Pseudo Hermitian Interactions in the Dirac Equation
Abstract
: We consider a (2 + 1)-dimensional massless Dirac equation in the presence of complex vector potentials. It is shown that such vector potentials (leading to complex magnetic fields) can produce bound states, and the Dirac Hamiltonians are η-pseudo Hermitian. Some examples have been explicitly worked out.1. Introduction
In recent years, the massless Dirac equation in (2 + 1) dimensions has drawn a lot of attention, primarily because of its similarity to the equation governing the motion of charge carriers in graphene [1,2]. In view of the fact that electrostatic fields alone cannot provide confinement of the electrons, there have been quite a number of works on exact solutions of the relevant Dirac equation with different magnetic field configurations, for example, square well magnetic barriers [3–5], non-zero magnetic fields in dots [6], decaying magnetic fields [7], solvable magnetic field configurations [8], etc. On the other hand, at the same time, there have been some investigations into the possible role of non-Hermiticity and




2. The Model
The (2 + 1)-dimensional massless Dirac equation is given by:
Then, from (3), the equations for the components are found to be (in units of ℏ = 1):
2.1. Complex Decaying Magnetic Field
It is now necessary to choose the function, f(x). Our first choice for this function is:
Now, from the second of Equation (7), we obtain:
Let us now examine the upper component, ϕ1. Since ϕ2 is known, one can always use the intertwining relation:
Therefore, we find that it is indeed possible to create bound states with an imaginary vector potential. We shall now demonstrate the above results for a second example.
2.2. Complex Hyperbolic Magnetic Field
Here, we choose f(x), which leads to an effective potential of the complex hyperbolic Rosen–Morse type:
3. η-Pseudo Hermiticity
Let us recall that a Hamiltonian is η-pseudo Hermitian if [21]:
We recall that in both the cases considered here, the Hamiltonian is of the form:
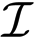 2, where
2, where
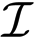 2 is the (2 × 2) unit matrix. Then, it can be shown that:
2 is the (2 × 2) unit matrix. Then, it can be shown that:
For the magnetic field given by Equation (19), the operator, η, can be found by using relations Equation (26). After a straightforward calculation, it can be shown that the η operator is given by:
4. Conclusions
Here, we have studied the (2 + 1)-dimensional massless Dirac equation (we note that if a massive particle of mass m is considered, the energy spectrum in the first example would become . Similar changes will occur in the second example, too). in the presence of complex magnetic fields, and it has been shown that such magnetic fields can create bound states. It has also been shown that Dirac Hamiltonians in the presence of such magnetic fields are η-pseudo Hermitian. We feel it would be of interest to study the generation of bound states using other types of magnetic fields, e.g., periodic magnetic fields.
Acknowledgments
One of us (P. R.) wishes to thank INFN Sezione di Perugia for supporting a visit during which part of this work was carried out. He would also like to thank the Physics Department of the University of Perugia for its hospitality.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Novoselov, K.S.; Geim, A.K.; Morozov, S.V.; Jiang, D.; Zhang, Y.; Dubonos, S.V.; Grigorieva, I.V.; Firsov, A.A. Electric field effect in atomically thin carbon films. Science 2004, 306, 666–669. [Google Scholar]
- Novoselov, K.S.; Geim, A.K.; Morozov, S.V.; Jiang, D.; Katsnelson, M.I.; Grigorieva, I.V.; Dubonos, S.V.; Firsov, A.A. Two-dimensional gas of massless Dirac fermions in graphene. Nature 2005, 438, 197–200. [Google Scholar]
- De Martino, A.; Dell'Anna, L.; Egger, R. Magnetic confinement of massless dirac fermions in graphene. Phys. Rev. Lett. 2007, 98, 066802:1–066802:4. [Google Scholar]
- De Martino, A.; Dell'Anna, L.; Eggert, R. Magnetic barriers and confinement of Dirac-Weyl quasiparticles in graphene. Solid State Commun. 2007, 144, 547–550. [Google Scholar]
- Dell'Anna, L.; de Martino, A. Multiple magnetic barriers in graphene. Phys. Rev. B 2009, 79, 045420:1–045420:9. [Google Scholar]
- Wang, D.; Jin, G. Bound states of Dirac electrons in a graphene-based magnetic quantum dot. Phys. Lett. A 2009, 373, 4082–4085. [Google Scholar]
- Ghosh, T.K. Exact solutions for a Dirac electron in an exponentially decaying magnetic field. J. Phys. Condens. Matter 2009, 21. [Google Scholar] [CrossRef]
- Kuru, S; Negro, J.M.; Nieto, L.M. Exact analytic solutions for a Dirac electron moving in graphene under magnetic fields. J. Phys. Condens. Matter 2009, 21. [Google Scholar] [CrossRef]
- Bender, C.M.; Boettcher, S. Real spectra in non-hermitian hamiltonians having PT symmetry. Phys. Rev. Lett. 1988, 80, 5243–5246. [Google Scholar]
- Fagotti, M; Bonati, C.; Logoteta, D.; Marconcini, P.; Macucci, M. Armchair graphene nanoribbons: PT-symmetry breaking and exceptional points without dissipation. Phys. Rev. B 2011, 83, 241406:1–241406:4. [Google Scholar]
- Szameit, A.; Rechtsman, M.C.; Bahat-Treidel, O.; Segev, M. PT-Symmetry in heoneycomeb photonic lattices. Phys. Rev. A 2011, 84, 021806(R):1–021806(R):5. [Google Scholar]
- Esaki, K.; Sato, M.; Hasebe, K.; Kohmoto, M. Edge states and topological phases in non-Hermitian systems. Phys. Rev. B 2011, 84, 205128:1–205128:19. [Google Scholar]
- Longhi, S. Classical simulation of relativistic quantum mechanics in periodic optical structures. Appl. Phys. B 2011, 104, 453–468. [Google Scholar]
- Longhi, S. Optical realization of relativistic non-hermitian quantum mechanics. Phys. Rev. Lett. 2010, 105, 013903:1–013903:4. [Google Scholar]
- Ramezani, H.; Kottos, T.; Kovanis, V.; Christodoulides, D.N. Exceptional-point dynamics in photoni honeycomb lattices with PT-symmetry. Phys. Rev. A 2012, 85, 013818:1–013818:6. [Google Scholar]
- Mandal, B.P.; Gupta, S. Pseudo-hermitian interactions in Dirac theory: Examples. Mod. Phys. Lett. A 2010, 25, 1723–1732. [Google Scholar]
- Hatano, N.; Nelson, D. Localization transitions in non-hermitian quantum mechanics. Phys. Rev. Lett. 1996, 77, 570–573. [Google Scholar]
- Feinberg, J.; Zee, A. Non-Hermitian localization and delocalization. Phys. Rev. E 1999, 59, 6433–6443. [Google Scholar]
- Mandal, B.P.; Mourya, B.K.; Yadav, R.K. PT phase transition in higher-dimensional quantum systems. Phys. Lett. A 2013, 377, 1043–1046. [Google Scholar]
- Tan, L.Z.; Park, C.-H.; Louie, S.G. Graphene Dirac fermions in one dimensional field profiles; Tansforming magnetic to electric field. Phys. Rev. B 2010, 81, 195426:1–195426:8. [Google Scholar]
- Mostafazadeh, A. Pseudo-hermiticity versus PT-symmetry III: Equivalence of pseudo-Hermiticity and the presence of antilinear symmetries. J. Math. Phys. 2002, 43, 3944–3951. [Google Scholar]
- Flügge, S. Practical Quantum Mechanics; Springer-Verlag: Berlin, Germany, 1974. [Google Scholar]
- Cooper, F.; Khare, A; Sukhatme, U. Supersymmetry in Quantum Mechanics; World Scientific Publishing Co. Pte. Ltd.: Singapore, 2001. [Google Scholar]
- Milpas, E.; Torres, M.; Murguía, G. Magnetic field barriers in graphene: An analytically solvable model. J. Phys. Condens. Matter 2011, 23, 245304:1–245304:7. [Google Scholar]
- Rosen, N.; Morse, P.M. On the vibrations of polyatomic molecules. Phys. Rev. 1932, 42, 210–217. [Google Scholar]
- Ahmed, Z. Pseudo-hermiticity of hamiltonians under imaginary shift of the coordinate: Real spectrum of complex potentials. Phys. Lett. A 2001, 290, 19–22. [Google Scholar]
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license( http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Panella, O.; Roy, P. Pseudo Hermitian Interactions in the Dirac Equation. Symmetry 2014, 6, 103-110. https://doi.org/10.3390/sym6010103
Panella O, Roy P. Pseudo Hermitian Interactions in the Dirac Equation. Symmetry. 2014; 6(1):103-110. https://doi.org/10.3390/sym6010103
Chicago/Turabian StylePanella, Orlando, and Pinaki Roy. 2014. "Pseudo Hermitian Interactions in the Dirac Equation" Symmetry 6, no. 1: 103-110. https://doi.org/10.3390/sym6010103



