Interplay between Point-Group Symmetries and the Choice of the Bloch Basis in Multiband Models
Abstract
:1. Introduction
2. General Tight-Binding Hamiltonian
2.1. Wannier Basis
2.2. Hybridizing and Non-Hybridizing Bloch Bases
3. Fourfold Symmetry: Emery Model without Oxygen-Oxygen Hopping
3.1. Model Hamiltonian
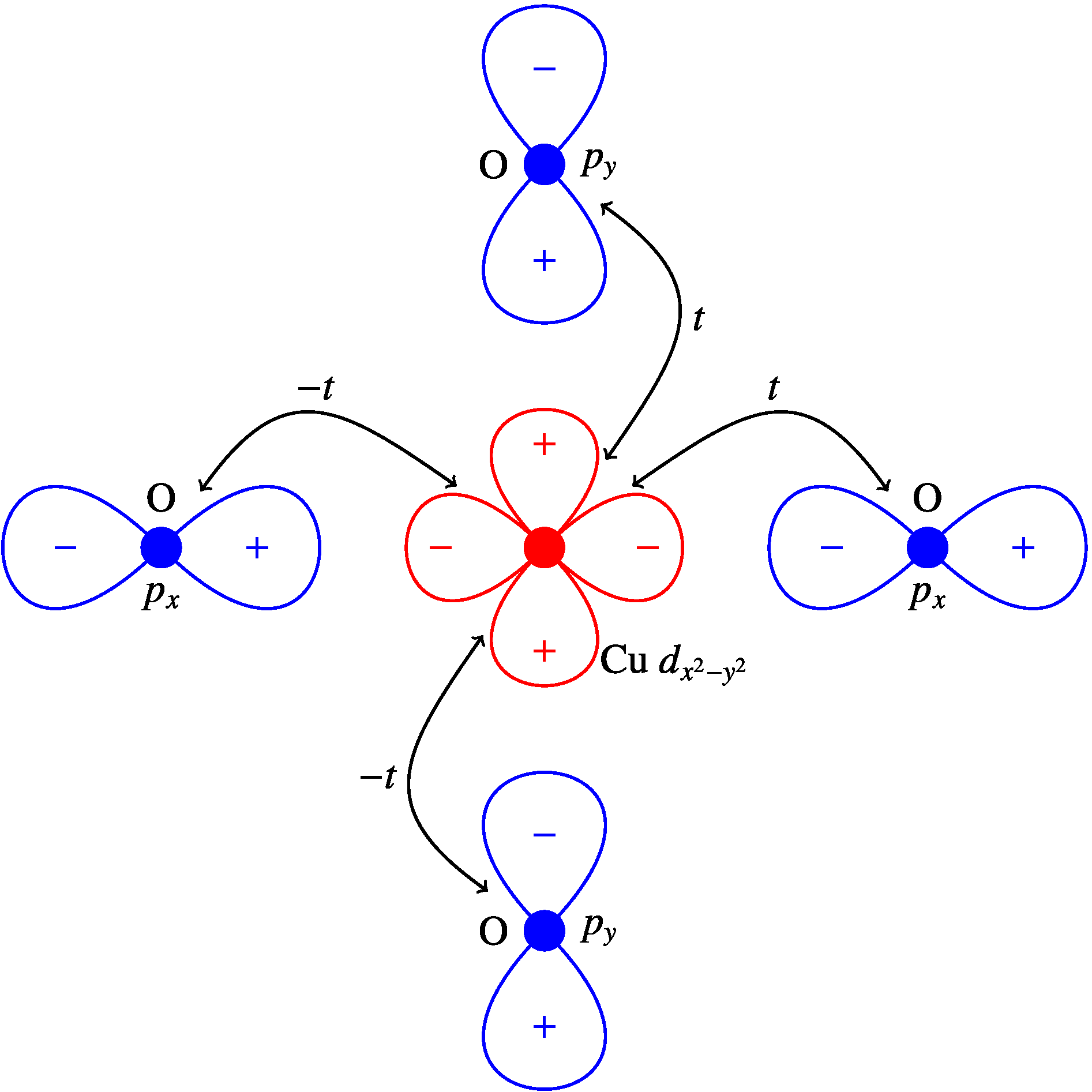
- (i)
- In what way is the point-group symmetry of the lattice manifest in the Emery model?
- (ii)
- Is there an alternative, explicitly -symmetric formulation of the Emery model with vertex functions that behave trivially under the point-group operations?
3.2. Symmetry
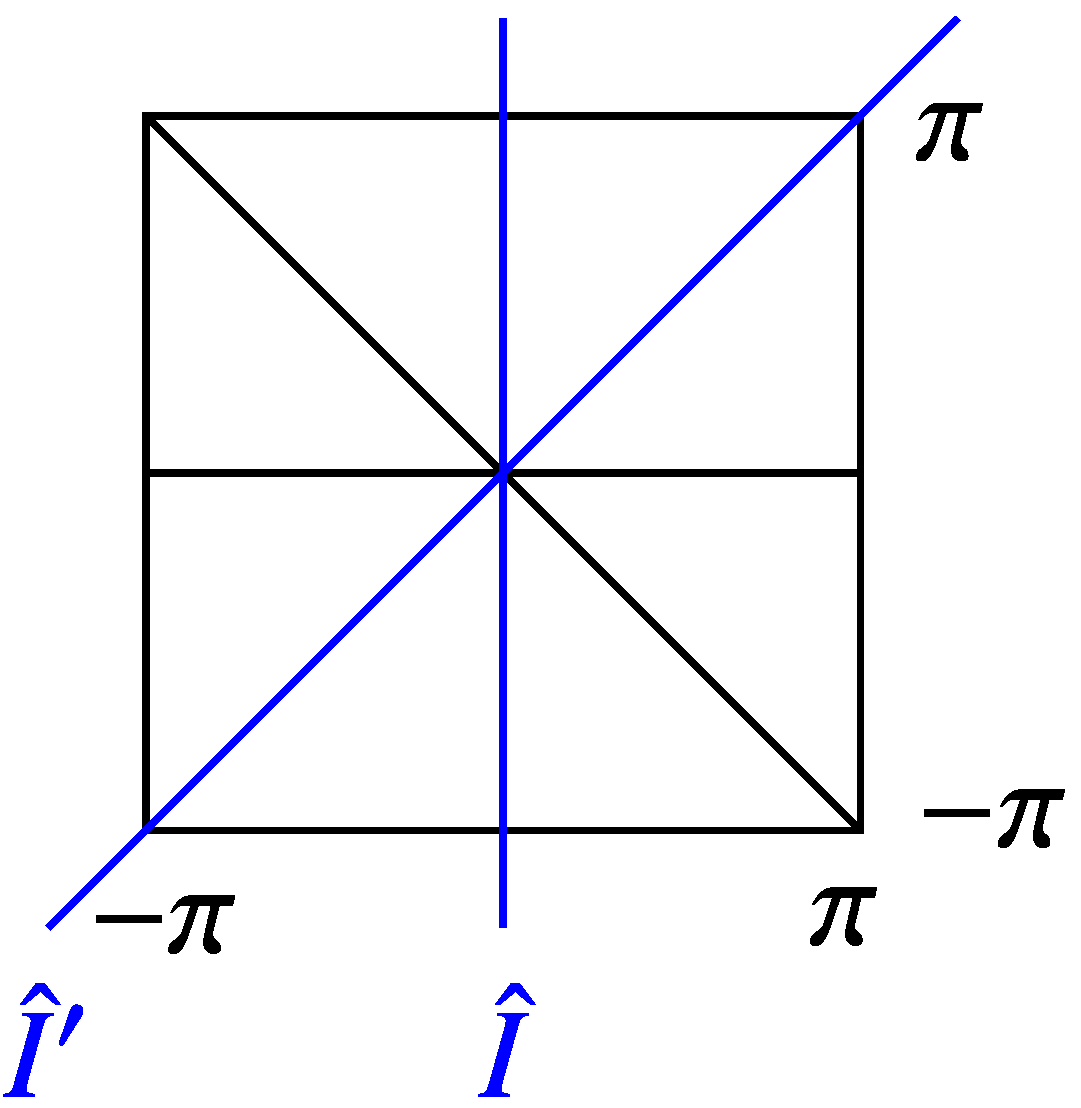
3.3. Band Language and Natural Bloch Basis
4. Sixfold Symmetry: Graphene
4.1. Model Hamiltonian
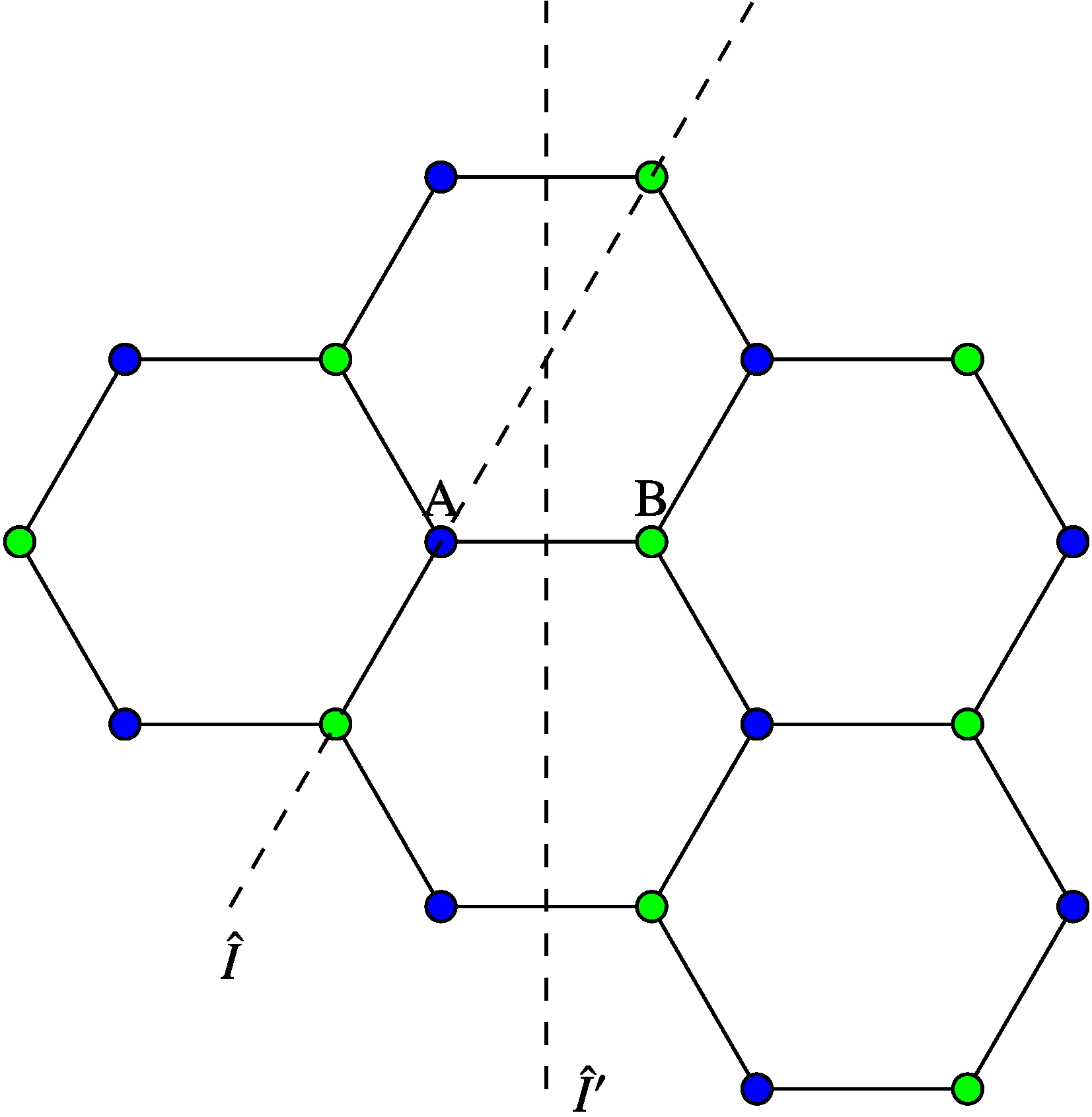
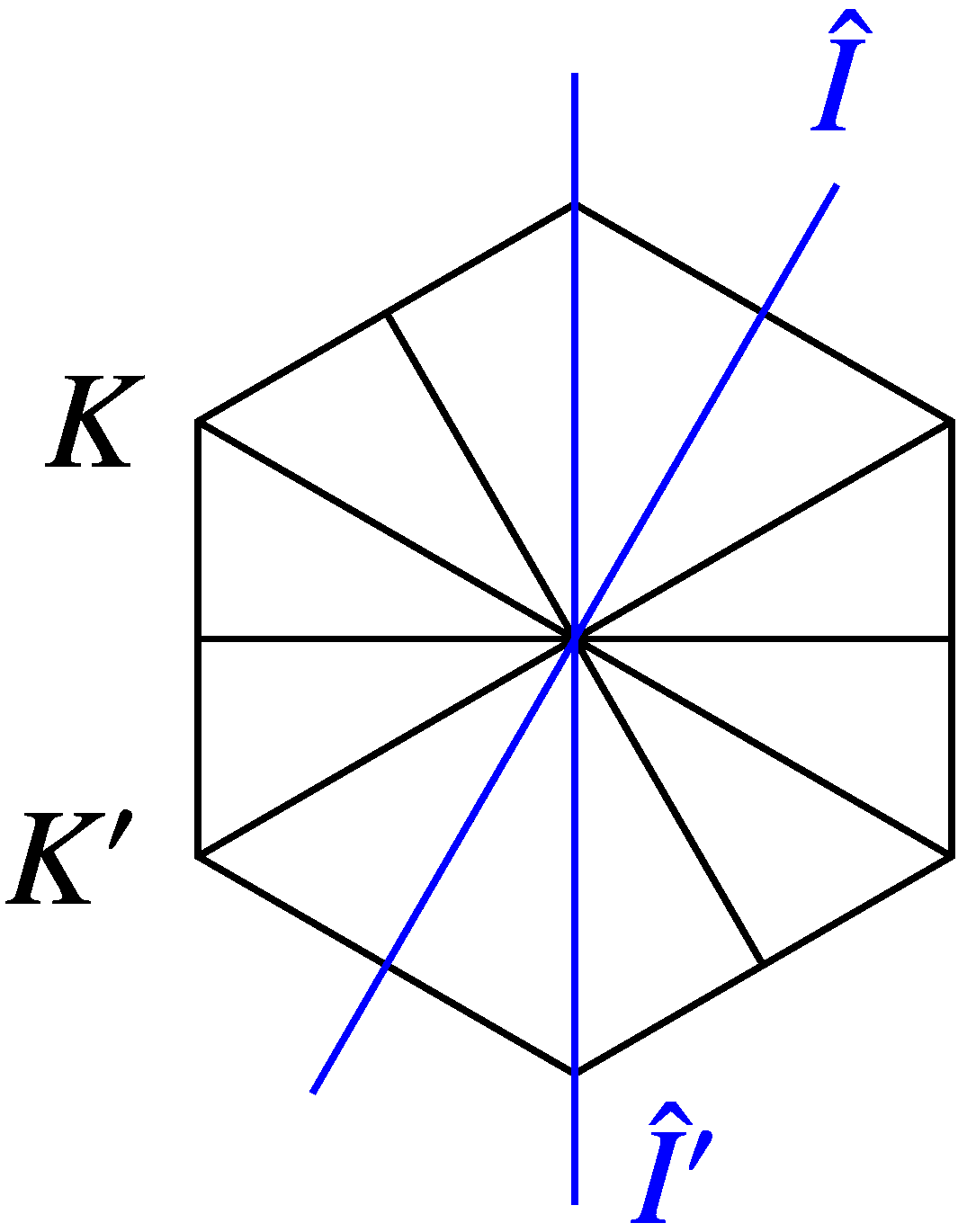
4.2. Band Language and Natural Basis
5. Natural Bloch Basis for the General Case
5.1. Point-Group Transformations
5.2. Basis Transformations in the Band Language
5.3. Consequences of the Existence of a Natural Basis
5.4. Construction of a Natural Bloch Basis
- (i)
- Select a minimal sector of the BZ , i.e., the smallest set of points from which can be generated according to:For , for example, corresponds to of the BZ.
- (ii)
- Choose the band phases in the orbital-to-band transformation, , arbitrarily on .
- (iii)
- Determine from for via Equation (101). Since for , this scheme is free of inconsistencies.
6. Summary and Outlook
Acknowledgments
Conflicts of Interest
Appendix
A. Alternative Proof of the Existence of a Natural Basis
A.1. Non-Degenerate Bands
A.2. General Case
References
- Tinkham, M. Group Theory and Quantum Mechanics; McGraw-Hill Book Company: New York, NY, USA, 1964. [Google Scholar]
- Berges, J.; Tetradis, N.; Wetterich, C. Non-perturbative renormalization flow in quantum field theory and statistical physics. Phys. Rep. 2002, 363, 223–386. [Google Scholar] [CrossRef]
- Metzner, W.; Salmhofer, M.; Honerkamp, C.; Meden, V.; Schönhammer, K. Functional renormalization group approach to correlated fermion systems. Rev. Mod. Phys. 2012, 84, 299–352. [Google Scholar] [CrossRef]
- Honerkamp, C. Density waves and cooper pairing on the honeycomb lattice. Phys. Rev. Lett. 2008, 100, 146404:1–146404:4. [Google Scholar] [CrossRef]
- Scherer, M.M.; Uebelacker, S.; Honerkamp, C. Instabilities of interacting electrons on the honeycomb bilayer. Phys. Rev. B 2012, 85, 235408:1–235408:5. [Google Scholar] [CrossRef]
- Lang, T.C.; Meng, Z.Y.; Scherer, M.M.; Uebelacker, S.; Assaad, F.F.; Muramatsu, A.; Honerkamp, C.; Wessel, S. Antiferromagnetism in the Hubbard model on the Bernal-stacked honeycomb bilayer. Phys. Rev. Lett. 2012, 109, 126402:1–126402:5. [Google Scholar] [CrossRef]
- Scherer, M.M.; Uebelacker, S.; Scherer, D.D.; Honerkamp, C. Interacting electrons on trilayer honeycomb lattices. Phys. Rev. B 2012, 86, 155415:1–155415:12. [Google Scholar] [CrossRef]
- Kiesel, M.L.; Platt, C.; Hanke, W.; Abanin, D.A.; Thomale, R. Competing many-body instabilities and unconventional superconductivity in graphene. Phys. Rev. B 2012, 86, 020507:1–020507:5. [Google Scholar] [CrossRef]
- Wang, F.; Zhai, H.; Lee, D.H. Antiferromagnetic correlation and the pairing mechanism of the cuprates and iron pnictides: A view from the functional renormalization group studies. EPL (Europhys. Lett.) 2009, 85. [Google Scholar] [CrossRef]
- Wang, F.; Zhai, H.; Lee, D.H. Nodes in the gap function of LaFePO, the gap function of the Fe(Se,Te) systems, and the STM signature of the s± pairing. Phys. Rev. B 2010, 81, 184512:1–184512:7. [Google Scholar] [CrossRef]
- Thomale, R.; Platt, C.; Hu, J.; Honerkamp, C.; Bernevig, B.A. Functional renormalization-group study of the doping dependence of pairing symmetry in the iron pnictide superconductors. Phys. Rev. B 2009, 80, 180505:1–180505:4. [Google Scholar] [CrossRef]
- Platt, C.; Honerkamp, C.; Hanke, W. Pairing in the iron arsenides: A functional RG treatment. New J. Phys. 2009, 11, 055058:1–055058:15. [Google Scholar] [CrossRef]
- Thomale, R.; Platt, C.; Hanke, W.; Bernevig, B.A. Mechanism for explaining differences in the order parameters of FeAs-based and FeP-based pnictide superconductors. Phys. Rev. Lett. 2011, 106, 187003:1–187003:4. [Google Scholar] [CrossRef]
- Platt, C.; Thomale, R.; Honerkamp, C.; Zhang, S.C.; Hanke, W. Mechanism for a pairing state with time-reversal symmetry breaking in iron-based superconductors. Phys. Rev. B 2012, 85, 180502:1–180502:4. [Google Scholar]
- Kiesel, M.L.; Thomale, R. Sublattice interference in the kagome Hubbard model. Phys. Rev. B 2012, 86, 121105:1–121105:4. [Google Scholar] [CrossRef]
- Wang, Q.H.; Platt, C.; Yang, Y.; Honerkamp, C.; Zhang, F.C.; Hanke, W.; Rice, T.M.; Thomale, R. Theory of superconductivity in a three-orbital model of Sr2RuO4. EPL (Europhys. Lett.) 2013, 104. [Google Scholar] [CrossRef]
- Vafek, O.; Yang, K. Many-body instability of Coulomb interacting bilayer graphene: Renormalization group approach. Phys. Rev. B 2010, 81, 041401:1–041401:4. [Google Scholar] [CrossRef]
- Wang, W.S.; Xiang, Y.Y.; Wang, Q.H.; Wang, F.; Yang, F.; Lee, D.H. Functional renormalization group and variational Monte Carlo studies of the electronic instabilities in graphene near doping. Phys. Rev. B 2012, 85, 035414:1–035414:6. [Google Scholar]
- Wang, W.S.; Li, Z.Z.; Xiang, Y.Y.; Wang, Q.H. Competing electronic orders on kagome lattices at van Hove filling. Phys. Rev. B 2013, 87, 115135:1–115135:8. [Google Scholar] [CrossRef]
- Salmhofer, M.; Honerkamp, C. Fermionic Renormalization Group Flows: Technique and Theory. Prog. Theor. Phys. 2001, 105, 1–35. [Google Scholar] [CrossRef]
- Husemann, C.; Salmhofer, M. Efficient parametrization of the vertex function, Ω scheme, and the t, t′ Hubbard model at van Hove filling. Phys. Rev. B 2009, 79, 195125:1–195125:17. [Google Scholar] [CrossRef]
- Eberlein, A.; Metzner, W. Parametrization of Nambu vertex in a singlet superconductor. Prog. Theor. Phys. 2010, 124, 471–491. [Google Scholar] [CrossRef]
- Marzari, N.; Mostofi, A.A.; Yates, J.R.; Souza, I.; Vanderbilt, D. Maximally localized Wannier functions: Theory and applications. Rev. Mod. Phys. 2012, 84, 1419–1475. [Google Scholar] [CrossRef] [Green Version]
- Fetter, A.L.; Walecka, J.D. Quantum Theory of Many-Particle Systems; McGraw Hill: Boston, MA, USA, 1971. [Google Scholar]
- Maier, T.A.; Graser, S.; Scalapino, D.J.; Hirschfeld, P.J. Origin of gap anisotropy in spin fluctuation models of the iron pnictides. Phys. Rev. B 2009, 79, 224510:1–224510:6. [Google Scholar] [CrossRef]
- Emery, V.J. Theory of high-Tc superconductivity in oxides. Phys. Rev. Lett. 1987, 58, 2794–2797. [Google Scholar] [CrossRef] [PubMed]
- Fulde, P. Electron Correlations in Molecules and Solids, 3rd ed.; Springer: Berlin/Heidelberg, Germany, 1995. [Google Scholar]
- Andersen, O.; Liechtenstein, A.; Jepsen, O.; Paulsen, F. LDA energy bands, low-energy Hamiltonians, t′,t″,t⊥(k), and J⊥. J. Phys. Chem. Solids 1995, 56, 1573–1591. [Google Scholar] [CrossRef]
- Weber, C.; Haule, K.; Kotliar, G. Optical weights and waterfalls in doped charge-transfer insulators: A local density approximation and dynamical mean-field theory study of La2−xSrxCuO4. Phys. Rev. B 2008, 78, 134519:1–134519:5. [Google Scholar] [CrossRef]
- Weber, C.; Haule, K.; Kotliar, G. Strength of correlations in electron- and hole-doped cuprates. Nat. Phys. 2010, 6, 574–578. [Google Scholar] [CrossRef]
- Weber, C.; Haule, K.; Kotliar, G. Apical oxygens and correlation strength in electron- and hole-doped copper oxides. Phys. Rev. B 2010, 82, 125107:1–125107:24. [Google Scholar] [CrossRef]
- Castro Neto, A.H.; Guinea, F.; Peres, N.M.R.; Novoselov, K.S.; Geim, A.K. The electronic properties of graphene. Rev. Mod. Phys. 2009, 81, 109–162. [Google Scholar] [CrossRef]
- Wallace, P.R. The band theory of graphite. Phys. Rev. 1947, 71, 622–634. [Google Scholar] [CrossRef]
- Kataev, V.; Möller, A.; Löw, U.; Jung, W.; Schittner, N.; Kriener, M.; Freimuth, A. Structural and magnetic properties of the new low-dimensional spin magnet. J. Magn. Magn. Mater. 2005, 290, 310–313. [Google Scholar] [CrossRef]
- Möller, A.; Löw, U.; Taetz, T.; Kriener, M.; André, G.; Damay, F.; Heyer, O.; Braden, M.; Mydosh, J.A. Structural domain and finite-size effects of the antiferromagnetic S = 1/2 honeycomb lattice in InCu2/3V1/3O3. Phys. Rev. B 2008, 78, 024420:1–024420:10. [Google Scholar] [CrossRef]
- Yan, Y.J.; Li, Z.Y.; Zhang, T.; Luo, X.G.; Ye, G.J.; Xiang, Z.J.; Cheng, P.; Zou, L.J.; Chen, X.H. Magnetic properties of the doped spin- honeycomb-lattice compound In3Cu2VO9. Phys. Rev. B 2012, 85, 085102:1–085102:5. [Google Scholar] [CrossRef]
- Slonczewski, J.C.; Weiss, P.R. Band structure of graphite. Phys. Rev. 1958, 109, 272–279. [Google Scholar] [CrossRef]
- Sun, K.; Fradkin, E. Time-reversal symmetry breaking and spontaneous anomalous Hall effect in Fermi fluids. Phys. Rev. B 2008, 78, 245122:1–245122:17. [Google Scholar] [CrossRef]
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Maier, S.A.; Honerkamp, C.; Wang, Q.-H. Interplay between Point-Group Symmetries and the Choice of the Bloch Basis in Multiband Models. Symmetry 2013, 5, 313-343. https://doi.org/10.3390/sym5040313
Maier SA, Honerkamp C, Wang Q-H. Interplay between Point-Group Symmetries and the Choice of the Bloch Basis in Multiband Models. Symmetry. 2013; 5(4):313-343. https://doi.org/10.3390/sym5040313
Chicago/Turabian StyleMaier, Stefan A., Carsten Honerkamp, and Qiang-Hua Wang. 2013. "Interplay between Point-Group Symmetries and the Choice of the Bloch Basis in Multiband Models" Symmetry 5, no. 4: 313-343. https://doi.org/10.3390/sym5040313



