2. Results and Discussion
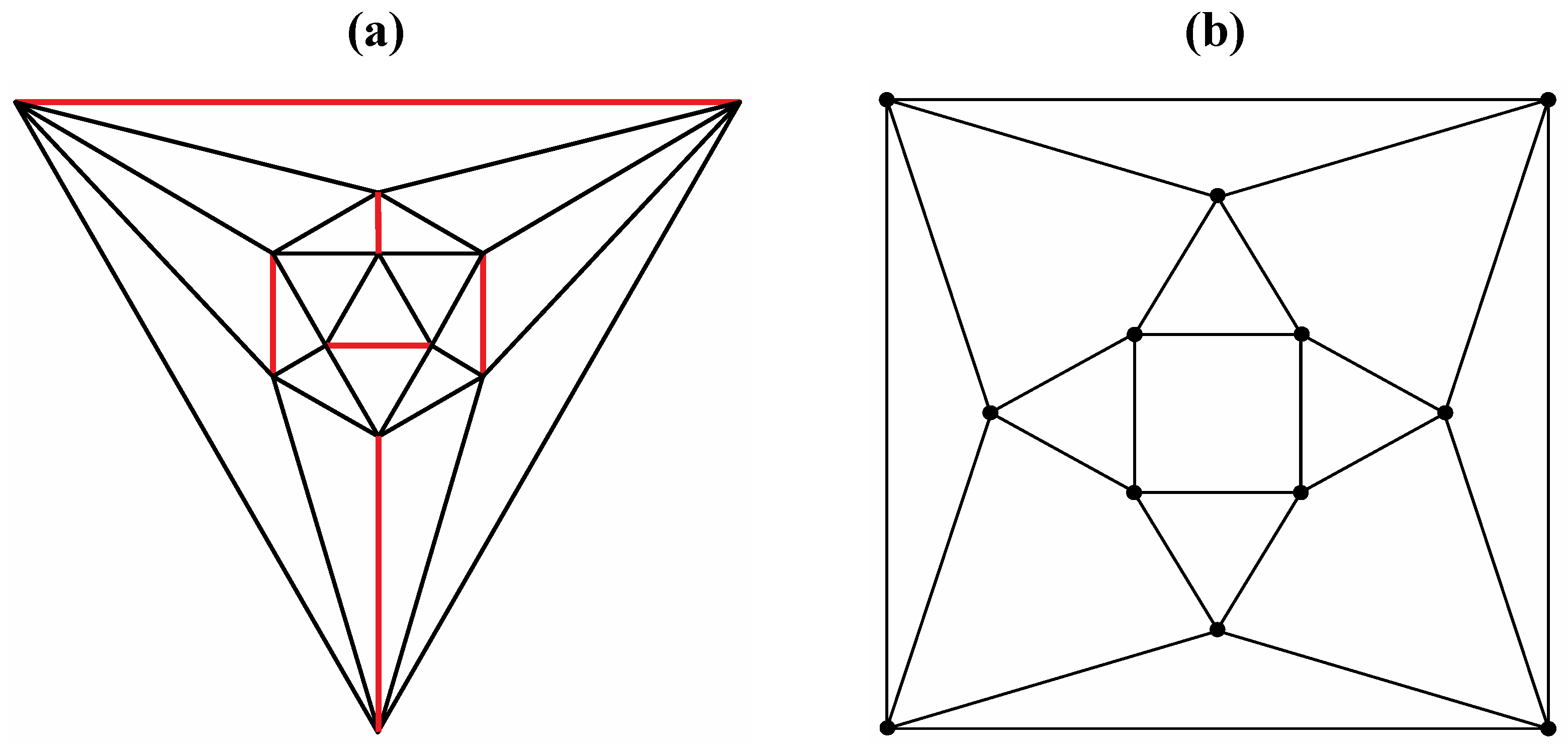
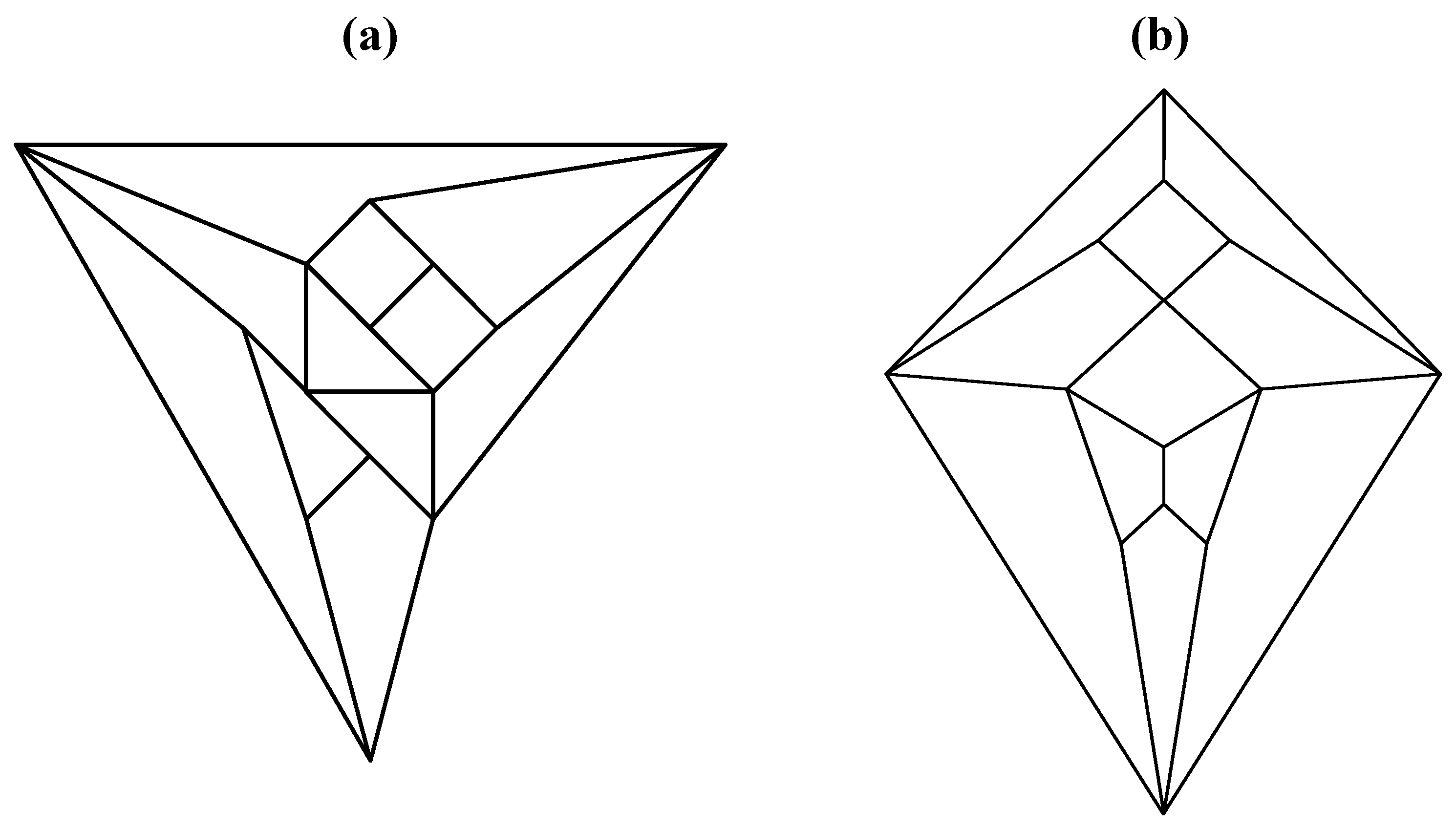
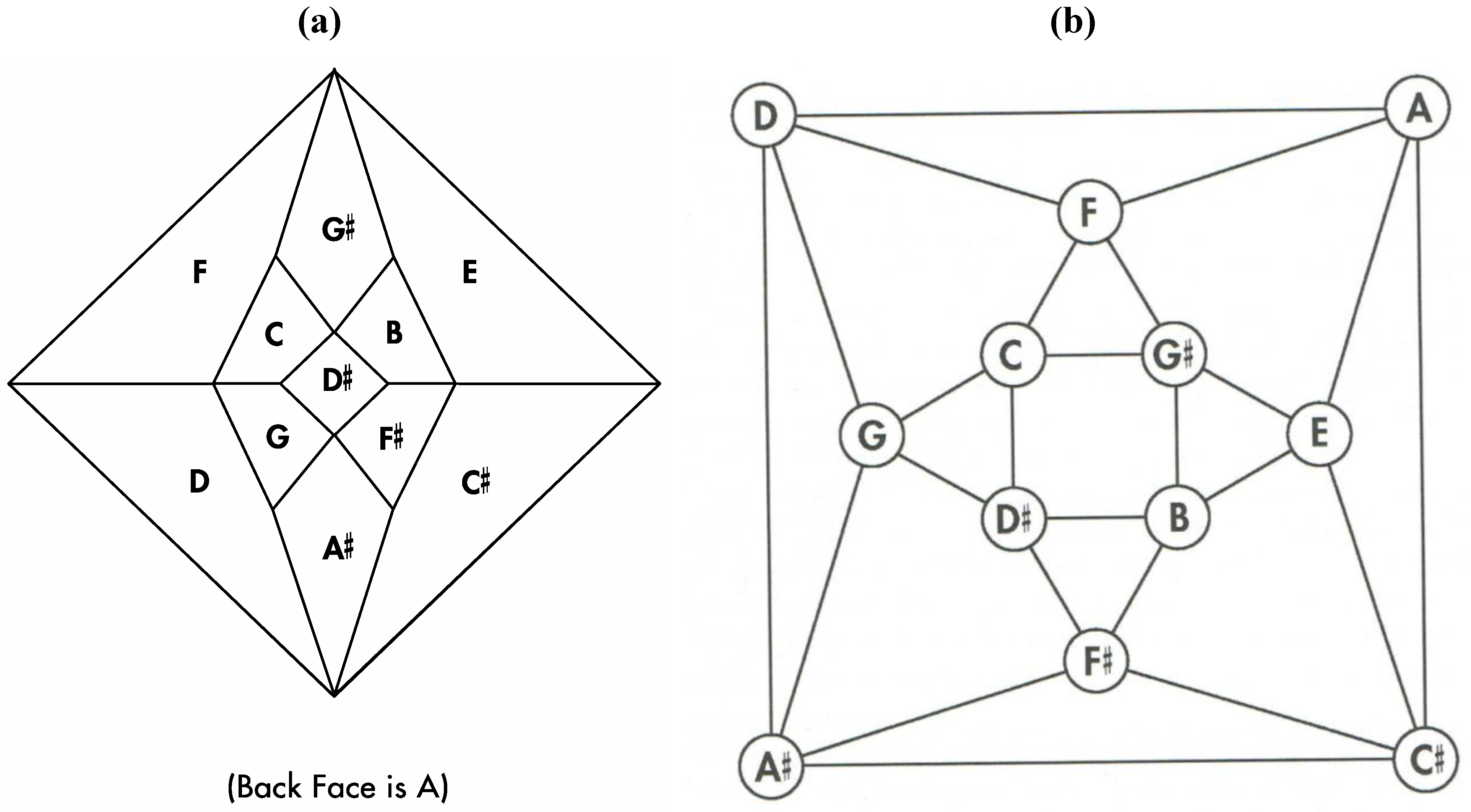
Good progress toward answering the aforementioned question can be achieved by removing a specific set of twelve edges from a tetrakis hexahedral graph as indicated in
Figure 4. Thus, removal of the
Figure 4 red edges yields
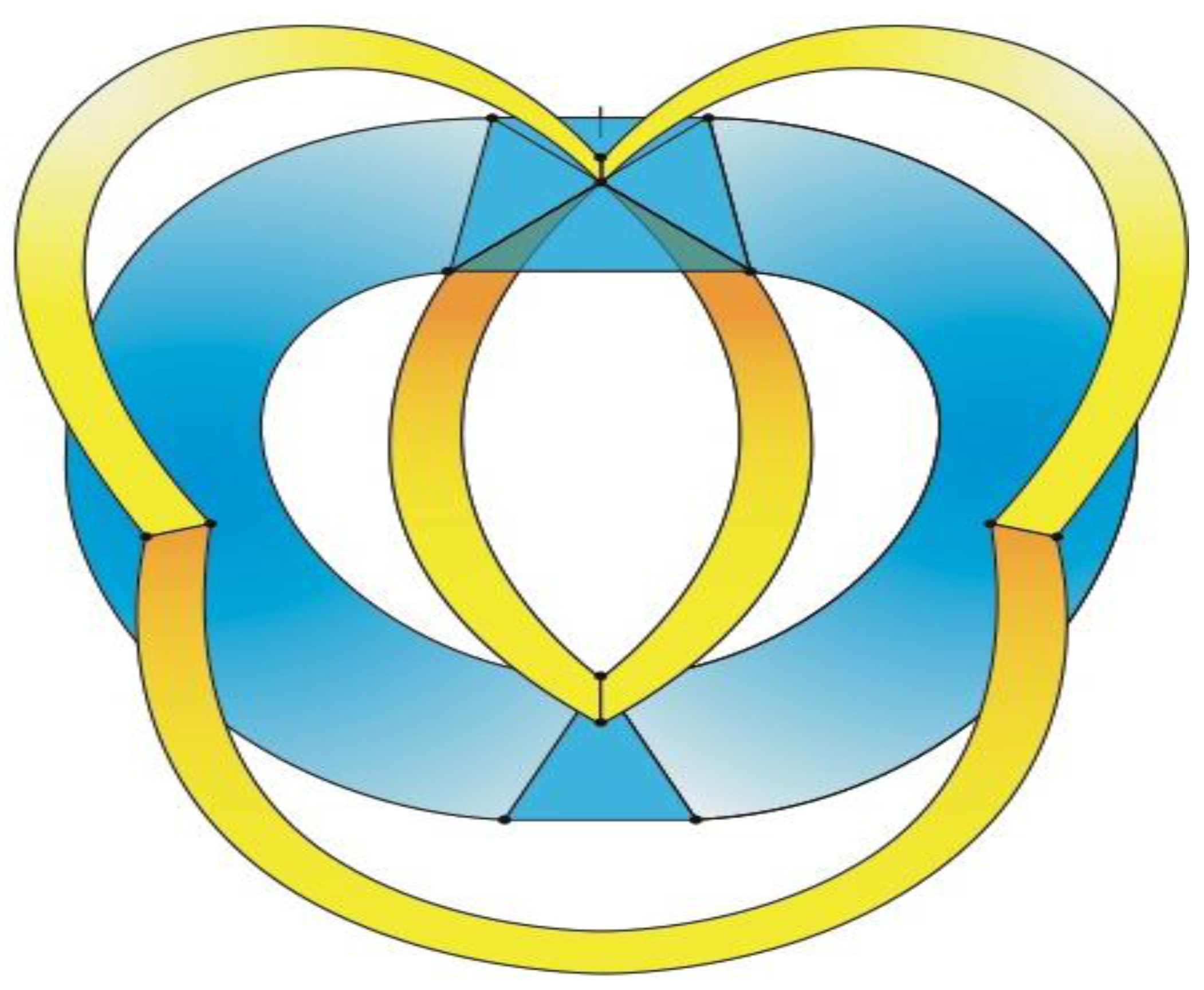
Figure 5a that can be stretched and rotated to yield the isomorphic graph in
Figure 5b. Curiously, the graph in
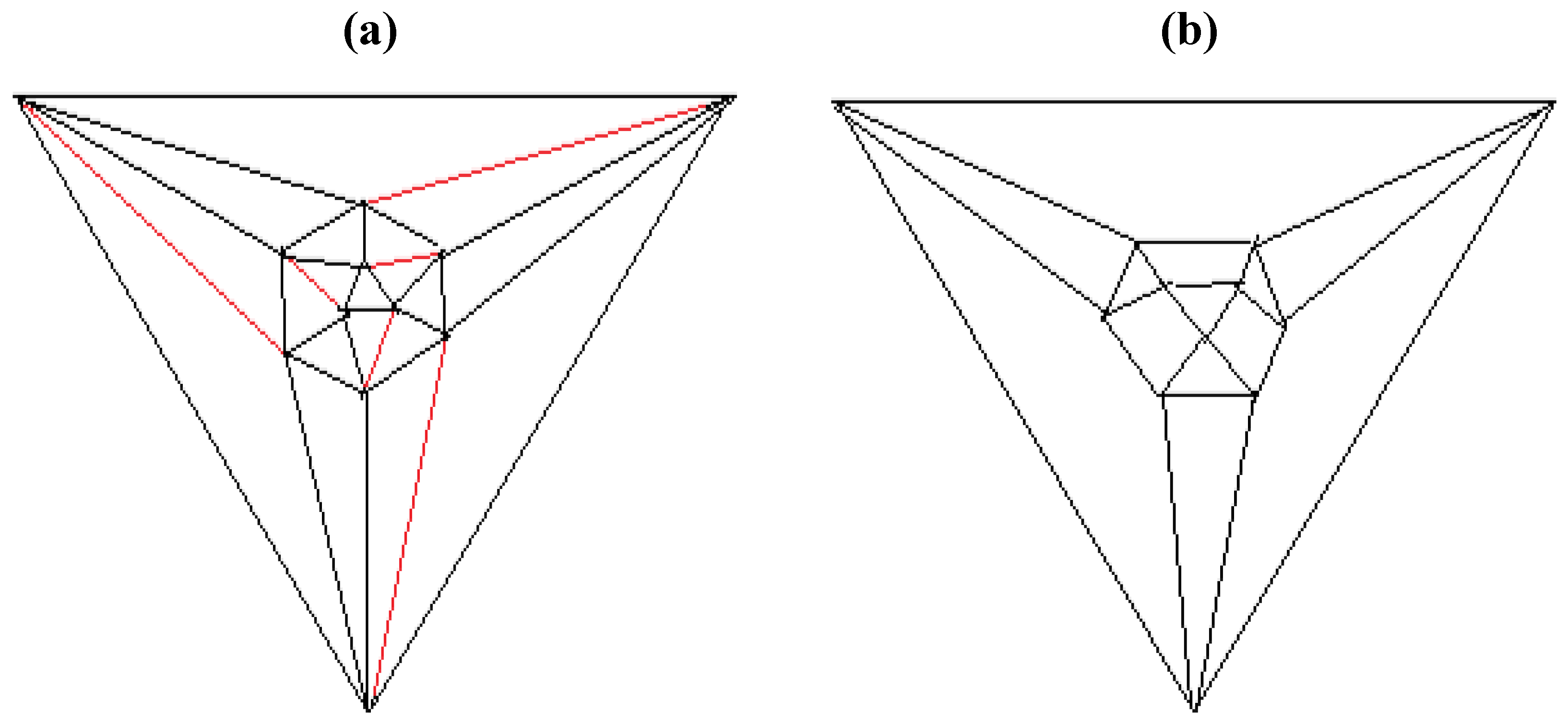
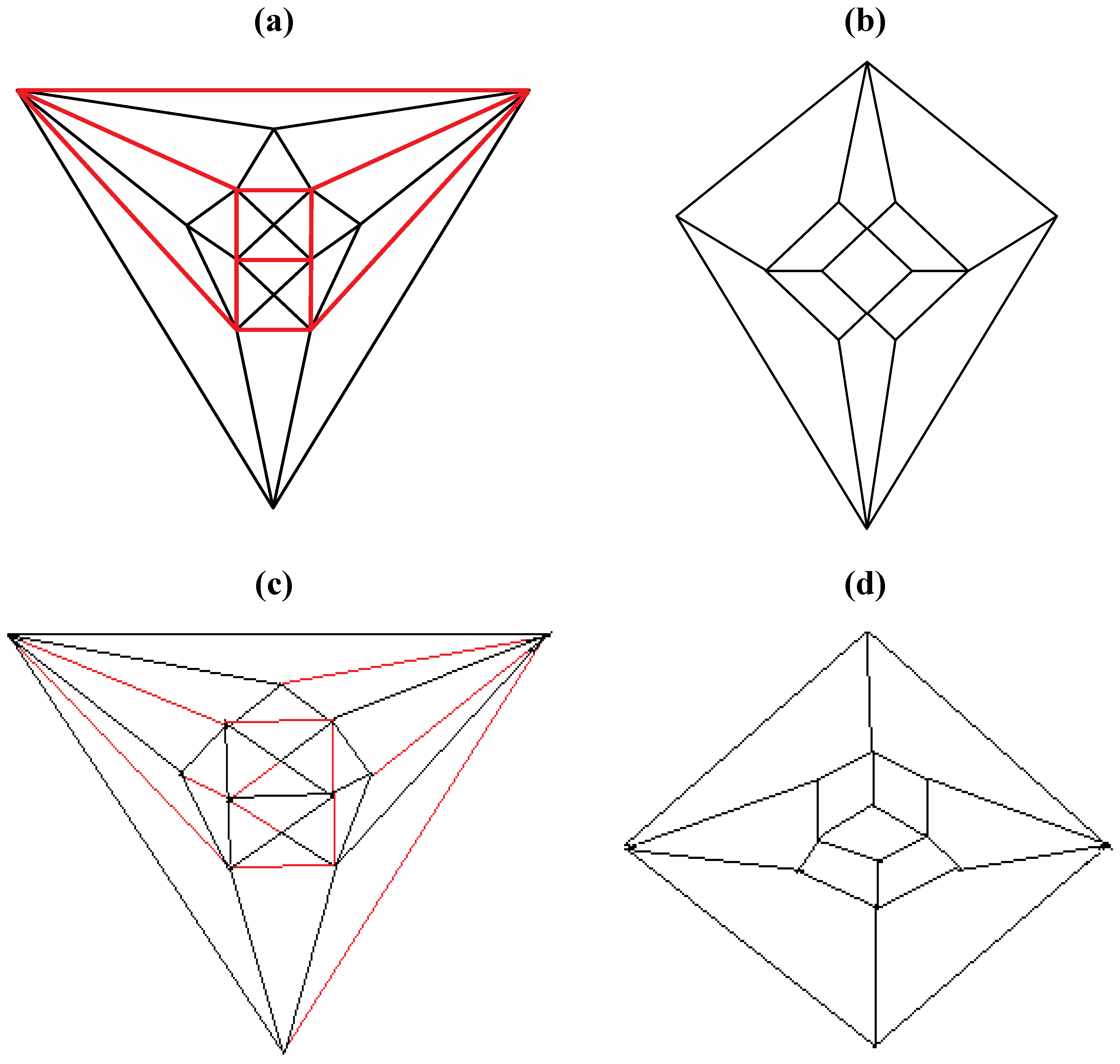
Figure 5b possesses only one C2 axis, unlike the graph of the rhombic dodecahedron or that of the trapezo-rhombic dodecahedron—both which can be obtained similarly from the tetrakis hexahedral graph by removing one of two different sets of twelve edges (as shown in
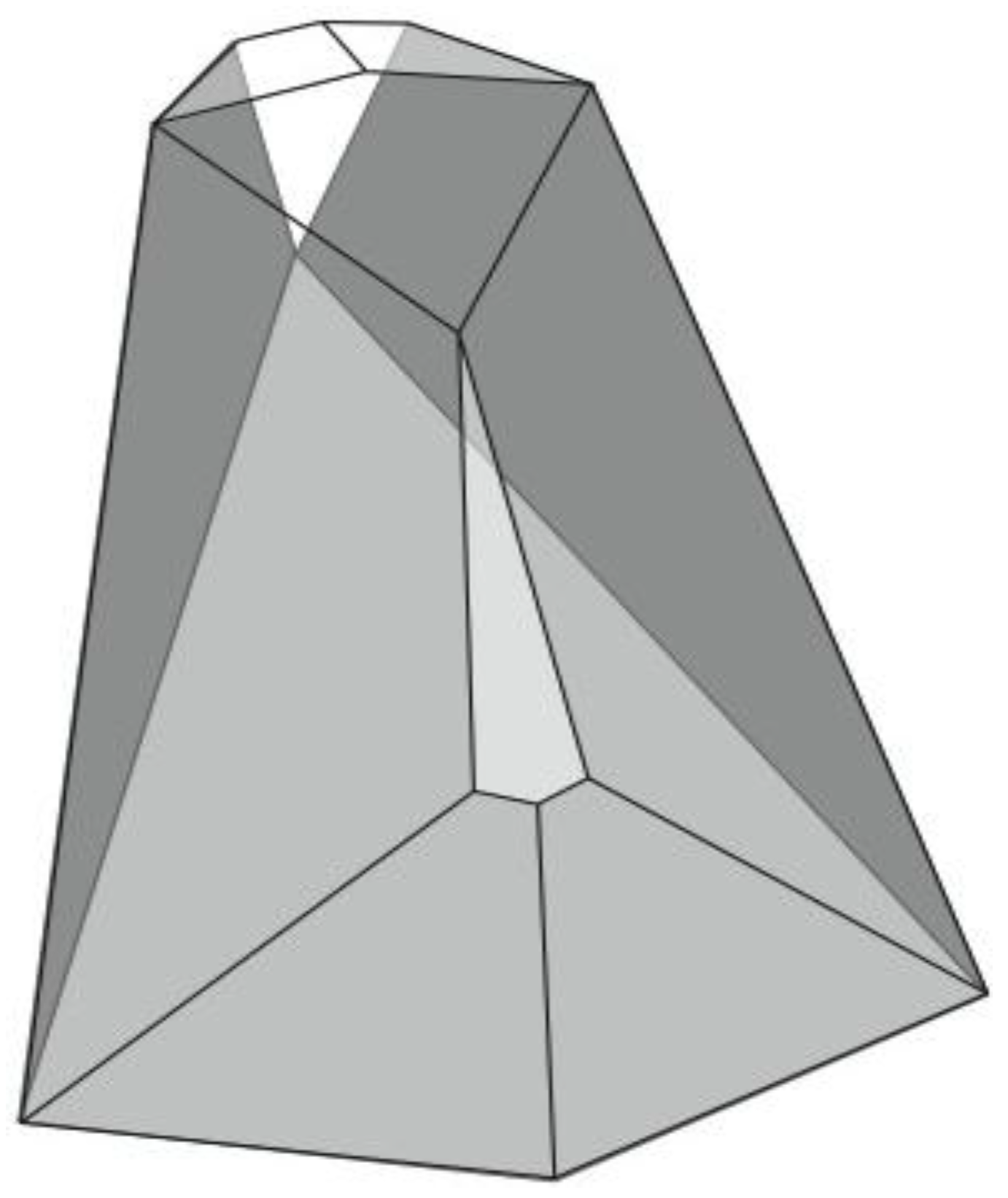
Figure 6). A convex dodecahedron that exemplifies the patterning within
Figure 5b is shown in
Figure 7 and displays striking bilateral symmetry.
Figure 4.
The twelve edges to be removed from (
a) the tetrakis hexahedral graph (in order to arrive at the patterning of the particular dodecahedron that is the dual of
Figure 3c) are indicated in (
b) in red.
Figure 4.
The twelve edges to be removed from (
a) the tetrakis hexahedral graph (in order to arrive at the patterning of the particular dodecahedron that is the dual of
Figure 3c) are indicated in (
b) in red.
Figure 5.
(
a) The graph obtained from the tetrakis hexahedral graph after removal of the twelve red edges in
Figure 4, can be redrawn as (
b), the isomorphic graph.
Figure 5.
(
a) The graph obtained from the tetrakis hexahedral graph after removal of the twelve red edges in
Figure 4, can be redrawn as (
b), the isomorphic graph.
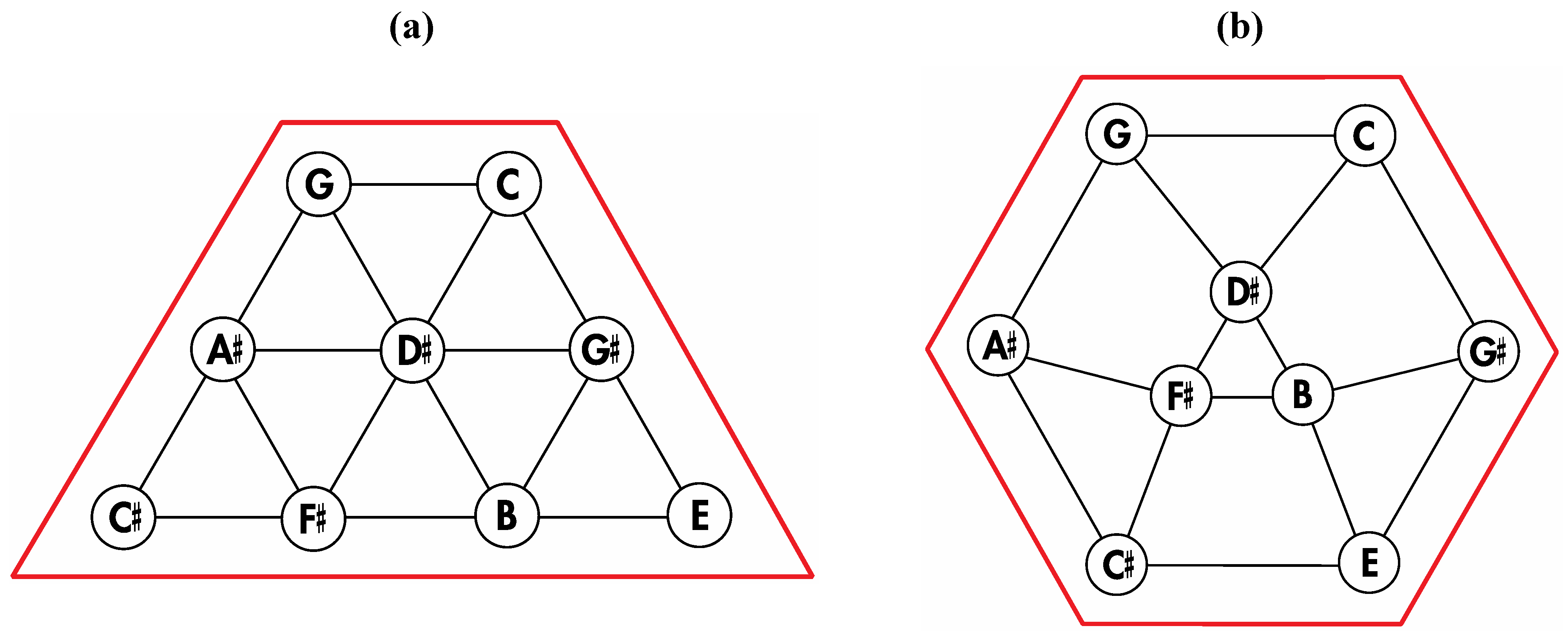
Figure 6.
Removal of the indicated red edges in (a) the tetrakis hexahedral graph generates (b) the rhombic dodecahedral graph, while removal of the twelve red edges from the tetrakis hexahedral graph as shown in (c) produces (d) the trapezo-rhombic dodecahedral graph.
Figure 6.
Removal of the indicated red edges in (a) the tetrakis hexahedral graph generates (b) the rhombic dodecahedral graph, while removal of the twelve red edges from the tetrakis hexahedral graph as shown in (c) produces (d) the trapezo-rhombic dodecahedral graph.
Figure 7.
A convex, bilaterally symmetrical dodecahedron that exemplifies the patterning in
Figure 5.
Figure 7.
A convex, bilaterally symmetrical dodecahedron that exemplifies the patterning in
Figure 5.
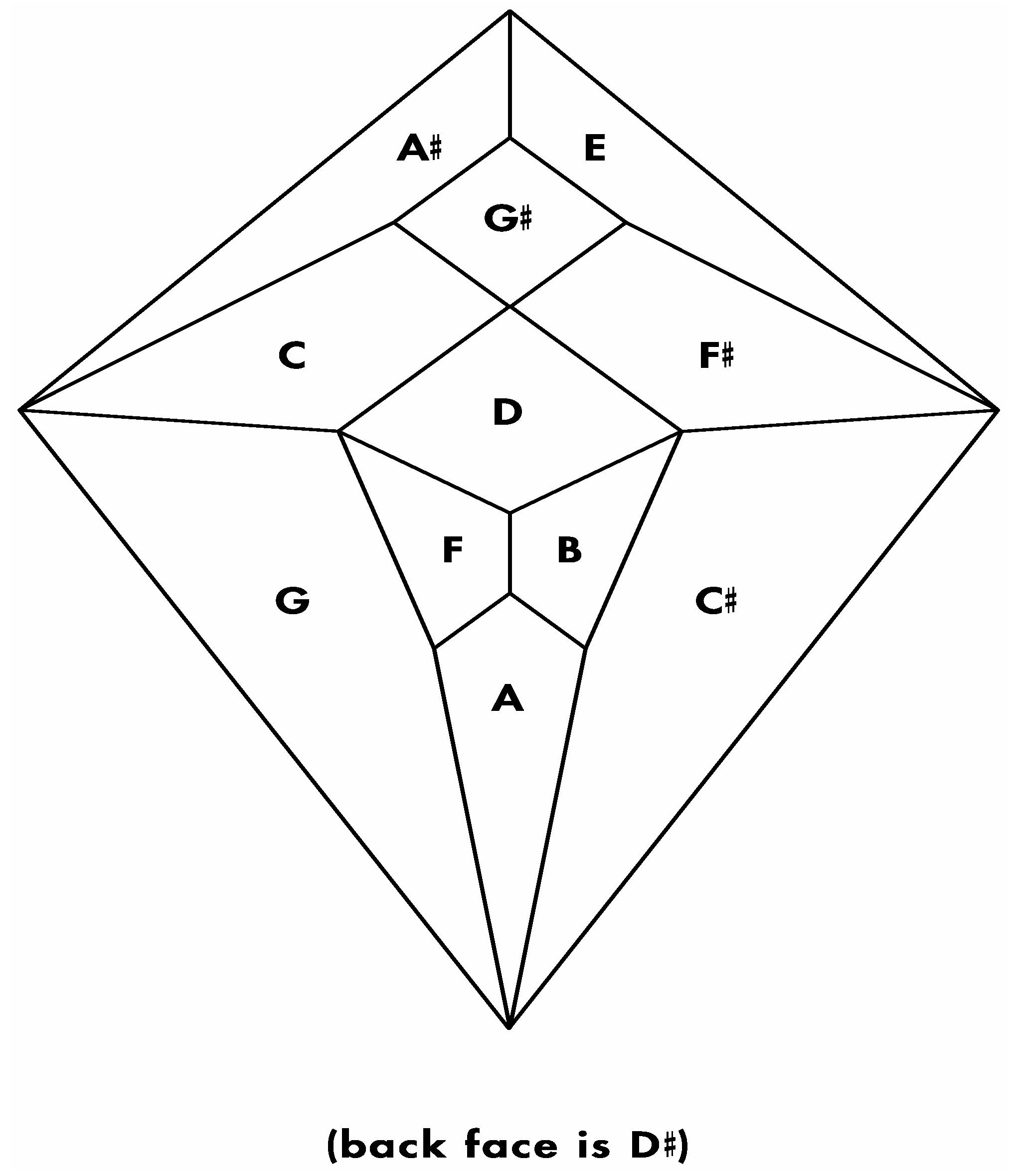
Remarkably, one of the 3,326,400 harmonically distinct intonations of the
Figure 7 zygo-dodecahedron—an intonation that can be produced by assigning each one of the twelve tones to one of each of the twelve quadrilateral faces as illustrated in
Figure 8a—exhibits both an important relationship to the Circle of Fifths [
3,
4] (vide infra) as well as a bilaterally symmetrical network of tones that features all six tritone pair midpoints in this zygo-dodecahedron’s single reflection plane.
Figure 8.
(a) A bilaterally symmetrical network of zygo-dodecahedral tones that encodes important jazz/blues sonorities and that is related to the Circle of Fifths; (b) The corresponding Schlegel diagram of the dual of the preceding zygo-dodecahedron.
Figure 8.
(a) A bilaterally symmetrical network of zygo-dodecahedral tones that encodes important jazz/blues sonorities and that is related to the Circle of Fifths; (b) The corresponding Schlegel diagram of the dual of the preceding zygo-dodecahedron.
Consider the twelve pentatonic sets that arise from the
Figure 8a dodecahedron as seen in
Figure 9. Each of these pentatonic sets is formed by combining any given tone with the tones assigned to each of the four faces that share an edge with the quadrilateral face that is assigned to the given tone. Interestingly, all twelve of these pentatonic sets can be construed as chords that are bedrock jazz/blues sonorities in the dominant seventh family. Moreover, as is demonstrated by the original song “Code of Blues”, compelling musical compositions in the blues genre can be assembled that employ chord progressions and melodies that stem directly from such pentatonic sets as they are encountered in sequence along a continuous path that moves from face to neighboring face of this intonated zygo-dodecahedron [
5].
Figure 9.
(
a) Sheet Music for the original composition “Code of Blues” (first page); (
b) Sheet music for the original composition “Code of Blues” (second page); (
c) Pentatonic sets from the intonated zygo-dodecahedron in
Figure 8a.
Figure 9.
(
a) Sheet Music for the original composition “Code of Blues” (first page); (
b) Sheet music for the original composition “Code of Blues” (second page); (
c) Pentatonic sets from the intonated zygo-dodecahedron in
Figure 8a.
With regard to the relationship between the
Figure 8a dodecahedral array of tones and the Circle of Fifths, the following analyses serve to reveal a powerful correspondence. First, it is widely known that Euler’s 2-D tonnetz, a music theoretical mainstay that emerged from seminal work reported in 1739 [
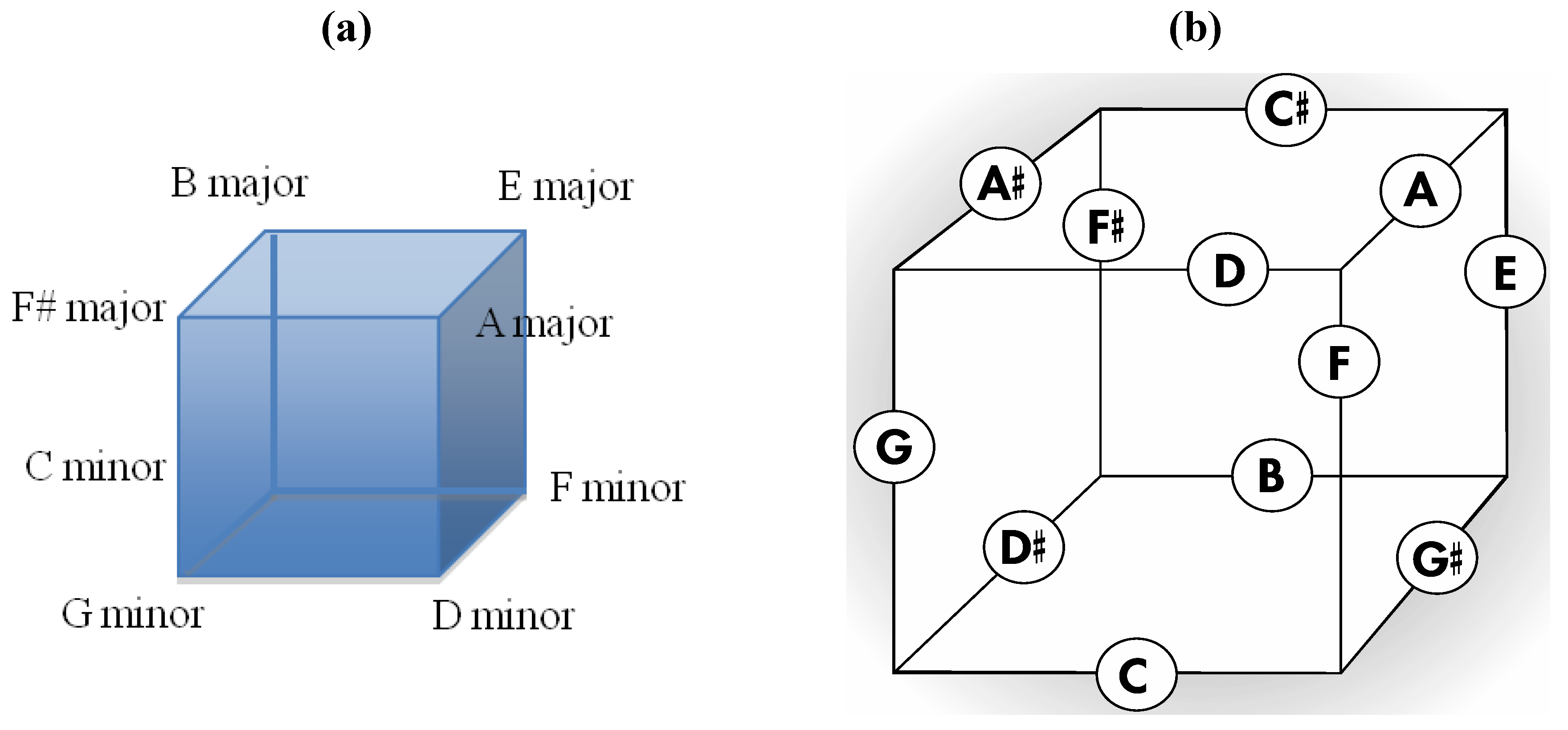
6], is a fundamental tonal geometry that maps important triads and that clearly features the Circle of Fifths within one of its rows. Second, it can be seen that Euler’s 2-D tonnetz is closely related to a three-dimensional arrangement of the twelve tones upon the twelve faces of a rhombic dodecahedron as presented in
Figure 10a. Thus, remembering that the dual polyhedron of the rhombic dodecahedron is the cuboctahedron, subtle rearrangement of nine particular tones of Euler’s 2-D tonnetz (highlighted by the trapezoidal perimeter in
Figure 11a) produces the geometry in
Figure 11b that constitutes a 2-D projection of the top half of a cuboctahedron (with correspondingly intonated vertices) that is resting upon one of its triangular faces.
Third, exactly half of the pentatonic sets (six of the twelve sets) that emanate from the rhombic dodecahedral geometry in
Figure 10a bear remarkable similarity to exactly half of the
Figure 9 pentatonic sets (six of the twelve sets) that originate from the zygo-dodecahedral geometry in
Figure 8a. Thus, three of the six pentatonic sets from the rhombic dodecahedral geometry in
Figure 10a can be viewed as major seventh chords with the added ninth (fully tertian major ninth chords), while three other such sets can be viewed as major seventh chords with the added thirteenth. The roots of these three sets with added thirteenths are a semitone lower than the roots of the three sets with added ninths. This same pattern is present among six of the
Figure 9 pentatonic sets from the
Figure 8a zygo-dodecahedral array—with a crucial difference being that the three zygo-dodecahedral seventh chords with added ninths (fully tertian dominant ninth chords) and the three zygo-dodecahedral seventh chords with added thirteenths (also containing ninths but no fifths) possess dominant seventh rather than major seventh cores. Moreover, these six pentatonic sets from
Figure 9 and the six corresponding pentatonic sets from
Figure 10 recapitulate important harmonic properties of the Circle of Fifths such as the fact that any set composed of five contiguous tones in the Circle of Fifths (the tones of fundamental major/minor pentatonic scales) comprises a major triad along with the respective ninth and thirteenth (typified in the key of F# by the harmonically coherent black keys of the piano).
Figure 10.
(
a) An important intonation of the rhombic dodecahedron with connections to Euler’s tonnetz, the Circle of Fifths, and the zygo-dodecahedral intonation in
Figure 8a. (
b) The corresponding dual cuboctahedral graph of the preceding rhombic dodecahedral graph.
Figure 10.
(
a) An important intonation of the rhombic dodecahedron with connections to Euler’s tonnetz, the Circle of Fifths, and the zygo-dodecahedral intonation in
Figure 8a. (
b) The corresponding dual cuboctahedral graph of the preceding rhombic dodecahedral graph.
Figure 11.
(
a) Nine particular tones from Euler’s tonnetz; (
b) A subtle rearrangement of the nine tones from Euler’s tonnetz in
Figure 11a reveals a cuboctahedral projection that corresponds to the rhombic dodecahedron in
Figure 10a (and the cuboctahedron in
Figure 10b).
Figure 11.
(
a) Nine particular tones from Euler’s tonnetz; (
b) A subtle rearrangement of the nine tones from Euler’s tonnetz in
Figure 11a reveals a cuboctahedral projection that corresponds to the rhombic dodecahedron in
Figure 10a (and the cuboctahedron in
Figure 10b).
Additionally, just as any tone in the Circle of Fifths is flanked by its respective dominant and sub-dominant tones to constitute a vital 1,4,5 relationship, so too are several striking 1,4,5 relationships present in the
Figure 10a rhombic dodecahedral tonal geometry such as in neighboring major ninths (E major ninth, A major ninth, B major ninth) and minor ninths (C minor ninth, F minor ninth, G minor ninth) in the six aforementioned
Figure 10 pentatonic sets. Likewise encoded within
Figure 10a are elements of the harmonically important cadence IV to V7 to I as occurs in three neighboring pentatonic sets in
Figure 10a (E major ninth, F# 7 + 9, B major ninth). The rhombic dodecahedral array in
Figure 10a also sports important 1,4,5 relationships in triads that are encoded by those eight of the fourteen rhombic dodecahedral vertices that define a cube. Thus, four of these eight triads are major (E, F#, A, B with 1,4,5 relationships in the key of E or B)) and four of the eight are minor (C, D, F, G with 1,4,5 relationships in the key of C or G). In three dimensions, the four major triads can be seen to be encoded by vertices comprising the top four cubic vertices while the bottom four such cubic vertices encode the four minor triads (
Figure 12a). With regard to the cube, it should be noted that the twelve face centers of the rhombic dodecahedron define the twelve edge centers of an appropriately sized cube such that the geometry in
Figure 10 can be redrawn on cube edges as in
Figure 12b. It is believed that the representation in
Figure 12b is the first tonal geometry that is related to prior music theoretical cornerstones (the Circle of Fifths and Euler’s tonnetz) and that captures important major/minor 1,4,5 relationships while utilizing all twelve tones upon a single cube (Douthett and Steinbach’s “Cube Dance” [
7,
8,
9] uses four interconnected cubes with each of the four cubes containing six of the twelve tones). Also noteworthy is the fact that important geometric properties concerning tritone pair midpoints exist in both the Circle of Fifths and in the Schlegel diagram corresponding to the
Figure 8a zygo-dodecahedron (shown in
Figure 13) such that all six tritone pair midpoints in the Circle of Fifths are copunctal at the center of the circle whereas all six tritone pair midpoints in
Figure 13 are centrally collinear. In three dimensions, as has been previously mentioned, all six tritone pair midpoints of the
Figure 8a zygo-dodecahedron lie conspicuously in its lone reflection plane.
Figure 12.
(
a) The four major triads and four minor triads encoded at those eight of the fourteen vertices of the rhombic dodecahedron in
Figure 10a that define a cube; (
b) A version of the intonated rhombic dodecahedron in
Figure 10a that features intonated cube edges.
Figure 12.
(
a) The four major triads and four minor triads encoded at those eight of the fourteen vertices of the rhombic dodecahedron in
Figure 10a that define a cube; (
b) A version of the intonated rhombic dodecahedron in
Figure 10a that features intonated cube edges.
Figure 13.
Schlegel diagram corresponding to the
Figure 8a zygo-dodecahedron.
Figure 13.
Schlegel diagram corresponding to the
Figure 8a zygo-dodecahedron.
Fourth, both the rhombic dodecahedral array of tones in
Figure 10a and the zygo-dodecahedral array of tones in
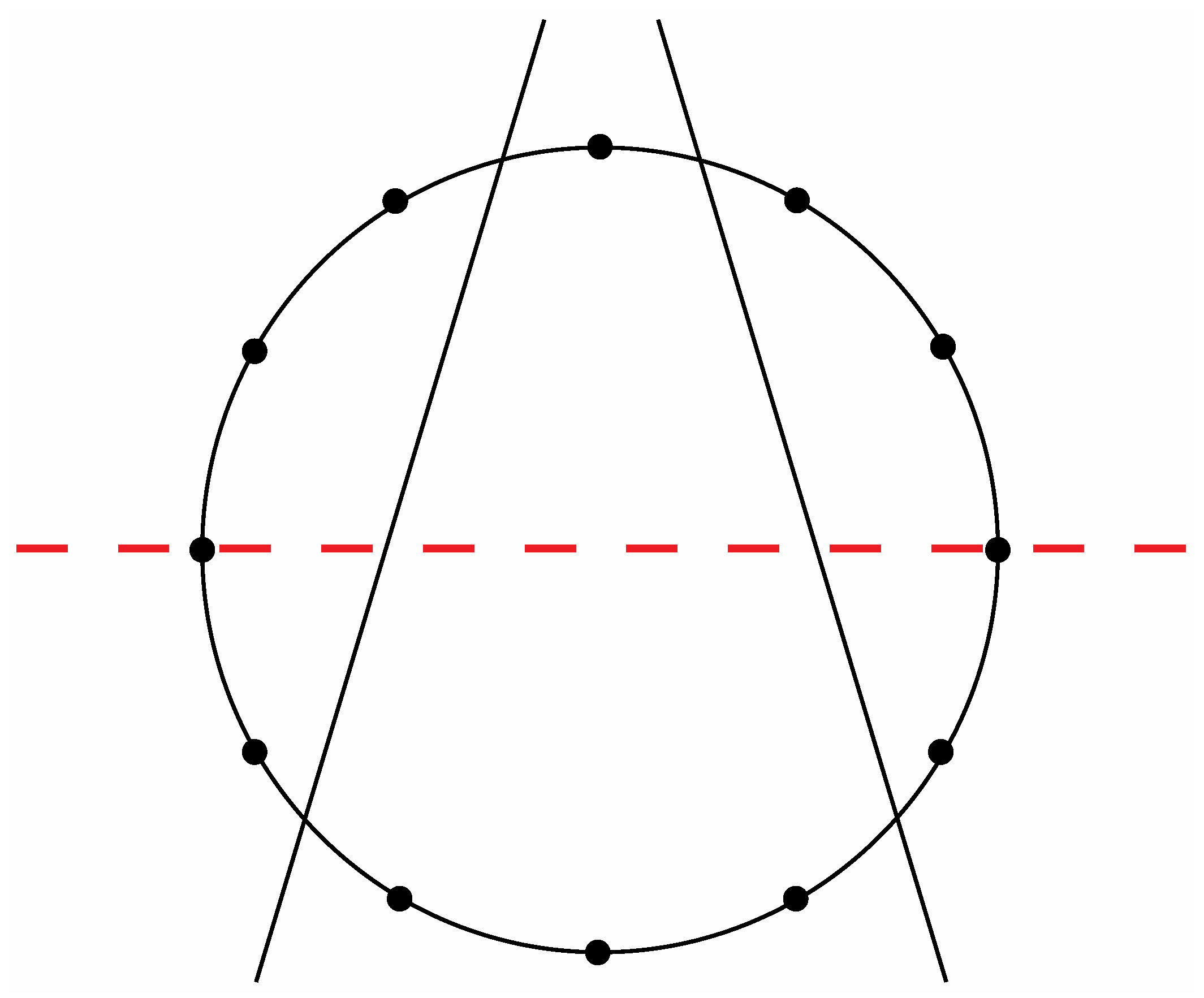
Figure 8a exhibit a precise correlation medially and laterally to one of the two possible ways that the Circle of Fifths can be bilaterally sectioned according to specific criteria that will become clear in the following discussion. Thus, for the sake of argument, consider the ways that a circle with twelve evenly spaced vertices can be divided in a bilaterally symmetrical manner with two straight lines to produce a medial group of four vertices, a left lateral group of four vertices, and a right lateral group of four vertices such that any one of these three groups of four vertices possesses at least one vertex on both sides of a third line that bisects the circle. There are exactly two solutions to such criteria as shown in
Figure 14 and
Figure 15.
Figure 14.
One of the two possible modes to section a circle with twelve evenly spaced vertices according to the criteria specified in the text.
Figure 14.
One of the two possible modes to section a circle with twelve evenly spaced vertices according to the criteria specified in the text.
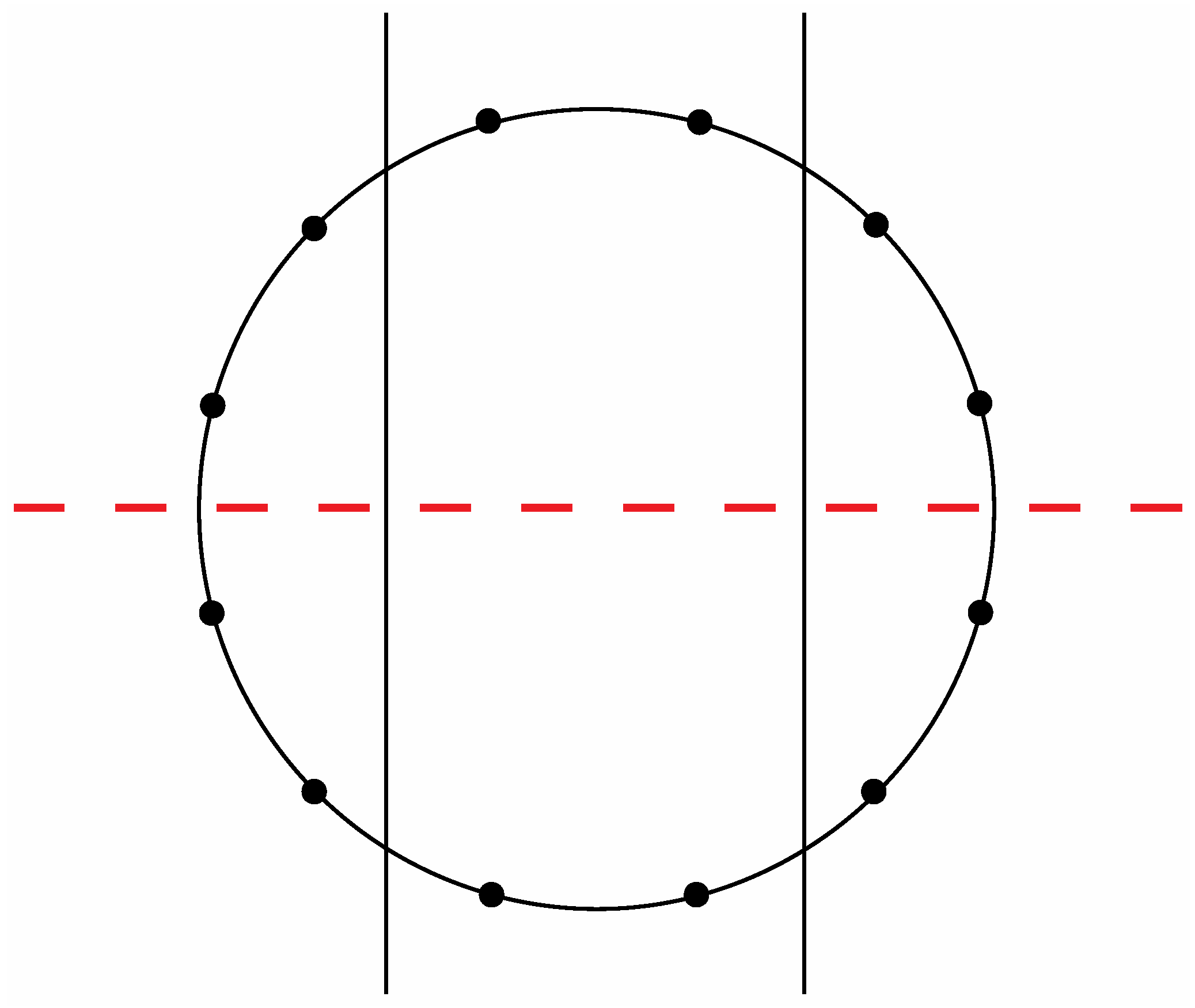
Figure 15.
The second of the two possible modes to section a circle with twelve evenly spaced vertices according to the criteria specified in the text.
Figure 15.
The second of the two possible modes to section a circle with twelve evenly spaced vertices according to the criteria specified in the text.
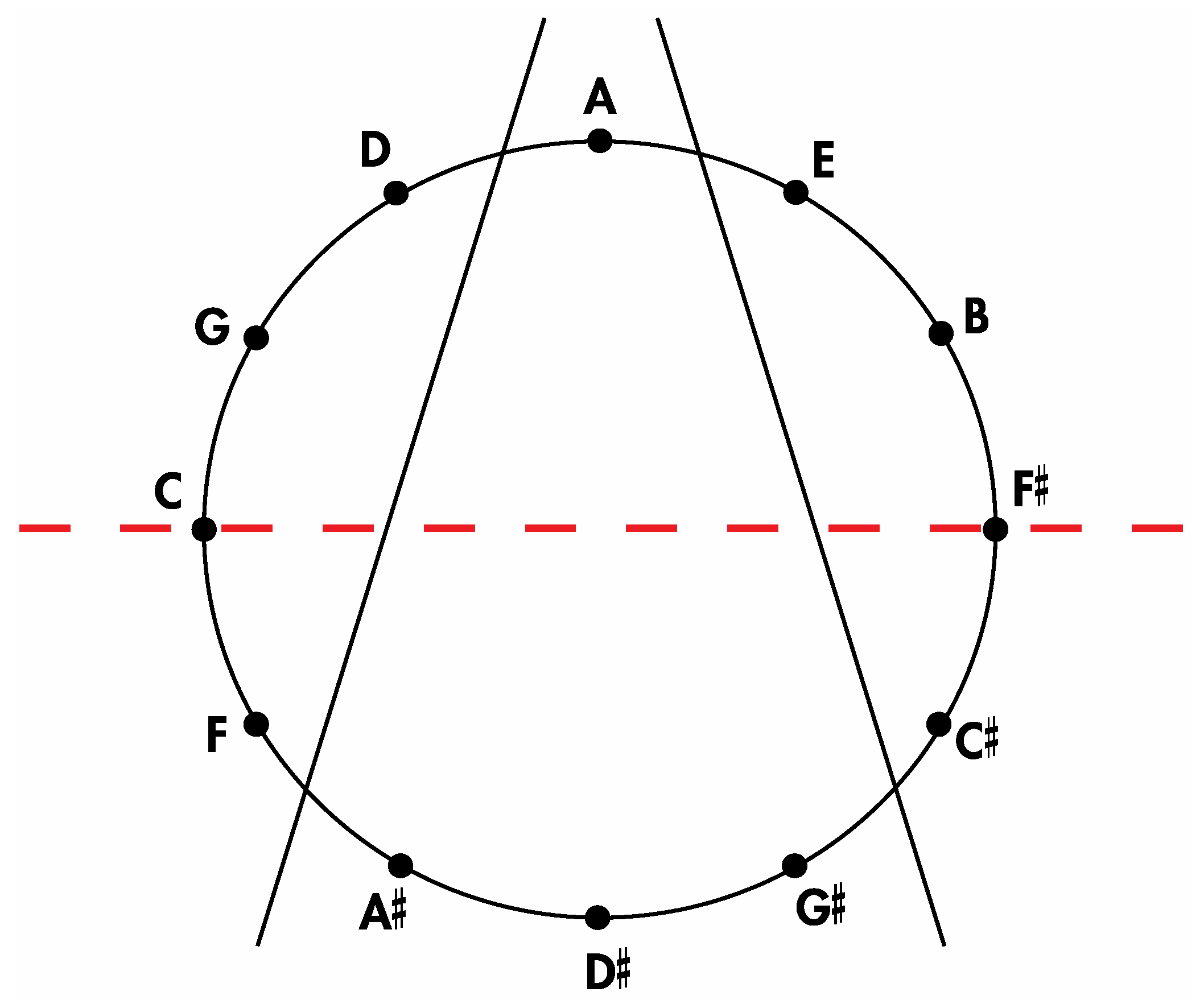
Insertion of the tones of the Circle of Fifths onto
Figure 14 and
Figure 15 in the manner shown respectively in
Figure 16 and
Figure 17 allows for the aforementioned correlations to be appreciated. Thus, it is evident that the four medial tones in
Figure 16 (D#, G#, A, A#) are indeed the same four tones on the four medial faces of the
Figure 10a rhombic dodecahedron when it is seated on the rhombic face assigned to the tone A and oriented such that the rhombic face assigned to the tone A# is closest to the viewer. Moreover, the four left lateral tones in
Figure 16 (F, C, G, D) perfectly match the four left lateral tones on this rhombic dodecahedron. The correlation is complete after confirming that the four right lateral tones in
Figure 16 (E, B, F#, C#) are the same as this particularly oriented
Figure 10a rhombic dodecahedron’s four right lateral tones.
Figure 16.
An installation of the tones of the Circle of Fifths onto the sectioned circle in
Figure 14.
Figure 16.
An installation of the tones of the Circle of Fifths onto the sectioned circle in
Figure 14.
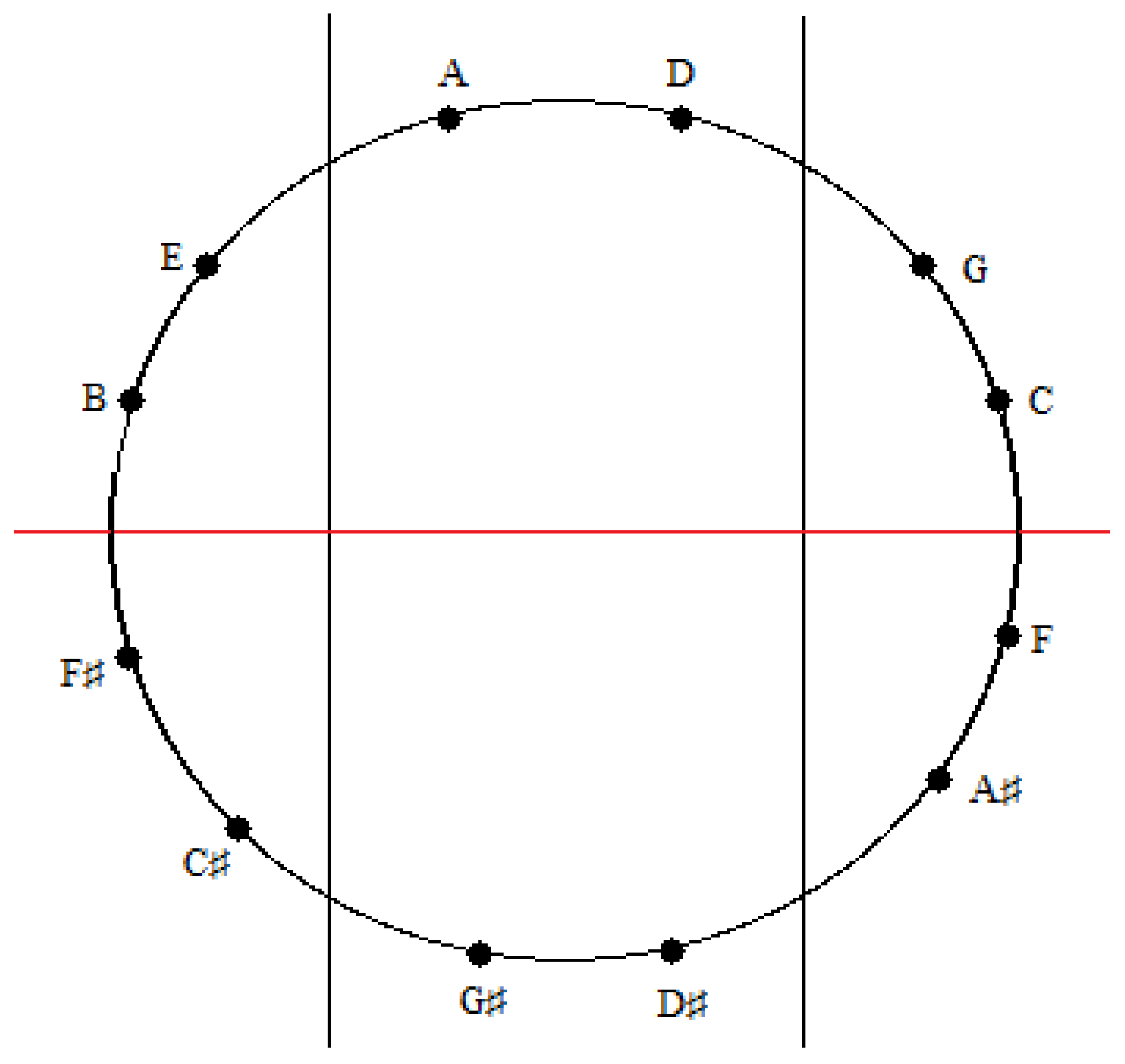
Figure 17.
An installation of the tones of the Circle of Fifths onto the sectioned circle in
Figure 15.
Figure 17.
An installation of the tones of the Circle of Fifths onto the sectioned circle in
Figure 15.
A similar correspondence is gleaned upon comparing the medial and lateral groups of tones in the zygo-dodecahedral tonal geometry in
Figure 8a to the medial and lateral groups of tones in
Figure 17. As can be seen, the medial tones in both
Figure 8a and
Figure 17 are identical (D, G#, D#, A) as are the left lateral tones (A#, F, C, G) and the right lateral tones (E, B, F#, C#). In view of the fact that there are only two possible trisections of the Circle of Fifths according to the preceding criteria—both of which showing perfect correspondence to one of the two featured dodecahedral arrays of tones—and in view of the fact that there are only two types of seventh chords that can result via the addition of a seventh on top of a major triad in root position (major seventh or dominant seventh)—both of which are paradigmatically exemplified in one or the other of the two intonated dodecahedral geometries as seen within the respective aforementioned pentatonic ninth and thirteenth chords—it is tempting to conclude that these two dodecahedral tone networks are in fact fundamental twin expansions of the Circle of Fifths into the third dimension.
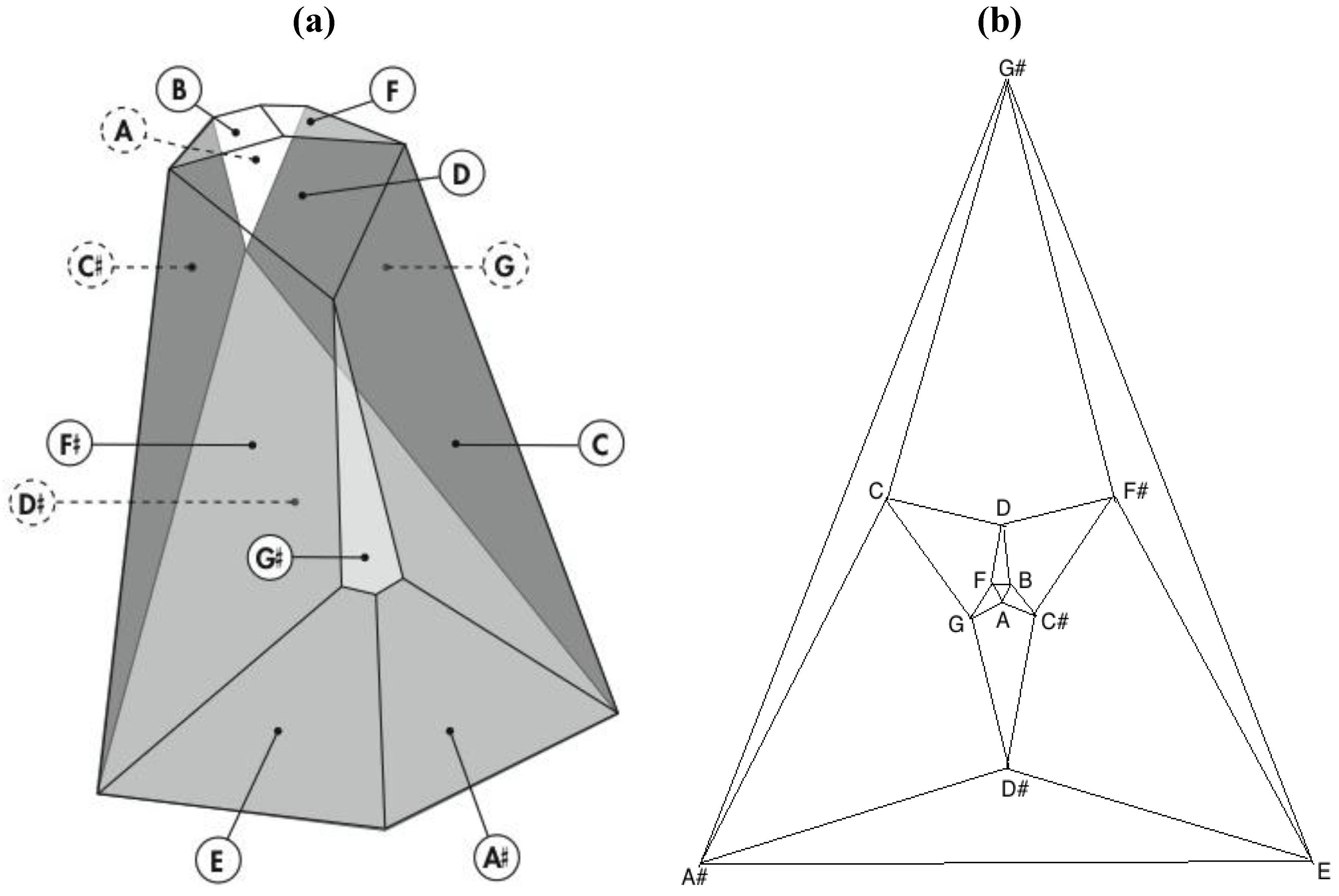
It has thus far been put forth that an obscure (and perhaps completely overlooked) bilaterally symmetrical dodecahedron consisting of twelve convex quadrilaterals (with eight different shapes and sizes) harbors a bilaterally symmetrical harmonic assembly of the twelve tones in an axiomatic manner. Curiously, close inspection of
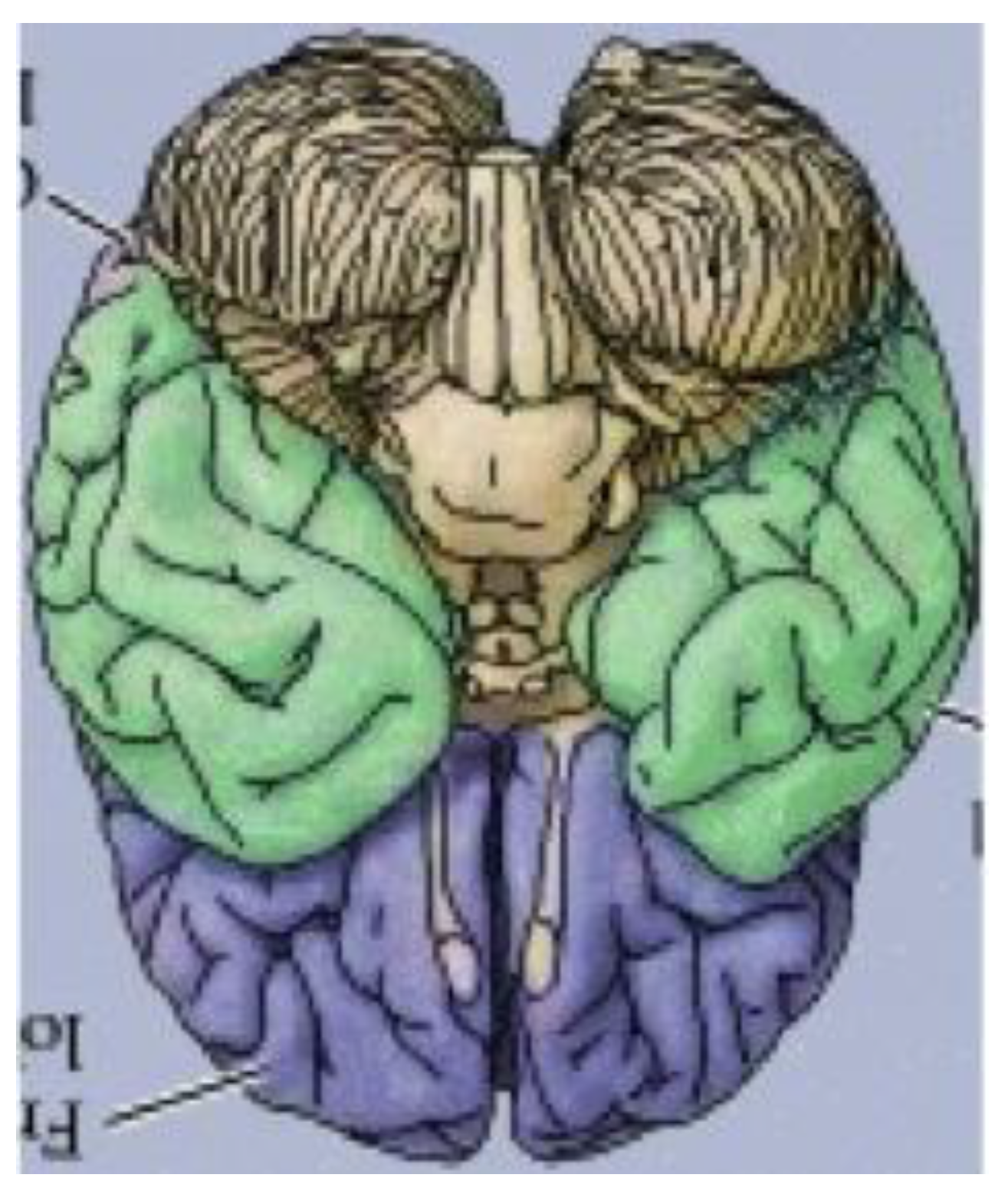
Figure 18, a rendering of the ventral view of the human brain (an image that appears on an NIH webpage [
10]), reveals remarkable similarities to the delineated zygo-dodecahedral paradigm.
Figure 18.
Ventral view of the human brain (image reproduced with permission from [
10], copyright 2001).
Figure 18.
Ventral view of the human brain (image reproduced with permission from [
10], copyright 2001).
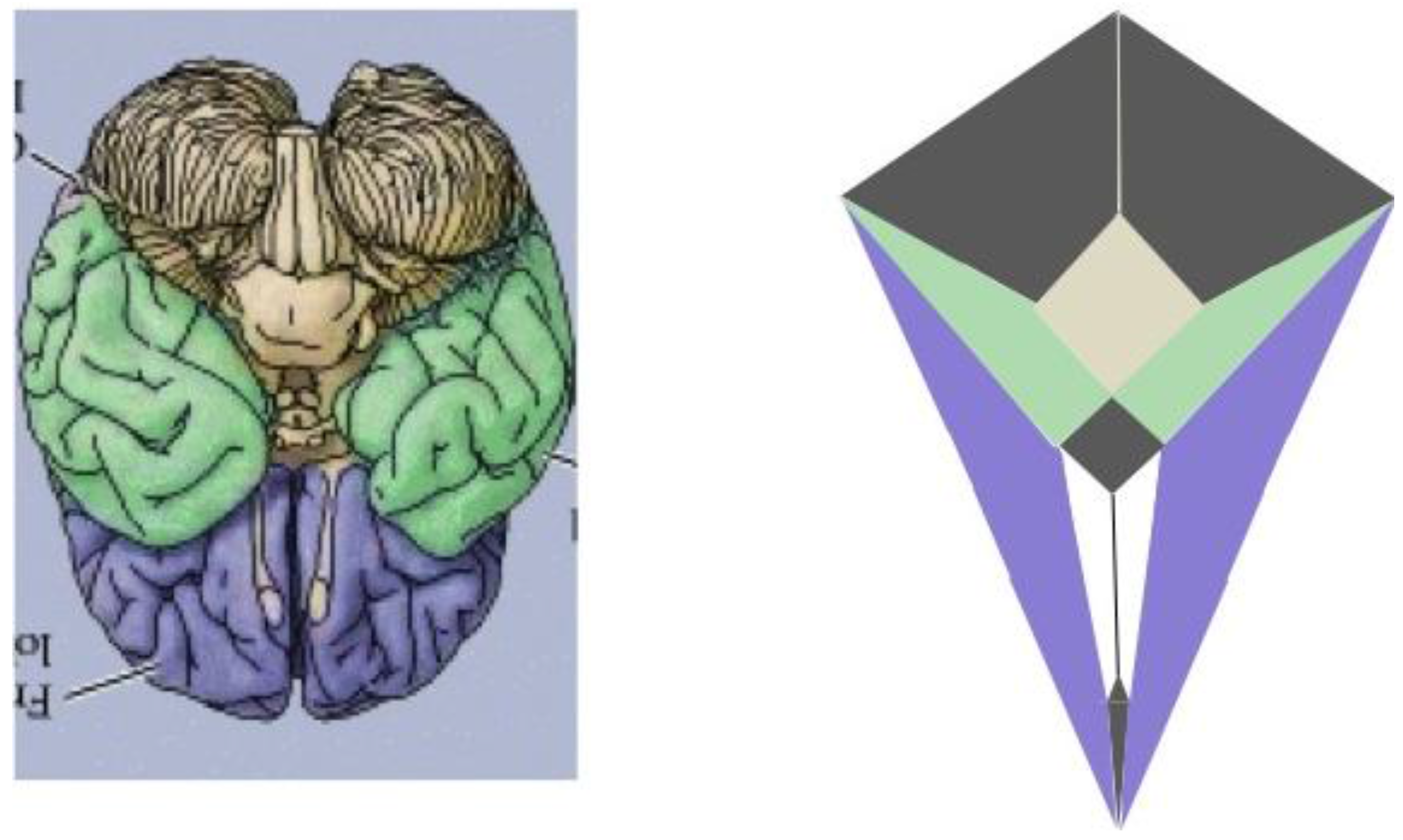
Thus, as indicated in the side-by-side comparison within
Figure 19, the four major paired structures in the aforementioned image show substantial congruence with the respectively color-coded regions of the zygo-dodecahedral Schlegel diagram such that the cerebellar lobes are depicted in black, the temporal lobes in green, the frontal lobes in violet, and the olfactory bulbs in white. The three medial structures in the Schlegel diagram in
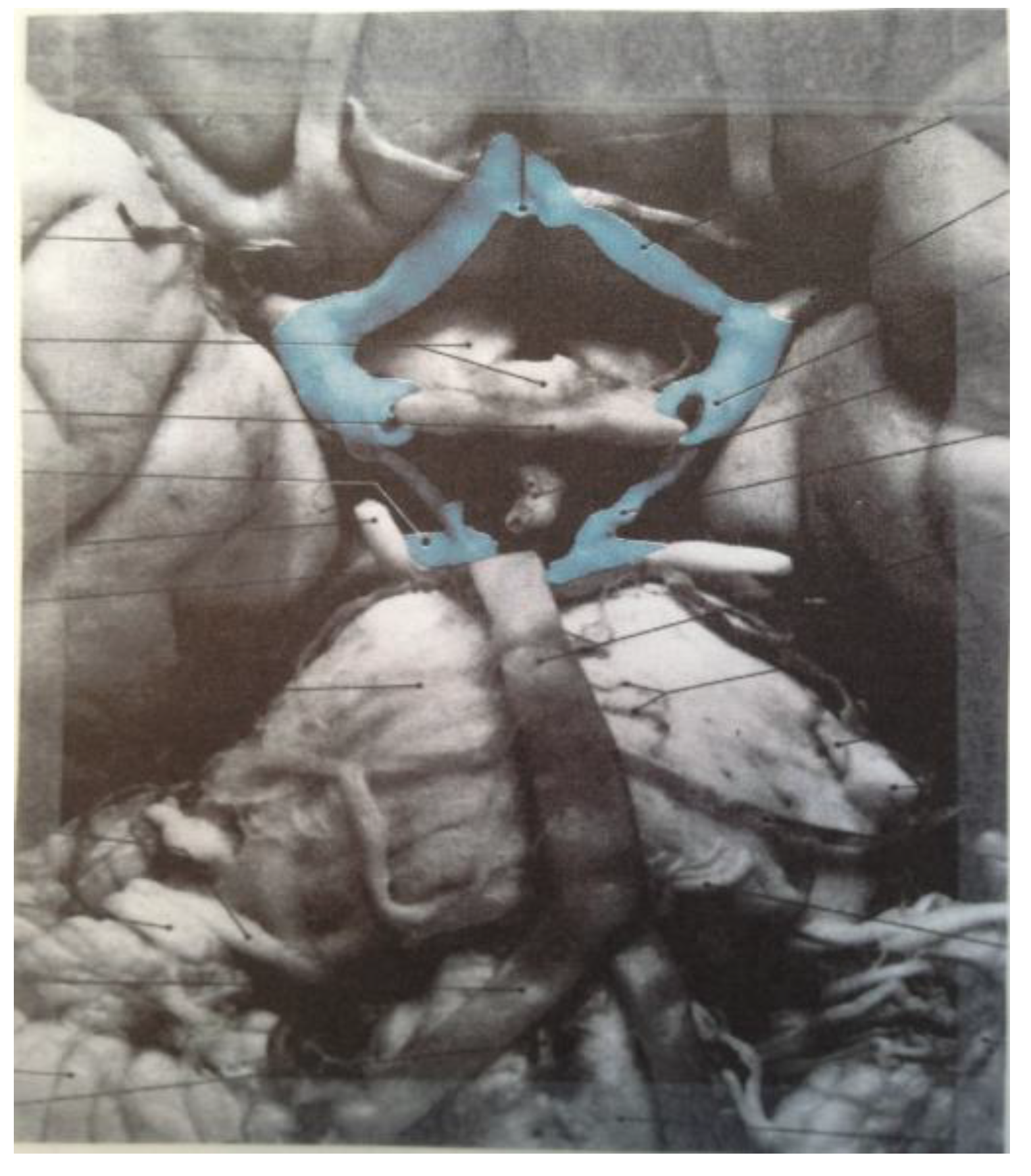
Figure 19 correspond to the medulla/pons (yellow), the diencephalon (black), and the corpus callosum (black). The large quadrilateral region (on the underside of the Schlegel diagram’s two-dimensional projection) is attributed to the cerebral cortex. It is interesting to note that certain quadrilateral boundaries define well-recognized anatomical brain structures. For example, the Circle of Willis (highlighted in blue in the image in
Figure 20) [
11] has been referred to as a diamond-shaped network of vasculature at the diencephalon’s perimeter [
11] (attributed to the perimeter of the large medial black region in
Figure 19). Another pertinent quadrilateral region of the brain is the rhomboid fossa—a structure forming the floor of the fourth ventricle that grossly defines the ventral brain boundaries of the medulla and pons [
12] (attributed to the yellow region in
Figure 19).
Figure 19.
A side-by-side comparison between a color-coded ventral view of the human brain and a correspondingly colored Schlegel diagram of the
Figure 7 zygo-dodecahedron (ventral view of the human brain reproduced with permission from [
10], copyright 2001).
Figure 19.
A side-by-side comparison between a color-coded ventral view of the human brain and a correspondingly colored Schlegel diagram of the
Figure 7 zygo-dodecahedron (ventral view of the human brain reproduced with permission from [
10], copyright 2001).
Figure 20.
The diamond shape of the Circle of Willis (highlighted in blue) is readily apparent (image reproduced with permission from [
11], copyright 2005).
Figure 20.
The diamond shape of the Circle of Willis (highlighted in blue) is readily apparent (image reproduced with permission from [
11], copyright 2005).
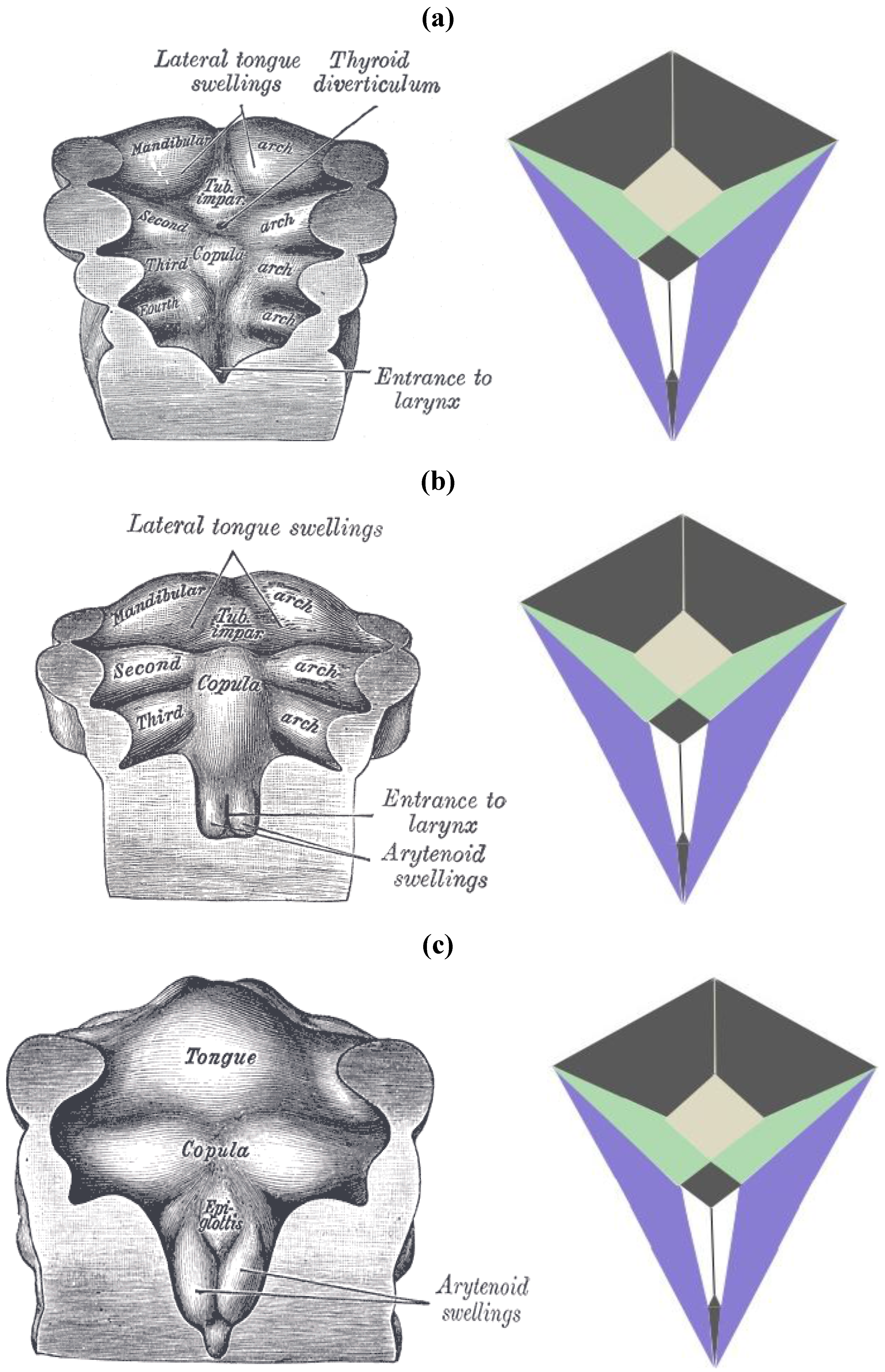
The zygo-dodecahedral pattern emphasized herein can also be arguably discerned during the development of the embryonic pharynx as illustrated within vintage diagrams in Gray’s Anatomy [
13]. Three drawings from Henry Gray’s classic tome on human anatomy display the morphogenesis of the pharynx from approximately 26 to 30 days of gestation and examination of
Figure 21a–c allows the following putative zygo-dodecahedral correspondences to be made.
Figure 21.
(
a) A discernible zygo-dodecahedral motif in the developing pharynx; (
b) Several days later, the discernible zygo-dodecahedral motif becomes more pronounced with the development of the arytenoid swellings; (
c) Several days later still, the entrance to the larynx temporarily closes. Images of the pharynx reproduced from [
13].
Figure 21.
(
a) A discernible zygo-dodecahedral motif in the developing pharynx; (
b) Several days later, the discernible zygo-dodecahedral motif becomes more pronounced with the development of the arytenoid swellings; (
c) Several days later still, the entrance to the larynx temporarily closes. Images of the pharynx reproduced from [
13].
Thus, the paired black quadrilaterals match the lateral lingual swellings, the medial yellow quadrilateral is assigned to the tuberculum impar, the paired green quadrilaterals are ascribed to the second pharyngeal arch, the paired white quadrilaterals correspond to the arytenoid swellings, the black medial quadrilateral at the bottom is attributed to the larynx, the large black medial quadrilateral is assigned to the copula linguae, and the paired violet quadrilaterals roughly match the remaining pre-fused pharyngeal arches. The large quadrilateral on the underside of the zygo-dodecahedral projection corresponds to the hypopharynx. That quadrilateral regions could well be involved in workings of the tongue beyond embryonic stages is bolstered by a condition known as median rhomboid glossitis [
14] that is characterized by the appearance of a red diamond-shaped zone of medial inflammation toward the back of the tongue that is believed to reflect pathology within the remnant tissue of the tuberculum impar (persistent tuberculum impar is another name for the condition).
Similarities between the dolichocephalic skull/head morphology of certain canine breeds and the structure of the
Figure 7 zygo-dodecahedron are also worthy of consideration as seen in
Figure 22. Assignments that match each one of the dodecahedral quadrilaterals to major bone/cartilaginous structures can be made such that the white medial dodecahedral face is assigned to the maxilla, the large medial light gray face to the mandible, the paired dark gray faces to the temporal bones, the paired white faces to the nasal bones, the paired gray faces at the rear to the auricles, the remaining paired faces to the parietal bones, the thin medial gray quadrilateral toward the rear to the occipital bone, and the remaining medial face to the frontal bone.
Figure 22.
Similarity between the overall morphology of (
a) the
Figure 7 zygo-dodecahedron and (
b) the head of a dolichocephalic dog.
Figure 22.
Similarity between the overall morphology of (
a) the
Figure 7 zygo-dodecahedron and (
b) the head of a dolichocephalic dog.
A non-convex version of the
Figure 7 zygo-dodecahedron is more akin to the human skull/head as seen in
Figure 23. Biologically speaking, it is well known that cephalization is strongly linked to the emergence of a bilaterally symmetrical body plan [
15]. It is possible that simple icosahedral modifications that lead to zygomorphic structures—such as those icosahedral modifications leading to the zygo-dodecahedron featured in this work—could underlie primary events that take place during cephalogenesis.
Figure 23.
A non-convex version of the dodecahedron in
Figure 7 is discernibly cephaloid such that the bottom yellow medial face corresponds to the mandible, the upper two yellow faces are assigned to the auricles, the two central yellow faces are attributed to the nasal bones, the lower blue medial triangle is ascribed to the maxilla, the two large central blue faces are assigned to the temporal bones, the top blue medial triangle corresponds to the occipital bone (the hash mark at the top of this face indicates the mid-line), the other blue medial triangle is ascribed to the frontal bone, and the remaining two blue triangles are ascribed to the parietal bones.
Figure 23.
A non-convex version of the dodecahedron in
Figure 7 is discernibly cephaloid such that the bottom yellow medial face corresponds to the mandible, the upper two yellow faces are assigned to the auricles, the two central yellow faces are attributed to the nasal bones, the lower blue medial triangle is ascribed to the maxilla, the two large central blue faces are assigned to the temporal bones, the top blue medial triangle corresponds to the occipital bone (the hash mark at the top of this face indicates the mid-line), the other blue medial triangle is ascribed to the frontal bone, and the remaining two blue triangles are ascribed to the parietal bones.
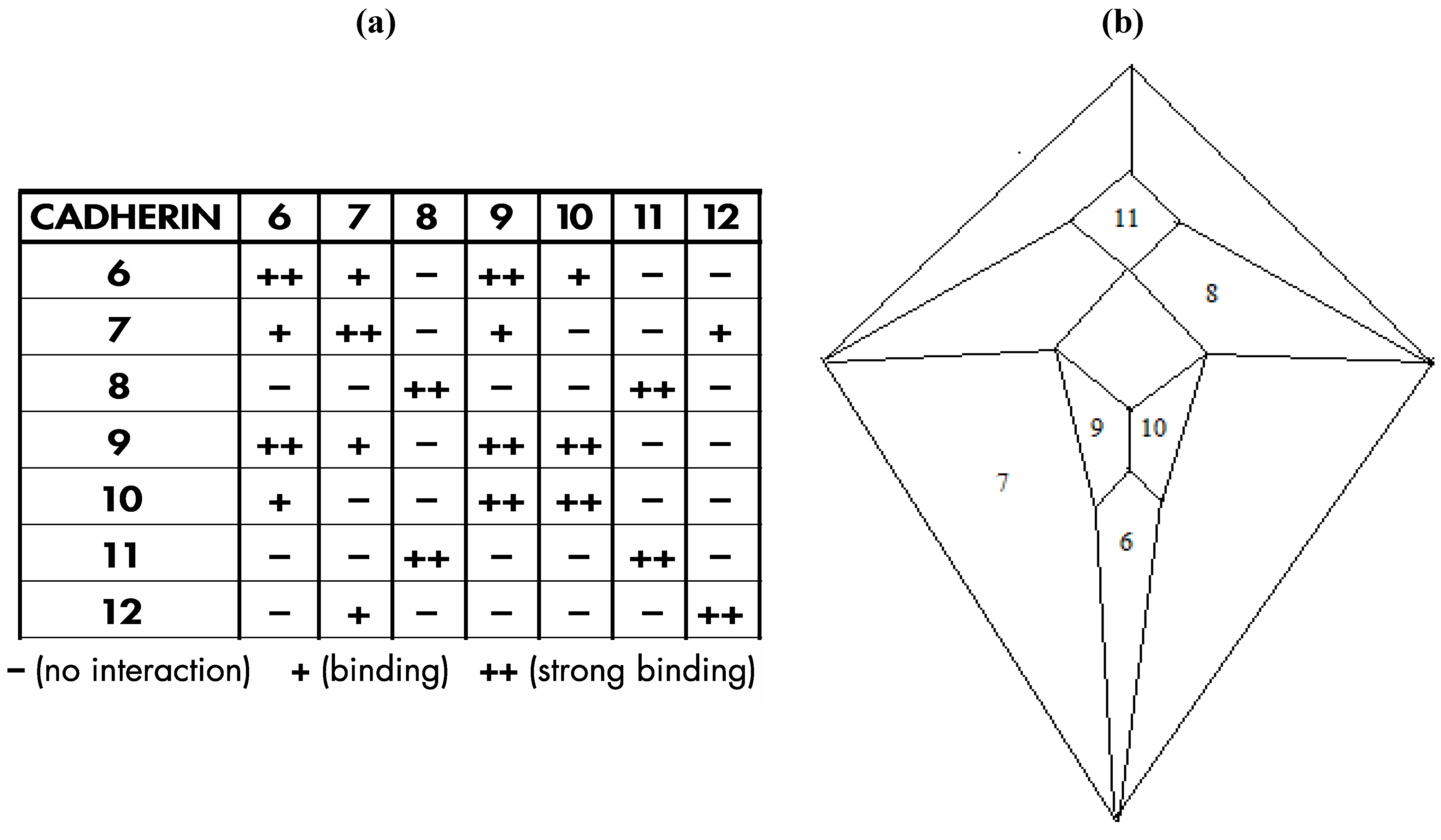
Interestingly, a relatively recent paper by Shimoyama
et al. [
16] documents heterophilic binding data (shown in
Figure 24a) for certain members of an important class of cell adhesion proteins; namely, the type II cadherins, that, with respect to a group of seven of the eight examined proteins in which distinct binding preferences are displayed, perfectly conforms in four possible modes to the
Figure 3c graph, as is detailed, in one of the four possible modes, within
Figure 24b.
The particular mode shown in
Figure 24b is the only one of the four possible modes in which three prominent cadherins (cadherin-6, cadherin-11, and cadherin-12) occupy medial positions and that places cadherin-6, in view of its documented role in forebrain development [
17], at the most anterior medial quadrilateral. The medial quadrilateral corresponding to the medulla/pons has been assigned to cadherin-11 on the basis of data that indicates high cadherin-11 expression in the spinal cord [
18]. Cadherin-12, also known as BR-cadherin or brain-cadherin, has been placed at the large medial quadrilateral corresponding to the cerebral cortex and this assignment is supported by the detection of abundant quantities of this particular cadherin in the developing and adult cerebral cortex [
19]. At the time of publication of the Shimoyama studies (in the year 2000), it was not possible to investigate the heterophilic binding properties of all type II cadherins because not all of them were then known. It is now known that the number of vertebrate type II cadherin genes is thirteen [
20]—a number conspicuously close to the twelve that would be expected in a dodecahedral network. Moreover, the number thirteen is significant in terms of the repeat motif for either the fcc (affiliated with the rhombic dodecahedron) or hcp (affiliated with the trapezo-rhombic dodecahedron) lattices in which uniform spheres aggregate with twelve spheres surrounding a central sphere. The number thirteen may also be significant in the context of the zygo-dodecahedral network wherein a thirteenth type II cadherin could theoretically promote the growth of a cluster of cells at an interior region near or at the center of this bilaterally symmetrical dodecahedron.
The analysis in
Figure 24b leaves out one of the eight type II cadherins in the Shimoyama study; namely, cadherin-18 (formerly known as cadherin-14). This cadherin is excluded for several reasons. First, as described above, a presumed dodecahedral network would seem to suggest that one of the thirteen type II cadherins should be removed in order to generate a system with twelve postulated components. Second, the Shimoyama data shows that cadherin-18 has fully redundant binding proclivities when compared to cadherin-7. Third, cadherin-18 is the only one of the type II cadherins with the amino acid sequence nye in a rather highly conserved region of the third extracellular domain (nine of the other twelve possess a dfe sequence, two possess a dye sequence, and one possesses the sequence sfe).
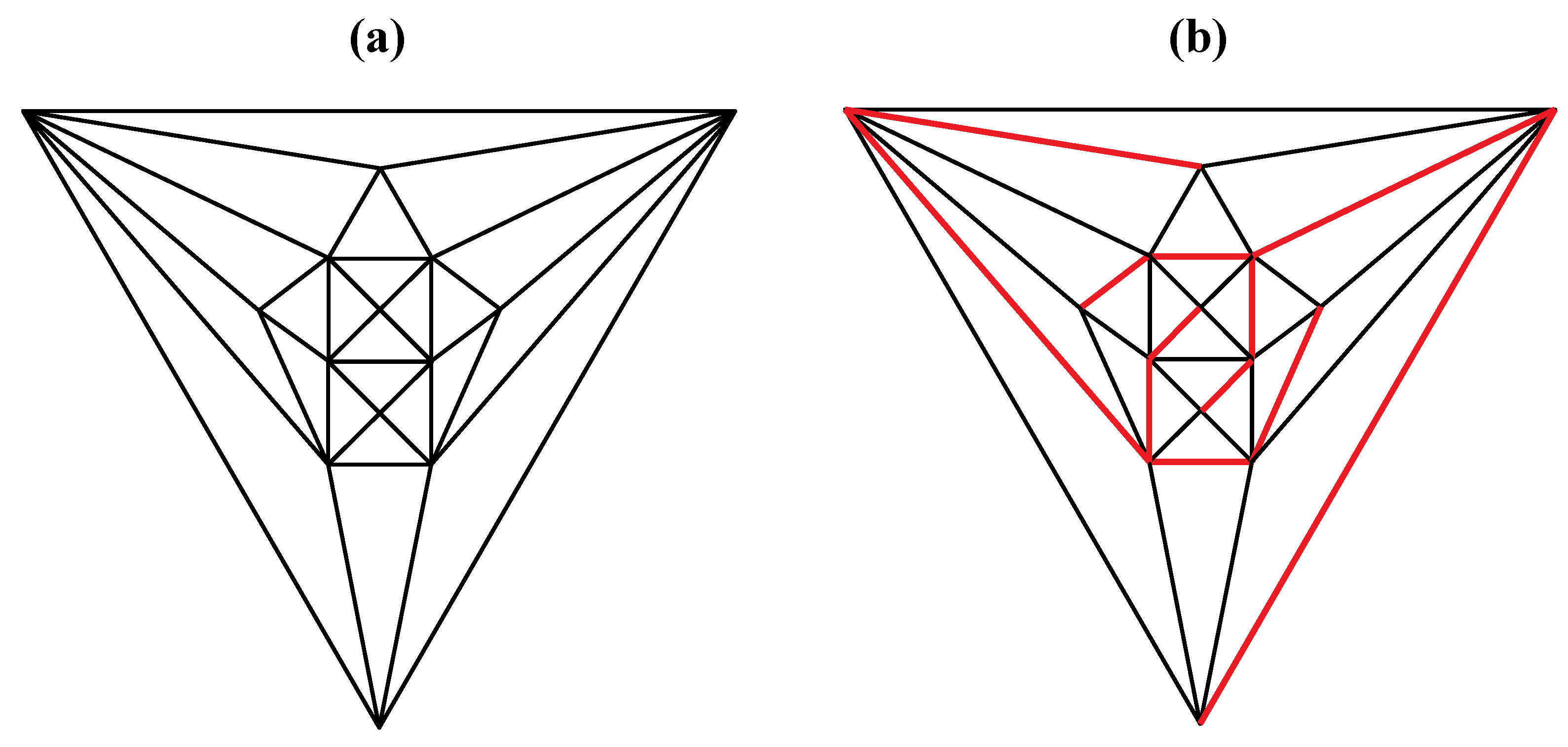
Figure 24.
(
a) Shimoyama type II cadherin binding data for cadherins six through twelve; (
b) An installation of cadherins six through twelve onto the
Figure 5 zygo-dodecahedral Schlegel diagram in a manner that is consistent with the Shimoyama binding data in
Figure 24a (the back face is assigned to cadherin-12).
Figure 24.
(
a) Shimoyama type II cadherin binding data for cadherins six through twelve; (
b) An installation of cadherins six through twelve onto the
Figure 5 zygo-dodecahedral Schlegel diagram in a manner that is consistent with the Shimoyama binding data in
Figure 24a (the back face is assigned to cadherin-12).
An intriguing experimental finding in a 2005 Nature article [
21], known cerebellar type II cadherin expression patterns [
22], and data within an elegant 2009 article by Hulpiau and van Roy [
23] are instrumental in completing the assemblage of the putative zygo-dodecahedral type II cadherin network by assigning the remaining five type II cadherins to the five vacant quadrilaterals in
Figure 24b. Thus, affinity capture mass spectrometry has demonstrated a protein-protein interaction between cadherin-19 and cadherin-6 [
21]. Strikingly, with respect to experimentally determined protein-protein interactions of cadherin-19, the website interlogfinder.com lists cadherin-6 as the single currently known cadherin-19 binding partner [
24]. Within
Figure 24b, only one quadrilateral is vacant wherein one of its four edges is shared by the quadrilateral that bears cadherin-6 (the aforementioned vacant quadrilateral has been, as previously discussed, assigned to one of the two lateral frontal lobes), and therefore, cadherin-19 is placed at this particular quadrilateral. In the cerebellum, according to available data such as that in the Body Atlas of the website nextbio.com, expression of cadherin-24 is higher than in any other brain region [
22]. Of the two vacant cerebellar lobes, cadherin-24, by virtue of the Hulpiau/van Roy data—a phylogenetic analysis of the first extracellular domains of each of the thirteen type II cadherins such that the hierarchy shown in
Figure 25 is obtained to reflect a succession of closest relatives within this group of proteins [
23]—is placed into that cerebellar quadrilateral which shares an edge with cadherin-8. Likewise, in view of its pronounced cerebellar expression [
22], cadherin-22 is placed into the other cerebellar quadrilateral. Placement of cadherin-5 into the medial quadrilateral representing the diencephalon is made because cadherin-5 and cadherin-8 are neighbors in the Hulpiau/van Roy hierarchy [
23]. By process of elimination, cadherin-20 is assigned to the only remaining vacant quadrilateral (that which represents one of the temporal lobes). Cadherin-20 is highly expressed in major temporal lobe substructures such as the tail of the caudate nucleus and hippocampus [
22,
25].
Figure 25.
The Hulpiau/van Roy phylogenetic analysis of Type II cadherins yields a linear map of structural relatives (CDH18 has been excluded for reasons explained in the text).
Figure 25.
The Hulpiau/van Roy phylogenetic analysis of Type II cadherins yields a linear map of structural relatives (CDH18 has been excluded for reasons explained in the text).
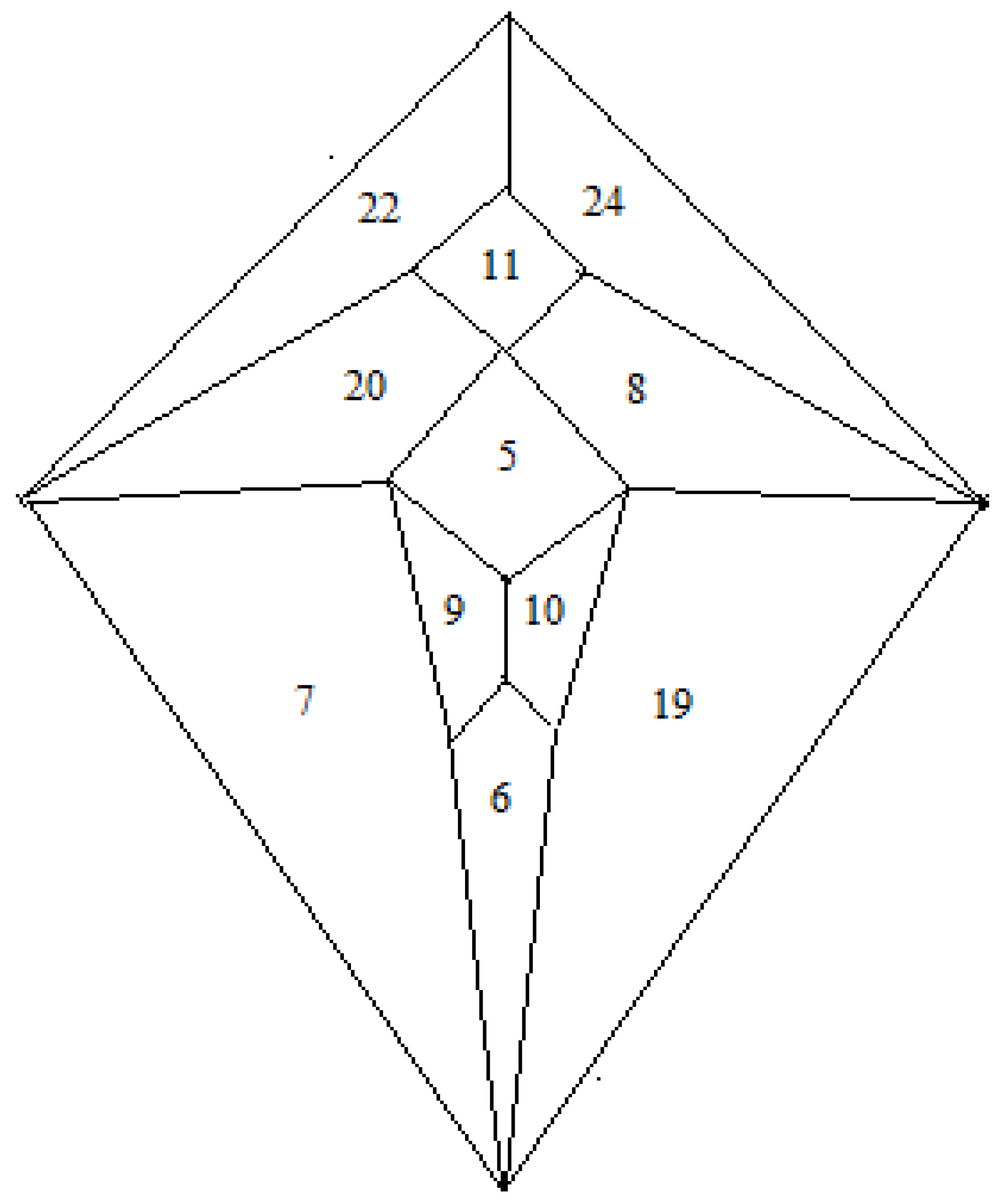
Thus, combination of the Shimoyama data and the Hulpiau/van Roy data allows the zygo-dodecahedral network in
Figure 26 to be proposed that utilizes all of the type II cadherins except for cadherin-18. The network in
Figure 26 places, on average, each cadherin next to nearly three of four closest neighbors in the
Figure 25 Hulpiau/van Roy hierarchy while retaining the binding preferences in the Shimoyama data. It is interesting to note that experimental binding evidence exists to link cadherin-6 to all four of its nearest neighbors in the
Figure 26 array [
16,
21]. It is also noteworthy that
Figure 26 places cadherin-8 in a manner such that it is surrounded by all four of its nearest cadherin neighbors in the Hulpiau/van Roy hierarchy. The assignment of cadherin-5 (vascular endothelial cadherin or VE-cadherin), a protein that affects the development of the vasculature, to the diencephalon is reasonable in light of the fact that the Circle of Willis constitutes the major route by which blood is supplied to the brain in a quadrilateral-shaped loop around the diencephalon. Indeed, while some researchers strictly limit the presence of cadherin-5 to endothelial cells, there are recent reports of cadherin-5 expression in astrocytes [
26] and within cells of the embryonic diencephalon of the zebrafish [
27].
It is important to keep in mind that it is common that several members of the type II cadherin family are expressed simultaneously at most points in the life cycle of many cells [
28], but that does not preclude the existence of the proposed zygo-dodecahedral network. While an initial impulse to hastily dismiss the zygo-dodecahedral cadherin map in
Figure 26 as far-fetched may be understandable, it can also be said that when this protein array is considered against the backdrop of the highly cited Shimoyama binding studies, the compelling Hulpiau/van Roy hierarchy, the experimentally established binding interaction between cadherin-19 and cadherin-6, the high cerebellar expression of both cadherin-24 and cadherin-22, and the acute resemblance of the aforementioned ventral patterning of the brain to that of the icosahedrally-derived zygo-dodecahedron featured herein, even the most hardened skeptic would likely find it difficult to argue counter to the assertion that the
Figure 26 model is well beyond a random fit of the data. Knockout experiments are consistent with some degree of redundancy [
29] for some of the type II cadherins but more work with compound knockouts seems necessary to provide further clarity with respect to determining which type II cadherins (or pairs thereof) are indispensable morphogenetic constituents.
Figure 26.
A zygo-dodecahedral brain map of type II cadherins that conforms to the Shimoyama binding data and that reflects substantial agreement with the Hulpiau/van Roy cadherin map in
Figure 25. CDH22 and CDH24 are assigned to the cerebellar lobes; CDH8 and CDH20 are assigned to the temporal lobes; CDH7 and CDH19 are assigned to the frontal lobes; CDH9 and CDH10 are assigned to the olfactory bulbs; CDH11 is assigned to the medulla/pons; CDH5 is assigned to the diencephalon; CDH6 is assigned to the corpus callosum (the back face has been assigned to cadherin-12 and corresponds to the cerebral cortex).
Figure 26.
A zygo-dodecahedral brain map of type II cadherins that conforms to the Shimoyama binding data and that reflects substantial agreement with the Hulpiau/van Roy cadherin map in
Figure 25. CDH22 and CDH24 are assigned to the cerebellar lobes; CDH8 and CDH20 are assigned to the temporal lobes; CDH7 and CDH19 are assigned to the frontal lobes; CDH9 and CDH10 are assigned to the olfactory bulbs; CDH11 is assigned to the medulla/pons; CDH5 is assigned to the diencephalon; CDH6 is assigned to the corpus callosum (the back face has been assigned to cadherin-12 and corresponds to the cerebral cortex).
The proposed network in
Figure 26 would require asymmetric brain expression of certain type II cadherins, but such asymmetric expression of cadherins has precedent in that cadherin-2 (a type I cadherin also known as N-cadherin) is expressed to a greater extent in the left hemisphere than in that on the right [
30]. In view of recent findings by Monaco
et al. that link mutations in the type II cadherin gene for cadherin-8 to the incidence of autism [
31], the elucidation of cadherin and protocadherin networks in brain morphogenesis is an important matter that continues to be a focus of extensive research efforts [
32]. It is interesting to note that recent work suggests that the number twelve may hold special significance in the context of brain connectivity as van den Heuvel and Sporns have posited that the human brain contains a bilaterally symmetrical “Rich Club” of twelve major interconnected neuronal hubs [
33]. That the brain’s twelve pairs of cranial nerves may also be pertinent to the proposed zygo-dodecahedral model is a topic for further deliberation.