Abstract
Non-periodic systems have become more important in recent years, both theoretically and practically. Their description via Delone sets requires the extension of many standard concepts of crystallography. Here, we summarise some useful notions of symmetry and aperiodicity, with special focus on the concept of the hull of a Delone set. Our aim is to contribute to a more systematic and consistent use of the different notions.
1. Introduction
The notion of symmetry for (fully) periodic objects such as perfect crystals is well established and has a long history. While there are slightly different approaches, for instance via direct or via Fourier space, there is little dispute what the symmetry of a given structure really is. As it turns out, an important ingredient is the underlying periodicity, which brings in a deep connection with lattices and their structures; see [1] for a systematic mathematical exposition.
Things are more complex in the setting of general (discrete) structures, in particular in the absence of non-trivial periods. In particular, rather different notions are in use regarding what the terms such as “periodicity" or “symmetry" are supposed to mean. While this should be no problem in principle, experience proves otherwise. Quite some confusion emerges from the comparison of “results” that were phrased in different contexts, which asks for some clarification, as has been noted in this context in [2] (Chapter 10).
The purpose of this article is to contribute to this question, via some notions that have proved particularly useful in the setting of non-periodic and aperiodic structures; see [3,4] for background. We present some definitions and results, all example-driven and designed for Euclidean space , and add some arguments in favour of their systematic use, one being a higher degree of consistency.
In view of the well-established equivalence concept of mutual local derivability (MLD), compare [5,6] and the discussion below, we do this mainly for Delone sets, and leave it to the reader to rephrase results in terms of his or her favourite structure, be it a tiling, a marked pattern, an ornament or any other MLD representative. Some of our examples will also be drawn from the tiling zoo, but we primarily view them as Delone sets (for instance, via their vertex points) in the spirit of [7].
Very little (if anything) of what we discuss below is really new. However, the bits and pieces are scattered over the literature, both in mathematics and physics. Due to the renewed interest in non-periodic systems following the award of the 2011 Nobel Prize in Chemistry to Dan Shechtman for his discovery of quasicrystals [8], it seems necessary to recapitulate and slightly adjust some of the most relevant concepts in a more coherent fashion. We hope that our brief exposition below will help to clarify the notions and avoid future misunderstandings.
2. General Notions and Definitions
A central concept for our discussion is that of a Delone set , by which we mean a point set (a countable subset of ) that is neither “too crowded” nor “too sparse”. More precisely, there are positive radii r and R such that no open ball contains more than one point of Λ, irrespective of the centre x, while each ball contains at least one point of Λ. More generally, one can consider other point sets as well. In view of the applications in crystallography, we often consider point sets that are at least uniformly discrete, which is the above condition with the ball alone, while we might sometimes omit the relative denseness (which is the other condition). A reasonable minimal assumption is the local finiteness of Λ, by which we mean that is a finite set for any compact . Local finiteness of Λ is equivalent to Λ being discrete (each possesses an open neighbourhood that contains no other point of Λ) and closed. Note that the set is discrete, but not closed (and clearly not locally finite).
A Delone (or, more generally, a locally finite) set Λ is said to have a non-trivial period when holds for some , and non-periodic otherwise, where . The set
is the set of periods of Λ, which is always a subgroup of . Clearly, Λ is non-periodic if and only if , which means that is the trivial group. When t is a non-trivial period of Λ, contains the subgroup . A Delone set Λ is called crystallographic (or fully periodic) when the -span of is . The simplest examples are lattices, by which we mean discrete co-compact subgroups of . They are thus point sets of the form
where is a basis of .
Let us emphasise that, as soon as , a Delone set can be periodic without being crystallographic (some authors call this sub-periodic, though we will not use this term). If is locally finite and is a (discrete) group of rank , Λ is said to be periodic of rank r. In particular, non-crystallographic (for ) is weaker than non-periodic. Later, we shall also introduce the term aperiodic, which refers to a yet stronger property than non-periodicity. Our notion of aperiodicity will be consistent with the one introduced in [2].
The symmetries of crystallographic point sets are fully understood, and completely classified in small dimensions [1,9]. Particularly simple are lattices, and it may be this widely discussed class that makes the adjustment of suitable symmetry concepts to other (and in particular non-periodic) cases so unfamiliar. Let us thus first look at symmetries under (linear) isometries in more detail.
3. Rotations and Reflections of Individual Delone Sets
In one dimension, the reflection in the point x is defined by . Clearly, is the identity on . A point set is called reflection symmetric in the point x, if
Observing , which means that the product of two reflections in is a translation, the existence of more than one reflection centre has the following consequence.
Lemma 1
Let be a point set that is reflection symmetric in the distinct points x and y. Then, Λ is periodic with period . ☐
If is locally finite, the existence of two distinct reflection centres implies, via Lemma 1, the existence of a non-trivial period, wherefore Λ must also be uniformly discrete. Consequently, there are also two reflection centres of minimal distance, and say. In this case, Λ is crystallographic, with as lattice of periods. Moreover, the set comprises all reflection centres of Λ.
In dimension d, one inherits this structure when the point set Λ is reflection symmetric in two parallel, but distinct, co-dimension one hyperplanes; see [10] for background material, including a classification of finite and affine reflection groups.
Let us now take a closer look at individual rotation symmetries in the Euclidean plane. Our (actually rather classic) arguments will revolve around the consequences of multiple symmetry centres. For convenience, we observe and use complex numbers. Consider a uniformly discrete point set and assume that it has two distinct fivefold rotation centres, z and say, which means that
where is a primitive fifth root of unity. Note that either rotation centre may be, but need not be, an element of Λ. Still, the uniform discreteness of Λ implies that there is such a pair with being minimal. Figure 1 shows how each rotation centre produces five centres of the other type, namely and with . Here, pairs of opposite centres have distance
where the first factor takes a non-zero value for some ℓ. This contradicts the separation assumption on the position of the rotation centres, wherefore we conclude that two rotation centres are impossible. This also implies that a uniformly discrete point set with fivefold symmetry cannot possess a non-trivial period. This is the reason why fivefold symmetry is called a non-crystallographic symmetry of the plane; compare [10,11].
The above argument applies to all other non-crystallographic rotation symmetries ( or ) of the plane in an analogous way. In contrast, the crystallographic symmetries “escape” this argument, see also [10] (Section 6.6), because the prefactor is either always (for ) or the only value is zero (which happens for ). Together, this gives the following result.
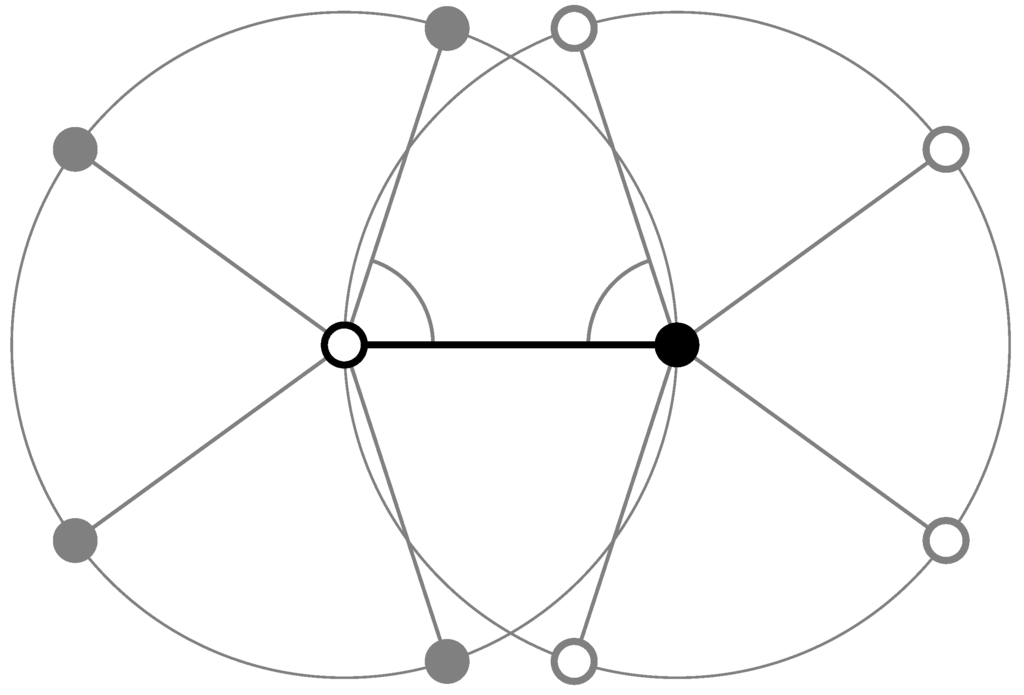
Figure 1.
Sketch of the incompatibility between points of fivefold rotational symmetry at minimal distance (black line) and periodicity in the Euclidean plane.
Proposition 1
Let be a uniformly discrete point set with an exact n-fold rotational symmetry. If n is non-crystallographic, which means or , there can only be one such rotation centre. When , the existence of more than one rotation centre is possible, and then implies lattice periodicity of Λ. When , the existence of another rotation centre means that Λ is at least rank-1 periodic.
PROOF.
The claim about the impossibility of more than one rotation centre for non-crystallographic values of n follows from our above arguments. The case (in standard orientation) leads to rotation centres on the lattice , which results in . Similarly, produces a triangular lattice, while the choice generates rotation centres on the vertices of a honeycomb packing. Finally, produces rotation centres along a line. This is (via an embedding) a consequence of Lemma 1. ☐
For a systematic discussion of non-crystallographic root systems and their reflections in higher dimensions, we refer to [11] and references therein in conjunction with [10]. Let us just mention that a uniformly discrete point set in 3-space can at most have one symmetry centre for icosahedral symmetry, which is the most relevant case for quasicrystals in 3-space.
The exact symmetry of an individual point set or pattern is an important concept, but it is of limited use for non-periodic structures. Let us briefly explain this well-known observation with a classic example. We employ an inflation rule for a tiling made from a square (which is dissected into two triangles) and a rhombus, as displayed in Figure 2. It is known as the (undecorated) Ammann–Beenker tiling; see [2,12,13] and references therein for details. In an inflation step, a tiling is scaled by a factor (in this case ) and the inflated tiles are then dissected into copies of the original size, as indicated in the left panel of Figure 2. Iterating this procedure on an appropriate initial patch (which may consist of a single tile) will lead to a space-filling tiling of the plane.
The patch shown in Figure 2 is part of a tiling of the plane that is a fixed point under the square of the inflation rule (with a single square as its central seed). It has no rotational symmetry at all, and a reflection symmetry only in the diagonal.
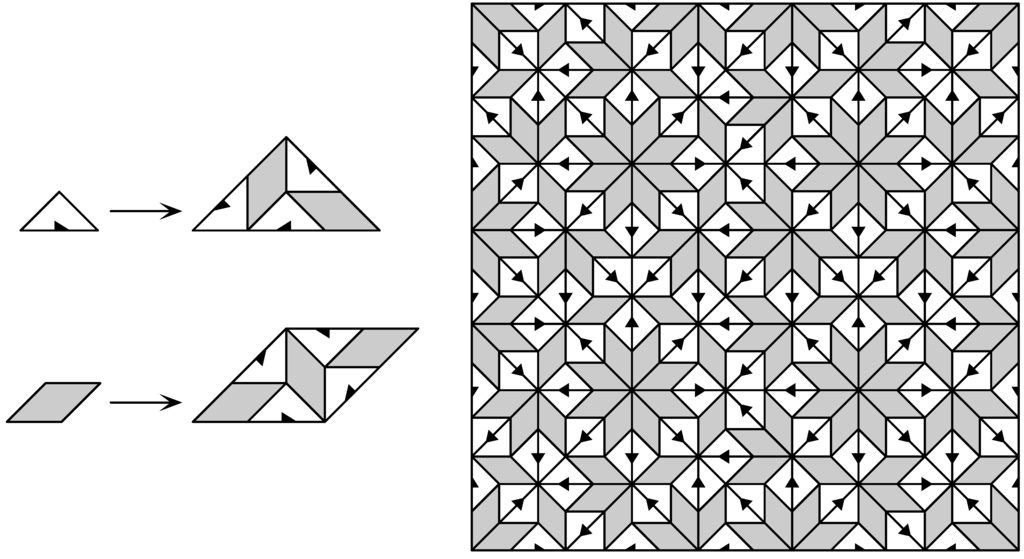
Figure 2.
Inflation rule for the (essentially undecorated) Ammann–Beenker tiling (left), and a patch (right) obtained by three inflation steps from a square-shaped patch (consisting of two triangles) in the centre; see text for details. The patch has no rotation symmetry, but is reflection symmetric in the diagonal.
In contrast, Figure 3 shows the central patch of a fixed point tiling (for the same inflation rule, but starting from an eightfold symmetric seed; the patch shown is obtained by two inflation steps from the central octagonal patch comprising 16 triangles and 16 rhombuses), this time with complete symmetry. Although these two tilings are distinct, they are locally indistinguishable in the sense that any finite patch of one occurs in the other (and vice versa); see below for a precise definition. In fact, any finite patch re-occurs in a relatively dense fashion. This property is called repetitivity, and is a direct consequence of the underlying (stone) inflation structure (where stone inflation refers to the property that the inflated tiles are dissected into complete tiles in the inflation rule of Figure 2). Both from a mathematical and from a physical perspective, structures that are locally indistinguishable should be considered from a unified point of view; see also the discussion in [14]. In particular, one needs a suitably adapted notion of symmetry. For example, the diffraction patterns of our two examples are identical and show perfect symmetry; see [15,16] for details and an illustration.
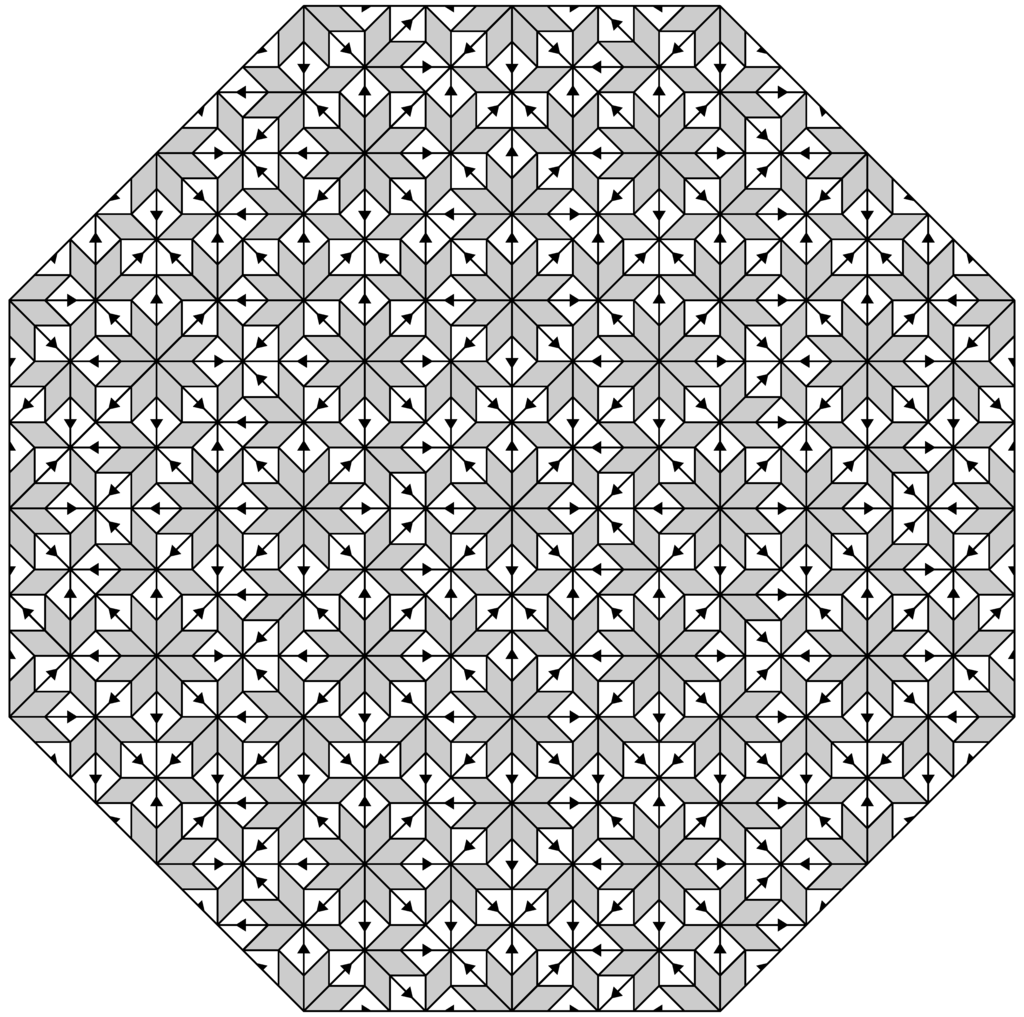
Figure 3.
Central patch of an Ammann–Beenker tiling with exact symmetry.
4. Symmetries of LI Classes and Hulls
Two Delone sets Λ and in are called locally indistinguishable (or LI for short) if any finite cluster of Λ (which is a non-empty set of the form for some compact ) is, up to translation, also a cluster of and vice versa. More formally, for any compact , there are translations such that
Note that also the terms locally isomorphic or locally isometric are in use for this property (but have the same abbreviation). Clearly, LI is an equivalence relation on the class of Delone sets, and the equivalence class of a single Λ is called its LI class, denoted by .
Beyond LI, one needs a notion to formalise relations between point sets and tilings, or, more generally, between distinct but related patterns. A useful concept, called local derivability, was introduced in [6]; see also [5]. A pattern (where we are thinking mainly of tilings or point sets here, though more general structures are possible) in is said to be locally derivable from a pattern T in , when a compact neighbourhood of 0 exists such that, whenever the K-patches (defined as suitable intersections with K) of T centred at two positions and coincide, also looks the same in the vicinity of x and y; we refer to [6,12] for further details and formal aspects. This means that there exists a strictly local rule to construct from T.
Next, two patterns T and in are called mutually locally derivable or MLD if is locally derivable from T and vice versa. An example of two patterns that are MLD are the (undecorated) Ammann–Beenker tiling of Figure 3 and the set of its vertex points—clearly, knowing the tiling one then knows the position of the vertices, while it is slightly less obvious that knowing the vertices one can locally reconstruct the squares and the rhombuses, including the arrow direction. Mutual local derivability is an equivalence concept, and we refer to the corresponding equivalence classes as MLD classes. For the Ammann–Beenker tiling of Figure 2 and Figure 3, the set of vertex points is thus a Delone set representative of the corresponding MLD class. Note that mutual local derivability consistently extends from tilings or Delone sets to the corresponding LI classes, wherefore an MLD class is naturally composed of entire LI classes.
In our setting, a linear isometry is called an LI symmetry of , if Λ and RΛ are LI, or (equivalently) if . Some further thought reveals that each element of shares the same symmetry in this sense, so that the symmetry is actually a property of the entire LI class. This definition resolves the problem encountered with the two Ammann–Beenker tilings (respectively their representing Delone sets) above, both now having symmetry group in this sense. This is true because the non-symmetric version has the property that all its rotated copies (by multiples of ) are in the same LI class. Due to the orientations of the structural elements, no further symmetries are possible in this example.
In general, an LI class can have a larger symmetry group than any of its members individually. For instance, this happens for the rhombic Penrose tiling. Here, the maximal exact or individual symmetry group is , as in the example shown in Figure 4, while any such Penrose tiling is LI with a copy that is rotated through . In particular, the images of any finite patch under the operations occur in the same tiling. Consequently, the symmetry group in the LI sense is , which is also the symmetry of the diffraction pattern of any rhombic Penrose tiling.
This approach is adequate and satisfactory as long as the LI class is a closed set in the local rubber topology [17], where two Delone sets Λ and are ε-close when they agree on a central ball of radius , possibly after moving the individual points of one set (Λ, say) by at most a distance ε. This means that each individual point may be independently displaced to match , but only within . This topology is induced by the Hausdorff metric [18,19].
In general, however, LI classes are not closed. As a trivial example, consider the set , which may be considered as a set with a single “defect”. This set is clearly LI with any translate of itself, and one has
In other words, the LI class is the orbit of Λ under the translation action of the group . However, this LI class is not closed in the local rubber topology, because
where is arbitrary but fixed, and n is integer. Consequently, one finds
with , which is a closed subset. Obviously, the different components behave differently under reflections, although they still have reflection symmetry in the LI sense. Repeating this exercise with leads to an orbit closure with components of distinct symmetry. For physical aspects such as diffraction, the defects are immaterial, so that the relevant symmetry is not the individual symmetry of Λ, but rather that of . The latter is a closed subset of . We will come back to this point below in Section 6 in a measure-theoretic setting.
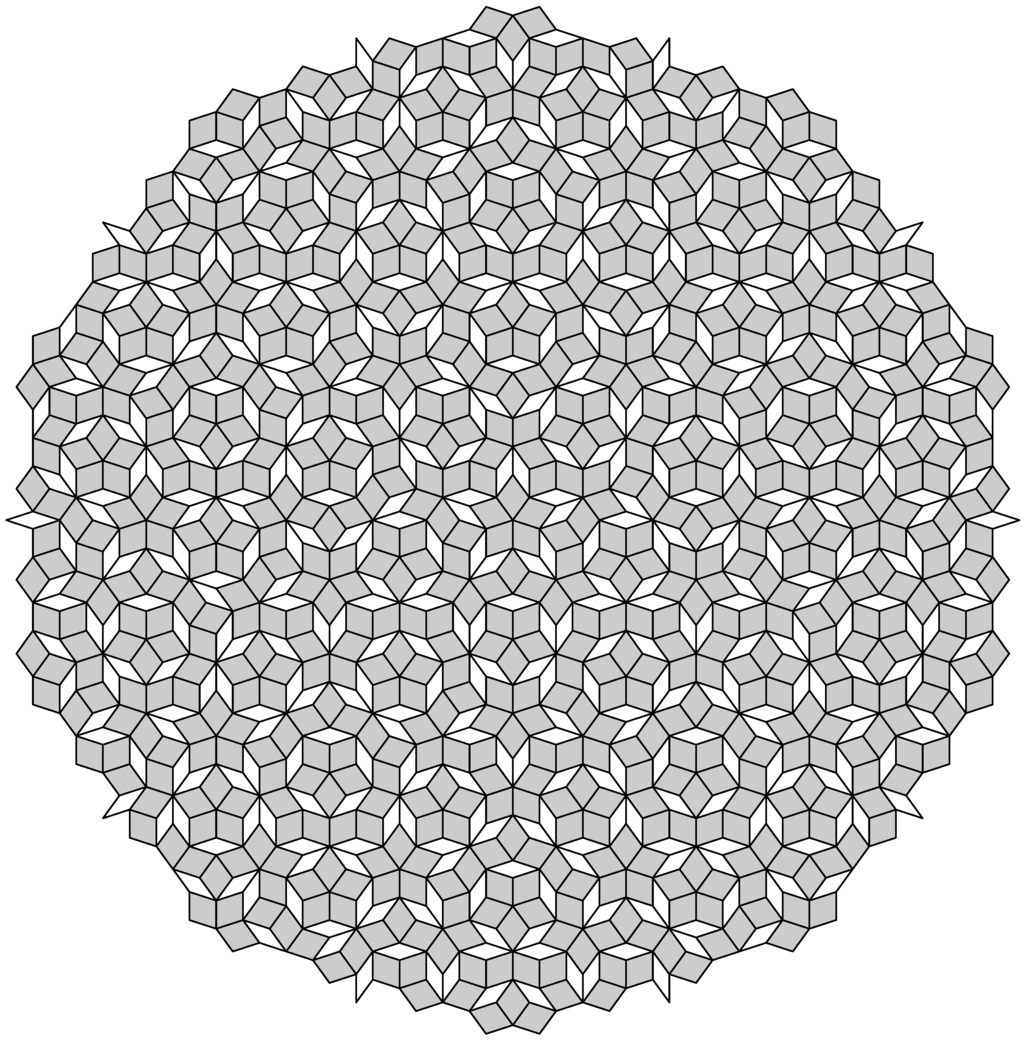
Figure 4.
Central patch of a rhombic Penrose tiling with exact symmetry.
To simplify our further discussion, let us assume that the point set has finite local complexity (FLC). By this we mean that, given any compact , there are only finitely many distinct clusters (with ) up to translations. If Λ is FLC, it must be uniformly discrete. Let us recall a characterisation of FLC sets due to Schlottmann [20].
Lemma 2
A point set is FLC if and only if is locally finite. ☐
The advantage is that, for FLC sets, we may replace the local rubber topology by the simpler local topology (both agree on FLC sets [17]). In the local topology, two FLC sets Λ and are ε-close when for some , so that only the entire set Λ may be displaced (rather than its points individually as before).
Given an FLC set , we define its (continuous) hull as
where the closure is taken in the local topology; compare [21] and references therein. A classic result on is the following [18,20,21].
Proposition 2
If is an FLC set, its hull is compact in the local topology. ☐
If is a crystallographic Delone set, with Γ as its lattice of periods, one obtains the hull
where is a (measurable) fundamental domain of the lattice Γ and denotes the d-torus. This is an example of a particularly simple hull. In contrast, the hull of the Ammann–Beenker point set, say, is a rather complicated topological space, which locally looks like a product of with a Cantor set [21,22].
In many important cases, the hull and the LI class of a Delone set Λ coincide. This happens if and only if Λ is repetitive [20]. Examples include the Ammann–Beenker and Penrose vertex point sets from above. In general, the hull is a larger set than the LI class. In such a case, one defines the symmetry of Λ via the hull , where is a hull symmetry of Λ if . This is the symmetry concept from dynamical systems theory [18,23], where the compact space is invariant under the translation action of . Since translations are used to define the hull, the built-in translation invariance implies that isometries and translations have to be treated differently. Let us now turn our attention to appropriate notions of non-periodicity in this context.
5. Non-Periodicity versus Aperiodicity
Let us define a concept of aperiodicity that is in line with the notion used in [2] (Chapter 10). As introduced above, a locally finite point set is called non-periodic when . The set is non-periodic as a subset of . However, the hull contains as an element, which is clearly periodic. This motivates the following refining definition.
Definition 1
A locally finite point set is called topologically aperiodic, or aperiodic for short, when all elements of its hull are non-periodic.
The notion of aperiodicity is thus stronger than that of non-periodicity. One has the implications
none of which is reversible in general. The Ammann–Beenker and Penrose point sets from above are aperiodic in this stronger sense. The importance of the concept of aperiodicity stems from the fact that it discards “trivial” cases of non-periodicity, as in our initial example.
Let us move on to a three-dimensional structure with interesting properties, which will lead to a further refinement of our definition of aperiodicity. Consider a bi-prism with rhombic basis, such as the one shown in the left panel of Figure 5. Depending on the angle φ between the two “roof ridges”, we call the prototile commensurate (for ) or incommensurate (for ). The incommensurate SCD prototile was introduced by Schmitt, Conway and Danzer, see [24,25] for details and background, as an example of a monotile or “einstein”, which is a single prototile that admits space-filling tilings, but no tiling with non-trivial periods. Note that we do not allow the use of the reflected tile here. As before, one can replace any tiling by a suitable Delone set (for instance via the vertices of the Delone complex, which is the dual of the Voronoi complex). For convenience, we use the tiling language for this example, but phrase results for a suitable Delone representative of the corresponding MLD class.
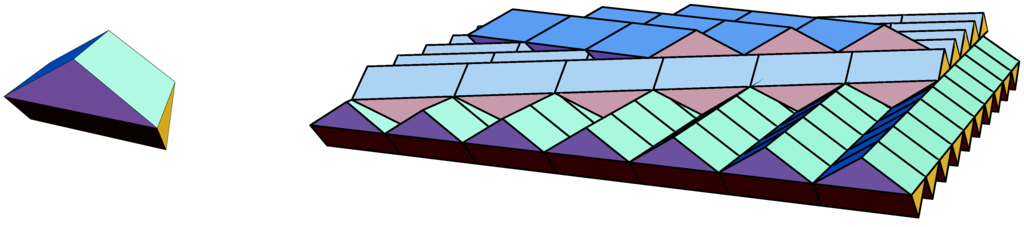
Figure 5.
The SCD monotile (left) and the layer structure of the corresponding tiling (right).
Joining SCD tiles face to face at the triangular facets, one can (only) form a closed planar layer, which is periodic with a two-dimensional lattice of periods Γ. The top of this layer shows ridges and valleys, all parallel to each other, while the bottom shows the corresponding structure “upside down”, with the directions of the ridges related by an angle φ. In order to continue the tiling process, one has to stack such layers as indicated in the right panel of Figure 5. Each layer is rotated with respect to the previous layer by the angle φ. For a finite number of layers, it is still possible that non-trivial periods persist, which happens precisely if the rotation is a coincidence rotation of the planar lattice of periods of a single layer, so when Γ and Γ share a common sublattice of finite index. However, with each layer added, the common sublattice gets sparser, and . Consequently, a space-filling tiling built from an incommensurate SCD tile cannot have any non-trivial periods, and hence is non-periodic.
In general, an SCD tiling is not repetitive, even when this property is considered with respect to Euclidean motions, which is appropriate here. Repetitive SCD tilings can be obtained [24] if . For a repetitive tiling, the corresponding hull is again a compact set, and contains only congruent copies of a single SCD tiling and limits of convergent sequences of congruent copies. This construction leaves no freedom to generate non-trivial periods, which implies the following result according to Definition 1.
Proposition 3
Consider a repetitive, incommensurate SCD tiling, and let Λ be a Delone representative of its MLD class. Then, Λ is aperiodic. ☐
Clearly, one then also calls the corresponding tiling itself aperiodic, after the obvious extension of our above definitions to tilings and (more generally) to patterns; see [12] for details. Consequently, the rhombic Penrose tiling is aperiodic, as is the Ammann–Beenker tiling (and many others).
The SCD tile is an example of an aperiodic prototile set, a term frequently met in the literature; compare [2]. This refers to a (usually finite) set of prototiles (possibly with markers) which admit space-filling tilings, but only non-periodic ones. An example of an aperiodic prototile set is the two decorated Penrose rhombuses of Figure 6, with the imposed local rules (or matching rules) that arrows on adjacent edges have to match (and the tiling has to be face to face). Note that the two “naked” Penrose rhombuses (without arrow decorations) fail to form an aperiodic set (because they are obviously compatible with periodic tilings), while the decorated versions of Figure 6 do the job, via these arrow matching rules [2], in the sense that any space-filling tiling of the plane that obeys the arrow matching rules is MLD with the Penrose tiling of Figure 4. Note that in any infinite rhombic Penrose tiling, the arrow decorations of the edges can be reconstructed from the undecorated version in a local fashion, so the decorated and undecorated tilings are indeed MLD.
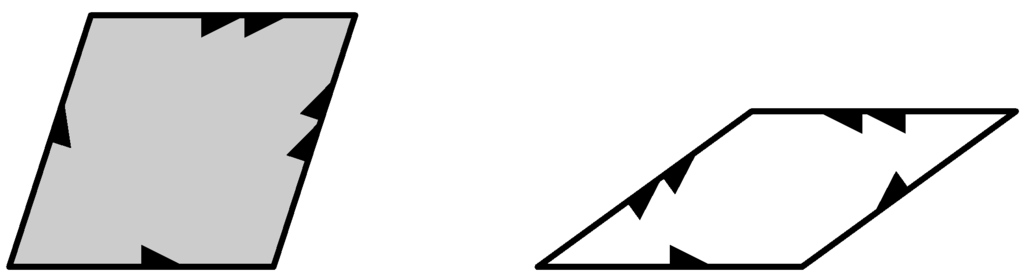
Figure 6.
Aperiodic prototile set for the rhombic Penrose tiling.
This property is not met by most of the other tilings of the aperiodic tiling zoo, including the Ammann–Beenker tiling. The latter also possesses aperiodic local rules, which can be realised as additional decorations, but these cannot be locally reconstructed from the undecorated tiling (while removing the additional decorations clearly provides a local rule in the converse direction). In that case, the decorated and undecorated tilings form different MLD classes; see [26] for a proof of this statement.
Given an aperiodic prototile set, all admissible space-filling tilings together form a space , wherefore our above notion of aperiodicity fits this situation as well. However, note that a tiling can be aperiodic in our setting without emerging from an aperiodic prototile set, and the undecorated Ammann–Beenker tiling is an example (as are any one-dimensional aperiodic tilings, since aperiodicity cannot be enforced by local rules in one dimension). Note that, for the Ammann–Beenker tiling, an aperiodic prototile set with additional markings exist [2], yielding the decorated Ammann–Beenker tilings from which the undecorated Ammann–Beenker tilings can be locally derived (by removing the additional markings), but not vice versa, as the additional markings cannot be locally recovered. A similar result holds more generally for inflation tilings [27], in the sense that there is an, in principle, constructive method to add local information to obtain an aperiodic prototile set; however, this usually leads to a much larger number of prototiles and is thus not used in practice.
As this discussion shows, the meaning of “aperiodicity” depends on the context, but our main point here is that the notion built on the LI class (rather than on an individual tiling or Delone set) is consistent.
Returning to the SCD tiling, the result of Proposition 3 is perhaps not entirely satisfactory, since an individual SCD tiling of this type may still possess a symmetry in the form of a screw axis. Even though the tiling admits no non-trivial translation symmetry, its symmetry group thus contains an infinite subgroup. The following definition introduces a stronger notion that separates such structures from examples like the Ammann–Beenker or Penrose tilings considered above, where the remaining symmetry groups are always finite.
Definition 2
A locally finite point set is called strongly aperiodic when it is aperiodic and when the individual symmetry group of each element of is a finite group.
With this notion, repetitive incommensurate SCD tilings are aperiodic, but not strongly aperiodic. Note that it is possible to have strong aperiodicity in the presence of continuous symmetries of the hull. An example is provided by the pinwheel tiling [28]. This is a tiling of the plane with a single triangular prototile (and its reflected version), defined by the inflation rule shown in the left panel of Figure 7, where the dots indicate a possible choice of representative (or control) points for an MLD Delone set [29]. The reflected tile is inflated using the reflected rule. The inflation rule introduces an angle which is incommensurate with π, so a “new" direction is introduced in each inflation step. Thus a fixed point tiling shows complete circular symmetry (while and individual tiling has at most a reflection symmetry) and as a consequence has circularly symmetric diffraction [29,30] (although a complete description of the diffraction measure is still lacking). A small patch of a pinwheel tiling is shown in the right panel of Figure 7. Various generalisation of pinwheel tilings exist [31], including higher-dimensional “quaquaversal" tilings [32]; see also [33] (Chapter 4.3).
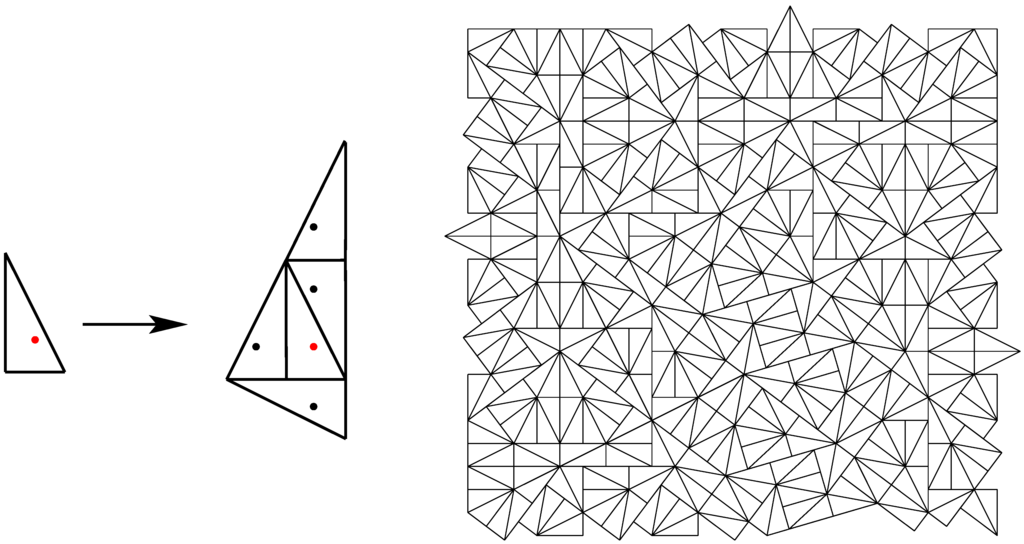
Figure 7.
Inflation rule (left) and patch (right) of the pinwheel tiling. The prototiles are right triangles with side length 1, 2 and . The dots represent control points of an equivalent Delone set. Starting from a single triangle with the control point in the origin leads to a fixed point tiling with circular symmetry.
6. Probabilistic Extensions and Outlook
The notion of a hull is an example of an ensemble of point sets, which is a well-known concept in statistical physics, too. For instance, consider the (discrete) ensemble of all subsets of (which can later be extended to a continuous ensemble by translations). This ensemble can be identified with the compact set and may be considered as a model for a lattice gas. In ergodic theory, this is known as the full shift space [34]. Note that is the orbit closure (under the action of ) of a typical element of , but not of every element. More precisely, there exists a probability measure μ (in fact, more than one) on that quantifies this statement in a certain way. One possibility is conveniently described via the “obvious" Bernoulli measure on . For , the latter is defined via the measure of cylinder sets, giving probability p for 1 (occupied) and for 0 (empty) per site; see [34] for details on the construction. Any such measure is -invariant by construction. Consequently, one obtains a measure-theoretic dynamical system .
In such a dynamical system, μ-almost all elements are non-periodic, while also contains lots of periodic or even crystallographic elements (such as the completely occupied lattice). However, all periodic elements together are still a subset of of measure 0. This motivates the following probabilistic counterpart of Definition 1.
Definition 3
A measure-theoretic dynamical system is called statistically (or metrically) aperiodic when the subset of elements of with non-trivial periods is a null set for the measure μ.
The term “metric" is often used in number theory or dynamical systems theory to refer to a situation where certain properties hold almost surely relative to a reference measure.
Returning to our example from above, one can show that the corresponding hull admits only one invariant probability measure. This has support on and hence gives no weight at all to the subset . This means that, in the probabilistic setting, the dynamical systems point of view tells us that Λ should be considered as an essentially periodic system, and not as a non-periodic one—quite in agreement with the physical intuition about the role of a single defect in an otherwise periodic structure.
It is clear that one can use this probabilistic setting to also extend the notion of symmetry, then often referred to as statistical symmetry. There are several possible variants of it. For any given Delone set with well-defined patch frequencies, one could speak of a statistical rotation or reflection symmetry when the image of each patch of the set occurs with the same frequency. For instance, each Penrose point set from above has statistical symmetry in this sense. This coincides with the symmetry of the LI class, because the latter is closed and uniquely ergodic as a dynamical system [23] under the action of .
A larger class would comprise equilibrium systems, which essentially are ensembles together with a translation invariant Gibbs measure; see [35] for a systematic exposition. Such systems, and probabilistic methods in general, are presently receiving growing attention, both theoretically and practically; see [16] and references therein. It is thus desirable and necessary to further extend the classic notions of crystallography to this viewpoint. We believe that this will be vital for a better understanding of important stochastic system such as random tilings or disordered structures.
Acknowledgment
This work was supported by the German Research Council (DFG), within the CRC 701.
References
- Schwarzenberger, R.L.E. N-Dimensional Crystallography; Pitman: London, UK, 1980. [Google Scholar]
- Grünbaum, B.; Shephard, G.C. Tilings and Patterns; Freeman: New York, NY, USA, 1987. [Google Scholar]
- Directions in Mathematical Quasicrystals; Baake, M.; Moody, R.V (Eds.) CRM Monograph Series; AMS: Providence, RI, USA, 2000.
- Quasicrystals and Discrete Geometry; Patera, J. (Ed.) Fields Institute Monographs; AMS: Providence, RI, USA, 1998.
- Baake, M. A guide to mathematical quasicrystals. In Quasicrystals—An Introduction to Structure, Physical Properties and Applications; Suck, J.-B., Schreiber, M., Häussler, P., Eds.; Springer: Berlin, Germany, 2002; pp. 17–48. [Google Scholar]
- Baake, M.; Schlottmann, M.; Jarvis, P.D. Quasiperiodic patterns with tenfold symmetry and equivalence with respect to local derivability. J. Phys. A: Math. Gen. 1991, 24, 4637–4654. [Google Scholar] [CrossRef]
- Lagarias, J.C. Geometric models for quasicrystals I. Delone sets of finite type. Discrete Comput. Geom. 1999, 21, 161–191. [Google Scholar] [CrossRef]
- Shechtman, D.; Blech, I.; Gratias, D.; Cahn, J.W. Metallic phase with long-range orientational order and no translational symmetry. Phys. Rev. Lett. 1984, 53, 1951–1953. [Google Scholar] [CrossRef]
- Brown, H.; Bülow, R.; Neubüser, J.; Wondratschek, H.; Zassenhaus, H. Crystallographic Groups of Four-dimensional Space; Wiley: New York, NY, USA, 1978. [Google Scholar]
- Humphreys, J.E. Reflection Groups and Coxeter Groups, 2nd ed.; Cambridge University Press: Cambridge, UK, 1992. [Google Scholar]
- Chen, L.; Moody, R.V.; Patera, J. Non-crystallographic root systems. In Quasicrystals and Discrete Geometry; Patera, J., Ed.; Fields Institute Monographs; AMS: Providence, RI, USA, 1998; pp. 135–178. [Google Scholar]
- Baake, M.; Grimm, U. Theory of Aperiodic Order: A Mathematical Invitation; Cambridge University Press: Cambridge, UK, in preparation.
- Ammann, R.; Grünbaum, B.; Shephard, G.C. Aperiodic tiles. Discrete Comput. Geom. 1992, 8, 1–25. [Google Scholar] [CrossRef]
- Lifshitz, R. The symmetry of quasiperiodic crystals. Physica A 1996, 232, 633–647. [Google Scholar] [CrossRef]
- Baake, M.; Grimm, U. Kinematic diffraction from a mathematical viewpoint. Z. Kristallogr. 2011, 226, 711–725. [Google Scholar] [CrossRef]
- Baake, M.; Grimm, U. Mathematical diffraction of aperiodic structures. Chem. Soc. Rev. 2012, 41, 6821–6843. [Google Scholar] [CrossRef] [PubMed]
- Baake, M.; Lenz, D. Dynamical systems on translation bounded measures: Pure point dynamical and diffraction spectra. Ergod. Theory Dyn. Syst. 2004, 24, 1867–1893. [Google Scholar] [CrossRef]
- Radin, C.; Wolff, M. Space tilings and local isomorphism. Geom. Dedicata 1992, 42, 355–360. [Google Scholar] [CrossRef]
- Solomyak, B. Spectrum of dynamical systems arising from Delone sets. In Quasicrystals and Discrete Geometry; Patera, J., Ed.; Fields Institute Monographs; AMS: Providence, RI, USA, 1998; pp. 265–275. [Google Scholar]
- Schlottmann, M. Generalised model sets and dynamical systems. In Directions in Mathematical Quasicrystals; Baake, M., Moody, R.V., Eds.; CRM Monograph Series; AMS: Providence, RI, USA, 2000; pp. 143–159. [Google Scholar]
- Bellissard, J.; Herrmann, D.J.L.; Zarrouati, M. Hulls of aperiodic solids and gap labeling theorems. In Directions in Mathematical Quasicrystals; Baake, M., Moody, R.V., Eds.; CRM Monograph Series; AMS: Providence, RI, USA, 2000; pp. 207–258. [Google Scholar]
- Sadun, L. Topology of Tiling Spaces; AMS: Providence, RI, USA, 2008. [Google Scholar]
- Robinson, E.A. The dynamical properties of Penrose tilings. Trans. Amer. Math. Soc. 1996, 348, 4447–4464. [Google Scholar] [CrossRef]
- Baake, M.; Frettlöh, D. SCD patterns have singular diffraction. J. Math. Phys. 2005, 46, 033510:1-10. [Google Scholar] [CrossRef]
- Danzer, L. A family of 3D-spacefillers not permitting any periodic or quasiperiodic tiling. In Aperiodic ’94; Chapuis, G., Paciorek, W., Eds.; World Scientific: Singapore, 1995; pp. 11–17. [Google Scholar]
- Gähler, F. Matching rules for quasicrystals: The composition-decomposition method. J. Non-Cryst. Solids 1993, 153–154, 160–164. [Google Scholar] [CrossRef]
- Goodman-Strauss, C. Matching rules and substitution tilings. Ann. Math. 1998, 147, 181–223. [Google Scholar] [CrossRef]
- Radin, C. The pinwheel tilings of the plane. Ann. Math. 1994, 139, 661–702. [Google Scholar] [CrossRef]
- Baake, M.; Frettlöh, D.; Grimm, U. A radial analogue of Poisson’s summation formula with applications to powder diffraction and pinwheel patterns. J. Geom. Phys. 2007, 57, 1331–1343. [Google Scholar] [CrossRef]
- Moody, R.V.; Postnikoff, D.; Strungaru, N. Circular symmetry of pinwheel diffraction. Ann. Henri Poincaré 2006, 7, 711–730. [Google Scholar] [CrossRef]
- Frettlöh, D. Substitution tilings with statistical circular symmetry. Eur. J. Combin. 2008, 29, 1881–1893. [Google Scholar] [CrossRef]
- Conway, J.H.; Radin, C. Quaquaversal tilings and rotations. Invent. Math. 1998, 132, 179–188. [Google Scholar] [CrossRef]
- Radin, C. Miles of Tiles; AMS: Providence, RI, USA, 1999. [Google Scholar]
- Walters, P. An Introduction to Ergodic Theory; reprint; Springer: New York, NY, USA, 2000. [Google Scholar]
- Georgii, H.-O. Gibbs Measures and Phase Transitions, 2nd ed.; de Gruyter: Berlin, Germany, 2011. [Google Scholar]
© 2012 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license ( http://creativecommons.org/licenses/by/3.0/).