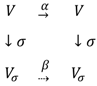1. Introduction
The concept of hidden symmetries of an object was introduced by Weyl [
1]. Underlying this is the notion that if
X is an
H-set, where
H is a symmetry group (the group of
obvious symmetries) acting on
X, additional
hidden symmetries associated with
X may correspond to elements of a larger group which also acts upon
X and contains
H as a subgroup. Sophisticated approaches based upon Weyl’s concept for finding hidden symmetries in physical systems have found application in solving and understanding a variety of problems of scientific interest (e.g., [
2,
3,
4,
5]), including numerous applications in computer science (see, for example, the survey [
6] and the monograph [
7]).
The primary objective of this paper is to show that each element
σ in the normalizer of the automorphism group
Aut(
G) of a simple graph
G with labeled vertex set
V is an
Aut(
G) invariant isomorphism between
G and the graph obtained from
G by the
σ relabeling of
V (
i.e.,
σ is a
hidden permutation symmetry of
G). The remainder of this paper is organized as follows: the relevant topics in graph theory and group theory are summarized in the next section (for additional depth and clarification the reader is invited to consult such standard texts as [
8] and [
9]). The hidden permutation symmetries of a simple vertex labeled graph
G are identified in
Section 3. A simple example is presented in
Section 4 to illustrate the theory. Closing remarks comprise the final section of this paper.
2. Preliminaries
A simple graph G is the pair G = (V, E), where V is a finite set of at least two vertices and the edge set E is either a set of doubleton subsets of V or the empty set ∅. If {u, v}∈ E, then u and v are adjacent in G. The order of a graph G is the cardinality |V| of V, |E| is its size, and G is a (|V|, |E|) graph. G is vertex labeled when V = {1,2,3,…,n}. A labeled graph which is relabeled by a permutation σ of it vertices is the graph where vertex i is relabeled as σ(i). The complement Gc of G is the graph with vertex set V and edge set Ec = {{u, v}, u, v ∈ V: {u, v}∉ E}. Graph G1 = (V1, E1) is isomorphic to graph G2 = (V2, E2) if there is a bijection φ : V1→ V2 such that {u, v}∈ E1 if and only if {φ(u), φ(v)}∈ E2. Thus, a graph isomorphism preserves adjacency. The bijection φ is the isomorphism between G1 and G2 and the associated graph isomorphism is denoted φ : G1→ G2.
An automorphism of G is an isomorphism of G with itself. The set of all automorphisms of G under the operation “composition of functions” forms the automorphism (or symmetry) group Aut(G) of G. When G is vertex labeled, then Aut(G) is a subgroup of the symmetric group SV of all permutations of V, denoted Aut(G) ⊂ SV. Furthermore, Aut(G) = Aut(Gc) and if G1 and G2 are isomorphic graphs, then Aut(G1) is isomorphic to Aut(G2), denoted Aut(G1) ~ Aut(G2).
The order of a group X is |X| and the order of x ∈ X is the least positive integer m such that xm = e, where e is the identity element in X. If X ⊂ Y and yXy−1 = X for every y ∈ Y, then X is a normal subgroup of Y, denoted X ⊲ Y. Here y−1 ∈ Y is the inverse of y. The normalizer N(Aut(G)) of Aut(G) in SV is the group defined by
and is the largest subgroup in SV for which Aut(G) ⊲ N(Aut(G)).
3. Hidden Symmetries of G
The automorphisms of the symmetry group Aut(G) of G are the obvious symmetries of G. The objective of this section is to show that each σ ∈ N(Aut(G)) is a hidden permutation symmetry of G—i.e., it is an Aut(G) invariant graph isomorphism between G and the graph obtained from G by the application of σ to G’s vertex labels (thus, σ ∈ Aut(G) is both a G automorphism and a hidden permutation symmetry of G). The next two lemmas are required to prove this.
Lemma 3.1 Let G = (V, E) be a simple vertex labeled graph. If σ ∈ SV and Gσ is the graph obtained by relabeling the vertices of G as prescribed by σ, then σ : G → Gσ is an isomorphism.
Proof. The relabeling of G’s vertices is specified by the permutation σ : V → V so that the associated relabeled edges are the set Eσ = {{σ(i), σ(j)}: {i, j} ∈ E}. Now let Vσ = V, define Gσ = (Vσ, Eσ), and observe that σ : V → Vσ is a bijection with the property that {i, j} ∈ E if and only if {σ(i), σ(j)} ∈ Eσ. Thus, σ : G → Gσ is an isomorphism.
Lemma 3.2 Let G = (V, E) be a simple vertex labeled graph, σ ∈ SV, and Gσ = (Vσ, Eσ) be the graph obtained by the σ relabeling of G’s vertices. If α ∈ Aut(G), then σασ −1∈ Aut(Gσ).
Proof. Since σ : G → Gσ is an isomorphism (Lemma 3.1), then so is σ −1: Gσ → G and diagram (2) commutes, where “⇢” denotes that the diagram is completed by the map β = σασ −1. But β is an isomorphism because it is a composition of the isomorphisms σ, α, and σ −1. Therefore, β = σασ −1∈ Aut(Gσ) since it is the isomorphism β : Gσ → Gσ.
Theorem 3.3 (Hidden Permutation Symmetries) Let G = (V, E) be a simple vertex labeled graph and Gσ be the graph obtained by the σ relabeling of G’s vertices. If σ ∈ N(Aut(G)), then σ : G → Gσ is an isomorphism for which Aut(Gσ) = Aut(G).
Proof. The fact that σ : G → Gσ is an isomorphism is established by Lemma 3.1. Recall from Lemma 3.2 that—since σ ∈ N(Aut(G)) ⊂ SV—for each α ∈ Aut(G) there is a distinct β = σασ −1 ∈ Aut(Gσ). However, because σ ∈ N(Aut(G)), then by definition (1) it is also the case that β ∈ Aut(G) so that Aut(Gσ) ⊆ Aut(G). Furthermore, β ∈ Aut(G) implies β = σασ −1 for some α ∈ Aut(G) and σ ∈ N(Aut(G)). Consequently, β ∈ Aut(Gσ) so that Aut(G) ⊆ Aut(Gσ). Thus, Aut(Gσ) = Aut(G).
Note that in general Aut(Gσ) ~ Aut(G) when σ ∈ SV. However, when σ ∈ N(Aut(G)) the group isomorphism is the identity map.
Corollary 3.4 σ ∈ N(Aut(G)) is a hidden permutation symmetry for Gc.
Proof. Since Aut(Gc) = Aut(G), then it must be the case that N(Aut(Gc)) = N(Aut(G)) so that σ ∈ N(Aut(G)) if and only if σ ∈ N(Aut(Gc)). It follows from Theorem 3.3 that σ : Gc→ Gcσ is an isomorphism for which Aut(Gcσ) = Aut(Gc).
4. Example: Hidden Symmetries of a Simple Vertex Labeled (4, 5) Graph
Let G = (V, E), where V = {1,2,3,4} and E = {{1,2}, {2,3}, {3,4}, {1,4}, {2,4}}.
4.1. The Automorphism and Normalizer Groups for G
By inspection it is found that
where
—when expressed in Cayley cycle notation—
i = (1)(2)(3)(4), α1 = (13)(2)(4), α2 = (24)(1)(3), and
α3 = (13)(24) (here,
i is clearly the group identity element). The Cayley table for
Aut(G) is easily determined from these and is given by
Table 1.
Table 1.
The Cayley table for Aut(G).
Table 1.
The Cayley table for Aut(G).
| i | α1 | α2 | α3 |
|---|
| i | i | α1 | α2 | α3 |
| α1 | α1 | i | α3 | α2 |
| α2 | α2 | α3 | i | α1 |
| α3 | α3 | α2 | α1 | i |
It is interesting to note that up to (group) isomorphism there are only two groups of order four—the cyclic group
Z4 and the
Viergruppe V of Felix Klein. Inspection of
Table 1 reveals that
Aut(G) ≁
Z4 because there is no fourth order element in
Aut(G). Thus, it must be the case that
Aut(G)∼
V (this is further corroborated from the table by the facts that
Aut(G) is an abelian group and that every
Aut(G) element is order two—which are properties of
V).
In order to find N(Aut(G)) it is necessary to apply definition Equation (1) to the elements of SV. Trial and error yields
where
σ1 = (1234), σ2 = (1432), σ3 = (14)(23), and
σ4 = (12)(34). The Cayley table for
N(Aut(G)) is presented as
Table 2. As an aside—observe from
Table 2 that
N(Aut(G)) is a nonabelian group. Consequently,
N(Aut(G)) must be isomorphic to either the quaternion group
Q or the dihedral group
D4 since these are the only nonabelian groups of order eight. It is also seen from a closer examination of
Table 2 that
N(Aut(G)) is generated by
σ1 and
α1 which satisfy the relations
(σ1)4 = i, (α1)2 = i, and
α1σ1α1 = σ2 = σ1 −1. Since these are precisely the generators and relations that define
D4 then it must be the case that
N(Aut(G)) ∼
D4.
Table 2.
The Cayley table for N(Aut(G)).
Table 2.
The Cayley table for N(Aut(G)).
| i | α1 | α2 | α3 | σ1 | σ2 | σ3 | σ4 |
|---|
| i | i | α1 | α2 | α3 | σ1 | σ2 | σ3 | σ4 |
| α1 | α1 | i | α3 | α2 | σ3 | σ4 | σ1 | σ2 |
| α2 | α2 | α3 | i | α1 | σ4 | σ3 | σ2 | σ1 |
| α3 | α3 | α2 | α1 | i | σ2 | σ1 | σ4 | σ3 |
| σ1 | σ1 | σ4 | σ3 | σ2 | α3 | i | α1 | α2 |
| σ2 | σ2 | σ3 | σ4 | σ1 | i | α3 | α2 | α1 |
| σ3 | σ3 | σ2 | σ1 | σ4 | α2 | α1 | i | α3 |
| σ4 | σ4 | σ1 | σ2 | σ3 | α1 | α2 | α3 | i |
4.2. The Hidden Permutation Symmetries of G
In order to illustrate Theorem 3.3, first note that
i, α1, α2, and
α3 either fix vertex labels
2 and
4 or permutes them, whereas
σ1, σ2, σ3, and
σ4 relabel
2 and
4 as
1 and
3, or vice versa. Thus—as automorphisms—
i, α1, α2, and
α3 must preserve adjacency by mapping edge {
2,4} in
G to edge {
2,4} in the associated relabeled graphs and—as isomorphisms—
σ1, σ2, σ3, and σ
4 must preserve adjacency by mapping edge {
2,4} in
G to edge {
1,3} in the associated relabeled graphs. This is evidenced in
Table 3 which lists the
N(Aut(G)) image of each edge in
G in the associated relabeled graph. There the bold face first column lists the edges in
G and the bold face first row lists the elements of
N(Aut(G)). The table entries are the
N(Aut(G)) images of
G edges in the corresponding relabeled graphs. For example, the image of edge {
2,3} in
G under the map
α3 is the edge {
1,4} in the graph with vertices relabeled by
α3. It is obvious from this table that
σ : G → Gσ, σ ∈ N(Aut(G)), is an isomorphism because {
i,j}
∈ E if and only if
{σ(i),σ(j)} ∈ Eσ (
i.e., σ : V → Vσ = V is an edge preserving bijection).
Table 3.
The N(Aut(G)) images of E.
Table 3.
The N(Aut(G)) images of E.
| i | α1 | α2 | α3 | σ1 | σ2 | σ3 | σ4 |
|---|
| {1,2} | {1,2} | {2,3} | {1,4} | {3,4} | {2,3} | {1,4} | {3,4} | {1,2} |
| {2,3} | {2,3} | {1,2} | {3,4} | {1,4} | {3,4} | {1,2} | {2,3} | {1,4} |
| {3,4} | {3,4} | {1,4} | {2,3} | {1,2} | {1,4} | {2,3} | {1,2} | {3,4} |
| {1,4} | {1,4} | {3,4} | {1,2} | {2,3} | {1,2} | {3,4} | {1,4} | {2,3} |
| {2,4} | {2,4} | {2,4} | {2,4} | {2,4} | {1,3} | {1,3} | {1,3} | {1,3} |
To see that
Aut(G) is the automorphism group for each graph relabeled by
σ ∈ {σ1, σ2, σ3, σ4} = N(Aut(G)) - Aut(G) (
i.e., that each such isomorphism
σ : G → Gσ is
Aut(G) invariant), observe that the automorphisms of
Aut(G) are the only bijective vertex maps which preserve adjacency in each
Gσ and map edge {
1,3} in each
Gσ to itself. For example, the set of edges in the graph relabeled by
σ2 (the sixth column in
Table 3) is bijectively mapped in an adjacency preserving manner onto itself by
α2 ∈ Aut(G) according to the mappings given by (3) (the associated vertex maps appear in parentheses). Similar results also hold for
i, α1, and
α3 so that
Aut(G) is the automorphism group for this
σ2 relabeled graph,
i.e.,
Aut(G) is invariant under the isomorphism
σ2.