Self-Dual, Self-Petrie Covers of Regular Polyhedra

Abstract

The well-known duality and Petrie duality operations on maps have natural analogs for abstract polyhedra. Regular polyhedra that are invariant under both operations have a high degree of both “external” and “internal” symmetry. The mixing operation provides a natural way to build the minimal common cover of two polyhedra, and by mixing a regular polyhedron with its five other images under the duality operations, we are able to construct the minimal self-dual, self-Petrie cover of a regular polyhedron. Determining the full structure of these covers is challenging and generally requires that we use some of the standard algorithms in combinatorial group theory. However, we are able to develop criteria that sometimes yield the full structure without explicit calculations. Using these criteria and other interesting methods, we then calculate the size of the self-dual, self-Petrie covers of several polyhedra, including the regular convex polyhedra.

1. Introduction

Abstract polyhedra are partially-ordered sets that generalize the face-lattices of convex polyhedra. They are closely related to maps on surfaces (i.e., 2-cell decompositions of surfaces), and indeed, every abstract polyhedron has a natural realization as such a map. The regular polyhedra are the most extensively studied. These are the polyhedra such that the automorphism group acts transitively on the flags (which consist of a vertex, an edge, and a face that are all mutually incident). There is a natural way to build a regular polyhedron from a finitely generated group satisfying certain properties, yielding a bijection between (isomorphism classes of) regular polyhedra and such groups. The ability to view a regular polyhedron as either a map on a surface or as a group has fostered the development of a rich theory.

The well-known duality and Petrie duality operations on maps can be easily applied to polyhedra, though in some rare cases, the Petrie dual of a polyhedron is not a polyhedron. A regular polyhedron that is invariant under both operations has a high degree of “external” symmetry in addition to the “internal” symmetry that regularity measures. In [1], the authors describe a way to build a self-dual, self-Petrie cover of a regular map. Using a similar construction, we show how to build a self-dual, self-Petrie cover of a regular polyhedron. Determining the local structure of the cover is simple. However, finding a presentation for the automorphism group of the cover is generally infeasible. Therefore, our goal is to develop criteria that give us information about the cover without requiring direct calculation.

We start by giving some background on abstract polyhedra, regularity, and the duality operations in Section 2. In Section 3, we present the mixing operation for regular polyhedra and show how to use it to construct self-dual, self-Petrie covers. We then show how to calculate the size of these covers in certain cases. Finally, in Section 4 we calculate the size of the self-dual, self-Petrie covers of several polyhedra, including the regular convex polyhedra.

2. Abstract Polyhedra

Let $\mathcal{P}$ be a ranked partially ordered set of vertices, edges, and faces, which have rank 0, 1, and 2, respectively. If $F\le G$ or $G\le F$, we say that F and G are incident. A flag of $\mathcal{P}$ is a maximal chain, and two flags are adjacent if they differ in exactly one element. We say that $\mathcal{P}$ is an (abstract) polyhedron if it satisfies the following properties:

• Each flag of $\mathcal{P}$ consists of a vertex, an edge, and a face.
• Each edge is incident on exactly two vertices and two faces.
• If F is a vertex and G is a face such that $F\le G$, then there are exactly two edges that are incident to both F and G.
• $\mathcal{P}$ is strongly flag-connected, meaning that if $\mathsf{\Phi }$ and $\mathsf{\Psi }$ are two flags of $\mathcal{P}$, then there is a sequence of flags $\mathsf{\Phi }={\mathsf{\Phi }}_0,{\mathsf{\Phi }}_1,\dots ,{\mathsf{\Phi }}_k=\mathsf{\Psi }$ such that for $i=0,\dots ,k-1$, the flags ${\mathsf{\Phi }}_i$ and ${\mathsf{\Phi }}_{i+1}$ are adjacent, and each ${\mathsf{\Phi }}_i$ contains $\mathsf{\Phi }\cap \mathsf{\Psi }$.

As a consequence of the second and third properties above, every flag $\mathsf{\Phi }$ has a unique flag ${\mathsf{\Phi }}^i$ that differs from $\mathsf{\Phi }$ only in its element of rank i. We say that ${\mathsf{\Phi }}^i$ is i-adjacent to $\mathsf{\Phi }$.

For polyhedra $\mathcal{P}$ and $\mathcal{Q}$, an isomorphism from $\mathcal{P}$ to $\mathcal{Q}$ is an incidence- and rank-preserving bijection, and an isomorphism from $\mathcal{P}$ to itself is an automorphism. We denote the group of all automorphisms of $\mathcal{P}$ by $\mathsf{\Gamma }\left(\mathcal{P}\right)$. There is a natural action of $\mathsf{\Gamma }\left(\mathcal{P}\right)$ on the flags of $\mathcal{P}$, and we say that $\mathcal{P}$ is regular if this action is transitive. The faces of a regular polyhedron all have the same number of sides, and the vertices all have the same valency. In general, we say that a polyhedron is of type $\{p,q\}$ if every face is a p-gon and every vertex is q-valent.

Given a regular polyhedron $\mathcal{P}$, fix a base flag$\mathsf{\Phi }$. Then the automorphism group $\mathsf{\Gamma }\left(\mathcal{P}\right)$ is generated by involutions ${\rho }_0,$${\rho }_1,$ and ${\rho }_2$, where ${\rho }_i$ maps the base flag $\mathsf{\Phi }$ to ${\mathsf{\Phi }}^i$. This completely determines the action of each ${\rho }_i$ on all flags, since for any automorphism $\phi$ and flag $\mathsf{\Psi }$,

$$\left({\mathsf{\Psi }}^i\right)\phi ={\left(\mathsf{\Psi }\phi \right)}^i$$

If $\mathcal{P}$ is of type $\{p,q\}$, then these generators satisfy (at least) the relations

$${\left({\rho }_0{\rho }_1\right)}^p={\left({\rho }_0{\rho }_2\right)}^2={\left({\rho }_1{\rho }_2\right)}^q=ϵ$$

If these are the only defining relations, then we denote $\mathcal{P}$ by $\{p,q\}$, and $\mathsf{\Gamma }\left(\mathcal{P}\right)$ is a Coxeter group, denoted $[p,q]$. We note that whenever $\mathcal{P}$ is the face-lattice of a regular convex polyhedron, then its denotation is the same as the usual Schläfli symbol for that polyhedron (see [2]).

For $I\subseteq \{0,1,2\}$ and a group $\mathsf{\Gamma }=\langle {\rho }_0,{\rho }_1,{\rho }_2\rangle$, we define ${\mathsf{\Gamma }}_I:=\langle {\rho }_i\mid i\in I\rangle$. The strong flag-connectivity of polyhedra induces the following intersection property in the group:

$${\mathsf{\Gamma }}_I\cap {\mathsf{\Gamma }}_J={\mathsf{\Gamma }}_{I\cap J}\mathrm{for}I,J\subseteq \{0,1,2\}$$

(1)

In general, if $\mathsf{\Gamma }=\langle {\rho }_0,{\rho }_1,{\rho }_2\rangle$ is a group such that each ${\rho }_i$ has order 2 and such that ${\left({\rho }_0{\rho }_2\right)}^2=ϵ$, then we say that Γ is a string group generated by involutions on 3 generators (or sggi). If Γ also satisfies the intersection property given above, then we call Γ a string C-group on 3 generators. There is a natural way of building a regular polyhedron $\mathcal{P}\left(\mathsf{\Gamma }\right)$ from a string C-group Γ such that $\mathsf{\Gamma }\left(\mathcal{P}\right(\mathsf{\Gamma }\left)\right)=$ Γ [3] (Theorem 2E11). Therefore, we get a one-to-one correspondence between regular polyhedra and string C-groups on 3 specified generators.

Let $\mathcal{P}$ and $\mathcal{Q}$ be two polyhedra (not necessarily regular). A function $\gamma :\mathcal{P}\to \mathcal{Q}$ is called a covering if it preserves adjacency of flags, incidence, and rank; then $\gamma$ is necessarily surjective, by the flag-connectedness of $\mathcal{Q}$. We say that $\mathcal{P}$ covers $\mathcal{Q}$ if there exists a covering $\gamma :\mathcal{P}\to \mathcal{Q}$. If $\mathcal{P}$ and $\mathcal{Q}$ are both regular polyhedra, then their automorphism groups are both quotients of

$$W:=[\infty ,\infty ]=\langle {\rho }_0,{\rho }_1,{\rho }_2\mid {\rho }_0^2={\rho }_1^2={\rho }_2^2={\left({\rho }_0{\rho }_2\right)}^2=ϵ\rangle$$

Therefore there are normal subgroups M and K of W such that $\mathsf{\Gamma }\left(\mathcal{P}\right)=W/M$ and $\mathsf{\Gamma }\left(\mathcal{Q}\right)=W/K$. Then $\mathcal{P}$ covers $\mathcal{Q}$ if and only if $M\le K$.

2.1. Duality Operations

There are two well-known duality operations on maps on surfaces, described in [1] and earlier articles. These naturally give rise to corresponding operations on polyhedra. The first is known simply as duality, and the dual of $\mathcal{P}$ (denoted ${\mathcal{P}}^{\delta }$) is obtained from $\mathcal{P}$ by reversing the partial order. If a polyhedron is isomorphic to its dual, then it is called self-dual.

In order to formulate the second duality operation, we need to define the Petrie polygons of a polyhedron. Consider a walk along edges of the polyhedron such that at each successive step, we alternate between taking the first exit on the left and the first exit on the right. When we start with a finite polyhedron, such a walk will eventually take us to a vertex we have already visited, leaving in the same direction as we have before. This closed walk is one of the Petrie polygons of the polyhedron.

We can now describe the second duality operation. Given a polyhedron $\mathcal{P}$, its Petrie dual ${\mathcal{P}}^{\pi }$ consists of the same vertices and edges as $\mathcal{P}$, but its faces are the Petrie polygons of $\mathcal{P}$. Taking the Petrie dual of a polyhedron also forces the old faces to be the new Petrie polygons, so that ${\mathcal{P}}^{\pi \pi }\simeq \mathcal{P}$. If $\mathcal{P}$ is isomorphic to ${\mathcal{P}}^{\pi }$, then we say that $\mathcal{P}$ is self-Petrie.

Since Petrie polygons play a central role in this paper, we expand some of our earlier terminology. If $\mathcal{P}$ is a regular polyhedron, then its Petrie polygons all have the same length, and that length is the order of ${\rho }_0{\rho }_1{\rho }_2$ in $\mathsf{\Gamma }\left(\mathcal{P}\right)$. A regular polyhedron of type $\{p,q\}$ and with Petrie polygons of length r is also said to be of type ${\{p,q\}}_r$. If $\mathcal{P}$ is of type ${\{p,q\}}_r$ and it covers every other polyhedron of type ${\{p,q\}}_r$, then we call it the universal polyhedron of type ${\{p,q\}}_r$ and we denote it by ${\{p,q\}}_r$. The automorphism group of ${\{p,q\}}_r$ is denoted by ${[p,q]}_r$, and this group is the quotient of $[p,q]$ by the single extra relation ${\left({\rho }_0{\rho }_1{\rho }_2\right)}^r=ϵ$. We will also extend our notation and use ${[p,q]}_r$ for the group with presentation

$$\langle {\rho }_0,{\rho }_1,{\rho }_2\mid {\rho }_0^2={\rho }_1^2={\rho }_2^2={\left({\rho }_0{\rho }_1\right)}^p={\left({\rho }_0{\rho }_2\right)}^2={\left({\rho }_1{\rho }_2\right)}^q={\left({\rho }_0{\rho }_1{\rho }_2\right)}^r=ϵ\rangle$$

even when there is no universal polyhedron of type ${\{p,q\}}_r$.

The operations $\delta$ and $\pi$ form a group of order 6, isomorphic to $S_3$. A regular polyhedron that is self-dual and self-Petrie is invariant under all 6 operations; such a polyhedron must be of type ${\{n,n\}}_n$ for some $n\ge 2$. In general, if $\mathcal{P}$ is of type ${\{p,q\}}_r$, then ${\mathcal{P}}^{\delta }$ is of type ${\{q,p\}}_r$, and ${\mathcal{P}}^{\pi }$ is of type ${\{r,q\}}_p$. Furthermore, the dual and the Petrie dual of a universal polyhedron is again universal.

3. Mixing Polyhedra

The mixing construction on polyhedra is analogous to the join of two maps or hypermaps [4]. Using it, we can find the minimal common cover of two or more polyhedra, which will enable us to describe the self-dual, self-Petrie covers of regular polyhedra.

We begin by describing the mixing operation on groups (also called the parallel product in [5]). Let $\mathcal{P}$ and $\mathcal{Q}$ be regular polyhedra with $\mathsf{\Gamma }\left(\mathcal{P}\right)=\langle {\rho }_0,{\rho }_1,{\rho }_2\rangle$ and $\mathsf{\Gamma }\left(\mathcal{Q}\right)=\langle {\rho }_0^{\prime },{\rho }_1^{\prime },{\rho }_2^{\prime }\rangle$. Let ${\alpha }_i=({\rho }_i,{\rho }_i^{\prime })\in \mathsf{\Gamma }\left(\mathcal{P}\right)\times \mathsf{\Gamma }\left(\mathcal{Q}\right)$ for $i\in \{0,1,2\}$. Then we define the mix of $\mathsf{\Gamma }\left(\mathcal{P}\right)$ and $\mathsf{\Gamma }\left(\mathcal{Q}\right)$ to be the group

$$\mathsf{\Gamma }\left(\mathcal{P}\right)\diamond \mathsf{\Gamma }\left(\mathcal{Q}\right):=\langle {\alpha }_0,{\alpha }_1,{\alpha }_2\rangle$$

Note that the order of any word ${\alpha }_{i_1}\dots {\alpha }_{i_t}$ is the least common multiple of the orders of ${\rho }_{i_1}\dots {\rho }_{i_t}$ and ${\rho }_{i_1}^{\prime }\dots {\rho }_{i_t}^{\prime }$. In particular, each ${\alpha }_i$ is an involution, and ${\left({\alpha }_0{\alpha }_2\right)}^2=ϵ$. Therefore, $\mathsf{\Gamma }\left(\mathcal{P}\right)\diamond \mathsf{\Gamma }\left(\mathcal{Q}\right)$ is a string group generated by involutions. As we shall see, it also satisfies the intersection property (Equation (1)). Recall that ${\mathsf{\Gamma }}_I:=\langle {\rho }_i\mid i\in I\rangle$.

Proposition 3.1.

Let $\mathcal{P}$ and $\mathcal{Q}$ be regular polyhedra, and let $I,J\subseteq \{0,1,2\}$. Let $\mathsf{\Lambda }=\mathsf{\Gamma }\left(\mathcal{P}\right)$, $\Delta =\mathsf{\Gamma }\left(\mathcal{Q}\right)$, and $\mathsf{\Gamma }=\mathsf{\Lambda }\diamond \Delta$. Then ${\mathsf{\Gamma }}_I\cap {\mathsf{\Gamma }}_J\subseteq {\mathsf{\Lambda }}_{I\cap J}\times {\Delta }_{I\cap J}$.

Proof. 

Let $g\in {\mathsf{\Gamma }}_I\cap {\mathsf{\Gamma }}_J$, and write $g=(g_1,g_2)$. Then $g_1\in {\mathsf{\Lambda }}_I\cap {\mathsf{\Lambda }}_J$ and $g_2\in {\Delta }_I\cap {\Delta }_J$. Now, since $\mathcal{P}$ and $\mathcal{Q}$ are polyhedra, we have that ${\mathsf{\Lambda }}_I\cap {\mathsf{\Lambda }}_J={\mathsf{\Lambda }}_{I\cap J}$ and ${\Delta }_I\cap {\Delta }_J={\Delta }_{I\cap J}$. Therefore, $g\in {\mathsf{\Lambda }}_{I\cap J}\times {\Delta }_{I\cap J}$. □

Corollary 3.2.

Let $\mathcal{P}$ and $\mathcal{Q}$ be regular polyhedra. Let $\mathsf{\Lambda }=\mathsf{\Gamma }\left(\mathcal{P}\right)$, $\Delta =\mathsf{\Gamma }\left(\mathcal{Q}\right)$, and $\mathsf{\Gamma }=\mathsf{\Lambda }\diamond \Delta$. Then Γ satisfies the intersection property (Equation(1)).

Proof. 

Let $\mathsf{\Lambda }=\langle {\rho }_0,{\rho }_1,{\rho }_2\rangle$ and let $\Delta =\langle {\rho }_0^{\prime },{\rho }_1^{\prime },{\rho }_2^{\prime }\rangle$. Let $\mathsf{\Gamma }=\langle {\alpha }_0,{\alpha }_1,{\alpha }_2\rangle$. We need to show that for subsets I and J of $N=\{0,1,2\}$, ${\mathsf{\Gamma }}_I\cap {\mathsf{\Gamma }}_J\le {\mathsf{\Gamma }}_{I\cap J}$. If $I\cap J=\varnothing$, the claim follows immediately from Proposition 3.1. If $I\subseteq J$, the claim also clearly holds. The only remaining case is when $I=N\setminus \left\{i\right\}$ and $J=N\setminus \left\{j\right\}$ for $i\ne j$. We will prove the case $I=\{0,1\}$ and $J=\{1,2\}$; the other cases are similar. Now, from Proposition 3.1, we know that ${\mathsf{\Gamma }}_I\cap {\mathsf{\Gamma }}_J\subseteq \langle {\rho }_1\rangle \times \langle {\rho }_1^{\prime }\rangle$. We want to show that $({\rho }_1,ϵ)$ and $(ϵ,{\rho }_1^{\prime })$ are not in ${\mathsf{\Gamma }}_I\cap {\mathsf{\Gamma }}_J$. We have that ${\mathsf{\Lambda }}_I=\langle {\rho }_0,{\rho }_1\rangle$, which is a dihedral group. In particular, all relations of ${\mathsf{\Lambda }}_I$ have even length. The same is true of ${\Delta }_I$. Therefore, when we reduce a word $({\rho }_{i_1}\dots {\rho }_{i_k},{\rho }_{i_1}^{\prime }\dots {\rho }_{i_k}^{\prime })$ in ${\mathsf{\Gamma }}_I$, the length of each component must have the same parity. In particular, we cannot have $({\rho }_1,ϵ)\in {\mathsf{\Gamma }}_I$ or $(ϵ,{\rho }_1^{\prime })\in {\mathsf{\Gamma }}_I$. Therefore, ${\mathsf{\Gamma }}_I\cap {\mathsf{\Gamma }}_J\le \langle {\alpha }_1\rangle$, which is what we wanted to show. □

Since the group $\mathsf{\Gamma }\left(\mathcal{P}\right)\diamond \mathsf{\Gamma }\left(\mathcal{Q}\right)$ satisfies the intersection property, we can build a regular polyhedron from the group. We call this polyhedron the mix of $\mathcal{P}$ and $\mathcal{Q}$, and we denote it $\mathcal{P}\diamond \mathcal{Q}$. By construction, $\mathsf{\Gamma }(\mathcal{P}\diamond \mathcal{Q})=\mathsf{\Gamma }\left(\mathcal{P}\right)\diamond \mathsf{\Gamma }\left(\mathcal{Q}\right)$.

Note that whether we mix $\mathcal{P}$ and $\mathcal{Q}$ as regular polyhedra, or take their join as maps, we get the same structure. Therefore, Corollary 3.2 tells us that when we take the join of two maps that correspond to polyhedra, we get another map that corresponds to a polyhedron.

There is another way to describe the mix of $\mathsf{\Gamma }\left(\mathcal{P}\right)$ and $\mathsf{\Gamma }\left(\mathcal{Q}\right)$ using quotients of the group W, which was described in Section 2. Let $\mathcal{P}$ and $\mathcal{Q}$ be regular polyhedra with $\mathsf{\Gamma }\left(\mathcal{P}\right)=W/M$ and $\mathsf{\Gamma }\left(\mathcal{Q}\right)=W/K$. Then the homomorphism from W to $W/M\times W/K$, sending a word w to the pair of cosets $(wM,wK)$, has kernel $M\cap K$ and image $W/M\diamond W/K$. Thus we see that $\mathsf{\Gamma }\left(\mathcal{P}\right)\diamond \mathsf{\Gamma }\left(\mathcal{Q}\right)\simeq W/(M\cap K)$. Therefore, $\mathcal{P}\diamond \mathcal{Q}$ is the minimal regular polyhedron that covers both $\mathcal{P}$ and $\mathcal{Q}$.

Now we can describe how to construct the self-dual, self-Petrie cover of a polyhedron. Let $G=\langle \delta ,\pi \rangle$, the group of polyhedron operations generated by duality and Petrie duality, and let $\mathcal{P}$ be a regular polyhedron with $\mathsf{\Gamma }\left(\mathcal{P}\right)=W/M$. For any $\phi \in G$, define ${\mathcal{P}}^{\phi }$ to be the regular poset (usually a polyhedron) built from the group $W/\phi \left(M\right)$. Now consider

$${\mathcal{P}}^{\ast }:=\mathcal{P}\diamond {\mathcal{P}}^{\delta }\diamond {\mathcal{P}}^{\pi }\diamond {\mathcal{P}}^{\delta \pi }\diamond {\mathcal{P}}^{\pi \delta }\diamond {\mathcal{P}}^{\delta \pi \delta }$$

Then $\mathsf{\Gamma }\left({\mathcal{P}}^{\ast }\right)$ is the quotient of W by

$$M\cap \delta \left(M\right)\cap \pi \left(M\right)\cap \delta \pi \left(M\right)\cap \pi \delta \left(M\right)\cap \delta \pi \delta \left(M\right)$$

and since this subgroup is fixed by both $\delta$ and $\pi$, it follows that ${\mathcal{P}}^{\ast }$ is self-dual and self-Petrie. Now, if ${\mathcal{P}}^{\pi }$ and ${\mathcal{P}}^{\delta \pi }$ are both polyhedra, then Corollary 3.2 tells us that ${\mathcal{P}}^{\ast }$ is also a polyhedron. In the rare cases where ${\mathcal{P}}^{\pi }$ is not a polyhedron, we can use the “quotient criterion” [3, Theorem 2E17] to show that $\mathcal{P}\diamond {\mathcal{P}}^{\pi }$ is nevertheless a polyhedron, since the natural epimorphism from $\mathsf{\Gamma }\left(\mathcal{P}\right)\diamond \mathsf{\Gamma }\left({\mathcal{P}}^{\pi }\right)=\langle {\alpha }_0,{\alpha }_1,{\alpha }_2\rangle$ to $\mathsf{\Gamma }\left(\mathcal{P}\right)$ is one-to-one on the subgroup $\langle {\alpha }_1,{\alpha }_2\rangle$. In any case, ${\mathcal{P}}^{\ast }$ is the minimal regular, self-dual, self-Petrie polyhedron that covers $\mathcal{P}$.

If $\mathcal{P}$ is a regular polyhedron of type ${\{p,q\}}_r$, then ${\mathcal{P}}^{\ast }$ is of type ${\{n,n\}}_n$, where n is the least common multiple of p, q, and r. This gives us a full picture of the local structure of ${\mathcal{P}}^{\ast }$. Determining the global structure, such as the size, isomorphism type, and presentation of $\mathsf{\Gamma }\left({\mathcal{P}}^{\ast }\right)$, is much more challenging. With the tools presented so far, the only way we can determine $\mathsf{\Gamma }\left({\mathcal{P}}^{\ast }\right)$ is by looking at the intersection of six subgroups of W, or finding the diagonal subgroup of the direct product of six groups. Neither alternative is feasible in general.

There is another construction, dual to mixing, that helps us calculate the size of $\mathsf{\Gamma }\left(\mathcal{P}\right)\diamond \mathsf{\Gamma }\left(\mathcal{Q}\right)$. If $\mathsf{\Gamma }\left(\mathcal{P}\right)$ has presentation $\langle {\rho }_0,{\rho }_1,{\rho }_2\mid R\rangle$ and $\mathsf{\Gamma }\left(\mathcal{Q}\right)$ has presentation $\langle {\rho }_0^{\prime },{\rho }_1^{\prime },{\rho }_2^{\prime }\mid S\rangle$, then we define the comix of $\mathsf{\Gamma }\left(\mathcal{P}\right)$ and $\mathsf{\Gamma }\left(\mathcal{Q}\right)$, denoted $\mathsf{\Gamma }\left(\mathcal{P}\right)\square \mathsf{\Gamma }\left(\mathcal{Q}\right)$, to be the group with presentation

$$\langle {\rho }_0,{\rho }_0^{\prime },{\rho }_1,{\rho }_1^{\prime },{\rho }_2,{\rho }_2^{\prime }\mid R,S,{\rho }_0^{-1}{\rho }_0^{\prime },{\rho }_1^{-1}{\rho }_1^{\prime },{\rho }_2^{-1}{\rho }_2^{\prime }\rangle$$

Informally speaking, we can just add the relations from $\mathsf{\Gamma }\left(\mathcal{Q}\right)$ to those of $\mathsf{\Gamma }\left(\mathcal{P}\right)$, rewriting them to use ${\rho }_i$ in place of ${\rho }_i^{\prime }$. As a result, the order of any word ${\rho }_{i_1}\dots {\rho }_{i_t}$ in $\mathsf{\Gamma }\left(\mathcal{P}\right)\square \mathsf{\Gamma }\left(\mathcal{Q}\right)$ divides the order of the corresponding word in $\mathsf{\Gamma }\left(\mathcal{P}\right)$ and in $\mathsf{\Gamma }\left(\mathcal{Q}\right)$.

Like the mix of two groups, the comix has a natural interpretation in terms of quotients of W. In particular, if $\mathsf{\Gamma }\left(\mathcal{P}\right)=W/M$ and $\mathsf{\Gamma }\left(\mathcal{Q}\right)=W/K$, then $\mathsf{\Gamma }\left(\mathcal{P}\right)\square \mathsf{\Gamma }\left(\mathcal{Q}\right)=W/MK$. That is, $\mathsf{\Gamma }\left(\mathcal{P}\right)\square \mathsf{\Gamma }\left(\mathcal{Q}\right)$ is the maximal common quotient of $\mathsf{\Gamma }\left(\mathcal{P}\right)$ and $\mathsf{\Gamma }\left(\mathcal{Q}\right)$ (with respect to the natural covering maps).

Proposition 3.3.

Let $\mathcal{P}$ and $\mathcal{Q}$ be finite regular polyhedra. Then

$$\left|\mathsf{\Gamma }\right(\mathcal{P})\diamond \mathsf{\Gamma }(\mathcal{Q}\left)\right|·\left|\mathsf{\Gamma }\right(\mathcal{P})\square \mathsf{\Gamma }(\mathcal{Q}\left)\right|=\left|\right(\mathsf{\Gamma }\mathcal{P}\left)\right|·\left|\right(\mathsf{\Gamma }\mathcal{Q}\left)\right|$$

Furthermore, if $\mathsf{\Gamma }\left(\mathcal{P}\right)\square \mathsf{\Gamma }\left(\mathcal{Q}\right)$ is trivial, then $\mathsf{\Gamma }\left(\mathcal{P}\right)\diamond \mathsf{\Gamma }\left(\mathcal{Q}\right)=\mathsf{\Gamma }\left(\mathcal{P}\right)\times \mathsf{\Gamma }\left(\mathcal{Q}\right)$.

Proof. 

Let $\mathsf{\Gamma }\left(\mathcal{P}\right)=W/M$ and $\mathsf{\Gamma }\left(\mathcal{Q}\right)=W/K$. Then $\mathsf{\Gamma }\left(\mathcal{P}\right)\diamond \mathsf{\Gamma }\left(\mathcal{Q}\right)=W/(M\cap K)$ and $\mathsf{\Gamma }\left(\mathcal{P}\right)\square \mathsf{\Gamma }\left(\mathcal{Q}\right)=W/MK$. Let $f:\mathsf{\Gamma }\left(\mathcal{P}\right)\diamond \mathsf{\Gamma }\left(\mathcal{Q}\right)\to \mathsf{\Gamma }\left(\mathcal{P}\right)$ and $g:\mathsf{\Gamma }\left(\mathcal{Q}\right)\to \mathsf{\Gamma }\left(\mathcal{P}\right)\square \mathsf{\Gamma }\left(\mathcal{Q}\right)$ be the natural epimorphisms. Then $\ker f\simeq M/(M\cap K)$ and $\ker g\simeq MK/K\simeq M/(M\cap K)$. Therefore, we have that

$$\begin{array}{cc}\hfill \left|\mathsf{\Gamma }\right(\mathcal{P})\diamond \mathsf{\Gamma }(\mathcal{Q}\left)\right|& =\left|\mathsf{\Gamma }\right(\mathcal{P}\left)\right|\left|\ker f\right|\hfill \\ & =\left|\mathsf{\Gamma }\right(\mathcal{P}\left)\right|\left|\ker g\right|\hfill \\ & =\left|\mathsf{\Gamma }\right(\mathcal{P}\left)\right|\left|\mathsf{\Gamma }\right(\mathcal{Q}\left)\right|/\left|\mathsf{\Gamma }\right(\mathcal{P})\square \mathsf{\Gamma }(\mathcal{Q}\left)\right|\hfill \end{array}$$

and the result follows. □

Using Proposition 3.3, it is often possible to determine the size of $\mathsf{\Gamma }\left(\mathcal{P}\right)\diamond \mathsf{\Gamma }\left(\mathcal{Q}\right)$ by hand or with the help of a computer algebra system. However, since finding the comix of two groups usually requires that we know their presentations, the result is somewhat less useful for determining the size of $\mathsf{\Gamma }\left({\mathcal{P}}^{\ast }\right)$, which is the mix of six groups. In a few nice cases, though, we can determine the size or structure of $\mathsf{\Gamma }\left({\mathcal{P}}^{\ast }\right)$ without any difficult calculations. We present a few such results here.

Theorem 3.4.

Let $\mathcal{P}$ be a self-Petrie polyhedron of type ${\{p,q\}}_p$. Suppose p is odd and that p and q are coprime. Then

$$\mathsf{\Gamma }\left({\mathcal{P}}^{\ast }\right)=\mathsf{\Gamma }\left(\mathcal{P}\right)\times \mathsf{\Gamma }\left({\mathcal{P}}^{\delta }\right)\times \mathsf{\Gamma }\left({\mathcal{P}}^{\delta \pi }\right)$$

Proof. 

First, we note that ${\mathcal{P}}^{\delta }$ is of type ${\{q,p\}}_p$. In $\mathsf{\Gamma }\left(\mathcal{P}\right)\square \mathsf{\Gamma }\left({\mathcal{P}}^{\delta }\right)$, the order of ${\rho }_0{\rho }_1$ divides p and q, and since p and q are coprime, we get ${\rho }_0{\rho }_1=ϵ$; that is, ${\rho }_0={\rho }_1$. Similarly, ${\rho }_1{\rho }_2=ϵ$, and so ${\rho }_1={\rho }_2$. Now, the order of ${\rho }_0{\rho }_1{\rho }_2$ divides p. On the other hand, ${\rho }_0{\rho }_1{\rho }_2={\rho }_0^3={\rho }_0$, and so the order divides 2 as well. Therefore, we must have that ${\rho }_0{\rho }_1{\rho }_2=ϵ$. This forces all of the generators to be trivial, and thus $\mathsf{\Gamma }\left(\mathcal{P}\right)\square \mathsf{\Gamma }\left({\mathcal{P}}^{\delta }\right)$ is trivial and $\mathsf{\Gamma }\left(\mathcal{P}\right)\diamond \mathsf{\Gamma }\left({\mathcal{P}}^{\delta }\right)=\mathsf{\Gamma }\left(\mathcal{P}\right)\times \mathsf{\Gamma }\left({\mathcal{P}}^{\delta }\right)$.

Now, $\mathcal{P}\diamond {\mathcal{P}}^{\delta }$ is of type ${\{pq,pq\}}_p$, and ${\mathcal{P}}^{\delta \pi }$ is of type ${\{p,p\}}_q$. Then in their comix, we get that ${\rho }_0{\rho }_1{\rho }_2$ has order dividing p and q, and thus it is trivial. Thus ${\rho }_0={\rho }_1{\rho }_2$, and so ${\left({\rho }_1{\rho }_2\right)}^2=ϵ$. On the other hand, we also have that ${\left({\rho }_1{\rho }_2\right)}^p=ϵ$ in the comix, and since p is odd, this means that ${\rho }_1{\rho }_2$ is trivial. So ${\rho }_0$ is trivial, and ${\rho }_1={\rho }_2$. Similarly, ${\rho }_2={\rho }_0{\rho }_1$, and thus ${\left({\rho }_0{\rho }_1\right)}^2=ϵ$. But again, we also have that ${\left({\rho }_0{\rho }_1\right)}^p=ϵ$, and thus ${\rho }_0{\rho }_1=ϵ$. So ${\rho }_0={\rho }_1={\rho }_2=ϵ$ and we see that the comix is trivial. Therefore, the mix is the direct product $\mathsf{\Gamma }\left(\mathcal{P}\right)\times \mathsf{\Gamma }\left({\mathcal{P}}^{\delta }\right)\times \mathsf{\Gamma }\left({\mathcal{P}}^{\delta \pi }\right)$.

Finally, we note that since $\mathcal{P}$ is self-Petrie, we have ${\mathcal{P}}^{\pi }=\mathcal{P}$, ${\mathcal{P}}^{\pi \delta }={\mathcal{P}}^{\delta }$, and ${\mathcal{P}}^{\pi \delta \pi }={\mathcal{P}}^{\delta \pi }$. Therefore, the self-dual, self-Petrie cover of $\mathcal{P}$ consists of just the three distinct polyhedra we have mixed. □

Corollary 3.5.

Let $\mathcal{P}$ be a regular polyhedron of type ${\{p,q\}}_r$. Suppose p and r are odd and both coprime to q. Let $\mathcal{Q}=\mathcal{P}\diamond {\mathcal{P}}^{\pi }$. Then

$$\mathsf{\Gamma }\left({\mathcal{P}}^{\ast }\right)=\mathsf{\Gamma }\left(\mathcal{Q}\right)\times \mathsf{\Gamma }\left({\mathcal{Q}}^{\delta }\right)\times \mathsf{\Gamma }\left({\mathcal{Q}}^{\delta \pi }\right)$$

Proof. 

We start by noting that any self-dual, self-Petrie polyhedron that covers $\mathcal{P}$ must also cover $\mathcal{Q}$; therefore, ${\mathcal{P}}^{\ast }={\mathcal{Q}}^{\ast }$. Now, the polyhedron $\mathcal{Q}$ is a self-Petrie polyhedron of type ${\{\ell ,q\}}_{\ell }$, where ℓ is the least common multiple of p and r. Since p and r are both odd and coprime to q, ℓ is also odd and coprime to q. Then we can apply Theorem 3.4 and the result follows. □

The condition in Theorem 3.4 that p is odd is essential. When p is even, we cannot tell from the type alone whether $\mathsf{\Gamma }\left(\mathcal{P}\right)\square \mathsf{\Gamma }\left({\mathcal{P}}^{\delta }\right)$ has order 1 or 2. However, if $\mathcal{P}$ is the universal polyhedron of type ${\{p,q\}}_p$, then we can still determine $\left|\mathsf{\Gamma }\right({\mathcal{P}}^{\ast }\left)\right|$.

Theorem 3.6.

Let $\mathcal{P}={\{p,q\}}_p$, the universal polyhedron of type ${\{p,q\}}_p$. Suppose p is even and that p and q are coprime. Then

$$|\mathsf{\Gamma }\left({\mathcal{P}}^{\ast }\right)|=|\mathsf{\Gamma }\left(\mathcal{P}\right){|}^3/8$$

Proof. 

Since p and q are coprime, a presentation for $\mathsf{\Gamma }\left(\mathcal{P}\right)\square \mathsf{\Gamma }\left({\mathcal{P}}^{\delta }\right)$ is given by

$$\langle {\rho }_0,{\rho }_1,{\rho }_2\mid {\rho }_0^2={\rho }_1^2={\rho }_2^2={\rho }_0{\rho }_1={\left({\rho }_0{\rho }_2\right)}^2={\rho }_1{\rho }_2={\left({\rho }_0{\rho }_1{\rho }_2\right)}^p=ϵ\rangle$$

and direct calculation shows that this is a group of order 2. Then by Proposition 3.3, $|\mathsf{\Gamma }\left(\mathcal{P}\right)\diamond \mathsf{\Gamma }\left({\mathcal{P}}^{\delta }\right)|=|\mathsf{\Gamma }\left(\mathcal{P}\right){|}^2/2$.

Now we consider $(\mathsf{\Gamma }\left(\mathcal{P}\right)\diamond \mathsf{\Gamma }\left({\mathcal{P}}^{\delta }\right))\square \mathsf{\Gamma }\left({\mathcal{P}}^{\delta \pi }\right)$. In this group, the order of ${\rho }_0{\rho }_1{\rho }_2$ divides both p and q, and thus ${\rho }_0{\rho }_1{\rho }_2=ϵ$. Therefore, ${\rho }_0{\rho }_1={\rho }_2$, which forces ${\rho }_0{\rho }_1$ to have order dividing 2, and similarly ${\rho }_0={\rho }_1{\rho }_2$, which forces ${\rho }_1{\rho }_2$ to have order dividing 2. Therefore, the comix is a (not necessarily proper) quotient of the group ${[2,2]}_1$, a group of order 4. Now, since $\mathsf{\Gamma }\left({\mathcal{P}}^{\delta \pi }\right)={[p,p]}_q$ and p is even, we see that $\mathsf{\Gamma }\left({\mathcal{P}}^{\delta \pi }\right)$ covers ${[2,2]}_1$. We similarly see that $\mathsf{\Gamma }\left(\mathcal{P}\right)$ covers ${[2,1]}_1$ and that $\mathsf{\Gamma }\left({\mathcal{P}}^{\delta }\right)$ covers ${[1,2]}_1$, and thus $\mathsf{\Gamma }\left(\mathcal{P}\right)\diamond \mathsf{\Gamma }\left({\mathcal{P}}^{\delta }\right)$ covers ${[2,1]}_1\diamond {[1,2]}_1$, which is equal to ${[2,2]}_1$. Thus we see that the group ${[2,2]}_1$ is the maximal group covered by both $\mathsf{\Gamma }\left(\mathcal{P}\right)\diamond \mathsf{\Gamma }\left({\mathcal{P}}^{\delta }\right)$ and $\mathsf{\Gamma }\left({\mathcal{P}}^{\delta \pi }\right)$, and therefore it is their comix. Therefore,

$$|\mathsf{\Gamma }\left(\mathcal{P}\right)\diamond \mathsf{\Gamma }\left({\mathcal{P}}^{\delta }\right)\diamond \mathsf{\Gamma }\left({\mathcal{P}}^{\delta \pi }\right)|=\frac{|\mathsf{\Gamma }\left(\mathcal{P}\right)\diamond \mathsf{\Gamma }\left({\mathcal{P}}^{\delta }\right)|·|\mathsf{\Gamma }\left({\mathcal{P}}^{\delta \pi }\right)|}{4}=\frac{{\left|\mathsf{\Gamma }\left(\mathcal{P}\right)\right|}^3}{8}$$

 □

We note here that the arguments used can be generalized to give bounds on $\left|\mathsf{\Gamma }\right({\mathcal{P}}^{\ast }\left)\right|$ even when we cannot calculate the exact value. In the next section, however, we will only consider cases where we can calculate $\left|\mathsf{\Gamma }\right({\mathcal{P}}^{\ast }\left)\right|$ exactly.

4. The Covers of Universal Polyhedra

In this section, we will consider several of the finite polyhedra $\mathcal{P}={\{p,q\}}_r$ and calculate $\left|\mathsf{\Gamma }\right({\mathcal{P}}^{\ast }\left)\right|$. The results are summarized in

Table 1. Self-dual, self-Petrie covers of finite polyhedra ${\{p,q\}}_r$.

$\mathcal{P}$	$\left|\mathsf{\Gamma }\right(\mathcal{P}\left)\right|$	$\left|\mathsf{\Gamma }\right({\mathcal{P}}^{\ast }\left)\right|$	Method
${\{2,2k+1\}}_{4k+2}$	$4(2k+1)$	$8{(2k+1)}^3$	Hand
${\{2,4k\}}_{4k}$	$16k$	$32k^3$	Hand
${\{2,4k+2\}}_{4k+2}$	$8(2k+1)$	$8{(2k+1)}^3$	Hand
${\{3,3\}}_4$	24	${\left(24\right)}^3$	Thm. 3.4
${\{3,4\}}_6$	48	${\left(48\right)}^3/8$	GAP
${\{3,5\}}_5$	60	${\left(60\right)}^3$	Thm. 3.4
${\{3,5\}}_{10}$	120	${\left(120\right)}^3$	GAP
${\{3,6\}}_6$	108	${\left(108\right)}^3/216$	GAP
${\{3,7\}}_8$	336	${\left(336\right)}^6/8$	Cor. 3.5
${\{3,7\}}_9$	504	${\left(504\right)}^6$	Cor. 3.5
${\{3,7\}}_{13}$	$1,092$	${(1,092)}^6$	Cor. 3.5
${\{3,7\}}_{15}$	$12,180$	${(12,180)}^6$	Cor. 3.5
${\{3,7\}}_{16}$	$21,504$	${(21,504)}^6/8$	Cor. 3.5
${\{3,8\}}_8$	672	${\left(672\right)}^3/8$	Thm. 3.6
${\{3,8\}}_{11}$	$12,144$	${(12,144)}^6/8$	Cor. 3.5
${\{3,9\}}_9$	$3,420$	${(3,420)}^3$	GAP
${\{3,9\}}_{10}$	$20,520$	${(20,520)}^6/216$	Cor. 3.5
${\{4,4\}}_{4k}$	$64k^2$	$64k^6$	Hand
${\{4,4\}}_{4k+2}$	$16{(2k+1)}^2$	$32{(2k+1)}^6$	Hand
${\{4,5\}}_5$	160	${\left(160\right)}^3$	Thm. 3.4
${\{4,5\}}_9$	$6,840$	${(6,840)}^6/8$	Cor. 3.5

. In most cases, the sizes are easily calculated by applying Corollary 3.5 to $\mathcal{P}$ or one of its images under the duality operations. A few others can be found by applying Theorem 3.6 or by calculating the size directly using GAP [6]. We cover the remaining cases here.

We start with $\mathcal{P}=\{2,2s\}$. The order of ${\rho }_0{\rho }_1{\rho }_2$ in $\mathsf{\Gamma }\left(\mathcal{P}\right)$ is $2s$, and therefore $\mathcal{P}={\{2,2s\}}_{2s}$, which has an automorphism group of order $8s$. If $s=1$, then $\mathcal{P}$ is already self-dual and self-Petrie. In any case, there are only 3 distinct images of $\mathcal{P}$ under the duality operations, and thus

$${\mathcal{P}}^{\ast }=\mathcal{P}\diamond {\mathcal{P}}^{\delta }\diamond {\mathcal{P}}^{\pi }$$

Now, $\mathcal{P}\diamond {\mathcal{P}}^{\delta }$ is a self-dual regular polyhedron of type ${\{2s,2s\}}_{2s}$. We note that for any s, the group $\mathsf{\Gamma }\left(\mathcal{P}\right)\square \mathsf{\Gamma }\left({\mathcal{P}}^{\delta }\right)$ is equal to ${[2,2]}_{2s}$. In fact, this group is equal to ${[2,2]}_2$, the group of order 8 generated by 3 commuting involutions (i.e., the direct product of three cyclic groups of order 2). Then by Proposition 3.3, we see that $|\mathsf{\Gamma }\left(\mathcal{P}\right)\diamond \mathsf{\Gamma }\left({\mathcal{P}}^{\delta }\right)|=8s^2$. In order to determine whether $\mathcal{P}\diamond {\mathcal{P}}^{\delta }$ is self-Petrie, we would like to determine the group $\mathsf{\Gamma }\left(\mathcal{P}\right)\diamond \mathsf{\Gamma }\left({\mathcal{P}}^{\delta }\right)$. A computation with GAP [6] suggests that the group is always the quotient of ${[2s,2s]}_{2s}$ by the extra relation ${\left({\rho }_1{\rho }_0{\rho }_1{\rho }_2\right)}^2=ϵ$. Since this extra relation also holds in $\mathsf{\Gamma }\left(\mathcal{P}\right)$ and $\mathsf{\Gamma }\left({\mathcal{P}}^{\delta }\right)$, this quotient must cover $\mathsf{\Gamma }\left(\mathcal{P}\right)\diamond \mathsf{\Gamma }\left({\mathcal{P}}^{\delta }\right)$. Therefore, to prove that this is in fact the mix, it suffices to show that this group has order $8s^2$.

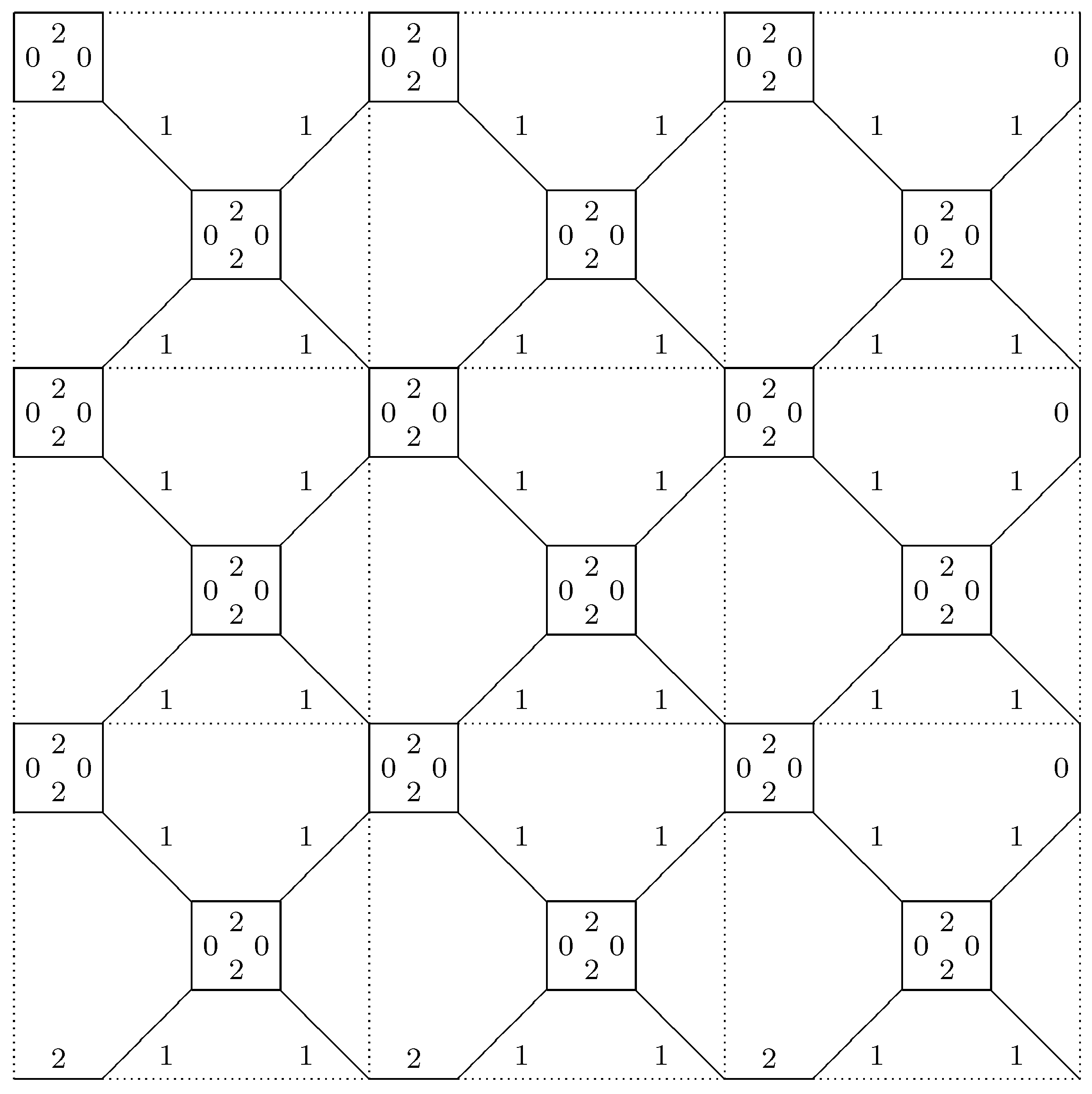
Start by considering the Cayley graph G of

$$\langle {\rho }_0,{\rho }_1,{\rho }_2\mid {\rho }_0^2={\rho }_1^2={\rho }_2^2={\left({\rho }_0{\rho }_2\right)}^2={\left({\rho }_1{\rho }_0{\rho }_1{\rho }_2\right)}^2=ϵ\rangle$$

Starting at a vertex and building out from it, we see that the Cayley graph of this group is the uniform tiling $\mathrm{4.8.8}$ of the plane by squares and octagons. Figure 1 gives a local picture of G.

Now, let us see what happens when we introduce the remaining relations ${\left({\rho }_0{\rho }_1\right)}^{2s}=ϵ$ and ${\left({\rho }_1{\rho }_2\right)}^{2s}=ϵ$. We note that the components of G induced by edges labeled 0 and 1 are vertical zigzags, while the components of G induced by edges labeled 1 and 2 are horizontal zigzags. Therefore, adding the relation ${\left({\rho }_0{\rho }_1\right)}^{2s}=ϵ$ forces an identification between points that are s tiles away vertically, and adding the relation ${\left({\rho }_1{\rho }_2\right)}^{2s}=ϵ$ forces an identification between points that are s tiles away horizontally. Therefore, the Cayley graph of $\mathsf{\Gamma }(\mathcal{P}\diamond {\mathcal{P}}^{\delta })$ consists of an $s\times s$ grid of tiles, with opposite sides identified. Each tile has 8 vertices, so there are a total of $8s^2$ vertices, which shows that the given group has $8s^2$ elements. Therefore the given group is indeed the mix.

Now we consider $(\mathsf{\Gamma }\left(\mathcal{P}\right)\diamond \mathsf{\Gamma }\left({\mathcal{P}}^{\delta }\right))\square \mathsf{\Gamma }\left({\mathcal{P}}^{\pi }\right)$, which is the quotient of ${[2s,2s]}_2$ by the extra relation ${\left({\rho }_1{\rho }_0{\rho }_1{\rho }_2\right)}^2=ϵ$. Put another way, we get the quotient of $\mathsf{\Gamma }\left(\mathcal{P}\right)\diamond \mathsf{\Gamma }\left({\mathcal{P}}^{\delta }\right)$ by the extra relation ${\left({\rho }_0{\rho }_1{\rho }_2\right)}^2=ϵ$. Using the Cayley graph from before, we see that the relation ${\left({\rho }_0{\rho }_1{\rho }_2\right)}^2=ϵ$ forces us to identify each tile with the tiles that touch it at a corner. When s is odd, this forces every tile to be identified, leaving us with a Cayley graph with 8 vertices. When s is even, we instead get 2 distinct tiles, and the Cayley graph has 16 vertices. Therefore, $|\mathsf{\Gamma }\left(\mathcal{P}\right)\diamond \mathsf{\Gamma }\left({\mathcal{P}}^{\delta }\right)\diamond \mathsf{\Gamma }\left({\mathcal{P}}^{\delta \pi }\right)|=8s^3$ if s is odd, and $4s^3$ if s is even. In other words, if $s=2k+1$, then $|\mathsf{\Gamma }\left({\mathcal{P}}^{\ast }\right)|=8{(2k+1)}^3$, and if $s=2k$, then $|\mathsf{\Gamma }\left({\mathcal{P}}^{\ast }\right)|=32k^3$.

Now suppose that $\mathcal{P}=\{2,2k+1\}$. This polyhedron is covered by $\mathcal{Q}=\{2,4k+2\}$ (which is equal to ${\{2,4k+2\}}_{4k+2}$, as we observed earlier); therefore, $\mathcal{Q}\diamond {\mathcal{Q}}^{\delta }$ covers $\mathcal{P}\diamond {\mathcal{P}}^{\delta }$. Calculating the size of the mix, we find that $|\mathsf{\Gamma }\left(\mathcal{Q}\right)\diamond \mathsf{\Gamma }\left({\mathcal{Q}}^{\delta }\right)|=|\mathsf{\Gamma }\left(\mathcal{P}\right)\diamond \mathsf{\Gamma }\left({\mathcal{P}}^{\delta }\right|$, and thus these two groups must be equal. From this it easily follows that ${\mathcal{Q}}^{\ast }={\mathcal{P}}^{\ast }$, and thus $|\mathsf{\Gamma }\left({\mathcal{P}}^{\ast }\right)|=8{(2k+1)}^3$.

Next we consider the polyhedra ${\{4,4\}}_{2s}$, which are the torus maps ${\{4,4\}}_{(s,s)}$ with $16s^2$ flags [7]. First, suppose that $s=2k$, so that $\mathcal{P}={\{4,4\}}_{4k}$. Then $\mathsf{\Gamma }\left(\mathcal{P}\right)\square \mathsf{\Gamma }\left({\mathcal{P}}^{\pi }\right)={[4,4]}_4$, which has order 64. Therefore, by Proposition 3.3,

$$|\mathsf{\Gamma }\left(\mathcal{P}\right)\diamond \mathsf{\Gamma }\left({\mathcal{P}}^{\pi }\right)|=|\mathsf{\Gamma }\left(\mathcal{P}\right)\left|\right|\mathsf{\Gamma }\left({\mathcal{P}}^{\pi }\right)|/64=64k^4$$

Now, $\mathcal{P}\diamond {\mathcal{P}}^{\pi }$ is of type ${\{4k,4\}}_{4k}$, and ${\mathcal{P}}^{\pi \delta }$ is the universal polyhedron of type ${\{4,4k\}}_4$. Thus $(\mathsf{\Gamma }\left(\mathcal{P}\right)\diamond \mathsf{\Gamma }\left({\mathcal{P}}^{\pi }\right))\square \mathsf{\Gamma }\left({\mathcal{P}}^{\pi \delta }\right)$ is ${[4,4]}_4$ or a proper quotient. Since $\mathsf{\Gamma }\left(\mathcal{P}\right)$ covers ${[4,4]}_4$, so does $\mathsf{\Gamma }\left(\mathcal{P}\right)\diamond \mathsf{\Gamma }\left({\mathcal{P}}^{\pi }\right)$. Then since $\mathsf{\Gamma }\left({\mathcal{P}}^{\pi \delta }\right)$ also covers ${[4,4]}_4$, so does $(\mathsf{\Gamma }\left(\mathcal{P}\right)\diamond \mathsf{\Gamma }\left({\mathcal{P}}^{\pi }\right))\square \mathsf{\Gamma }\left({\mathcal{P}}^{\pi \delta }\right)$, and thus the comix is the whole group ${[4,4]}_4$. Thus we see that

$$|\mathsf{\Gamma }\left(\mathcal{P}\right)\diamond \mathsf{\Gamma }\left({\mathcal{P}}^{\pi }\right)\diamond \mathsf{\Gamma }\left({\mathcal{P}}^{\pi \delta }\right)|=|\mathsf{\Gamma }\left(\mathcal{P}\right)\diamond \mathsf{\Gamma }\left({\mathcal{P}}^{\pi }\right)|·|\mathsf{\Gamma }\left({\mathcal{P}}^{\pi \delta }\right)|/64=64k^6$$

Now suppose that $s=2k+1$, so that $\mathcal{P}={\{4,4\}}_{4k+2}$. Then $\mathsf{\Gamma }\left(\mathcal{P}\right)\square \mathsf{\Gamma }\left({\mathcal{P}}^{\pi }\right)={[2,4]}_2$, which has size 8. Therefore,

$$|\mathsf{\Gamma }\left(\mathcal{P}\right)\diamond \mathsf{\Gamma }\left({\mathcal{P}}^{\pi }\right)|=|\mathsf{\Gamma }\left(\mathcal{P}\right)|·|\mathsf{\Gamma }\left({\mathcal{P}}^{\pi }\right)|/8=32{(2k+1)}^4$$

Now, $\mathcal{P}\diamond {\mathcal{P}}^{\pi }$ is of type ${\{8k+4,4\}}_{8k+4}$ and ${\mathcal{P}}^{\pi \delta }$ is the universal polyhedron ${\{4,4k+2\}}_4$. Thus $(\mathsf{\Gamma }\left(\mathcal{P}\right)\diamond \mathsf{\Gamma }\left({\mathcal{P}}^{\pi }\right))\square \mathsf{\Gamma }\left({\mathcal{P}}^{\pi \delta }\right)$ is ${[4,2]}_4$ or a proper quotient. Clearly, $\mathsf{\Gamma }\left({\mathcal{P}}^{\pi \delta }\right)$ covers ${[4,2]}_4$. Furthermore, $\mathsf{\Gamma }\left(\mathcal{P}\right)$ covers ${[4,4]}_2$ and $\mathsf{\Gamma }\left({\mathcal{P}}^{\pi }\right)$ covers ${[2,4]}_4$; therefore, their mix covers ${[4,4]}_2\diamond {[2,4]}_4$, which covers ${[4,2]}_4$. Therefore, the comix is the whole group ${[4,2]}_4$ of order 16, and we see that

$$|\mathsf{\Gamma }\left(\mathcal{P}\right)\diamond \mathsf{\Gamma }\left({\mathcal{P}}^{\pi }\right)\diamond \mathsf{\Gamma }\left({\mathcal{P}}^{\pi \delta }\right)|=|\mathsf{\Gamma }\left(\mathcal{P}\right)\diamond \mathsf{\Gamma }\left({\mathcal{P}}^{\pi }\right)|·|\mathsf{\Gamma }\left({\mathcal{P}}^{\pi \delta }\right)|/16=32{(2k+1)}^6$$

It would be natural here to consider the torus maps ${\{3,6\}}_{2s}={\{3,6\}}_{(s,0)}$. However, in this case there are 6 distinct polyhedra under the duality operations, and the problem seems to be intractable.

Finally, we note that the self-dual, self-Petrie covers of ${\{3,3\}}_4$ and ${\{3,4\}}_6$ have groups of the same order. In fact, since ${\{3,4\}}_6$ covers ${\{3,4\}}_3$, these two polyhedra have the same self-dual, self-Petrie cover.