Study of Dynamical Chiral Symmetry Breaking in (2 + 1) Dimensional Abelian Higgs Model
Abstract
:1. Introduction
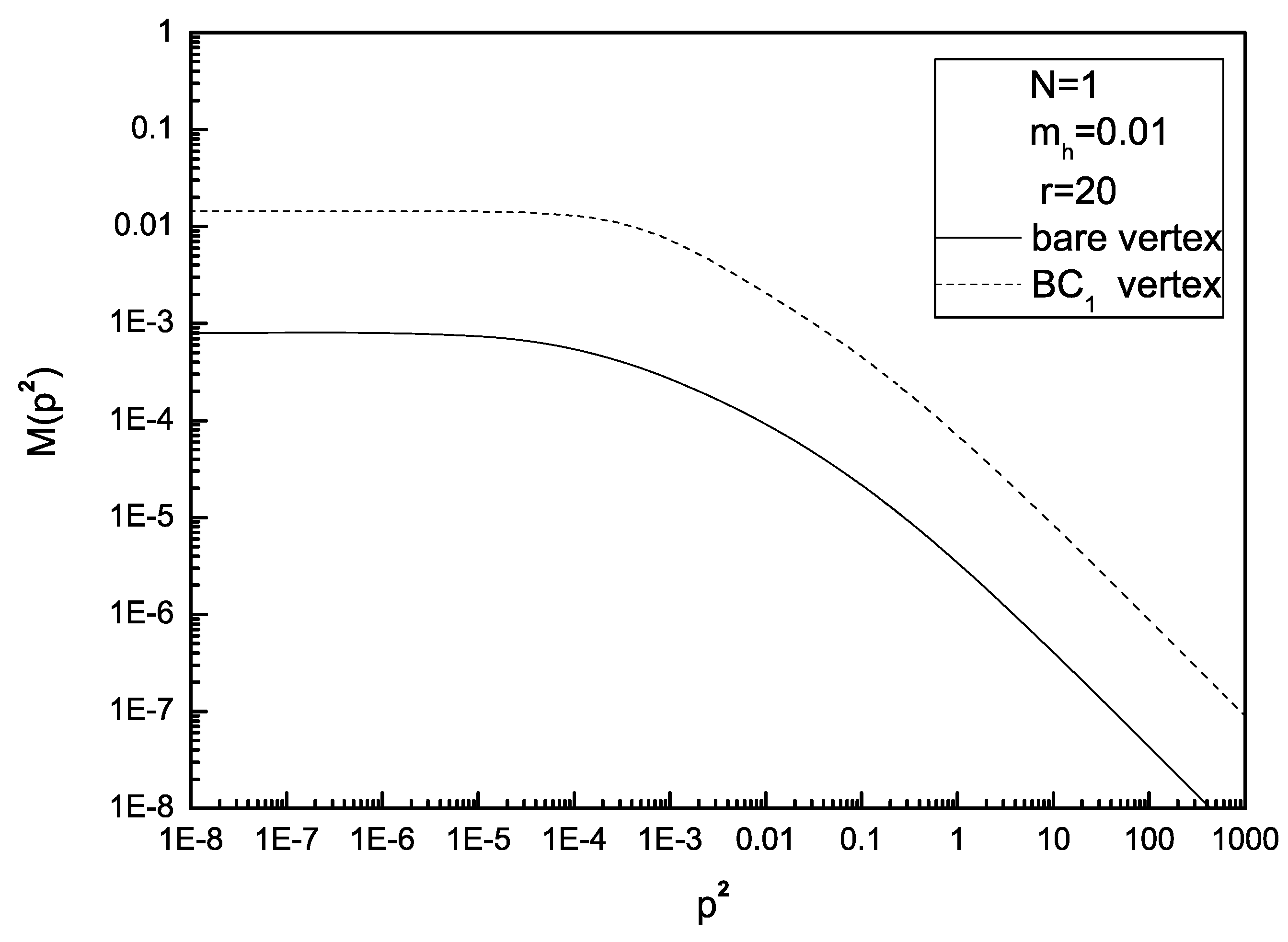
2. Results and Discussions
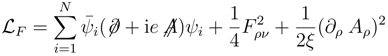
3. Conclusions
Acknowledgments
References
- Cornwall, J.M. Confinement and chiral-symmetry breakdown: estimates of Fπ and of effective quark masses. Phys.Rev. D 1980, 22, 1452–1468. [Google Scholar] [CrossRef]
- Pisarski, R.D. Chiral-symmetry breaking in three-dimensional electrodynamics. Phys. Rev. D 1984, 29, 2423–2426. [Google Scholar] [CrossRef]
- Appelquist, T.W.; Bowick, M.; Karabali, D; Wijewardhana, L.C.R. Spontaneous chiral-symmetry breaking in three-dimensional QED. Phys. Rev. D 1986, 33, 3704–3713. [Google Scholar] [CrossRef]
- Appelquist, T.; Nash, D.; Wijewardhana, L.C.R. Critical behavior in (2+1)-dimensional QED. Phys. Rev. Lett. 1988, 60, 2575–2578. [Google Scholar] [CrossRef] [PubMed]
- Nash, D. Higher-order corrections in (2+1)-dimensional QED. Phys. Rev. Lett. 1989, 62, 3024–3026. [Google Scholar] [CrossRef] [PubMed]
- Burden, C.J.; Roberts, C.D. Light-cone regular vertex in three-dimensional quenched QED. Phys. Rev. D 1991, 44, 540–550. [Google Scholar] [CrossRef]
- Maris, P. Confinement and complex singularities in three-dimensional QED. Phys. Rev. D 1995, 52, 6087–6097. [Google Scholar] [CrossRef]
- Maris, P. Influence of the full vertex and vacuum polarization on the fermion propagator in (2+1)-dimensional QED. Phys. Rev. D 1996, 54, 4049–4058. [Google Scholar] [CrossRef]
- Kondo, K.-I.; Maris, P. Spontaneous chiral-symmetry breaking in three-dimensional QED with a Chern-Simons term. Phys. Rev. D 1995, 52, 1212–1233. [Google Scholar] [CrossRef]
- Burden, C.J.; Praschifka, J.; Roberts, C.D. Photon polarization tensor and gauge dependence in three-dimensional quantum electrodynamics. Phys. Rev. D 1992, 46, 2695–2702. [Google Scholar] [CrossRef]
- Grignani, G.; Semenoff, G.; Sodano, P. Confinement-deconfinement transition in three-dimensional QED. Phys. Rev. D 1996, 53, 7157–7161. [Google Scholar] [CrossRef]
- Bashir, A.; Raya, A.; Cloët, I.C.; Roberts, C.D. Confinement and dynamical chiral symmetry breaking in QED3. Phys. Rev. C 2008, 78, 055201–055207. [Google Scholar]
- Bashir, A.; Raya, A.; Sanchez-Madrigal, S.; Roberts, C.D. Gauge invariance of a critical number of flavours in QED3. Few Body Syst 2009, 46, 229–237. [Google Scholar] [CrossRef]
- Wen, X.G.; Zee, A. Neutral superfluid modes and magnetic monopoles in multilayered quantum Hall systems. Phys. Rev. Lett. 1992, 69, 1811–1814. [Google Scholar] [CrossRef] [PubMed]
- Rantner, W.; Wen, X.G. Electron spectral function and algebraic spin liquid for the normal state of underdoped high Tc superconductors. Phys. Rev. Lett. 2001, 86, 3871–3874. [Google Scholar] [CrossRef] [PubMed]
- Lee, P.A.; Wen, X.G. Theory of underdoped cuprates. Phys. Rev. Lett. 1996, 76, 503–506. [Google Scholar]
- Lee, P.A.; Nagaosa, N.; Wen, X.G. Doping a mott insulator: physics of high-temperature superconductivity. Rev. Mod. Phys. 2006, 78, 17–85. [Google Scholar] [CrossRef]
- Kim, D.H.; Lee, P.A.; Wen, X.G. Massless Dirac fermions, gauge fields, and underdoped cuprates. Phys. Rev. Lett. 1997, 79, 2109–2112. [Google Scholar] [CrossRef]
- Kim, D.H.; Lee, P.A. Theory of spin excitations in undoped and underdoped cuprates. Ann. Phys. 1999, 272, 130–164. [Google Scholar] [CrossRef]
- Franz, M.; Tesaanovic, Z. Algebraic Fermi liquid from phase fluctuations: topological fermions, vortex Berryons, and QED3 theory of cuprate superconductors. Phys. Rev. Lett. 2001, 87, 257003–257006. [Google Scholar] [CrossRef]
- Herbut, I.F. Antiferromagnetism from phase disordering of a d-wave superconductor. Phys. Rev. Lett. 2002, 88, 047006–047009. [Google Scholar] [CrossRef] [PubMed]
- Herbut, I.F. QED3 theory of underdoped high-temperature superconductors. Phys. Rev. B 2002, 66, 094504–094522. [Google Scholar] [CrossRef]
- Herbut, I.F. Effective theory of high-temperature superconductors. Phys. Rev. Lett. 2005, 94, 237001–237004. [Google Scholar] [CrossRef] [PubMed]
- Marston, J.B. Instantons and massless fermions in (2+1)-dimensional lattice QED and antiferromagnets. Phys. Rev. Lett. 1990, 64, 1166–1169. [Google Scholar] [CrossRef] [PubMed]
- Hermele, B.I.; Lee, P.A.; Read, N. Theory of the half-filled Landau level. Phys. Rev. B 1993, 47, 7312–7343. [Google Scholar]
- Gusynin, V.P.; Sharapov, S.G. Unconventional integer quantum Hall effect in graphene. Phys. Rev. Lett. 2005, 95, 146801–146804. [Google Scholar] [CrossRef]
- Gusynin, V.P.; Sharapov, S.G.; Carbotte, J.P. Unusual microwave response of Dirac quasiparticles in graphene. Phys. Rev. Lett. 2006, 96, 256802–256805. [Google Scholar] [CrossRef]
- Durt, J.E.; Lahde, T.A. Lattice field theory simulations of graphene. Phys. Rev. B 2009, 79, 165425–165438. [Google Scholar]
- Nambu, Y.; Lasinio, G.J. Dynamical model of elementary particles based on an analogy with superconductivity. I. Phys. Rev. 1961, 122, 345–358. [Google Scholar] [CrossRef]
- Fisher, C.S.; Alkofer, R.; Dahm, T.; Maris, P. Dynamical chiral symmetry breaking in unquenched QED3. Phys. Rev. D 2004, 70, 073007-1-19. [Google Scholar] [CrossRef]
- Liu, G.Z.; Cheng, G. Effect of gauge boson mass on chiral symmetry breaking in three-dimensional QED. Phys. Rev. D 2003, 67, 065010-1-11. [Google Scholar] [CrossRef]
- Liu, G.Z.; Jiang, H.; Li, W.; Cheng, G. Quantum electrodynamics in three dimensions: dynamical chiral symmetry breaking, confinement, and disorder effects. Phys. Rev. B 2009, 79, 014507-1-5. [Google Scholar] [CrossRef]
- Jiang, H.; Liu, G.Z.; Cheng, G. Chiral symmetry breaking in three-dimensional QED with Abelian Higgs model. J. Phys. A 2008, 41, 255402–255410. [Google Scholar] [CrossRef]
- Gusynin, V.; Hams, A.; Reenders, M. Nonperturbative infrared dynamics of three-dimensional QED with a four-fermion interaction. Phys. Rev. D 2001, 63, 045025-1-19. [Google Scholar] [CrossRef]
- Kleinert, H.; Nogueira, F.S. Charged fixed point found in superconductor below T(c). Nucl. Phys. B 2003, 651, 361–386. [Google Scholar] [CrossRef]
- Kizilersü, A.; Pennington, M. Building the full fermion-photon vertex of QED by imposing multiplicative renormalizability of the Schwinger-Dyson equations for the fermion and photon propagators. Phys. Rev. D 2009, 79, 125020-1-25. [Google Scholar]
- Bashir, A.; Raya, A. Constructing the fermion-boson vertex in three-dimensional QED. Phys. Rev. D 2001, 64, 105001-1-10. [Google Scholar] [CrossRef]
- Bashir, A.; Huet, A.; Raya, A. Gauge dependence of mass and condensate in chirally asymmetric phase of quenched three-dimensional QED. Phys. Rev. D 2002, 66, 025029-1-8. [Google Scholar] [CrossRef]
- Curtis, D.C.; Peninington, M.R. Truncating the Schwinger-Dyson equations: How multiplicative renormalizability and the Ward identity restrict the three-point vertex in QED. Phys. Rev. D 1990, 42, 4165–4169. [Google Scholar] [CrossRef]
- King, J.E. Transverse vertex and gauge technique in quantum electrodynamics. Phys. Rev. D 1982, 27, 1821–1829. [Google Scholar] [CrossRef]
- Kizilersü, A.; Reenders, M.; Pennington, M.R. One-loop QED vertex in any covariant gauge: Its complete analytic form. Phys. Rev. D 1995, 52, 1242–1259. [Google Scholar]
- Burden, C.J.; Tjiang, P.C. Deconstructing the vertex Ansatz in three-dimensional quantum electrodynamics. Phys. Rev. D 1998, 58, 085019-1-8. [Google Scholar] [CrossRef]
- Bashir, A.; Kizilersü, A.; Peninington, M.R. Does the weak coupling limit of the Burden-Tjiang deconstruction of the massless quenched three-dimensional QED vertex agree with perturbation theory? Phys. Rev. D 2000, 62, 085002-1-8. [Google Scholar] [CrossRef]
- Bashir, A.; Peninington, M.R. Gauge-independent chiral symmetry breaking in quenched QED. Phys. Rev. D 1994, 50, 7679–7689. [Google Scholar] [CrossRef]
- Ball, J.S.; Chiu, T.W. Analytic properties of the vertex function in gauge theories. Phys. Rev. D 1980, 22, 2542–2549. [Google Scholar] [CrossRef]
- Kondo, K.; Nakatani, H. Strong coupling unquenched QED.2. Prog. Theor. Phys. 1992, 87, 193–206. [Google Scholar] [CrossRef]
- Feng, H.T.; Sun, W.M.; Hu, F.; Zong, H.S. The influence of the gauge boson mass on the critical number of the fermion flavors in QED(3). Int. J. Mod. Phys. A 2005, 20, 2753–2762. [Google Scholar] [CrossRef]
- Feng, H.T.; Sun, W.M.; He, D.K.; Zong, H.S. Influence of finite chemical potential on the fermion chiral condensate in QED3. Phys. Lett. B 2008, 661, 57–65. [Google Scholar] [CrossRef]
- Marston, J.; Affleck, I. Large-n limit of the Hubbard-Heisenberg model. Phys. Rev. B 1989, 39, 11538–11558. [Google Scholar] [CrossRef]
- Ioffe, L.B.; Larkin, A.I. Gapless fermions and gauge fields in dielectrics. Phys. Rev. B 1989, 39, 8988–8999. [Google Scholar] [CrossRef]
- Marston, J.B. Instantons and massless fermions in (2+1)-dimensional lattice QED and antiferromagnets. Phys. Rev. Lett. 1990, 64, 1166–1169. [Google Scholar] [CrossRef] [PubMed]
- Laughlin, R.B.; Zou, Z. Properties of the chiral-spin-liquid state. Phys. Rev. B 1990, 41, 664–687. [Google Scholar] [CrossRef]
© 2010 by the authors; licensee MDPI, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license http://creativecommons.org/licenses/by/3.0/.
Share and Cite
Li, J.-F.; Huang, S.-S.; Feng, H.-T.; Sun, W.-M.; Zong, H.-S. Study of Dynamical Chiral Symmetry Breaking in (2 + 1) Dimensional Abelian Higgs Model. Symmetry 2010, 2, 907-915. https://doi.org/10.3390/sym2020907
Li J-F, Huang S-S, Feng H-T, Sun W-M, Zong H-S. Study of Dynamical Chiral Symmetry Breaking in (2 + 1) Dimensional Abelian Higgs Model. Symmetry. 2010; 2(2):907-915. https://doi.org/10.3390/sym2020907
Chicago/Turabian StyleLi, Jian-Feng, Shi-Song Huang, Hong-Tao Feng, Wei-Min Sun, and Hong-Shi Zong. 2010. "Study of Dynamical Chiral Symmetry Breaking in (2 + 1) Dimensional Abelian Higgs Model" Symmetry 2, no. 2: 907-915. https://doi.org/10.3390/sym2020907



