Investigation of Buckling Behavior of Cracked FG Cylindrical Panels Reinforced by Graphene Platelets
Abstract
:1. Introduction
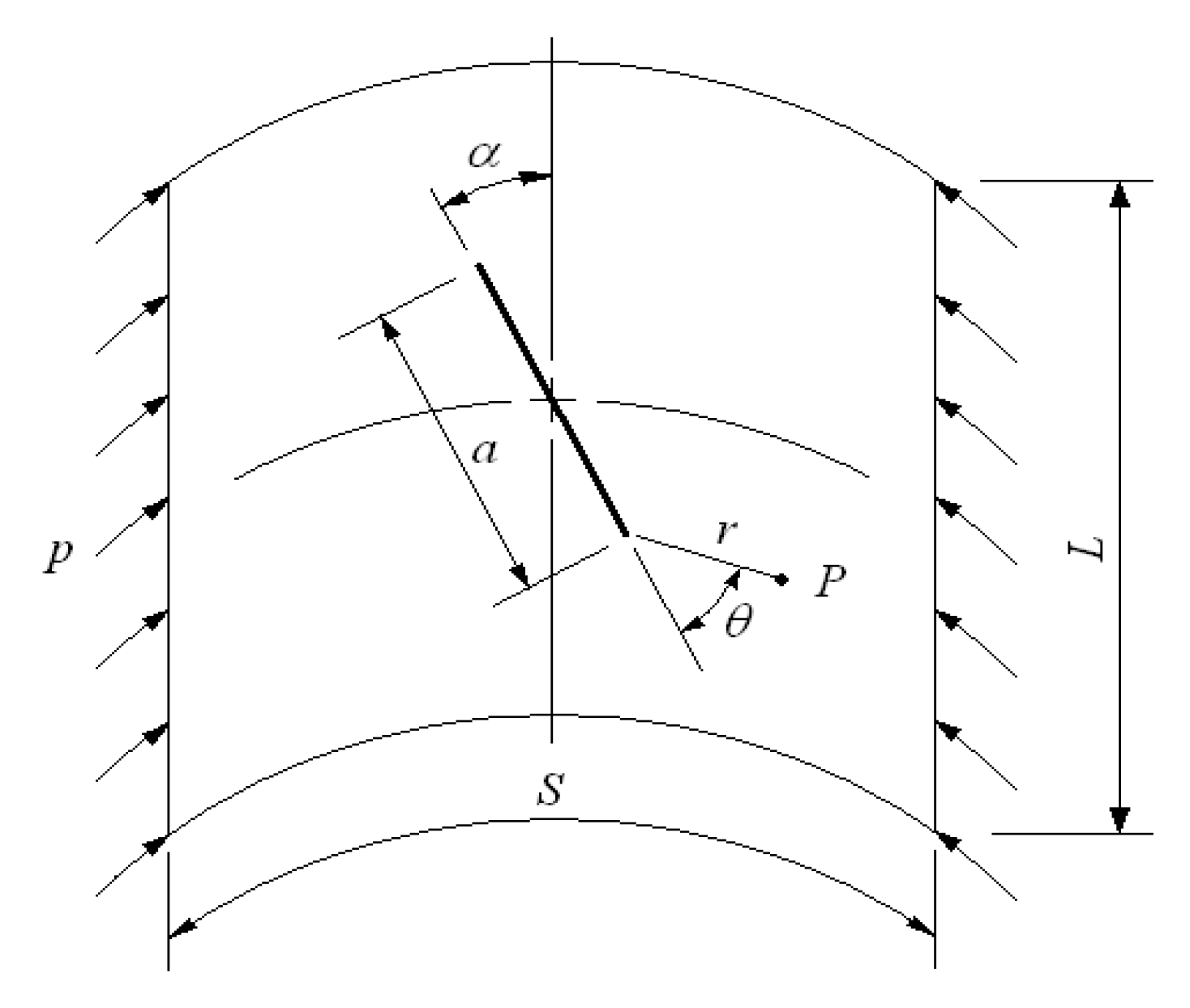
2. FG-GPLRC Cylindrical Panel
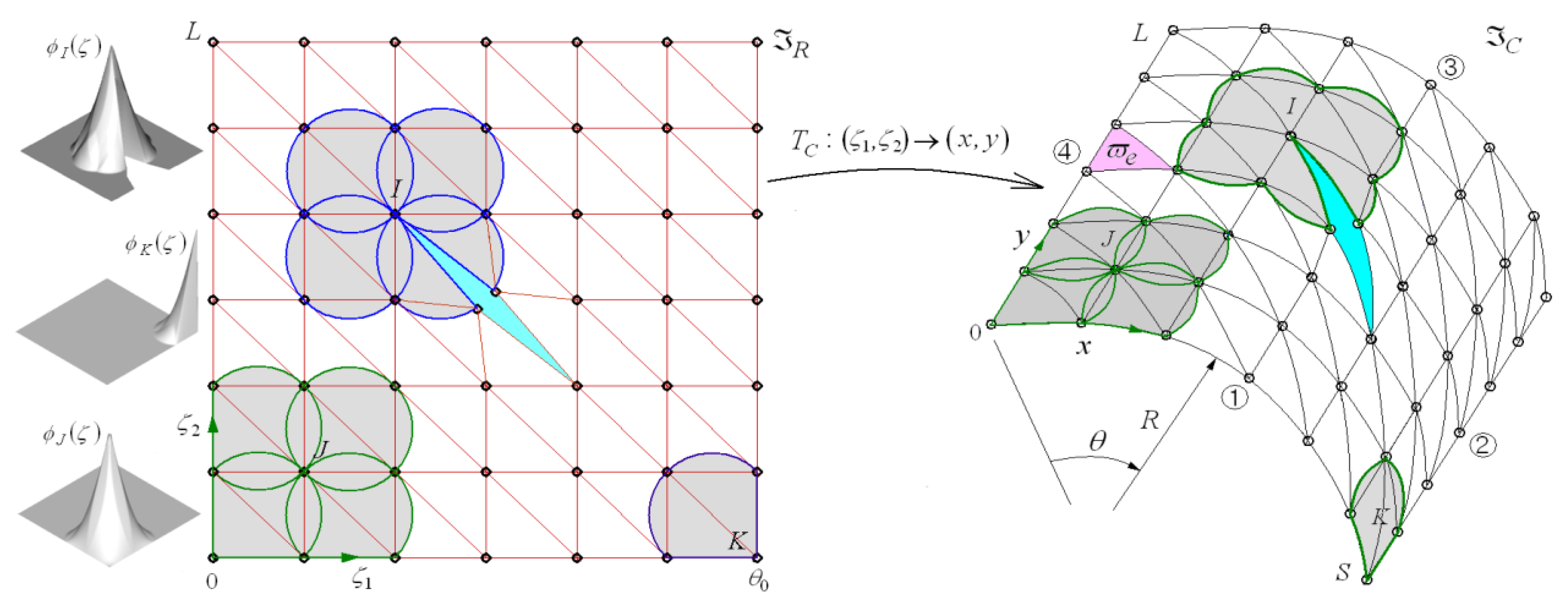
3. Natural Element Buckling Load Approximation
4. Results and Discussion
5. Conclusions
- The developed 2-D XNEM effectively analyzes the buckling of FG-GPLRC cylindrical panel having a central crack, with reasonable numerical accuracy;
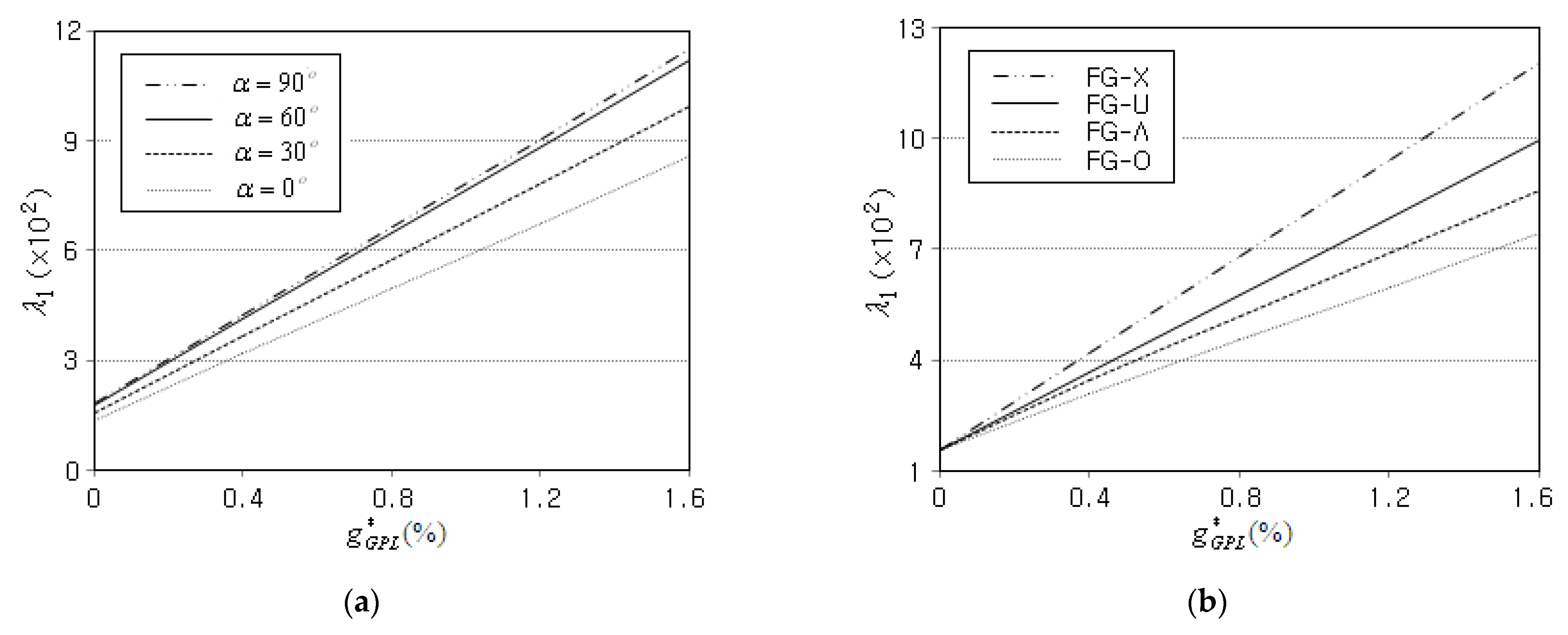
- The fundamental buckling load linearly increases proportional to the amount of GPLs, regardless of the crack inclination angle. The relative order in the fundamental buckling loads among the four GPL distribution patterns is FG-X > FG-U > FG-Λ > FG-O;
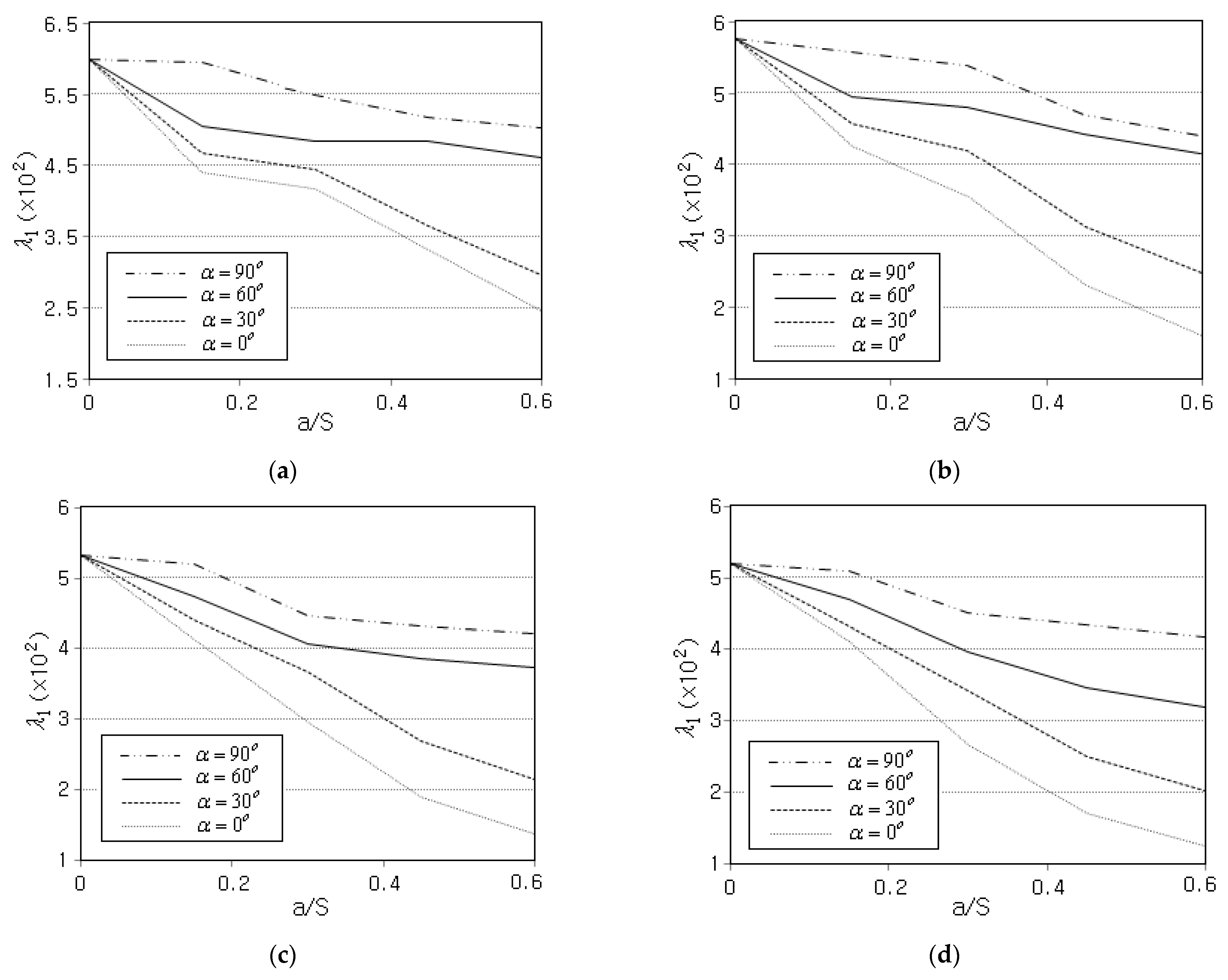
- The fundamental buckling load increases proportionally to the crack inclination angle, but this increase trend is slightly saturated for CCCC, regardless of the GPL distribution pattern. However, it uniformly decreases proportionally to the crack’s relative length.
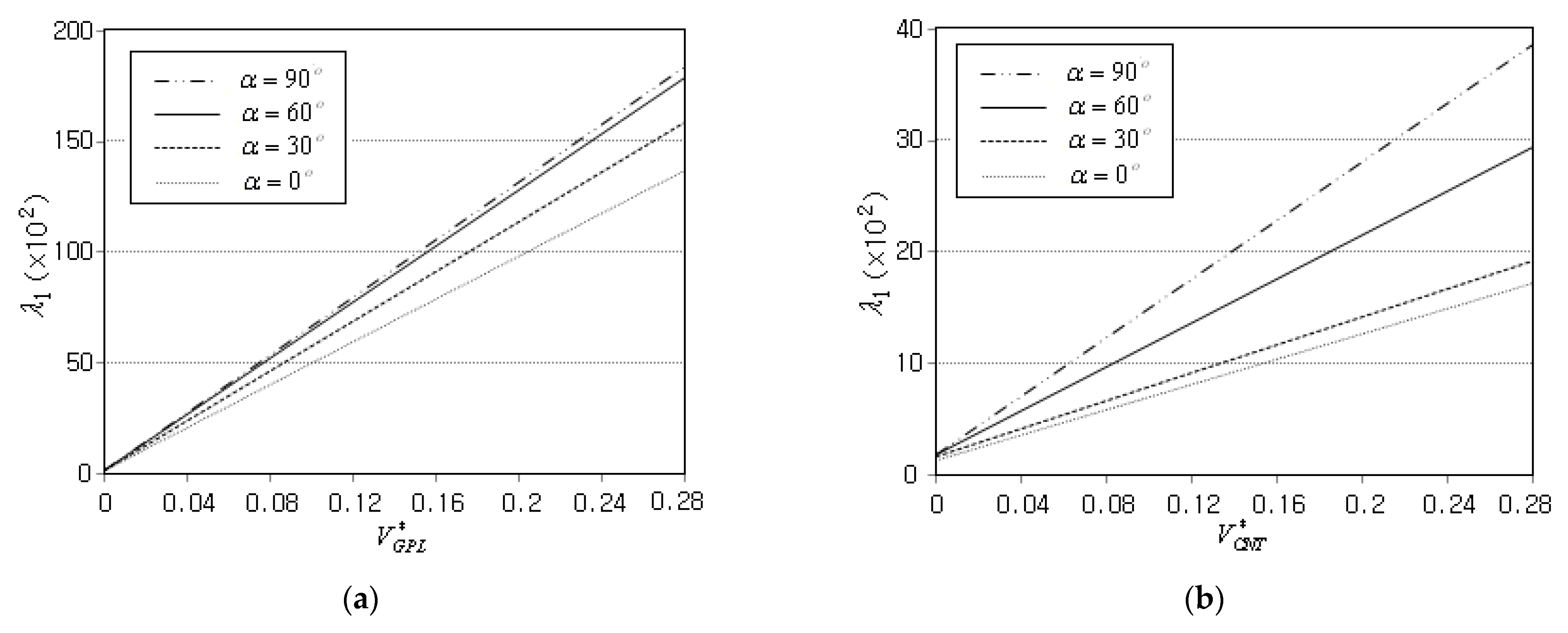
- For the same volume fraction, the buckling stiffness of the cylindrical panel reinforced with GPLs is almost five times as large as that of a CNT-reinforced cylindrical panel.
Funding
Conflicts of Interest
Nomenclature
| Radius, subtended angle and thickness of the cylindrical panel | |
| Width and length of the cylindrical panel | |
| Neutral surface and its radial distance from the panel midsurface | |
| Volume fractions of GPL and the matrix | |
| Total volume fractions of GPLs and CNTs | |
| Elastic moduli of GPLRC, matrix and GPL | |
| Length, thickness and width of GPL | |
| Poisson’s ratios of GPLRC, matrix and GPL | |
| Densities of GPLRC, matrix and GPL | |
| Length and inclination angle of central crack | |
| Translation components at the neutral surface of cylindrical panel | |
| Rotational components at the neutral surface | |
| Non-singular nodal vector at node J | |
| Singular nodal vector corresponding to the k-th singular function | |
| In-plane strain components | |
| In-plane stress components | |
| Transverse shear strains and stresses | |
| Physical and computational NEM grids | |
| J-th critical buckling load and buckling mode | |
| Shear correction factor | |
| Shear stabilization parameter | |
| Panel aspect ratio and relative crack length | |
| CNT efficiency parameters | |
| Power-law index and calibrated J-th critical buckling load |
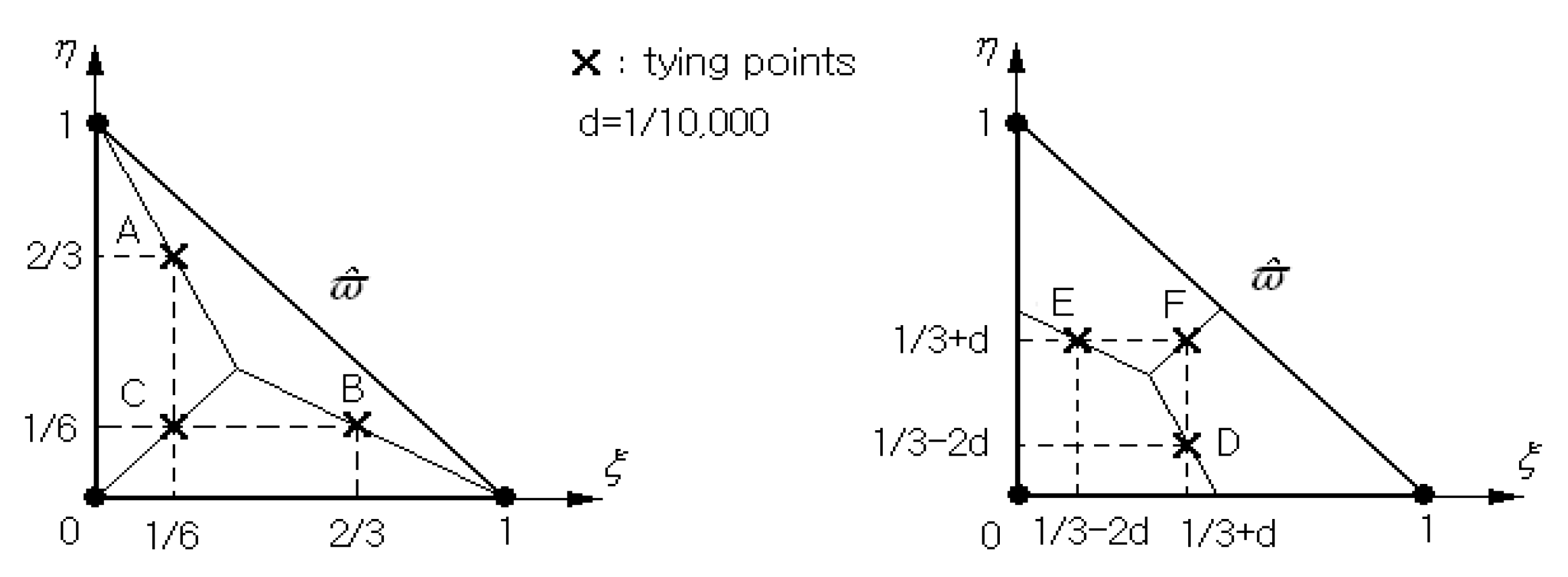
Appendix A
References
- Ramanathan, T.; Abdala, A.A.; Stankovich, S.; Dikin, D.A.; Herrera-Alonso, M.; Piner, R.D.; Adamson, D.H.; Schniepp, H.C.; Chen, X.; Ruoff, R.S.; et al. Functionalized graphene sheets for polymer nanocomposites. Nat. Nanotechnol. 2008, 3, 327–331. [Google Scholar] [CrossRef]
- Cho, J.R. Free vibration analysis of functionally graded porous cylindrical panels reinforced with graphene platerets. Nanomaterials 2023, 13, 1441. [Google Scholar] [CrossRef]
- Young, R.J.; Kinloch, I.A.; Gong, I.; Novoselov, K.S. The mechanics of graphene nano-composites: A review. Compos. Sci. Technol. 2012, 72, 1459–1476. [Google Scholar] [CrossRef]
- Rafiee, M.A.; Rafiee, J.; Wang, Z.; Song, H.; Yu, Z.Z.; Koratkar, N. Enhanced mechanical properties of nanocomposites at low graphene content. ACS Nano 2009, 3, 3884–3890. [Google Scholar] [CrossRef] [PubMed]
- Shen, H.S.; Xiang, Y.; Lin, F. Nonlinear vibration of functionally graded graphene-reinforced composite laminated plates in thermal environments. Comput. Methods Appl. Mech. Eng. 2017, 319, 175–193. [Google Scholar] [CrossRef]
- Zhao, S.; Zhao, Z.; Yang, Z.; Ke, L.L.; Kitipornchai, S.; Yang, J. Functionally graded graphene reinforced composite structures: A review. Eng. Struct. 2020, 210, 110339. [Google Scholar] [CrossRef]
- Kumar, A.; Sharma, K.; Dixit, A.R. Carbon nanotube- and graphene-reinforced multiphase polymeric composites: Review on their properties and applications. J. Mater. Sci. 2020, 55, 2682–2724. [Google Scholar] [CrossRef]
- Cho, J.R.; Oden, J.T. Functionally graded material: A parametric study on thermal-stress characteristics using the Crack-Nicolson-Galerkin scheme. Comput. Methods Appl. Mech. Eng. 2000, 188, 17–38. [Google Scholar] [CrossRef]
- Birman, V.; Byrd, L.W. Modeling and analysis of functionally graded materials and structures. Appl. Mech. Rev. 2007, 60, 195–216. [Google Scholar] [CrossRef]
- Zhou, W.; Ai, S.; Chen, M.; Zhang, R.; He, R.; Pei, Y.; Fang, D. Preparation and thermodynamic analysis of the porous ZrO2/(ZrO2+ Ni) functionally graded bolted joint. Compos. Part B 2015, 82, 13–22. [Google Scholar] [CrossRef]
- Cho, J.R.; Ha, D.Y. Optimal tailoring of 2D volume-fraction distributions for heat-resisting functionally graded materials using FDM. Comput. Methods Appl. Mech. Eng. 2002, 191, 3195–3211. [Google Scholar] [CrossRef]
- Nikbakht, S.; Kamarian, S.; Shakeri, M. A review on optimization of composite structures, Part II: Functionally graded materials. Compos. Struct. 2019, 214, 83–102. [Google Scholar] [CrossRef]
- Shen, H.S. Nonlinear bending of functionally graded carbon nanotube-reinforced composite plates in thermal environments. Compos. Struct. 2009, 91, 9–19. [Google Scholar] [CrossRef]
- Ke, L.L.; Yang, J.; Kitipornchai, S. Nonlinear free vibration of functionally graded carbon nanotube-reinforced composite beams. Compos. Struct. 2010, 92, 676–683. [Google Scholar] [CrossRef]
- García-Macías, E.; Rodríguez-Tembleque, L.; Sáez, A. Bending and free vibration analysis of functionally graded graphene vs. carbon nanotube reinforced composite plates. Compos. Struct. 2018, 186, 123–138. [Google Scholar] [CrossRef]
- Shen, H.-S.; Xiang, Y.; Lin, F. Thermal buckling and postbuckling of functionally graded graphene-reinforced composite laminated plates resting on elastic foundations. Thin-Walled Struct. 2017, 118, 229–237. [Google Scholar] [CrossRef]
- Wu, H.; Kitipornchai, S.; Yang, J. Thermal buckling and postbuckling of functionally graded graphene nanocomposite plates. Mater. Des. 2017, 132, 430–441. [Google Scholar] [CrossRef]
- Song, M.; Yang, J.; Kitipornchai, S. Bending and buckling analyses of functionally graded polymer composite plates reinforced with graphene nanoplaterets. Compos. Part B Eng. 2018, 134, 106–113. [Google Scholar] [CrossRef]
- Huang, Y.; Yang, Z.; Liu, A.; Fu, J. Nonlinear buckling analysis of functionally graded graphene reinforced composite shallow arches with elastic rotational constraints under uniform radial load. Materials 2018, 11, 910. [Google Scholar] [CrossRef]
- Wang, Y.; Feng, C.; Zhao, Z.; Lu, F.; Yang, J. Torsional buckling of graphene platerets (GPLs) reinforced functionally graded cylindrical shell with cutout. Compos. Struct. 2018, 197, 72–79. [Google Scholar] [CrossRef]
- Kiani, Y. Buckling of functionally graded graphene reinforced conical shells under external pressure in thermal environment. Compos. Part B Eng. 2019, 156, 128–137. [Google Scholar] [CrossRef]
- Mao, J.J.; Zhang, W. Buckling and post-buckling analyses of functionally graded graphene reinforced piezoelectric plate subjected to electric potential and axial forces. Compos. Struct. 2019, 216, 392–405. [Google Scholar] [CrossRef]
- Thai, C.H.; Ferreira, A.J.M.; Tran, T.D.; Phung-Van, O. Free vibration, buckling and vbending analyses of multilayer functionally graded graphene nanoplaterets reinforced composite plates using the NURBS formulation. Compos. Struct. 2019, 220, 749–759. [Google Scholar] [CrossRef]
- Shahgholian, D.; Safarpour, M.; Rahimi, A.R.; Alibeigloo, A. Buckling analyses of functionally graded graphene-reinforced porous cylindrical shell using the Rayleigh–Ritz method. Acta Mech. 2020, 231, 1887–1902. [Google Scholar] [CrossRef]
- Zeverdejani, M.K.; Beni, Y.T.; Kiani, Y. Multi-scale buckling and post-buckling analysis of functionally graded laminated composite plates reinforced by defective graphene sheets. Int. J. Struct. Stab. Dyn. 2020, 20, 2050001. [Google Scholar] [CrossRef]
- Allahkarami, F. Dynamic buckling of functionally graded multilayer graphene nanocomposite annular plate under different boundary conditions in thermal environment. Eng. Comput. 2022, 38, 583–606. [Google Scholar] [CrossRef]
- Zhang, L.; Xu, Z.; Gao, M.; Xu, R.; Wang, G. Static, dynamic and buckling responses of random functionally graded beams reinforced by graphene platerets. Eng. Struct. 2023, 291, 116476. [Google Scholar] [CrossRef]
- Wang, K.; Chen, L.; Wu, J.; Toh, M.L.; He, C.; Yee, A.F. Epoxy nanocomposites with highly exfolidated clay: Mechcanical properties and fracture mechanisms. Macromolecules 2005, 38, 788–800. [Google Scholar] [CrossRef]
- Cho, J.R. Buckling analysis of functionally graded plates resting on elastic foundation by natural element method. Steel Compos. Struct. 2022, 44, 157–167. [Google Scholar]
- Halphin, J.C.; Kardos, J.L. The Haplin-Tsai equations: A review. Polym. Eng. Sci. 1976, 16, 344–352. [Google Scholar]
- Sukumar, N.; Moran, B.; Belytschko, T. The natural element method in solid mechanics. Int. J. Numer. Methods Eng. 1998, 43, 839–887. [Google Scholar] [CrossRef]
- Cho, J.R.; Lee, H.W. A Petrov-Galerkin natural element method securing the numerical integration accuracy. J. Mech. Sci. Technol. 2006, 20, 94–109. [Google Scholar] [CrossRef]
- Pitkaranta, J. The problem of membrane locking in finite element analysis of cylindrical shells. Numer. Math. 1992, 61, 523–542. [Google Scholar] [CrossRef]
- Cho, J.R.; Oden, J.T. Locking and boundary layer in hierarchical models for thin elastic structures. Comput. Methods Appl. Mech. Eng. 1997, 149, 33–48. [Google Scholar] [CrossRef]
- Bayesteh, H.; Mohammadi, S. XFEM fracture analysis of shells: The effect of crack tip enrichments. Comput. Mater. Sci. 2011, 50, 2793–2813. [Google Scholar] [CrossRef]
- Nasirmanesh, A.; Mohammadi, S. Eigenvalue buckling analysis of cracked functionally graded cylindrical shells in the framework of the extended finite element method. Compos. Struct. 2017, 159, 548–566. [Google Scholar] [CrossRef]
- Yang, B.; Yang, J.; Kitipornchai, S. Thermoelastic analysis of functionally graded graphene reinforced rectangular plates based on 3D elasticity. Meccanica 2017, 52, 2275–2292. [Google Scholar] [CrossRef]
- Reddy, J.N. Mechanics of Laminated Composite Plates and Shells, Theory and Analysis, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2004. [Google Scholar]
- Niu, Y.; Yao, M. Linear and nonlinear vibrations of graphene platelet reinforced composite tapered plates and cylindrical panels. Aerosp. Sci. Technol. 2021, 115, 106798. [Google Scholar] [CrossRef]
- Lee, Y.; Lee, P.-S.; Bathe, K.-J. The MITC3+ shell finite element and its performance. Comput. Struct. 2014, 138, 12–23. [Google Scholar] [CrossRef]
- Chau-Dinh, T. Analysis of shell structures by an improved 3-node triangular flat shell element with a bubble function and cell-based strain smoothing. Thin-Walled Struct. 2023, 182, 110222. [Google Scholar] [CrossRef]
- Lyly, M.; Stenberg, R.; Vihinen, T. A stable bilinear element for the Reissner-mindlin plate model. Comput. Methods Appl. Mech. Eng. 1993, 110, 343–357. [Google Scholar] [CrossRef]
- Cho, J.R.; Lee, H.W. Calculation of stress intensity factors in 2-D linear fracture mechanics by Petrov–Galerkin natural element method. Int. J. Numer. Methods Eng. 2014, 98, 819–839. [Google Scholar] [CrossRef]
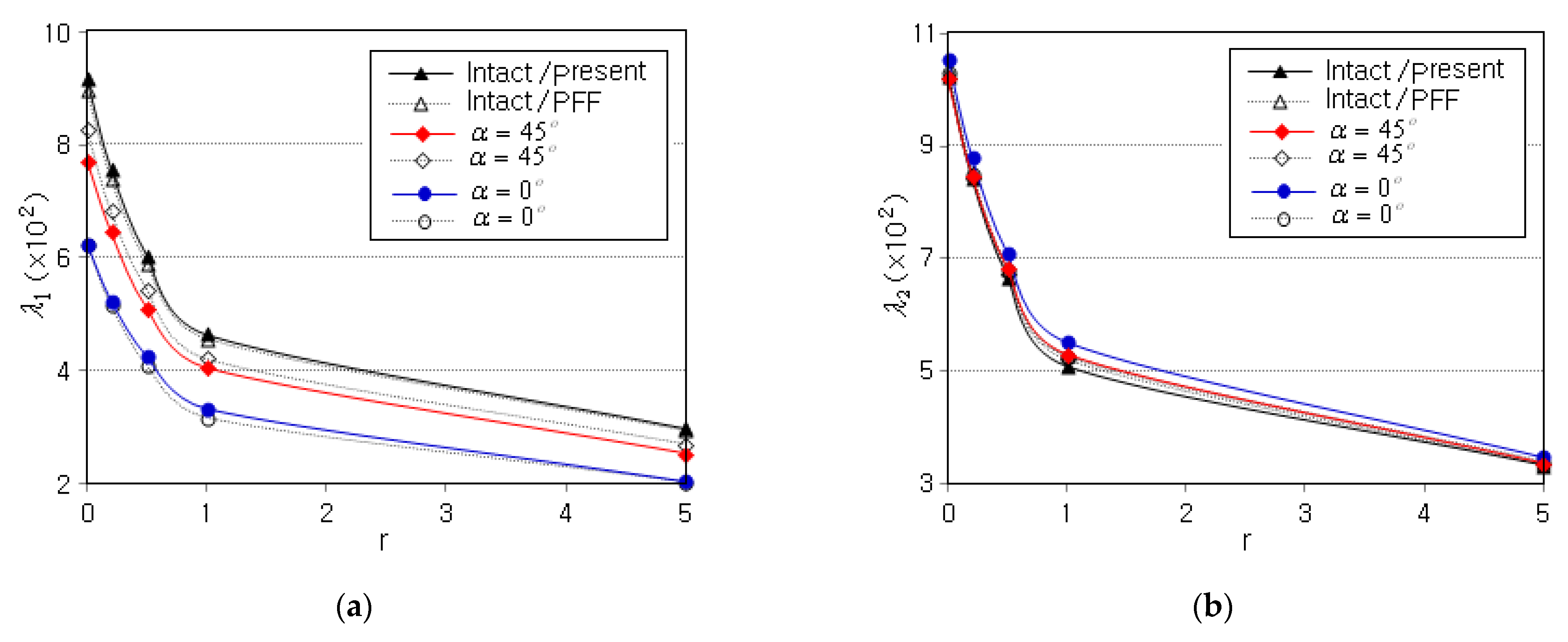
- Torabi, J.; Ansari, R. Numerical investigation on the buckling and vibration of cracked FG cylindrical panels based on the phase-field formulation. Eng. Fract. Mech. 2020, 228, 106895. [Google Scholar] [CrossRef]
- Ambati, M.; Gerasimov, T.; De Lorenzis, L. A review on phase-field models of brittle fracture and a new fast hybrid formulation. Comput. Mech. 2015, 55, 383–405. [Google Scholar] [CrossRef]
- Liang, Z.; Gou, J.J.; Zhang, C.; Wang, B.; Kramer, L. Investigation of molecular interactions between (10, 10) single-walled nanotube and Epon 862 resin/DETDA curing agent molecules. Mater. Sci. Eng. A 2004, 365, 228–234. [Google Scholar] [CrossRef]
- Zhu, P.; Lei, Z.X.; Liew, K.M. Static and free vibration analyses of carbon nanotube-reinforced composite plates using finite element method with first order shear deformation plate theory. Compos. Struct. 2012, 94, 1450–1460. [Google Scholar] [CrossRef]
- Baker, E.B.; Oden, J.T.; Carey, G.F. Finite Elements: An Introoduction; Prentice-Hall: Hoboken, NJ, USA, 1981; Volume 1. [Google Scholar]





| Items | Grid Density | ||||||
|---|---|---|---|---|---|---|---|
| 333.36 | 285.52 | 256.11 | 236.35 | 222.14 | 211.44 | 203.13 | |
| 64.11 | 40.56 | 26.08 | 16.35 | 9.36 | 4.09 | - | |
| Method | CBL | ||||||
|---|---|---|---|---|---|---|---|
| 0 | 0.2 | 0.5 | 1 | 5 | |||
| PFF [44] | Intact | 896.21 | 739.69 | 589.83 | 456.89 | 293.36 | |
| 1034.66 | 855.02 | 682.26 | 528.50 | 338.72 | |||
| 0 | 624.52 | 514.50 | 409.52 | 316.63 | 202.72 | ||
| 1030.11 | 851.56 | 679.88 | 526.91 | 336.65 | |||
| 45 | 826.08 | 681.53 | 543.20 | 420.56 | 269.69 | ||
| 1021.45 | 843.85 | 673.15 | 521.30 | 334.09 | |||
| 90 | 857.26 | 706.91 | 562.89 | 435.41 | 280.80 | ||
| 1023.02 | 845.07 | 674.02 | 521.88 | 334.56 | |||
| Present | Intact | 916.85 | 758.12 | 604.18 | 464.34 | 297.71 | |
| 1025.20 | 843.15 | 667.27 | 508.09 | 332.64 | |||
| 0 | 624.28 | 523.97 | 425.01 | 332.89 | 203.84 | ||
| 1054.42 | 879.79 | 707.95 | 550.78 | 346.69 | |||
| 45 | 771.78 | 644.99 | 519.25 | 404.32 | 252.76 | ||
| 1019.26 | 848.31 | 682.25 | 529.94 | 336.25 | |||
| 90 | 855.52 | 704.49 | 556.60 | 422.59 | 277.56 | ||
| 1080.01 | 901.52 | 726.01 | 559.74 | 359.09 | |||
| (%) | GPL Distribution Pattern | |||||
|---|---|---|---|---|---|---|
| FG-U | FG-O | FG-X | FG-Λ | |||
| 0.4 | 0 | 0.3 | 316.77 | 271.86 | 356.96 | 302.75 |
| 0.6 | 152.32 | 130.05 | 173.50 | 155.12 | ||
| 30 | 0.3 | 366.94 | 306.21 | 420.80 | 343.82 | |
| 0.6 | 214.71 | 184.49 | 242.64 | 198.83 | ||
| 60 | 0.3 | 413.23 | 338.52 | 480.32 | 383.46 | |
| 0.6 | 362.90 | 305.70 | 415.85 | 335.89 | ||
| 90 | 0.3 | 424.03 | 345.90 | 497.97 | 393.26 | |
| 0.6 | 374.39 | 308.85 | 436.16 | 349.08 | ||
| 0.8 | 0 | 0.3 | 496.85 | 405.29 | 558.78 | 456.70 |
| 0.6 | 239.29 | 194.36 | 281.43 | 238.49 | ||
| 30 | 0.3 | 576.37 | 452.59 | 682.77 | 519.28 | |
| 0.6 | 337.31 | 275.97 | 392.74 | 297.36 | ||
| 60 | 0.3 | 649.06 | 497.25 | 781.48 | 578.72 | |
| 0.6 | 570.04 | 454.20 | 675.06 | 502.39 | ||
| 90 | 0.3 | 666.03 | 508.43 | 812.90 | 598.02 | |
| 0.6 | 588.09 | 466.46 | 702.20 | 530.33 | ||
| Young’s Moduli (GPa) | Poisson’s Ratios | Shear Moduli (GPa) | ||||||
|---|---|---|---|---|---|---|---|---|
| 5646.6 | 7080.0 | 7080.0 | 0.175 | 0 | 0 | 1944.5 | 1944.5 | 1944.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cho, J.-R. Investigation of Buckling Behavior of Cracked FG Cylindrical Panels Reinforced by Graphene Platelets. Symmetry 2023, 15, 2162. https://doi.org/10.3390/sym15122162
Cho J-R. Investigation of Buckling Behavior of Cracked FG Cylindrical Panels Reinforced by Graphene Platelets. Symmetry. 2023; 15(12):2162. https://doi.org/10.3390/sym15122162
Chicago/Turabian StyleCho, Jin-Rae. 2023. "Investigation of Buckling Behavior of Cracked FG Cylindrical Panels Reinforced by Graphene Platelets" Symmetry 15, no. 12: 2162. https://doi.org/10.3390/sym15122162





