Statistical Analyses of a Class of Random Cyclooctatetraene Chain Networks with Respect to Several Topological Properties
Abstract
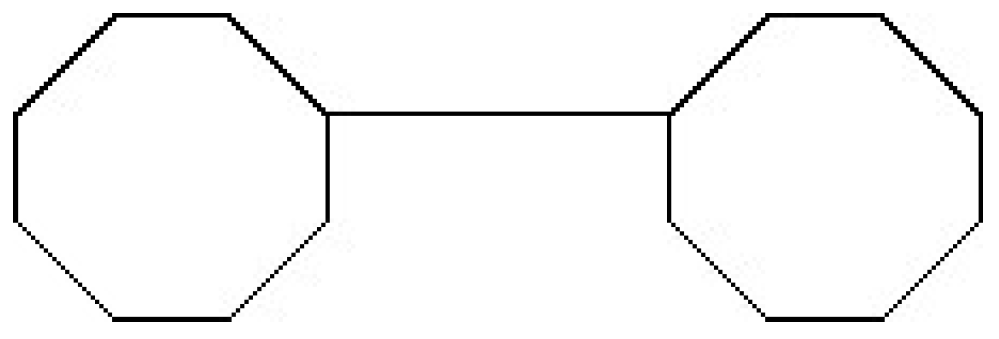
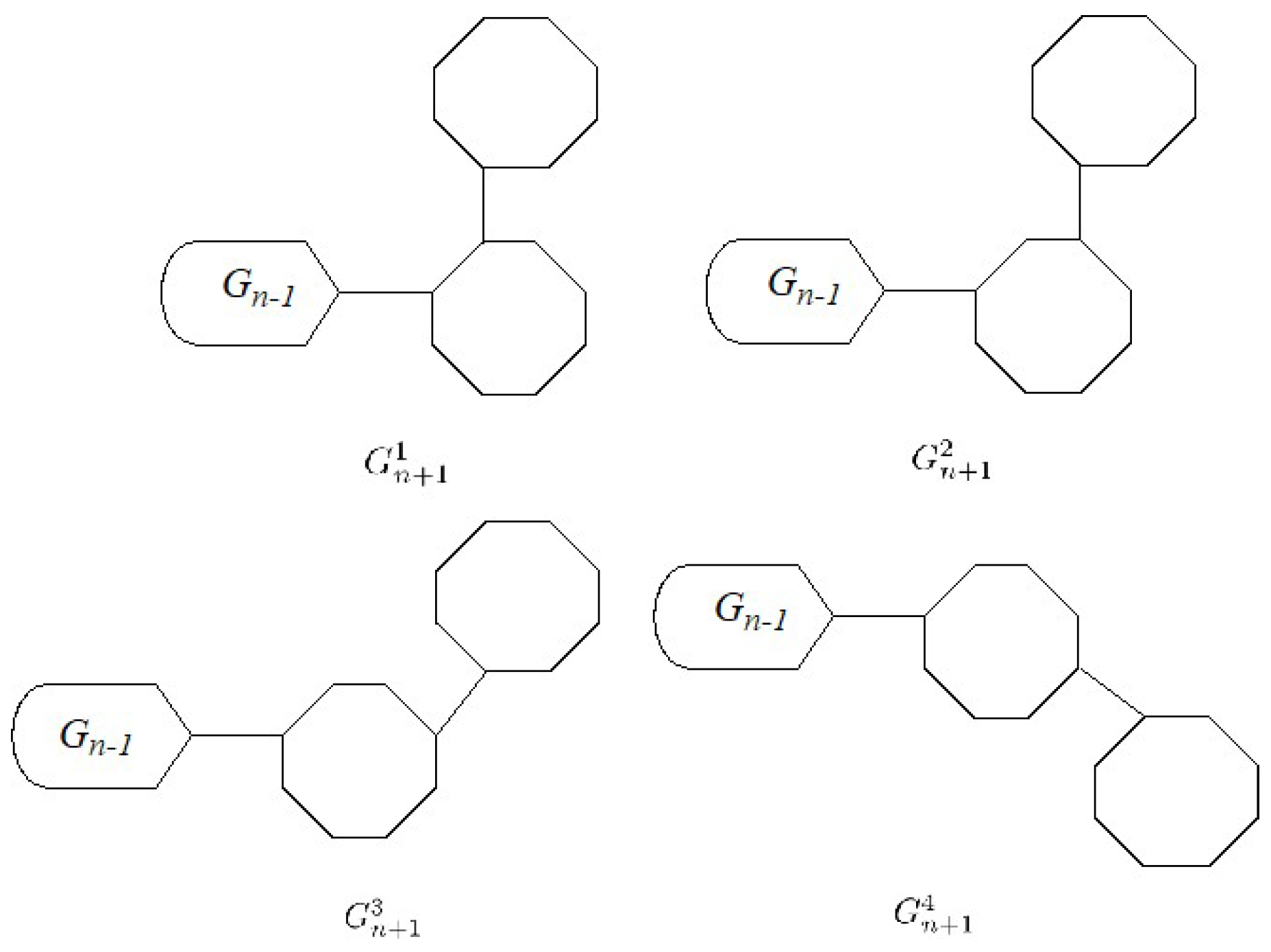
:1. Introduction
- is the probability that ;
- is the probability that
- is the probability that
- is the probability that .
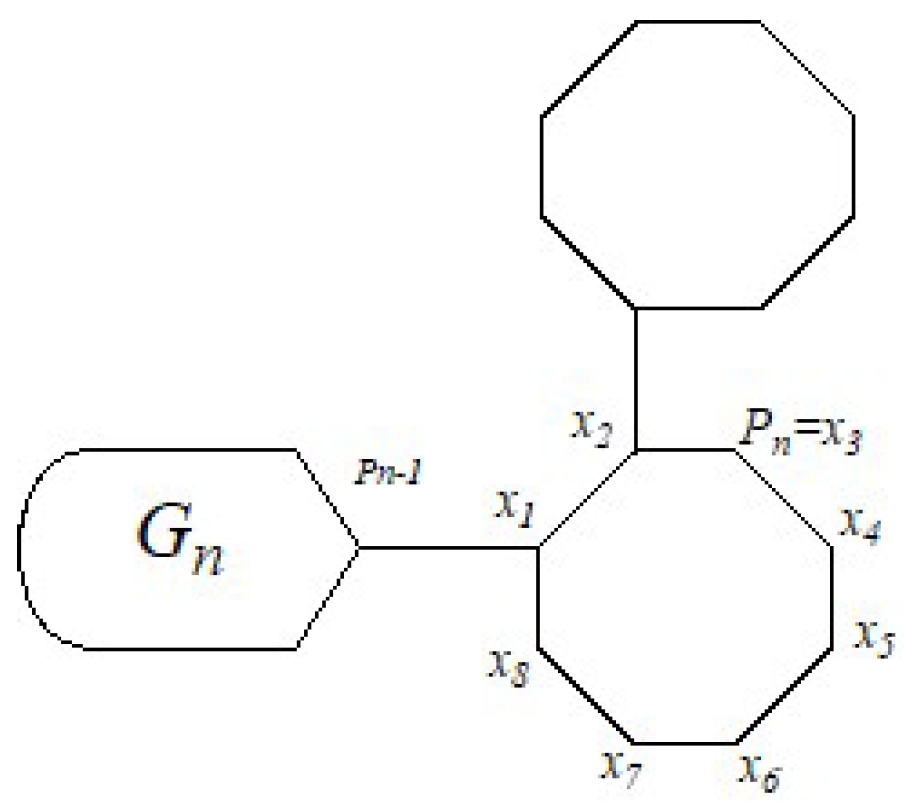
2. The Variances for the Gutman Index and Schultz Index of a Random Cyclooctatetraene Chain
3. The Variances of Multiplicative and Additive Degree-Kirchhoff Indices of a Random Cyclooctatetraene Chain
4. Concluding Remarks
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bondy, J.A.; Murty, U.S.R. Graph Theory; Springer: New York, NY, USA, 2008. [Google Scholar]
- Haruo, H.; Index, T. A Newly Proposed Quantity Characterizing the Topological Nature of Structural Isomers of Saturated Hydrocarbons. J. Bull. Chem. Soc. Jpn. 2006, 44, 2332–2339. [Google Scholar]
- Estrada, E. Edge Adjacency Relationships and a Novel Topological Index Related to Molecular Volume. J. Chem. Inf. Comput. Sci. 1995, 35, 31–33. [Google Scholar] [CrossRef]
- Person, W.B.; Pimentel, G.C.; Pitzer, K.S. The Structure of Cyclooctatetraene. J. Am. Chem. Soc. 1952, 74, 3437–3438. [Google Scholar] [CrossRef]
- Cope, A.C.; Pike, R.M.; Polyolefins, C. Cyclooctatetraene Derivatives from Copolymerization and Side Chain Modification. J. Am. Chem. Soc. 1953, 75, 3220–3223. [Google Scholar] [CrossRef]
- Luthe, G.; Jacobus, J.A.; Robertson, L.W. Receptor interactions by polybrominated diphenyl ethers versus polychlorinated biphenyls: A theoretical structure-activity assessment. Environ. Toxicol. Pharm. 2008, 25, 202–210. [Google Scholar] [CrossRef] [PubMed]
- Mathews, F.S.; Lipscomb, W.N. The Structure of Silver Cyclooctatetraene Nitrate. J. Phys. Chem. 1959, 63, 845–850. [Google Scholar] [CrossRef]
- Garavelli, M.; Bernardi, F.; Cembran, A. Cyclooctatetraene Computational Photo- and Thermal Chemistry: A Reactivity Model for Conjugated Hydrocarbons. J. Am. Chem. Soc. 2002, 124, 13770–13789. [Google Scholar] [CrossRef]
- Lo, D.H.; Whitehead, M.A. Molecular geometry and bond energy. III. Cyclooctatetraene and related compounds. J. Am. Chem. Soc. 1969, 91, 238–242. [Google Scholar] [CrossRef]
- Schwamm, R.J.; Anker, M.D.; Lein, M. Reduction vs. Addition: The Reaction of an Aluminyl Anion with 1,3,5,7-Cyclooctatetraene. J. Chem. 2019, 58, 1489–1493. [Google Scholar]
- Milas, N.; Nolan, J., Jr.; Otto, P.H.L. Notes-Ozonization of Cyclooctatetraene. J. Org. Chem. 1958, 23, 624–625. [Google Scholar] [CrossRef]
- Wiener, H. Structrual determination of paraffin boiling points. J. Am. Chem. Soc. 1947, 69, 17–20. [Google Scholar] [CrossRef] [PubMed]
- Buckley, F.; Harary, F. Distance in Graphs; Addison-Wesley: Reading, UK, 1989. [Google Scholar]
- Chen, A.L.; Zhang, F.J. Wiener index and perfect matchings in random phenylene chains. MATCH Commun. Math. Comput. Chem. 2009, 61, 623–630. [Google Scholar]
- Entringer, R.C.; Jackson, D.E.; Snyder, D.A. Distance in graphs. Czechoslov. Math. J. 1976, 26, 283–296. [Google Scholar] [CrossRef]
- Zhou, Q.N.; Wang, L.G.; Lu, Y. Wiener index and Harary index on Hamilton-connected graphs with large minimum degree. Discrete Appl. Math. 2018, 247, 180–185. [Google Scholar] [CrossRef]
- Zhang, L.I.; Li, Q.S.; Li, S.C.; Zhang, M.J. The expected values for the Schultz index, Gutman index, multiplicative degree-Kirchhoff index and additive degree-Kirchhoff index of a random polyphenylene chain. J. Discret. Appl. Math. 2020, 282, 243–256. [Google Scholar] [CrossRef]
- Zhang, J.L.; Peng, X.H.; Chen, H.L. The limiting behaviours for the Gutman index, Schultz index, multiplicative degree-Kirchhoff index and additive degree-Kirchhoff index of a random polyphenylene chain. Discrete Appl. Math. 2021, 299, 62–73. [Google Scholar] [CrossRef]
- Ayache, A.; Alameri, A. Topological indices of the mk-graph. J. Assoc. Arab. Univ. Basic Appl. Sci. 2017, 24, 283–291. [Google Scholar]
- Gutman, I. Selected properties of the Schultz molecular topological index. J. Chem. Inf. Comput. Sci. 1994, 34, 1087–1089. [Google Scholar] [CrossRef]
- Chen, S. Modified Schultz index of zig-zag polyhex nanotubes. J. Comput. Theor. Nanosci. 2009, 6, 1499–1503. [Google Scholar] [CrossRef]
- Farahani, M.R. Hosoya, Schultz, modified Schultz polynomials and their topological indices of benzene molecules: First members of polycyclic aromatic hydrocarbons (PAHs). Int. J. Theor. Chem. 2013, 1, 9–16. [Google Scholar]
- Heydari, A. On the modified Schultz index of C4C8(S) nanotubes and nanotorus. Digest. J. Nanomater. Biostruct. 2010, 5, 51–56. [Google Scholar]
- Xiao, Z.; Chen, S. The modified Schultz index of armchair polyhex nanotubes. J. Comput. Theor. Nanosci. 2009, 6, 1109–1114. [Google Scholar] [CrossRef]
- Mukwembi, S.; Munyira, S. MunyiraDegree distance and minimum degree. Bull. Aust. Math. Soc. 2013, 87, 255–271. [Google Scholar] [CrossRef]
- Qi, X.L.; Zhou, B.; Du, Z.B. The Kirchhoff indices and the matching numbers of unicyclic graphs. J. Appl. Math. Comput. 2016, 289. [Google Scholar] [CrossRef]
- Georgakopoulos, A. Uniqueness of electrical currents in a network of finite total resistance. J. Lond. Math. Soc. 2010, 82, 256–272. [Google Scholar] [CrossRef]
- Huang, S.B.; Zhou, J.; Bu, C.J. Some results on Kirchhoff index and degree-Kirchhoff index. MATCH Commun. Math. Comput. Chem. 2016, 75, 207–222. [Google Scholar]
- Cinkir, Z. Deletion and contraction identities for the resistance calues and the Kirchhoff index. Int. J. Quantum Chem. 2011, 111, 4030–4041. [Google Scholar] [CrossRef]
- Gupta, S.; Singh, M.; Madan, A.K. Eccentric distance sum: A novel graph invariant for predicting biological and physical properties. J. Math. Anal. Appl. 2002, 275, 386–401. [Google Scholar] [CrossRef]
- Klein, D.J.; Randić, M. Resistance distance. J. Math. Chem. 1993, 12, 81–95. [Google Scholar] [CrossRef]
- He, F.G.; Zhu, Z.X. Cacti with maximum eccentricity resistance-distance sum. Discret. Appl. Math. 2017, 219, 117–125. [Google Scholar] [CrossRef]
- Huang, Z.W.; Xi, X.Z.; Yuan, S.L. Some further results on the eccentric distance sum. J. Math. Anal. Appl. 2019, 470, 145–158. [Google Scholar] [CrossRef]
- Li, S.C.; Wei, W. Some edge-grafting transformations on the eccentricity resistance-distance sum and their applications. Discret. Appl. Math. 2016, 211, 130–142. [Google Scholar] [CrossRef]
- Somodi, M. On the Ihara zeta function and resistance distance-based indices. Linear Algebra Appl. 2017, 513, 201–209. [Google Scholar] [CrossRef]
- Yang, Y.J.; Klein, D.J. A note on the Kirchhoff and additive degree-Kirchhoff indices of graphs. Z. Naturforsch. A 2015, 70, 459–463. [Google Scholar] [CrossRef]
- Chen, H.; Zhang, F. Resistance distance and the normalized Laplacian spectrum. Discret. Appl. Math. 2007, 155, 654–661. [Google Scholar] [CrossRef]
- Tang, M.; Priebe, C.E. Limit theorems for eigenvectors of the normalized Laplacian for random graphs. Ann. Statist. 2018, 46, 2360–2415. [Google Scholar] [CrossRef]
- Chung, F.R.K. Spectral Graph Theory; American Mathematical Society: Providence, RI, USA, 1997. [Google Scholar]
- Gutman, I.; Feng, L.; Yu, G. Degree resistance distance of unicyclic graphs. Trans. Comb. 2012, 1, 27–40. [Google Scholar]
- Qi, J.F.; Ni, J.B.; Geng, X.Y. The expected values for the Kirchhoff indices in the random cyclooctatetraene and spiro chains. J. Discret. Appl. Math. 2022, 321, 240–249. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tao, C.; Tang, S.; Geng, X. Statistical Analyses of a Class of Random Cyclooctatetraene Chain Networks with Respect to Several Topological Properties. Symmetry 2023, 15, 1971. https://doi.org/10.3390/sym15111971
Tao C, Tang S, Geng X. Statistical Analyses of a Class of Random Cyclooctatetraene Chain Networks with Respect to Several Topological Properties. Symmetry. 2023; 15(11):1971. https://doi.org/10.3390/sym15111971
Chicago/Turabian StyleTao, Chen, Shengjun Tang, and Xianya Geng. 2023. "Statistical Analyses of a Class of Random Cyclooctatetraene Chain Networks with Respect to Several Topological Properties" Symmetry 15, no. 11: 1971. https://doi.org/10.3390/sym15111971



