Interval Fuzzy Segments

Abstract

In this paper, we bring together two concepts related to uncertainty and vagueness: fuzzy numbers and intervals. With them, we build a new structure whose elements we call interval fuzzy segments. We have undertaken this based on the conviction that the fuzzy numbers are a correct representation of the real numbers under situations of indeterminacy. We also believe that if it makes sense to consider the set of real numbers between two real bounds, then it also makes sense to consider the set of all the fuzzy numbers between two fuzzy number bounds. In this way, we extend the concept of real interval to the concept of interval fuzzy segment defined by two fuzzy bounds and a transition mapping that leads from the lower fuzzy bound to the upper fuzzy bound and this transition mapping generates the set of all the fuzzy numbers comprised between those fuzzy bounds. At the same time, this transition mapping brings the concept of interval fuzzy segment closer to the concept of line segment.

1. Introduction

We can apply both probabilistic and non-probabilistic methods in order to deal with uncertainty, imprecision, indiscernibility and vagueness. If we focus on non-probabilistic methods, the theory of fuzzy sets and interval theory have been widely used over the past few decades to quantify both uncertainty and imprecision.

The theory of fuzzy sets, introduced by Zadeh [1], provides a non-probabilistic way to represent uncertainty using membership functions. Interval analysis is mainly based on studies by Moore [2], using real intervals as a tool to treat non-probabilistic uncertainty and also imprecision.

In most traditional research, fuzzy set theory and interval theory are applied separately to carry out non-probabilistic analysis of uncertainty and imprecision. However, in some situations, it may be useful to combine fuzzy uncertainty and interval uncertainty in some way.

There are studies in which fuzzy numbers and intervals are combined to provide new tools to describe and treat uncertainty. For instance, in the field of engineering, to analyze structural response in special situations, the method called fuzzy interval uncertainty [3] has been proposed. In that method, structures simultaneously have fuzzy parameters and interval parameters, but these are independent. That is to say, the method works with variables that have a degree of uncertainty, evaluated with fuzzy numbers, and it also works with some other variables that have a degree of inaccuracy, which are quantified by intervals. In this way, all the operations necessary to be able to work simultaneously with fuzzy numbers and intervals are defined.

In some studies, we can also find the concept of fuzzy-boundary interval [4,5,6,7]. In this case, the uncertain parameters of structures are treated as interval variables, but the intervals, instead of having two real (determined) bounds, the lower and upper bounds are considered to be fuzzy numbers. A fuzzy-boundary interval is the set formed by all the real numbers bounded by two fuzzy numbers. However, the idea of fuzzy-boundary intervals is not the same that we propose in this paper.

The best-known proposal that combines fuzzy numbers and intervals is the called interval-valued fuzzy numbers also called interval type-2 fuzzy numbers [8,9,10]. The interval-valued fuzzy numbers arise when we attempt to represent the numerical uncertainty related to the degree of membership. When working with fuzzy numbers, membership functions associate an exact number with each element of the support of the fuzzy number which is understood as a membership value. When working with interval-valued fuzzy numbers, the degree of membership is given by an interval. We can find applications of interval type-2 fuzzy numbers in many scientific disciplines, such as decision-making [11,12,13,14,15], engineering applications [16,17,18], graph theory [19] and control theory [20,21] among others.

Nowadays, there has been a significant increase of the research on higher order forms of fuzzy logic systems [22,23,24,25].

A generalization of interval-valued fuzzy numbers are the so-called generalized type-2 fuzzy numbers, formally introduced by Zadeh in [8], where the membership degree of each element is given by another fuzzy set defined over the interval $\left[0,1\right]$. Several authors have studied these sets, as [26,27].

The interval fuzzy segments introduced in this paper are not meant to generalize the set of fuzzy numbers just as the interval-valued fuzzy numbers and the type-2 fuzzy numbers do.

Interval fuzzy segments are based on a generalization of intervals or segments from the point of view of sets of fuzzy numbers comprised between two fuzzy bounds. Hence, an interval fuzzy segment can be considered as closer to a fuzzy-boundary interval and not closer to type-2 fuzzy numbers.

The goal we want to achieve with this article is to provide a tool that is useful not only to solve situations where there is uncertainty or inaccuracy, but also to treat those in which there appears inaccuracy in the uncertainty. There are other tools, such as intervals or fuzzy numbers, that allow us to work efficiently in front of problems in which there is uncertainty or inaccuracy separately. The results obtained when working with intervals is also an interval, that is, we obtain two bounds that define the set of real numbers that we must consider globally as the result, and we can’t highlight any value in the interval. Working with fuzzy numbers, we obtain a result that is also a fuzzy number, which means that we can establish a graduation of the membership for specific values given by the fuzzy result. Both intervals and fuzzy numbers are useful tools in the appropriate contexts. However, they do not allow to express the inaccuracy in the uncertainty neither of the data nor the result. Moreover, using interval fuzzy segments, we introduce elements of variation that allow us to represent in a more realistic way the approach of real problems.

2. Preliminaries

2.1. Intervals

Given $a,b\in \mathbb{R}$ such that $a\le b$, the classical interval $\left[a,b\right]$ is defined as $\left[a,b\right]=\left\{x\in \mathbb{R}\mid a\le x\le b\right\}$, where $\mathbb{R}$ is the set of real numbers. The set of classical intervals is represented by $I\left(\mathbb{R}\right)$ and it has been extensively studied. We can highlight the preliminary studies by Sunaga [28], and further consolidation of classical interval theory by Moore [2] and Nickel [29]. Operations between classical intervals have been studied by Kaucher [30].

Classical intervals present some deficiencies. Perhaps one of the most fundamental difficulties arises from the fact that interval subtraction is not the inverse operation of interval addition: if $\left[a,b\right]$ is an interval with $a\ne b$, there exists no interval $\left[x,y\right]$ such that $\left[a,b\right]+\left[x,y\right]=\left[0,0\right]$ because the addition rule would imply $\left[a,b\right]+\left[x,y\right]=\left[a+x,b+y\right]=\left[0,0\right]$ and then $\left[x,y\right]=\left[-a,-b\right]$ with $a<b$ implying $-a>-b$; that is to say, $\left[-a,-b\right]$ would be no interval at all.

More generally, the solution $\left[x,y\right]$ of the interval equation $\left[a,b\right]+\left[x,y\right]=\left[c,d\right]$ satisfies $a+x=c$ and $b+y=d$. This solution exists in $I\left(\mathbb{R}\right)$ only under the condition $b-a\le d-c$, but even when the interval equation has a solution, this solution cannot be obtained by any interval syntactic computation on $I\left(\mathbb{R}\right)$.

With the dual operator introduced by Gardeñes [31] and represented by $dual\left(\left[a,b\right]\right)$, we can consider:

$$\left[a,b\right]-dual\left(\left[c,d\right]\right)=\left[a-c,b-d\right].$$

(1)

The dual operator allows us to find a solution to some interval problems in which no solution was possible without using this operator. Using the dual operator, we can solve some equations. For instance, the solution to the equation $\left[2,5\right]+\left[x,y\right]=\left[3,7\right]$ is $\left[x,y\right]=\left[3,7\right]-dual\left(\left[2,5\right]\right)$ and hence $\left[x,y\right]=\left[1,2\right].$ For more information, see Sainz [32].

Two important relationships in the set of classical intervals are the inequality $\left(\le \right)$ and the inclusion $\left(\subseteq \right)$ relationships. The former, between two intervals $\left[a,b\right]$ and $\left[c,d\right]$ is defined as:

$$\left[a,b\right]\le \left[c,d\right]\mathrm{iff}a\le c\mathrm{and}b\le d.$$

(2)

Although it is unusual, the interval inequality ≤ can be characterized by:

$$\left[a,b\right]\le \left[c,d\right]\mathrm{iff}\forall \lambda \in \left[0,1\right]\left(\left(1-\lambda \right)a+\lambda b\right)\le \left(\left(1-\lambda \right)c+\lambda d\right).$$

(3)

The inequality relationship ≤ between intervals is not a total order, since, given two intervals $\left[a,b\right]$ and $\left[c,d\right],$ we cannot always verify one of the relations $\left[a,b\right]\le \left[c,d\right]$ or $\left[c,d\right]\le \left[a,b\right]$, but the following will always exist: $inf\left\{\left[a,b\right],\left[c,d\right]\right\}=\left[min\left\{a,c\right\},min\left\{b,d\right\}\right]$ and $sup\left\{\left[a,b\right],\left[c,d\right]\right\}=\left[max\left\{a,c\right\},max\left\{b,d\right\}\right]$, although they do not necessarily have to coincide with the two given intervals. Hence, the set of classical intervals is a lattice with regard to the ≤ relation.

We have also mentioned the inclusion relationship, defined by set inclusion, which can be expressed using the interval coordinates as:

$$\left[a,b\right]\subseteq \left[c,d\right]\mathrm{iff}a\ge c\mathrm{and}b\le d.$$

(4)

The infimum and supremum of two intervals with regard to the inclusion relationship are named Meet and Join, respectively, and they do not always exist. This is why the set of classical intervals with regard to the inclusion relationship is not a lattice.

2.2. Fuzzy Numbers

Fuzzy sets were introduced by Zadeh [1]. Although they are without a doubt the most widely accepted tool to represent uncertainty, there are some other non-probabilistic tools used to represent indiscernibility, vagueness, imprecision and also uncertainty: rough sets [33,34,35]; marks [32]; and numerical clouds [36], among others.

If X is a universal set, a fuzzy set A in X can be defined by its membership function. The membership function of a fuzzy set A is a mapping ${\mu }_A:X\to \left[0,1\right]$ which assigns a real number ${\mu }_A\left(x\right)\in \left[0,1\right]$ to each element $x\in X$. The value ${\mu }_A\left(x\right)$ quantifies the level of membership that the element x has of the fuzzy set A.

A fuzzy number A is a fuzzy set of the real line. The set of fuzzy numbers is represented by $FN.$ Its membership function, ${\mu }_A:\mathbb{R}\to \left[0,1\right]$ must be normal (that is, $\exists x\in \mathbb{R}$ such that ${\mu }_A\left(x\right)=1$), fuzzy convex ($\forall x,y\in \mathbb{R}\forall \lambda \in \left[0,1\right],{\mu }_A\left(\lambda x+\left(1-\lambda \right)y\right)\ge {\mu }_A\left(x\right)\wedge {\mu }_A\left(y\right)$), upper semi-continuous and such that the closure of the set $\left\{x\in \mathbb{R}\mid {\mu }_A\left(x\right)>0\right\}$ is bounded [37].

The membership function of a fuzzy number A can be described as:

$${\mu }_A\left(x\right)=\left\{\begin{array}{cc}{f}_L\left(x\right),& \mathrm{if}{a}_1\le x<a_2,\\ 1,& \mathrm{if}{a}_2\le x\le a_3,\\ f_U\left(x\right),& \mathrm{if}{a}_3<x\le a_4,\\ 0,& \mathrm{otherwise},\end{array}\right.$$

(5)

where $a_1,a_2,a_3$ and $a_4$ are real numbers such that $a_1<a_2\le a_3<a_4$; $f_L$ is a real-valued strictly increasing and right-continuous function; and $f_U$ is a real-valued strictly decreasing and left-continuous function.

Given a fuzzy set A of X with membership function ${\mu }_A$, and given a real number $\alpha \in \left[0,1\right]$, the $\alpha$-cut of A is the crisp set denoted by $A^{\alpha }$ and is defined by:

$$A^{\alpha }=\left\{\begin{array}{cc}\left\{x\in X\mid {\mu }_A\left(x\right)\ge \alpha \right\},& \mathrm{if}\alpha \in \left(0,1\right],\hfill \\ \\ \overline{\left\{x\in X\mid {\mu }_A\left(x\right)>0\right\}},& \mathrm{if}\alpha =0,\hfill \end{array}\right.$$

(6)

where $\overline{\left\{x\in X\mid {\mu }_A\left(x\right)>0\right\}}$ is the closure of the set $\left\{x\in X\mid {\mu }_A\left(x\right)>0\right\}$.

A fuzzy number A can be represented by its membership function or alternatively by the set of its $\alpha$-cuts: $A={\left\{A^{\alpha }\right\}}_{\alpha \in \left[0,1\right]}.$

The $\alpha$-cut $A^0$ is called the support of A and it is denoted by $supp\left(A\right).$ The $\alpha$-cut $A^1$ is called the core of A and is denoted by $core\left(A\right)$.

When the core of a fuzzy number is point-wise, we will refer to it as a punctual-core fuzzy number. The set of the punctual-core fuzzy numbers will be represented by $\stackrel{•}{FN}$.

The arithmetic operations on fuzzy numbers can be approached either by the direct use of the membership function by Zadeh’s extension principle [1] or in terms of arithmetic operations on their $\alpha$-cuts that we will use in this paper. Thus, given A and B two fuzzy numbers expressed by $A={\left\{A^{\alpha }\right\}}_{\alpha \in \left[0,1\right]}$ and $B={\left\{B^{\alpha }\right\}}_{\alpha \in \left[0,1\right]}$, if $\omega$ is an interval binary operator, the extension of $\omega$ on A and B, denoted by W, is defined as

$$AWB={\left\{A^{\alpha }\omega B^{\alpha }\right\}}_{\alpha \in \left[0,1\right].}$$

(7)

The partial ordering of fuzzy numbers is defined from the partial ordering of their $\alpha$-cuts (see [38]), that is, let A and B be two fuzzy numbers:

$$A\le B\mathrm{iff}\forall \alpha \in \left[0,1\right],A^{\alpha }\le B^{\alpha }.$$

(8)

Note that on this basis of the concept of the partial order, we can also introduce the concept of the fuzzy number with definite sign: positive or negative.

$$A\ge 0\mathrm{iff}\forall \alpha \in \left[0,1\right],A^{\alpha }\ge \left[0,0\right]\mathrm{or}A\le 0\mathrm{iff}\forall \alpha \in \left[0,1\right],A^{\alpha }\le \left[0,0\right].$$

(9)

3. Interval Fuzzy Segments

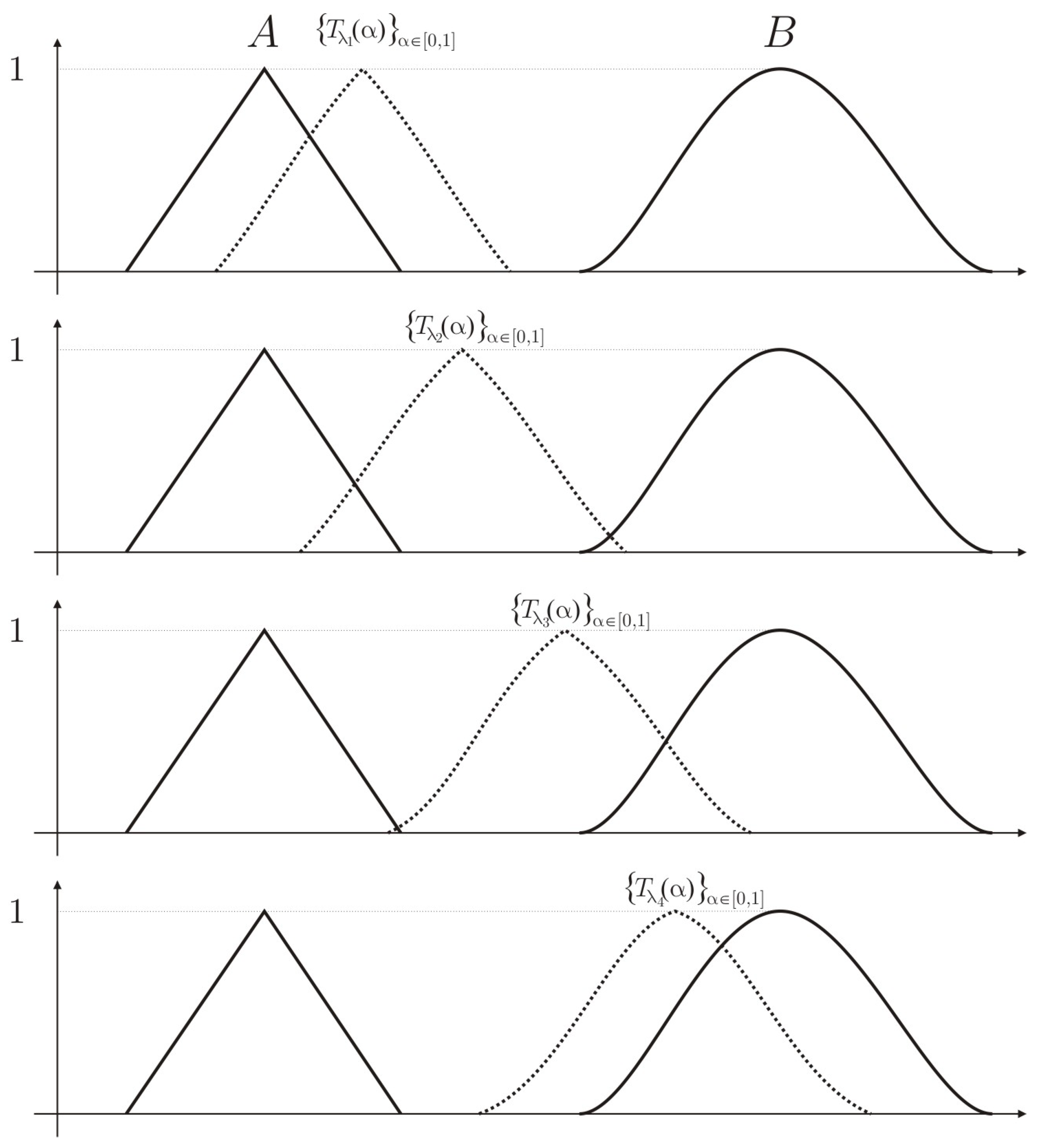
In this section, we will introduce a new set whose elements will be called interval fuzzy segments, as a generalization of a real interval. In the interval fuzzy segments, we will consider fuzzy numbers whose core is a point-wise interval instead of considering real numbers. To obtain a consistent definition of interval fuzzy segments, we will first introduce what we define as a fuzzy numbers S-transformation.

Definition 1. (Fuzzy numbers S-transformation)

Let A and B be two punctual-core fuzzy numbers, that is $A,B\in \stackrel{•}{FN},$ such that $A\le B$. The fuzzy numbers S-transformation from A to B is a mapping

$$\begin{array}{ccc}T:\left[0,1\right]& ⟶& F\left(\left[0,1\right];I\left(\mathbb{R}\right)\right)\\ \lambda & ⟼& T_{\lambda },\end{array}$$

where $\forall \lambda \in \left[0,1\right],T_{\lambda }$ is a function

$$\begin{array}{ccc}{T}_{\lambda }:\left[0,1\right]& ⟶& I\left(\mathbb{R}\right)\\ \alpha & ⟼& T_{\lambda }\left(\alpha \right)\end{array}$$

that satisfies the following properties:

1.

${\left\{T_0\left(\alpha \right)\right\}}_{\alpha \in \left[0,1\right]}=A,$

2.

${\left\{T_1\left(\alpha \right)\right\}}_{\alpha \in \left[0,1\right]}=B,$

3.

$\forall \lambda \in \left[0,1\right]{\left\{T_{\lambda }\left(\alpha \right)\right\}}_{\alpha \in \left[0,1\right]}\in \stackrel{•}{FN},$

4.

$\forall {\lambda }_1,{\lambda }_2\in \left[0,1\right]$ if ${\lambda }_1<{\lambda }_2$, then ${\left\{T_{{\lambda }_1}\left(\alpha \right)\right\}}_{\alpha \in \left[0,1\right]}\le {\left\{T_{{\lambda }_2}\left(\alpha \right)\right\}}_{\alpha \in \left[0,1\right]}$.

Given $A,B\in \stackrel{•}{FN},$ such that $A\le B$, the existence of fuzzy numbers S-transformation from A to B is proved in Proposition 8.

Definition 2. (Interval fuzzy segment)

Given $A,B\in \stackrel{•}{FN}$ such that $A\le B$ and given T, a fuzzy numbers S-transformation, if we consider the set of all the punctual-core fuzzy numbers between A and B obtained by the S-transformation T, that is:

$$\left\{C\in \stackrel{•}{FN}\mid \exists \lambda \in \left[0,1\right]\left({\left\{T_{\lambda }\left(\alpha \right)\right\}}_{\alpha \in \left[0,1\right]}=C\right)\right\}.$$

(10)

Then, the interval fuzzy segment with bounds A and B and S-transformation T is represented by ${\left[A,B\right]}_T$ and is defined as the pair:

$${\left[A,B\right]}_T=\left(\left\{C\in \stackrel{•}{FN}\mid \exists \lambda \in \left[0,1\right]\left({\left\{T_{\lambda }\left(\alpha \right)\right\}}_{\alpha \in \left[0,1\right]}=C\right)\right\},T\right).$$

(11)

The set of the interval fuzzy segments is represented by $IFS.$

We call the set:

$$\left\{C\in \stackrel{•}{FN}\mid \exists \lambda \in \left[0,1\right]\left({\left\{T_{\lambda }\left(\alpha \right)\right\}}_{\alpha \in \left[0,1\right]}=C\right)\right\},$$

(12)

the support of an interval fuzzy segment with bounds A and B and S-transformation T, and we represent it by supp$\left({\left[A,B\right]}_T\right)$.

Notice that given $A,B\in \stackrel{•}{FN}$ such that $A\le B,$ there may be various S-transformations that generate the same support. For instance, the S-transformations $T_{\lambda }\left(\alpha \right)=A^{\alpha }+\lambda \left(B^{\alpha }-dual\left(A^{\alpha }\right)\right)$ and $T_{\lambda }^{\prime }\left(\alpha \right)=A^{\alpha }+{\lambda }^2\left(B^{\alpha }-dual\left(A^{\alpha }\right)\right)$ generate the same support, that is supp$\left({\left[A,B\right]}_T\right)=$supp$\left({\left[A,B\right]}_{T^{\prime }}\right)$; however, the interval fuzzy segments will not be the same: ${\left[A,B\right]}_T\ne {\left[A,B\right]}_{T^{\prime }}$ as the interval fuzzy segments will take into account not only the support generated, but also how that support has been generated. We will study different S-transformations in Section 6.

Definition 3. ($\left(\lambda ,\alpha \right)$-cut of an interval fuzzy segment)

Given $\mathcal{A}={\left[A,B\right]}_T\in IFS$ and given a pair of real numbers $\left(\lambda ,\alpha \right)\in \left[0,1\right]\times \left[0,1\right]$, the $\left(\lambda ,\alpha \right)$-cut of $\mathcal{A}$ is the interval denoted by ${\mathcal{A}}_{\lambda }^{\alpha }$ and defined as:

$${\mathcal{A}}_{\lambda }^{\alpha }=T_{\lambda }\left(\alpha \right).$$

(13)

Notice that the set of $\left(0,\alpha \right)$-cuts ${\left\{{\mathcal{A}}_0^{\alpha }\right\}}_{\alpha \in \left[0,1\right]}$ and the set of $\left(1,\alpha \right)$-cuts ${\left\{{\mathcal{A}}_1^{\alpha }\right\}}_{\alpha \in \left[0,1\right]}$ correspond to the fuzzy bounds of the interval fuzzy segment $\mathcal{A}$, that is, ${\left\{{\mathcal{A}}_0^{\alpha }\right\}}_{\alpha \in \left[0,1\right]}=A$ and ${\left\{{\mathcal{A}}_1^{\alpha }\right\}}_{\alpha \in \left[0,1\right]}=B$.

An interval fuzzy segment $\mathcal{A}$ can be represented as the pair that consists of the set of its $\left(\lambda ,\alpha \right)$-cuts and the fuzzy numbers S-transformation T, thus:

$$\mathcal{A}=\left({\left\{{\left\{{\mathcal{A}}_{\lambda }^{\alpha }\right\}}_{\alpha \in \left[0,1\right]}\right\}}_{\lambda \in \left[0,1\right]},T\right).$$

(14)

Using the fuzzy numbers S-transformation from A to B, we can evaluate the membership function of every fuzzy number $C\in$supp$\left({\left[A,B\right]}_T\right),$ taking into account that there will exist a value $\lambda \in \left[0,1\right]$ such that $C={\left\{T_{\lambda }\left(\alpha \right)\right\}}_{\alpha \in \left[0,1\right]}$ (see Figure 1). As the infimum and supremum of a real interval $\left[a,b\right]$ are defined by $inf\left(\left[a,b\right]\right)=a$ and $sup\left(\left[a,b\right]\right)=b$, it follows that:

$$T_{\lambda }\left(\alpha \right)=\left[inf\left(T_{\lambda }\left(\alpha \right)\right),sup\left(T_{\lambda }\left(\alpha \right)\right)\right]\in I\left(\mathbb{R}\right)$$

(15)

and hence:

$${\mu }_C\left(x\right)=\left\{\begin{array}{cc}{\left(inf\left(T_{\lambda }\right)\right)}^{-1}\left(x\right),& \mathrm{if}inf\left(T_{\lambda }\left(0\right)\right)\le x<T_{\lambda }\left(1\right),\hfill \\ 1,& \mathrm{if}x=T_{\lambda }\left(1\right),\hfill \\ {\left(sup\left(T_{\lambda }\right)\right)}^{-1}\left(x_{}\right),& \mathrm{if}{T}_{\lambda }\left(1\right)<x\le sup\left(T_{\lambda }\left(0\right)\right),\hfill \\ 0,& \mathrm{otherwise}.\hfill \end{array}\right.$$

(16)

4. Arithmetic Operations on $\mathit{IFS}$

Arithmetic operators on the set of the interval fuzzy segments are based on the following two properties:

• Each interval fuzzy segment can fully and uniquely be represented by its $\left(\lambda ,\alpha \right)$-cuts.
• For all $\lambda ,\alpha \in \left[0,1\right]$, the $\left(\lambda ,\alpha \right)$-cuts of each interval fuzzy segment constitute a closed interval of real numbers.

These properties enable us to define arithmetic operations on $IFS$ in terms of the arithmetic operations of their $\left(\lambda ,\alpha \right)$-cuts.

Definition 4. (Arithmetic operations)

Let $\mathcal{A}={\left[\underline{A},\overline{A}\right]}_T$ and $\mathcal{B}={\left[\underline{B},\overline{B}\right]}_{T^{\prime }}$ be two $IFS$. Then, the four arithmetic operations on $IFS$ are defined as follows:

(a) 

${\left[\underline{A},\overline{A}\right]}_T+{\left[\underline{B},\overline{B}\right]}_{T^{\prime }}={\left[\underline{A}+\underline{B},\overline{A}+\overline{B}\right]}_{\mathcal{T}}$ where ${\mathcal{T}}_{\lambda }=T_{\lambda }+T_{\lambda }^{\prime }.$

(b) 

${\left[\underline{A},\overline{A}\right]}_T-{\left[\underline{B},\overline{B}\right]}_{T^{\prime }}={\left[\underline{A}-\overline{B},\overline{A}-\underline{B}\right]}_{\mathcal{T}}$ where ${\mathcal{T}}_{\lambda }=T_{\lambda }-T_{1-\lambda }^{\prime }$.

(c) 

If $\underline{A},\overline{A},\underline{B},\overline{B}$ they all have definite sign, ${\left[\underline{A},\overline{A}\right]}_T\ast {\left[\underline{B},\overline{B}\right]}_{T^{\prime }}=\mathcal{C}$ and

(c.1) 

$\mathcal{C}={\left[\underline{A}\ast \underline{B},\overline{A}\ast \overline{B}\right]}_{\mathcal{T}}$ where ${\mathcal{T}}_{\lambda }=T_{\lambda }\ast T_{\lambda }^{\prime }$ if $\underline{A}\ge 0,\overline{A}\ge 0,\underline{B}\ge 0,\overline{B}\ge 0,$

(c.2) 

$\mathcal{C}={\left[\overline{A}\ast \underline{B},\overline{A}\ast \overline{B}\right]}_{\mathcal{T}}$ where ${\mathcal{T}}_{\lambda }=T_1\ast T_{\lambda }^{\prime }$ if $\underline{A}\ge 0,\overline{A}\ge 0,\underline{B}<0,\overline{B}\ge 0,$

(c.3) 

$\mathcal{C}={\left[\overline{A}\ast \underline{B},\underline{A}\ast \overline{B}\right]}_{\mathcal{T}}$ where ${\mathcal{T}}_{\lambda }=T_{1-\lambda }\ast T_{\lambda }^{\prime }$ if $\underline{A}\ge 0,\overline{A}\ge 0,\underline{B}<0,\overline{B}<0,$

(c.4) 

$\mathcal{C}={\left[\underline{A}\ast \overline{B},\overline{A}\ast \overline{B}\right]}_{\mathcal{T}}$ where ${\mathcal{T}}_{\lambda }=T_{\lambda }\ast T_1^{\prime }$ if $\underline{A}<0,\overline{A}\ge 0,\underline{B}\ge 0,\overline{B}\ge 0,$

(c.5) 

$\mathcal{C}={\left[\overline{A}\ast \underline{B},\underline{A}\ast \underline{B}\right]}_{\mathcal{T}}$ where ${\mathcal{T}}_{\lambda }=T_{1-\lambda }\ast T_0^{\prime }$ if $\underline{A}<0,\overline{A}\ge 0,\underline{B}<0,\overline{B}<0,$

(c.6) 

$\mathcal{C}={\left[\underline{A}\ast \overline{B},\overline{A}\ast \underline{B}\right]}_{\mathcal{T}}$ where ${\mathcal{T}}_{\lambda }=T_{\lambda }\ast T_{1-\lambda }^{\prime }$ if $\underline{A}<0,\overline{A}<0,\underline{B}\ge 0,\overline{B}\ge 0,$

(c.7) 

$\mathcal{C}={\left[\underline{A}\ast \overline{B},\underline{A}\ast \underline{B}\right]}_{\mathcal{T}}$ where ${\mathcal{T}}_{\lambda }=T_0\ast T_{1-\lambda }^{\prime }$ if $\underline{A}<0,\overline{A}<0,\underline{B}<0,\overline{B}\ge 0,$

(c.8) 

$\mathcal{C}={\left[\overline{A}\ast \overline{B},\underline{A}\ast \underline{B}\right]}_{\mathcal{T}}$ where ${\mathcal{T}}_{\lambda }=T_{1-\lambda }\ast T_{1-\lambda }^{\prime }$ if $\underline{A}<0,\overline{A}<0,\underline{B}<0,\overline{B}<0,$

(c.9) 

$\mathcal{C}={\left[min\left(\underline{A}\ast \overline{B},\overline{A}\ast \underline{B}\right),max\left(\underline{A}\ast \underline{B},\overline{A}\ast \overline{B}\right)\right]}_{\mathcal{T}}$ if $\underline{A}<0,\overline{A}\ge 0,\underline{B}<0,\overline{B}\ge 0$, and there exist $min\left(\underline{A}\ast \overline{B},\overline{A}\ast \underline{B}\right)$ and $max\left(\underline{A}\ast \underline{B},\overline{A}\ast \overline{B}\right),$ where ${\mathcal{T}}_{\lambda }$ can be deduced from the previous cases.

(d) 

If $\underline{A},\overline{A},\underline{B},\overline{B}$ all have definite signs and $\forall C\in \mathcal{B},0\notin$supp$\left(C\right),$ then ${\left[\underline{A},\overline{A}\right]}_T/{\left[\underline{B},\overline{B}\right]}_{T^{\prime }}={\left[\underline{A},\overline{A}\right]}_T\ast {\left[1/\overline{B},1/\underline{B}\right]}_{1/T_{1-\lambda }^{\prime }}$

Proposition 1.

If we denote by ⨀ an operator, and $⨀\in \left\{+,-,\ast ,/\right\},$ then given $\mathcal{A}$ and $\mathcal{B}$, two $IFS$, the calculus $\mathcal{C}=\mathcal{A}⨀\mathcal{B}$, where $\mathcal{C}=$${\left[\underline{C},\overline{C}\right]}_{\mathcal{T}}$ is an interval fuzzy segment, that is, the application $\mathcal{T}$ is a fuzzy numbers S-transformation as it satisfies:

1.

${\left\{{\mathcal{T}}_0\left(\alpha \right)\right\}}_{\alpha \in \left[0,1\right]}=\underline{C},$

2.

${\left\{{\mathcal{T}}_1\left(\alpha \right)\right\}}_{\alpha \in \left[0,1\right]}=\overline{C},$

3.

$\forall \lambda \in \left[0,1\right]{\left\{{\mathcal{T}}_{\lambda }\left(\alpha \right)\right\}}_{\alpha \in \left[0,1\right]}\in \stackrel{•}{FN},$

4.

$\forall {\lambda }_1,{\lambda }_2\in \left[0,1\right]$if ${\lambda }_1<{\lambda }_2$, then ${\left\{{\mathcal{T}}_{{\lambda }_1}\left(\alpha \right)\right\}}_{\alpha \in \left[0,1\right]}\le {\left\{{\mathcal{T}}_{{\lambda }_2}\left(\alpha \right)\right\}}_{\alpha \in \left[0,1\right]}$.

Proof. 

We will prove the cases (b) , (c.3) and (c.4) (Definition 4). The demonstration in the other cases follows in a similar way.

(b) 

${\left[\underline{A},\overline{A}\right]}_T-{\left[\underline{B},\overline{B}\right]}_{T^{\prime }}={\left[\underline{A}-\overline{B},\overline{A}-\underline{B}\right]}_{\mathcal{T}}$, where ${\mathcal{T}}_{\lambda }=T_{\lambda }-T_{1-\lambda }^{\prime }.$

• If $\lambda =0$, ${\left\{{\mathcal{T}}_0\left(\alpha \right)\right\}}_{\alpha \in \left[0,1\right]}={\left\{T_0\left(\alpha \right)-T_1^{\prime }\left(\alpha \right)\right\}}_{\alpha \in \left[0,1\right]}=\underline{A}-\overline{B}.$
• If $\lambda =1$, ${\left\{{\mathcal{T}}_1\left(\alpha \right)\right\}}_{\alpha \in \left[0,1\right]}={\left\{T_1\left(\alpha \right)-T_0^{\prime }\left(\alpha \right)\right\}}_{\alpha \in \left[0,1\right]}=\overline{A}-\underline{B}.$
• Given $\lambda \in \left[0,1\right]$, if ${\alpha }_1\le {\alpha }_2,$ then, as ${\left\{T_{\lambda }\left(\alpha \right)\right\}}_{\alpha \in \left[0,1\right]}$ is a fuzzy number, it will be $T_{\lambda }\left({\alpha }_2\right)\subseteq T_{\lambda }\left({\alpha }_1\right)$. In the same way, as $1-\lambda \in \left[0,1\right]$, ${\left\{T_{1-\lambda }^{\prime }\left(\alpha \right)\right\}}_{\alpha \in \left[0,1\right]}$ is also a fuzzy number and $T_{1-\lambda }^{\prime }\left({\alpha }_2\right)\subseteq T_{1-\lambda }^{\prime }\left({\alpha }_1\right)$. Applying the inclusivity property of the interval difference (see [32]), it follows that $T_{\lambda }\left({\alpha }_2\right)-T_{1-\lambda }^{\prime }\left({\alpha }_2\right)\subseteq T_{\lambda }\left({\alpha }_1\right)-T_{1-\lambda }^{\prime }\left({\alpha }_1\right)$ hence ${\mathcal{T}}_{\lambda }\left({\alpha }_2\right)\subseteq {\mathcal{T}}_{\lambda }\left({\alpha }_1\right).$
  Moreover, ${\mathcal{T}}_{\lambda }\left(1\right)$ is a point-wise interval, as both $T_{\lambda }\left(1\right)$ and $T_{1-\lambda }^{\prime }\left(1\right)$ are point-wise intervals, since ${\left\{T_{\lambda }\left(\alpha \right)\right\}}_{\alpha \in \left[0,1\right]}$ and ${\left\{T_{1-\lambda }^{\prime }\left(\alpha \right)\right\}}_{\alpha \in \left[0,1\right]}$ are punctual-core fuzzy numbers.
• If ${\lambda }_1,{\lambda }_2\in \left[0,1\right]$ and ${\lambda }_1<{\lambda }_2$, then $1-{\lambda }_1>1-{\lambda }_2,$ hence $T_{1-{\lambda }_1}^{\prime }\left(\alpha \right)\ge T_{1-{\lambda }_2}^{\prime }\left(\alpha \right)$ and $-T_{1-{\lambda }_1}^{\prime }\left(\alpha \right)\le -T_{1-{\lambda }_2}^{\prime }\left(\alpha \right).$ As $T_{{\lambda }_1}\left(\alpha \right)\le T_{{\lambda }_2}\left(\alpha \right),$ it follows $T_{{\lambda }_1}\left(\alpha \right)-T_{1-{\lambda }_1}^{\prime }\left(\alpha \right)\le T_{{\lambda }_2}\left(\alpha \right)-T_{1-{\lambda }_2}^{\prime }\left(\alpha \right)$, which is ${\mathcal{T}}_{{\lambda }_1}\left(\alpha \right)\le {\mathcal{T}}_{{\lambda }_2}\left(\alpha \right).$

(c.3) 

${\left[\underline{A},\overline{A}\right]}_T\ast {\left[\underline{B},\overline{B}\right]}_{T^{\prime }}={\left[\overline{A}\ast \underline{B},\underline{A}\ast \overline{B}\right]}_{\mathcal{T}}$, where ${\mathcal{T}}_{\lambda }=T_{1-\lambda }\ast T_{\lambda }^{\prime }$ if $\underline{A}\ge 0,\overline{A}\ge 0,\underline{B}<0,\overline{B}<0.$

• If $\lambda =0$, ${\left\{{\mathcal{T}}_0\left(\alpha \right)\right\}}_{\alpha \in \left[0,1\right]}={\left\{T_1\left(\alpha \right)\ast T_0^{\prime }\left(\alpha \right)\right\}}_{\alpha \in \left[0,1\right]}=\overline{A}\ast \underline{B}.$
• If $\lambda =1$, ${\left\{{\mathcal{T}}_1\left(\alpha \right)\right\}}_{\alpha \in \left[0,1\right]}={\left\{T_0\left(\alpha \right)-T_1^{\prime }\left(\alpha \right)\right\}}_{\alpha \in \left[0,1\right]}=\underline{A}\ast \overline{B}.$
• Given $\lambda \in \left[0,1\right]$, if ${\alpha }_1\le {\alpha }_2,$ then, as ${\left\{T_{\lambda }^{\prime }\left(\alpha \right)\right\}}_{\alpha \in \left[0,1\right]}$ is a fuzzy number, it will be $T_{\lambda }^{\prime }\left({\alpha }_2\right)\subseteq T_{\lambda }^{\prime }\left({\alpha }_1\right)$ . In the same way, as $1-\lambda \in \left[0,1\right]$, ${\left\{T_{1-\lambda }\left(\alpha \right)\right\}}_{\alpha \in \left[0,1\right]}$ is also a fuzzy number and $T_{1-\lambda }\left({\alpha }_2\right)\subseteq T_{1-\lambda }\left({\alpha }_1\right)$. Applying the inclusivity property of the product, it follows that $T_{1-\lambda }\left({\alpha }_2\right)\ast T_{\lambda }^{\prime }\left({\alpha }_2\right)\subseteq T_{1-\lambda }\left({\alpha }_1\right)\ast T_{\lambda }^{\prime }\left({\alpha }_1\right),$ hence ${\mathcal{T}}_{\lambda }\left({\alpha }_2\right)\subseteq {\mathcal{T}}_{\lambda }\left({\alpha }_1\right).$
  Moreover, ${\mathcal{T}}_{\lambda }\left(1\right)$ is a point-wise interval, as both $T_{1-\lambda }\left(1\right)$ and $T_{\lambda }^{\prime }\left(1\right)$ are point-wise intervals, since ${\left\{T_{1-\lambda }\left(\alpha \right)\right\}}_{\alpha \in \left[0,1\right]}$ and ${\left\{T_{\lambda }^{\prime }\left(\alpha \right)\right\}}_{\alpha \in \left[0,1\right]}$ are punctual-core fuzzy numbers.
• If ${\lambda }_1,{\lambda }_2\in \left[0,1\right]$ and ${\lambda }_1<{\lambda }_2$, then $1-{\lambda }_2<1-{\lambda }_1.$ Consequently, $T_{1-{\lambda }_2}\left(\alpha \right)\le T_{1-{\lambda }_1}\left(\alpha \right)$ and $T_{{\lambda }_1}^{\prime }\left(\alpha \right)\le T_{{\lambda }_2}^{\prime }\left(\alpha \right)$. Moreover, as $\underline{A}\ge 0,\overline{A}\ge 0$, $\underline{B}<0,\overline{B}<0$, it will be $0\le T_{1-{\lambda }_2}\left(\alpha \right)\le T_{1-{\lambda }_1}\left(\alpha \right)$ and $T_{{\lambda }_1}^{\prime }\left(\alpha \right)\le T_{{\lambda }_2}^{\prime }\left(\alpha \right)<0,$ thus $T_{1-{\lambda }_1}\left(\alpha \right)\ast T_{{\lambda }_1}^{\prime }\left(\alpha \right)\le T_{1-{\lambda }_2}\left(\alpha \right)\ast T_{{\lambda }_2}^{\prime }\left(\alpha \right),$ which is ${\mathcal{T}}_{{\lambda }_1}\left(\alpha \right)\le {\mathcal{T}}_{{\lambda }_2}\left(\alpha \right).$

(c.4) 

${\left[\underline{A},\overline{A}\right]}_T\ast {\left[\underline{B},\overline{B}\right]}_{T^{\prime }}={\left[\underline{A}\ast \overline{B},\overline{A}\ast \overline{B}\right]}_{\mathcal{T}},$ where ${\mathcal{T}}_{\lambda }=T_{\lambda }\ast T_1^{\prime }$ if $\underline{A}<0,\overline{A}\ge 0,\underline{B}\ge 0,\overline{B}\ge 0.$

• If $\lambda =0$, ${\left\{{\mathcal{T}}_0\left(\alpha \right)\right\}}_{\alpha \in \left[0,1\right]}={\left\{T_0\left(\alpha \right)\ast T_1^{\prime }\left(\alpha \right)\right\}}_{\alpha \in \left[0,1\right]}=\underline{A}\ast \overline{B}.$
• If $\lambda =1$, ${\left\{{\mathcal{T}}_1\left(\alpha \right)\right\}}_{\alpha \in \left[0,1\right]}={\left\{T_1\left(\alpha \right)-T_1^{\prime }\left(\alpha \right)\right\}}_{\alpha \in \left[0,1\right]}=\overline{A}\ast \overline{B}.$
• Given $\lambda \in \left[0,1\right]$, if ${\alpha }_1\le {\alpha }_2$, then, as ${\left\{T_{\lambda }\left(\alpha \right)\right\}}_{\alpha \in \left[0,1\right]}$ is a fuzzy number, $T_{\lambda }\left({\alpha }_2\right)\subseteq T_{\lambda }\left({\alpha }_1\right)$. Moreover, ${\left\{T_1^{\prime }\left(\alpha \right)\right\}}_{\alpha \in \left[0,1\right]}$ is also a fuzzy number, and, consequently, $T_1^{\prime }\left({\alpha }_2\right)\subseteq T_1^{\prime }\left({\alpha }_1\right)$. Applying the inclusivity property of the product, it follows that $T_{\lambda }\left({\alpha }_2\right)\ast T_1^{\prime }\left({\alpha }_2\right)\subseteq T_{\lambda }\left({\alpha }_1\right)\ast T_1^{\prime }\left({\alpha }_1\right)$ hence ${\mathcal{T}}_{\lambda }\left({\alpha }_2\right)\subseteq {\mathcal{T}}_{\lambda }\left({\alpha }_1\right).$
  Moreover, ${\mathcal{T}}_{\lambda }\left(1\right)$ is a point-wise interval, as both $T_{\lambda }\left(1\right)$ and $T_1^{\prime }\left(1\right)$ are point-wise intervals since ${\left\{T_{\lambda }\left(\alpha \right)\right\}}_{\alpha \in \left[0,1\right]}$ and ${\left\{T_1^{\prime }\left(\alpha \right)\right\}}_{\alpha \in \left[0,1\right]}$ are punctual-core fuzzy numbers.
• If ${\lambda }_1,{\lambda }_2\in \left[0,1\right]$ and ${\lambda }_1<{\lambda }_2$ then $T_{{\lambda }_1}\left(\alpha \right)\le T_{{\lambda }_2}\left(\alpha \right).$ Moreover, $T_1^{\prime }\left(\alpha \right)\ge 0$ as $\underline{B}\ge 0$ and $\overline{B}\ge 0.$ Thus, $T_{{\lambda }_1}\left(\alpha \right)\ast T_1^{\prime }\left(\alpha \right)\le T_{{\lambda }_2}\left(\alpha \right)\ast T_1^{\prime }\left(\alpha \right)$ that is ${\mathcal{T}}_{{\lambda }_1}\left(\alpha \right)\le {\mathcal{T}}_{{\lambda }_2}\left(\alpha \right).$

 ☐

In all the cases, $\underline{C}$ and $\overline{C}$ are fuzzy numbers as they are obtained operating fuzzy numbers. Moreover, $\underline{C}\le \overline{C}$ since $\mathcal{T}$ verifies the properties 1, 2 and 4.

5. Inequality and Inclusion Relationship

In this section, we define the inequality and the inclusion relationships between interval fuzzy segments and we analyze some of their properties.

5.1. Inequality Relationship: The Lattice $\left(IFS,\le \right)$

From the expression for the interval inequality relationship ≤ described in Equation (3), we define the inequality relationship between interval fuzzy segments as follows:

Definition 5.

Given ${\left[A,B\right]}_T$ and ${\left[C,D\right]}_{T^{\prime }}$ two interval fuzzy segments, we define

$${\left[A,B\right]}_T\le {\left[C,D\right]}_{T^{\prime }}\iff \left(\forall \lambda \in \left[0,1\right]\forall \alpha \in \left[0,1\right]\left(T_{\lambda }\left(\alpha \right)\le T_{\lambda }^{\prime }\left(\alpha \right)\right)\right).$$

(17)

From this definition, it is obvious that, if ${\left[A,B\right]}_T\le {\left[C,D\right]}_{T^{\prime }}$, then $A\le C$ and $B\le D$, as $\forall \alpha \in \left[0,1\right]$ $A^{\alpha }=T_0\left(\alpha \right)\le T_0^{\prime }\left(\alpha \right)=B^{\alpha }.$ In the same way, $B^{\alpha }=T_1\left(\alpha \right)\le T_1^{\prime }\left(\alpha \right)=D^{\alpha }$, but we must emphasize that the inequalities $A\le C$ and $B\le D$ are not enough to define the inequality ${\left[A,B\right]}_T\le {\left[C,D\right]}_{T^{\prime }}$.

Observe that given $\mathcal{X}={\left[\underline{X},\overline{X}\right]}_{{}_{\mathcal{T}}}\in IFS$, $\mathcal{X}\ge 0$ if $\forall \lambda \in \left[0,1\right]\forall \alpha \in \left[0,1\right]{\mathcal{T}}_{\lambda }\left(\alpha \right)\ge 0.$

In particular, this ensures that $\forall \alpha \in \left[0,1\right]\left({\underline{X}}^{\alpha }\ge 0\mathrm{and}{\overline{X}}^{\alpha }\ge 0\right).$

Proposition 2.

Given ${\left[A,B\right]}_T$,${\left[C,D\right]}_{T^{\prime }}\in IFS$, if there exists ${\left[X,Y\right]}_{\mathcal{T}}\ge 0$ such that ${\left[A,B\right]}_T+{\left[X,Y\right]}_{\mathcal{T}}={\left[C,D\right]}_{T^{\prime }}$, then ${\left[A,B\right]}_T\le {\left[C,D\right]}_{T^{\prime }}$

Proof. 

If there exists ${\left[X,Y\right]}_{\mathcal{T}}\ge 0$ such that ${\left[A,B\right]}_T+{\left[X,Y\right]}_{\mathcal{T}}={\left[C,D\right]}_{T^{\prime }}$, from the addition of interval fuzzy segments (Definition 4), it follows that:

$$\forall \lambda \in \left[0,1\right]\forall \alpha \in \left[0,1\right]\left({\left(T+\mathcal{T}\right)}_{\lambda }\left(\alpha \right)=T_{\lambda }^{\prime }\left(\alpha \right)\right)$$

(18)

and then $\forall \lambda \in \left[0,1\right]\forall \alpha \in \left[0,1\right]\left(T_{\lambda }\left(\alpha \right)+{\mathcal{T}}_{\lambda }\left(\alpha \right)=T_{\lambda }^{\prime }\left(\alpha \right)\right).$ As ${\mathcal{T}}_{\lambda }\left(\alpha \right)\ge 0,$ we obtain $T_{\lambda }\left(\alpha \right)\le T_{\lambda }^{\prime }\left(\alpha \right).$ ☐

This proposition is not an equivalence, as can be observed by taking ${\left[A,B\right]}_T={\left[\left(1,2,3\right),\left(7,9,11\right)\right]}_T$ and ${\left[C,D\right]}_{T^{\prime }}={\left[\left(5,7,9\right),\left(10,13,16\right)\right]}_{T^{\prime }}$. It is the case that ${\left[\left(1,2,3\right),\left(7,9,11\right)\right]}_T\le {\left[\left(5,7,9\right),\left(10,13,16\right)\right]}_{T^{\prime }}$, but the expression ${\left[A,B\right]}_T+{\left[X,Y\right]}_{\mathcal{T}}={\left[C,D\right]}_{T^{\prime }}$ has no solution in the set of the interval fuzzy segments, as X and Y should be $X=\left(4,5,6\right)$ and $Y=\left(3,4,5\right)$, for which it is not the case that $X\le Y$.

Proposition 3.

The inequality relationship ≤ studied in Definition 5 is a partial order.

Proof. 

Given $\mathcal{A}={\left[\underline{A},\overline{A}\right]}_T,$ $\mathcal{M}={\left[\underline{M},\overline{M}\right]}_{T^{\prime }}$ and $\mathcal{P}={\left[\underline{P},\overline{P}\right]}_{T^{″}}$ then:

• $\mathcal{A}\le \mathcal{A}$ as $T_{\lambda }\left(\alpha \right)\le T_{\lambda }\left(\alpha \right).$
• If $\mathcal{A}\le \mathcal{M}$ and $\mathcal{M}\le \mathcal{A}$, then $T_{\lambda }\left(\alpha \right)\le T_{\lambda }^{\prime }\left(\alpha \right)$ and $T_{\lambda }^{\prime }\left(\alpha \right)\le T_{\lambda }\left(\alpha \right)$ and thus $T_{\lambda }\left(\alpha \right)=T_{\lambda }^{\prime }\left(\alpha \right)$, which is $\mathcal{A}=\mathcal{M}.$
• If $\mathcal{A}\le \mathcal{M}$ and $\mathcal{M}\le \mathcal{P}$, then $T_{\lambda }\left(\alpha \right)\le T_{\lambda }^{\prime }\left(\alpha \right)$ and $T_{\lambda }^{\prime }\left(\alpha \right)\le T_{\lambda }^{″}\left(\alpha \right)$ and thus $T_{\lambda }\left(\alpha \right)\le T_{\lambda }^{″}\left(\alpha \right),$ which is $\mathcal{A}\le \mathcal{P}.$

 ☐

The inequality relationship ≤ on the interval fuzzy segments is not a total order, as neither the interval nor the fuzzy inequality are.

Proposition 4.

Given $\mathcal{A}={\left[\underline{A},\overline{A}\right]}_T$ and $\mathcal{M}={\left[\underline{M},\overline{M}\right]}_{T^{\prime }}$ two interval fuzzy segments, then:

1.

$inf\left\{\mathcal{A},\mathcal{M}\right\}=\mathcal{X}={\left[\underline{X},\overline{X}\right]}_{\mathcal{T}}$, where

$\underline{X}=inf\left\{\underline{A},\underline{M}\right\},$$\overline{X}=inf\left\{\overline{A},\overline{M}\right\}$ and ${\mathcal{T}}_{\lambda }\left(\alpha \right)=inf\left\{T_{\lambda }\left(\alpha \right),T_{\lambda }^{\prime }\left(\alpha \right)\right\}.$

2.

$sup\left\{\mathcal{A},\mathcal{M}\right\}=\mathcal{Y}={\left[\underline{Y},\overline{Y}\right]}_{\mathcal{T}}$, where

$\underline{Y}=sup\left\{\underline{A},\underline{M}\right\},$$\overline{Y}=sup\left\{\overline{A},\overline{M}\right\}$ and ${\mathcal{T}}_{\lambda }\left(\alpha \right)=sup\left\{T_{\lambda }\left(\alpha \right),T_{\lambda }^{\prime }\left(\alpha \right)\right\}.$

Proof. 

• As $\underline{A}\le \overline{A}$ and $\underline{M}\le \overline{M}$, then $inf\left\{\underline{A},\underline{M}\right\}\le inf\left\{\overline{A},\overline{M}\right\}$ and as all the cores are point-wise intervals, their infimum will also be a point-wise interval. Moreover, the conditions required in Definition 1 are fulfilled, as we prove below:

  (a)

  If $\lambda =0,$ then ${\mathcal{T}}_0\left(\alpha \right)=inf\left\{T_0\left(\alpha \right),T_0^{\prime }\left(\alpha \right)\right\}=inf\left\{\underline{A},\underline{M}\right\}.$

  (b)

  If $\lambda =1,$ then ${\mathcal{T}}_1\left(\alpha \right)=inf\left\{T_1\left(\alpha \right),T_1^{\prime }\left(\alpha \right)\right\}=inf\left\{\overline{A},\overline{M}\right\}.$

  (c)

  $\left(\forall \lambda \in \left[0,1\right]\right),{\mathcal{T}}_{\lambda }\left(\alpha \right)=inf\left\{T_{\lambda }\left(\alpha \right),T_{\lambda }^{\prime }\left(\alpha \right)\right\}\in \stackrel{•}{FN}$ as both $T_{\lambda }\left(\alpha \right)$ and $T_{\lambda }^{\prime }\left(\alpha \right)$ are punctual-core fuzzy numbers.

  (d)

  If ${\lambda }_1,{\lambda }_2\in \left[0,1\right]$ and ${\lambda }_1<{\lambda }_2$, then ${\mathcal{T}}_{{\lambda }_1}\left(\alpha \right)\le {\mathcal{T}}_{{\lambda }_2}\left(\alpha \right)$ as ${\mathcal{T}}_{{\lambda }_1}\left(\alpha \right)=inf\left\{T_{{\lambda }_1}\left(\alpha \right),T_{{\lambda }_1}^{\prime }\left(\alpha \right)\right\}\le inf\left\{T_{{\lambda }_2}\left(\alpha \right),T_{{\lambda }_2}^{\prime }\left(\alpha \right)\right\}={\mathcal{T}}_{{\lambda }_2}\left(\alpha \right).$

  Moreover, $\left(\forall \lambda \in \left[0,1\right]\right)\left(\forall \alpha \in \left[0,1\right]\right)\left({\mathcal{T}}_{\lambda }\left(\alpha \right)\le T_{\lambda }\left(\alpha \right)\mathrm{and}{\mathcal{T}}_{\lambda }\left(\alpha \right)\le T_{\lambda }^{\prime }\left(\alpha \right)\right).$
  Thus,

  $${\left[\underline{X},\overline{X}\right]}_{\mathcal{T}}\le {\left[\underline{A},\overline{A}\right]}_T\mathrm{and}{\left[\underline{X},\overline{X}\right]}_{\mathcal{T}}\le {\left[\underline{M},\overline{M}\right]}_{T^{\prime }}.$$

  (19)
  Moreover, if $\mathcal{P}={\left[\underline{P},\overline{P}\right]}_{T^{\prime \prime }}\in IFS$ is such that ${\left[\underline{P},\overline{P}\right]}_{T^{″}}\le {\left[\underline{A},\overline{A}\right]}_T$ and ${\left[\underline{P},\overline{P}\right]}_{T^{″}}\le {\left[\underline{M},\overline{M}\right]}_{T^{\prime }}$, then it will follow that:

  $$\begin{array}{ccc}\left({\left[\underline{P},\overline{P}\right]}_{T^{″}}\le {\left[\underline{A},\overline{A}\right]}_T\right)\hfill & \iff & \left(\forall \lambda \in \left[0,1\right]\right)\left(\forall \alpha \in \left[0,1\right]\right)\left(T_{\lambda }^{″}\left(\alpha \right)\le T_{\lambda }\left(\alpha \right)\right),\hfill \\ \left({\left[\underline{P},\overline{P}\right]}_{T^{″}}\le {\left[\underline{M},\overline{M}\right]}_{T^{\prime }}\right)\hfill & \iff & \left(\forall \lambda \in \left[0,1\right]\right)\left(\forall \alpha \in \left[0,1\right]\right)\left(T_{\lambda }^{″}\left(\alpha \right)\le T_{\lambda }^{\prime }\left(\alpha \right)\right),\hfill \end{array}$$

  and therefore

  $$T_{\lambda }^{″}\left(\alpha \right)\le inf\left\{T_{\lambda }\left(\alpha \right),T_{\lambda }^{\prime }\left(\alpha \right)\right\},$$

  (20)

  thus

  $${\left[\underline{P},\overline{P}\right]}_{T^{″}}\le {\left[\underline{X},\overline{X}\right]}_{\mathcal{T}}.$$

  (21)
• In a similar way:

 ☐

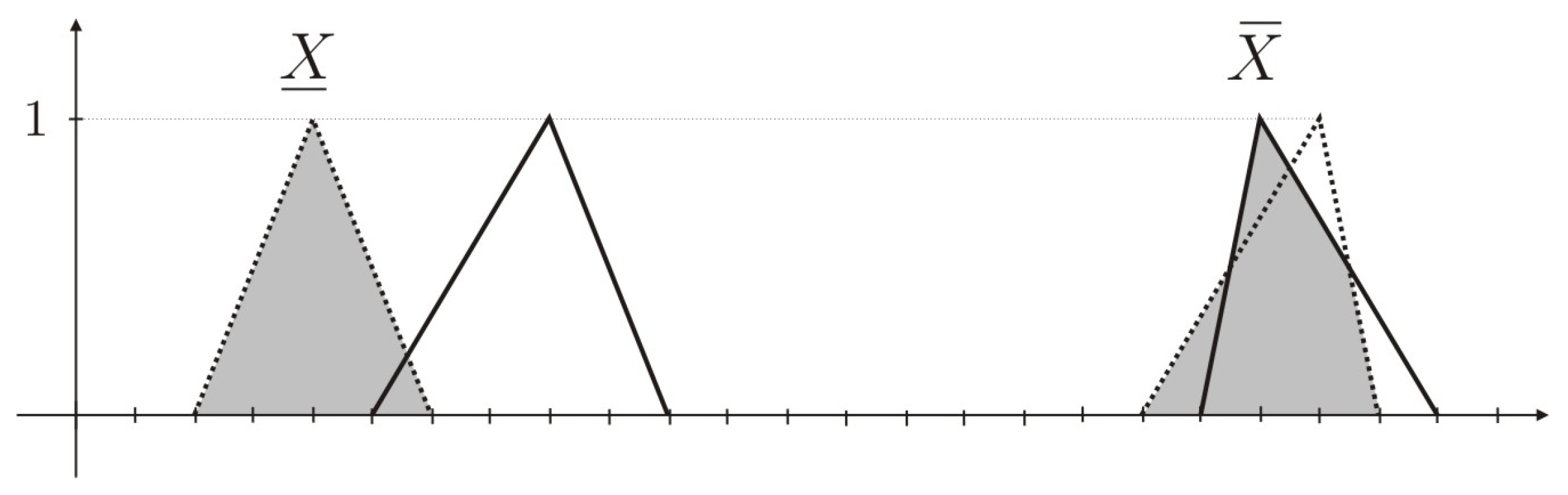
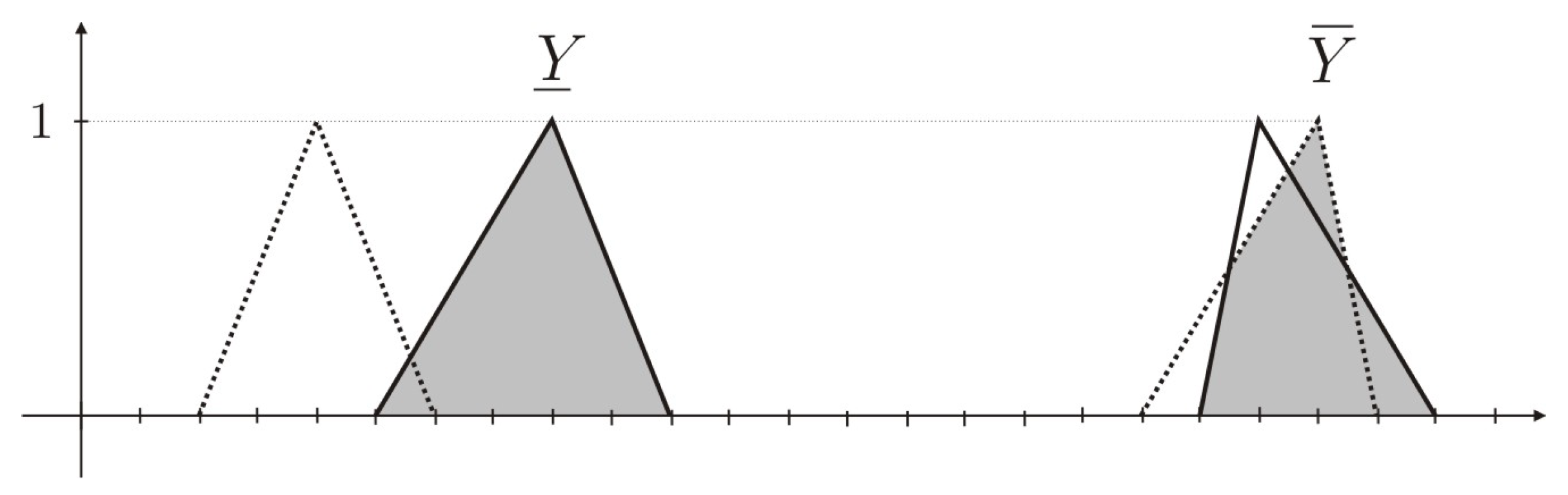
Example 1.

Considering $\mathcal{A}={\left[\underline{A},\overline{A}\right]}_T$ and $\mathcal{M}={\left[\underline{M},\overline{M}\right]}_{T^{\prime }}$ where $\underline{A},\overline{A},\underline{M}$ and $\overline{M}$ are the triangular fuzzy numbers $\underline{A}=\left(2,4,6\right)$, $\overline{A}=\left(18,21,22\right)$, $\underline{M}=\left(5,8,10\right)$ and $\overline{M}=\left(19,20,23\right)$ (Figure 2), the infimum $\mathcal{X}={\left[\underline{X},\overline{X}\right]}_{\mathcal{T}}=inf\left\{\mathcal{A},\mathcal{M}\right\}$ is illustrated in Figure 3 and the supremum $\mathcal{Y}={\left[\underline{Y},\overline{Y}\right]}_{\mathcal{T}}=sup\left\{\mathcal{A},\mathcal{M}\right\}$ is illustrated in Figure 4.

5.2. Inclusion Relationship

The definition of the inclusion of two interval fuzzy segments is based on the inclusion relationship between their supports.

Definition 6. (Inclusion in $IFS$)

Given $\mathcal{A}={\left[\underline{A},\overline{A}\right]}_T$ and $\mathcal{M}={\left[\underline{M},\overline{M}\right]}_{T^{\prime }}$ two interval fuzzy segments, we define:

$$\mathcal{A}\subseteq \mathcal{M}iffsupp\left(\mathcal{A}\right)\subseteq supp\left(\mathcal{M}\right).$$

(22)

Proposition 5.

Given $\mathcal{A}={\left[\underline{A},\overline{A}\right]}_T$ and $\mathcal{M}={\left[\underline{M},\overline{M}\right]}_{T^{\prime }}$ two interval fuzzy segments, from Definition 6 above, it follows that:

$$\mathcal{A}\subseteq \mathcal{M}\iff \forall \lambda \in \left[0,1\right]\exists \mu \in \left[0,1\right]\left({\left\{T_{\lambda }\left(\alpha \right)\right\}}_{\alpha \in \left[0,1\right]}={\left\{T_{\mu }^{\prime }\left(\beta \right)\right\}}_{\beta \in \left[0,1\right]}\right).$$

(23)

Proposition 6. (Necessary condition for inclusivity)

Given $\mathcal{A}={\left[\underline{A},\overline{A}\right]}_T$ and $\mathcal{M}={\left[\underline{M},\overline{M}\right]}_{T^{\prime }}$ two interval fuzzy segments, it is the case that:

$${\left[\underline{A},\overline{A}\right]}_T\subseteq {\left[\underline{M},\overline{M}\right]}_{T^{\prime }}\Rightarrow \underline{A}\ge \underline{M}and\overline{A}\le \overline{M}.$$

(24)

Proof. 

Let $\lambda =0,$ then there exists $\mu \in \left[0,1\right]$such that${\left\{T_0\left(\alpha \right)\right\}}_{\alpha \in \left[0,1\right]}={\left\{T_{\mu }^{\prime }\left(\alpha \right)\right\}}_{\alpha \in \left[0,1\right]}$, which is $\underline{A}={\left\{T_{\mu }^{\prime }\left(\alpha \right)\right\}}_{\alpha \in \left[0,1\right]}$.

As $0\le \mu ,$ then, by applying Definition 1, we have:

$$\forall \alpha \in \left[0,1\right]\left(T_0^{\prime }\left(\alpha \right)\le T_{\mu }^{\prime }\left(\alpha \right)\right),$$

(25)

and thus $\underline{A}={\left\{T_{\mu }^{\prime }\left(\alpha \right)\right\}}_{\alpha \in \left[0,1\right]}\ge {\left\{T_0^{\prime }\left(\alpha \right)\right\}}_{\alpha \in \left[0,1\right]}=\underline{M}.$

In the same way, $\overline{A}\le \overline{M}$. ☐

Proposition 7.

The inclusion relationship studied in Definition 6 is a partial order in $IFS$.

Proof. 

Given $\mathcal{A}={\left[\underline{A},\overline{A}\right]}_T,$ $\mathcal{B}={\left[\underline{B},\overline{B}\right]}_{T^{\prime }},$ $\mathcal{C}={\left[\underline{C},\overline{C}\right]}_{T^{″}}\in IFS,$ the following properties are fulfilled:

Reflexive: $\mathcal{A}\subseteq \mathcal{A}$ as $\forall \lambda \in \left[0,1\right]\left({\left\{T_{\lambda }\left(\alpha \right)\right\}}_{\alpha \in \left[0,1\right]}={\left\{T_{\lambda }\left(\beta \right)\right\}}_{\beta \in \left[0,1\right]}\right).$

Anti-symmetric: If $\mathcal{A}\subseteq \mathcal{B}$ and $\mathcal{B}\subseteq \mathcal{A}$, it follows

$\forall \lambda \in \left[0,1\right]\exists \mu \in \left[0,1\right]\left({\left\{T_{\lambda }\left(\alpha \right)\right\}}_{\alpha \in \left[0,1\right]}={\left\{T_{\mu }^{\prime }\left(\beta \right)\right\}}_{\beta \in \left[0,1\right]}\right),$

$\forall \mu \in \left[0,1\right]\exists \lambda \in \left[0,1\right]\left({\left\{T_{\mu }^{\prime }\left(\beta \right)\right\}}_{\beta \in \left[0,1\right]}={\left\{T_{\lambda }\left(\alpha \right)\right\}}_{\alpha \in \left[0,1\right]}\right),$

and consequently $\mathcal{A}=\mathcal{B}$.

Transitive: If $\mathcal{A}\subseteq \mathcal{B}$ and $\mathcal{B}\subseteq \mathcal{C}$, it follows

$\forall \lambda \in \left[0,1\right]\exists \mu \in \left[0,1\right]\left({\left\{T_{\lambda }\left(\alpha \right)\right\}}_{\alpha \in \left[0,1\right]}={\left\{T_{\mu }^{\prime }\left(\beta \right)\right\}}_{\beta \in \left[0,1\right]}\right),$

$\forall \mu \in \left[0,1\right]\exists \eta \in \left[0,1\right]\left({\left\{T_{\mu }^{\prime }\left(\beta \right)\right\}}_{\beta \in \left[0,1\right]}={\left\{T_{\eta }^{″}\left(\gamma \right)\right\}}_{\gamma \in \left[0,1\right]}\right),$

thus $\forall \lambda \in \left[0,1\right]\exists \eta \in \left[0,1\right]\left({\left\{T_{\lambda }\left(\alpha \right)\right\}}_{\alpha \in \left[0,1\right]}={\left\{T_{\eta }^{″}\left(\gamma \right)\right\}}_{\gamma \in \left[0,1\right]}\right),$

and consequently $\mathcal{A}\subseteq \mathcal{C}.$ ☐

The inclusion relationship cannot be a total order in the set $IFS$, as the interval inclusion is not. Thus, the structure $\left(IFS,\subseteq \right)$ is not a lattice, as the structure $\left(I\left(\mathbb{R}\right),\subseteq \right)$ is not either.

6. Some Fuzzy Number S-Transformations

Next, we will study interval fuzzy segments by considering different fuzzy number S-transformations. We will illustrate each of these S-transformations by an application. The first S-transformation we present is called linear S-transformation and it represents the transition from the lower bound of an interval fuzzy segment to the upper bound that corresponds to a linear mapping. The second S-transformation we consider has been named exponential S-transformation, as it represents the transition from the lower bound of an interval fuzzy segment to the upper bound that corresponds to an exponential mapping.

Proposition 8.

Let $f:\left[0,1\right]⟶\left[0,1\right]$ be a continuous increasing function such that $f\left(0\right)=0$, $f\left(1\right)=1$. If $A,B\in \stackrel{•}{FN}$ and $A\le B$, then the mapping

$$\begin{array}{ccc}T:\left[0,1\right]& ⟶& F\left(\left[0,1\right];I\left(\mathbb{R}\right)\right)\\ \lambda & ⟼& T_{\lambda },\end{array}$$

where $\forall \alpha \in \left[0,1\right],T_{\lambda }\left(\alpha \right)=A^{\alpha }+f\left(\lambda \right)\left(B^{\alpha }-dual\left(A^{\alpha }\right)\right)$ is a fuzzy number S-transformation (Definition 1) from A to $B.$

Proof. 

• If $\lambda =0,$ ${\left\{T_0\left(\alpha \right)\right\}}_{\alpha \in \left[0,1\right]}={\left\{A^{\alpha }+f\left(0\right)\left(B^{\alpha }-dual\left(A^{\alpha }\right)\right)\right\}}_{\alpha \in \left[0,1\right]}={\left\{A^{\alpha }\right\}}_{\alpha \in \left[0,1\right]}=A.$
• If $\lambda =1,$ ${\left\{T_1\left(\alpha \right)\right\}}_{\alpha \in \left[0,1\right]}={\left\{A^{\alpha }+f\left(1\right)\left(B^{\alpha }-dual\left(A^{\alpha }\right)\right)\right\}}_{\alpha \in \left[0,1\right]}={\left\{A^{\alpha }+B^{\alpha }-dual\left(A^{\alpha }\right)\right\}}_{\alpha \in \left[0,1\right]}=B.$
• ${\alpha }_1,{\alpha }_2\in \left[0,1\right].$ We can express $A^{{\alpha }_1}=\left[{\underline{a}}^{{\alpha }_1},{\overline{a}}^{{\alpha }_1}\right],$ $A^{{\alpha }_2}=\left[{\underline{a}}^{{\alpha }_2},{\overline{a}}^{{\alpha }_2}\right],$ $B^{{\alpha }_1}=\left[{\underline{b}}^{{\alpha }_1},{\overline{b}}^{{\alpha }_1}\right],$ $B^{{\alpha }_2}=\left[{\underline{b}}^{{\alpha }_2},{\overline{b}}^{{\alpha }_2}\right]$. As $A^{{\alpha }_1}$, $A^{{\alpha }_2}$, $B^{{\alpha }_1}$, $B^{{\alpha }_2}$ are fuzzy numbers, if ${\alpha }_1\le {\alpha }_2$ then $A^{{\alpha }_2}\subseteq A^{{\alpha }_1}$ and $B^{{\alpha }_2}\subseteq B^{{\alpha }_1},$ which is ${\underline{a}}^{{\alpha }_2}\ge {\underline{a}}^{{\alpha }_1}$, ${\overline{a}}^{{\alpha }_2}\le {\overline{a}}^{{\alpha }_1}$, ${\underline{b}}^{{\alpha }_2}\ge {\underline{b}}^{{\alpha }_1}$, ${\overline{b}}^{{\alpha }_2}\le {\overline{b}}^{{\alpha }_1}$.
  If $\lambda \in \left[0,1\right]$ and ${\alpha }_1\le {\alpha }_2$ $T_{\lambda }\left({\alpha }_2\right)=A^{{\alpha }_2}+f\left(\lambda \right)\left(B^{{\alpha }_2}-dual\left(A^{{\alpha }_2}\right)\right)$ and $T_{\lambda }\left({\alpha }_1\right)=A^{{\alpha }_1}+f\left(\lambda \right)\left(B^{{\alpha }_1}-dual\left(A^{{\alpha }_1}\right)\right)$. As $A\le B,$ then $B-dual\left(A\right)\ge 0.$ Moreover, $f\left(\lambda \right)\ge 0$, so the distributive law is fulfilled, thus

  $$T_{\lambda }\left({\alpha }_2\right)=\left[{\underline{a}}^{{\alpha }_2}\left(1-f\left(\lambda \right)\right)+{\underline{b}}^{{\alpha }_2}f\left(\lambda \right),{\overline{a}}^{{\alpha }_2}\left(1-f\left(\lambda \right)\right)+{\overline{b}}^{{\alpha }_2}f\left(\lambda \right)\right]$$

  and

  $$T_{\lambda }\left({\alpha }_1\right)=\left[{\underline{a}}^{{\alpha }_1}\left(1-f\left(\lambda \right)\right)+{\underline{b}}^{{\alpha }_1}f\left(\lambda \right),{\overline{a}}^{{\alpha }_1}\left(1-f\left(\lambda \right)\right)+{\overline{b}}^{{\alpha }_1}f\left(\lambda \right)\right].$$

  Moreover,

  $$\begin{array}{ccc}{\underline{a}}^{{\alpha }_2}\hfill & \ge & {\underline{a}}^{{\alpha }_1}\mathrm{and}1-f\left(\lambda \right)\ge 0\Rightarrow {\underline{a}}^{{\alpha }_2}\left(1-f\left(\lambda \right)\right)\ge {\underline{a}}^{{\alpha }_1}\left(1-f\left(\lambda \right)\right),\hfill \\ {\underline{b}}^{{\alpha }_2}\hfill & \ge & {\underline{b}}^{{\alpha }_1}\mathrm{and}f\left(\lambda \right)\ge 0\Rightarrow {\underline{b}}^{{\alpha }_2}f\left(\lambda \right)\ge {\underline{b}}^{{\alpha }_1}f\left(\lambda \right).\hfill \end{array}$$
  In the same way, ${\overline{a}}^{{\alpha }_2}\left(1-f\left(\lambda \right)\right)\le {\overline{a}}^{{\alpha }_1}\left(1-f\left(\lambda \right)\right)$ and ${\overline{b}}^{{\alpha }_2}f\left(\lambda \right)\le {\overline{b}}^{{\alpha }_1}f\left(\lambda \right).$ Consequently, $T_{\lambda }\left({\alpha }_2\right)\subseteq T_{\lambda }\left({\alpha }_1\right).$
  As A and B are punctual-core fuzzy numbers, then $A^1$ and $B^1$ are real numbers, hence $T_{\lambda }\left(1\right)$ is also a real number.
• If $0\le {\lambda }_1<{\lambda }_2\le 1$, as f is an increasing function and $B-dual\left(A\right)\ge 0$, it will be

  $$A^{\alpha }+f\left({\lambda }_1\right)\left(B^{\alpha }-dual\left(A^{\alpha }\right)\right)\le A^{\alpha }+f\left({\lambda }_2\right)\left(B^{\alpha }-dual\left(A^{\alpha }\right)\right),$$

  which is $T_{{\lambda }_1\left(\alpha \right)}\le T_{{\lambda }_2\left(\alpha \right)}$.

 ☐

6.1. Linear Interval Fuzzy Segment

Let A and B be two fuzzy numbers such that $A\le B.$

Let us consider the following linear mapping:

$$\begin{array}{ccccc}T:\left[0,1\right]& ⟶& F\left(\left[0,1\right];I\left(\mathbb{R}\right)\right)& & \\ \lambda & ⟼& T_{\lambda }:\left[0,1\right]& \to & I\left(\mathbb{R}\right)\hfill \\ & & \alpha & \mapsto & T_{\lambda }\left(a\right)=A^{\alpha }+\lambda \left(B^{\alpha }-dual\left(A^{\alpha }\right)\right)\hfill \end{array}$$

(26)

Applying Proposition 8 to this mapping, T, is a fuzzy number S-transformation and it holds that:

• $T_0\left(\alpha \right)=A^{\alpha }$,
• $T_1\left(\alpha \right)=A^{\alpha }+\left(B^{\alpha }-dual\left(A^{\alpha }\right)\right)=B^{\alpha }$,
• $\left(\forall \lambda \in \left[0,1\right]\right){\left\{T_{\lambda }\left(\alpha \right)\right\}}_{\alpha \in \left[0,1\right]}={\left\{A^{\alpha }+\lambda \left(B^{\alpha }-dual\left(A^{\alpha }\right)\right)\right\}}_{\alpha \in \left[0,1\right]}\in \stackrel{•}{FN}$,
• If ${\lambda }_1,{\lambda }_2\in \left[0,1\right]$ with ${\lambda }_1<{\lambda }_2$, as $\forall \alpha \in \left[0,1\right],A^{\alpha }\le B^{\alpha }$, then it will be the case that $\left(B^{\alpha }-dual\left(A^{\alpha }\right)\right)\ge 0$ and hence ${\lambda }_1\left(B^{\alpha }-dual\left(A^{\alpha }\right)\right)<{\lambda }_2\left(B^{\alpha }-dual\left(A^{\alpha }\right)\right)$, which implies $T_{{\lambda }_1}\left(\alpha \right)\le T_{{\lambda }_2}\left(\alpha \right)$.

From the fuzzy numbers $A,B\in \stackrel{•}{FN}$ and from the associated linear S-transformation T, we can define the linear interval fuzzy segment ${\left[A,B\right]}_T$.

In a particular way, we can illustrate these linear interval fuzzy segments considering that the bounds A and B are triangular fuzzy numbers, $A=\left(a_1,a_2,a_3\right)$ and $B=\left(b_1,b_2,b_3\right)$, then the characteristic functions are:

$${\mu }_A\left(x\right)=\left\{\begin{array}{cc}\frac{x-a_1}{a_2-a_1},& \mathrm{if}{a}_1\le x<a_2,\hfill \\ 1,& \mathrm{if}x=a_2,\hfill \\ \frac{a_3-x}{a_3-a_2},& \mathrm{if}{a}_2<x\le a_3,\hfill \\ 0,& \mathrm{otherwise},\hfill \end{array}\right.\mathrm{and}{\mu }_B\left(x\right)=\left\{\begin{array}{cc}\frac{x-b_1}{b_2-b_1},& \mathrm{if}{b}_1\le x<b_2,\hfill \\ 1,& \mathrm{if}x=b_2,\hfill \\ \frac{b_3-x}{b_3-b_2},& \mathrm{if}{b}_2<x\le b_3,\hfill \\ 0,& \mathrm{otherwise},\hfill \end{array}\right.$$

(27)

and the respective $\alpha -$cuts are:

$$\begin{array}{ccc}{A}^{\alpha }\hfill & =& \left[\alpha \left(a_2-a_1\right)+a_1,\alpha \left(a_2-a_3\right)+a_3\right],\hfill \\ B^{\alpha }\hfill & =& \left[\alpha \left(b_2-b_1\right)+b_1,\alpha \left(b_2-b_3\right)+b_3\right],\hfill \end{array}$$

thus, the linear S-transformation is expressed by:

$$\begin{array}{ccc}{T}_{\lambda }\left(\alpha \right)\hfill & =& \left(1-\lambda \right)\left[\alpha \left(a_2-a_1\right)+a_1,\alpha \left(a_2-a_3\right)+a_3\right]\hfill \\ & & +\lambda \left[\alpha \left(b_2-b_1\right)+b_1,\alpha \left(b_2-b_3\right)+b_3\right].\hfill \end{array}$$

The membership function of a fuzzy number $C\in$supp$\left({\left[A,B\right]}_T\right)$ can be evaluated as:

If $\left(1-\lambda \right)a_1+\lambda b_1\le x<\left(1-\lambda \right)a_2+\lambda b_2,$ then

$$x=\left(1-\lambda \right)\alpha \left(a_2-a_1\right)+\left(1-\lambda \right)a_1+\lambda \alpha \left(b_2-b_1\right)+\lambda b_1,$$

(28)

which results in:

$$\alpha =\frac{x-\left(1-\lambda \right)a_1-\lambda b_1}{\left(1-\lambda \right)\left(a_2-a_1\right)+\lambda \left(b_2-b_1\right)}.$$

(29)

If $\left(1-\lambda \right)a_2+\lambda b_2<x\le \left(1-\lambda \right)a_3+\lambda b_3,$ then

$$x=\left(1-\lambda \right)\alpha \left(a_2-a_3\right)+\left(1-\lambda \right)a_3+\lambda \alpha \left(b_2-b_3\right)+\lambda b_3,$$

(30)

which results in:

$$\alpha =\frac{x-\left(1-\lambda \right)a_3-\lambda b_3}{\left(1-\lambda \right)\left(a_2-a_3\right)+\lambda \left(b_2-b_3\right)}.$$

(31)

It is obvious that if $\alpha =1$, we obtain $x=\left(1-\lambda \right)\left(a_2-a_1\right)+\left(1-\lambda \right)a_1+\lambda \left(b_2-b_1\right)+\lambda b_1=\left(1-\lambda \right)a_2+\lambda b_2$, which corresponds to the linear S-transformation (linear segment) of the cores of the fuzzy bounds A and B of the interval fuzzy segment ${\left[A,B\right]}_T$.

The membership function of a fuzzy number $C\in$supp$\left({\left[A,B\right]}_T\right)$ is:

$${\mu }_C\left(x\right)=\left\{\begin{array}{cc}\frac{x-\left(1-\lambda \right)a_1-\lambda b_1}{\left(1-\lambda \right)\left(a_2-a_1\right)+\lambda \left(b_2-b_1\right)},& \mathrm{if}\left(1-\lambda \right)a_1+\lambda b_1\le x<\left(1-\lambda \right)a_2+\lambda b_2,\hfill \\ \\ 1,& \mathrm{if}x=\left(1-\lambda \right)a_2+\lambda b_2,\hfill \\ \\ \frac{x-\left(1-\lambda \right)a_3-\lambda b_3}{\left(1-\lambda \right)\left(a_2-a_3\right)+\lambda \left(b_2-b_3\right)},& \mathrm{if}\left(1-\lambda \right)a_2+\lambda b_2<x\le \left(1-\lambda \right)a_3+\lambda b_3,\hfill \\ \\ 0,& \mathrm{otherwise}.\hfill \end{array}\right.$$

(32)

Example 2.

Let us suppose that we have a digital thermometer and the temperature range to be measured is from −15 ${}^{\circ }$C to +45 ${}^{\circ }$C. Every temperature reading with this thermometer is subject to inaccuracy, such as the sensitivity of the device and/or the accuracy of the display. If x is the real temperature we want to measure and p is the temperature read from the thermometer, we require that they satisfy $\left|x-p\right|\le ϵ$. Thus, for every temperature p read from the display of the thermometer, we can consider we have obtained a triangular fuzzy number P whose core is the temperature reading p and whose support is the real interval $\left[p-ϵ,p+ϵ\right]$. If the thermometer display has a single decimal place, and the accuracy of the device is complete, we can then consider a value for ϵ such as $0.1$. However, if we want to take into account the accuracy of the device, we should increase the value $ϵ>0$. As this is a descriptive example, we can take, for example, $ϵ=0.11$. In this way, the thermometer would measure a temperature that can be expressed as an $IFS$, thus:

$${\left[A,B\right]}_T={\left[\left(-15.11,-15,-14.89\right),\left(44.89,45,45.11\right)\right]}_T.$$

(33)

The $\alpha -cuts$ of the interval bounds are $A^{\alpha }=\left[0.11\alpha -15.11,-0.11\alpha -14.89\right]$ and $B^{\alpha }=\left[0.11\alpha +44.89,-0.11\alpha +45.11\right]$.

The linear fuzzy number S-transformation is:

$$T_{\lambda }\left(a\right)=A^{\alpha }+\lambda \left(B^{\alpha }-dual\left(A^{\alpha }\right)\right),$$

(34)

$$T_{\lambda }\left(\alpha \right)=\left[60\lambda +0.11\alpha -15.11,60\lambda -0.11\alpha -14.89\right].$$

(35)

Example 3.

Considering the same situation as in the previous example, let us now suppose that the temperature range we want to measure is from +10 ${}^{\circ }$C to +30 ${}^{\circ }$C. Let us also suppose a margin of related error $\left(e_r\right)$ of the device, and $e_r=$ 5%. Thus, the fuzzy bounds A and B of the interval fuzzy segment are:

$$A=10\left(1\pm 0.05\right)=\left(9.5,10,10.5\right)$$

(36)

and

$$B=30\left(1\pm 0.05\right)=\left(28.5,30,31.5\right).$$

(37)

Assuming a linear S-transformation for the thermometer readings, we obtain:

$${\left[A,B\right]}_T={\left[\left(9.5,10,10.5\right),\left(28.5,30,31.5\right)\right]}_T,$$

(38)

where $T_{\lambda }\left(a\right)=A^{\alpha }+\lambda \left(B^{\alpha }-dual\left(A^{\alpha }\right)\right)$ and thus:

$$T_{\lambda }\left(\alpha \right)=\left[0.5\alpha +9.5+\lambda \left(\alpha +19\right),-0.5\alpha +10.5+\lambda \left(-\alpha +21\right)\right].$$

(39)

As all the temperatures in the established range are positives, it is easy to prove that this transition function maintains the related error $e_r$ of 5%, as for every $\lambda \in \left[0,1\right]$ it is $A_{\lambda }^0=\left[9.5+19\lambda ,10.5+21\lambda \right]$ and also $A_{\lambda }^1=\left[10+20\lambda ,10+20\lambda \right]$. Thus, $e_r=\frac{\left|10.5+21\lambda -\left(10+20\lambda \right)\right|}{10+20\lambda }=\frac{0.5+\lambda }{10+20\lambda }=0.05=5\%$.

6.2. Exponential Interval Fuzzy Segment

Although the linear S-transformation is one of the easiest to use, there are some situations in which it can be useful to work with other nonlinear S-transformations. In some models, it can be useful to work with an exponential S-transformation, as this can better represent the problem to be solved.

Let $A,B\in \stackrel{•}{FN}$ such that $A\le B.$

Considering the following exponential mapping:

$$\begin{array}{ccccc}T:\left[0,1\right]& ⟶& F\left(\left[0,1\right];I\left(\mathbb{R}\right)\right)& & \\ \lambda & ⟼& T_{\lambda }:\left[0,1\right]& \to & I\left(\mathbb{R}\right)\hfill \\ & & \alpha & \mapsto & T_{\lambda }\left(a\right)=A^{\alpha }+\frac{e^{\lambda }-1}{e-1}\left(B^{\alpha }-dual\left(A^{\alpha }\right)\right).\hfill \end{array}$$

(40)

Applying Proposition 8 to this mapping, T, is a fuzzy number S-transformation and it holds that:

• $T_0\left(\alpha \right)=A^{\alpha }+\frac{e^0-1}{e-1}\left(B^{\alpha }-dual\left(A^{\alpha }\right)\right)=A^{\alpha }$.
• $T_1\left(\alpha \right)=A^{\alpha }+\frac{e^1-1}{e-1}\left(B^{\alpha }-dual\left(A^{\alpha }\right)\right)=A^{\alpha }+\left(B^{\alpha }-dual\left(A^{\alpha }\right)\right)=B^{\alpha }$.
• $\left(\forall \lambda \in \left[0,1\right]\right){\left\{T_{\lambda }\left(\alpha \right)\right\}}_{\alpha \in \left[0,1\right]}={\left\{A^{\alpha }+\frac{e^{\lambda }-1}{e-1}\left(B^{\alpha }-dual\left(A^{\alpha }\right)\right)\right\}}_{\alpha \in \left[0,1\right]}\in \stackrel{•}{FN}$.
• If ${\lambda }_1,{\lambda }_2\in \left[0,1\right]$ with ${\lambda }_1<{\lambda }_2$, then $\frac{e^{{\lambda }_1}-1}{e-1}<\frac{e^{{\lambda }_2}-1}{e-1}.$ As $\forall \alpha \in \left[0,1\right],A^{\alpha }\le B^{\alpha },$ it follows that $B^{\alpha }-dual\left(A^{\alpha }\right)\ge 0$ and thus:

  $$\frac{e^{{\lambda }_1}-1}{e-1}\left(B^{\alpha }-dual\left(A^{\alpha }\right)\right)<\frac{e^{{\lambda }_2}-1}{e-1}\left(B^{\alpha }-dual\left(A^{\alpha }\right)\right),$$

  (41)

  that is, $T_{{\lambda }_1}\left(\alpha \right)\le T_{{\lambda }_2}\left(\alpha \right).$

From the punctual-core fuzzy numbers $A,B\in \stackrel{•}{FN}$ and the associated exponential S-transformation T, we can define the interval fuzzy segment ${\left[A,B\right]}_T$.

In particular, we can consider the bounds A and B of these interval fuzzy segments as the triangular fuzzy numbers $A=\left(a_1,a_2,a_3\right)$ and $B=\left(b_1,b_2,b_3\right)$, with their respective membership functions ${\mu }_A\left(x\right)$ and ${\mu }_B\left(x\right)$ as laid out previously.

The exponential S-transformation is expressed as:

$$\begin{array}{ccc}{T}_{\lambda }\left(\alpha \right)\hfill & =& \left[a_1+\alpha \left(a_2-a_1\right)+\frac{e^{\lambda }-1}{e-1}\left(b_1-a_1+\alpha \left(\left(b_2-b_1\right)-\left(a_2-a_1\right)\right)\right),\right.\hfill \\ & & \left.a_3+\alpha \left(a_2-a_3\right)+\frac{e^{\lambda }-1}{e-1}\left(b_3-a_3+\alpha \left(\left(b_2-b_3\right)-\left(a_2-a_3\right)\right)\right)\right]\hfill \end{array}$$

and the membership function of a fuzzy number $C\in$supp$\left({\left[A,B\right]}_T\right)$ can be evaluated as:

If $a_1+\frac{e^{\lambda }-1}{e-1}\left(b_1-a_1\right)\le x<a_2+\frac{e^{\lambda }-1}{e-1}\left(b_2-a_2\right),$ then

$$\alpha =\frac{x-a_1-\frac{e^{\lambda }-1}{e-1}\left(b_1-a_1\right)}{a_2-a_1+\frac{e^{\lambda }-1}{e-1}\left(b_2-a_2-b_1+a_1\right)}.$$

(42)

If $a_2+\frac{e^{\lambda }-1}{e-1}\left(b_2-a_2\right)<x\le a_3+\frac{e^{\lambda }-1}{e-1}\left(b_3-a_3\right),$ then

$$\alpha =\frac{x-a_3-\frac{e^{\lambda }-1}{e-1}\left(b_3-a_3\right)}{a_2-a_3+\frac{e^{\lambda }-1}{e-1}\left(b_2-a_2-b_3+a_3\right)}$$

(43)

and ${\mu }_C\left(x\right)$ is

$$\left\{\begin{array}{cc}\frac{x-a_1-\frac{e^{\lambda }-1}{e-1}\left(b_1-a_1\right)}{a_2-a_1+\frac{e^{\lambda }-1}{e-1}\left(b_2-a_2-b_1+a_1\right)},& \mathrm{if}{a}_1+\frac{e^{\lambda }-1}{e-1}\left(b_1-a_1\right)\le x<a_2+\frac{e^{\lambda }-1}{e-1}\left(b_2-a_2\right),\hfill \\ \\ 1,& \mathrm{if}x=a_2+\frac{e^{\lambda }-1}{e-1}\left(b_2-a_2\right),\hfill \\ \\ \frac{x-a_3-\frac{e^{\lambda }-1}{e-1}\left(b_3-a_3\right)}{a_2-a_3+\frac{e^{\lambda }-1}{e-1}\left(b_2-a_2-b_3+a_3\right)},& \mathrm{if}{a}_2+\frac{e^{\lambda }-1}{e-1}\left(b_2-a_2\right)<x\le a_3+\frac{e^{\lambda }-1}{e-1}\left(b_3-a_3\right),\hfill \\ \\ 0,& \mathrm{otherwise}.\hfill \end{array}\right.$$

(44)

Example 4.

We have an exponential variable resistor and its extreme values are 50 Ω and 390 Ω. If we have a tolerance of $10\%$, we can express the values of this exponential variable resistor as an interval fuzzy segment ${\left[A,B\right]}_T$ where A and B are the fuzzy triangular numbers which express the upper and lower values respectively, of the variable resistor, taking into account the value of the tolerance. Finally, T would be the associated exponential S-transformation modeling the behavior of the resistor.

Thus, we obtain $A=\left(45,50,55\right),$ $B=\left(351,390,429\right)$ and the α-cuts of A and B are:

$$A^{\alpha }=\left[5\alpha +45,55-5\alpha \right]and{B}^{\alpha }=\left[39\alpha +351,429-39\alpha \right].$$

(45)

The exponential S-transformation T is:

$$T_{\lambda }\left(\alpha \right)=\left[5\alpha +45,55-5\alpha \right]+\frac{e^{\lambda }-1}{e-1}\left(\left[34\alpha +306,374-34\alpha \right]\right),$$

(46)

that is:

$$T_{\lambda }\left(\alpha \right)=\left[5\alpha +45+\frac{e^{\lambda }-1}{e-1}\left(34\alpha +306\right),55-5\alpha +\frac{e^{\lambda }-1}{e-1}\left(374-34\alpha \right)\right].$$

(47)

To complete this section, we will present an example that shows how this model works in a real-life problem, and will compare the results obtained using interval fuzzy segments in front of the results obtained working with intervals and working with fuzzy numbers, highlighting the advantages obtained using interval fuzzy segments.

Example 5.

Consider a simplified circuit of voltage regulation using the LM317 circuit and detailed in the following diagram (Figure 5)

We will assume that, for a given input voltage $V_{IN},$ we obtain a constant value $V_{PQ}=1.25V$. The output voltage $V_{OUT}$ is

$$V_{OUT}=1.25\left(1+\frac{R_2}{R_1}\right)+I_{ADJ}·R_2.$$

We will not take into account the value $I_{ADJ}$ because it is small enough not to affect significantly the study we are doing.

Let us consider that $R_1$ is a resistor whose value is 1000 Ω with a tolerance of $5\%$ and $R_2$ is a variable resistor whose value is comprised between 0 Ω and 10,000 Ω with a tolerance of $5\%.$ We will study the different values obtained for $V_{OUT}$ using interval calculus, fuzzy numbers and interval fuzzy segments with both linear S-transformation and exponential S-transformation.

1.

Interval calculus.

When working with intervals, the values for the resistors are $R_1=\left[950,1050\right]$ and $R_2=\left[0,10500\right]$. Thus, using the arithmetical rules for intervalar calculus, it will be $V_{OUT}=\left[1.25,15.06\right].$

2.

Fuzzy numbers.

Using fuzzy numbers, the values for the resistors are the trapezoidal fuzzy numbers $R_1=\left(950,1000,1000,1050\right)$ and $R_2=\left(0,0,10000,10500\right)$. Doing the calculations using $\alpha -$cuts, the fuzzy result for $V_{OUT}$ is $V_{OUT}={\left\{\left[1.25,1.25+\frac{-500\alpha +10500}{40\alpha +760}\right]\right\}}_{\alpha \in \left[0,1\right]}$.

For $\alpha =0$, the $\alpha -$cut of $V_{OUT},$ (that is the support of $V_{OUT}$) is the interval $\left[1.25,15.06\right]$ and for $\alpha =1$, the $\alpha -$cut of $V_{OUT}$ (that is the core of $V_{OUT})$ is the interval $\left[1.25,13.75\right]$. Notice that the support of $V_{OUT}$ coincides with the intervalar result obtained.

3.

Interval fuzzy segments.

(a) 

Using linear interval fuzzy segment for the variable resistor.

The resistor $R_1$ is the triangular fuzzy number expressed by its $\alpha -$cuts as $R_1={\left\{\left[50\alpha +950,-50\alpha +1050\right]\right\}}_{\alpha \in \left[0,1\right]}$. We will consider that the lower bound for the resistor $R_2$ is the triangular fuzzy number $\left(0,0,10\right)$; then, the resistor $R_2$ is the IFS expressed by its $\left(\lambda ,\alpha \right)-$cuts as

$R_2={\left\{{\left\{\left[\lambda \left(500\alpha +9500\right),-10\alpha +10+\lambda \left(-490\alpha +10490\right)\right]\right\}}_{\alpha \in \left[0,1\right]}\right\}}_{\lambda \in \left[0,1\right]}$.

From these data, we obtain $V_{OUT}$ whose value is

${\left\{{\left\{\left[1.25+\frac{\lambda \left(500\alpha +9500\right)}{-40\alpha +840},1.25+\frac{-10\alpha +10+\lambda \left(-490\alpha +10490\right)}{40\alpha +760}\right]\right\}}_{\alpha \in \left[0,1\right]}\right\}}_{\lambda \in \left[0,1\right]}$.

Using the values $\lambda =0,$ $\lambda =1$, we obtain the fuzzy bounds for $V_{OUT}$:

$\underline{V_{OUT}}={\left\{\left[1.25,1.25+\frac{-10\alpha +10}{40\alpha +760}\right]\right\}}_{\alpha \in \left[0,1\right]}$ and

$\overline{V_{OUT}}={\left\{\left[1.25+\frac{\left(500\alpha +9500\right)}{-40\alpha +840},1.25+\frac{\left(-500\alpha +10500\right)}{40\alpha +760}\right]\right\}}_{\alpha \in \left[0,1\right]}$.

(b) 

Using exponential interval fuzzy segment for the variable resistor.

As in the previous case, $R_1={\left\{\left[50\alpha +950,-50\alpha +1050\right]\right\}}_{\alpha \in \left[0,1\right]}$. The lower bound for the resistor $R_2$ is the triangular fuzzy number $\left(0,0,10\right)$ and then $R_2$ is

${\left\{{\left\{\left[\frac{e^{\lambda }-1}{e-1}\left(500\alpha +9500\right),-10\alpha +10+\frac{e^{\lambda }-1}{e-1}\left(-490\alpha +10490\right)\right]\right\}}_{\alpha \in \left[0,1\right]}\right\}}_{\lambda \in \left[0,1\right]}$.

The output voltage $V_{OUT}$ is

${\left\{{\left\{\left[1.25+\frac{\frac{e^{\lambda }-1}{e-1}\left(500\alpha +9500\right)}{-40\alpha +840},1.25+\frac{-10\alpha +10+\frac{e^{\lambda }-1}{e-1}\left(-490\alpha +10490\right)}{40\alpha +760}\right]\right\}}_{\alpha \in \left[0,1\right]}\right\}}_{\lambda \in \left[0,1\right]}$.

Using the values $\lambda =0$ and $\lambda =1$, the fuzzy bounds for $V_{OUT}$ are

$\underline{V_{OUT}}={\left\{\left[1.25,1.25+\frac{-10\alpha +10}{40\alpha +760}\right]\right\}}_{\alpha \in \left[0,1\right]}$ and

$\overline{V_{OUT}}={\left\{\left[1.25+\frac{\left(500\alpha +9500\right)}{-40\alpha +840},1.25+\frac{\left(-500\alpha +10500\right)}{40\alpha +760}\right]\right\}}_{\alpha \in \left[0,1\right]}$.

As can be seen, the information expressed using interval analysis only gives us the margin of variation of the resulting output voltage. When we use fuzzy numbers, we obtain a little more information, as the fuzzy value for $V_{OUT}$ incorporates, from the $\alpha -$cuts of $V_{OUT}$, a vagueness component of the output voltage. Although fuzzy numbers provide a better understanding of the problem than intervals, they can not naturally include the modeling of the variation of the resistor $R_2$, and therefore they can not express the modeling of the output voltage $V_{OUT}$. Interval fuzzy segments can describe the modeling of the output voltage as they describe the problem taking into account their uncertainties and inaccuracies, describing the dynamic procedure and not just the end result. Using interval fuzzy segments, we know which is the variation of the output voltage depending on the variation of the resistors. In addition to this variation, the result also reflects the uncertainty and inaccuracy that are propagated throughout the calculation, depending on the uncertainty and inaccuracy in the data.

Note that the value $\underline{V_{OUT}}$ obtained using a linear interval fuzzy segment and exponential interval fuzzy segment is the same in both cases and the same goes for $\overline{V_{OUT}}$. This is explained from the concept of support of an interval fuzzy segment. The support of both IFSs is the same, but for a given λ such that $\lambda \ne 0$ and $\lambda \ne 1,$ the fuzzy number obtained using linear fuzzy interval segments and exponential fuzzy interval segments are different.

7. Conclusions

Both fuzzy numbers and intervals are powerful tools to represent uncertainty, inaccuracy, indiscernibility and vagueness. In this work, we combine these tools to create a new concept: the interval fuzzy segment.

We have generalized intervals, as a set of real values between two real bounds, in terms of the set of fuzzy numbers comprised between two fuzzy numbers and generated by a function that we have treated as a transition function.

We have gone a little beyond the generic concept of interval, since by introducing the S-transformation to generate all the elements of the interval fuzzy segment, this new concept would be closer to the concept of segment or path between two points than to the concept of interval.

Taking advantage of the structures and operations of both fuzzy numbers and intervals, we have built on this new set of interval fuzzy segments the main arithmetic operators. We have also studied the inequality relationship, and proved that this relationship gives a lattice structure to the set of interval fuzzy segments. Furthermore, we introduced the inclusion relationship in the set of interval fuzzy segments.

The interval fuzzy segments that we have defined and studied here reflect, in a very realistic way, situations in which there is uncertainty, inaccuracy and even inaccuracy in the uncertainty.

Many measurements are uncertain and a good way to represent these is to adopt fuzzy numbers. However, when these measurements are lower and upper bounded, a good tool to represent them is obtained using interval fuzzy segments.

If we consider future research lines and applications of the new structure that we have created here, we think that it would be interesting to move beyond the idea of interval and go deeper into the idea of a segment of fuzzy numbers, without any inequality restriction on the bounds.