Intelligent Prognostics of Degradation Trajectories for Rotating Machinery Based on Asymmetric Penalty Sparse Decomposition Model
Abstract
:1. Introduction
- (1)
- The historical data with long-terms, including normal and abnormal time series data, should be collected using sensors and other portable testing devices. Typically, good degradation data must capture the physical transitions that the rotating machinery such as rolling bearing undergo during different stages of its running life; fortunately, most of the historical data are easy to collect since the rotating machinery is frequently updated in real time.
- (2)
- The health indicators (e.g., peak-to-peak value and Kurtosis) should be extracted to assess and continuously track the health condition of rotating machines or system. The health indicators are used to design a suitable prediction model that captures the evolution of the degradation trend of rotating machines.
- (3)
- The reliable prediction models and possible failure models should be established and the remaining useful life (RUL) or future trajectory of rotating machines could be effectively predicted.
- (1)
- Generally, the penalty functions that are established in a low-rank matrix approximation model are symmetric function, e.g., absolute value function; the common drawback is that this penalty function is non-differentiable at zero point, which can lead to some numerical issues such as local optimum and early termination of algorithm.
- (2)
- In conventional SLMD methods, the convex regularizer (e.g., L1-norm) which usually underestimates the sparse signal when the absolute value function is used as a sparsity regularizer. Additionally, both the convex and nonconvex methods shrink all the coefficients equally and remove too much energy of useful information, resulting in the separation of the LFC and HFC becoming more challenging.
- (1)
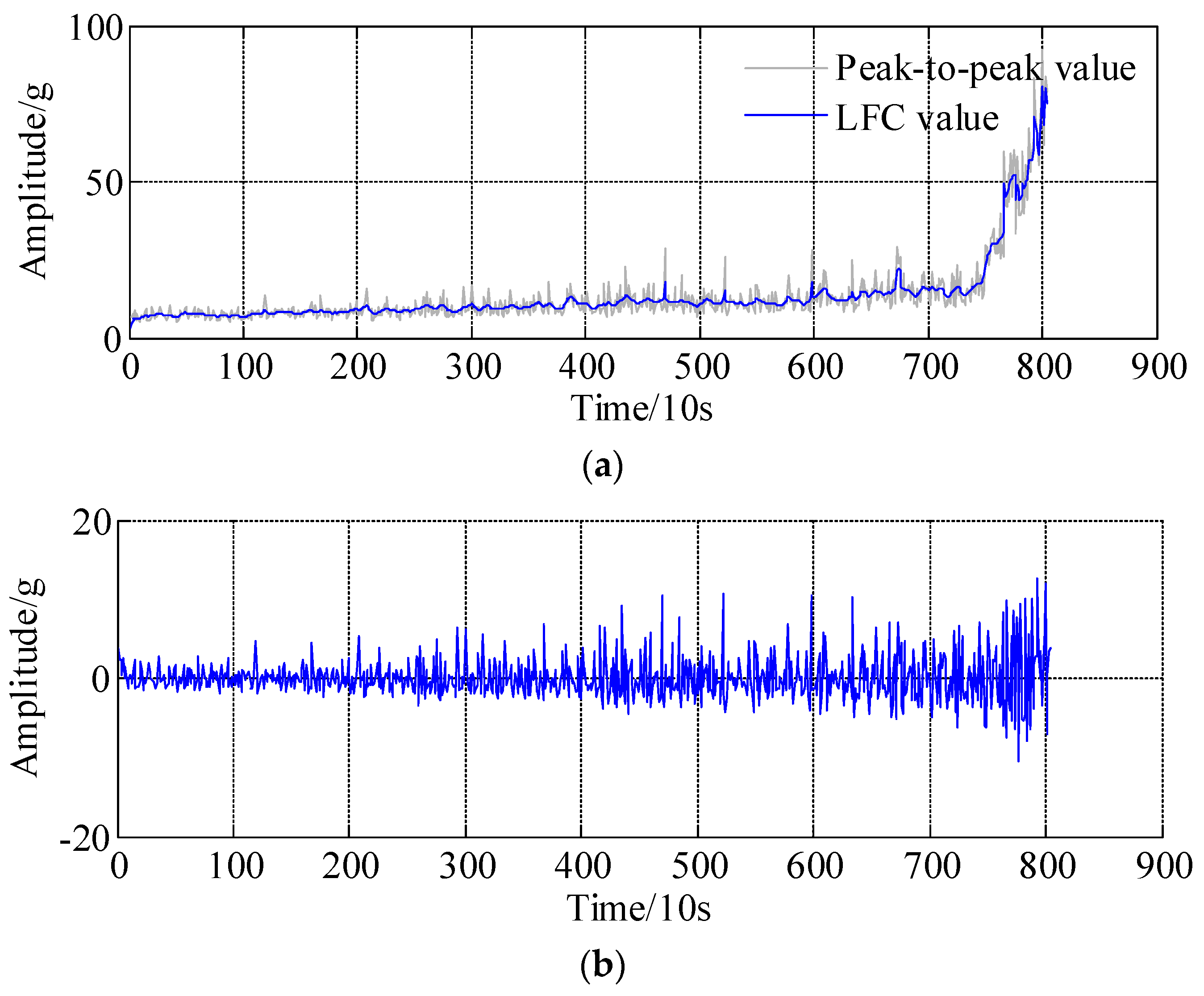
- To address the issue of models merging and improve the prediction accuracy, the health indicators time series (HITS) is decomposed into different sub-components, i.e., low frequency component (LFC) and high frequency component (HFC), using the APSD algorithm.
- (2)
- To address the drawback that penalty function is non-differentiable at zero point, a new asymmetric penalty function is proposed.
- (3)
- To solve the proposed non-convex regularization problem based on asymmetric penalty function, the majorization-minimization (MM) algorithm is introduced.
- (4)
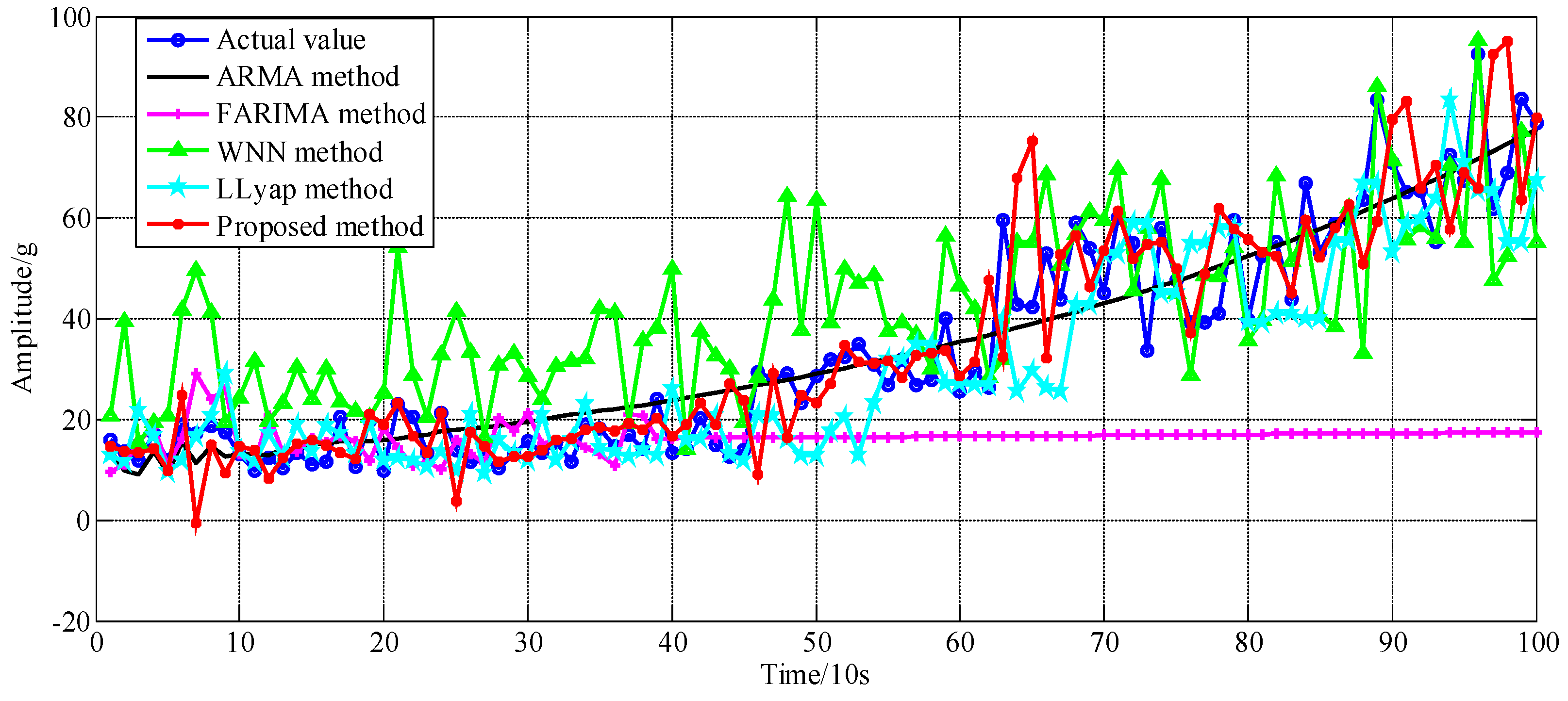
- The decomposed LFC and HFC components can be predicted using the wavelet neural network (WNN) and ARMA combined with recursive least squares algorithm (ARMA-RLS) methods, respectively.
- (5)
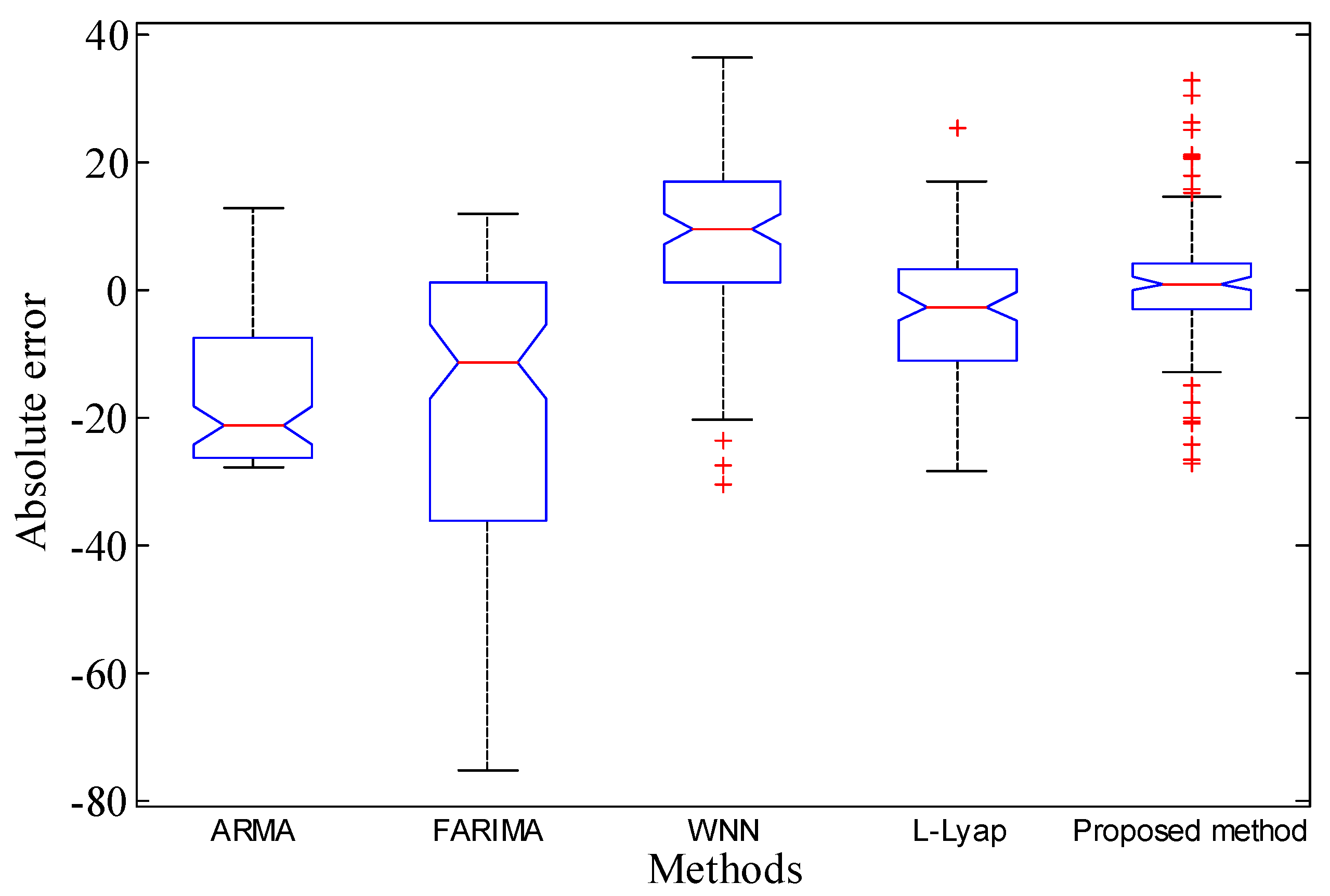
- The prediction accuracy is greatly improved compared with some state-of-the-art models, and the presented approach has powerful application potentials.
2. Asymmetric Penalty Sparse Decomposition (APSD) Algorithm
2.1. Sparse Representation and Filter Banks
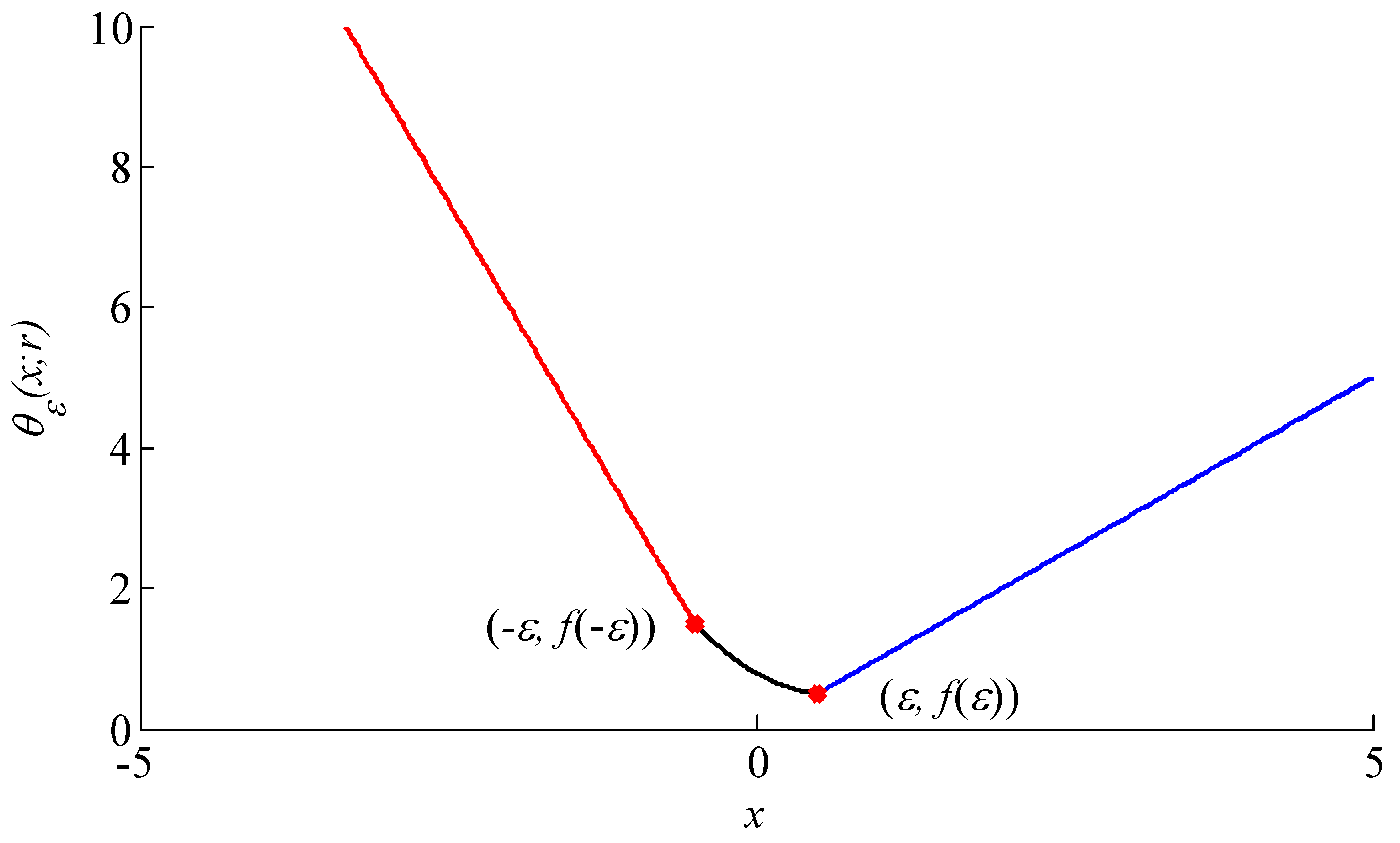
2.2. Asymmetric Penalty Regularization Model
- (I)
- The M-term compound regularizers to estimate the fault transient impulses;
- (II)
- The compound regularizer model consists of symmetric and asymmetric penalty functions, wherein the symmetric penalty function is a differentiable function compared with the nondifferentiable function at point i = 0.
- (III)
- The MM algorithm is introduced for the solution of proposed compound regularization method, i.e., the OCF.
2.3. The Solution of Proposed Model Based on Majorization-Minimization Algorithm
- (a)
- Majorizer of symmetric and differentiable function based on MM algorithm.
- (b)
- Majorizer of asymmetric and differentiable function based on MM algorithm.
- (c)
- Majorizer of objective cost F(x) based on MM algorithm.
- (1)
- Inputs: signal y, r ≥ 1, matrix A, matrix B, , k = 0;
- (2)
- (3)
- Initialize x = y;
- (4)
- Repeat the following iterations:
- (5)
- If the stopping criterion is satisfied, then output signal x, otherwise, k = k + 1, and go to step (4).
- (6)
- Output: signal x.
2.4. Parameters Selection
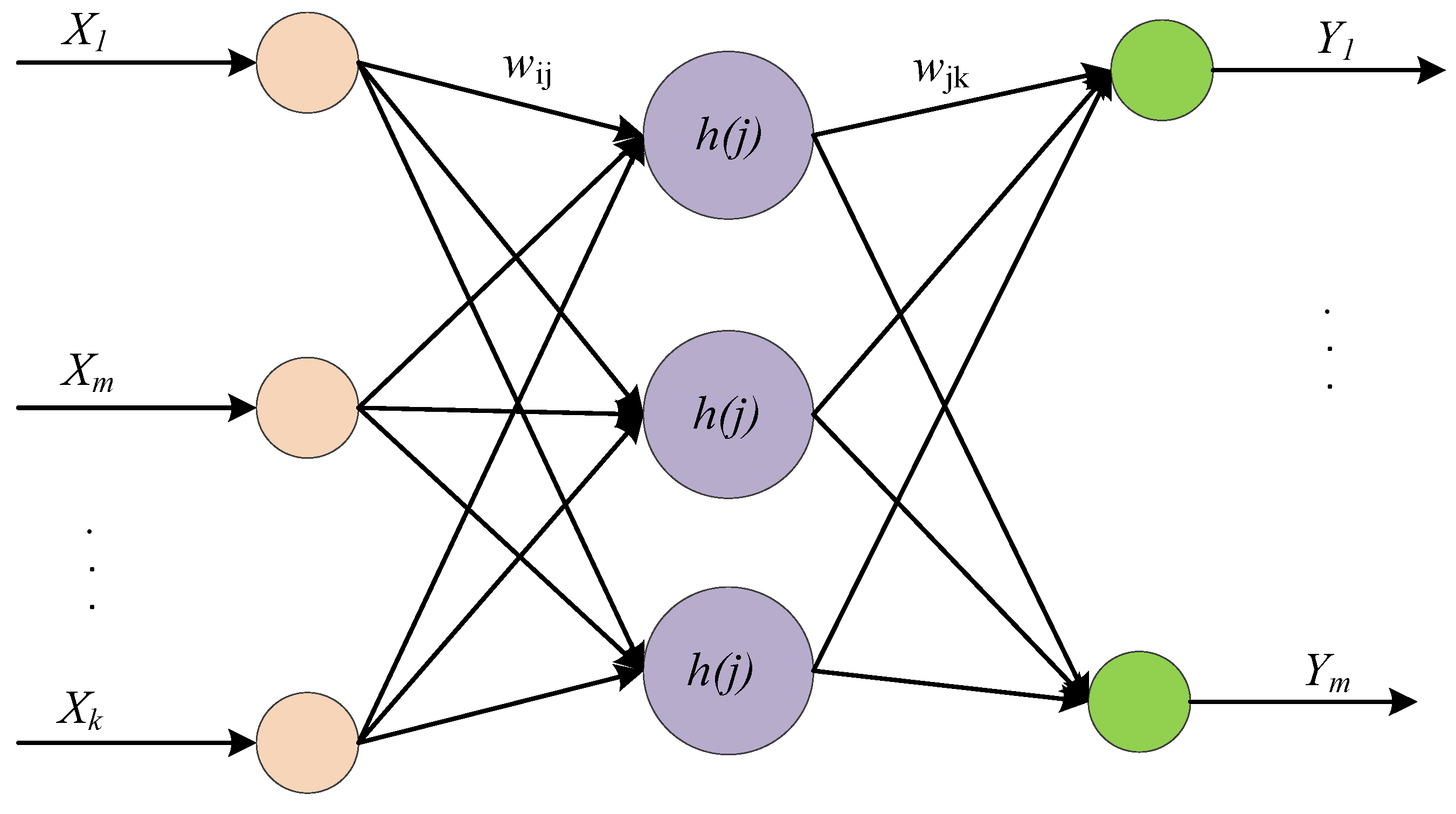
3. Wavelet Neural Network and ARMA-RLS Algorithm
3.1. Wavelet Neural Network Algorithm
3.2. ARMA Combined With Recursive Least Squares (RLS) Algorithm
3.2.1. ARMA Review of ARMA Model
3.2.2. Recursive Least Squares (RLS) Algorithm
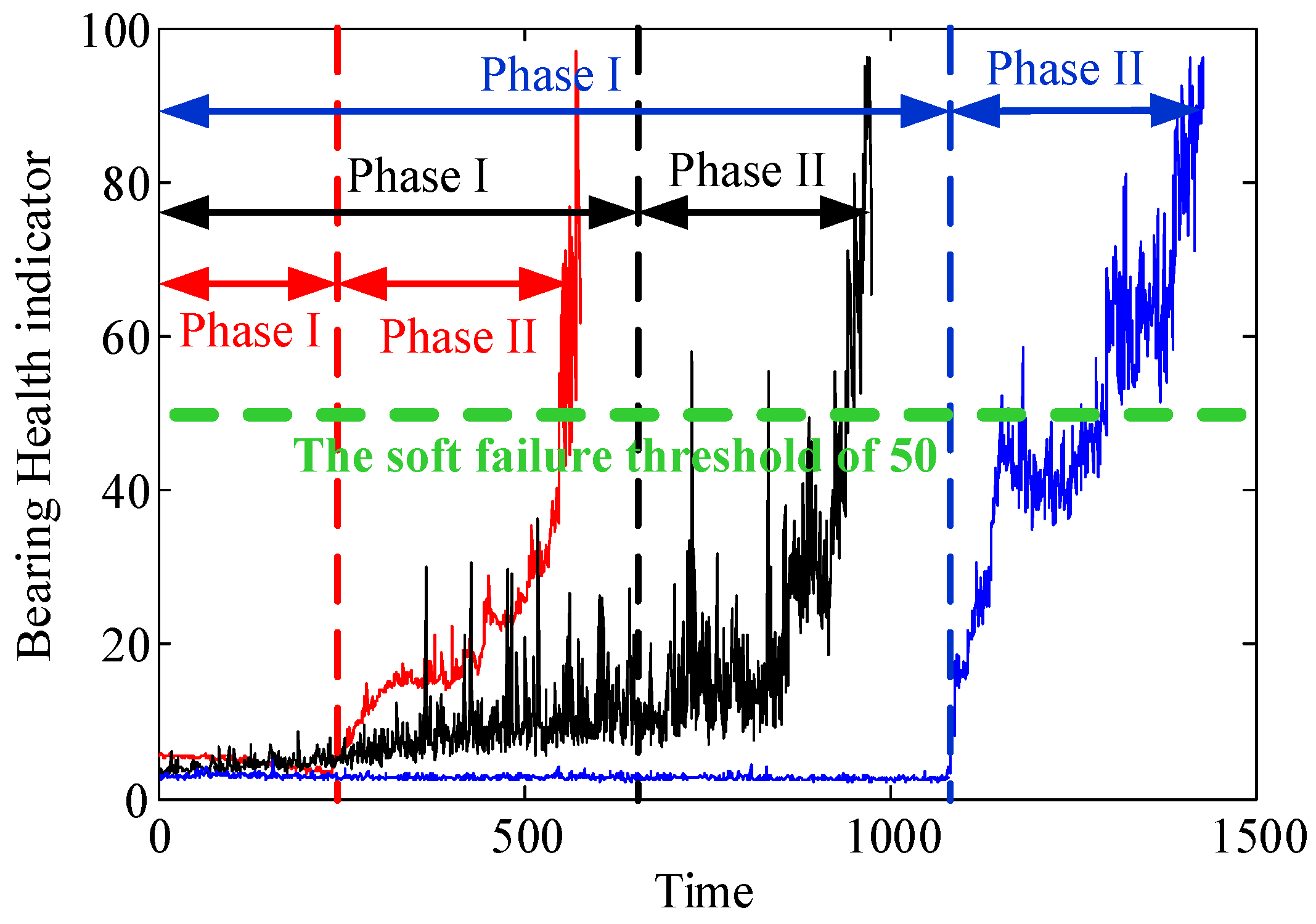
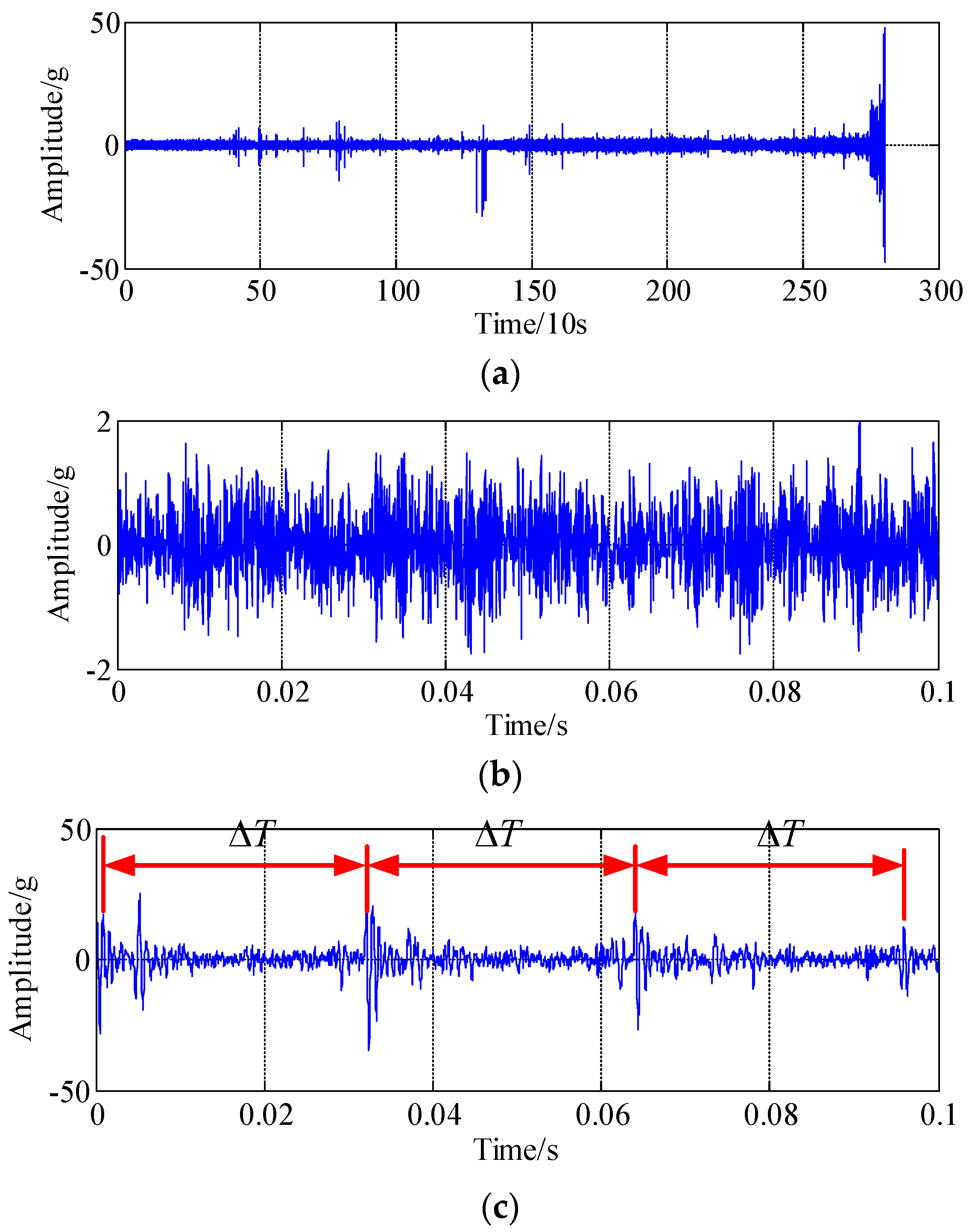
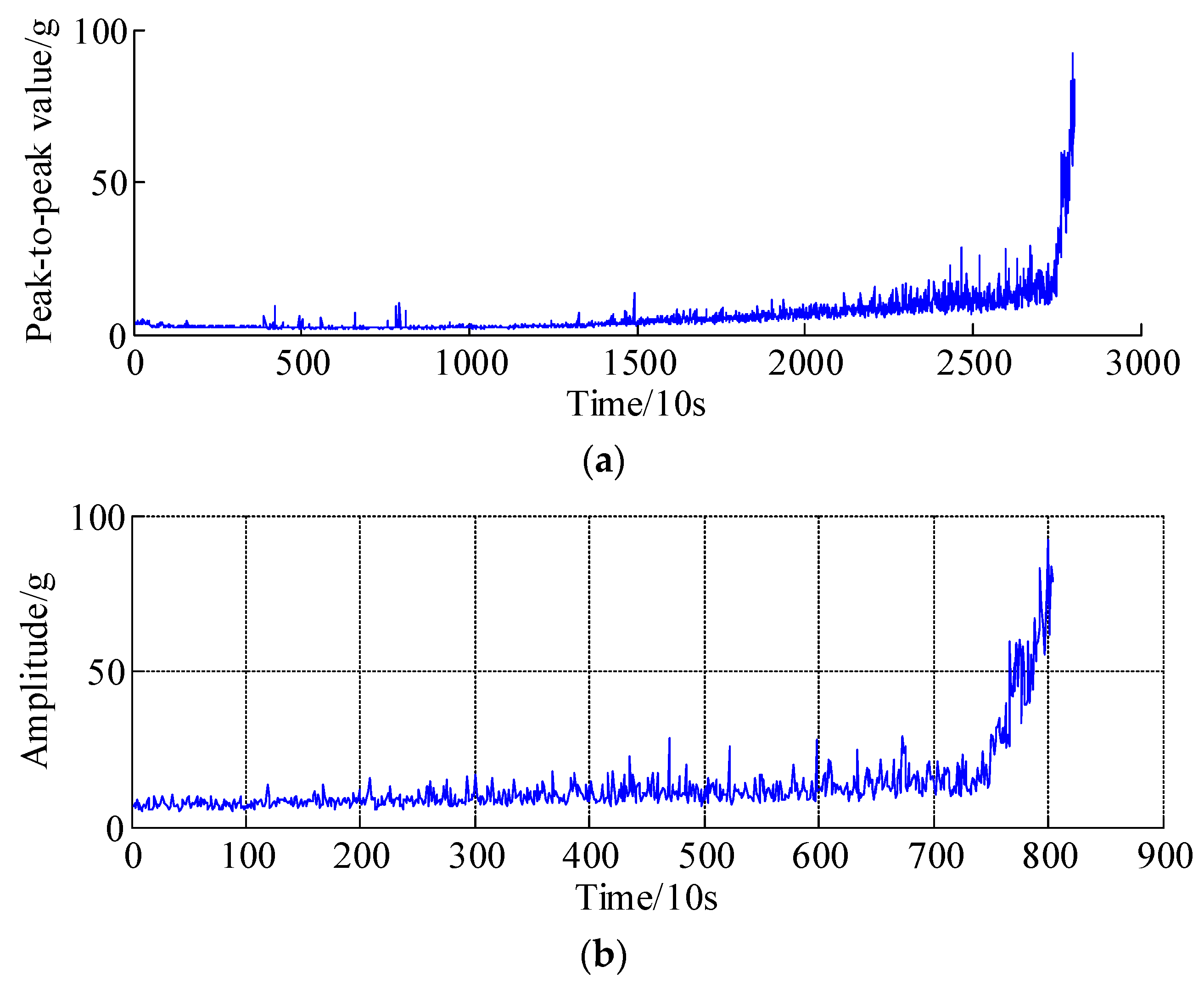
4. Experimental Validations
- (1)
- bearing 1: operating conditions: speed 1800 rpm and load 4000 N; whole test life: 28,030 s;
- (1)
- bearing 2: operating conditions: speed 1800 rpm and load 4000 N; whole test life: 18,020 s;
- (1)
- bearing 3: operating conditions: speed 1650 rpm and load 4200 N; whole test life: 7970 s;
- (1)
- bearing 4: operating conditions: speed 1800 rpm and load 4000 N; whole test life: 14,280 s.
5. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Chen, Z.Y.; Li, W.H. Multisensor feature fusion for bearing fault diagnosis using sparse autoencoder and deep belief network. IEEE Trans. Instrum. Meas. 2017, 66, 1693–1702. [Google Scholar] [CrossRef]
- Singleton, R.K.; Strangas, E.G.; Aviyente, S. The use of bearing currents and vibrations in lifetime estimation of bearings. IEEE Trans. Ind. Inform. 2017, 13, 1301–1309. [Google Scholar] [CrossRef]
- Li, Q.; Ji, X.; Liang, S.Y. Incipient fault feature extraction for rotating machinery based on improved AR-minimum entropy deconvolution combined with variational mode decomposition approach. Entropy 2017, 19, 317. [Google Scholar] [CrossRef]
- Lei, Y.G.; Li, N.P.; Guo, L.; Li, N.B.; Yan, T.; Lin, J. Machinery health prognostics: A systematic review from data acquisition to RUL prediction. Mech. Syst. Signal Process. 2018, 104, 799–834. [Google Scholar] [CrossRef]
- Li, Q.; Liang, S.Y.; Song, W.Q. Revision of bearing fault characteristic spectrum using LMD and interpolation correction algorithm. Procedia CIRP 2016, 56, 182–187. [Google Scholar] [CrossRef]
- Li, Q.; Hu, W.; Peng, E.F.; Liang, S.Y. Multichannel signals reconstruction based on tunable Q-factor wavelet transform-morphological component analysis and sparse Bayesian iteration for rotating machines. Entropy 2018, 20, 263. [Google Scholar] [CrossRef]
- Hong, S.; Zhou, Z.; Zio, E.; Wang, W.B. An adaptive method for health trend prediction of rotating bearings. Digit. Signal Process. 2014, 35, 17–123. [Google Scholar] [CrossRef]
- Rojas, I.; Valenzuela, O.; Rojasa, F.; Guillen, A.; Herrera, L.J.; Pomares, H.; Marquez, L.; Pasadas, M. Soft-computing techniques and ARMA model for time series prediction. Neurocomputing 2008, 71, 519–537. [Google Scholar] [CrossRef]
- Li, Q.; Liang, S.Y.; Yang, J.G.; Li, B.Z. Long range dependence prognostics for bearing vibration intensity chaotic time series. Entropy 2016, 18, 23. [Google Scholar] [CrossRef]
- Li, M.; Zhang, P.D.; Leng, J.X. Improving autocorrelation regression for the Hurst parameter estimation of long-range dependent time series based on golden section search. Phys. A 2016, 445C, 189–199. [Google Scholar] [CrossRef]
- Li, Q.; Liang, S.Y. Degradation trend prognostics for rolling bearing using improved R/S statistic model and fractional Brownian motion approach. IEEE Access 2018, 6, 21103–21114. [Google Scholar] [CrossRef]
- Song, W.; Li, M.; Liang, J.K. Prediction of bearing fault using fractional brownian motion and minimum entropy deconvolution. Entropy 2016, 18, 418. [Google Scholar] [CrossRef]
- Peng, Y.; Dong, M. A prognosis method using age-dependent hidden semi-Markov model for equipment health prediction. Mech. Syst. Signal Process. 2011, 25, 237–252. [Google Scholar] [CrossRef]
- Yan, J.H.; Guo, C.Z.; Wang, X. A dynamic multi-scale Markov model based methodology for remaining life prediction. Mech. Syst. Signal Process. 2011, 25, 1364–1376. [Google Scholar] [CrossRef]
- Tien, T.L. A research on the prediction of machining accuracy by the deterministic grey dynamic model DGDM (1,1,1). Appl. Math. Comput. 2005, 161, 923–945. [Google Scholar] [CrossRef]
- Abdulshahed, A.M.; Longstaff, A.P.; Fletcher, S.; Potdar, A. Thermal error modelling of a gantry-type 5-axis machine tool using a grey neural network model. J. Manuf. Syst. 2016, 41, 130–142. [Google Scholar] [CrossRef]
- Santhosh, T.V.; Gopika, V.; Ghosh, A.K.; Fernandes, B.G. An approach for reliability prediction of instrumentation & control cables by artificial neural networks and Weibull theory for probabilistic safety assessment of NPPs. Reliab. Eng. Syst. Saf. 2018, 170, 31–44. [Google Scholar]
- Torkashvand, A.M.; Ahmadi, A.; Nikravesh, N.L. Prediction of kiwifruit firmness using fruit mineral nutrient concentration by artificial neural network (ANN) and multiple linear regressions (MLR). J. Integr. Agric. 2017, 16, 1634–1644. [Google Scholar] [CrossRef]
- Lazakis, I.; Raptodimos, Y.; Varelas, T. Predicting ship machinery system condition through analytical reliability tools and artificial neural networks. Ocean Eng. 2018, 152, 404–415. [Google Scholar] [CrossRef]
- Dhamande, L.S.; Chaudhari, M.B. Detection of combined gear-bearing fault in single stage spur gear box using artificial neural network. Procedia Eng. 2016, 144, 759–766. [Google Scholar] [CrossRef]
- Chen, C.C.; Vachtsevanos, G. Bearing condition prediction considering uncertainty: An interval type-2 fuzzy neural network approach. Robot. Comput. Int. Manuf. 2012, 28, 509–516. [Google Scholar] [CrossRef]
- Ren, L.; Cui, J.; Sun, Y.Q.; Cheng, X.J. Multi-bearing remaining useful life collaborative prediction: A deep learning approach. J. Manuf. Syst. 2017, 43, 248–256. [Google Scholar] [CrossRef]
- Deutsch, J.; He, D. Using deep learning-based approach to predict remaining useful life of rotating components. IEEE Trans. Syst. Man Cybern. Syst. 2018, 48, 11–20. [Google Scholar] [CrossRef]
- Selesnick, I.W.; Bayram, I. Enhanced sparsity by non-separable regularization. IEEE Trans. Signal Process. 2016, 64, 2298–2313. [Google Scholar] [CrossRef]
- He, W.P.; Ding, Y.; Zi, Y.Y.; Selesnick, I.W. Repetitive transients extraction algorithm for detecting bearing faults. Mech. Syst. Signal Process. 2017, 84, 227–244. [Google Scholar] [CrossRef] [Green Version]
- Li, Q.; Liang, S.Y. Multiple faults detection for rotating machinery based on Bi-component sparse low-rank matrix separation approach. IEEE Access 2018, 6, 20242–20254. [Google Scholar] [CrossRef]
- Li, Q.; Liang, S.Y. Bearing incipient fault diagnosis based upon maximal spectral kurtosis TQWT and group sparsity total variation de-noising approach. J. Vibroeng. 2018, 20, 1409–1425. [Google Scholar] [CrossRef]
- Wang, S.B.; Selesnick, I.W.; Cai, G.G.; Feng, Y.N.; Sui, X.; Chen, X.F. Nonconvex sparse regularization and convex optimization for bearing fault diagnosis. IEEE Trans. Ind. Electron. 2018, 65, 7332–7342. [Google Scholar] [CrossRef]
- Parekh, A.; Selesnick, I.W. Enhanced low-rank matrix approximation. IEEE Signal Process. Lett. 2016, 23, 493–497. [Google Scholar] [CrossRef]
- Parekh, A.; Selesnick, I.W. Convex fused lasso denoising with non-convex regularization and its use for pulse detection. In Proceedings of the IEEE Signal Processing in Medicine and Biology Symposium, Philadelphia, PA, USA, 12 December 2015; pp. 1–6. [Google Scholar]
- Ding, Y.; He, W.P.; Chen, B.Q.; Zi, Y.Y.; Selesnick, I.W. Detection of faults in rotating machinery using periodic time-frequency sparsity. J. Sound Vib. 2016, 382, 357–378. [Google Scholar] [CrossRef] [Green Version]
- Donoho, D.L. Compressed sensing. IEEE Trans. Inf. Theory 2006, 52, 1289–1306. [Google Scholar] [CrossRef]
- Donoho, D.L.; Tsaig, Y. Fast solution of ℓ1-norm minimization problems when the solution may be sparse. IEEE Trans. Inf. Theory 2008, 54, 4789–4812. [Google Scholar] [CrossRef]
- Donoho, D.L. De-noising by soft-thresholding. IEEE Trans. Inf. Theory 1995, 41, 613–627. [Google Scholar] [CrossRef] [Green Version]
- Selesnick, I.W. Total variation denoising via the Moreau envelope. IEEE Signal Process. Lett. 2017, 24, 216–220. [Google Scholar] [CrossRef]
- Selesnick, I.W.; Parekh, A.; Bayram, I. Convex 1-D total variation denoising with non-convex regularization. IEEE Signal Process. Lett. 2015, 22, 141–144. [Google Scholar] [CrossRef]
- Selesnick, I.W.; Graber, H.L.; Pfeil, D.S.; Barbour, R.L. Simultaneous low-pass filtering and total variation denoising. IEEE Trans. Signal Process. 2014, 62, 1109–1124. [Google Scholar] [CrossRef]
- Ning, X.R.; Selesnick, I.W.; Duval, L. Chromatogram baseline estimation and denoising using sparsity (BEADS). Chemom. Intell. Lab. Syst. 2014, 139, 156–167. [Google Scholar] [CrossRef]
- Mourad, N.; Reilly, J.P.; Kirubarajan, T. Majorization-minimization for blind source separation of sparse sources. Signal Process. 2017, 131, 120–133. [Google Scholar] [CrossRef]
- Hunter, D.R.; Lange, K. Quantile Regression via an MM Algorithm. J. Comput. Graph. Stat. 2000, 9, 60–77. [Google Scholar] [Green Version]
- Donoho, D.; Johnstone, I.; Johnstone, I.M. Ideal spatial adaptation by wavelet shrinkage. Biometrika 1993, 81, 425–455. [Google Scholar] [CrossRef]
- Singh, K.R.; Chaudhury, S. Efficient technique for rice grain classification using back-propagation neural network and wavelet decomposition. IET Comput. Vis. 2016, 10, 780–787. [Google Scholar] [CrossRef]
- Heermann, P.D.; Khazenie, N. Classification of multispectral remote sensing data using a back-propagation neural network. IEEE Trans. Geosci. Remote 1992, 30, 81–88. [Google Scholar] [CrossRef]
- Chen, F.C. Back-propagation neural networks for nonlinear self-tuning adaptive control. IEEE Control. Syst. Mag. 1990, 10, 44–48. [Google Scholar] [CrossRef] [Green Version]
- Zeng, Y.R.; Zeng, Y.; Choi, B.; Wang, L. Multifactor-influenced energy consumption forecasting using enhanced back-propagation neural network. Energy 2017, 127, 381–396. [Google Scholar] [CrossRef]
- Osofsky, S.S. Calculation of transient sinusoidal signal amplitudes using the Morlet wavelet. IEEE Trans. Signal Process. 1999, 47, 3426–3428. [Google Scholar] [CrossRef]
- Büssow, R. An algorithm for the continuous Morlet wavelet transform. Mech. Syst. Signal Process. 2007, 21, 2970–2979. [Google Scholar] [CrossRef] [Green Version]
- Ji, W.; Chee, K.C. Prediction of hourly solar radiation using a novel hybrid model of ARMA and TDNN. Sol. Energy 2011, 85, 808–817. [Google Scholar] [CrossRef]
- Brockwell, P.J.; Davis, R.A. Time Series: Theory and Methods, 2nd ed.; Springer: New York, NY, USA, 2009; ISBN 9781441903198. [Google Scholar]
- Ogasawara, H. Bias correction of the Akaike information criterion in factor analysis. J. Multivar. Anal. 2016, 149, 144–159. [Google Scholar] [CrossRef]
- Nectoux, P.; Gouriveau, R.; Medjaher, K.; Ramasso, E.; Morello, B.; Zerhouni, N.; Varnier, C. Pronostia: An experimental platform for bearings accelerated life test. In Proceedings of the IEEE International Conference on Prognostics and Health Management, Denver, CO, USA, 12 June 2012. [Google Scholar]
- Benkedjouh, T.; Medjaher, K.; Zerhouni, N.; Rechak, S. Remaining useful life estimation based on nonlinear feature reduction and support vector regression. Eng. Appl. Artif. Intell. 2013, 26, 1751–1760. [Google Scholar] [CrossRef]





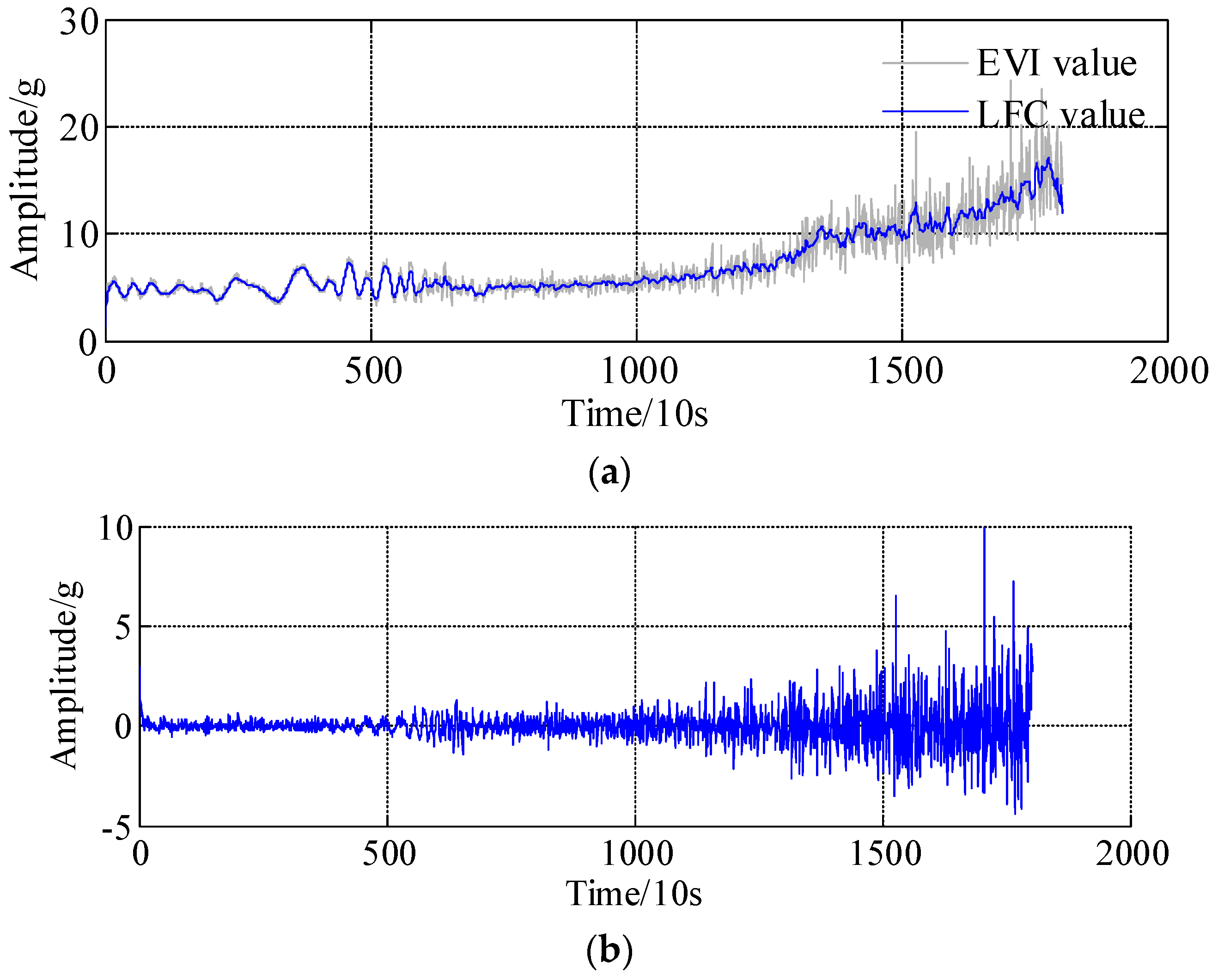

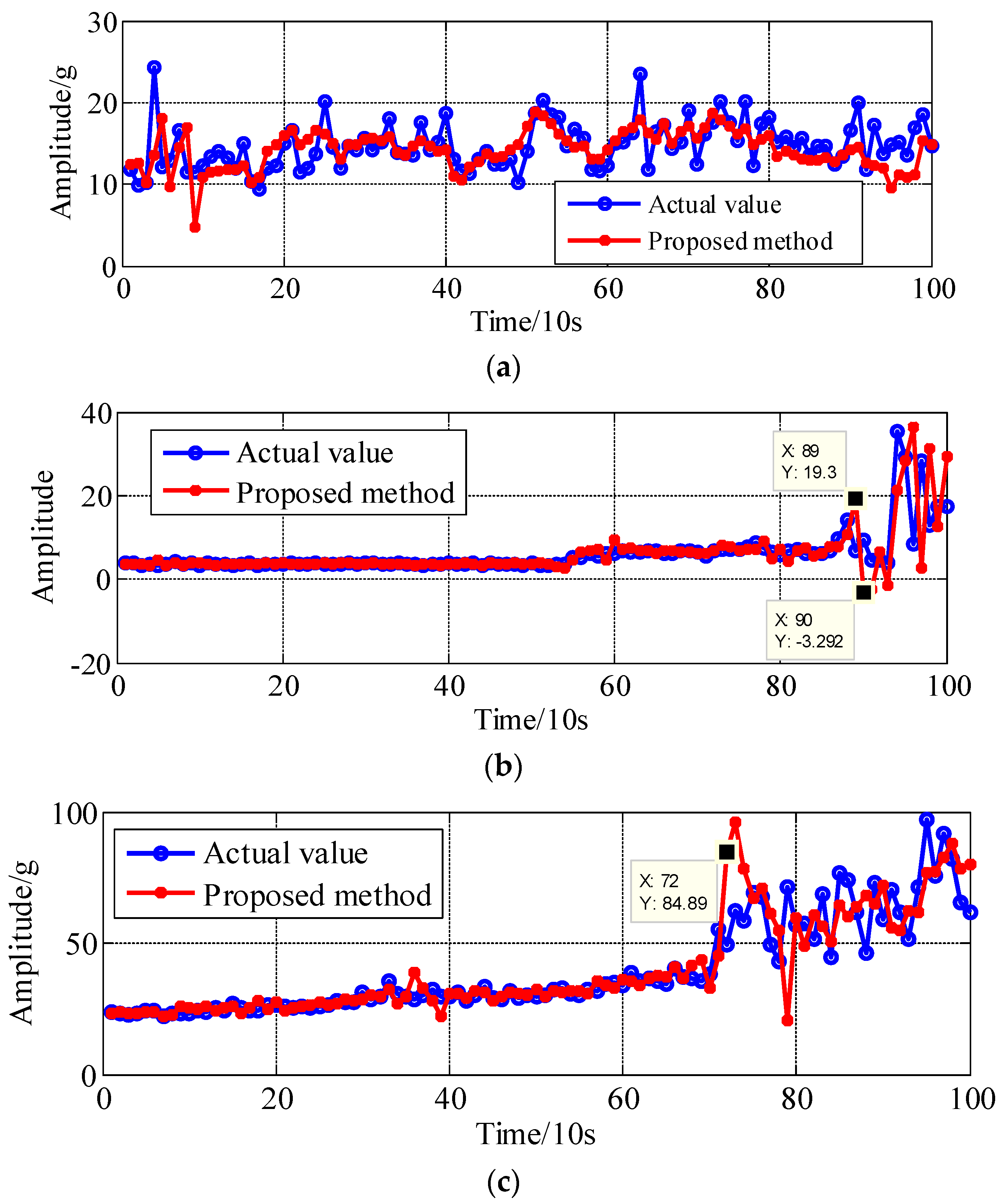
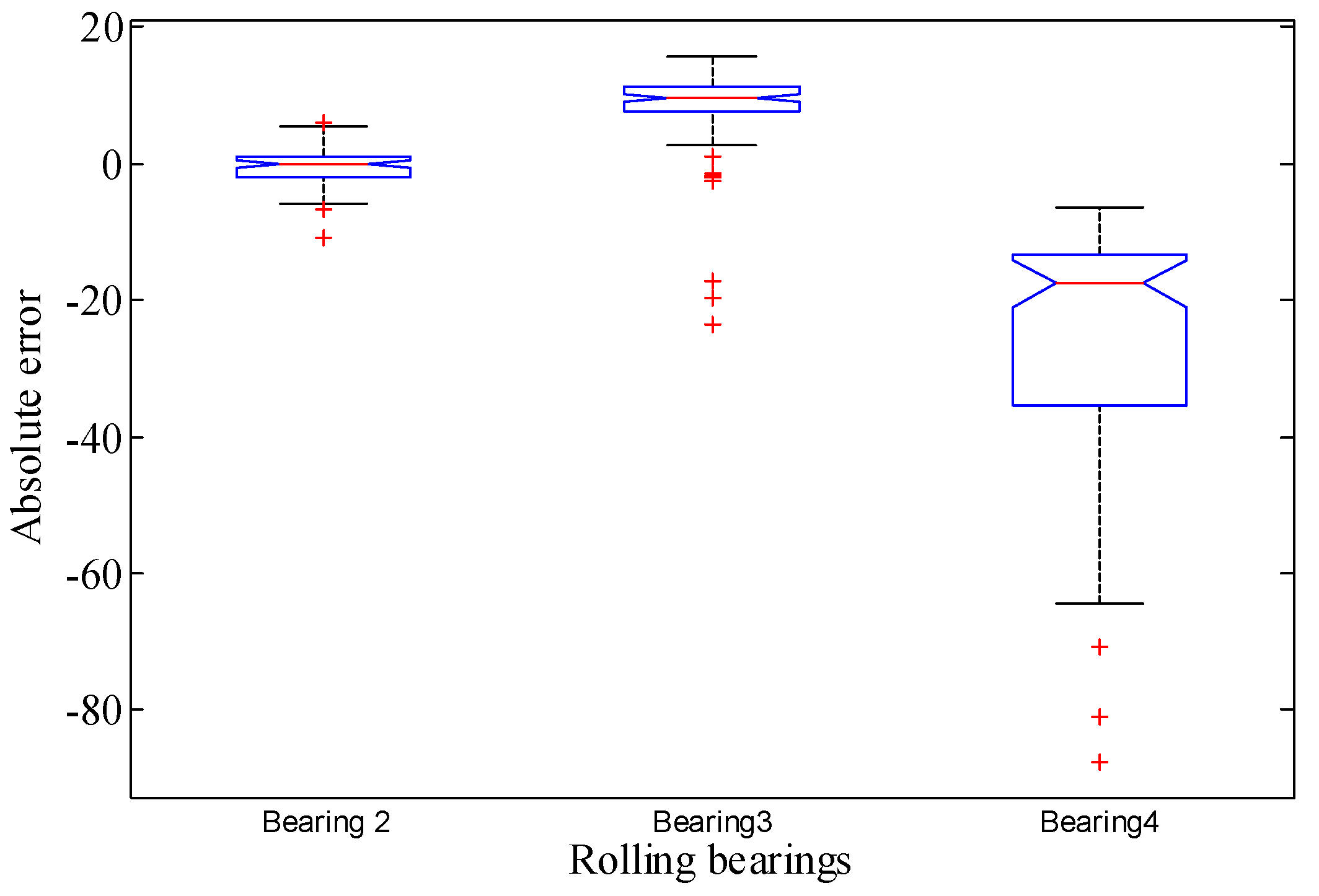
| Functions | ||
|---|---|---|
| Parameters β0 | Parameters γ | Regularization Parameter λ0 | Regularization Parameter λ1 | Regularization Parameter λ2 | M-Term | Iteration Times |
|---|---|---|---|---|---|---|
| β0 = 0.8 | γ = 7.5 | λ0 = 1.7400 | λ1 = 3.2625 | λ2 = 1.7400 | 2 | 50 |
| Index | ARMA | FARIMA | WNN | L-Lyap | Proposed |
|---|---|---|---|---|---|
| Mean Absolute Error-MAE | 0.5880 | 17.2700 | 8.2364 | 3.2453 | 0.9770 |
| Average relative error-ARE | 0.1872 | 0.4666 | 0.1583 | 0.2691 | 0.2599 |
| Root-Mean-Square Error-RMSE | 5.9094 | 173.5702 | 82.7793 | 32.6164 | 9.8190 |
| Normalized Mean Square Error-NMSE | 0.1657 | 2.4144 | 0.7173 | 0.3008 | 0.2244 |
| Maximum of Absolute Error-MaxAE | 21.9865 | 75.0981 | 36.4112 | 28.3548 | 32.9561 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Q.; Liang, S.Y. Intelligent Prognostics of Degradation Trajectories for Rotating Machinery Based on Asymmetric Penalty Sparse Decomposition Model. Symmetry 2018, 10, 214. https://doi.org/10.3390/sym10060214
Li Q, Liang SY. Intelligent Prognostics of Degradation Trajectories for Rotating Machinery Based on Asymmetric Penalty Sparse Decomposition Model. Symmetry. 2018; 10(6):214. https://doi.org/10.3390/sym10060214
Chicago/Turabian StyleLi, Qing, and Steven Y. Liang. 2018. "Intelligent Prognostics of Degradation Trajectories for Rotating Machinery Based on Asymmetric Penalty Sparse Decomposition Model" Symmetry 10, no. 6: 214. https://doi.org/10.3390/sym10060214





