Dynamics of Trapped Solitary Waves for the Forced KdV Equation
Abstract
:1. Introduction
2. The Forced KdV Equation
2.1. Model Equation with Two-Bump Configurations
2.2. Semi-Implicit Finite Difference Method
3. Numerical Simulations
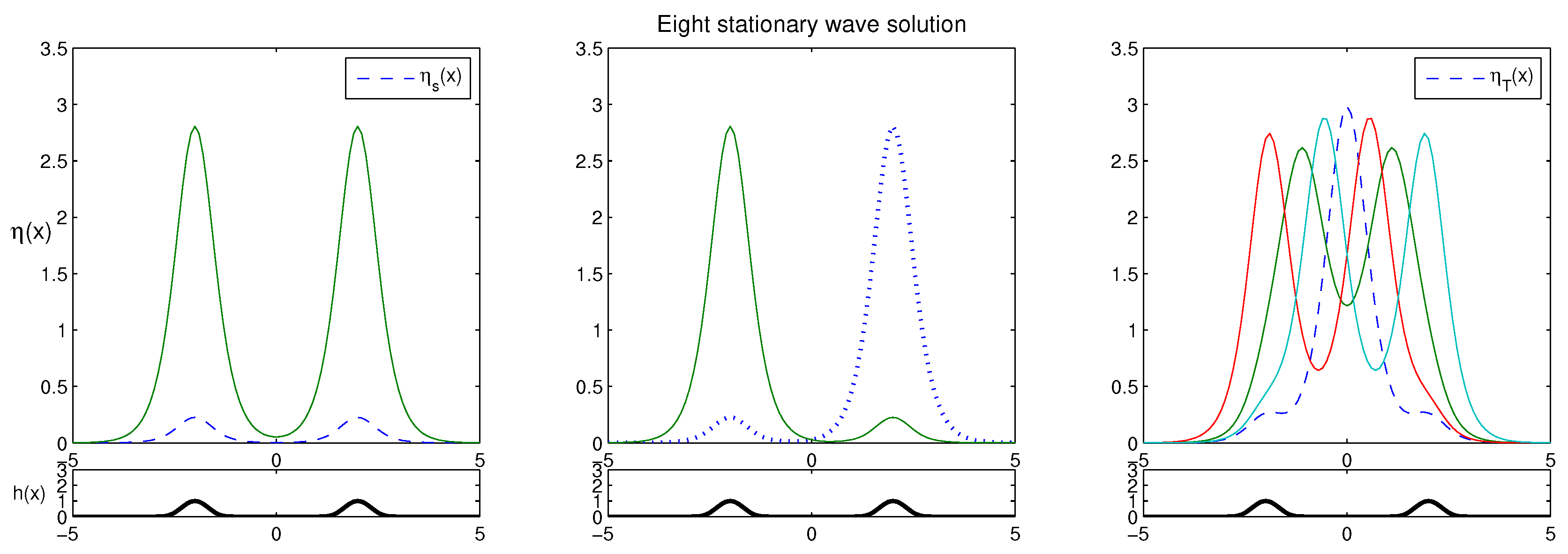
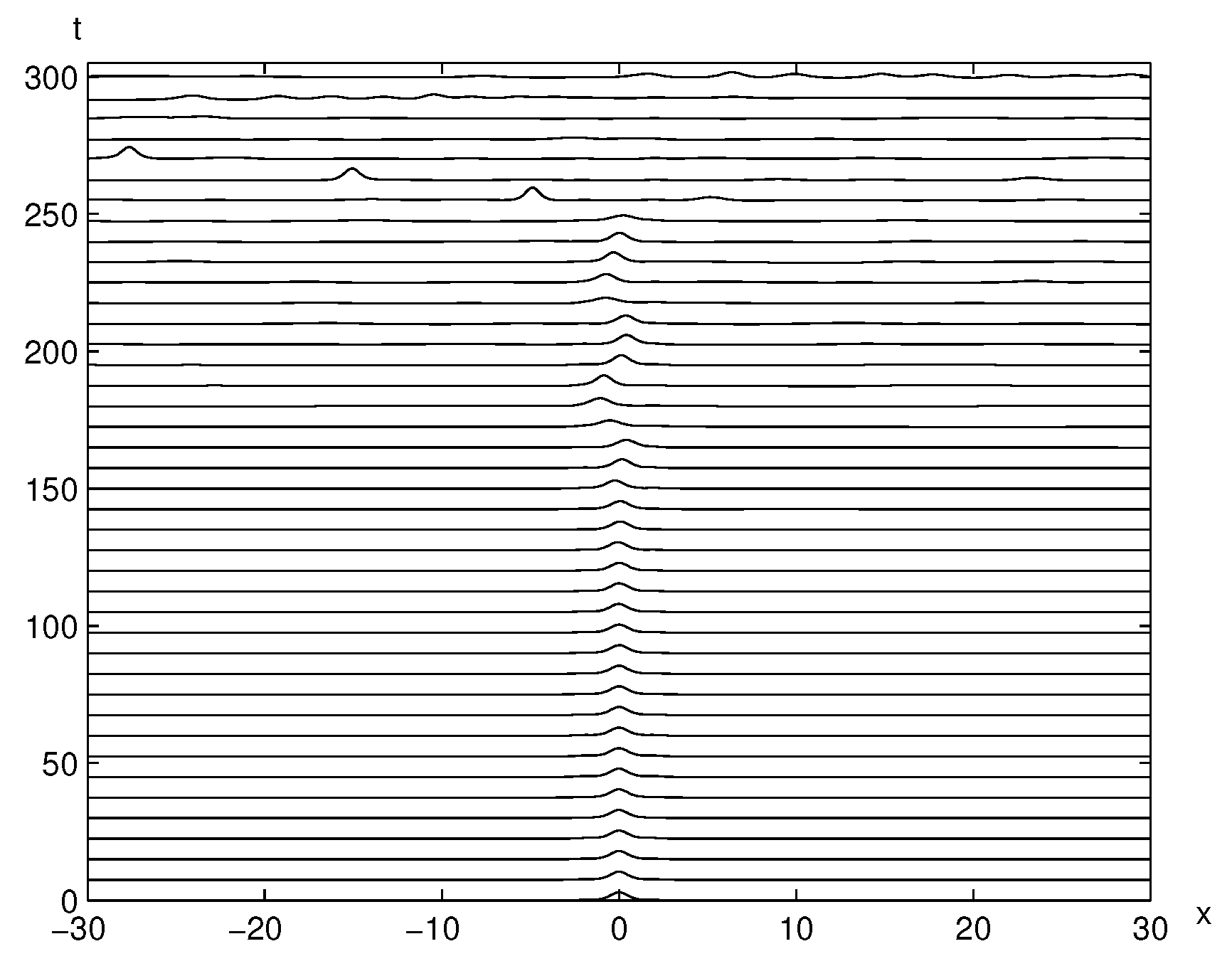
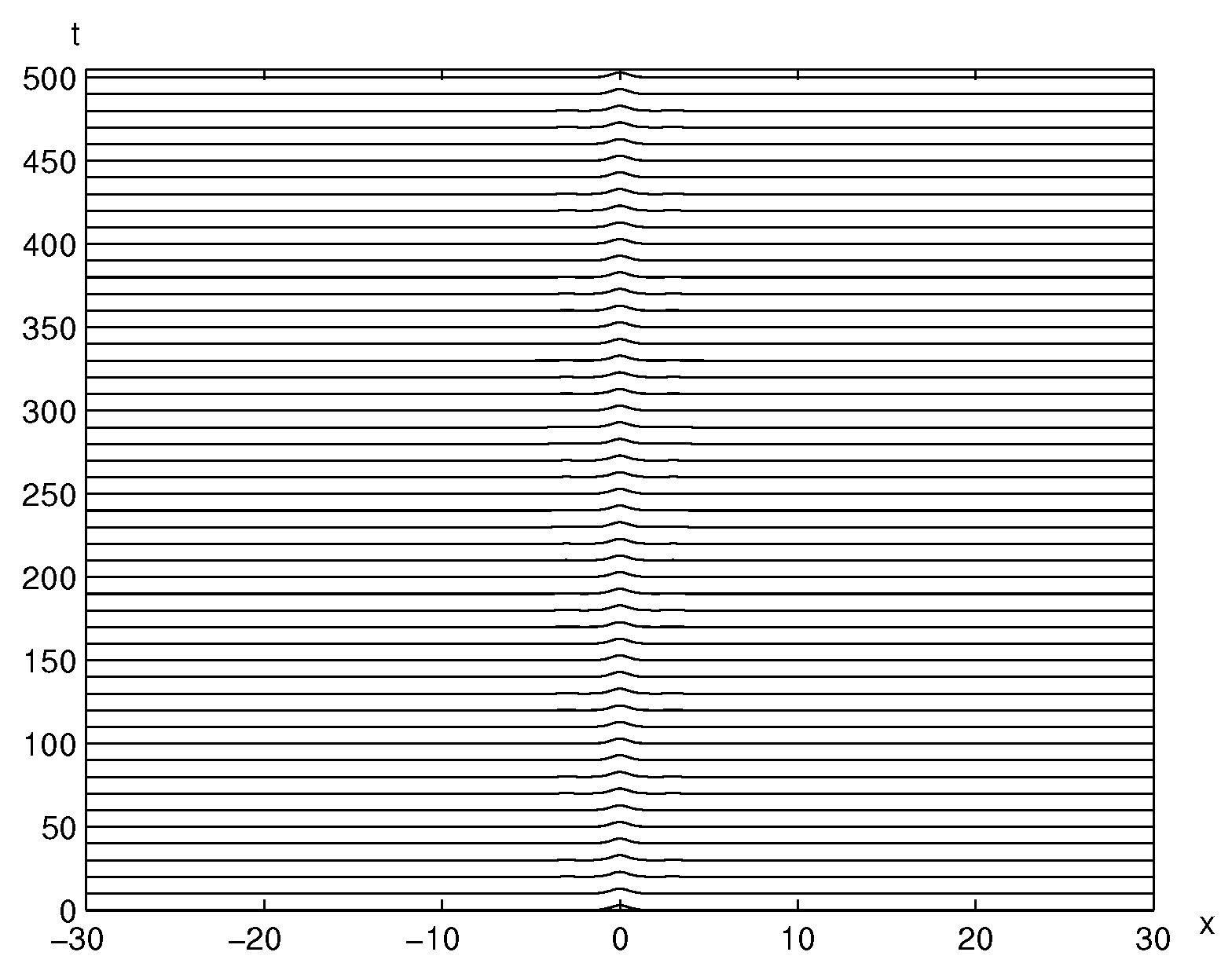
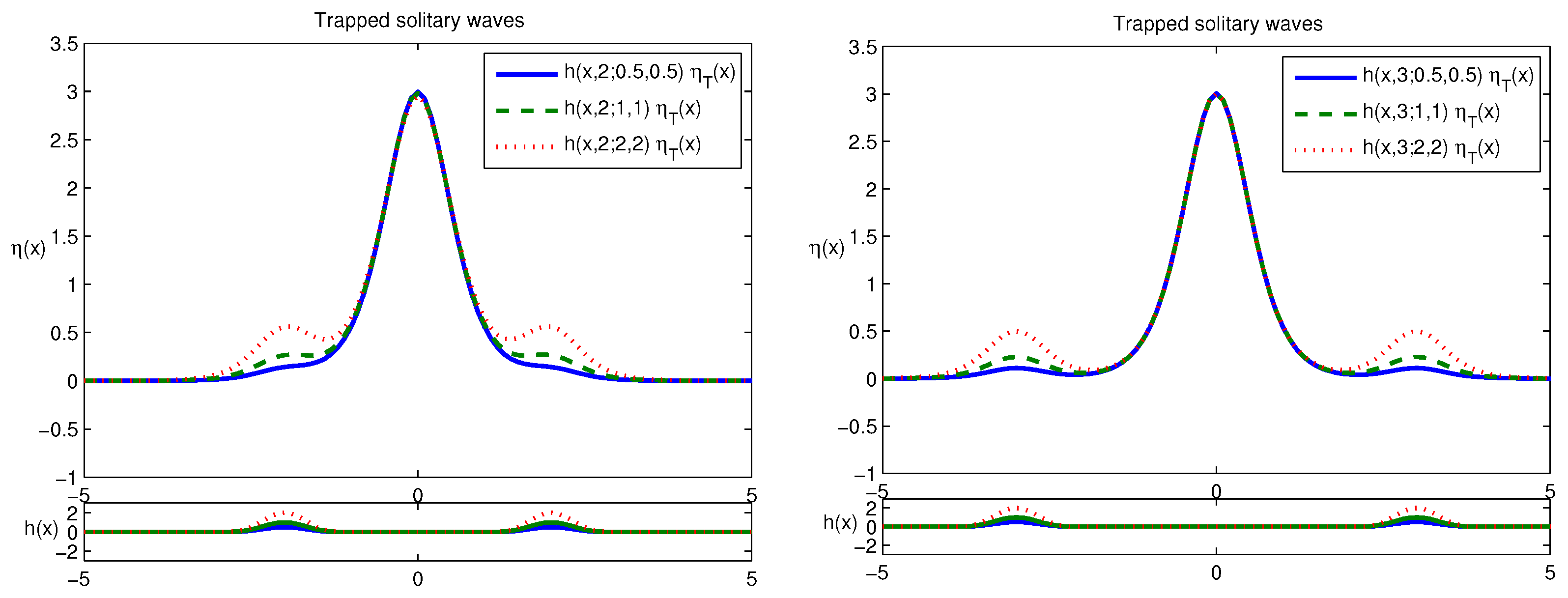
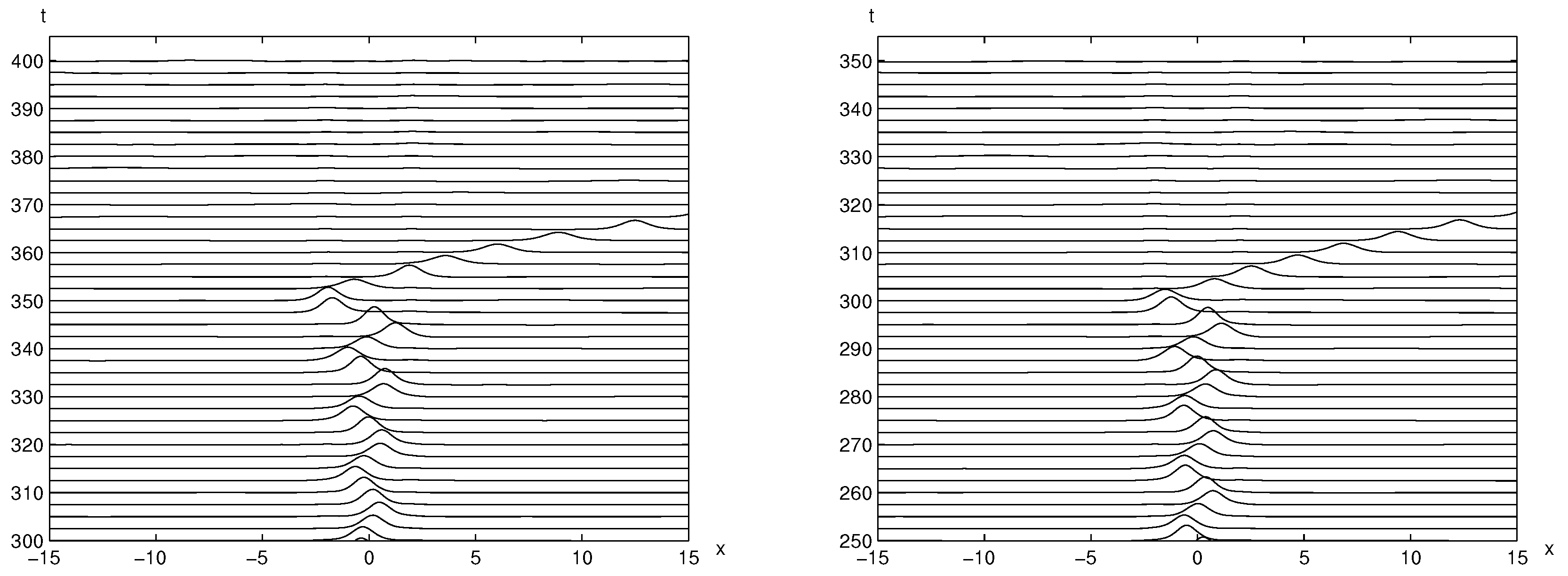
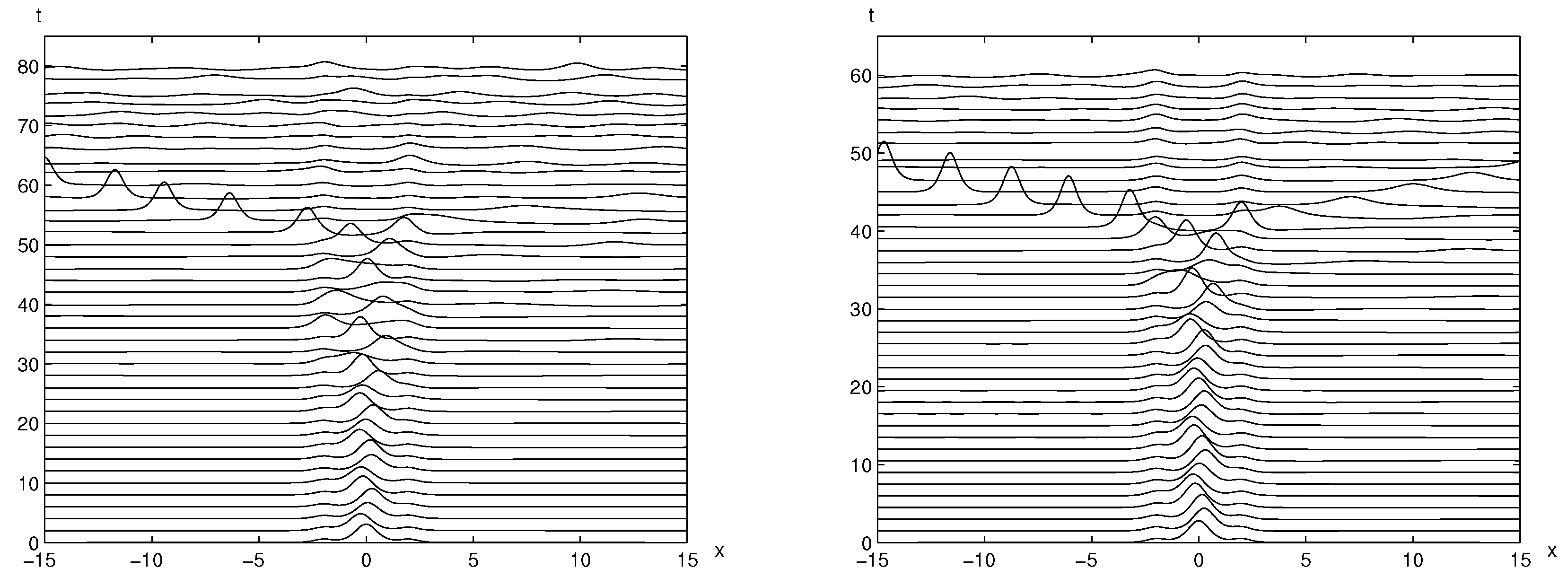
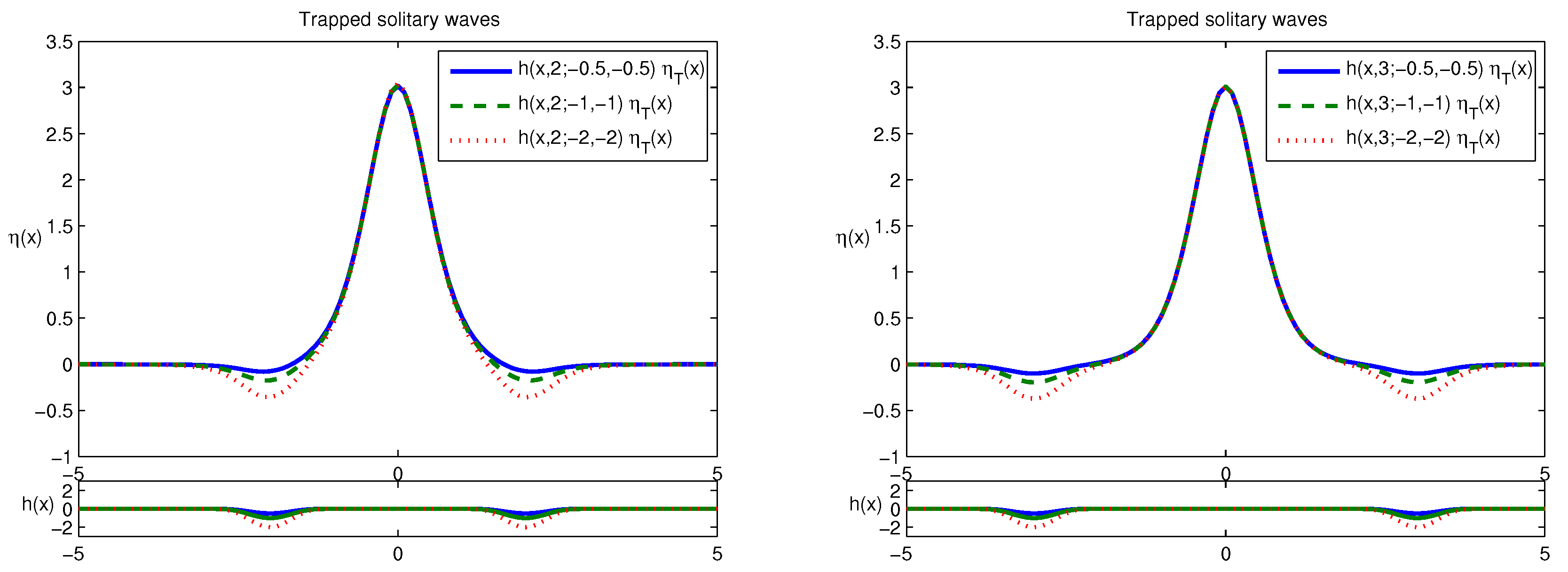
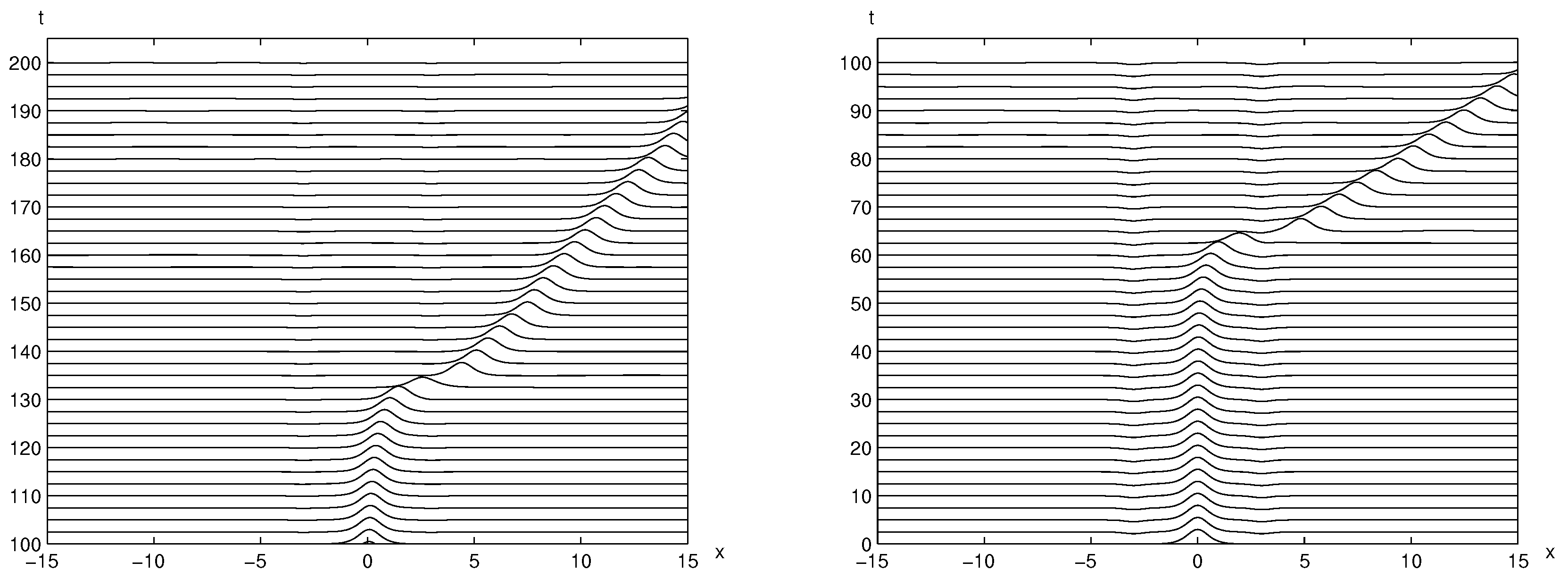
3.1. Trapped Solitary Waves between Two Positive Bumps
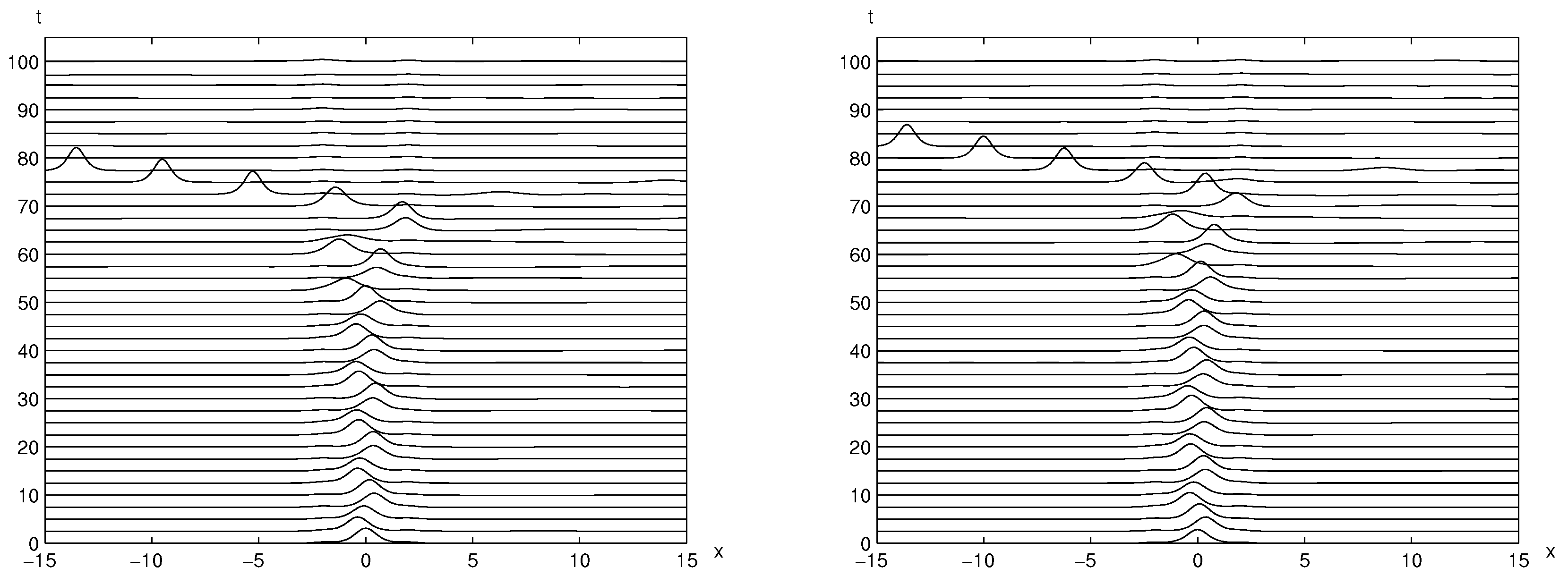
3.2. The Impact of the Bump Distance on the Stability of
3.3. The Impact of the Bump Size on the Stability of
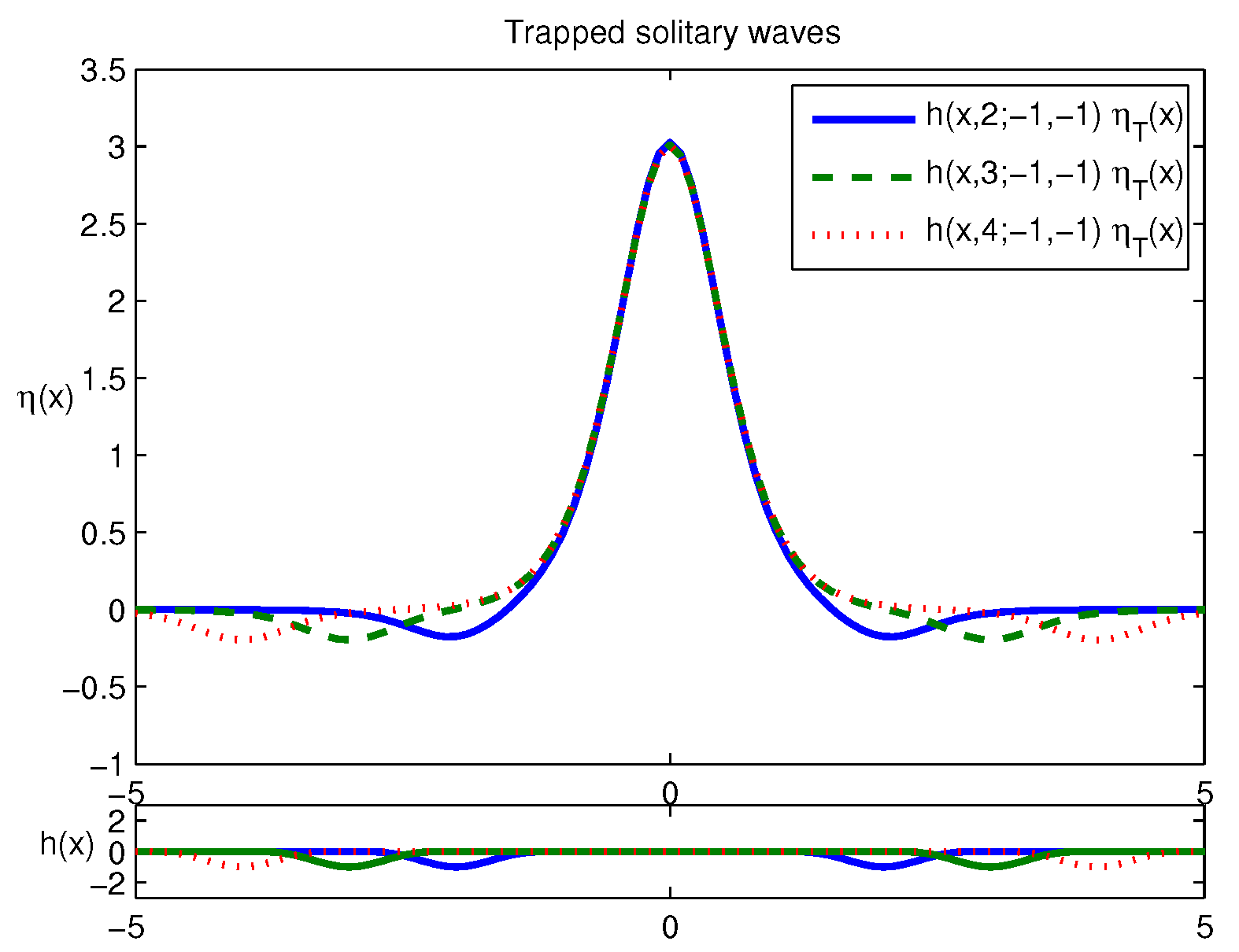
3.4. Trapped Solitary Waves between Two Negative Holes
4. Conclusions
Acknowledgments
Conflicts of Interest
Abbreviations
| MDPI | Multidisciplinary Digital Publishing Institute |
| DOAJ | Directory of open access journals |
| TLA | Three letter acronym |
| LD | linear dichroism |
References
- Camassa, R.; Wu, T. Stability of forced solitary waves. Philos. Trans. R. Soc. Lond. A 1991, 337, 429–466. [Google Scholar] [CrossRef]
- Zabuski, N.J.; Kruskal, M.D. Interaction of “solitons” in a collisionless plasma and the recurrence of initial states. Phys. Rev. Lett. 1965, 15, 240–243. [Google Scholar] [CrossRef]
- Dias, F.; Vanden-Broeck, J.M. Generalized critical free-surface flows. J. Eng. Math. 2002, 42, 291–301. [Google Scholar] [CrossRef]
- Shen, S.S. On the accuracy of the stationary forced Korteweg-De Vries equation as a model equation for flows over a bump. Q. Appl. Math. 1995, 53, 701–719. [Google Scholar] [CrossRef]
- Crighton, D.G. Applications of KdV. Acta Appl. Math. 1995, 39, 39–67. [Google Scholar] [CrossRef]
- Hereman, W. Shallow Water Waves and Solitary Waves. In Mathematics of Complexity and Dynamical Systems; Meyers, R., Ed.; Springer: New York, NY, USA, 2012. [Google Scholar]
- Choi, J.W.; Sun, S.M.; Whang, S.I. Supercritical surface gravity waves generated by a positive forcing. Eur. J. Mech. B Fluids 2008, 27, 750–770. [Google Scholar] [CrossRef]
- Shen, S.S.; Shen, M.C.; Sun, S.M. A model equation for steady surface waves over a bump. J. Eng. Math. 1989, 23, 315–323. [Google Scholar] [CrossRef]
- Shen, S.S.; Manohar, R.P.; Gong, L. Stability of the lower cusped solitary waves. Phys. Fluids 1995, 7, 2507–2509. [Google Scholar] [CrossRef]
- Forbes, L.K. Critical free-surface flow over a semi-circular obstruction. J. Eng. Math. 1988, 22, 3–13. [Google Scholar] [CrossRef]
- Grimshaw, R.; Maleewong, M. Stability of steady gravity waves generated by a moving localised pressure disturbance in water of finite depth. Phys. Fluids 2013, 25, 006705. [Google Scholar] [CrossRef]
- Pratt, L.J. On nonlinear flow with multiple obstructions. Geophys. Astrphys. Fluid Dyn. 1984, 41, 1214–1225. [Google Scholar] [CrossRef]
- Dias, F.; Vanden-Broeck, J.M. Trapped waves between submerged obstacles. J. Fluid Mech. 2004, 509, 93–102. [Google Scholar] [CrossRef]
- Binder, B.J.; Dias, F.; Vanden-Broeck, J.M. Influence of rapid changes in a channel bottom on free-surface flows. IMA J. Appl. Math. 2008, 73, 254–273. [Google Scholar] [CrossRef]
- Binder, B.J.; Blyth, M.G.; McCue, S.W. Free-surface flow past arbitrary topography and an inverse approach for wave-free solutions. IMA J. Appl. Math. 2013, 78, 685–696. [Google Scholar] [CrossRef]
- Ee, B.K.; Grimshaw, R.H.J.; Zang, D.H.; Chow, K.W. Steady transcritical flow over a hole: Parametric map of solutions of the forced Korteweg-de Vries equation. Phys. Fluids 2010, 22, 056602. [Google Scholar] [CrossRef]
- Chardard, F.; Dias, F.; Nguyen, H.Y.; Vanden-Broeck, J.M. Stability of some stationary solutions to the forced KdV equation with one or two bumps. J. Eng. Math. 2011, 70, 175–189. [Google Scholar] [CrossRef]
- Gong, L.; Shen, S.S. Multiple wave solutions of the staionary forced Korteweg-De Vries equation and their stability. SIAM J. Appl. Math. 1994, 54, 1268–1290. [Google Scholar] [CrossRef]
- Choi, J.W.; Lin, T.; Sun, S.M.; Whang, S.I. Supercritical surface waves generated by negative or oscillatory forcing. Discret. Contin. Dyn. Syst. B 2010, 14, 1313–1335. [Google Scholar] [CrossRef]
- Choi, J.W. Free surface waves over a depression. Bull. Aust. Math. Soc. 2002, 65, 329–335. [Google Scholar] [CrossRef]
- Whang, S.I.; Lee, S.M. Absorbing boundary conditions for the stationary forced KdV equation. Appl. Math. Comput. 2008, 202, 511–519. [Google Scholar] [CrossRef]
- Lee, S.M.; Whang, S.I. Trapped Supercritical wave for the forced KdV equation with two bumps. Appl. Math. Model. 2014, 39, 2649–2660. [Google Scholar] [CrossRef]
- Feng, B.; Mitsui, T. A finite difference method for the Korteweg-de Vries and the Kadomtsev-Petviashvili equations. J. Comput. Appl. Math. 1998, 90, 95–116. [Google Scholar] [CrossRef]
- Djidjeli, K.; Price, W.; Twizell, E.; Wang, Y. Numerical methods for the solution of the third- and fifth-order dispersive Korteweg-de Vries equations. J. Comput. Appl. Math. 1995, 58, 307–336. [Google Scholar] [CrossRef]




© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, S. Dynamics of Trapped Solitary Waves for the Forced KdV Equation. Symmetry 2018, 10, 129. https://doi.org/10.3390/sym10050129
Lee S. Dynamics of Trapped Solitary Waves for the Forced KdV Equation. Symmetry. 2018; 10(5):129. https://doi.org/10.3390/sym10050129
Chicago/Turabian StyleLee, Sunmi. 2018. "Dynamics of Trapped Solitary Waves for the Forced KdV Equation" Symmetry 10, no. 5: 129. https://doi.org/10.3390/sym10050129




