High-Resolution Vegetation Mapping in Japan by Combining Sentinel-2 and Landsat 8 Based Multi-Temporal Datasets through Machine Learning and Cross-Validation Approach
Abstract
:1. Introduction
2. Methodology
2.1. Preparation of Input Features
2.2. Machine Learning, Cross-Validation, and Mapping
3. Results
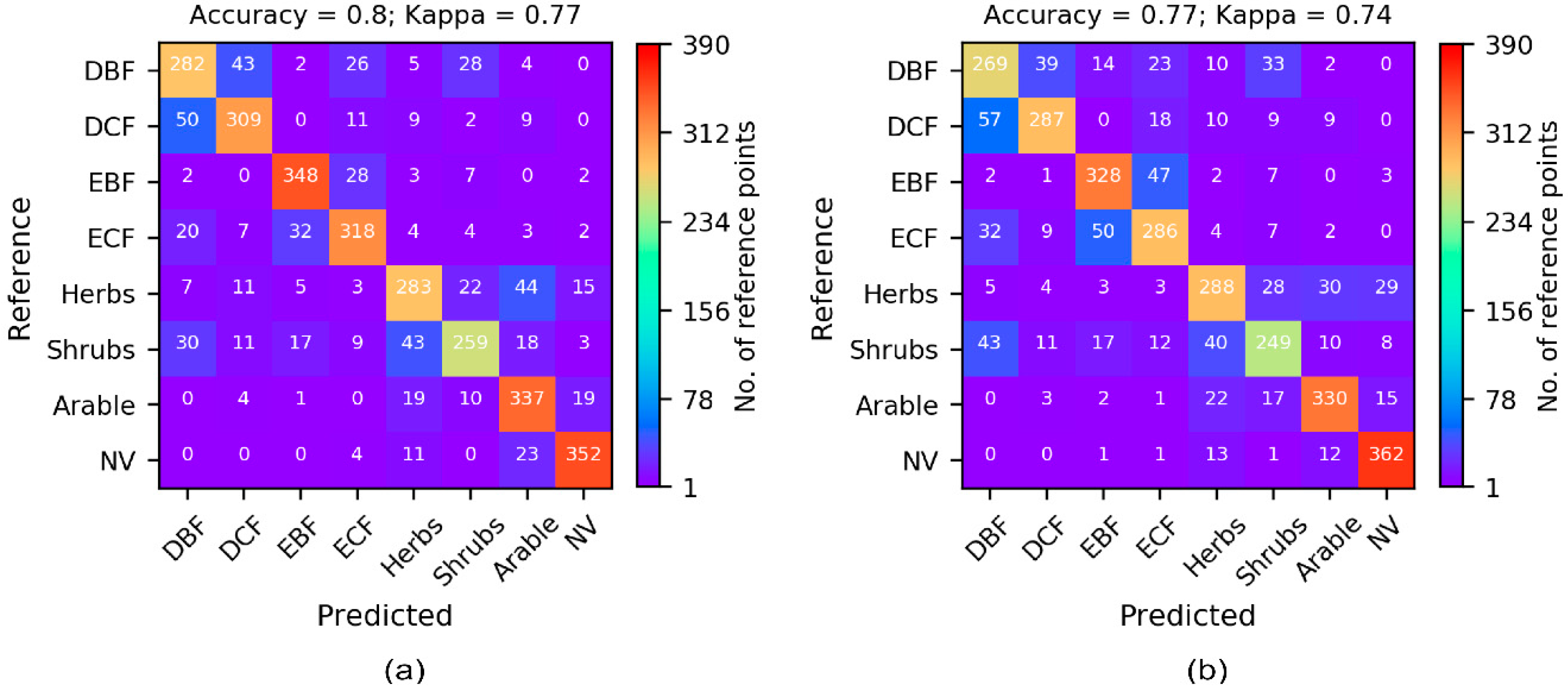
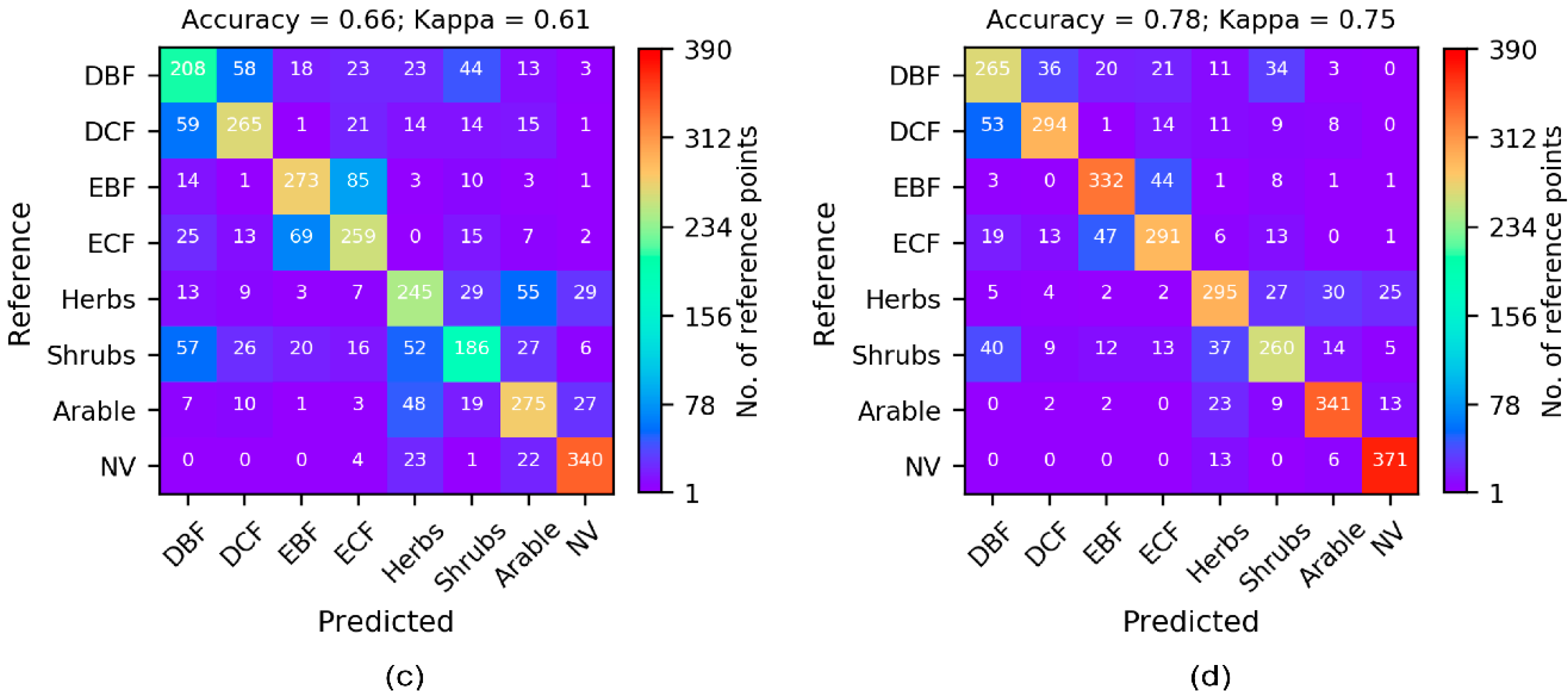
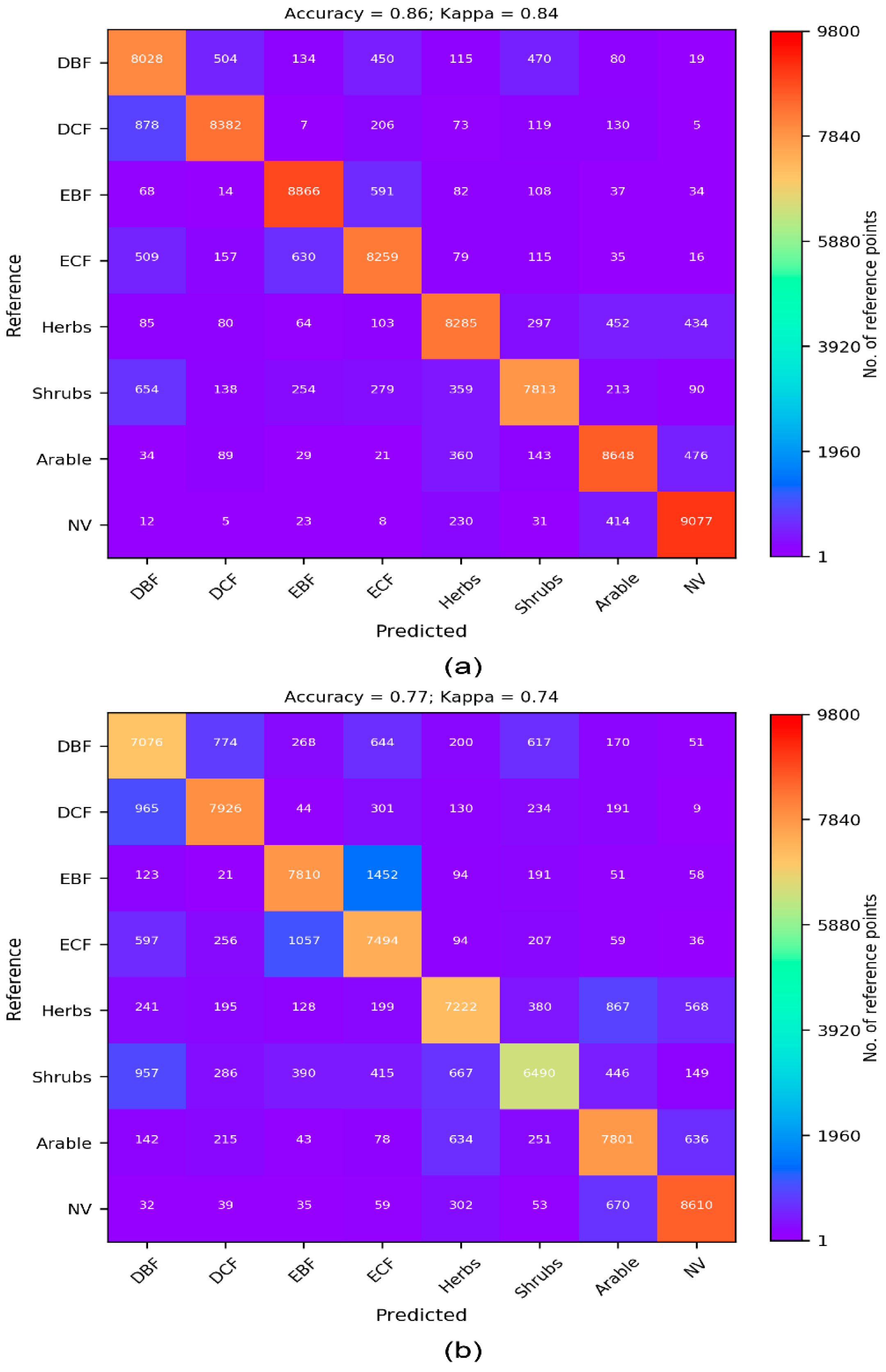
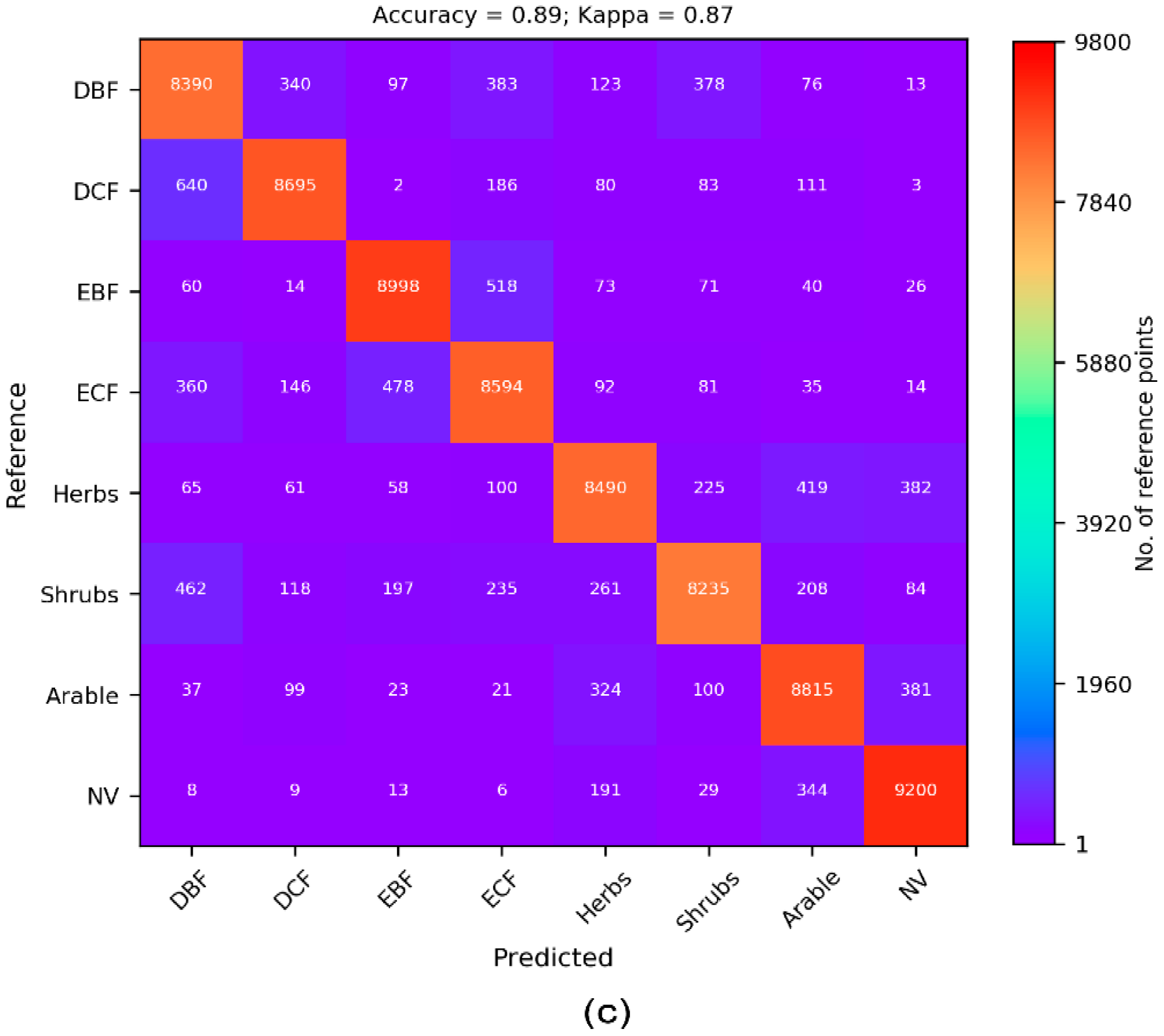
3.1. Cross-Validation Results
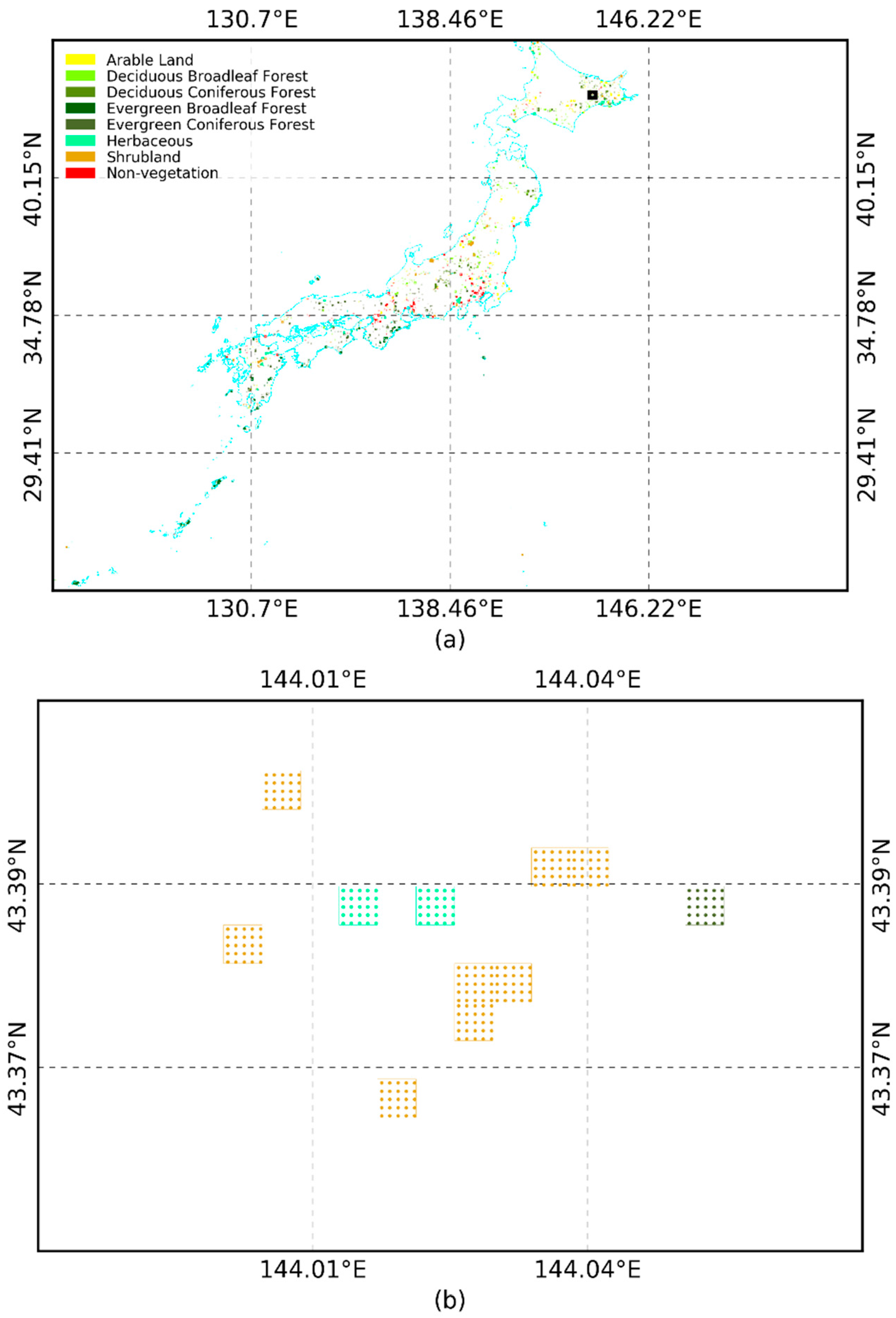
3.2. Production of Vegetation Map
4. Discussion and Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Ohba, H. The flora of Japan and the implication of global climatic change. J. Plant Res. 1994, 107, 85–89. [Google Scholar] [CrossRef]
- Leonelli, G.; Pelfini, M.; di Cella, U.M.; Garavaglia, V. Climate warming and the recent treeline shift in the European Alps: The role of geomorphological factors in high-altitude sites. Ambio 2011, 40, 264–273. [Google Scholar] [CrossRef] [PubMed]
- Kirdyanov, A.V.; Hagedorn, F.; Knorre, A.A.; Fedotova, E.V.; Vaganov, E.A.; Naurzbaev, M.M.; Moiseev, P.A.; Rigling, A. 20th century tree-line advance and vegetation changes along an altitudinal transect in the Putorana Mountains, northern Siberia. Boreas 2012, 41, 56–67. [Google Scholar] [CrossRef]
- Büntgen, U.; Hellmann, L.; Tegel, W.; Normand, S.; Myers-Smith, I.; Kirdyanov, A.V.; Nievergelt, D.; Schweingruber, F.H. Temperature-induced recruitment pulses of Arctic dwarf shrub communities. J. Ecol. 2015, 103, 489–501. [Google Scholar] [CrossRef]
- Seim, A.; Treydte, K.; Trouet, V.; Frank, D.; Fonti, P.; Tegel, W.; Panayotov, M.; Fernández-Donado, L.; Krusic, P.; Büntgen, U. Climate sensitivity of Mediterranean pine growth reveals distinct east-west dipole: East-West dipole in climate sensitivity of Mediterranean pines. Int. J. Clim. 2015, 35, 2503–2513. [Google Scholar] [CrossRef]
- Beard, J.S. The Physiognomic Approach. In Classification of Plant Communities; Whittaker, R.H., Ed.; Springer: Dordrecht, The Netherlands, 1978; pp. 33–64. [Google Scholar]
- Sharma, R.C.; Hara, K.; Hirayama, H. A Machine Learning and Cross-Validation Approach for the Discrimination of Vegetation Physiognomic Types Using Satellite Based Multispectral and Multitemporal Data. Scientifica 2017, 2017, 8. [Google Scholar] [CrossRef] [PubMed]
- Gitas, I.; Karydas, C.; Kazakis, G. Land cover mapping of Mediterranean landscapes, using SPOT4-Xi and IKONOS imagery-A preliminary investigation. Options Mediterr. Ser. B 2003, 2003, 27–41. [Google Scholar]
- Salovaara, K.J.; Thessler, S.; Malik, R.N.; Tuomisto, H. Classification of Amazonian primary rain forest vegetation using Landsat ETM+ satellite imagery. Remote Sens. Environ. 2005, 97, 39–51. [Google Scholar] [CrossRef]
- Li, L.; Ustin, S.L.; Lay, M. Application of multiple endmember spectral mixture analysis (MESMA) to AVIRIS imagery for coastal salt marsh mapping: A case study in China Camp, CA, USA. Int. J. Remote Sens. 2005, 26, 5193–5207. [Google Scholar] [CrossRef]
- Rosso, P.H.; Ustin, S.L.; Hastings, A. Mapping marshland vegetation of San Francisco Bay, California, using hyperspectral data. Int. J. Remote Sens. 2005, 26, 5169–5191. [Google Scholar] [CrossRef]
- Helmer, E.H.; Ruzycki, T.S.; Benner, J.; Voggesser, S.M.; Scobie, B.P.; Park, C.; Fanning, D.W.; Ramnarine, S. Detailed maps of tropical forest types are within reach: Forest tree communities for Trinidad and Tobago mapped with multiseason Landsat and multiseason fine-resolution imagery. For. Ecol. Manag. 2012, 279, 147–166. [Google Scholar] [CrossRef]
- Zweig, C.L.; Burgess, M.A.; Percival, H.F.; Kitchens, W.M. Use of Unmanned Aircraft Systems to Delineate Fine-Scale Wetland Vegetation Communities. Wetlands 2015, 35, 303–309. [Google Scholar] [CrossRef]
- Su, Y.; Guo, Q.; Fry, D.L.; Collins, B.M.; Kelly, M.; Flanagan, J.P.; Battles, J.J. A Vegetation Mapping Strategy for Conifer Forests by Combining Airborne LiDAR Data and Aerial Imagery. Can. J. Remote Sens. 2016, 42, 1–15. [Google Scholar] [CrossRef]
- Sankey, T.T.; McVay, J.; Swetnam, T.L.; McClaran, M.P.; Heilman, P.; Nichols, M. UAV hyperspectral and LiDAR data and their fusion for arid and semi-arid land vegetation monitoring. Remote Sens. Ecol. Conserv. 2017. [Google Scholar] [CrossRef]
- Koch, M.; Schmid, T.; Reyes, M.; Gumuzzio, J. Evaluating Full Polarimetric C- and L-Band Data for Mapping Wetland Conditions in a Semi-Arid Environment in Central Spain. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2012, 5, 1033–1044. [Google Scholar] [CrossRef]
- Betbeder, J.; Rapinel, S.; Corpetti, T.; Pottier, E.; Corgne, S.; Hubert-Moy, L. Multitemporal classification of TerraSAR-X data for wetland vegetation mapping. J. Appl. Remote Sens. 2014, 8, 083648. [Google Scholar] [CrossRef]
- Balzter, H.; Cole, B.; Thiel, C.; Schmullius, C. Mapping CORINE Land Cover from Sentinel-1A SAR and SRTM Digital Elevation Model Data using Random Forests. Remote Sens. 2015, 7, 14876–14898. [Google Scholar] [CrossRef]
- Furtado, L.F.deA.; Silva, T.S.F.; Novo, E.M.L.deM. Dual-season and full-polarimetric C band SAR assessment for vegetation mapping in the Amazon várzea wetlands. Remote Sens. Environ. 2016, 174, 212–222. [Google Scholar] [CrossRef]
- Rouse, J.; Haas, R.; Schell, J.; Deering, D. Monitoring Vegetation Systems in the Great Plains with ERTS. In Proceedings of the Third ERTS Symposium, Washington, DC, USA, 10–14 December 1974; Freden, S.C., Mercanti, E.P., Eds.; U.S. Govt. Printing Office: Washington DC, USA, 1974; Volume 351, p. 309. [Google Scholar]
- Tucker, C.J. Red and photographic infrared linear combinations for monitoring vegetation. Remote Sens. Environ. 1979, 8, 127–150. [Google Scholar] [CrossRef]
- Roberts, D.A.; Gardner, M.E.; Church, R.; Ustin, S.L.; Green, R.O. Optimum strategies for mapping vegetation using multiple-endmember spectral mixture models. Proc. SPIE 3118 1997, 108–119. [Google Scholar] [CrossRef]
- Udelhoven, T. Long term data fusion for a dense time series analysis with MODIS and Landsat imagery in an Australian Savanna. J. Appl. Remote Sens. 2012, 6, 063512. [Google Scholar] [CrossRef]
- Schmidt, M.; Lucas, R.; Bunting, P.; Verbesselt, J.; Armston, J. Multi-resolution time series imagery for forest disturbance and regrowth monitoring in Queensland, Australia. Remote Sens. Environ. 2015, 158, 156–168. [Google Scholar] [CrossRef] [Green Version]
- Murray, H.; Lucieer, A.; Williams, R. Texture-based classification of sub-Antarctic vegetation communities on Heard Island. Int. J. Appl. Earth Obs. Geoinf. 2010, 12, 138–149. [Google Scholar] [CrossRef]
- Stuart, N.; Barratt, T.; Place, C. Classifying the Neotropical savannas of Belize using remote sensing and ground survey. J. Biogeogr. 2006, 33, 476–490. [Google Scholar] [CrossRef]
- Vanselow, K.; Samimi, C. Predictive Mapping of Dwarf Shrub Vegetation in an Arid High Mountain Ecosystem Using Remote Sensing and Random Forests. Remote Sen. 2014, 6, 6709–6726. [Google Scholar] [CrossRef]
- Torbick, N.; Ledoux, L.; Salas, W.; Zhao, M. Regional Mapping of Plantation Extent Using Multisensor Imagery. Remote Sens. 2016, 8, 236. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, Q.; Zhao, L.; Wu, X.; Yue, G.; Zou, D.; Nan, Z.; Liu, G.; Pang, Q.; Fang, H.; et al. Mapping the vegetation distribution of the permafrost zone on the Qinghai-Tibet Plateau. J. Mt. Sci. 2016, 13, 1035–1046. [Google Scholar] [CrossRef]
- Schwieder, M.; Leitão, P.J.; da Cunha Bustamante, M.M.; Ferreira, L.G.; Rabe, A.; Hostert, P. Mapping Brazilian savanna vegetation gradients with Landsat time series. Int. J. Appl. Earth Obs. Geoinf. 2016, 52, 361–370. [Google Scholar] [CrossRef]
- Filippi, A.M.; Jensen, J.R. Fuzzy learning vector quantization for hyperspectral coastal vegetation classification. Remote Sens. Environ. 2006, 100, 512–530. [Google Scholar] [CrossRef]
- Carpenter, G.A.; Gopal, S.; Macomber, S.; Martens, S.; Woodcock, C.E. A neural network method for mixture estimation for vegetation mapping. Remote Sens. Environ. 1999, 70, 138–152. [Google Scholar] [CrossRef]
- Zhang, C.; Xie, Z. Combining object-based texture measures with a neural network for vegetation mapping in the Everglades from hyperspectral imagery. Remote Sens. Environ. 2012, 124, 310–320. [Google Scholar] [CrossRef]
- Antropov, O.; Rauste, Y.; Astola, H.; Praks, J.; Häme, T.; Hallikainen, M.T. Land cover and soil type mapping from spaceborne PolSAR data at L-band with probabilistic neural network. IEEE Trans. Geosci. Remote Sens. 2014, 52, 5256–5270. [Google Scholar] [CrossRef]
- Sharma, R.C.; Hara, K.; Hirayama, H.; Harada, I.; Hasegawa, D.; Tomita, M.; Geol Park, J.; Asanuma, I.; Short, K.M.; Hara, M.; et al. Production of Multi-Features Driven Nationwide Vegetation Physiognomic Map and Comparison to MODIS Land Cover Type Product. Adv. Remote Sens. 2017, 6, 54–65. [Google Scholar] [CrossRef]
- Sharma, R.; Tateishi, R.; Hara, K.; Iizuka, K. Production of the Japan 30-m Land Cover Map of 2013–2015 Using a Random Forests-Based Feature Optimization Approach. Remote Sens. 2016, 8, 429. [Google Scholar] [CrossRef]
- Homer, C.G.; Dewitz, J.A.; Yang, L.; Jin, S.; Danielson, P.; Xian, G.; Coulston, J.; Herold, N.D.; Wickham, J.; Megown, K. Completion of the 2011 National Land Cover Database for the conterminous United States-Representing a decade of land cover change information. Photogram. Eng. Remote Sens. 2015, 81, 345–354. [Google Scholar]
- Chen, J.; Chen, J.; Liao, A.; Cao, X.; Chen, L.; Chen, X.; He, C.; Han, G.; Peng, S.; Lu, M.; et al. Global land cover mapping at 30m resolution: A POK-based operational approach. ISPRS J. Photogram. Remote Sens. 2015, 103, 7–27. [Google Scholar] [CrossRef]
- Pelletier, C.; Valero, S.; Inglada, J.; Champion, N.; Marais Sicre, C.; Dedieu, G. Effect of Training Class Label Noise on Classification Performances for Land Cover Mapping with Satellite Image Time Series. Remote Sens. 2017, 9, 173. [Google Scholar] [CrossRef]
- Sharma, R.C.; Tateishi, R.; Hara, K.; Gharechelou, S.; Iizuka, K. Global mapping of urban built-up areas of year 2014 by combining MODIS multispectral data with VIIRS nighttime light data. Int. J. Digit. Earth 2016, 9, 1004–1020. [Google Scholar] [CrossRef]
- Sharma, R.; Tateishi, R.; Hara, K.; Nguyen, L. Developing Superfine Water Index (SWI) for Global Water Cover Mapping Using MODIS Data. Remote Sens. 2015, 7, 13807–13841. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Cohen, J. A coefficient of agreement for nominal scales. Educ. Psychol. Meas. 1960, 20, 37–46. [Google Scholar] [CrossRef]
- Harada, I.; Hara, K.; Tomita, M.; Short, K.; Park, J. Monitoring Landscape Changes in Japan Using Classification of Modis Data Combined with a Landscape Transformation Sere (LTS) Model. J. Landsc. Ecol. 2015, 7. [Google Scholar] [CrossRef]
- Roy, P.; Roy, A.; Joshi, P.; Kale, M.; Srivastava, V.; Srivastava, S.; Dwevidi, R.; Joshi, C.; Behera, M.; Meiyappan, P.; et al. Development of Decadal (1985–1995–2005) Land Use and Land Cover Database for India. Remote Sens. 2015, 7, 2401–2430. [Google Scholar] [CrossRef]
- Hayes, M.M.; Miller, S.N.; Murphy, M.A. High-resolution landcover classification using Random Forest. Remote Sens. Lett. 2014, 5, 112–121. [Google Scholar] [CrossRef]
- Sharma, R.; Tateishi, R.; Hara, K. A Biophysical Image Compositing Technique for the Global-Scale Extraction and Mapping of Barren Lands. ISPRS Int. J. Geo-Inf. 2016, 5, 225. [Google Scholar] [CrossRef]

| Datasets | f = 5 | f = 10 | f = 25 | f = 50 | f = 75 |
|---|---|---|---|---|---|
| MODIS (s = 390) | 0.74 (0.71) | 0.78 (0.75) | 0.79 (0.76) | 0.80 (0.77) | 0.80 (0.77) |
| Landsat 8 (s = 390) | 0.68 (0.64) | 0.76 (0.72) | 0.77 (0.74) | 0.77 (0.74) | 0.77 (0.74) |
| Landsat 8 (s = 9800) | 0.73 (0.69) | 0.83 (0.81) | 0.86 (0.84) | 0.86 (0.84) | 0.86 (0.84) |
| Sentinel 2 (s = 390) | 0.54 (0.48) | 0.61 (0.55) | 0.63 (0.58) | 0.66 (0.61) | 0.66 (0.61) |
| Sentinel 2 (s = 9800) | 0.61 (0.55) | 0.71 (0.67) | 0.76 (0.72) | 0.77 (0.74) | 0.77 (0.74) |
| Landsat 8 + Sentinel 2 (s = 390) | 0.68 (0.64) | 0.76 (0.72) | 0.77 (0.73) | 0.77 (0.73) | 0.78 (0.75) |
| Landsat 8 + Sentinel 2 (s = 9800) | 0.75 (0.71) | 0.83 (0.81) | 0.87 (0.85) | 0.88 (0.86) | 0.89 (0.87) |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sharma, R.C.; Hara, K.; Tateishi, R. High-Resolution Vegetation Mapping in Japan by Combining Sentinel-2 and Landsat 8 Based Multi-Temporal Datasets through Machine Learning and Cross-Validation Approach. Land 2017, 6, 50. https://doi.org/10.3390/land6030050
Sharma RC, Hara K, Tateishi R. High-Resolution Vegetation Mapping in Japan by Combining Sentinel-2 and Landsat 8 Based Multi-Temporal Datasets through Machine Learning and Cross-Validation Approach. Land. 2017; 6(3):50. https://doi.org/10.3390/land6030050
Chicago/Turabian StyleSharma, Ram C., Keitarou Hara, and Ryutaro Tateishi. 2017. "High-Resolution Vegetation Mapping in Japan by Combining Sentinel-2 and Landsat 8 Based Multi-Temporal Datasets through Machine Learning and Cross-Validation Approach" Land 6, no. 3: 50. https://doi.org/10.3390/land6030050
APA StyleSharma, R. C., Hara, K., & Tateishi, R. (2017). High-Resolution Vegetation Mapping in Japan by Combining Sentinel-2 and Landsat 8 Based Multi-Temporal Datasets through Machine Learning and Cross-Validation Approach. Land, 6(3), 50. https://doi.org/10.3390/land6030050





