Experimental Design of a Prescribed Burn Instrumentation
Abstract
:1. Introduction
2. Methods
2.1. Coupled Atmosphere-Fire Simulation
2.2. Statistical Analysis of Typical Burn Dates
2.3. Statistical Optimization of Sensor Placement
2.3.1. Repeated Latin Hypercube Sampling and Sobol Variance Decomposition
- is the total variability of the output Y over the range of the parameters . We take this as the strength of the signal from the sensor.
- , called the Variance of the Conditional Expectation (VCE), is an estimate of the variability of the output Y due to the parameter .
3. Results
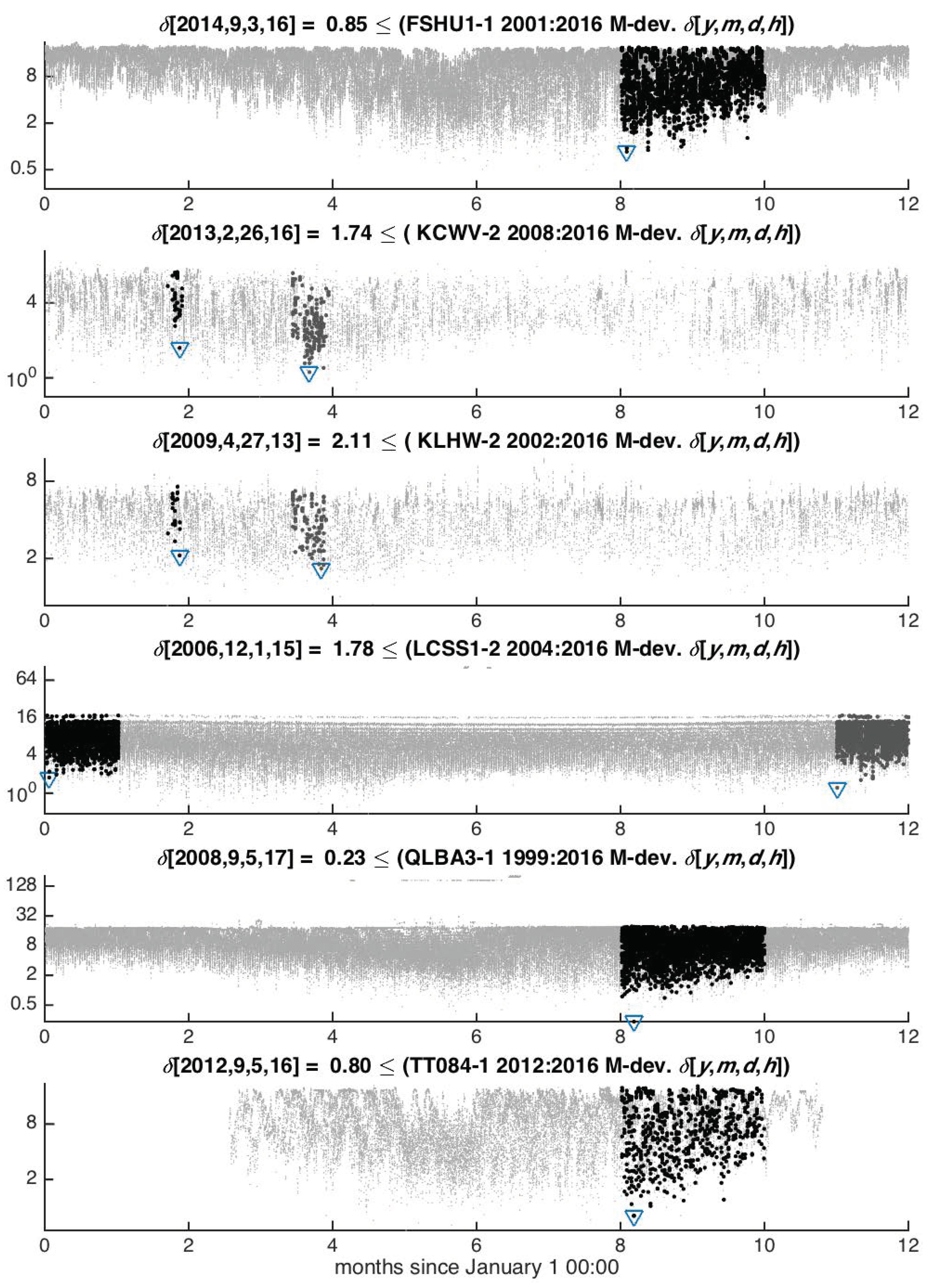
3.1. Determination of Typical Burn Days
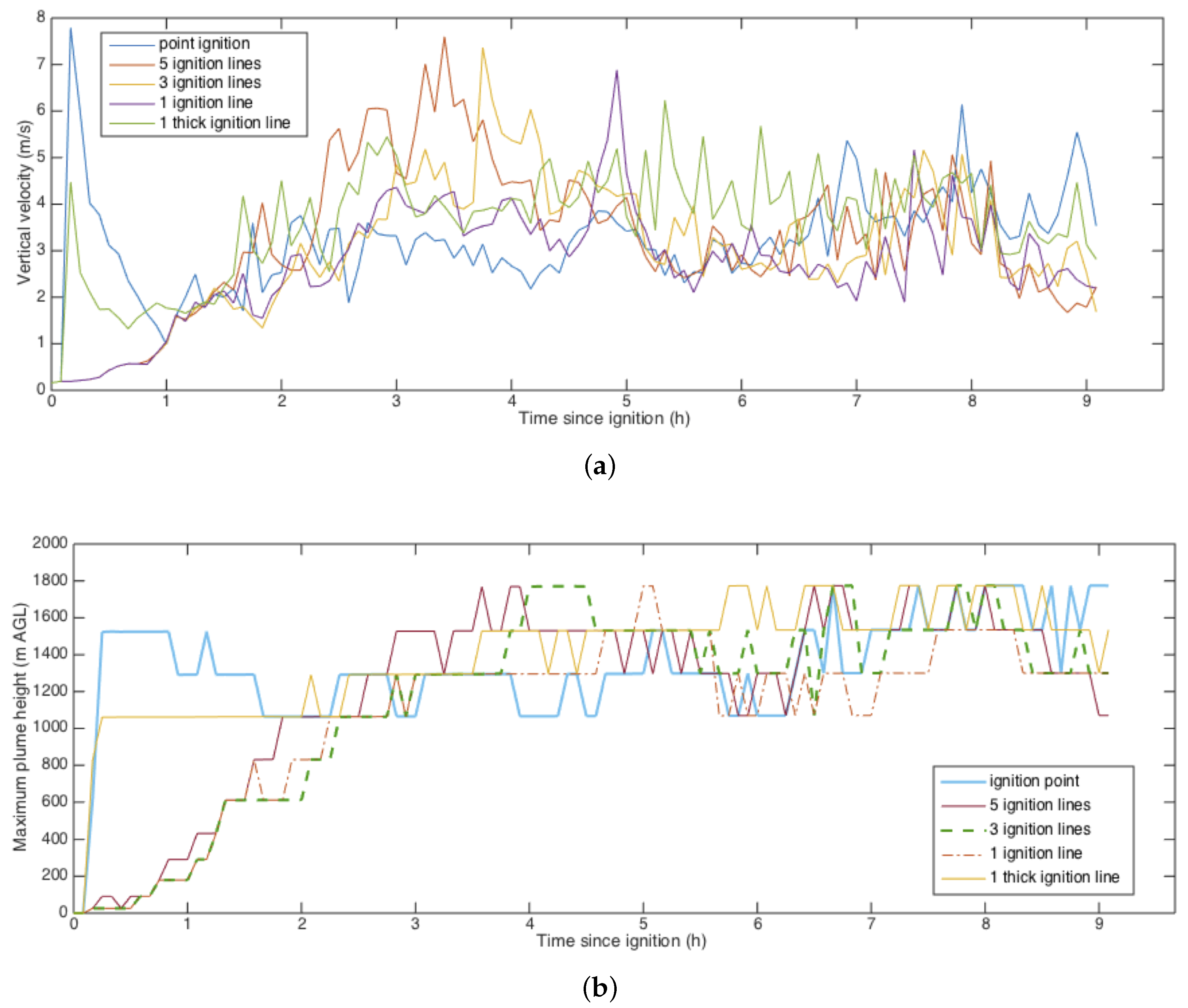
3.2. Results from Numerical Experiments
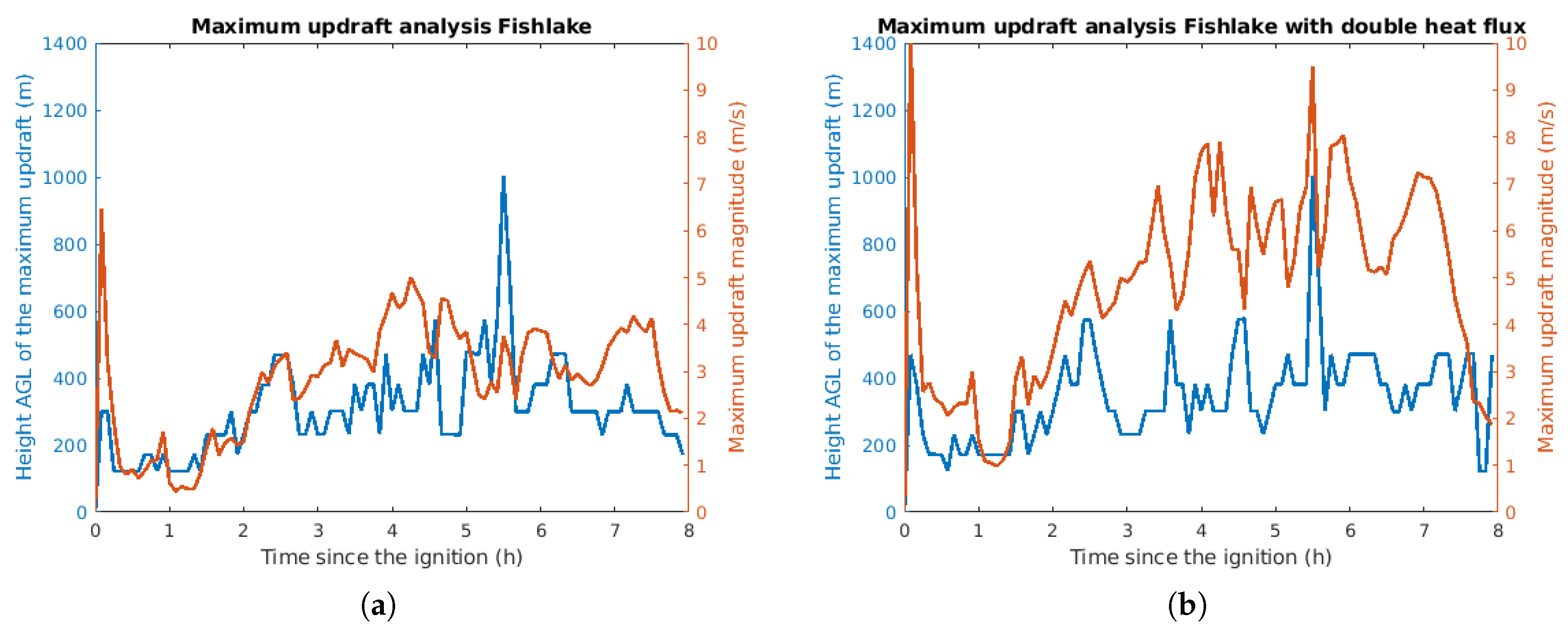
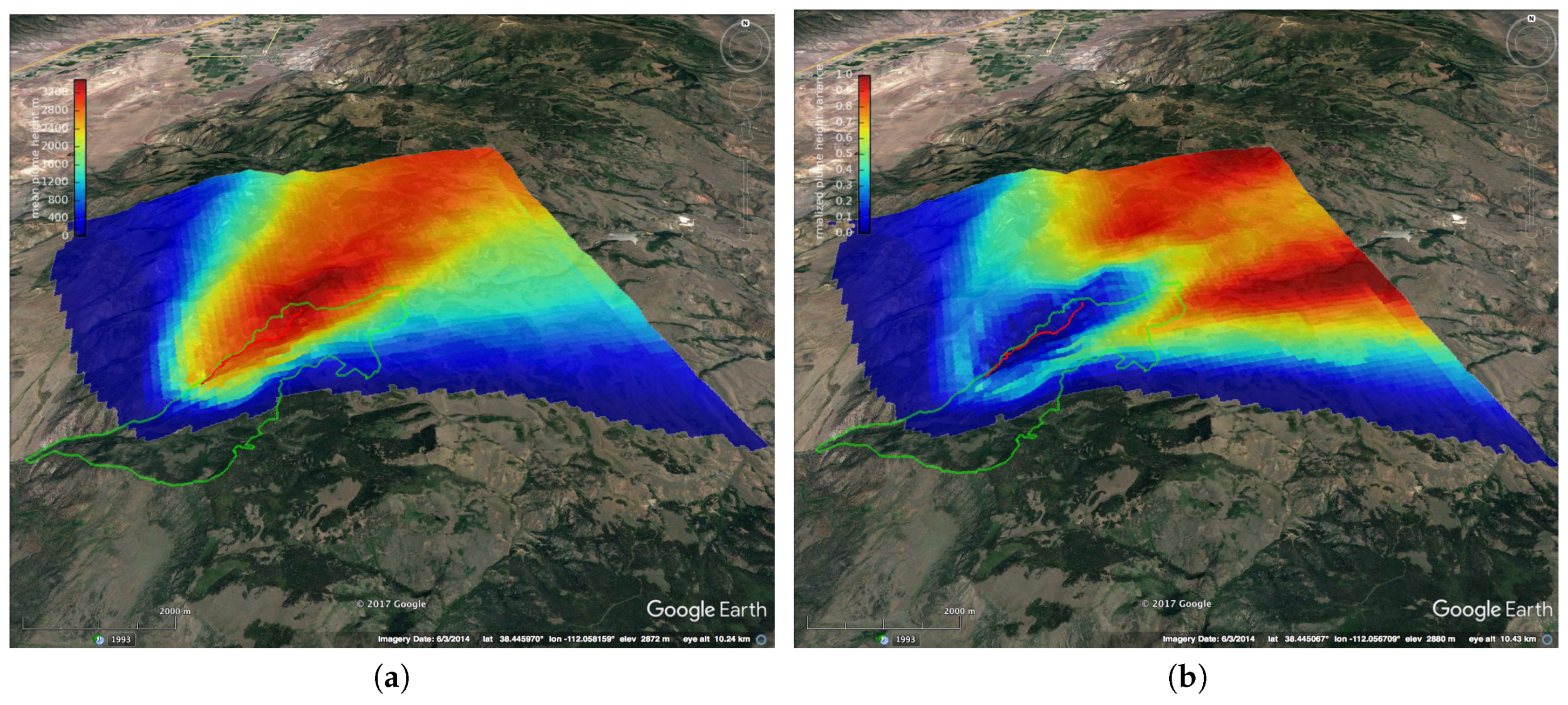
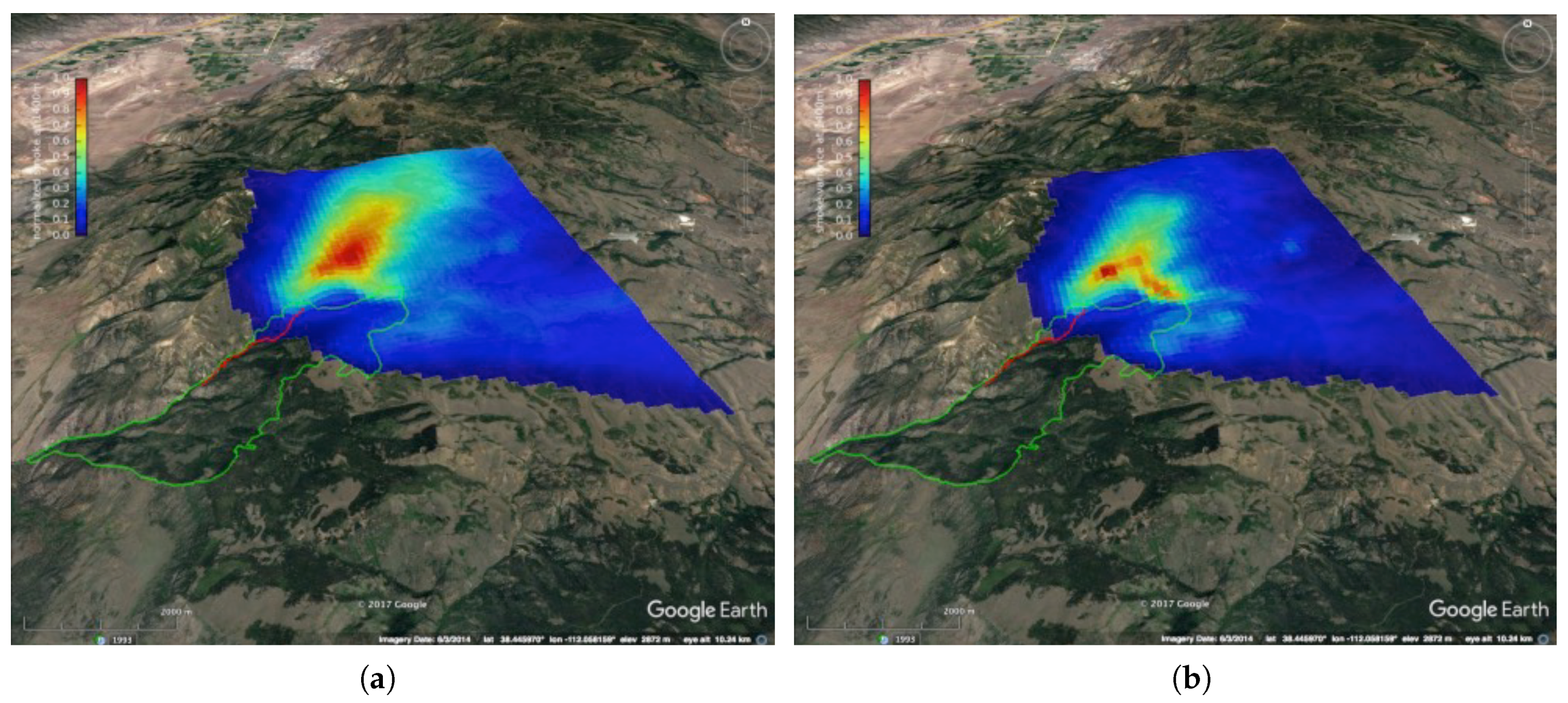
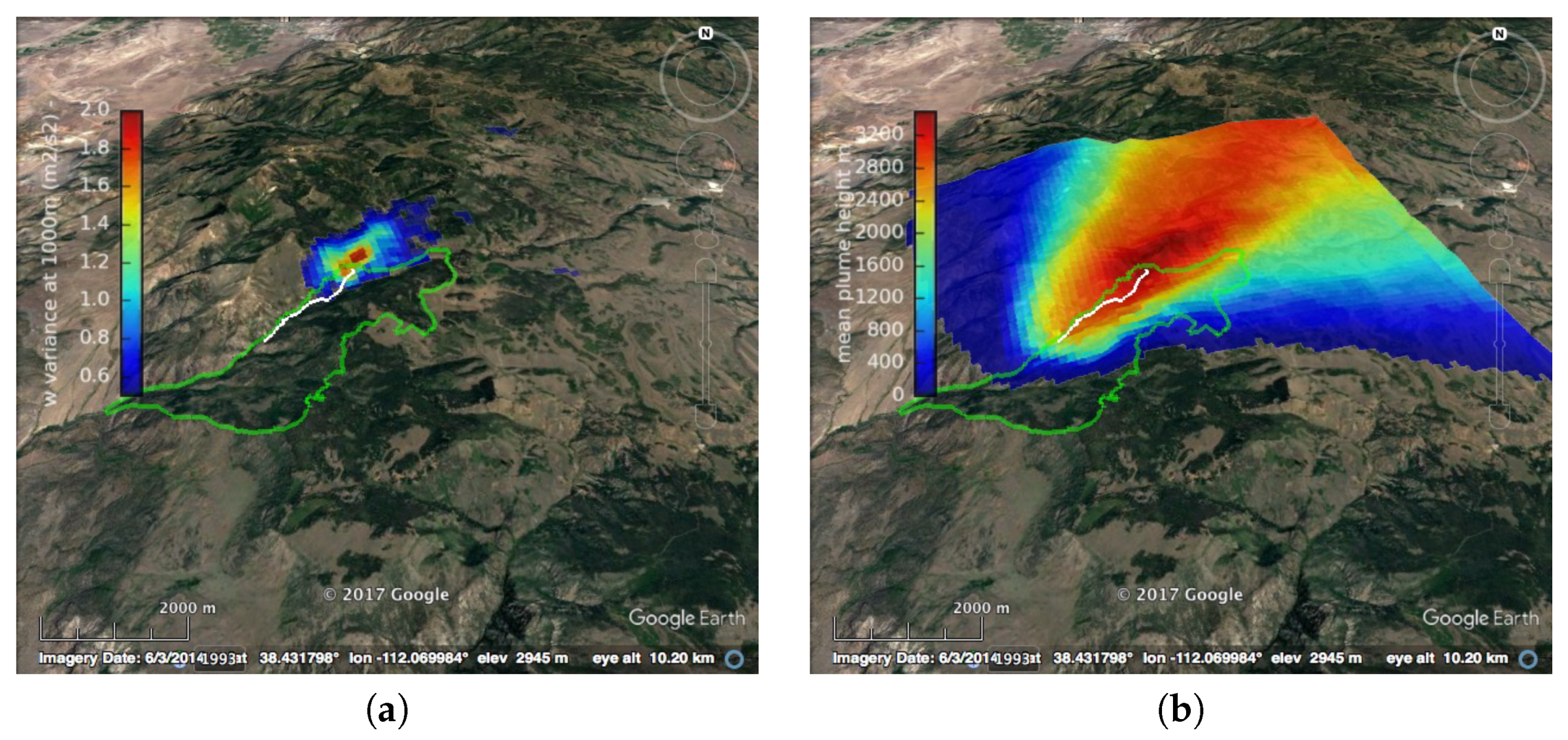
3.2.1. Simulations of Planned Experimental Burns in Fishlake
- reference simulation without fire,
- standard simulation with fire, and
- simulation with fire and doubled heat flux from the fire to the atmosphere.
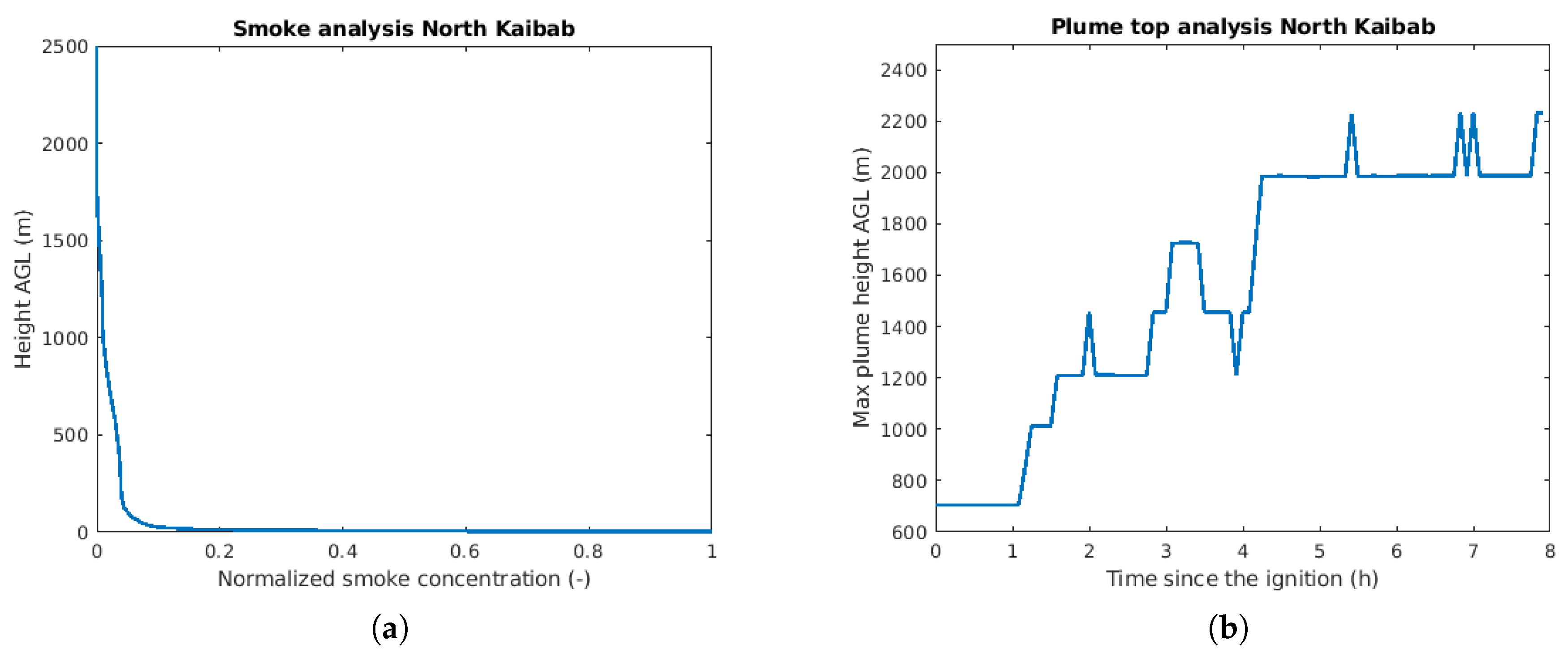
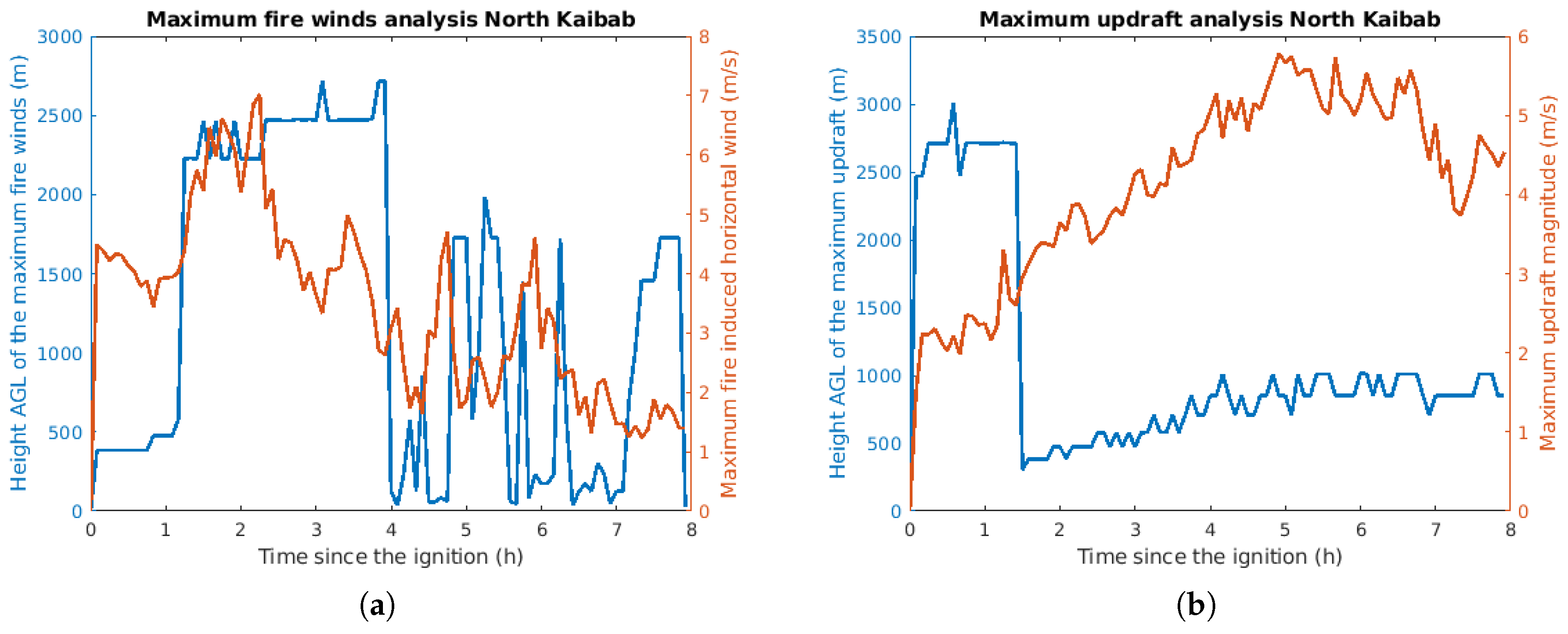
3.2.2. Simulations of Planned Experimental Burns in North Kaibab
3.2.3. Simulations of Planned Experimental Burns in Fort Stewart
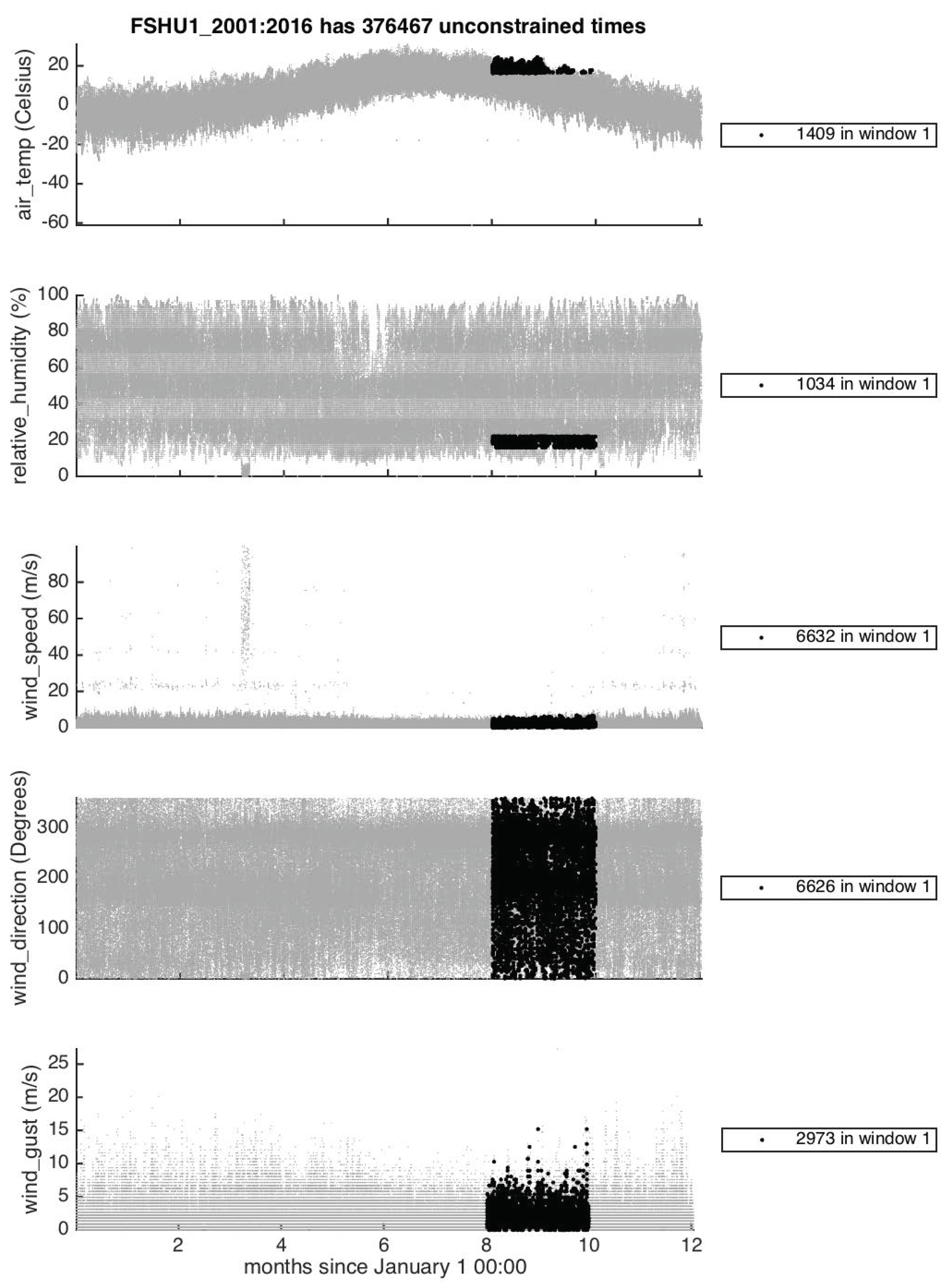
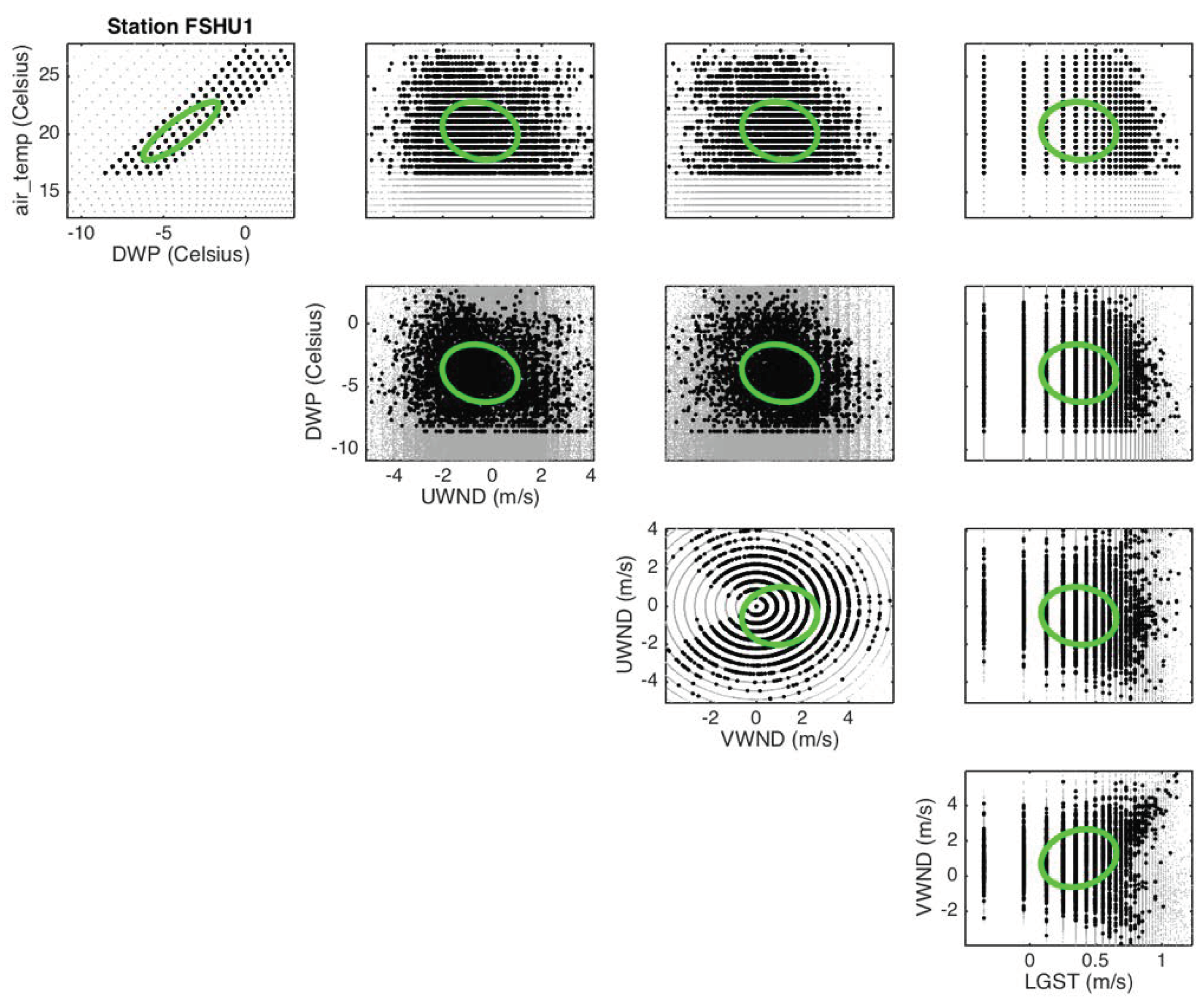
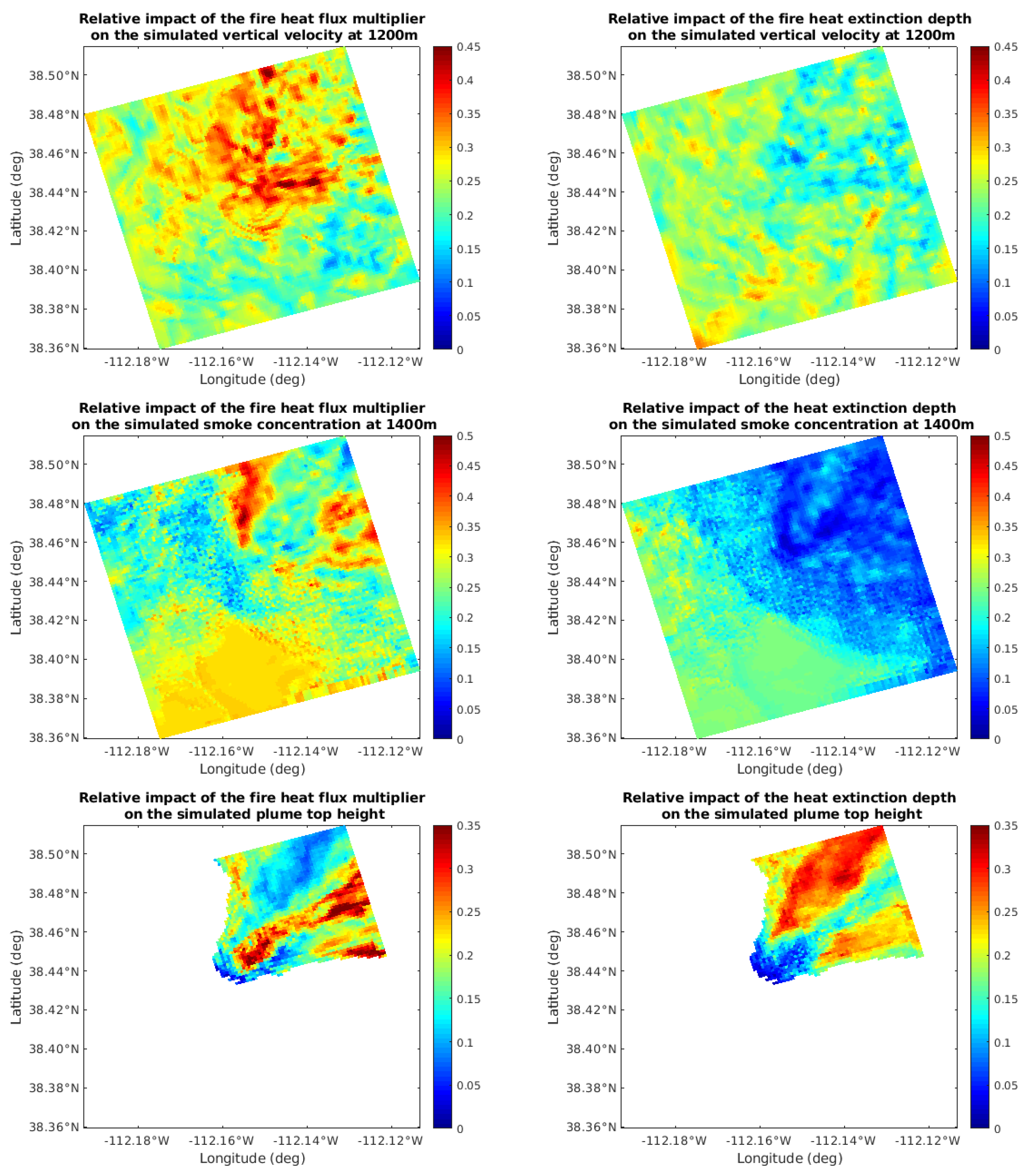
3.3. Sensitivity Study of Sensor Placement
3.3.1. Sampling Setup
- 10 h fuel moisture content, varying from 0.04 to 0.14 water mass/dry fuel mass. 1 h fuel moisture was 10 h fuel moisture minus 0.01, 100 h fuel moisture was 10 h fuel moisture plus 0.01, and live fuel moisture was 0.78. These values were entered as initial moisture values and did not change with time. See [1,19] for a further description of the fuel moisture in WRF-SFIRE.
- Heat extinction depth, varying from 6 m to 50 m. The fire heat flux is entered into WRF boundary layer with exponential decay, rather than all into the bottom layer of cells. The heat is apportioned depending on the height of the cell center above the terrain, with weight 1 at the ground and at the heat extinction depth. This gradual heat insertion is a parameterization for unresolved mixing and radiative heat transfer.
- Heat flux multiplier, varying from 0.5 to 2. The heat flux multiplier was chosen as a measure of the fire effect on the atmosphere; unlike the fuel load, it does not influence the rate of spread.
- Multiplier for the omnidirectional component R in the approximate fire rate of spread (ROS) formula following [34],
- Multiplier for the wind-induced ROS component
- Multiplier for the slope-induced ROS component
- The simulation day, selected from the “typical” burn days
- The vertical velocity vector component W, interpolated to a given height above the terrain, or to a given altitude above the sea level.
- The smoke intensity (the concentration of WRF tracer tr17_1), interpolated to a given height above the terrain, or to a given altitude above the sea level.
- Plume-top height, derived from the smoke concentration.
3.4. Computational Results for the Fishlake Burn Simulation
4. Conclusions
4.1. Estimation of Typical Days
4.2. Results from Numerical Experiments
4.3. Sensitivity Study of Sensor Placement
- The statistical analysis of runs with carefully sampled parameter sets was shown to provide clear guidelines on placing the measurements in space and time.
- Also, some measurements were found more affected by certain parameters, which can inform what parameters can be indirectly constrained by observations.
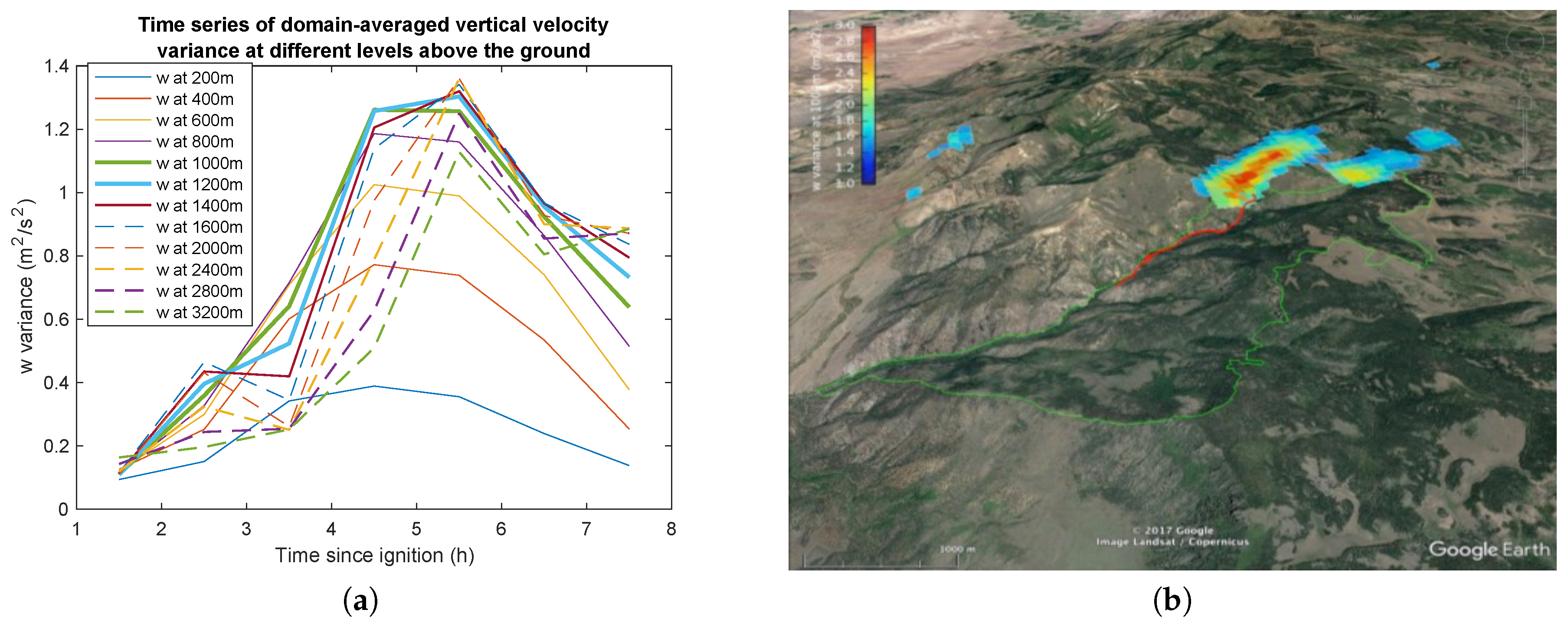
- Analyses of the variance in smoke concentration vertical velocity and plume top height from runs executed for different days and with different parameter sets show similar patterns indicating that typical day statistics managed to identify statistically similar days from the standpoint of plume rise and dispersion.
- The variability of the plume at higher altitudes (here, 1000–1400 m above the ground) is concentrated up to couple kilometers downwind from the plot, which suggests that sampling right above the fire, optimal for the fire heat flux measurements, may not be optimal for sampling most active parts of the plume.
- Additional parameters can be considered. The cost of one repetition does not increase with the number of parameters, but more repetitions need to be done for statistical convergence. The variability of the outputs will increase and the added parameters will help model additional uncertainty, which is always present in reality.
4.4. Computing Resources
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Statistics of Weather Data










References
- Mandel, J.; Amram, S.; Beezley, J.D.; Kelman, G.; Kochanski, A.K.; Kondratenko, V.Y.; Lynn, B.H.; Regev, B.; Vejmelka, M. Recent advances and applications of WRF-SFIRE. Nat. Hazards Earth Syst. Sci. 2014, 14, 2829–2845. [Google Scholar] [CrossRef]
- Larkin, N.K.; O’Neill, S.M.; Solomon, R.; Raffuse, S.; Strand, T.; Sullivan, D.C.; Krull, C.; Rorig, M.; Peterson, J.; Ferguson, S.A. The BlueSky smoke modeling framework. Int. J. Wildland Fire 2009, 18, 906–920. [Google Scholar] [CrossRef]
- Seiler, W.; Crutzen, P.J. Estimates of gross and net fluxes of carbon between the biosphere and the atmosphere from biomass burning. Clim. Chang. 1980, 2, 207–247. [Google Scholar] [CrossRef]
- Urbanski, S.P.; Hao, W.M.; Nordgren, B. The wildland fire emission inventory: Western United States emission estimates and an evaluation of uncertainty. Atmos. Chem. Phys. 2011, 11, 12973–13000. [Google Scholar] [CrossRef] [Green Version]
- Liu, Y.; Qu, J.J.; Wang, W.; Hao, X. Estimates of Wildland Fire Emissions. In Remote Sensing and Modeling Applications to Wildland Fires; Qu, J.J., Sommers, W.T., Yang, R., Riebau, A.R., Eds.; Springer: Berlin/Heidelberg, Germany, 2013; pp. 117–133. [Google Scholar] [CrossRef]
- Colarco, P.R.; Schoeberl, M.R.; Doddridge, B.G.; Marufu, L.T.; Torres, O.; Welton, E.J. Transport of smoke from Canadian forest fires to the surface near Washington, D.C.: Injection height, entrainment, and optical properties. J. Geophys. Res. Atmos. 2004, 109, D06203. [Google Scholar] [CrossRef]
- Liu, Y.; Achtemeier, G.; Goodrick, S. Sensitivity of air quality simulation to smoke plume rise. J. Appl. Remote Sens. 2008, 2, 021503. [Google Scholar] [CrossRef]
- Goodrick, S.L.; Achtemeier, G.L.; Larkin, N.K.; Liu, Y.; Strand, T.M. Modelling smoke transport from wildland fires: A review. Int. J. Wildland Fire 2013, 22, 83–94. [Google Scholar] [CrossRef]
- Ottmar, R.; Brown, T.J.; French, N.H.F.; Larkin, N.K. Fire and Smoke Model Evaluation Experiment (FASMEE) Study Plan. 2017. Available online: https://www.fasmee.net/wp-content/uploads/2017/07/FASMEE_StudyPlan_Final_07-11-17.pdf (accessed on 30 June 2018).
- Liu, Y.; Kochanski, A.; Baker, K.; Mell, R.; Linn, R.; Paugam, R.; Mandel, J.; Fournier, A.; Jenkins, M.A.; Goodrick, S.; et al. Fire and Smoke Model Evaluation Experiment (FASMEE): Modeling Gaps and Data Needs. In Proceedings of the 2nd International Smoke Symposium, Long Beach, CA, USA, 14–17 November 2016; Available online: https://www.fs.fed.us/rm/pubs_journals/2017/rmrs_2017_liu_y001.pdf (accessed on 30 June 2018).
- Mandel, J.; Beezley, J.D.; Kochanski, A.K. Coupled atmosphere-wildland fire modeling with WRF 3.3 and SFIRE 2011. Geosci. Model Dev. 2011, 4, 591–610. [Google Scholar] [CrossRef] [Green Version]
- Kochanski, A.K.; Jenkins, M.A.; Yedinak, K.; Mandel, J.; Beezley, J.; Lamb, B. Toward an integrated system for fire, smoke, and air quality simulations. Int. J. Wildland Fire 2016, 25, 534–546. [Google Scholar] [CrossRef]
- The “Matash” Fire-Prediction System. 2017. Available online: http://mops.gov.il/English/HomelandSecurityENG/NFServices/Pages/FirePredictionSystem.aspx (accessed on 14 May 2017).
- Val Martin, M.; Logan, J.A.; Kahn, R.A.; Leung, F.Y.; Nelson, D.L.; Diner, D.J. Smoke injection heights from fires in North America: Analysis of 5 years of satellite observations. Atmos. Chem. Phys. 2010, 10, 1491–1510. [Google Scholar] [CrossRef]
- Mallia, D.V.; Kochanski, A.K.; Urbanski, S.P.; Lin, J.C. Optimizing Smoke and Plume Rise Modeling Approaches at Local Scales. Atmosphere 2018, 9, 166. [Google Scholar] [CrossRef]
- Kochanski, A.; Mandel, J.; Fournier, A.; Jenkins, M.A. Modeling Support for FASMEE Experimental Design Using WRF-SFIRE-CHEM; Final Report for Joint Fire Science Program Project JFSP 16-4-05-3, 2017. Available online: https://www.firescience.gov/projects/16-4-05-3/project/16-4-05-3_final_report.pdf (accessed on 15 July 2018).
- Kochanski, A.K.; Jenkins, M.A.; Mandel, J.; Beezley, J.D.; Clements, C.B.; Krueger, S. Evaluation of WRF-SFIRE Performance with Field Observations from the FireFlux experiment. Geosci. Model Dev. 2013, 6, 1109–1126. [Google Scholar] [CrossRef]
- Kochanski, A.K.; Jenkins, M.A.; Kondratenko, V.; Schranz, S.; Vejmelka, M.; Clements, C.B.; Davis, B. Ignition from fire perimeter and assimilation into a coupled fire-atmosphere model. Proceedings for the 5th International Fire Behavior and Fuels Conference, Portland, OR, USA, 11–15 April 2016; International Association of Wildland Fire: Missoula, MT, USA, 2016; pp. 80–85. Available online: https://www.iawfonline.org/conference-proceedings (accessed on 27 July 2018).
- Mandel, J.; Beezley, J.D.; Kochanski, A.K.; Kondratenko, V.Y.; Kim, M. Assimilation of Perimeter Data and Coupling with Fuel Moisture in a Wildland Fire—Atmosphere DDDAS. Procedia Comput. Sci. 2012, 9, 1100–1109. [Google Scholar] [CrossRef]
- Mesinger, F.; DiMego, G.; Kalnay, E.; Mitchell, K.; Shafran, P.C.; Ebisuzaki, W.; Jović, D.; Woollen, J.; Rogers, E.; Berbery, E.H.; et al. North American Regional Reanalysis. Bull. Am. Meteorol. Soc. 2006, 87, 343–360. [Google Scholar] [CrossRef] [Green Version]
- Vejmelka, M. WRFxpy. 2016. Available online: https://github.com/openwfm/wrfxpy (accessed on 15 June 2018).
- Mandel, J.; Beezley, J.D.; Coen, J.L.; Kim, M. Data Assimilation for Wildland Fires: Ensemble Kalman filters in coupled atmosphere-surface models. IEEE Control Syst. Mag. 2009, 29, 47–65. [Google Scholar] [CrossRef]
- Mandel, J.; Beezley, J.D.; Kochanski, A.K.; Kondratenko, V.Y.; Zhang, L.; Anderson, E.; Daniels, J., II; Silva, C.T.; Johnson, C.R. A Wildland Fire Modeling and Visualization Environment; Paper 6.4, Ninth Symposium on Fire and Forest Meteorology, Palm Springs, October 2011. Available online: http://ams.confex.com/ams/9FIRE/webprogram/Paper192277.html (accessed on 27 July 2018).
- Clark, T.L.; Jenkins, M.A.; Coen, J.; Packham, D. A Coupled Atmospheric-Fire Model: Convective Feedback on Fire Line Dynamics. J. Appl. Meteorol. 1996, 35, 875–901. [Google Scholar] [CrossRef]
- Clark, T.L.; Coen, J.; Latham, D. Description of a Coupled Atmosphere-Fire Model. Int. J. Wildland Fire 2004, 13, 49–64. [Google Scholar] [CrossRef]
- Coen, J.L.; Cameron, M.; Michalakes, J.; Patton, E.G.; Riggan, P.J.; Yedinak, K. WRF-Fire: Coupled Weather-Wildland Fire Modeling with the Weather Research and Forecasting Model. J. Appl. Meteorol. Climatol. 2013, 52, 16–38. [Google Scholar] [CrossRef]
- Jiménez, P.A.; Muñoz-Esparza, D.; Kosović, B. A High Resolution Coupled Fire-Atmosphere Forecasting System to Minimize the Impacts of Wildland Fires: Applications to the Chimney Tops II Wildland Event. Atmosphere 2018, 9, 197. [Google Scholar] [CrossRef]
- Muñoz-Esparza, D.; Kosović, B.; Jiménez, P.A.; Coen, J.L. An Accurate Fire-Spread Algorithm in the Weather Research and Forecasting Model Using the Level-Set Method. J. Adv. Model. Earth Syst. 2018, 10, 908–926. [Google Scholar] [CrossRef] [Green Version]
- McKay, M.D.; Beckman, R.J.; Conover, W.J. A comparison of three methods for selecting values of input variables in the analysis of output from a computer code. Technometrics 1979, 21, 239–245. [Google Scholar] [CrossRef]
- McKay, M.D. Evaluating Prediction Uncertainty; Technical Report NUREG/CR-6311 LA-12915-MS; Los Alamos National Laboratory: Los Alamos, NM, USA, 1995; Available online: http://www.iaea.org/inis/collection/NCLCollectionStore/_Public/26/051/26051087.pdf (accessed on 16 October 2016).
- Saltelli, A.; Tarantola, S.; Campolongo, F.; Ratto, M. Sensitivity Analysis in Practice; John Wiley & Sons, Ltd.: Chichester, UK, 2004; p. xii+219. [Google Scholar]
- Sobol’, I.M. Global sensitivity indices for nonlinear mathematical models and their Monte Carlo estimates. Math. Comput. Simul. 2001, 55, 271–280. [Google Scholar] [CrossRef]
- Chugunov, N.; Ramakrishnan, T.S.; Moldoveanu, N.; Fournier, A.; Osypov, K.S.; Altundas, Y.B. Targeted Survey Design Under Uncertainty. US Patent Application No. 0278110 A1, 18 September 2014. [Google Scholar]
- Rothermel, R.C. A Mathematical Model for Predicting Fire Spread in Wildland Fires; USDA Forest Service Research Paper INT-115, 1972. Available online: https://www.fs.fed.us/rm/pubs_int/int_rp115.pdf (accessed on 15 March 2018).
- Clements, C.B.; Davis, B.; Seto, D.; Contezac, J.; Kochanski, A.; Filippi, J.B.; Lareau, N.; Barboni, T.; Butler, B.; Krueger, S.; et al. Overview of the 2013 FireFlux-II Grass Fire Field Experiment. In Advances in Forest Fire Research; Viegas, D.X., Ed.; Coimbra University Press: Coimbra, Portugal, 2014; pp. 392–400. [Google Scholar] [CrossRef]






| Burn Site | Fishlake | North Kaibab | Fort Stewart |
|---|---|---|---|
| Meteo forcing | NARR | NARR | NARR |
| Number of domains | 5 (realistic) | 5 (realistic) | 5 (realistic) |
| Domain sizes(XYZ) | |||
| Model top | 13.2 km | 13.2 km | 13.2 km |
| Horizontal resolution | 12 km/4 km/1.33 km/444 m/148 m | 12 km/4 km/1.33 km/444 m/148 m | 12 km/4 km/1.33 km/444 m/148 m |
| Vertical resolution | 5.3 m–2233 m | 5.3 m–2233 m | 5.3 m–2233 m |
| Fire mesh resolution | 29.6 m | 29.6 m | 29.6 m |
| Total number of runs | 7 | 4 | 10 |
| Ignition | Helicopter | Point | Straight Line/Point |
| Simulation start | 09/03/2014 00:00 UTC | 09/05/2008 00:00 UTC | 04/22/2014 00:00 UTC |
| 09/11/2016 00:00 UTC | 09/19/2015 00:00 UTC | 04/27/2009 00:00 UTC | |
| 09/22/2012 00:00 UTC | 09/01/2001 00:00 UTC | 02/27/2013 00:00 UTC | |
| 09/26/2015 00:00 UTC | 09/02/2011 00:00 UTC | 02/26/2008 00:00 UTC | |
| Ignition Time | 15:00 UTC (9:00 local) | 15:00 UTC (9:00 local) | 15:00 UTC (11:00 local) |
| Simulation Length | 48 h | 48 h | 48 h |
| Fire Output Interval | 5 min | 5 min | 5 min |
| Time step (d05) | 0.5 s | 0.5 s | 0.74 s |
| 1 h fuel moisture | 6.0% | 6.0% | 15.0% |
| 10 h fuel moisture | 8.0% | 8.0% | 13.0% |
| 100 h fuel moisture | 9.0% | 9.0% | 13.0% |
| 1000 h fuel moisture | 12.0% | 12.0% | 18.0% |
| Station | Burn Season | Min T | Max T | Min | Max | Min s | Max s |
|---|---|---|---|---|---|---|---|
| FSHU1 | 09/01 16:00 UTC–10/31 18:00 UTC | 61 F | 85 F | 16% | 22% | 0 | 15 mph |
| KCWV | 02/20 16:00 UTC–02/28 18:00 UTC | 60 | 90 | 30 | 55 | 6 | 20 |
| 04/15 13:00UTC–04/30 14:00 UTC | 60 | 90 | 30 | 55 | 6 | 20 | |
| KLHW | 02/20 16:00 UTC–02/28 18:00 UTC | 60 | 90 | 30 | 55 | 6 | 20 |
| 04/15 13:00 UTC–04/30 14:00 UTC | 60 | 90 | 30 | 55 | 6 | 20 | |
| LCSS1 | 01/01 15:00 UTC–02/01 19:00 UTC | 60 | 90 | 30 | 55 | 6 | 20 |
| 12/01 15:00 UTC–12/31 19:00 UTC | 60 | 90 | 30 | 55 | 6 | 20 | |
| QLBA3 | 09/01 17:00 UTC–10/31 19:00 UTC | 61 | 85 | 16 | 22 | 0 | 15 |
| TT084 | 09/01 16:00 UTC–10/31 18:00 UTC | 61 | 85 | 16 | 22 | 0 | 15 |
| Burn Site | Fishlake | North Kaibab | Fort Stewart | ||
|---|---|---|---|---|---|
| Weather Station | FSHU1 | TT084 | QLBA3 | KCWV | KLHW |
| Typical days | 09/03/2014 | 09/05/2012 | 09/05/2008 | 04/22/2014 | 04/27/2009 |
| 09/26/2015 | 09/04/2012 | 09/19/2005 | 02/24/2013 | 02/26/2013 | |
| Sampling Point | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| 10-fuel moisture (kg/kg) | 0.0459 | 0.0613 | 0.0748 | 0.0914 | 0.1219 |
| Heat extinction depth (m) | 7.5830 | 12.3531 | 17.3205 | 24.2854 | 39.5620 |
| Heat flux multiplier (1) | 0.5827 | 0.8017 | 1.0000 | 1.2473 | 1.7161 |
| Multiplier for R (1) | 0.5827 | 0.8017 | 1.0000 | 1.2473 | 1.7161 |
| Multiplier for (1) | 0.5827 | 0.8017 | 1.0000 | 1.2473 | 1.7161 |
| Multiplier for (1) | 0.5827 | 0.8017 | 1.0000 | 1.2473 | 1.7161 |
| Simulation day (date) | 09/03/2014 | 09/11/2016 | 09/22/2012 | 09/26/2015 | 09/27/2015 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kochanski, A.K.; Fournier, A.; Mandel, J. Experimental Design of a Prescribed Burn Instrumentation. Atmosphere 2018, 9, 296. https://doi.org/10.3390/atmos9080296
Kochanski AK, Fournier A, Mandel J. Experimental Design of a Prescribed Burn Instrumentation. Atmosphere. 2018; 9(8):296. https://doi.org/10.3390/atmos9080296
Chicago/Turabian StyleKochanski, Adam K., Aimé Fournier, and Jan Mandel. 2018. "Experimental Design of a Prescribed Burn Instrumentation" Atmosphere 9, no. 8: 296. https://doi.org/10.3390/atmos9080296





