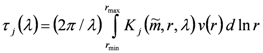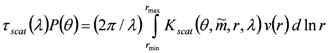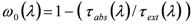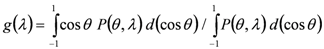1. Introduction
According to the Intergovernmental Panel on Climate Change [
1], the impact of atmospheric aerosols on the radiation budget remains uncertain and its magnitude and sign depend strongly on the aerosol amount and absorption. Under clear-sky conditions, this impact is commonly described by direct aerosol radiative forcing (DARF) defined as a difference between net clear-sky fluxes obtained with and without aerosols [
2,
3]. Consequently, accurate assessment of the DARF requires reliable estimations of aerosol optical properties on both the regional and global scales with high temporal resolution [
4,
5]. The corresponding uncertainties of the DARF assessment stem mostly from the well-known fact that aerosol properties exhibit high temporal and spatial variability compared to the greenhouse gases, and understanding this variability is an ongoing focus of many observational and model studies [
6,
7].
Abundant literature exists on the DARF assessment using aerosol properties obtained from satellite [
8,
9] and surface [
10,
11] observations, including aerosol retrievals from the Aerosol Robotic Network (AERONET; [
12];
http://aeronet.gsfc.nasa.gov/) and a suite of instruments supported by the Atmospheric Radiation Measurement (ARM) Program ([
13];
http://www.arm.gov/instruments). The AERONET-supported sunphotometer measurements at four specific wavelengths (0.44, 0.674, 0.87 and 1.02 μm) have been used for deriving aerosol optical properties from the retrieved size distributions and complex refractive index [
14,
15]. The largest uncertainties of the AERONET-based aerosol retrievals and, consequently, of downwelling flux estimations, were obtained in regions dominated by mineral dust and mixed aerosols [
16]. The AERONET-based microphysical and optical properties of natural and anthropogenic aerosols collected around the world were applied for the DARF assessment [
11,
17].
Substantial progress in understanding atmospheric aerosols has been made in the recent years by the use of aircraft
in situ and radiative measurements ([
18] and references therein). Aircraft observations of aerosol microphysical and optical properties provided an important baseline for constraining and evaluating satellite aerosol retrievals [
19,
20]. Moreover, these measurements in conjunction with aerosol remote sensing from surface and space served as a valuable basis for the DARF assessment [
21,
22,
23]. In particular, aircraft measurements of aerosol optical depth (
τa) from the NASA Ames 14-channel Airborne Tracking Sunphotometer (AATS-14), and upwelling and downwelling irradiances from a pair of Solar Spectral Flux Radiometers were successfully utilized for estimating spectral values of the aerosol radiative forcing efficiency, which describes the changes of the net irradiance per change of
τa [
24,
25].
Multi-spectral remote sensing applications of the airborne AATS-14 instrument have mostly focused on extracting important information of atmospheric aerosol and gas constituents from direct solar beam transmission at 14 wavelengths [
19]. Recently, the NASA Ames Research Center in collaboration with the Pacific Northwest National Laboratory have made substantial technical improvements and developed the next airborne generation of AATS-14, named Spectrometer for Sky-Scanning, Sun-Tracking Atmospheric Research (4STAR) with ultraviolet, visible and near-infrared spectral coverage, increased number of channels (more than 1,500 pixels) and the sky-scanning ability of the ground-based AERONET sun/sky photometers (
Figure 1; [
26,
27]). It is expected that for the first time the 4STAR on board the G-1 aircraft will provide retrievals of aerosol microphysical and optical properties during the ongoing Two-Column Aerosol Project supported by the ARM Program (
http://campaign.arm.gov/tcap/).
Figure 1.
Schematic diagram illustrating that the 4STAR instrument combines the sun-tracking ability of the airborne AATS-14 with the sky-scanning ability of the ground-based AERONET sun/sky photometer.
Figure 1.
Schematic diagram illustrating that the 4STAR instrument combines the sun-tracking ability of the airborne AATS-14 with the sky-scanning ability of the ground-based AERONET sun/sky photometer.
Compared to the AERONET-supported sun/sky photometer, the 4STAR is a compact flyable instrument with considerably shorter entrance optics (
Figure 1). Preflight assessment of the 4STAR performance illustrates that an apparent and noticeable enhancement (
E) of sky radiance can occur at small scattering angles (≤6° from sun) and this enhancement has a “half-bell” shape with its maximum at the smallest (~3° from sun) scattering angle. Note that the smallest scattering angle is the same for the AERONET and 4STAR measurements. To exclude data contaminated by stray light, the scattering angles smaller than 3° are not used in the AERONET retrievals. Also, this assessment demonstrated that the enhancement is spectrally-dependent: it could reach up to 25% and 50% at 0.44 and 1.02 μm wavelength, respectively. The angular and spectral shape of the enhancement of the sky radiance at near-sun angles was directly measured by pointing the 4STAR at numerous angles near the sun while alternately introducing and removing a shade between the 4STAR and the sun. The placement of the shade when introduced was such as to insulate the entrance optic from incident sunlight without impacting the actual sky view of the instrument. For a given angle, the enhancement was defined as a ratio of shaded measurement over unshaded measurement at four wavelengths (0.44, 0.674, 0.87 and 1.02 μm).
How this enhancement may alter the 4STAR-based aerosol retrievals was unknown. This paper quantifies the potential impact of the enhancement on the retrieved aerosol microphysical and optical properties (
Section 3.1 and
Section 3.2) by adapting a sensitivity study described by Dubovik
et al. [
28]. The importance of this impact is quantified in the context of the DARF (
Section 3.3) using representative cases with different aerosol loading and absorption selected from multi-year AERONET observations. Our paper further considers the impact of a spectrally neutral offset (
O) in the sky radiance measurements, as may be expected due to radiometric calibration uncertainties.
2. Approach
Sensitivity studies have proven to be a powerful tool in terms of theoretical error analysis [
28,
29]. For example, Dubovik
et al. [
28] used the forward modeling of sky radiances at four wavelengths (0.44, 0.674, 0.87 and 1.02 μm) for assessing the accuracy that could be anticipated for aerosol retrievals from AERONET measurements. The AERONET-based aerosol retrieval relies on statistically optimized multivariable fitting of model aerosol optical depth and sky radiance (at 4 specified wavelengths) to their observed counterparts [
14,
28]. Among several important findings, Dubovik
et al. [
28] demonstrated that systematic errors in sky radiances (or offsets) associated, for example, with miscalibrations, may have a large impact on the retrieved imaginary part of the refractive index, and consequently, on the retrieved single-scattering albedo (
ω0), which is the ratio of the scattering and extinction coefficients. The retrieved single scattering albedo is indicative of aerosol absorption:
ω0 = 1 and
ω0 < 1 for non-absorbing and absorbing aerosols, respectively. It was assumed that the instrumental offset (
O) does not depend on the scattering angle and wavelength [
28].
It becomes increasingly evident that
ω0 is the largest contributor (after
τa) to the DARF uncertainty [
10,
30] and the greatest variability of
ω0 (globally) is typically observed for biomass burning aerosol [
15]. For our sensitivity study, cases have been selected to be representative of the multi-year averages of biomass burning aerosol [
15]. More precisely, we select 4 days with cloud-screened and quality–assured data (level 2.0) collected at an AERONET site in Singapore with a wide range of
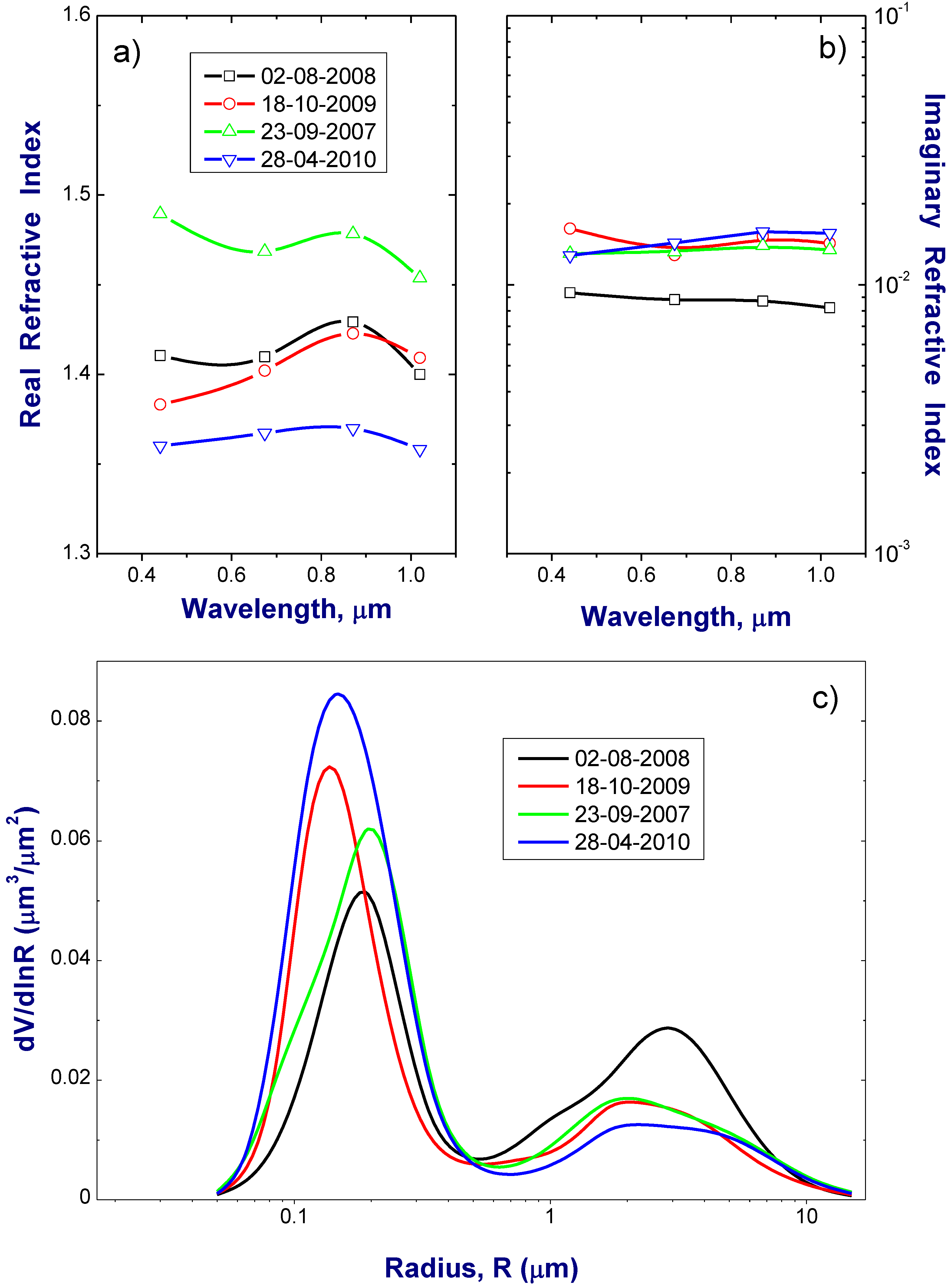
ω0 values. The overall time span of the considered AERONET data covers 2 years from 2008 to 2010. The AERONET retrieval product includes the real (
n) and imaginary (
k) parts of the complex refractive index, size distribution (
Figure 2), as well as
τa,
ω0, asymmetry factor (
g) and scattering phase function (
Figure 3). Sources (both local and remote) and meteorology are responsible for the seasonal variability of the optical and microphysical properties at this AERONET site [
31]. For example, the dry season (August–November) is typically characterized by a strong biomass component with quite large aerosol loading: the corresponding mean value of
τa at 0.5 μm is about 0.41 [
31]. The sources of this biomass component are forest and peat fires from local and remote regions. Episodically, aerosol in this region can also be due to waste burning in urban areas.
Figure 2.
The real (a) and imaginary (b) parts of the complex reflective index and volume size distribution (c) from the AERONET aerosol retrieval for the selected four days. These aerosol microphysical properties are considered as “true” microphysical properties in our sensitivity study.
Figure 2.
The real (a) and imaginary (b) parts of the complex reflective index and volume size distribution (c) from the AERONET aerosol retrieval for the selected four days. These aerosol microphysical properties are considered as “true” microphysical properties in our sensitivity study.
Figure 3.
The aerosol optical depth (a), single-scattering albedo and asymmetry factor (b), and scattering phase function (c) as part of the AERONET operational product for the selected four days. These aerosol optical properties are considered as “true” optical properties in our sensitivity study.
Figure 3.
The aerosol optical depth (a), single-scattering albedo and asymmetry factor (b), and scattering phase function (c) as part of the AERONET operational product for the selected four days. These aerosol optical properties are considered as “true” optical properties in our sensitivity study.
Figure 4.
Example of the observed sky radiance (
R) at four wavelengths (
a) and the relative difference (Δ
R) between the observed radiance and constructed artificial radiance (
b,
c) as a function of scattering angle. These differences are obtained for a given range of the spectrally dependent enhancement: from 0 to 25% at 0.44 μm (b) and from 0 to 50% at 1.02 μm (c) wavelengths, respectively. The conversion of the constructed radiances gives the retrieved values of microphysical (
Figure 5 and
Figure 6) and optical (
Figure 7,
Figure 8 and
Figure 9) parameters.
Figure 4.
Example of the observed sky radiance (
R) at four wavelengths (
a) and the relative difference (Δ
R) between the observed radiance and constructed artificial radiance (
b,
c) as a function of scattering angle. These differences are obtained for a given range of the spectrally dependent enhancement: from 0 to 25% at 0.44 μm (b) and from 0 to 50% at 1.02 μm (c) wavelengths, respectively. The conversion of the constructed radiances gives the retrieved values of microphysical (
Figure 5 and
Figure 6) and optical (
Figure 7,
Figure 8 and
Figure 9) parameters.
Here we adapted a three-step approach described by Dubovik
et al. [
28] for the expected 4STAR observations, where angular and spectral shape of the perturbations are based on the preflight assessment. The first step involves the construction of synthetic radiances by adding a spectrally-dependent enhancement to the observed sky radiances. We assume that possible
E values at 0.44 μm wavelength do not exceed 25% and increase linearly with the wavelength such that the highest values (50%) occur at 1.02 μm wavelength.
Figure 4 shows an example of the observed sky radiances and the corresponding relative differences between them and their synthetic counterparts. Note that the sky radiance decreases strongly (about two orders of magnitude) with the scattering angle (
Figure 4(a)). The second step provides the inversion product using the synthetic 4STAR-like radiances and the operational AERONET aerosol retrieval. The third step contrasts the inversion results with the corresponding references and provides the relative difference between them: Δ =
retrieved/true − 1, (%). The selected microphysical (
Figure 2) and optical (
Figure 3) aerosol properties from the AERONET climatology are considered as references (“true” values) in our sensitivity study. The aerosol properties inverted from the synthetic radiances during step 2 are considered as retrieved values and that is how the term “retrieved” has to be understood. The main objective of the outlined three-step approach is to estimate the potential impact of the enhancement
E (% stray light at small scattering angles) on the 4STAR-retrieved aerosol microphysical and optical properties. To estimate the corresponding impact of the offset
O (% radiance calibration error), we repeat the outlined three steps for an additional set of synthetic radiances. Similar to Dubovik
et al. [
28], this set is developed by adding the spectrally- and angular-independent offset to the observed sky radiances, keeping its values within the expected range (±5%) for the 4STAR measurements.
Previous sensitivity studies [
28] used the inversion algorithm (Version 1) originally developed by Dubovik and King [
14]. Here, we apply the operational AERONET retrieval, which utilizes an improved inversion scheme (Version 2). Recently, this scheme was generalized successfully for estimating aerosol properties from multi-angle polarimetric satellite observations [
32]. In comparison with the original version, the Version 2 includes several valuable improvements, such as providing one set of aerosol retrievals for mixed (spherical and non-spherical) aerosols and an estimate of the percentage of spherical particle scattering, the so-called sphericity parameter [
33]. For the cases considered here, the sphericity parameter is almost 100%. Also, the Version 2 includes a new radiative transfer module as part of the AERONET inversion product for calculating instantaneous values of the solar broadband (0.2–4 μm) fluxes at the top-of-atmosphere (TOA) and bottom-of-atmosphere (BOA) and the corresponding values of the DARF. The radiative properties at the TOA and BOA are calculated using the correlated k-distribution [
34] coupled with the discrete ordinate method embodied in DISORT [
35,
36]. The water vapor and total ozone contents are obtained from the AERONET retrieval of the instantaneous water vapor content at the 0.94 μm channel [
37] and monthly climatological averages based on the NASA Total Ozone Mapping Spectrometer (TOMS) measurements, respectively. For the atmospheric gaseous profiles, the US standard 1976 atmospheric model is applied. Details of the radiative transfer calculations can be found in Garcia
et al. [
16] and Derimian
et al. [
11]. The retrieved optical properties, namely
τa,
ω0 and scattering phase function, are applied for calculating these radiative properties. Moreover, the Version 2 replaces Lambertian surface reflectance model by bidirectional reflectance distribution functions (BRDFs). The Moderate Resolution Imaging Spectroradiometer (MODIS) surface albedo [
38] is used for normalization the BDRF functions at noon. For the radiative transfer calculations, the spectral and broadband values of the surface albedo are estimated from these BDRFs.
Using multiyear AERONET observations and collocated ground-based broadband solar radiation measurements at 13 sites around the world, Garcia
et al. [
16] validated the AERONET radiative product for different aerosol types and demonstrated good agreement between the calculated and measured total (direct and diffuse) downwelling fluxes at the BOA: for all considered sites the overall difference between them is about 15 W∙m
−2 (within 5% for fluxes measured at the BOA) and it is comparable with uncertainties of measured fluxes.
The AERONET-based calculations of downwelling (
F↓) and upwelling (
F↑) fluxes at the TOA and BOA are used for estimating the corresponding values of the DARF [
17]
In Equation (1), subscripts “a” and “0” define fluxes computed with and without aerosol, respectively. The negative (positive) values of the DARF represent aerosol cooling (warming) effect. For a given surface albedo, the magnitude and sign of the DARF is defined by the aerosol optical properties. To illustrate, the critical value of columnar
ω0 at which the DARF at TOA changes its sign from negative to positive occurs between 0.86 and 0.91 [
39].
Table 1 and
Table 2 include the calculated instantaneous downwelling and upwelling fluxes and DARF at TOA and BOA, as well as the corresponding values of the solar zenith angle (SZA), which cover a quite narrow (60–75°) range for the cases considered here. For the majority of aerosol and surface types, the DARF at TOA varies nonlinearly with the SZA such that its largest negative values typically occur at intermediate-to-large (60–75°) SZA [
11,
40]. Instantaneous values of DARF at these angles typically exceed their daily-averaged counterparts [
11,
41,
42]. Thus, one can expect that results of our sensitivity study represent an upper limit for the effects of
E and
O in the context of DARF at TOA.
The next section describes the sensitivity of the considered fluxes and DARF to potential uncertainties in the aerosol microphysical and optical properties retrieved from the expected 4STAR observations. We consider two major potential sources of these perturbations, namely the enhancement (
E) and offset (
O), and compare their relative impact on the retrieved aerosol properties and, consequently, on the calculated fluxes and DARF. These sensitivity tests are conducted in the framework of previous studies [
28] using the operational AERONET retrieval. We will start with an illustration of the impact of
E and
O on the microphysical (
Section 3.1) and optical (
Section 3.2) properties, and then consider the sensitivity of the radiative characteristics (
Section 3.3) to the potential unceratinties in aerosol optical properties.
Table 1.
Instantaneous broadband upwelling diffuse (Fdiff↑), downwelling diffuse (Fdiff↓) and downwelling total (F↓) fluxes calculated for four selected days using the AERONET-retrieved aerosol optical properties as part of the AERONET operational product for given solar zenith angles (SZA). Unit of these fluxes is W∙m−2. Note that for the upwelling radiation, the diffuse flux is equal to the total flux.
Table 1.
Instantaneous broadband upwelling diffuse (Fdiff↑), downwelling diffuse (Fdiff↓) and downwelling total (F↓) fluxes calculated for four selected days using the AERONET-retrieved aerosol optical properties as part of the AERONET operational product for given solar zenith angles (SZA). Unit of these fluxes is W∙m−2. Note that for the upwelling radiation, the diffuse flux is equal to the total flux.
| | 02-08-2008 | 18-10-2009 | 23-09-2007 | 28-04-2010 |
|---|
| Fdiff↓ (BOA) | 98.5 | 78.2 | 77.6 | 127.9 |
| Ftotal↓ (BOA) | 229.9 | 181.6 | 135.5 | 409.1 |
| Fdiff↑ (TOA) | 95.9 | 89.9 | 87.5 | 113.1 |
| SZA | 71.9 | 75.1 | 76.0 | 58.6 |
Table 2.
Similar to
Table 1, except that values of the direct aerosol radiative forcing (DARF) at the top of atmosphere (TOA) and the bottom of atmosphere (BOA) are calculated using Equation (1).
Table 2.
Similar to Table 1, except that values of the direct aerosol radiative forcing (DARF) at the top of atmosphere (TOA) and the bottom of atmosphere (BOA) are calculated using Equation (1).
| | 02-08-2008 | 18-10-2009 | 23-09-2007 | 28-04-2010 |
|---|
| DARFBOA | −47.1 | −52.6 | −55.4 | −77.2 |
| DARFBOA | −20.1 | −16.3 | −22.6 | −18.1 |
3. Results
Before discussing quantitative estimates in the following sections, let us outline the main distinguishing features associated with the anticipated impact of
E and
O on the aerosol retrievals and calculated DARF. The sky radiance
R(λ,θ) can be represented as a sum of multi-scattering
RM and single-scattering
R1 components. The latter is directly proportional to the scattering phase function
P(θ) and the single-scattering albedo [
43]: R
1(λ,θ) ~
ω0(λ)P(λ,θ), where
θ and
λ are the scattering angle and wavelength, respectively. The relative contribution of
RM to the sky radiance is greater for shorter wavelengths and larger scattering angles. For example,
RM is comparable with
R1 at
λ = 0.5 μm and
θ = 60° for moderate aerosol loading [
44]. To illustrate the physical processes involved, let us consider in the following paragraph the single-scattering component only. The single-scattering-approximation is used there as a guide for a qualitative description of the anticipated contribution of the enhancement Δ
RE(λ,θ) and offset Δ
R0 to the “measured” monochromatic sky radiance
R1′(λ,θ) and the corresponding retrieved values of the single-scattering albedo
ω0'(λ) and scattering phase function
P′(λ,θ). For a given wavelength, these retrieved values can be expressed as
ω0' = ω0 ± Δ
ω0 and
P'(θ) = P(θ) ± Δ
P(θ), where Δ
ω0 and Δ
P(θ) are the corresponding uncertainties associated with
E and
O.
The positive (negative) offset of sky radiance defines situations with apparently “brighter” (“dimmer”) sky. We emphasize that the offset does not change the angular distribution of the scattered light:
R1'(θ) = R1(θ) ± Δ
R0. Such artificial sky “brightening” (“dimming”) results mostly in the increase (decrease) of the retrieved
ω0:
ω0' = ω0 ± Δ
ω0 [
28]. This is consistent with conventional wisdom that a sky with absorbing aerosols looks dimmer than that with non-absorbing aerosols for the same aerosol loading. Alternatively, the enhancement of sky radiance at small scattering angles defines situations when the angular distribution of the scattering light is redistributed in a such way that an artificial sky “brightening” occurs mostly in the near-aureole region:
R1'(θ) = R1(θ) ± Δ
RE(θ*),
θ*≤ 10
0. For this region (e.g.,
θ* ≤ 10
0), diffraction effects contribute substantially to the aureole radiance [
45]. As a result, the aureole radiance shows a fairly weak sensitivity to the imaginary refractive index [
44] and, consequently, to
ω0. This suggests that such artificial sky “brightening” at the small scattering angles, would increase mostly the retrieved scattering phase function
P'(θ*) = P(θ*) + Δ
P(θ*) and, hence, the asymmetry factor, which becomes larger with an increase of the forward scattering fraction [
45,
46].
Since the impact of
E and
O on
τa is negligible (not shown), we will consider their impact on the intensive optical properties (
ω0 and
g) only (
Section 3.2). In comparison with
ω0, the asymmetry factor typically has a smaller impact on the DARF at both the TOA and BOA [
10]. Therefore, the expected different sensitivity of the retrieved aerosol properties (
ω0 and
g) to changes of
E and
O suggests that the enhancement (as compared with offset) would have a smaller influence on the DARF. Below we discuss the impact of the enhancement and offset on the aerosol retrievals and calculated DARF and provide the corresponding quantitative estimates.
3.1. Microphysical Properties
The AERONET inversion scheme is designed as a statistically optimized multivariable fitting where the microphysical properties are directly included in a set of the retrieved parameters. The retrieved microphysical properties are: (1) the real and imaginary parts of the complex refractive index and (2) the size distribution (
υ(
r) =
dV(
r)/
dln
r), which represents the aerosol particle volume in the total atmospheric column per unit of surface area (μm
3/μm
2). The uncertainties of these properties caused by changes of
E and
O are responsible for uncertainties of the corresponding optical parameters (
Section 3.2) and radiative fluxes and DARF (
Section 3.3).
Our sensitivity results demonstrate a weak (~1%) sensitivity of the real part
n to
E and
O changes (not shown). Therefore, we consider below the corresponding sensitivity of the imaginary part
k (
Figure 5) and size distribution (
Figure 6) only. As expected, the positive (negative) offset results in a reduction (increase) of the imaginary part and, consequently, in a reduction (increase) of the relative difference between its “true” and retrieved values (
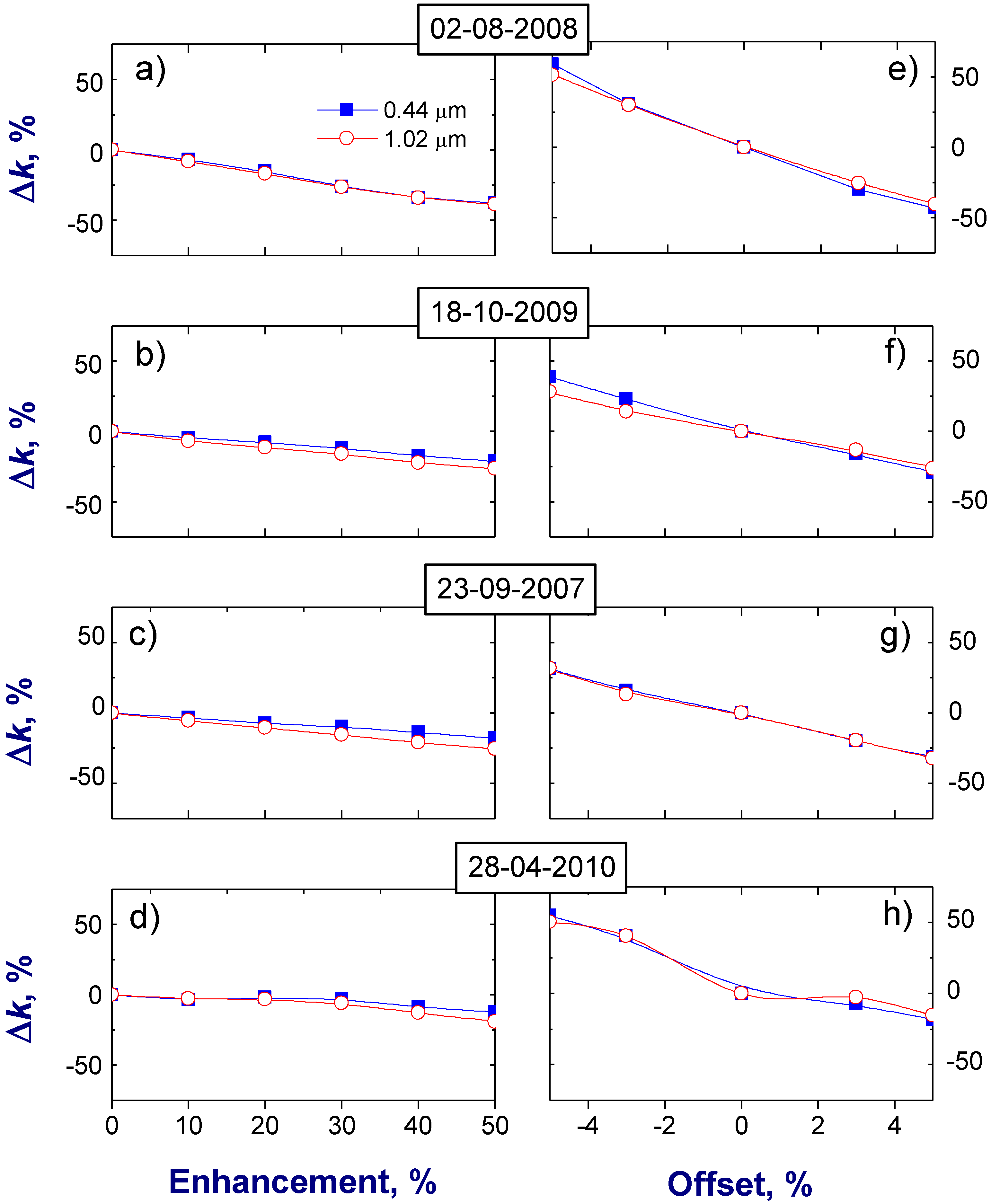
Figure 5). The obtained differences are within a ±50% range and consistent with those from previous studies [
28]. The weak spectral variations of the “true”
k values (
Figure 2(a)) and the spectrally-independent offset (
Section 2) explain the observed weak spectral variations of the corresponding retrieved
k values (
Figure 5, right column). In contrast to the offset
O (% radiance calibration error), the enhancement
E (% stray light at small scattering angles) increases with wavelength substantially (
Section 2). However, such spectral variations of
E have a quite small impact on the retrieved
k values as well (
Figure 5, left column). Thus, the retrieved
k is not sensitive to these spectral changes of
E. Results from
Figure 5 suggest that the large
E values (up to 50% at 1.02 μm wavelength) and small
O values (up to 5%) have comparable impact (up to 50%) on the retrieved imaginary refractive index. This means that the retrieved
k values are more sensitive to the offset than to the enhancement.
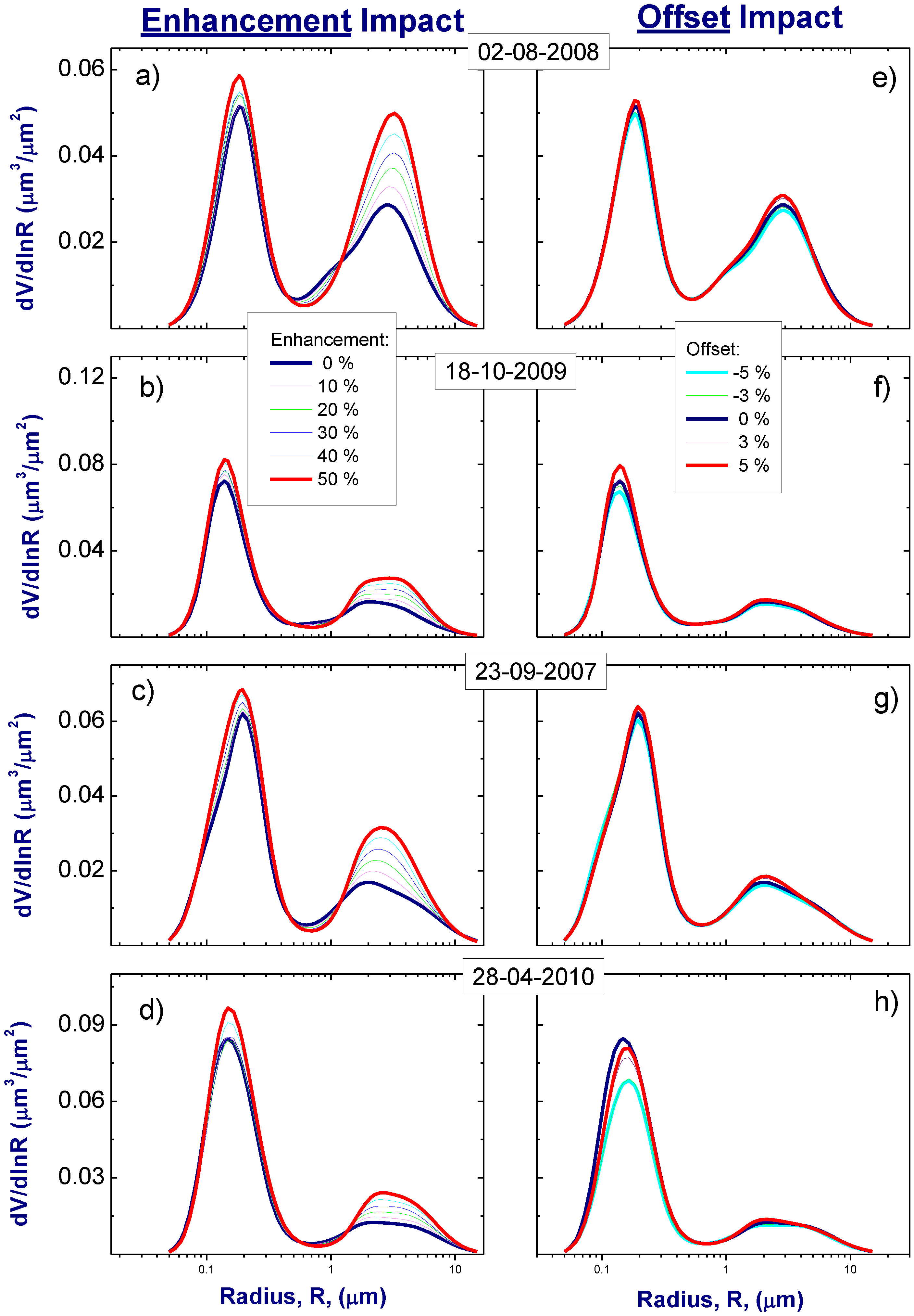
The opposite is true for the retrieved size distribution (
Figure 6), which covers the radius range from 0.05 to 15 μm and is composed of a sum of two lognormal distributions. These two distributions represent fine (submicron) and coarse (supermicron) modes, respectively. These lognormal distributions are described by three parameters: the particle volume concentration (
Cv), the median radius, and the standard deviation [
15].
Figure 6 shows that the offset (
O) modifies only slightly the fine and coarse modes of the retrieved size distribution. Comparable results were obtained earlier and discussed thoroughly in previous studies [
28].
Similarly to the offset, the enhancement does not change significantly the “positions” of these modes (
Figure 6) specified by the median radius. Contrary to the offset, the enhancement does change substantially the volume concentration of large particles (
Figure 6). As a result, the enhancement causes a large (up to 30%) increase of the coarse mode fraction (
Table 3) and a noticeable (up to 10%) decrease of the fine mode fraction (
Table 4). These volume fractions are defined as
where the indices denote the fine (
i = f) and coarse (
i = c) mode, respectively. The
ηf can be considered as a proxy of the aerosol fine mode fraction, which is described as the ratio of fine mode to the total aerosol optical depth [
47,
48]. The aerosol fine mode fraction is used commonly for identifying anthropogenic aerosols from remote sensing observations [
49,
50]. The combined changes of the fine and coarse modes associated with the
E and
O (
Table 3 and
Table 4) are responsible for the corresponding changes of the retrieved effective radius (
re) (
Table 5), defined as the ratio of the third to the second moment of a particle size distribution. In comparison with
ηc,
re and
ηf are less sensitive to the
E. These results indicate that the enhancement can affect substantially the retrieval of the detailed particle size distribution (
Figure 6) and the coarse mode volume fraction (
Table 3). Thus, the expected 4STAR observations may have limited capabilities for retrieving such information. However, they have potential for a reasonable retrieval (~10%) of the fine mode fraction and the effective radius. Note that
re is one of the most important bulk microphysical parameters, which control aerosol optical properties [
45].
Figure 5.
Relative difference between “true” and retrieved values of the imaginary part k of the refractive index for four selected days and two wavelengths: 0.44 μm (blue) and 1.02 μm (red). Left column: differences of k as a function of the assumed enhancement at 1.02 μm wavelength. Right column: differences of k as a function of the assumed offset.
Figure 5.
Relative difference between “true” and retrieved values of the imaginary part k of the refractive index for four selected days and two wavelengths: 0.44 μm (blue) and 1.02 μm (red). Left column: differences of k as a function of the assumed enhancement at 1.02 μm wavelength. Right column: differences of k as a function of the assumed offset.
Figure 6.
Volume size distributions for selected four days in the presence of enhancement (left column) and offset (right column).
Figure 6.
Volume size distributions for selected four days in the presence of enhancement (left column) and offset (right column).
Table 3.
The original values of the coarse volume mode fraction (ηc) calculated for four selected days using the AERONET-retrieved size distribution and Equation (2) (top row). Uncertainties in ηc (%) caused by a 50% enhancement at 1.02 μm wavelength (middle row) and a 5% positive spectrally-independent offset (bottom row) are also shown.
Table 3.
The original values of the coarse volume mode fraction (ηc) calculated for four selected days using the AERONET-retrieved size distribution and Equation (2) (top row). Uncertainties in ηc (%) caused by a 50% enhancement at 1.02 μm wavelength (middle row) and a 5% positive spectrally-independent offset (bottom row) are also shown.
| | 02-08-2008 | 18-10-2009 | 23-09-2007 | 28-04-2010 |
|---|
| ηc | 0.48 | 0.30 | 0.32 | 0.21 |
| Δηc, E(50%) | −13.2 | −17.1 | −19.5 | −31.1 |
| Δηc, O(5%) | 2.1 | -2.6 | 0.1 | 9.4 |
Table 4.
The same as
Table 3, except that these results correspond to the fine volume mode fraction (
ηf).
Table 4.
The same as Table 3, except that these results correspond to the fine volume mode fraction (ηf).
| | 02-08-2008 | 18-10-2009 | 23-09-2007 | 28-04-2010 |
|---|
| ηf | 0.52 | 0.70 | 0.68 | 0.79 |
| Δηf, E(50%) | 10.2 | 8.6 | 8.0 | 8.1 |
| Δηf, O(5%) | 0.0 | 1.1 | 0.0 | −1.4 |
Table 5.
The same as
Table 3, except that these results correspond to effective radius (
re).
Table 5.
The same as Table 3, except that these results correspond to effective radius (re).
| | 02-08-2008 | 18-10-2009 | 23-09-2007 | 28-04-2010 |
|---|
| re, μm | 0.297 | 0.197 | 0.225 | 0.183 |
| Δre, E(50%) | −10.8 | −10.2 | −11.6 | −11.5 |
| Δre, O(5%) | −1.0 | 0.0 | −0.9 | −5.5 |
3.2. Optical Properties
For the selected AERONET cases, the sphericity parameter is almost 100% (
Section 2), and therefore, the shape of aerosol particles for the cases considered here can be approximated by a sphere. For spherical particles, the microphysical (
Section 3.1) and optical properties are related by well-known equations based on the Lorenz-Mie theory [
28]:
where the indices denote the extinction (
j = ext), scattering (
j = scat) and absorption (
j = abs) components of the aerosol optical thickness, and
Kj (…) define the corresponding kernel functions. For a mixture of spherical and non-spherical particles, the corresponding general equations were obtained as well [
33].
These optical properties (Equations (3) and (4)) determine two important quantities frequently used for the DARF assessment, namely the single-scattering albedo and asymmetry factor
It follows from Equation (6) that the asymmetry factor represents the average of the cosine of the scattering angle and denotes how asymmetric the scattering of light is. Its values cover the theoretically possible range of −1≤ g ≤ 1. For example, values of −1 and 1 imply that the incoming light is scattered only in the back and forward directions, respectively; while a value of 0 (e.g., Rayleigh scattering) means light is scattered into both hemispheres symmetrically.
Figure 7.
The same as
Figure 5, except that these differences correspond to the scattering phase function (
P) at 0.44 μm wavelength.
Figure 7.
The same as
Figure 5, except that these differences correspond to the scattering phase function (
P) at 0.44 μm wavelength.
Figure 8.
The same as
Figure 5, except that these differences correspond to the scattering phase function (
P) at 1.02 µm wavelength.
Figure 8.
The same as
Figure 5, except that these differences correspond to the scattering phase function (
P) at 1.02 µm wavelength.
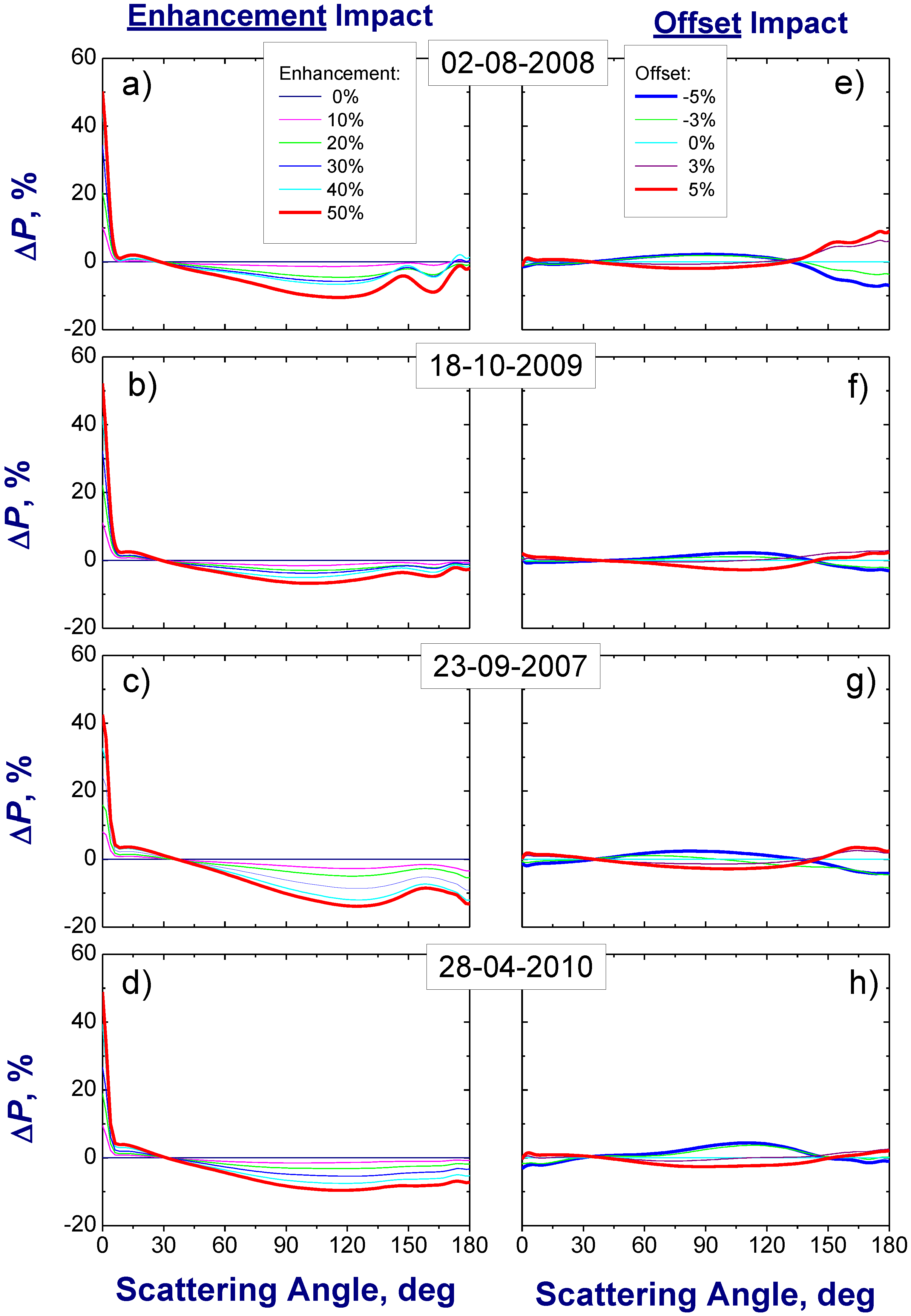
The enhancement
E in 4STAR measurements can increase substantially the sky radiance at small scattering angles (
θ* ≤ 10
0,
Figure 4(b,c)) and, thus, the retrieved scattering function at such angles. As a result, the corresponding difference for the scattering function Δ
P(θ*) is positive (
Figure 7 and
Figure 8; left column). Comparison
Figure 4(c) and
Figure 8 (left column) indicates that the relationship between Δ
P(θ*) and Δ
R(θ*) is almost linear at 1.02 μm wavelength. For example, a 50% enhancement in the sky radiance (
Figure 4(c)) produces about 40–50% enhancement in the retrieved scattering phase function (
Figure 8; left column). The observed almost linear relationship can be explained by a relatively small contribution of the multiple scattering for the cases considered here. This result is in accord with previous findings, which demonstrated that the aureole sky radiance is dominated by low-order light scattering [
44]. Since the importance of multiple scattering becomes larger at shorter wavelengths, the relationship between Δ
P(θ*) and Δ
R(θ*) is nonlinear at 0.47 μm wavelength: a 25% enhancement in the sky radiance (
Figure 4(b)) produces about 40–50% enhancement in the retrieved scattering phase function (
Figure 7, left column).
Let us consider the
E impact on the phase function for the moderate-to-large scattering angles (
θ > θ*) (
Figure 7 and
Figure 8, left column). Although Δ
P(θ) is zero for these angles (
Figure 4(b,c)), the corresponding differences of the scattering function Δ
P(θ) can be both positive and negative (
Figure 7 and
Figure 8; left column). The explanation of these differences (Δ
P(θ) versus Δ
P(θ)) lies mostly in the retrieval scheme, which provides the best fit between the measured and simulated sky radiance for all scattering angles [
28]. Thus, potential overestimation of
P(θ) for some scattering angles tends to be compensated, at least partially, by underestimation of
P(θ) for other angles. In contrast to the enhancement (
E), the offset (
O) does not depend on the scattering angle. However, the largest absolute values of Δ
P(θ) associated with the offset occur at moderate and large scattering angles (
Figure 7 and
Figure 8; right column), where the importance of multiple scattering becomes larger. In comparison with the enhancement, the offset is responsible for much smaller changes of the scattering phase function (
Figure 7 and
Figure 8; left
versus right columns).
The changes in the scattering function Δ
P(θ) associated with the offset have opposite signs and are comparable in magnitude (
Figure 7 and
Figure 8; right column). The overall impact of these changes on the asymmetry factor becomes negligible (
Figure 9; right column) after the integration of
P(θ) over all scattering angles (Equation (6)). In comparison with the offset, the enhancement causes the large positive values of Δ
P(θ) at small scattering angles (
Figure 7 and
Figure 8; left column) and these negative values are not completely balanced by their positive counterparts during the integration (Equation (6)). Thus, the overall impact of these
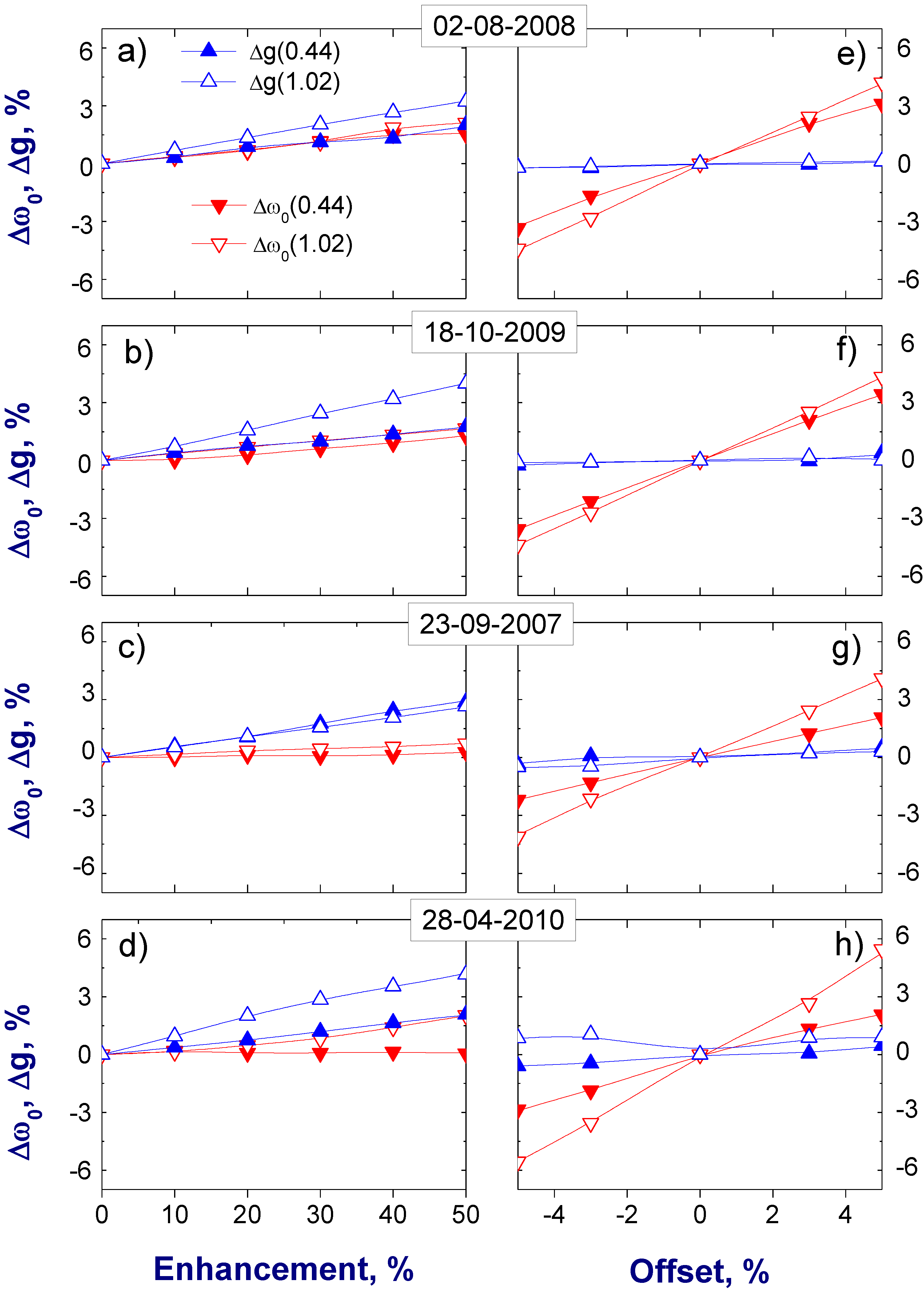
E-caused changes on
g is noticeable (up to 4%, or ±0.02 at 1.02 μm wavelength) and it becomes smaller at shorter wavelengths (
Figure 9; left column). These results indicate that the 4STAR observations have the potential for a reasonable (up to 4%, or ±0.02) retrieval of the asymmetry factor and the corresponding errors would be caused mostly by the enhancement. The retrieval errors of AERONET-derived
g are in the range of 3–5% [
51].
Similar to the asymmetry factor, the single-scattering albedo shows different sensitivity to
E and
O (
Figure 9). For example, a 5% positive offset leads to a similar (up to 6% or 0.04 at 1.02 μm wavelength) increases of
ω0 (
Figure 9; right column), while a 50% enhancement produces much smaller (up to 3% or 0.02 at 1.02 μm wavelength) increases of
ω0 (
Figure 9; left column). Note that uncertainties for the AERONET-derived
ω0 range from 0.03 and 0.05–0.07 for typical (
τa > 0.2) and low (
τa < 0.2) values of aerosol optical depth at 0.44 μm, respectively [
15]. The observed different sensitivity of
ω0 to
E and
O can be explained by noting that
ω0 changes are derived by the corresponding changes of the size distribution and the complex refractive index (see Equations (3) and (5)). For a given size distribution,
ω0 typically decreases with the increase of the imaginary part of the complex refractive index. Both the enhancement and positive offset decreases the retrieved imaginary part (
Figure 5): a 50% enhancement and a 5% positive offset define comparable (up to 50%) reduction of
k (
Figure 5), which leads to increase of the retrieved
ω0. However, the impact of
E and
O on the retrieved size distribution is very different (
Figure 6; left
versus right columns). It appears that the observed different sensitivity of the retrieved
ω0 to
E and
O (
Figure 9) is mainly attributed to different sensitivity of the retrieved size distribution to these two factors (
Figure 6). These results from
Figure 9 suggest that the 4STAR observations have the potential for a feasible retrieval of the asymmetry factor (up to 4%, or ±0.02) and single-scattering albedo (up to 6%, or ±0.04).
Figure 9.
The same as
Figure 5, except that these differences correspond to the single-scattering albedo (red) and asymmetry factor (blue) at two wavelengths: 0.44 μm (filled symbols) and 1.02 μm (open symbols), respectively.
Figure 9.
The same as
Figure 5, except that these differences correspond to the single-scattering albedo (red) and asymmetry factor (blue) at two wavelengths: 0.44 μm (filled symbols) and 1.02 μm (open symbols), respectively.
3.3.Radiative Properties
The clear-sky radiative fluxes are governed by the aerosol optical properties (τa, ω0 and scattering phase function or g). The offset and enhancement can modify noticeably two of them (ω0 and g), which define the amount and asymmetry of the scattered light. Thus, the expected impact of the E and O on the total (diffuse plus direct) downwelling flux is mainly caused by its diffuse component, which is positively correlated with both ω0 and g. In other words, changes of these two optical parameters work in the same direction and, thus, their combined effect is larger than their individual effects. In contrast to the downwelling radiation, these two parameters have opposite impact on the reflected radiation and individual effects of ω0 and g can cancel each other, at least partially.
The outlined distinct sensitivity of the transmitted and reflected radiation to these aerosol optical parameters is illustrated by
Figure 10 (left column). One can see that errors in the diffuse fluxes resulting from the joint increase of
ω0 and
g (
Figure 9; left column) are much smaller for the upwelling flux (~1%) compared to the downwelling flux (
Figure 10; left column). Note that enhancement
E causes the increase of
ω0, which is smaller than the corresponding increase of
g (
Figure 9; left column). The opposite is valid for
O: changes of
ω0 are larger than the corresponding changes of
g (
Figure 9; right column). Thus, the corresponding errors of the downwelling diffuse (up to 5%, or ±5 W∙m
−2) and upwelling (up to 3%, or ±3 W∙m
−2) fluxes (
Figure 10; right column) are mostly due to the
ω0 changes caused by the offset. Uncertainties of measured downwelling diffuse fluxes are about 4% (or ±4 W∙m
−2) [
52]; hence, the errors in calculated downwelling diffuse flux presented here are comparable to these uncertainties.
The observed sensitivity of the downwelling and upwelling fluxes (
Figure 10) to the controlling optical properties (
Figure 9) is important for understanding how the magnitude of the DARF at BOA and TOA (
Figure 11) depends on these parameters. Two main features of the obtained results (
Figure 11) should be emphasized. First, the response of the DARF to the
E changes is relatively weak (≤6%, or 1 W∙m
−2) primarily because of the weak dependence of the considered fluxes on the enhancement (
Figure 10; left column). In comparison with
E, the offset modifies these fluxes to a greater extent (
Figure 10; right column), and thus, the response of the DARF to the
O changes is stronger (up to 15%, or 3 W∙m
−2). Second, the largest differences of the DARF associated with the offset occur at the TOA. The observed stronger dependence of the DARF at TOA compared to the DARF at BOA results largely from the distinct dependences of the upwelling and downwelling fluxes on the offset (
Figure 10; right column). Similar to the DARF, the aerosol radiative forcing efficiency is commonly applied for describing aerosol impact of the radiative balance [
16]. It is defined as a ratio of the DARF and
τa (at 0.5 μm wavelength) and can be considered as the rate at which the atmosphere is forced per unit of aerosol optical depth. Since the impact of
E and
O on
τa is negligible, the DARF and aerosol radiative forcing efficiency have very similar dependence on the
E and
O (not shown).
Figure 10.
The same as
Figure 5, except that these differences correspond to the upwelling total (blue), downwelling total (green), and downwelling diffuse (red) fluxes at the TOA (blue) and BOA (green and red).
Figure 10.
The same as
Figure 5, except that these differences correspond to the upwelling total (blue), downwelling total (green), and downwelling diffuse (red) fluxes at the TOA (blue) and BOA (green and red).
Figure 11.
The same as
Figure 5, except that these differences correspond to the direct aerosol radiative forcing (DARF) at the top of atmosphere (TOA, red) and the bottom of atmosphere (BOA, blue).
Figure 11.
The same as
Figure 5, except that these differences correspond to the direct aerosol radiative forcing (DARF) at the top of atmosphere (TOA, red) and the bottom of atmosphere (BOA, blue).
4. Conclusions
This paper addresses the assessment of expected aerosol retrievals from the new airborne Spectrometer for Sky-Scanning, Sun-Tracking Atmospheric Research (4STAR) with multi-angular and multi-spectral observational capabilities [
26,
27]. The compact design of the 4STAR could result in an apparent enhancement of sky radiance at small scattering angles (≤6° from sun) with some spectral dependence (up to 25% and 50% at 0.44 and 1.02 μm wavelength, respectively). In contrast to the enhancement, the maximum expected offset (±5% skylight miscalibration) of the 4STAR observations is assumed independent of wavelength for this study.
To estimate the potential impact of the enhancement and offset on the anticipated aerosol retrievals, we performed a sensitivity study through application of the operational AERONET retrieval and development of synthetic 4STAR-like data. The development of the synthetic data involves (i) the selection of four days when the retrieved aerosol properties represent the multi-year averages of biomass burning aerosol, and (ii) adding the spectrally-dependent enhancement (at small scattering angles) or the spectrally independent offset (at all scattering angles) to the observed sky radiances for selected days. The relative sensitivity of the retrieved aerosol properties at four specified wavelengths (0.44, 0.674, 0.87 and 1.02 μm) to the expected enhancement and offset is treated in the framework of a theoretical approach previously developed and applied for the AERONET observations [
28]. Particular attention is given to what extent the uncertainties in the retrieved aerosol properties (associated with the enhancement and offset) affect the upwelling and downwelling broadband fluxes and the direct aerosol radiative forcing at the bottom and top of the atmosphere.
Results from numerical simulations offer two major conclusions related to the distinct sensitivity of the aerosol retrieval to the enhancement and offset. First, the enhancement at small scattering angles can prevent retrieving detailed information on the particle size distribution, including the coarse mode volume fraction, and the scattering phase function. For example, a 50% enhancement at 1.02 μm wavelength can result in a substantial overestimation of the phase function (up to 50%) at small scattering angles as well as the coarse mode volume fraction (up to 30%). However, the enhancement has a fairly small effect on the corresponding bulk parameters, such as the effective radius (up to 10%, or 0.03), asymmetry factor (up to 4%, or ±0.02), and single-scattering albedo (up to 2%, or ±0.01). Second, the offset in comparison with the enhancement modifies only slightly the retrieved size distribution and phase function. The offset-related changes of the phase function govern small uncertainties (~1%) of the retrieved asymmetry factor. In contrast to the asymmetry factor, the retrieved single-scattering albedo is sensitive to small changes of offset. To illustrate, a 5% positive offset causes a noticeable (up to 6%, or ±0.04) increase of the single-scattering albedo at 1.02 μm wavelength. Thus, large values of offset (radiance miscalibration >5%) would prevent accurate estimations of the single-scattering albedo.
The consequence of the outlined distinct impacts of E and O on the retrieved aerosol optical properties is a different sensitivity of the calculated fluxes and direct aerosol radiative forcing. The uncertainties of the asymmetry factor and single-scattering albedo caused by the offset have a larger relative impact on the radiative forcing at TOA (up to 15%, or 3 W∙m−2) than those caused by the enhancement (up to 6%, or 1 W∙m−2). Therefore, these uncertainties appear to be quite small in the context of the calculated fluxes and radiative forcing. The simulations indicate that the changes of the downwelling diffuse flux (up to 5% or 5 W∙m−2) resulting from uncertainties of the asymmetry factor and single-scattering albedo are comparable with the corresponding measurement uncertainties (±4 W∙m−2). Overall, the results from this sensitivity study suggest that limitations in the accuracy of 4STAR-retrieved particle size distribution and scattering phase function have diminished impact on the accuracy of retrieved bulk microphysical parameters, such as effective radius and the radiatively important optical properties, such as the asymmetry factor and single-scattering albedo.
We emphasize that these conclusions are obtained for four representative cases with biomass-burning aerosol. Since the aerosol optical properties for these cases match the corresponding climatological averages, we expect that the above conclusions may be valid for other situations when biomass burning aerosol is under consideration. The assessment of the expected aerosol retrievals from the 4STAR measurements for different observational conditions and types of aerosol will be the subject of future studies. An area worthy of further research is to extend the analysis of the promising 4STAR-based aerosol retrieval by using additional wavelengths provided by the 4STAR observations and different sampling strategies.