Modeling Multiple-Core Updraft Plume Rise for an Aerial Ignition Prescribed Burn by Coupling Daysmoke with a Cellular Automata Fire Model
Abstract
:1. Introduction
2. Materials and Methods
2.1. Fire Spread Model

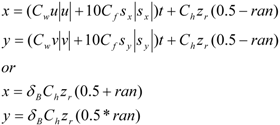
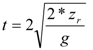
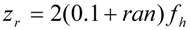
| fn | m1 | m2 | m3 | m4 | m5 | fh | vg | Ch | Cw | Cf | δB |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 01 | 0.5 | 0.0 | 0.0 | 0.0 | 0.0 | 0.65 | 2.00 | 1.00 | 0.25 | ---- | 1 |
| 02 | 0.1 | 0.0 | 0.0 | 0.0 | 0.0 | 1.00 | 1.00 | 1.00 | 0.25 | ---- | 1 |
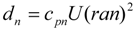
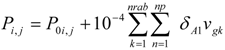
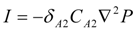
2.2. Daysmoke
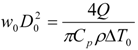
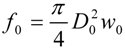
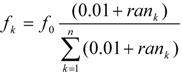
2.3. Data
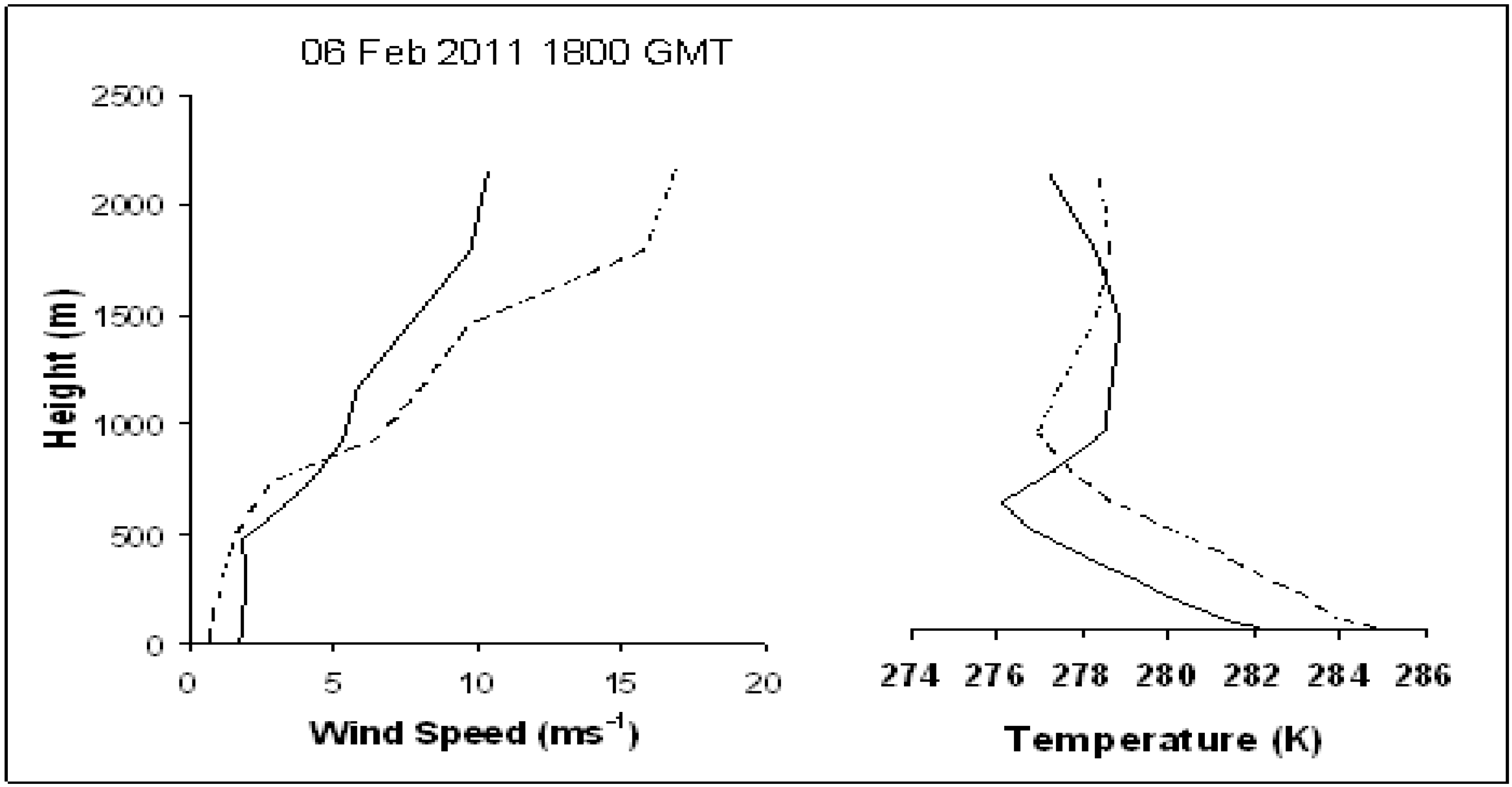
3. Results
3.1. Core Number and Other Plume Initial Variables via Rabbit Rules



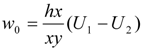
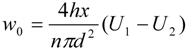
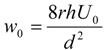

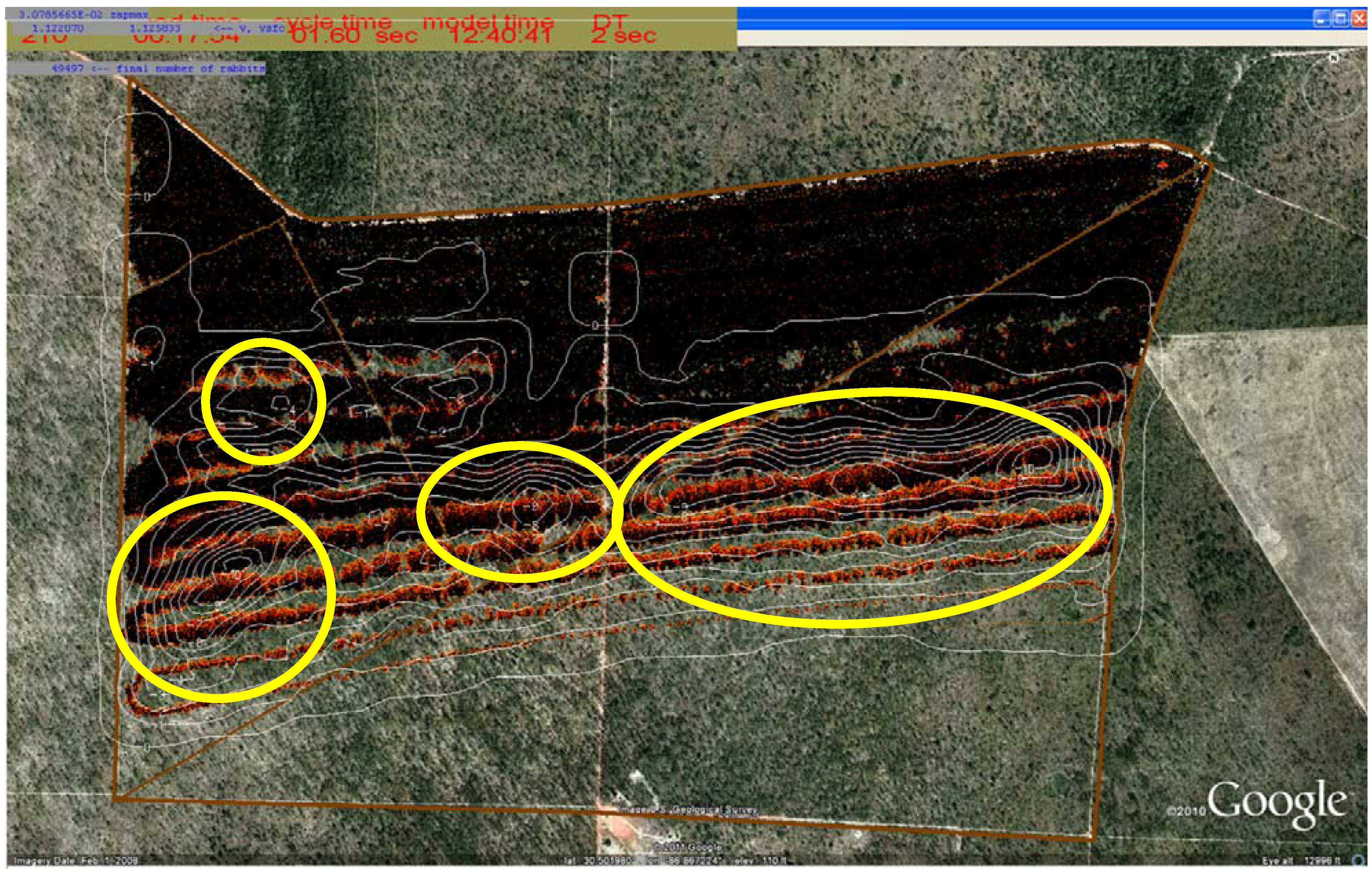


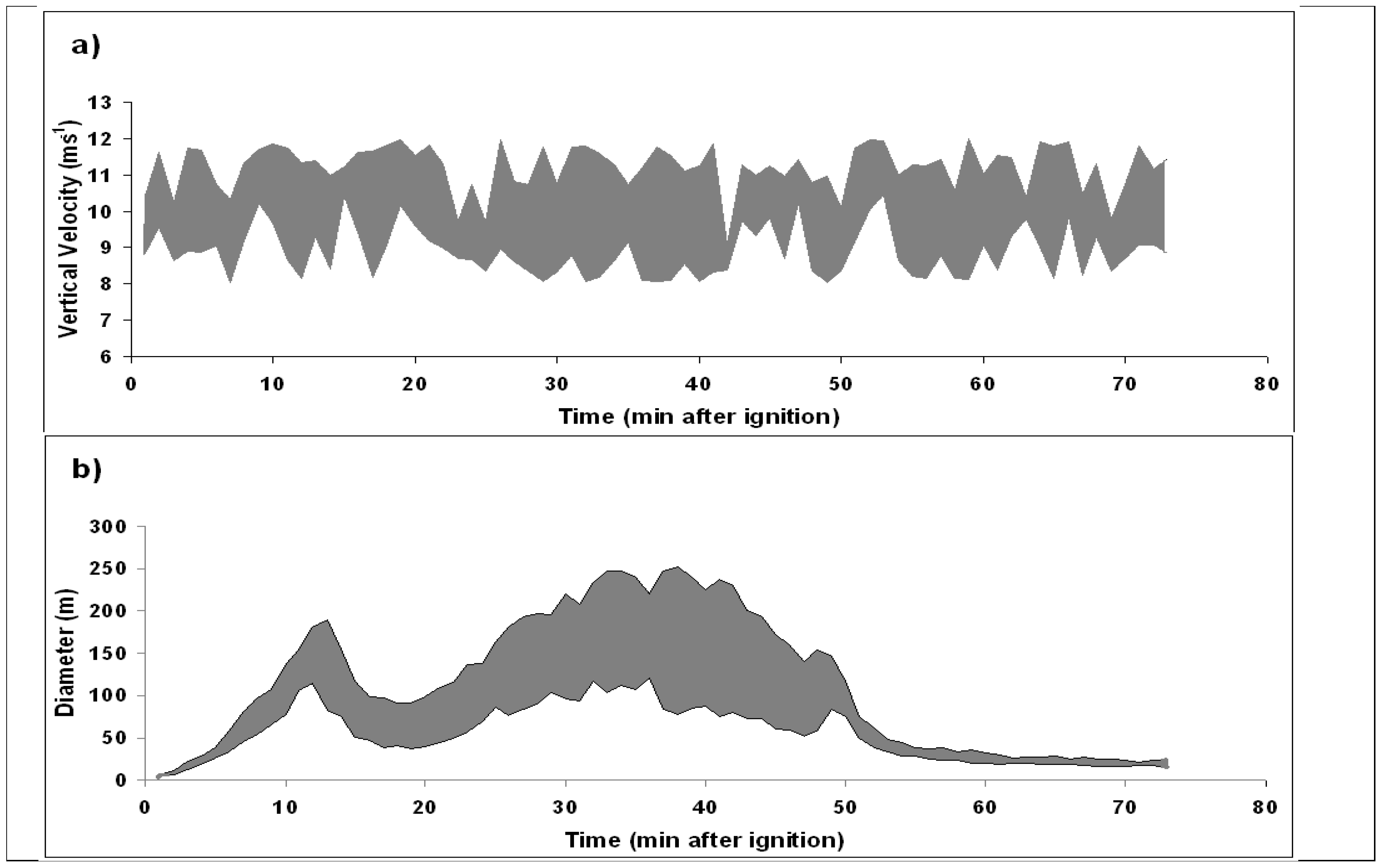
3.2. Plume Rise and Particulate Concentration via Daysmoke


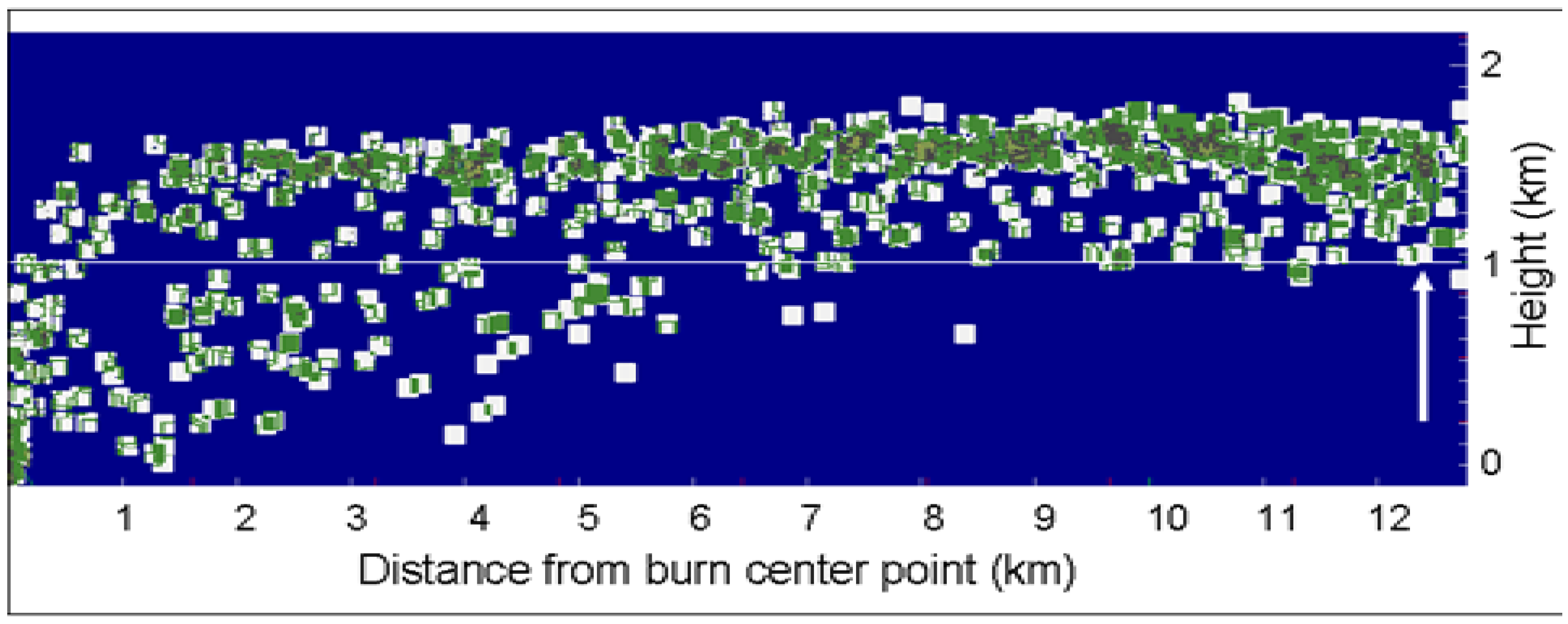
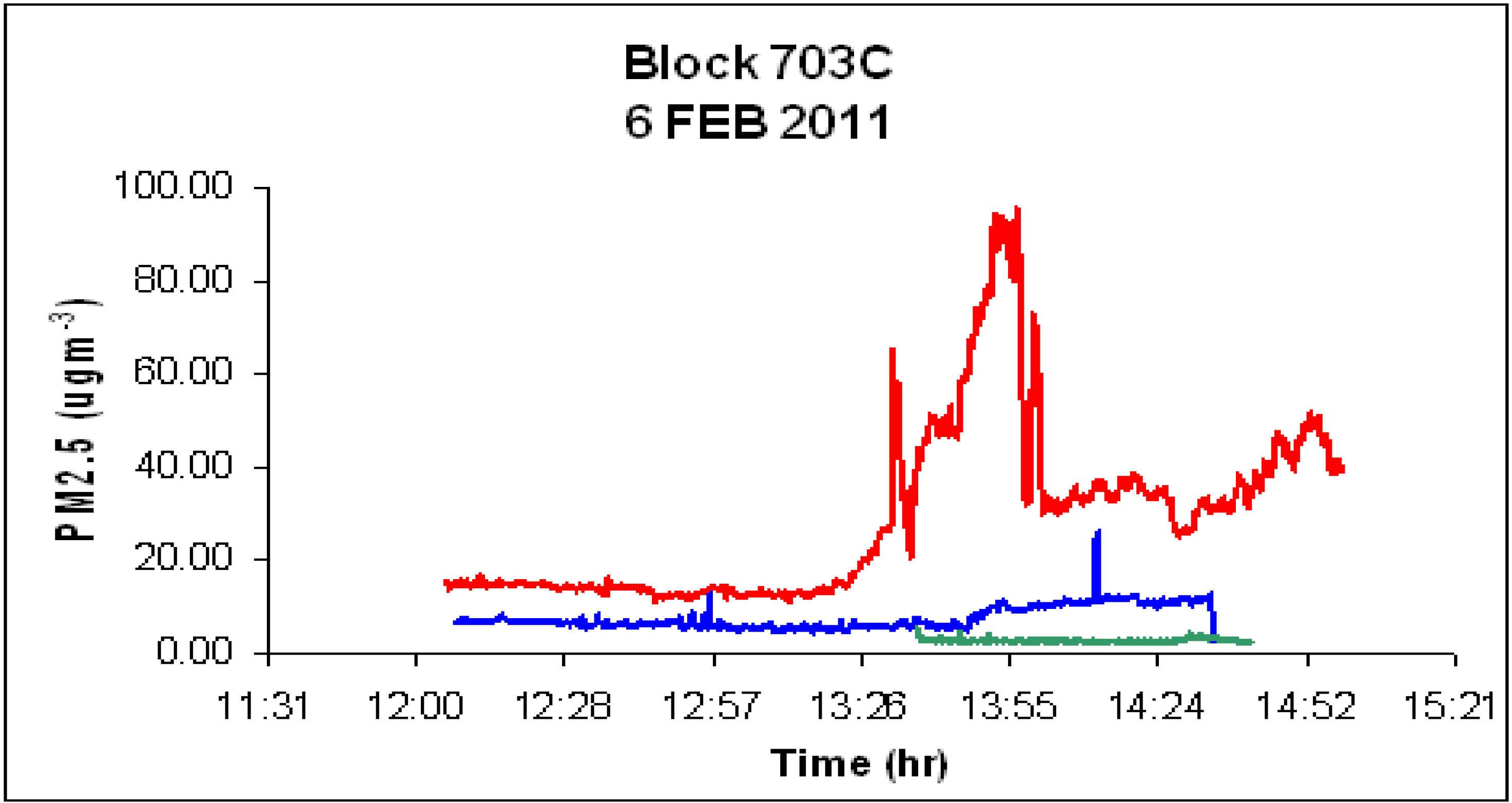
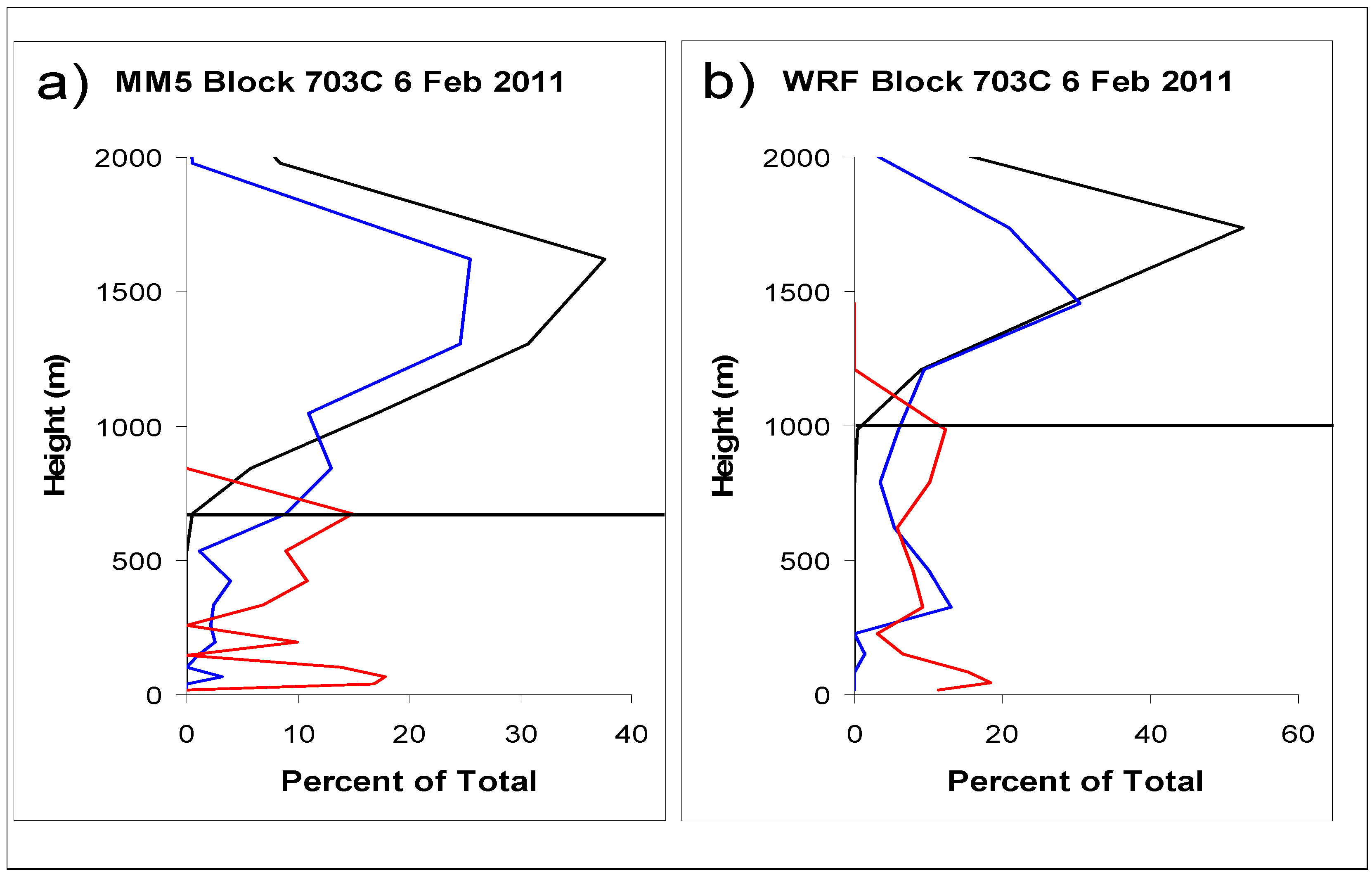
4. Discussion
5. Conclusions
Acknowledgements
References
- Wade, D.D.; Brock, B.L.; Brose, P.H.; Grace, J.B.; Hoch, G.A.; Patterson, W.A., III. Fire in Eastern Ecosystems. In Wildland Fire in Ecosystems: Effects of Fire on Flora; Brown, J.K., Smith, J.K., Eds.; Department of Agriculture: Forest Service, Rocky Mountain Research Station: Ogden, UT, USA, 2000; Volume 2, pp. 53–96. Chapter 4. [Google Scholar]
- Achtemeier, G.L. Effects of moisture released during forest burning on fog formation and implications for visibility. J. Appl. Meteorol. Climatol. 2008, 47, 1287–1296. [Google Scholar] [CrossRef]
- Achtemeier, G.L. On the formation and persistence of superfog in woodland smoke. Meteorol. Appl. 2009, 16, 215–225. [Google Scholar] [CrossRef]
- Naeher, L.P.; Achtemeier, G.L.; Glitzenstein, J.S.; MacIntosh, D.; Streng, D.R. Real-time and time-integrated PM2.5 and CO from prescribed burns in chipped and non-chipped plots—Firefighter and community exposure and health implications. J. Expo. Sci. Environ. Epidemiol. 2006. Available online: http://www.nature.com/doifinder/10.1038/sj.jea.7500497 (accessed on 10 July 2012).
- Lee, S.; Russell, A.G.; Baumann, K. Source apportionment of fine particulate matter in the southeastern United States. J. Air Waste Manag. Assoc. 2007, 57, 1123–1135. [Google Scholar] [CrossRef]
- Hu, Y.M.; Odman, T.; Chang, M.E.; Jackson, W.; Lee, S.; Edgerton, E.S.; Baumann, K. Simulation of air quality impacts from prescribed fires on an urban area. Environ. Sci. Technol. 2008, 42, 3676–3682. [Google Scholar]
- Byun, D.W.; Ching, J. Science Algorithms of the EPA Model-3 Community Multiscale Air Quality (CMAQ) Modeling System; EPA/600/R-99/030; National Exposure Research Laboratory: Research Triangle Park, NC, USA, 1999. [Google Scholar]
- Byun, D.W.; Schere, K.L. Review of the governing equations, computational algorithms, and other components of the Models-3 Community Multiscale Air Quality (CMAQ) modeling system. Appl. Mech. Rev. 2006, 59, 51–77. [Google Scholar] [CrossRef]
- Achtemeier, G.L.; Goodrick, S.A.; Liu, Y.; Garcia-Menendez, F.; Hu, Y.; Odman, M.T. Modeling plume-rise and smoke dispersion from southern United States prescribed burns. Atmosphere 2011, 2, 358–388. [Google Scholar]
- Oberhuber, J.M.; Herzog, M.; Graf, H.-F.; Schwanke, K. Volcanic plume simulation on large scales. J. Volcanol. Geotherm. Res. 1998, 87, 29–53. [Google Scholar]
- Herzog, M.; Graf, H.-F.; Textor, C.; Oberhuber, J.M. The effect of phase changes of water on the development of volcanic plumes. J. Volcanol. Geotherm. Res. 1998, 87, 55–74. [Google Scholar] [CrossRef]
- Freitas, S.R.; Longo, K.M.; Chatfield, R.; Latham, D.; Silva Dias, M.A.F.; Andreae, M.O.; Prins, E.; Santos, J.C.; Gielow, R.; Carvalho, J.A., Jr. Including the sub-grid scale plume rise of vegetation fires in low resolution atmospheric transport models. Atmos. Chem. Phys. 2007, 7, 3385–3398. [Google Scholar]
- Freitas, S.R.; Longo, K.; Trentmann, J.; Latham, D. Including the Environmental Wind Effects on Smoke Plume Rise of Vegetation Fires in 1D Cloud Models. In Proceedings of the Eighth Symposium on Fire and Forest Meteorology, Kalispell, MT, USA, 13–15 October 2009.
- Liu, Y.Q.; Achtemeier, G.L.; Goodrick, S.; Jackson, W.A. Important parameters for smoke plume rise simulation with Daysmoke. Atmos. Pollut. Res. 2010, 1, 250–259. [Google Scholar]
- Clarke, K.C.; Brass, J.A.; Riggan, P.J. A cellular automaton model of wildfire propagation and extinction. Photogramm. Eng. Remote Sens. 1994, 60, 1355–1367. [Google Scholar]
- Clarke, K.C.; Olsen, G. Refining a Cellular Automaton Model for Wildfire Propagation and Extinction. In GIS and Environmental Modeling: Progress and Research Issues; Goodchild, M.F., Louis, T., Steyaert, L.T., Bradley, O., Parks, B.O., Johnston, C., Eds.; John Wiley and Sons Publishers: Hoboken, NJ, USA, 1996. [Google Scholar]
- Karafyllidis, I.; Thanailakis, A. A model for predicting forest fire spreading using cellular automata. Ecol. Model. 1997, 99, 87–97. [Google Scholar] [CrossRef]
- Metzler, R.; Klafter, J. The random walk’s guide to anomalous diffusion: A fractional dynamics approach. Phys. Rep. 2000, 339, 1–77. [Google Scholar]
- Berjak, S.G.; Hearne, J.W. An improved cellular automaton model for simulating fire in a spatially heterogeneous Savanna system. Ecol. Model. 2002, 148, 133–151. [Google Scholar]
- Sullivan, A.L.; Knight, I.K. A Hybrid Cellular Automata/Semi-Physical Model of Fire Growth. In. In Proceedings of the 7th Asia-Pacific Conference on Complex Systems, Cairns, Australia, 6–10 December 2004; pp. 64–73.
- Encinas, A.H.; Encinas, L.H.; White, S.H.; Martin del Rey, A.; Rodriguez Sanchez, G. Simulation of forest fire fronts using cellular automata. Adv. Eng. Softw. 2007, 38, 372–378. [Google Scholar]
- Yassemi, S.; Dragicevic, S.; Schmidt, M. Design and implementation of an integrated GIS-based cellular automata model to characterize forest fire behavior. Ecol. Model. 2008, 210, 71–84. [Google Scholar]
- Adou, J.K.; Billaud, Y.; Brou, D.; Clerc, J.-P.; Consalvi, J.-L.; Fuentes, A.; Kaiss, A.; Nmira, F.; Porterie, B.; Zekri, L.; Zekri, N. Simulating wildfire patterns using a small-world network model. Ecol. Model. 2010. [Google Scholar]
- Achtemeier, G.L. Field validation of a free-agent cellular automata model of fire spread. Int. J. Wildland Fire 2012. [Google Scholar]
- Clark, T.L.; Jenkins, M.A.; Coen, J.; Packham, D. A coupled atmospheric-fire model: Convective Froude number and dynamic fingering. Int. J. Wildland Fire 1996, 6, 177–190. [Google Scholar]
- Linn, R.R.; Cunningham, P. Numerical simulations of grass fires using a coupled atmosphere-fire model: Basic fire behavior and dependence on wind speed. J. Geophys. Res. 2005, 110. [Google Scholar]
- Flakes, G.W. The Computational Beauty of Nature: Computer Explorations of Fractals, Chaos, Complex Systems, and Adaptation; MIT Press: Cambridge, MA, USA, 2000. [Google Scholar]
- Andrews, P.L.; Bevins, C.D.; Seli, R.C. BehavePlus Fire Modeling System, Version 3.0: User’s Guide; Gen. Tech. Rep. RMRS-GTR-106WWW Revised; U.S. Department of Agriculture: Forest Service, Rocky Mountain Research Station: Ogden, UT, USA, 2005. [Google Scholar]
- Hargrove, W.W.; Gardner, R.H.; Turner, M.G.; Romme, W.H.; Despain, D.G. Simulating fire patterns in heterogeneous landscapes. Ecol. Model. 2000, 135, 243–263. [Google Scholar] [CrossRef]
- Andrews, P.L. BehavePlus Fire Modeling System Version 4.0: Variables; Gen. Tech. Rep. RMRS-GTR-213WWW; U.S. Department of Agriculture: Forest Service, Rocky Mountain Research Station: Washington, DC, USA, 2008. [Google Scholar]
- Achtemeier, G.L. Planned burn-Piedmont. A local operational numerical meteorological model for tracking smoke on the ground at night: Model development and sensitivity tests. Int. J. Wildland Fire 2005, 14, 85–98. [Google Scholar] [CrossRef]
- Grell, G.A.; Dudhia, J.; Stauffer, D.R. A Description of the Fifth-generation Penn State/NCAR Mesoscale Model (MM5); NCAR Tech. Note NCAR/TN-3921STR; NCAR: Boulder, CO, USA, 1994. [Google Scholar]
- Skamarock, W.C.; Klemp, J.B.; Dudhia, J.; Gill, D.O.; Barker, D.M.; Wang, W.; Powers, J.G. A Description of the Advanced Research WRF Version 2; NCAR Technical Note: NCAR/TN-468+STR; NCAR: Boulder, CO, USA, 2005. [Google Scholar]
- Achtemeier, G.L. Predicting dispersion and deposition of ash from burning cane. Sugar Cane 1998, 1, 17–22. [Google Scholar]
- Achtemeier, G.L.; Adkins, C.W. Ash and smoke plumes produced from burning sugar cane. Sugar Cane 1997, 2, 16–21. [Google Scholar]
- Byram, G.M. Combustion of Forest Fuels. In Forest Fire Control and Use; Davis, K.P., Ed.; McGraw Hill: New York, NY, USA, 1959; pp. 155–182. [Google Scholar]
- Mercer, G.N.; Weber, R.O. Fire Plumes. In Forest Fires: Behavioral and Ecological Effects; Johnson, E.A., Miyanishi, K., Eds.; Academic Press: New York, NY, USA, 2001. [Google Scholar]
- Jenkins, M.A.; Clark, T.; Coen, J. Coupling Atmospheric and Fire Models. In Forest Fires: Behavior and Ecological Effects; Johnson, E.A., Miyanishi, K., Eds.; Academic Press: San Diego, CA, USA, 2001; pp. 258–301. [Google Scholar]
- Clements, C.B.; Zhong, S.; Goodrick, S.; Li, J.; Potter, B.E.; Bian, X.; Heilman, W.E.; Charney, J.J.; Perna, R.; Jang, M.; et al. Observing the dynamics of wildland grass fires: FireFlux-A field validation experiment. Bull. Am. Meteor. Soc. 2007, 88, 1369–1382. [Google Scholar] [CrossRef]
- Ottmar, R.D.; Vihnanek, R.E.; Mathey, J.W. Stereo Photo Series for Quantifying Natural Fuels. Vol. VIa: Sand Hill, Sand Pine Scrub, and Hardwoods with White Pine Types in the Southeast United States with Supplemental Sites for Volume VI; PMS 838 NFES 1119; US Department of the Interior: Washington, DC, USA, 2003; p. 22. [Google Scholar]
- Ottmar, R.D.; Anderson, G.K.; DeHerrera, P.J.; Reinhardt, T.E. Consume Version 2.1 User’s Guide; Department of Agriculture, Forest Service, Pacific Northwest Research Station: Portland, OR, USA, 1999. Available online: http://www.fs.fed.us/pnw/fera/products/consume/CONSUME21_USER_GUIDE.DOC (accessed on 10 July 2012).
- Liu, Y.Q.; Goodrick, S.A.; Achtemeier, G.L.; Forbus, K.; Combs, D. Smoke plume height measurements of prescribed burns in the southeastern United States. Int. J. Wildland Fire 2011. [Google Scholar]
- Liu, Y.Q.; Goodrick, S.; Achtemeier, G.L.; Jackson, W.A.; Qu, J.J.; Wang, W. Smoke incursions into urban areas: Simulation of a Georgia prescribed burn. Int. J. Wildland Fire 2009, 18, 336–348. [Google Scholar]
© 2012 by the authors; licensee MDPI, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Achtemeier, G.L.; Goodrick, S.A.; Liu, Y. Modeling Multiple-Core Updraft Plume Rise for an Aerial Ignition Prescribed Burn by Coupling Daysmoke with a Cellular Automata Fire Model. Atmosphere 2012, 3, 352-376. https://doi.org/10.3390/atmos3030352
Achtemeier GL, Goodrick SA, Liu Y. Modeling Multiple-Core Updraft Plume Rise for an Aerial Ignition Prescribed Burn by Coupling Daysmoke with a Cellular Automata Fire Model. Atmosphere. 2012; 3(3):352-376. https://doi.org/10.3390/atmos3030352
Chicago/Turabian StyleAchtemeier, Gary L., Scott A. Goodrick, and Yongqiang Liu. 2012. "Modeling Multiple-Core Updraft Plume Rise for an Aerial Ignition Prescribed Burn by Coupling Daysmoke with a Cellular Automata Fire Model" Atmosphere 3, no. 3: 352-376. https://doi.org/10.3390/atmos3030352




