Estimation of Daily Mean Land Surface Temperature over the Qinghai–Tibet Plateau Based on an RTM-DTC Model
Abstract
:1. Introduction
2. Materials and Methods
2.1. Data Source
2.1.1. In Situ Data
2.1.2. Remote Sensing Data
2.1.3. Reanalysis Data
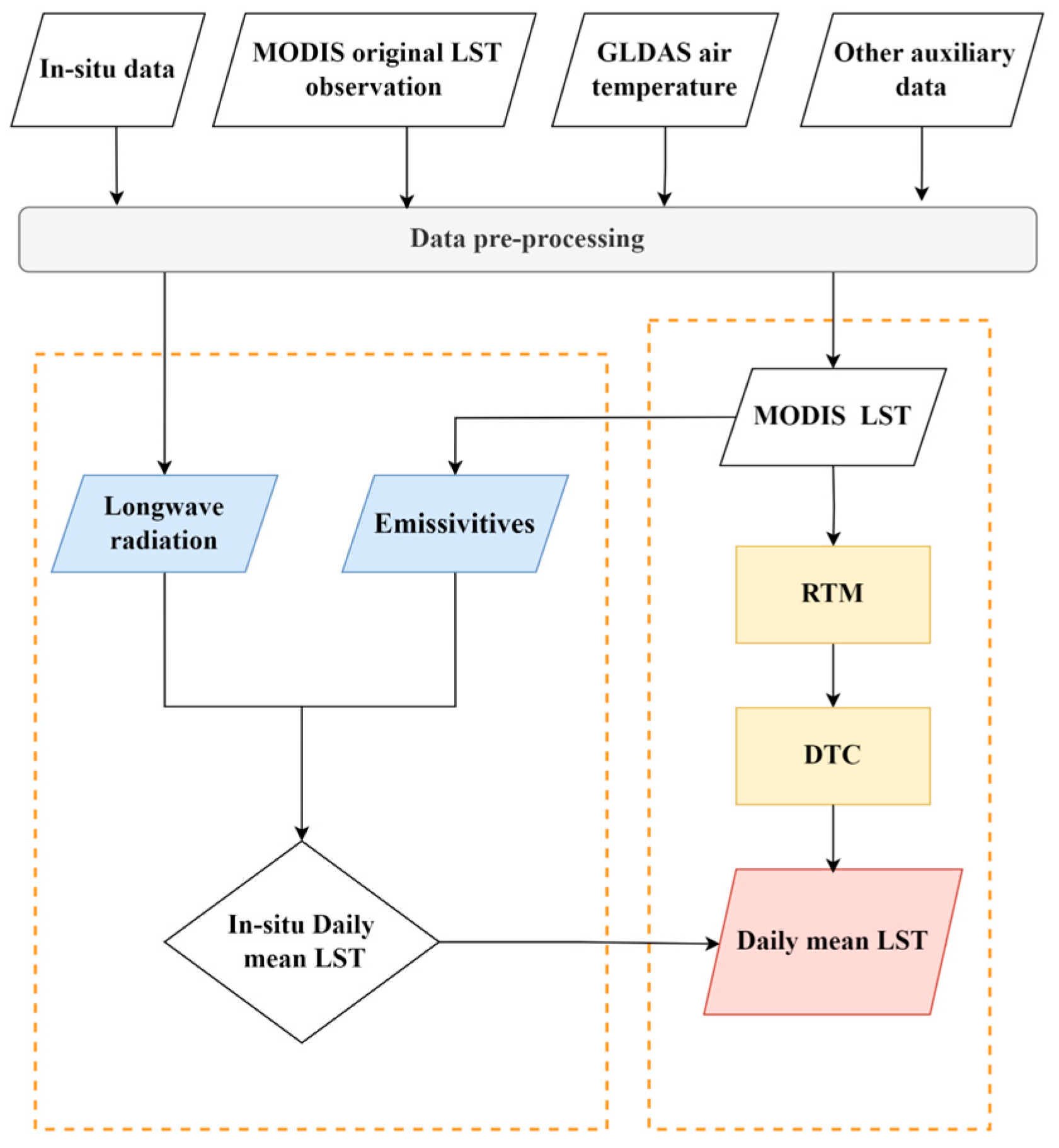
2.2. RTM-DTC Model
- (1)
- Data preprocessing is carried out on MOD11A1, reanalysis data (GLDAS), ground measured station data and other auxiliary data; after that, the preprocessed data re used to reconstruct the ground surface temperature under the cloud by the RTM method, and finally, it generates daily 1 km land surface temperature data twice a day, the accuracy of which is verified by the meteorological station data.
- (2)
- In this study, we used the land surface temperature data estimated by the RTM method and the surface temperature data of the day-by-day all-weather surface temperature dataset (TRIMS LST) published by Zhang et al., to generate 1-km surface temperature data four times a day [17].
- (3)
- The DTC modeling is carried out by using the 1 km land surface temperature data generated four times a day, and then the daily variation curve of the land surface temperature is simulated by the DTC model to estimate the average land surface temperature, and the accuracy of the estimation results is verified by the meteorological station data.
2.2.1. Reanalysis and Thermal Infrared Remote Sensing Merging (RTM) Model
2.2.2. Four-Parameter Diurnal Temperature Cycle (DTC) Model
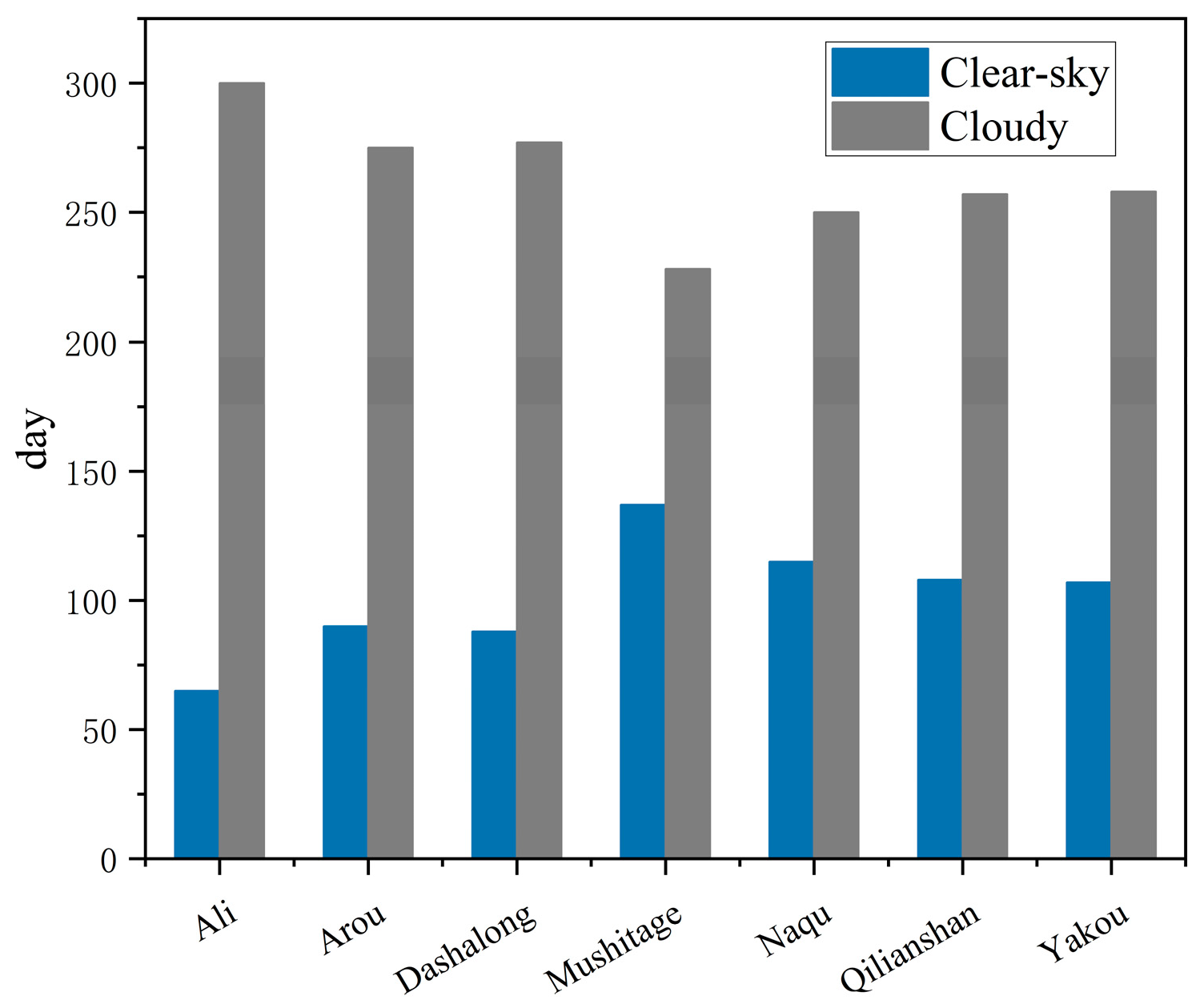
2.3. Validation Strategy
3. Results
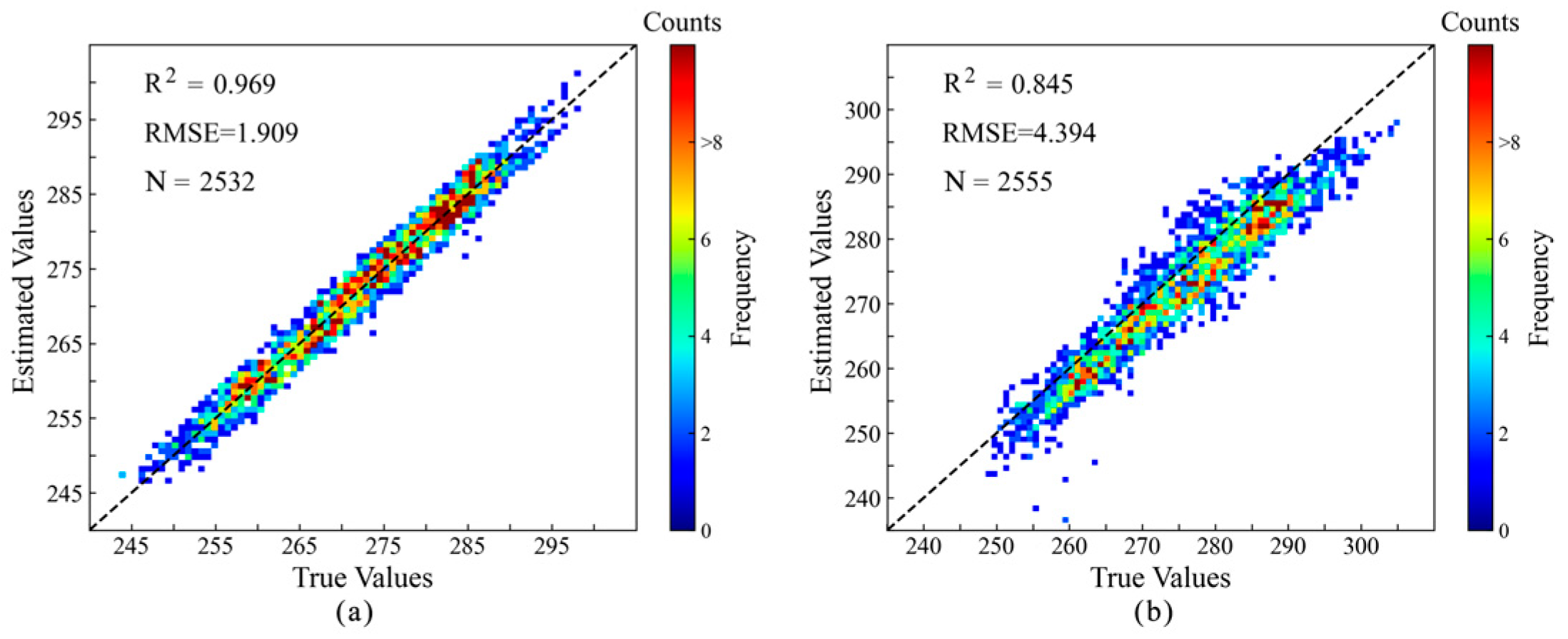
3.1. Comparative Analysis of RTM-DTC Model and Traditional Methods
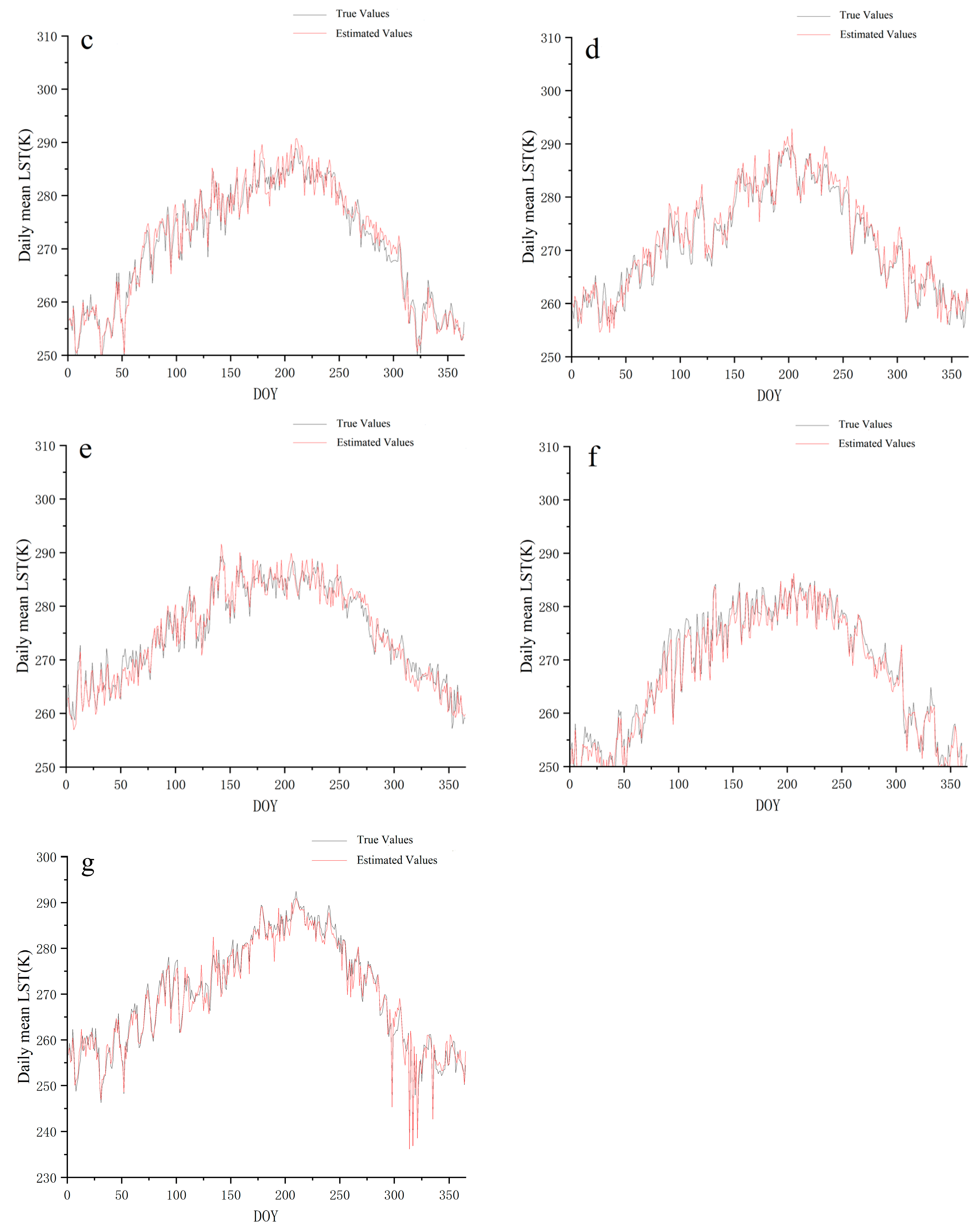
3.2. Daily Scale Verification
3.3. Monthly Scale Verification
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| Data Type | Product Name | Spatial Resolution | Data Source |
|---|---|---|---|
| Thermal Infrared Remote Sensing Data | MOD11A1 MYD11A1 | 1 KM | Level-1 and Atmosphere Archive and Distribution System Distributed Active Archive Center (https://ladsweb.modaps.eosdis.nasa.gov/) (accessed on 2 September 2023) |
| NDVI Data | MYD13A2 | 1 KM | EARTHDATA (https://earthdata.nasa.gov/) (accessed on 2 September 2023) |
| Surface Albedo Data | MCD43A3 | 1 KM | EARTHDATA (https://earthdata.nasa.gov/) (accessed on 2 September 2023) |
| DEM Data | SRTM | 250 m | Digital Elevation Data website of the American Spatial Information Society (http://srtm.csi.cgiar.org/) (accessed on 2 September 2023) |
| Reanalysis Data | GLDAS CLDAS | 0.25° 0.0625° | Goddard Space Flight Center (http://disc.sci.gsfc.nasa.gov) (accessed on 2 September 2023) China Meteorological Service Data Center (http://data.cma.cn/) (accessed on 2 September 2023) |
| Long-wave radiation data | / | High-cold region Observation and Research Network for Land surface processes and Environment of China (http://www.horn.ac.cn/index.jsp) (accessed on 2 September 2023) National Qinghai–Tibet Plateau Scientific Data Center (http://data.tpdc.ac.cn/zh-hans/) (accessed on 2 September 2023) | |
| The meteorological station data | / | the Qinghai–Tibet Plateau Data Center (http://data.tpdc.ac.cn/zh-hans/) (accessed on 2 September 2023) the China Alpine Surface Process and Research Network (http://www.horn.ac.cn/) (accessed on 2 September 2023) | |
References
- Jiang, L.; Islam, S. A methodology for estimation of surface evapotranspiration over large areas using remote sensing observations. Geophys. Res. Lett. 1999, 26, 2773–2776. [Google Scholar] [CrossRef]
- Leng, P.; Li, Z.-L.; Duan, S.-B.; Gao, M.-F.; Huo, H.-Y. A practical approach for deriving all-weather soil moisture content using combined satellite and meteorological data. ISPRS J. Photogramm. Remote Sens. 2017, 131, 40–51. [Google Scholar] [CrossRef]
- Wang, T.; Shi, J.; Ma, Y.; Letu, H.; Li, X. All-sky longwave downward radiation from satellite measurements: General parameterizations based on LST, column water vapor and cloud top temperature. ISPRS J. Photogramm. Remote Sens. 2020, 161, 52–60. [Google Scholar] [CrossRef]
- Weng, Q. Thermal infrared remote sensing for urban climate and environmental studies: Methods, applications, and trends. ISPRS J. Photogramm. Remote Sens. 2009, 64, 335–344. [Google Scholar] [CrossRef]
- Li, Y.; Zhao, M.; Motesharrei, S.; Mu, Q.; Kalnay, E.; Li, S. Local cooling and warming effects of forests based on satellite observations. Nat. Commun. 2015, 6, 6603. [Google Scholar] [CrossRef]
- Kleidon, A.; Renner, M. A simple explanation for the sensitivity of the hydrologic cycle to surface temperature and solar radiation and its implications for global climate change. Earth Syst. Dyn. 2013, 4, 455–465. [Google Scholar] [CrossRef]
- Rao, Y.; Liang, S.; Wang, D.; Yu, Y.; Song, Z.; Zhou, Y.; Shen, M.; Xu, B. Estimating daily average surface air temperature using satellite land surface temperature and top-of-atmosphere radiation products over the Tibetan Plateau. Remote Sens. Environ. 2019, 234, 111462. [Google Scholar] [CrossRef]
- Singh, S.; Bhardwaj, A.; Singh, A.; Sam, L.; Shekhar, M.; Martín-Torres, F.J.; Zorzano, M.-P. Quantifying the Congruence between Air and Land Surface Temperatures for Various Climatic and Elevation Zones of Western Himalaya. Remote Sens. 2019, 11, 2889. [Google Scholar] [CrossRef]
- Hu, T.; Renzullo, L.J.; van Dijk, A.I.J.M.; He, J.; Tian, S.; Xu, Z.; Zhou, J.; Liu, T.; Liu, Q. Monitoring agricultural drought in Australia using MTSAT-2 land surface temperature retrievals. Remote Sens. Environ. 2020, 236, 111419. [Google Scholar] [CrossRef]
- Ma, Z.; Sun, P.; Zhang, Q.; Yao, R. Research on Remote Sensing Drought Monitoring in North China Based on MODIS Data. Geogr. Sci. 2022, 42, 152–162. [Google Scholar] [CrossRef]
- Amiri, R.; Weng, Q.; Alimohammadi, A.; Alavipanah, S.K. Spatial–temporal dynamics of land surface temperature in relation to fractional vegetation cover and land use/cover in the Tabriz urban area, Iran. Remote Sens. Environ. 2009, 113, 2606–2617. [Google Scholar] [CrossRef]
- Han, H.; Yin, Y.; Zhao, Y.; Qin, F. Spatiotemporal Variations in Fractional Vegetation Cover and Their Responses to Climatic Changes on the Qinghai–Tibet Plateau. Remote Sens. 2023, 15, 2662. [Google Scholar] [CrossRef]
- Cong, N.; Shen, M.; Piao, S. Spatial variations in responses of vegetation autumn phenology to climate change on the Tibetan Plateau. J. Plant Ecol. 2016, 10, 744–752. [Google Scholar] [CrossRef]
- Weng, Q.; Firozjaei, M.K.; Kiavarz, M.; Alavipanah, S.K.; Hamzeh, S. Normalizing land surface temperature for environmental parameters in mountainous and urban areas of a cold semi-arid climate. Sci. Total Environ. 2019, 650, 515–529. [Google Scholar] [CrossRef]
- Xie, A.; Zhu, J.; Qin, X.; Wang, S. The Antarctic Amplification Based on MODIS Land Surface Temperature and ERA5. Remote Sens. 2023, 15, 3540. [Google Scholar] [CrossRef]
- Li, Z.; Duan, S.; Tang, B.; Wu, H.; Ren, H.; Yan, G.; Tang, R.; Leng, P. Review of methods for land surface temperature derived from thermal infrared remotely sensed data. Natl. Remote Sens. Bull. 2016, 20, 899–920. [Google Scholar] [CrossRef]
- Zhang, X.; Zhou, J.; Liang, S.; Wang, D. A practical reanalysis data and thermal infrared remote sensing data merging (RTM) method for reconstruction of a 1-km all-weather land surface temperature. Remote Sens. Environ. 2021, 260, 112437. [Google Scholar] [CrossRef]
- Xing, Z.; Li, Z.-L.; Duan, S.-B.; Liu, X.; Zheng, X.; Leng, P.; Gao, M.; Zhang, X.; Shang, G. Estimation of daily mean land surface temperature at global scale using pairs of daytime and nighttime MODIS instantaneous observations. ISPRS J. Photogramm. Remote Sens. 2021, 178, 51–67. [Google Scholar] [CrossRef]
- Zheng, G.; Yang, Y.; Yang, D.; Dafflon, B.; Yi, Y.; Zhang, S.; Chen, D.; Gao, B.; Wang, T.; Shi, R.; et al. Remote sensing spatiotemporal patterns of frozen soil and the environmental controls over the Tibetan Plateau during 2002–2016. Remote Sens. Environ. 2020, 247, 111927. [Google Scholar] [CrossRef]
- Shan, W.; Wang, Y.; Guo, Y.; Zhang, C.; Liu, S.; Qiu, L. Impacts of Climate Change on Permafrost and Hydrological Processes in Northeast China. Sustainability 2023, 15, 4974. [Google Scholar] [CrossRef]
- Ou, Y.; Che, T.; Dai, l.; Wang, Z. Estimating Mean Daily Surface Temperature over the Tibetan Plateau Based on MODIS LST Products. J. Glaciol. Geocryol. 2012, 34, 296–303. [Google Scholar] [CrossRef]
- Zhou, C.; Wang, K. Land surface temperature over global deserts: Means, variability, and trends. J. Geophys. Res. Atmos. 2016, 121, 14344–314357. [Google Scholar] [CrossRef]
- Xie, G.; Lu, C.; Leng, Y.; Zheng, D.; Li, S. Value assessment of ecological assets on the Qinghai-Tibet Plateau. J. Nat. Resour. 2003, 18, 189–196. [Google Scholar] [CrossRef]
- Yao, T.; Thompson, L.G.; Mosbrugger, V.; Zhang, F.; Ma, Y.; Luo, T.; Xu, B.; Yang, X.; Joswiak, D.R.; Wang, W.; et al. Third Pole Environment (TPE). Environ. Dev. 2012, 3, 52–64. [Google Scholar] [CrossRef]
- Lin, X.; Zhang, Z.; Wang, S.; Hu, Y.; Xu, G.; Luo, C.; Chang, X.; Duan, J.; Lin, Q.; Xu, B.; et al. Response of ecosystem respiration to warming and grazing during the growing seasons in the alpine meadow on the Tibetan plateau. Agric. For. Meteorol. 2011, 151, 792–802. [Google Scholar] [CrossRef]
- Zhu, Y.; Fan, G.; Hua, W.; Wang, Q. Analysis of temporal and spatial variation characteristics of surface temperature on the Qinghai-Tibet Plateau from 1981 to 2015. J. Southwest Univ. Nat. Sci. Ed. 2018, 40, 127–140. [Google Scholar] [CrossRef]
- Long, Z.; Ding, L.; Zhou, J.; Zhou, T. Toward the Estimation of All-Weather Daytime Downward Longwave Radiation over the Tibetan Plateau. Atmosphere 2021, 12, 1692. [Google Scholar] [CrossRef]
- Wu, K.; Chen, J.; Yang, H.; Yang, Y.; Hu, Z. Spatiotemporal Variations in the Sensitivity of Vegetation Growth to Typical Climate Factors on the Qinghai–Tibet Plateau. Remote Sens. 2023, 15, 2355. [Google Scholar] [CrossRef]
- Li, X.; Yao, Z.; Yuan, Q.; Xing, R.; Guo, Y.; Zhang, D.; Ahmad, I.; Liu, W.; Liu, H. Prediction of Potential Distribution Area of Two Parapatric Species in Triosteum under Climate Change. Sustainability 2023, 15, 5604. [Google Scholar] [CrossRef]
- Pan, B.; Li, J. The Qinghai-Tibet Plateau: The Driver and Amplifier of Global Climate Change—Ⅰ The Basic Characteristics of Cenozoic Climate Change. J. Lanzhou Univ. 1996, 32, 108–115. [Google Scholar]
- Bi, S. Best laboratory of the universal research for the earth’s global change and earth system science—The Qinghai-Tibet plateau. Syst. Eng. Theory Pract. 1997, 17, 72–77. [Google Scholar]
- Ding, L.; Zhou, J.; Zhang, X.; Liu, S.; Cao, R. Downscaling of surface air temperature over the Tibetan Plateau based on DEM. Int. J. Appl. Earth Obs. Geoinf. 2018, 73, 136–147. [Google Scholar] [CrossRef]
- Wei, Z.; Huang, R.; Dong, W. Interannual and interdecadal variations of air temperature and precipitation on the Qinghai-Tibet Plateau. Atmos. Sci. 2003, 27, 157–170. [Google Scholar]
- Qin, J.; Yang, K.; Liang, S.; Guo, X. The altitudinal dependence of recent rapid warming over the Tibetan Plateau. Clim. Change 2009, 97, 321–327. [Google Scholar] [CrossRef]
- Elmes, A.; Rogan, J.; Williams, C.; Ratick, S.; Nowak, D.; Martin, D. Effects of urban tree canopy loss on land surface temperature magnitude and timing. ISPRS J. Photogramm. Remote Sens. 2017, 128, 338–353. [Google Scholar] [CrossRef]
- Zhong, L.; Ma, Y.; Salama, M.S.; Su, Z. Assessment of vegetation dynamics and their response to variations in precipitation and temperature in the Tibetan Plateau. Clim. Change 2010, 103, 519–535. [Google Scholar] [CrossRef]
- Zhou, J.; Dai, F.; Zhang, X.; Zhao, S.; Li, M. Developing a temporally land cover-based look-up table (TL-LUT) method for estimating land surface temperature based on AMSR-E data over the Chinese landmass. Int. J. Appl. Earth Obs. Geoinf. 2015, 34, 35–50. [Google Scholar] [CrossRef]
- Xu, S.; Cheng, J. A new land surface temperature fusion strategy based on cumulative distribution function matching and multiresolution Kalman filtering. Remote Sens. Environ. 2021, 254, 112256. [Google Scholar] [CrossRef]
- Yang, J.; Zhou, J.; Göttsche, F.-M.; Long, Z.; Ma, J.; Luo, R. Investigation and validation of algorithms for estimating land surface temperature from Sentinel-3 SLSTR data. Int. J. Appl. Earth Obs. Geoinf. 2020, 91, 102136. [Google Scholar] [CrossRef]
- Liu, S.M.; Xu, Z.W.; Wang, W.Z.; Jia, Z.Z.; Zhu, M.J.; Bai, J.; Wang, J.M. A comparison of eddy-covariance and large aperture scintillometer measurements with respect to the energy balance closure problem. Hydrol. Earth Syst. Sci. 2011, 15, 1291–1306. [Google Scholar] [CrossRef]
- Liu, S.; Li, X.; Xu, Z.; Che, T.; Xiao, Q.; Ma, M.; Liu, Q.; Jin, R.; Guo, J.; Wang, L.; et al. The Heihe Integrated Observatory Network: A Basin-Scale Land Surface Processes Observatory in China. Vadose Zone J. 2018, 17, 1–21. [Google Scholar] [CrossRef]
- Lin, J.; Qiu, S.; Tan, X.; Zhuang, Y. Measuring the relationship between morphological spatial pattern of green space and urban heat island using machine learning methods. Build. Environ. 2023, 228, 109910. [Google Scholar] [CrossRef]
- Zhang, Q.; Cheng, J. An Empirical Algorithm for Retrieving Land Surface Temperature From AMSR-E Data Considering the Comprehensive Effects of Environmental Variables. Earth Space Sci. 2020, 7, e2019EA001006. [Google Scholar] [CrossRef]
- Duan, S.-B.; Li, Z.-L.; Wang, N.; Wu, H.; Tang, B.-H. Evaluation of six land-surface diurnal temperature cycle models using clear-sky in situ and satellite data. Remote Sens. Environ. 2012, 124, 15–25. [Google Scholar] [CrossRef]
- Göttsche, F.-M.; Olesen, F.-S.; Trigo, I.; Bork-Unkelbach, A.; Martin, M. Long Term Validation of Land Surface Temperature Retrieved from MSG/SEVIRI with Continuous in-Situ Measurements in Africa. Remote Sens. 2016, 8, 410. [Google Scholar] [CrossRef]
- Zhu, Z.; Shi, C.; Gu, J.; Liang, X. Analysis of the temporal and spatial variation characteristics of surface temperature on the Qinghai-Tibet Plateau in the past 10 years. Sci. Technol. Eng. 2020, 20, 3828–3837. [Google Scholar]
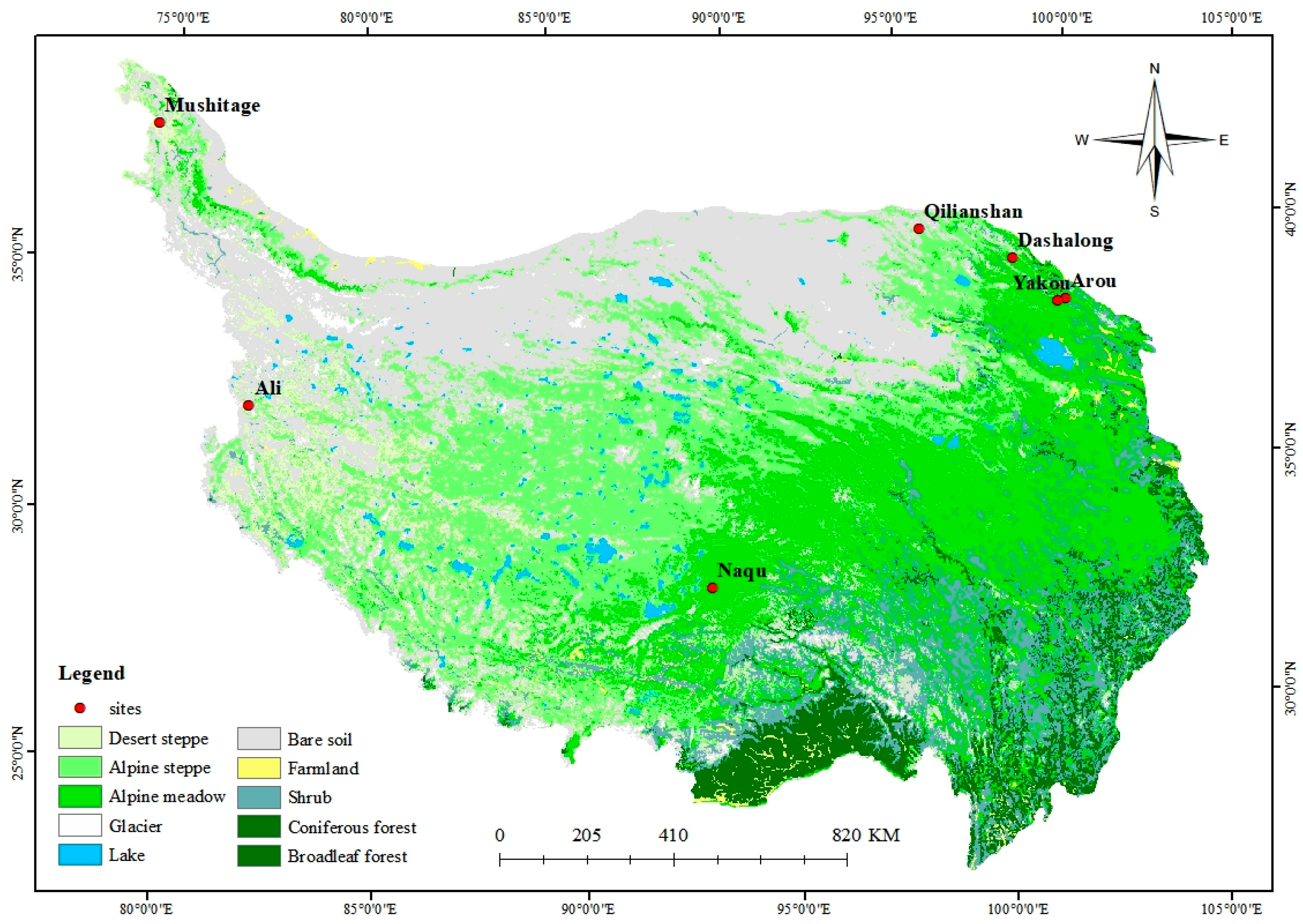
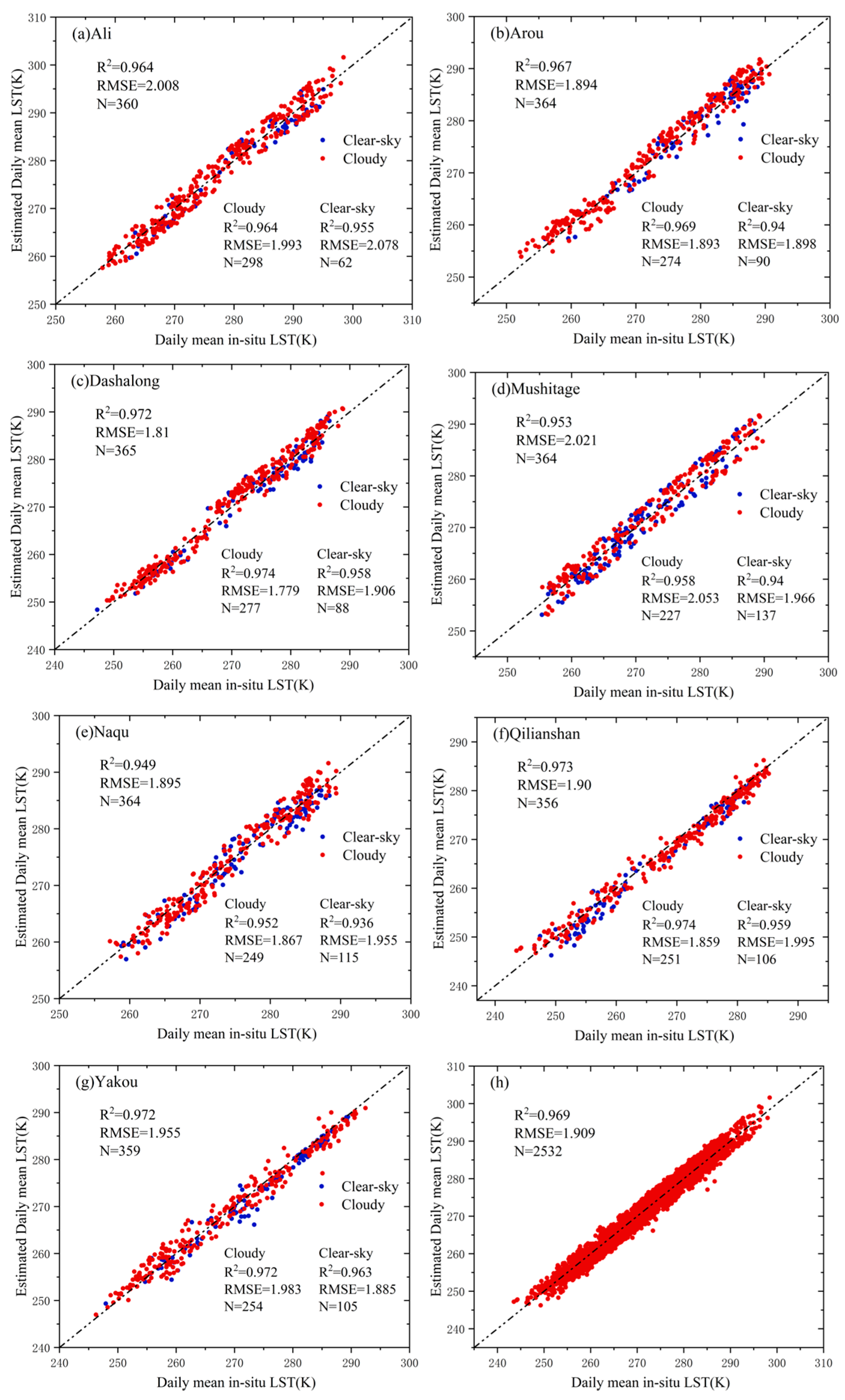
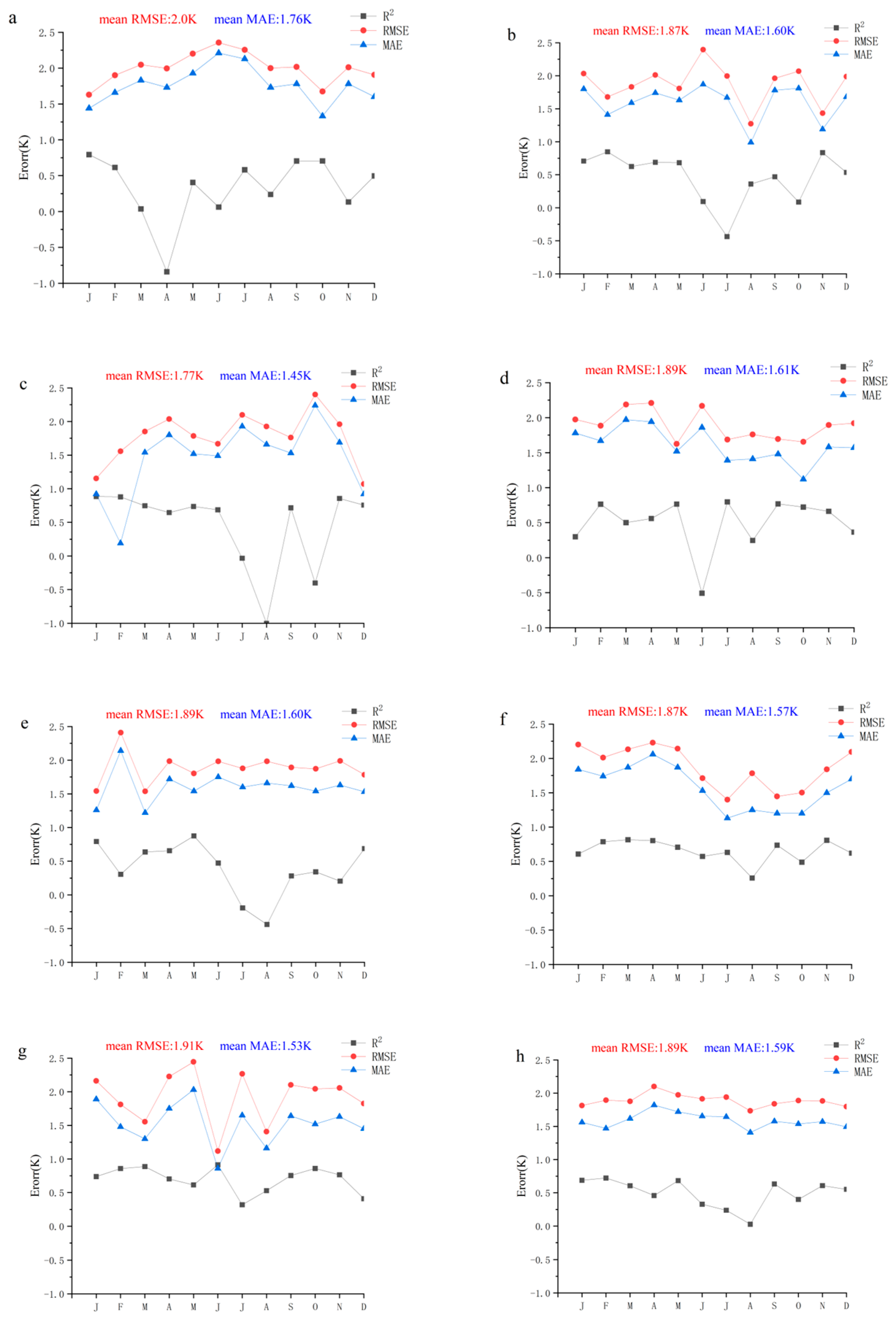
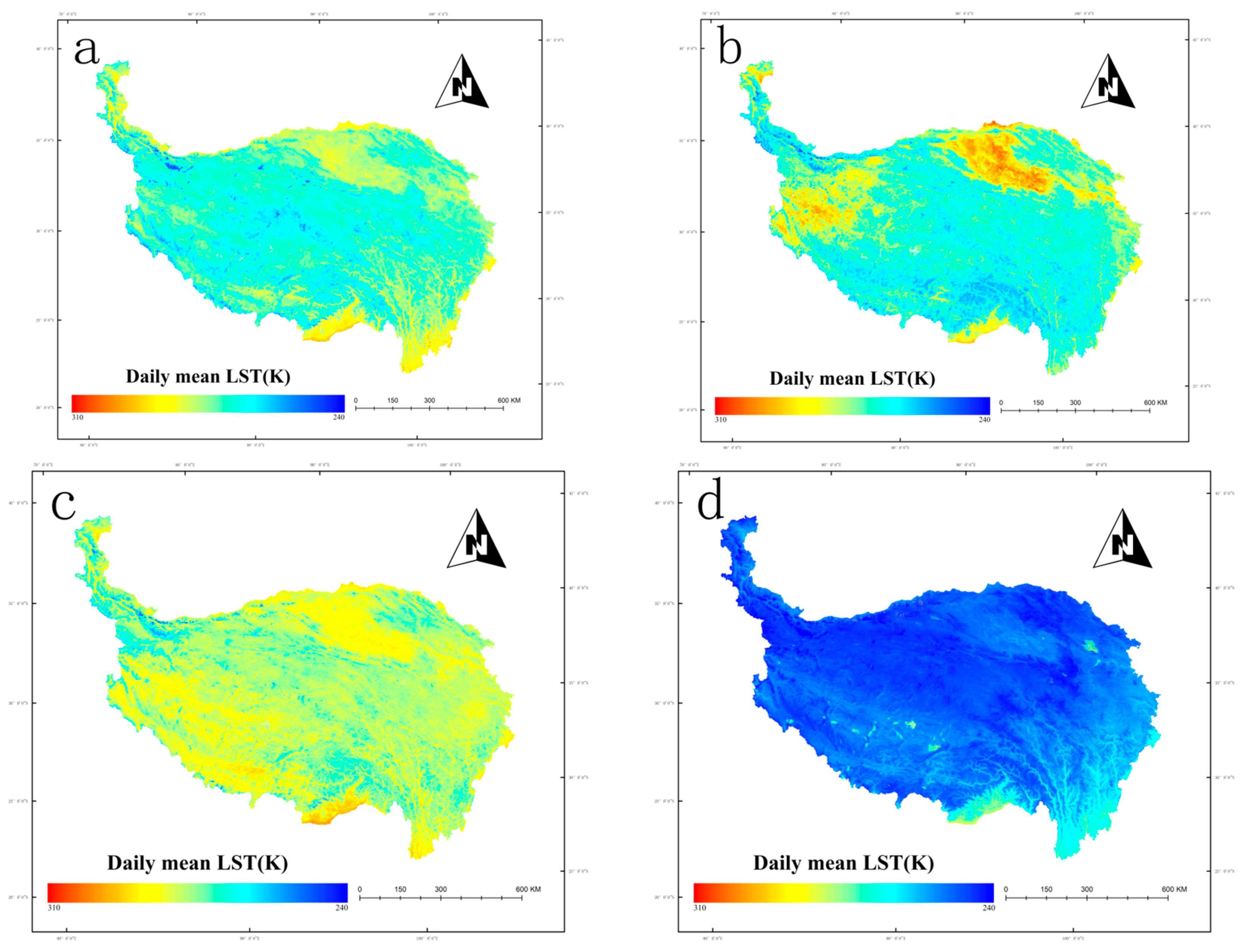
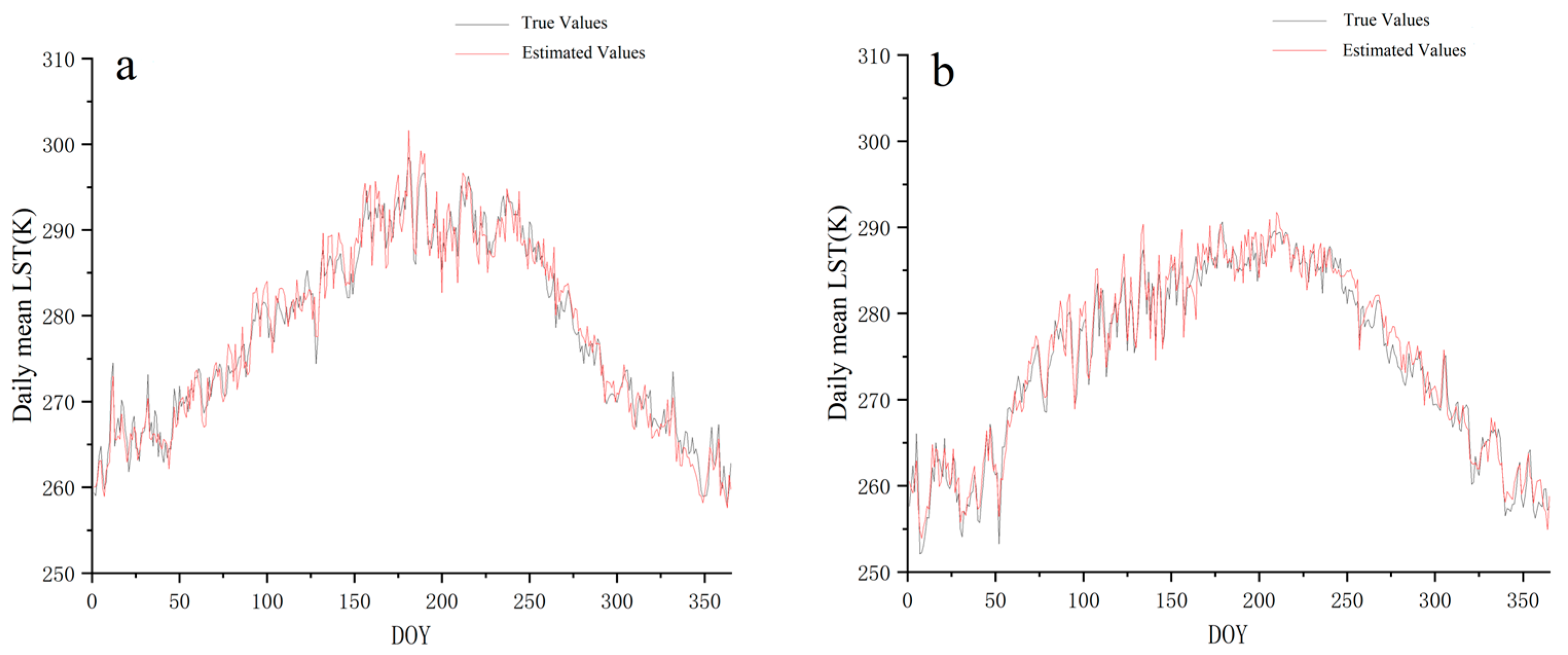
| Site Name | Latitude (°) | Longitude (°) | Altitude | Land Cover Type | Interval |
|---|---|---|---|---|---|
| Ali | 23.39 | 79.70 | 4272 | Desert steppe | 1 d |
| Arou | 38.05 | 100.46 | 3033 | Alpine meadow | 10 min |
| Dashalong | 38.84 | 98.94 | 3739 | Alpine meadow | 10 min |
| Mushitage | 38.41 | 75.05 | 3668 | Desert steppe | 1 d |
| Naqu | 31.37 | 91.90 | 4509 | Alpine steppe | 1 d |
| Qilianshan | 39.50 | 96.50 | 4250 | Alpine meadow | 1 d |
| Yakou | 38.01 | 100.24 | 4148 | Alpine steppe | 10 min |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, L.; Xue, D.; Zhang, X.; Fu, Y. Estimation of Daily Mean Land Surface Temperature over the Qinghai–Tibet Plateau Based on an RTM-DTC Model. Atmosphere 2023, 14, 1559. https://doi.org/10.3390/atmos14101559
Zhao L, Xue D, Zhang X, Fu Y. Estimation of Daily Mean Land Surface Temperature over the Qinghai–Tibet Plateau Based on an RTM-DTC Model. Atmosphere. 2023; 14(10):1559. https://doi.org/10.3390/atmos14101559
Chicago/Turabian StyleZhao, Lei, Dongjian Xue, Xiaoxuan Zhang, and Yudi Fu. 2023. "Estimation of Daily Mean Land Surface Temperature over the Qinghai–Tibet Plateau Based on an RTM-DTC Model" Atmosphere 14, no. 10: 1559. https://doi.org/10.3390/atmos14101559






