Unfolding Kinetics of a Wormlike Chain under Elongational Flow
Abstract
:1. Introduction
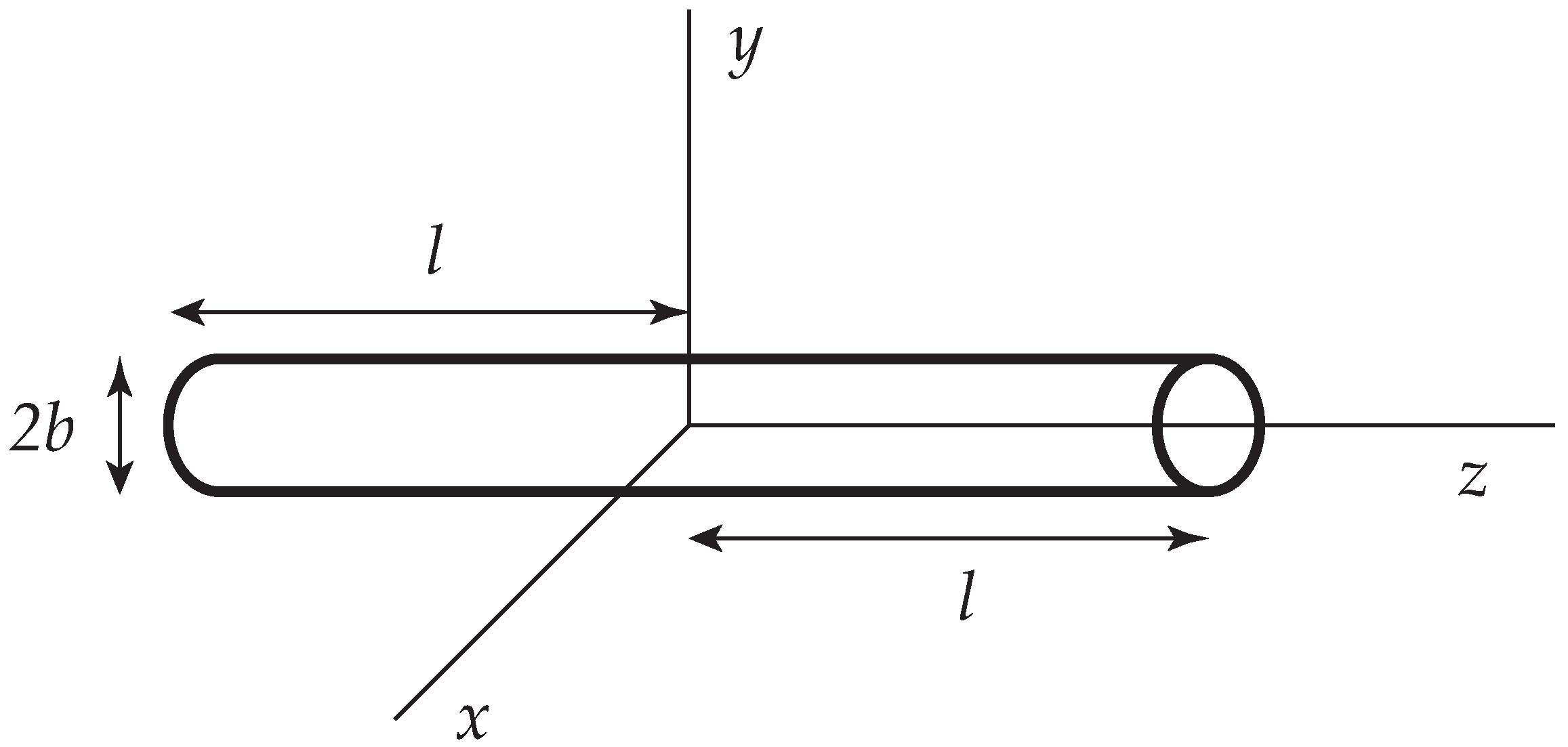
2. Slender Body Theory for Rods
3. Kramers-Type Theory for Unfolding Dynamics
4. Discussion
5. Concluding Remarks
Acknowledgments
Conflicts of Interest
References
- Lindner, A.; Shelley, M. Elastic fibers in flows. In Fluid-Structure Interactions at Low Reynolds Numbers; Duprut, C., Stone, H.A., Eds.; The Royal Society of Chemistry: Cambridge, UK, 2012. [Google Scholar]
- Kantsler, V.; Goldstein, R.E. Fluctuation, dynamics, and the stretch–coil transition of single actin filaments in extensional flows. Phys. Rev. Lett. 2012, 108, 038103. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, H.; Fauci, L. Hydrodynamics of diatom chains and semiflexible fibres. J. R. Soc. Interface 2014, 11, 20140314. [Google Scholar] [CrossRef] [PubMed]
- Young, Y.N.; Shelley, M.J. Stretch-coil transition and transport of fibers in cellular flows. Phys. Rev. Lett. 2007, 99, 058303. [Google Scholar] [CrossRef] [PubMed]
- Gugleilmini, L.; Kushwaha, A.; Shaqfeh, E.S.G.; Stone, H.A. Buckling transitions of an elastic filament in a viscous stagnation point flow. Phys. Fluids 2012, 24, 123601. [Google Scholar] [CrossRef]
- Manikantan, H.; Saintillan, D. Buckling transition of a semiflexible filament in extensional flow. Phys. Rev. E 2015, 92, 041002(R). [Google Scholar] [CrossRef] [PubMed]
- Odijk, T. Microfibrillar buckling within fibers under compression. J. Chem. Phys. 1998, 108, 6923–6928. [Google Scholar] [CrossRef]
- Emanuel, M.; Mohrbach, H.; Sayar, M.; Schiesel, H.; Kulić, I.M. Buckling of stiff polymers: Influence of thermal fluctuations. Phys. Rev. E 2007, 76, 061907. [Google Scholar] [CrossRef] [PubMed]
- Baczynski, K.; Lipowsky, R.; Kierfeld, J. Stretching of buckled filaments by thermal fluctuations. Phys. Rev. E 2007, 76, 061914. [Google Scholar] [CrossRef] [PubMed]
- Blundell, J.R.; Terentjev, E.M. Buckling of semiflexible filaments under compresstion. Soft Matter 2009, 5, 4015–4020. [Google Scholar] [CrossRef]
- Lee, N.L.; Johner, A.; Hong, S.C. Compressing a rigid filament: Buckling and cyclization. Eur. Phys. J. E 2007, 24, 229. [Google Scholar] [CrossRef] [PubMed]
- Pilyugina, E.; Krajina, B.; Spakowitz, A.J.; Schieber, J.D. Buckling a semiflexible polymer chain under compression. Polymers 2017, 9, 99. [Google Scholar] [CrossRef]
- Palenc̆ár, P.; Bleha, T. Bending and kinking in helical polymers. J. Polym. Sci. Polym. Phys. 2015, 53, 1345. [Google Scholar] [CrossRef]
- Strelnikova, N.; Göllner, M.; Pfohl, T. Direct observation of alternating stretch-coil and coil-stretch transitions of semiflexible polymers in microstructured flows. Macromol. Chem. Phys. 2017, 218, 1600474. [Google Scholar] [CrossRef]
- Reese, H.R.; Zimm, B.H. Fracture of polymer chains in extensional flow: Experiments with DNA and a molecular-dynamics simulation. J. Chem. Phys. 1990, 92, 2650–2662. [Google Scholar] [CrossRef]
- Perkins, T.T.; Smith, D.E.; Chu, S. Single polymer dyamics in an elongational flow. Science 1997, 276, 2016–2021. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Hsiao, K.W.; Brockman, C.A.; Yates, D.Y.; Robertson-Anderson, R.M.; Kornfield, J.A.; San Fransisco, M.J.; Schroeder, C.M.; McKenna, G.B. When ends meet: Circular DNA stretches differently in elongational flows. Macromolecules 2015, 48, 5997–6001. [Google Scholar]
- Zhou, Y.; Schroeder, C.M. Transient and average unsteady dynamics of single polymers in large-amplitude oscillatory extension. Macromolecules 2016, 49, 8018. [Google Scholar] [CrossRef]
- Pedersen, J.N.; Marie, R.; Kristensen, A.; Flyvbjerg, H. How to determine local stretching and tension in a flow-stretched DNA molecule. Phys. Rev. E 2016, 93, 042405. [Google Scholar] [CrossRef] [PubMed]
- Mai, D.J.; Schroeder, C.M. Single polymer dynamics of topologically complex DNA. Curr. Opin. Colloid Int. Sci. 2016, 26, 28. [Google Scholar] [CrossRef]
- Hariadi, R.F.; Yurke, B. Elongation-flow-induced scission of DNA nanotubes in laminar flow. Phys. Rev. E 2010, 82, 046307. [Google Scholar] [CrossRef] [PubMed]
- De Gennes, P.G. Coil-stretch transition of dilute flexible polymers under ultrahigh velocity gradients. J. Chem. Phys. 1974, 60, 5030–5042. [Google Scholar] [CrossRef]
- Hinch, E.J. Mechanical models of polymer solutions in strong flows. Phys. Fluids 1977, 10. [Google Scholar] [CrossRef]
- Chan, T.; Dean, D.S.; Jansons, K.M.; Rogers, L.C.G. On polymer conformations in elongated flows. Commun. Math. Phys. 1994, 160, 239–257. [Google Scholar] [CrossRef]
- Hinch, E.J. Uncoiling a polymer molecule in a strong extensional flow. J. Non Newton. Fluid Mech. 1994, 54, 209–230. [Google Scholar] [CrossRef]
- Larson, R.G.; Hu, H.; Smith, D.E.; Chu, S. Browian dynamics simulations of a DNA molecule in an extensional flow field. J. Rheol. 1999, 43, 267–304. [Google Scholar] [CrossRef]
- Lee, N.K.; Thirumalai, D. Pulling-speed-dependent force-extension profiles for semiflexible chains. Biophys. J. 2004, 86, 2641–2649. [Google Scholar] [CrossRef]
- Sunthar, P.; Prakash, J.R. Parameter-free prediction of DNA conformations in elongational flow by successive fine graining. Macromolecules 2005, 38, 617–640. [Google Scholar] [CrossRef]
- Burgers, J.M. Second Report on Viscosity and Plasticity of the Amsterdam Academy of Sciences, Part XVI, No. 4; North Holland: Amsterdam, The Netherlands, 1938. [Google Scholar]
- Lighthill, J. Mathematical Biofluiddynamics; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 1975. [Google Scholar]
- Yamakawa, H.; Yoshizaki, T. Helical Wormlike Chains in Polymer Solutions; Springer: Berlin, Germany, 2016. [Google Scholar]
- Batchelor, G.K. Slender-body theory for particles of arbitrary cross-section in Stokes flow. J. Fluid Mech. 1970, 44, 419–440. [Google Scholar] [CrossRef]
- Kramers, H.A. The behavior of macromolecules in inhomogeneous flow. J. Chem. Phys. 1946, 14, 415–430. [Google Scholar] [CrossRef]
- Swank, Z.; Deshpande, S.; Pfohl, T. Trapping, entrainment and synchronization of semiflexible polymers in narrow, asymmetric confinements. Soft Matter 2016, 12, 87–92. [Google Scholar] [CrossRef] [PubMed]
- Odijk, T. On the statistics and dynamics of confined or entangled stiff polymers. Macromolecules 1983, 16, 1340–1345. [Google Scholar] [CrossRef]
- Batchelor, G.K. Stress generated in a non-dilute suspension of elongated particles by pure straining motion. J. Fluid Mech. 1971, 46, 813–829. [Google Scholar] [CrossRef]
- Bird, R.B.; Hassager, O.; Armstrong, R.C.; Curtiss, C.F. Dynamics of Polymeric Liquids, Vol. 2; John Wiley: New York, NY, USA, 1977. [Google Scholar]
- Smith, D.E.; Chu, S. Response of flexible polymers to a sudden elongational flow. Science 1998, 281, 1335–1339. [Google Scholar] [CrossRef] [PubMed]
- Stone, P.A.; Hudson, S.D.; Dalheimer, P.; Discher, D.E.; Amis, E.J.; Migler, K.B. Dynamics of wormlike micelles in elongational flows. Macromolecules 2006, 39, 7144–7148. [Google Scholar] [CrossRef]

© 2017 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Odijk, T. Unfolding Kinetics of a Wormlike Chain under Elongational Flow. Polymers 2017, 9, 190. https://doi.org/10.3390/polym9060190
Odijk T. Unfolding Kinetics of a Wormlike Chain under Elongational Flow. Polymers. 2017; 9(6):190. https://doi.org/10.3390/polym9060190
Chicago/Turabian StyleOdijk, Theo. 2017. "Unfolding Kinetics of a Wormlike Chain under Elongational Flow" Polymers 9, no. 6: 190. https://doi.org/10.3390/polym9060190



