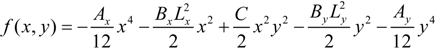Simplified Modeling of Rectangular Concrete Cross-Sections Confined by External FRP Wrapping
Abstract
:1. Introduction
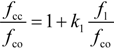
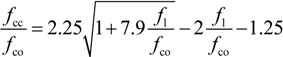
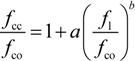
2. Theoretical Basis of the Proposed Simplified Approach
2.1. Refined Iterative Models
2.1.1. Airy’s Function f(x,y) for Non-Circular Cross-Section Confinement
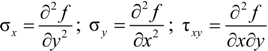
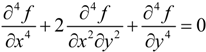
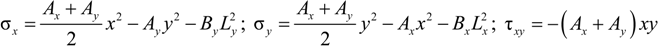
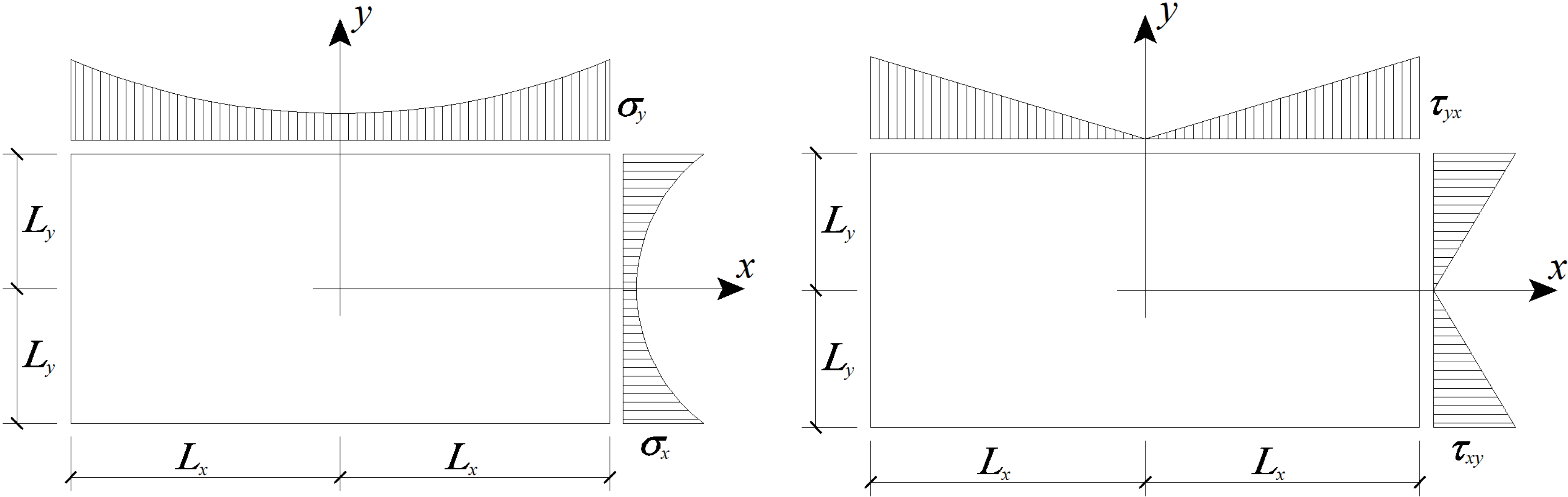
2.1.2. Displacement Compatibility
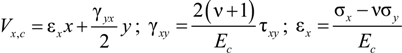
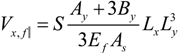
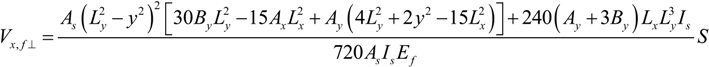
2.1.3. Evaluation of Parameters Ax, Ay, Bx and By
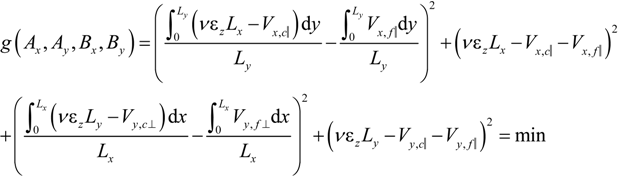
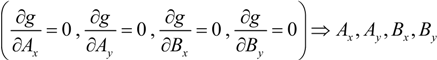
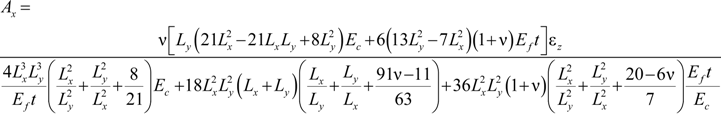
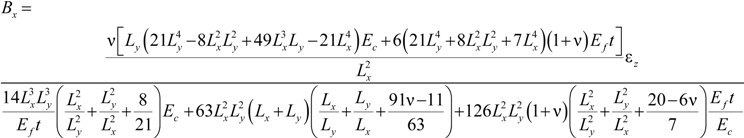
2.1.4. The Case of Square Cross-Sections
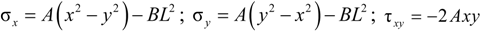
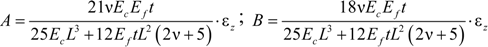
2.2. Simplified Model for Square Sections

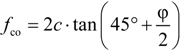
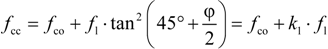
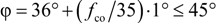
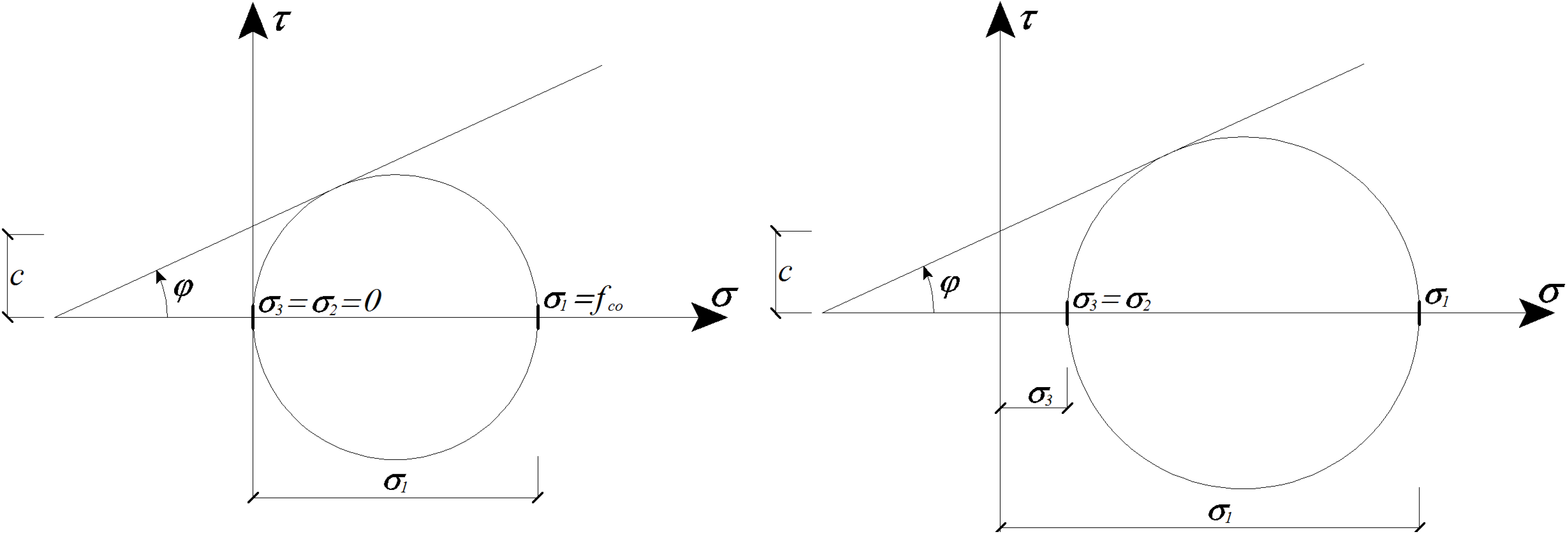
2.2.1. Conventional Procedures to Account for Non-Circular Cross-Sections
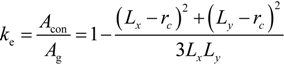
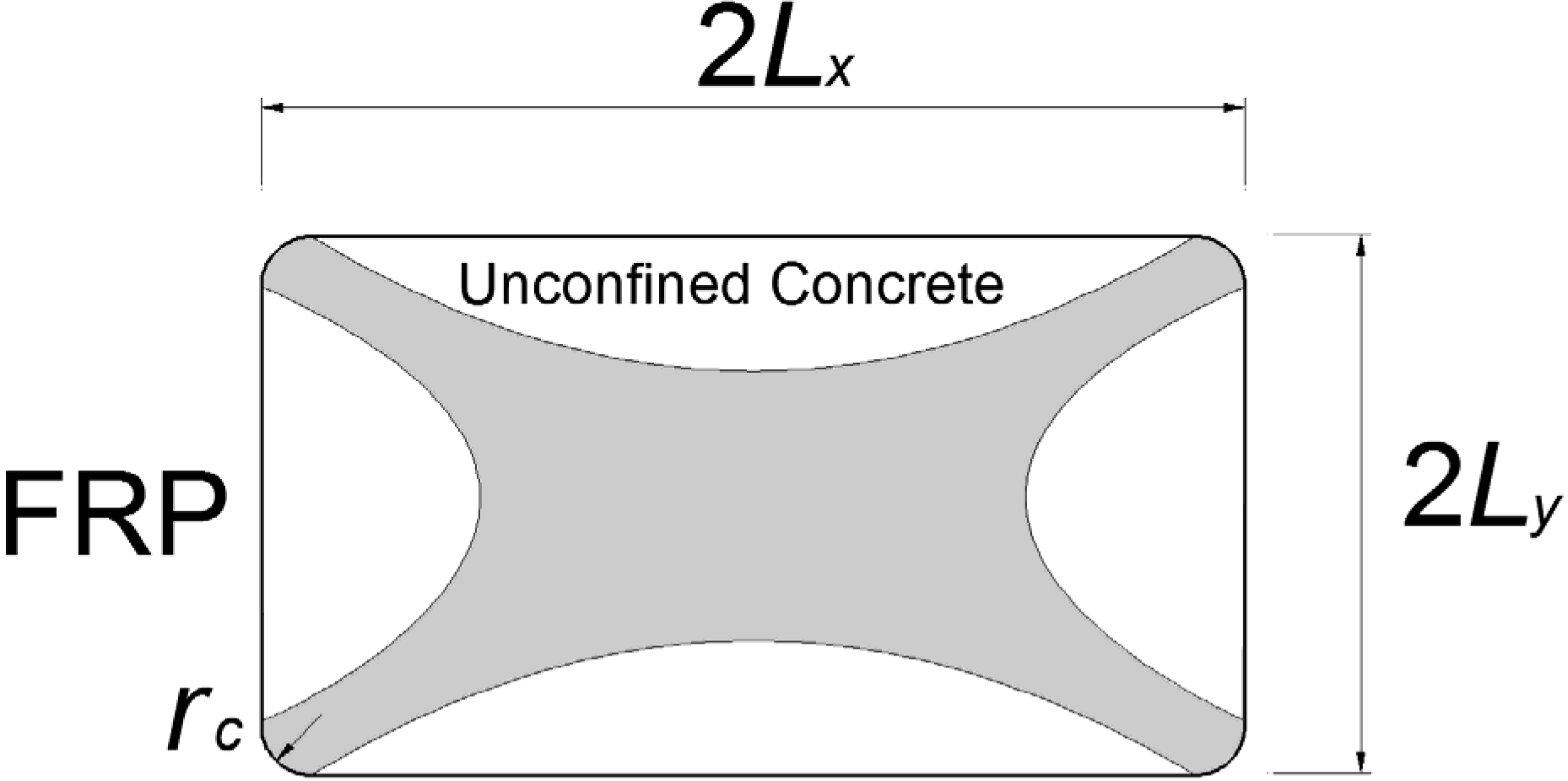
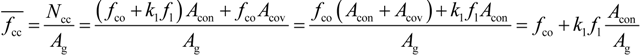
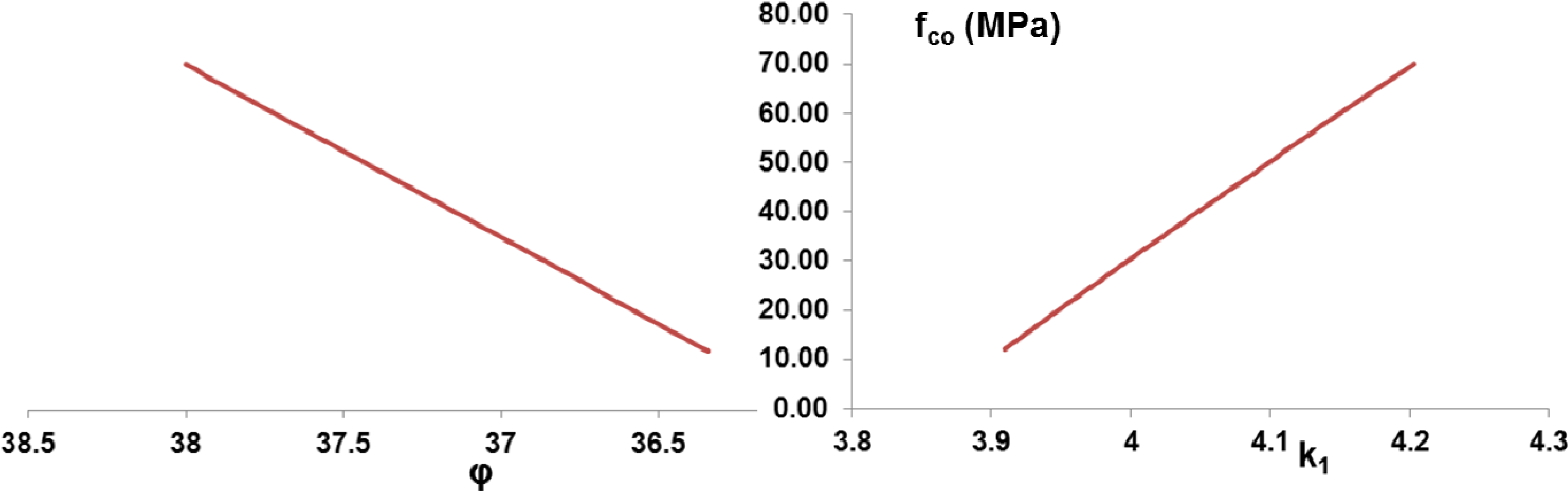
2.2.2. Novel Model for “Effective” Confining Pressure
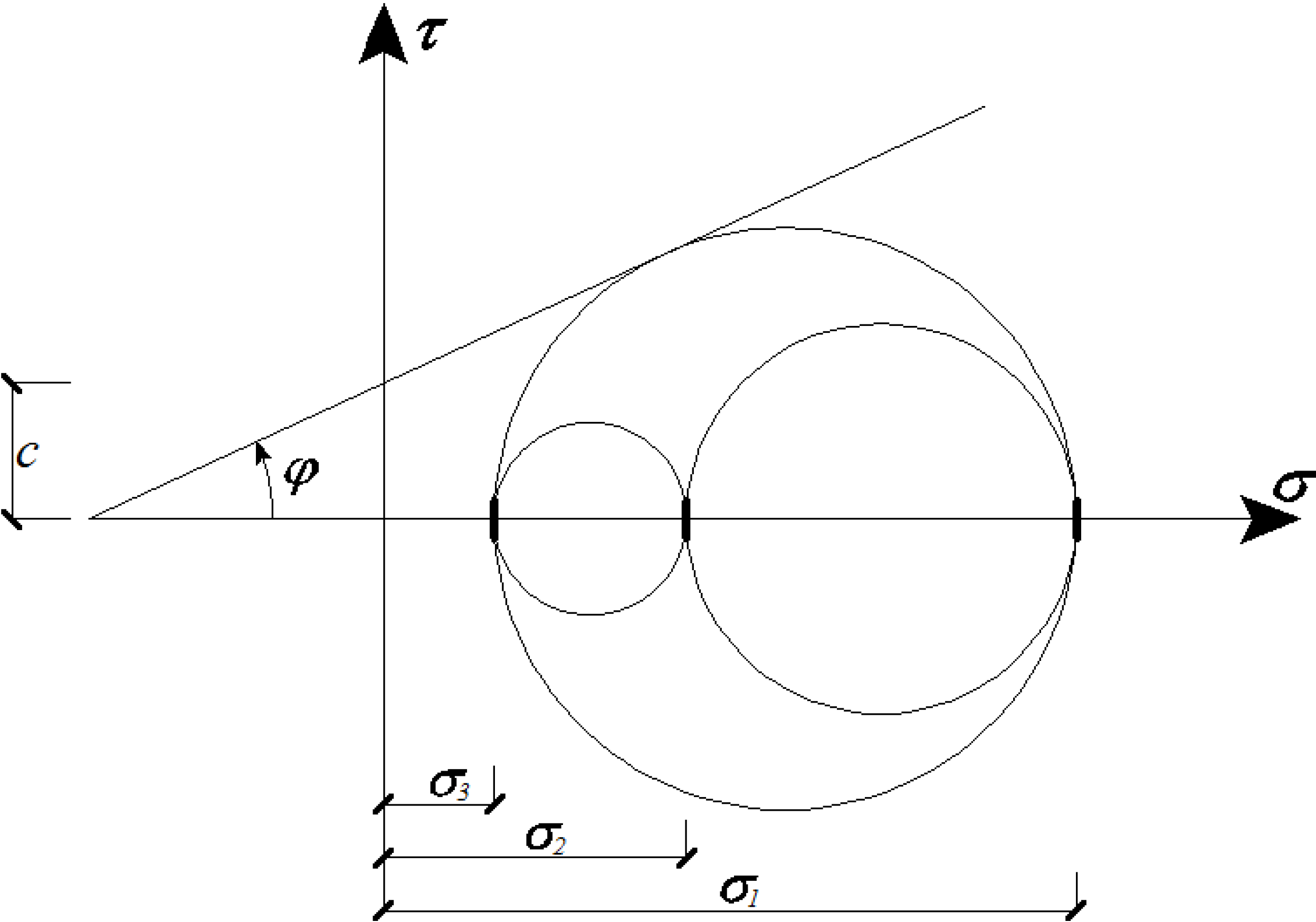
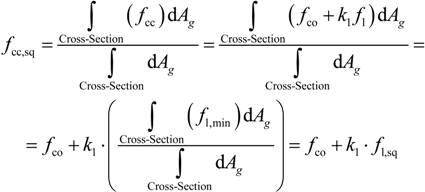
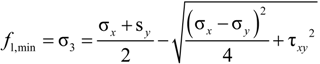
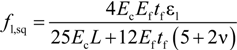
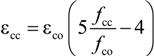
3. Proposed Simplified Confinement Model for Rectangular Sections
3.1. Implementation of the Model

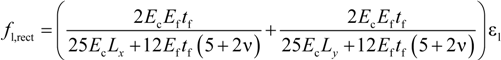
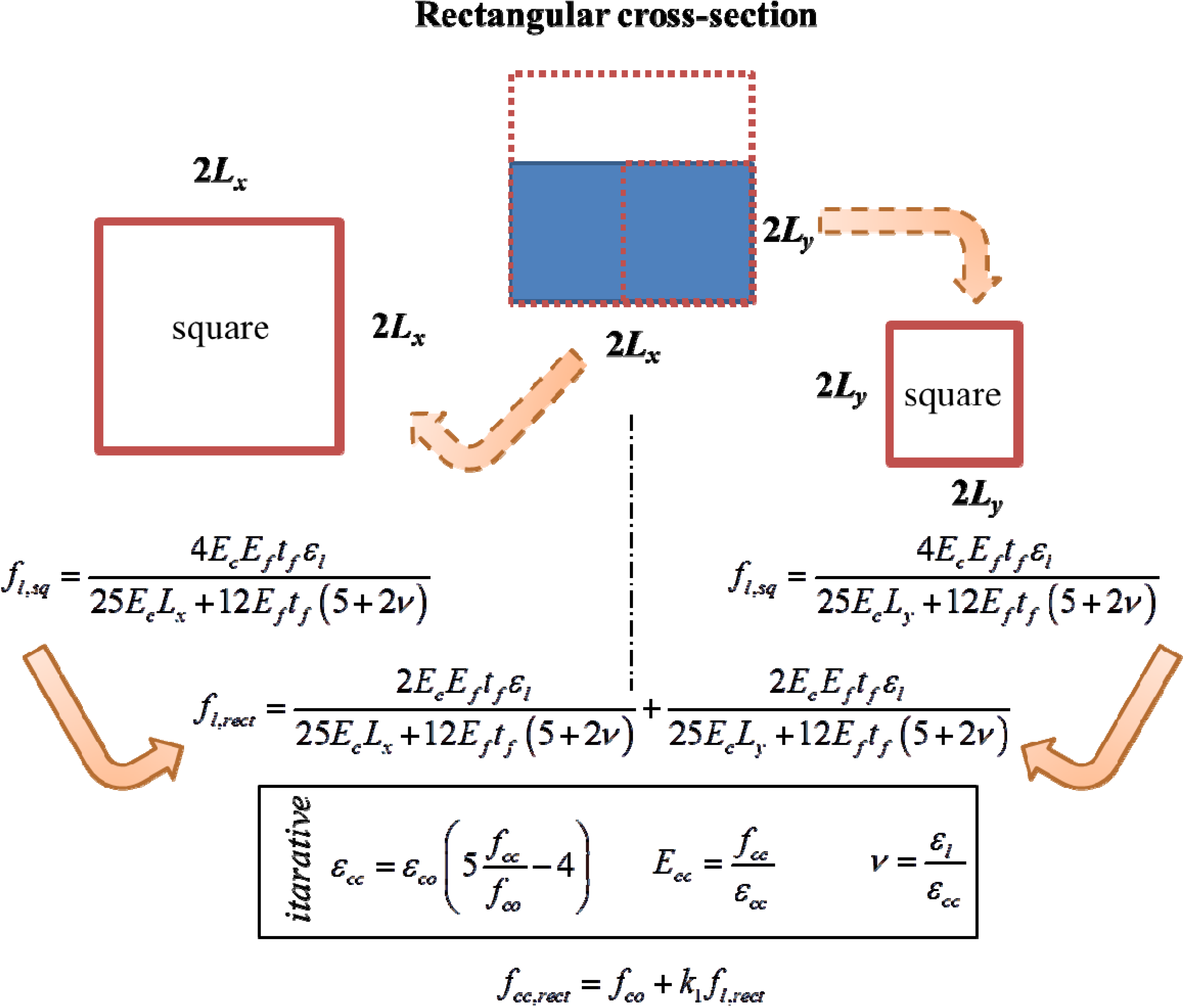
3.2. Validation of the Model
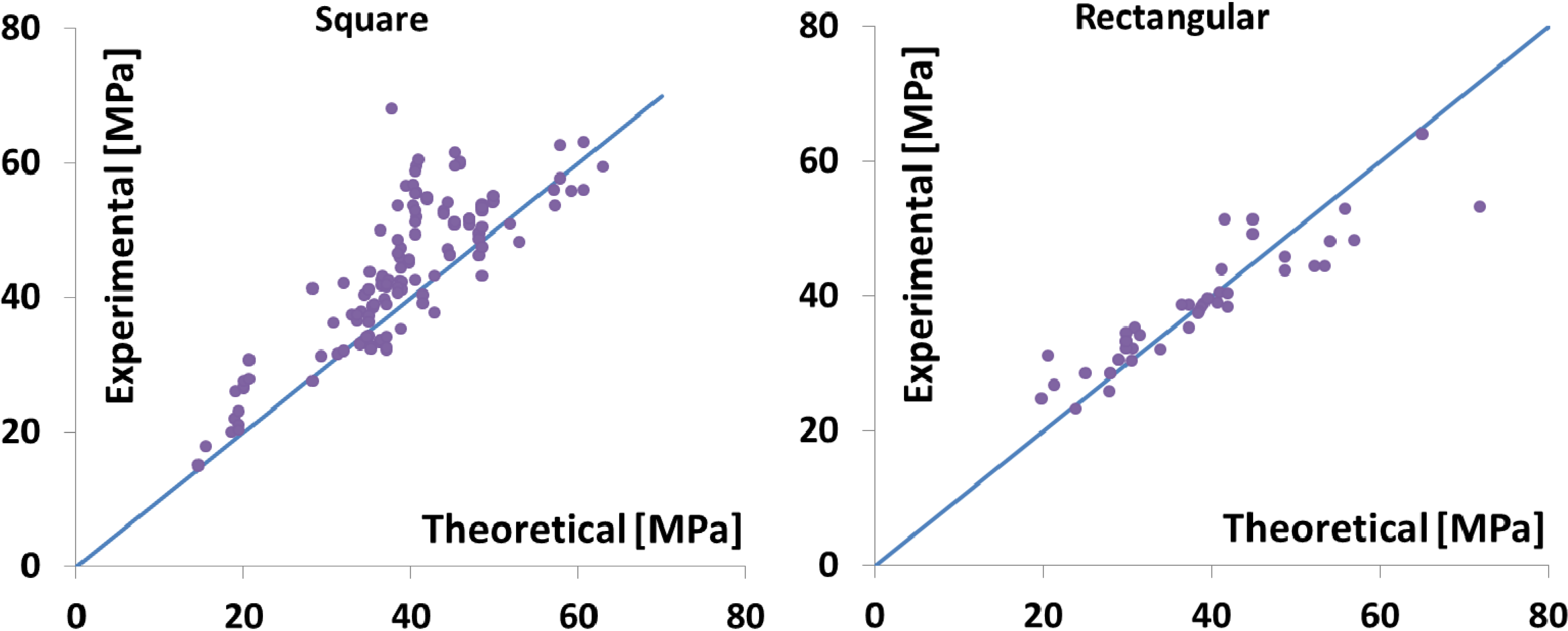
| Ref. | fco (MPa) | 2 L (mm) | Fiber | tf (mm) | Ef (GPa) | εl (%) | fcc, EXP (MPa) | fl, sq (MPa) | fcc, sq (MPa) | THEOR. EXP. |
|---|---|---|---|---|---|---|---|---|---|---|
| Campione (2006) [23] | 12.0 | 150 | CFRP | 0.165 | 230.0 | 1.50 | 15.1 | 0.84 | 15.27 | 1.01 |
| 12.0 | 150 | CFRP | 0.330 | 230.0 | 1.50 | 17.8 | 1.20 | 16.67 | 0.94 | |
| Rousakis et al. (2007) [24] | 33.0 | 200 | CFRP | 0.117 | 240.0 | 1.55 | 38.4 | 0.66 | 35.69 | 0.93 |
| 33.0 | 200 | CFRP | 0.117 | 240.0 | 1.55 | 38.8 | 0.66 | 35.69 | 0.92 | |
| 33.0 | 200 | CFRP | 0.351 | 240.0 | 1.55 | 45.9 | 1.72 | 39.94 | 0.87 | |
| 33.0 | 200 | CFRP | 0.351 | 240.0 | 1.55 | 42.4 | 1.72 | 39.94 | 0.94 | |
| 33.0 | 200 | CFRP | 0.585 | 240.0 | 1.55 | 55.6 | 2.48 | 42.98 | 0.77 | |
| 33.0 | 200 | CFRP | 0.585 | 240.0 | 1.55 | 59.5 | 2.48 | 42.98 | 0.72 | |
| 33.0 | 200 | GFRP | 0.351 | 65.0 | 2.80 | 42.6 | 0.97 | 36.94 | 0.87 | |
| 33.0 | 200 | GFRP | 0.351 | 65.0 | 2.80 | 41.8 | 0.97 | 36.94 | 0.88 | |
| 33.0 | 200 | GFRP | 0.702 | 65.0 | 2.80 | 44.4 | 1.83 | 40.37 | 0.91 | |
| 33.0 | 200 | GFRP | 0.702 | 65.0 | 2.80 | 47.3 | 1.83 | 40.37 | 0.85 | |
| 33.0 | 200 | GFRP | 1.053 | 65.0 | 2.80 | 51.9 | 2.56 | 43.29 | 0.83 | |
| 33.0 | 200 | GFRP | 1.053 | 65.0 | 2.80 | 55.5 | 2.56 | 43.29 | 0.78 | |
| 34.2 | 200 | CFRP | 0.117 | 240.0 | 1.55 | 42.2 | 0.66 | 36.84 | 0.87 | |
| 34.2 | 200 | CFRP | 0.117 | 240.0 | 1.55 | 41.9 | 0.66 | 36.84 | 0.88 | |
| 34.2 | 200 | CFRP | 0.351 | 240.0 | 1.55 | 45.2 | 1.71 | 41.07 | 0.91 | |
| 34.2 | 200 | CFRP | 0.351 | 240.0 | 1.55 | 45.7 | 1.71 | 41.07 | 0.90 | |
| 34.2 | 200 | CFRP | 0.585 | 240.0 | 1.55 | 54.6 | 2.46 | 44.06 | 0.81 | |
| 34.2 | 200 | CFRP | 0.585 | 240.0 | 1.55 | 54.9 | 2.46 | 44.06 | 0.80 | |
| 38.0 | 200 | GFRP | 0.351 | 65.0 | 2.80 | 40.4 | 0.97 | 41.88 | 1.04 | |
| 38.0 | 200 | GFRP | 0.351 | 65.0 | 2.80 | 39.1 | 0.97 | 41.88 | 1.07 | |
| 38.0 | 200 | GFRP | 0.702 | 65.0 | 2.80 | 52.8 | 1.81 | 45.28 | 0.86 | |
| 38.0 | 200 | GFRP | 0.702 | 65.0 | 2.80 | 52.4 | 1.81 | 45.28 | 0.86 | |
| 38.0 | 200 | GFRP | 1.053 | 65.0 | 2.80 | 59.8 | 2.52 | 48.14 | 0.81 | |
| 38.0 | 200 | GFRP | 1.053 | 65.0 | 2.80 | 60.2 | 2.52 | 48.14 | 0.80 | |
| 39.9 | 200 | GFRP | 0.351 | 65.0 | 2.80 | 43.1 | 0.78 | 43.06 | 1.00 | |
| 39.9 | 200 | GFRP | 0.351 | 65.0 | 2.80 | 37.7 | 0.78 | 43.06 | 1.14 | |
| 39.9 | 200 | GFRP | 0.702 | 65.0 | 2.80 | 54.2 | 1.21 | 44.79 | 0.83 | |
| 39.9 | 200 | GFRP | 0.702 | 65.0 | 2.80 | 47.1 | 1.21 | 44.79 | 0.95 | |
| 39.9 | 200 | GFRP | 1.053 | 65.0 | 2.80 | 59.5 | 1.46 | 45.82 | 0.77 | |
| 39.9 | 200 | GFRP | 1.053 | 65.0 | 2.80 | 61.5 | 1.46 | 45.82 | 0.74 | |
| Wang and Wu (2008) [25] | 31.7 | 150 | CFRP | 0.165 | 219.0 | 1.99 | 33.2 | 1.35 | 37.09 | 1.12 |
| 31.7 | 150 | CFRP | 0.330 | 219.0 | 1.99 | 35.2 | 2.30 | 40.90 | 1.16 | |
| 52.1 | 150 | CFRP | 0.165 | 225.7 | 1.92 | 53.7 | 1.42 | 57.91 | 1.08 | |
| 52.1 | 150 | CFRP | 0.330 | 225.7 | 1.92 | 55.9 | 2.58 | 62.67 | 1.12 | |
| 31.9 | 150 | CFRP | 0.165 | 219.0 | 1.99 | 33.6 | 1.35 | 37.29 | 1.11 | |
| 31.9 | 150 | CFRP | 0.330 | 219.0 | 1.99 | 42.2 | 2.31 | 41.12 | 0.97 | |
| 54.1 | 150 | CFRP | 0.165 | 225.7 | 1.92 | 55.8 | 1.42 | 59.94 | 1.07 | |
| 54.1 | 150 | CFRP | 0.330 | 225.7 | 1.92 | 59.4 | 2.60 | 64.77 | 1.09 | |
| 32.3 | 150 | CFRP | 0.165 | 219.0 | 1.99 | 39.8 | 1.35 | 37.71 | 0.95 | |
| 32.3 | 150 | CFRP | 0.330 | 219.0 | 1.99 | 56.5 | 2.32 | 41.56 | 0.74 | |
| 52.0 | 150 | CFRP | 0.165 | 225.7 | 1.92 | 55.9 | 1.42 | 57.81 | 1.03 | |
| 52.0 | 150 | CFRP | 0.330 | 225.7 | 1.92 | 63.0 | 2.58 | 62.56 | 0.99 | |
| 30.7 | 150 | CFRP | 0.165 | 219.0 | 1.99 | 43.7 | 1.34 | 36.05 | 0.83 | |
| 30.7 | 150 | CFRP | 0.330 | 219.0 | 1.99 | 68.0 | 2.28 | 39.80 | 0.59 | |
| 52.7 | 150 | CFRP | 0.165 | 225.7 | 1.92 | 57.6 | 1.42 | 58.52 | 1.02 | |
| 52.7 | 150 | CFRP | 0.330 | 225.7 | 1.92 | 80.3 | 2.58 | 63.30 | 0.79 | |
| 31.8 | 150 | CFRP | 0.165 | 219.0 | 1.99 | 50.0 | 1.35 | 37.19 | 0.74 | |
| 52.7 | 150 | CFRP | 0.165 | 225.7 | 1.92 | 62.6 | 1.42 | 58.52 | 0.93 | |
| 52.7 | 150 | CFRP | 0.330 | 225.7 | 1.92 | 89.8 | 2.58 | 63.30 | 0.70 | |
| Harries and Carey (2003) [26] | 32.4 | 152 | GFRP | 3.000 | 4.9 | 1.60 | 37.9 | 0.47 | 34.28 | 0.90 |
| 32.4 | 152 | GFRP | 9.000 | 4.9 | 1.60 | 43.2 | 1.23 | 37.30 | 0.86 | |
| 31.2 | 152 | GFRP | 3.000 | 4.9 | 1.60 | 37.4 | 0.48 | 33.11 | 0.89 | |
| 31.2 | 152 | GFRP | 9.000 | 4.9 | 1.60 | 39.0 | 1.31 | 36.43 | 0.93 | |
| Shehata et al. (2002) [27] | 23.7 | 150 | CFRP | 0.165 | 355.0 | 1.50 | 27.5 | 1.47 | 29.53 | 1.07 |
| 29.5 | 150 | CFRP | 0.165 | 355.0 | 1.50 | 40.4 | 1.55 | 35.69 | 0.88 | |
| Lam et al. (2006) [28] | 35.3 | 150 | CFRP | 0.167 | 230.0 | 1.50 | 41.2 | 1.02 | 39.39 | 0.96 |
| 35.3 | 150 | CFRP | 0.334 | 230.0 | 1.50 | 60.4 | 1.66 | 41.98 | 0.69 | |
| Ilki and Kumbasar (2003) [29] | 32.8 | 250 | CFRP | 0.165 | 230.0 | 1.50 | 32.7 | 0.68 | 35.53 | 1.09 |
| 32.8 | 250 | CFRP | 0.165 | 230.0 | 1.50 | 32.3 | 0.68 | 35.53 | 1.10 | |
| 32.8 | 250 | CFRP | 0.495 | 230.0 | 1.50 | 41.4 | 1.72 | 39.69 | 0.96 | |
| 32.8 | 250 | CFRP | 0.495 | 230.0 | 1.50 | 40.6 | 1.72 | 39.69 | 0.98 | |
| 32.8 | 250 | CFRP | 0.825 | 230.0 | 1.50 | 56.7 | 2.41 | 42.46 | 0.75 | |
| 32.8 | 250 | CFRP | 0.825 | 230.0 | 1.50 | 53.6 | 2.41 | 42.46 | 0.79 | |
| Al-Salloum (2006) [30] | 28.7 | 150 | CFRP | 1.200 | 75.1 | 1.50 | 41.2 | 1.99 | 36.62 | 0.89 |
| 30.9 | 150 | CFRP | 1.200 | 75.1 | 1.50 | 42.5 | 2.04 | 39.06 | 0.92 | |
| Harajli (2006) [31] | 42.0 | 152 | CFRP | 0.900 | 82.0 | 1.50 | 49.5 | 1.77 | 49.17 | 0.99 |
| 42.0 | 152 | CFRP | 0.900 | 82.0 | 1.50 | 46.2 | 1.77 | 49.17 | 1.06 | |
| 42.0 | 152 | CFRP | 0.900 | 82.0 | 1.50 | 48.7 | 1.77 | 49.17 | 1.01 | |
| Masia et al. (2004) [32] | 26.3 | 152 | GFRP | 1.000 | 19.1 | 2.40 | 31.3 | 0.89 | 29.83 | 0.95 |
| 26.3 | 152 | GFRP | 2.000 | 19.1 | 2.40 | 31.6 | 1.60 | 32.66 | 1.03 | |
| 26.3 | 152 | GFRP | 1.000 | 19.1 | 1.50 | 41.3 | 0.56 | 28.53 | 0.69 | |
| Mandal et al. (2005) [33] | 31.5 | 458 | GFRP | 3.000 | 19.1 | 1.50 | 36.5 | 0.56 | 33.76 | 0.92 |
| 31.5 | 458 | GFRP | 3.000 | 19.1 | 1.50 | 37.5 | 0.56 | 33.76 | 0.90 | |
| 31.9 | 152 | GFRP | 3.000 | 10.3 | 1.50 | 37.3 | 0.88 | 35.41 | 0.95 | |
| 31.9 | 152 | GFRP | 3.000 | 10.3 | 1.50 | 36.4 | 0.88 | 35.41 | 0.97 | |
| 31.9 | 152 | GFRP | 3.000 | 10.3 | 1.50 | 34.1 | 0.88 | 35.41 | 1.04 | |
| 31.9 | 152 | GFRP | 9.000 | 10.3 | 1.50 | 53.6 | 2.03 | 40.03 | 0.75 | |
| 31.9 | 152 | GFRP | 9.000 | 10.3 | 1.50 | 46.6 | 2.03 | 40.03 | 0.86 | |
| 31.9 | 152 | GFRP | 9.000 | 10.3 | 1.50 | 48.5 | 2.03 | 40.03 | 0.83 | |
| Wang and Wu (2008) [25] | 15.0 | 279 | GFRP | 2.000 | 87.0 | 1.40 | 26.0 | 1.35 | 20.27 | 0.78 |
| 15.0 | 279 | GFRP | 9.600 | 17.0 | 1.40 | 22.0 | 1.31 | 20.14 | 0.92 | |
| Tao et al. (2008) [34] | 43.0 | 152 | GFRP | 1.260 | 13.6 | 1.69 | 50.7 | 0.59 | 45.38 | 0.89 |
| 43.0 | 152 | GFRP | 2.520 | 13.6 | 1.69 | 51.6 | 1.12 | 47.53 | 0.92 | |
| 43.0 | 152 | GFRP | 3.780 | 13.6 | 1.69 | 53.8 | 1.59 | 49.44 | 0.92 | |
| 43.0 | 152 | GFRP | 5.040 | 13.6 | 1.69 | 54.2 | 2.00 | 51.12 | 0.94 | |
| 43.0 | 152 | GFRP | 1.260 | 13.6 | 1.69 | 51.2 | 0.59 | 45.38 | 0.89 | |
| 43.0 | 152 | GFRP | 2.520 | 13.6 | 1.69 | 51.2 | 1.12 | 47.53 | 0.93 | |
| 43.0 | 152 | GFRP | 3.780 | 13.6 | 1.69 | 53.3 | 1.59 | 49.44 | 0.93 | |
| 43.0 | 152 | GFRP | 5.040 | 13.6 | 1.69 | 55.0 | 2.00 | 51.12 | 0.93 | |
| 43.0 | 152 | GFRP | 2.520 | 13.6 | 1.69 | 50.7 | 1.12 | 47.53 | 0.94 | |
| 43.0 | 152 | GFRP | 3.780 | 13.6 | 1.69 | 52.9 | 1.59 | 49.44 | 0.93 | |
| Micelli and Modarelli (2013) [35] | 28.0 | 150 | CFRP | 0.330 | 221.0 | 1.40 | 32.0 | 1.13 | 32.50 | 1.02 |
| 28.0 | 150 | CFRP | 0.165 | 221.0 | 1.40 | 36.2 | 0.77 | 31.06 | 0.86 | |
| 28.0 | 150 | CFRP | 0.330 | 221.0 | 1.40 | 42.1 | 1.13 | 32.50 | 0.77 | |
| Faella et al. (2004) [36] | 30.0 | 150 | GFRP | 0.480 | 80.7 | 3.50 | 32.1 | 2.42 | 39.65 | 1.23 |
| 30.0 | 150 | GFRP | 0.480 | 80.7 | 3.50 | 32.5 | 2.42 | 39.65 | 1.22 | |
| 30.0 | 150 | GFRP | 0.480 | 80.7 | 3.50 | 41.5 | 2.42 | 39.65 | 0.95 | |
| 30.0 | 150 | GFRP | 0.480 | 80.7 | 3.50 | 34.1 | 2.42 | 39.65 | 1.16 | |
| 30.0 | 150 | GFRP | 0.480 | 80.7 | 3.50 | 41.9 | 2.42 | 39.65 | 0.95 | |
| 30.0 | 150 | GFRP | 0.480 | 80.7 | 3.50 | 38.9 | 2.42 | 39.65 | 1.02 | |
| 30.0 | 150 | GFRP | 0.960 | 80.7 | 3.50 | 42.5 | 3.93 | 45.69 | 1.07 | |
| 30.0 | 150 | GFRP | 0.960 | 80.7 | 3.50 | 49.3 | 3.93 | 45.69 | 0.93 | |
| 30.0 | 150 | GFRP | 0.960 | 80.7 | 3.50 | 51.2 | 3.93 | 45.69 | 0.89 | |
| 30.0 | 150 | GFRP | 0.960 | 80.7 | 3.50 | 52.9 | 3.93 | 45.69 | 0.86 | |
| 30.0 | 150 | GFRP | 0.960 | 80.7 | 3.50 | 58.7 | 3.93 | 45.69 | 0.78 | |
| 30.0 | 150 | GFRP | 0.960 | 80.7 | 3.50 | 55.5 | 3.93 | 45.69 | 0.82 | |
| Ombres (2006) [37] | 17.4 | 150 | CFRP | 0.047 | 240.0 | 1.42 | 20.0 | 0.32 | 18.68 | 0.93 |
| 17.4 | 150 | CFRP | 0.094 | 240.0 | 1.42 | 23.1 | 0.60 | 19.76 | 0.85 | |
| 17.4 | 150 | CFRP | 0.094 | 240.0 | 1.42 | 21.1 | 0.60 | 19.76 | 0.94 | |
| 17.4 | 150 | CFRP | 0.094 | 240.0 | 1.42 | 20.2 | 0.60 | 19.76 | 0.98 | |
| 17.4 | 150 | CFRP | 0.141 | 240.0 | 1.42 | 26.4 | 0.82 | 20.66 | 0.78 | |
| 17.4 | 150 | CFRP | 0.141 | 240.0 | 1.42 | 26.8 | 0.82 | 20.66 | 0.77 | |
| 17.4 | 150 | CFRP | 0.141 | 240.0 | 1.42 | 27.5 | 0.82 | 20.66 | 0.75 | |
| 17.4 | 150 | CFRP | 0.188 | 240.0 | 1.42 | 30.6 | 1.01 | 21.40 | 0.70 | |
| 17.4 | 150 | CFRP | 0.188 | 240.0 | 1.42 | 27.9 | 1.01 | 21.40 | 0.77 | |
| 17.4 | 150 | CFRP | 0.188 | 240.0 | 1.42 | 30.7 | 1.01 | 21.40 | 0.70 | |
| Demers and Neale (1999) [38] | 32.3 | 152 | GFRP | 1.050 | 10.5 | 2.00 | 33.1 | 0.45 | 34.10 | 1.03 |
| 32.3 | 152 | GFRP | 1.050 | 10.5 | 2.00 | 33.0 | 0.45 | 34.10 | 1.03 | |
| 32.3 | 152 | CFRP | 0.900 | 25.0 | 1.50 | 34.1 | 0.66 | 34.96 | 1.03 | |
| 42.2 | 152 | CFRP | 0.900 | 25.0 | 1.50 | 46.4 | 0.68 | 44.94 | 0.97 | |
| 42.2 | 152 | CFRP | 0.900 | 25.0 | 1.50 | 46.3 | 0.68 | 44.94 | 0.97 | |
| Rochette and Labossiere (2000) [39] | 42.0 | 152 | CFRP | 0.900 | 82.7 | 1.50 | 43.2 | 1.93 | 49.81 | 1.15 |
| 42.0 | 152 | CFRP | 0.900 | 82.7 | 1.50 | 47.4 | 1.93 | 49.81 | 1.05 | |
| 42.0 | 152 | CFRP | 0.900 | 82.7 | 1.50 | 50.4 | 1.93 | 49.81 | 0.99 | |
| 43.9 | 152 | CFRP | 1.500 | 82.7 | 1.50 | 48.3 | 2.82 | 55.33 | 1.15 | |
| 43.9 | 152 | CFRP | 1.200 | 82.7 | 1.50 | 50.9 | 2.42 | 53.71 | 1.06 | |
| 43.0 | 152 | AFRP | 1.260 | 13.6 | 1.70 | 50.7 | 0.59 | 45.40 | 0.90 | |
| 43.0 | 152 | AFRP | 2.520 | 13.6 | 1.70 | 51.6 | 1.13 | 47.59 | 0.92 | |
| 43.0 | 152 | AFRP | 3.780 | 13.6 | 1.70 | 53.7 | 1.62 | 49.55 | 0.92 | |
| 43.0 | 152 | AFRP | 5.040 | 13.6 | 1.70 | 54.2 | 2.05 | 51.30 | 0.95 | |
| 43.0 | 152 | AFRP | 1.260 | 13.6 | 1.70 | 51.2 | 0.59 | 45.40 | 0.89 |
| Ref. | fco (MPa) | 2 Lx (mm) | 2 Ly (mm) | Fiber | tf (mm) | Ef (GPa) | εl (%) | fcc, EXP (MPa) | fl, rect (MPa) | fcc, rect (MPa) | THEOR. EXP. |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Lam et al. (2006) [28] | 35.3 | 188 | 150 | CFRP | 0.334 | 230.0 | 1.50 | 51.4 | 1.55 | 41.53 | 0.81 |
| 35.3 | 225 | 150 | CFRP | 0.334 | 230.0 | 1.50 | 43.9 | 1.47 | 41.20 | 0.94 | |
| 35.3 | 263 | 150 | CFRP | 0.334 | 230.0 | 1.50 | 40.5 | 1.40 | 40.93 | 1.01 | |
| 35.3 | 300 | 150 | CFRP | 0.334 | 230.0 | 1.50 | 39.0 | 1.35 | 40.72 | 1.04 | |
| 35.3 | 188 | 150 | CFRP | 0.167 | 230.0 | 1.50 | 38.8 | 0.93 | 39.05 | 1.01 | |
| 35.3 | 225 | 150 | CFRP | 0.167 | 230.0 | 1.50 | 38.4 | 0.87 | 38.81 | 1.01 | |
| 35.3 | 263 | 150 | CFRP | 0.167 | 230.0 | 1.50 | 37.7 | 0.83 | 38.63 | 1.02 | |
| 35.3 | 300 | 150 | CFRP | 0.167 | 230.0 | 1.50 | 37.4 | 0.79 | 38.49 | 1.03 | |
| Ilki and Kumbasar (2003) [29] | 34.0 | 300 | 150 | CFRP | 0.165 | 230.0 | 1.50 | 35.2 | 0.83 | 37.33 | 1.06 |
| 34.0 | 300 | 150 | CFRP | 0.165 | 230.0 | 1.50 | 38.7 | 0.83 | 37.33 | 0.96 | |
| 34.0 | 300 | 150 | CFRP | 0.495 | 230.0 | 1.50 | 40.4 | 2.00 | 42.00 | 1.04 | |
| 34.0 | 300 | 150 | CFRP | 0.495 | 230.0 | 1.50 | 38.4 | 2.00 | 42.00 | 1.09 | |
| 34.0 | 300 | 150 | CFRP | 0.825 | 230.0 | 1.50 | 49.2 | 2.71 | 44.88 | 0.91 | |
| 34.0 | 300 | 150 | CFRP | 0.825 | 230.0 | 1.50 | 51.3 | 2.71 | 44.88 | 0.87 | |
| Rochette and Laboissiere (2000) [39] | 42.0 | 203 | 152 | GFRP | 0.900 | 86.0 | 1.50 | 45.8 | 1.66 | 48.72 | 1.06 |
| 42.0 | 203 | 152 | GFRP | 0.900 | 86.0 | 1.50 | 43.7 | 1.66 | 48.72 | 1.11 | |
| 43.9 | 203 | 152 | GFRP | 1.500 | 86.0 | 1.50 | 44.3 | 2.36 | 53.49 | 1.21 | |
| 43.9 | 203 | 152 | GFRP | 1.200 | 86.0 | 1.50 | 44.4 | 2.05 | 52.23 | 1.18 | |
| Demers and Neale (1999) [38] | 17.6 | 200 | 150 | CFRP | 0.165 | 221.0 | 1.40 | 24.8 | 0.56 | 19.79 | 0.80 |
| 17.6 | 200 | 150 | CFRP | 0.330 | 221.0 | 1.40 | 31.2 | 0.75 | 20.54 | 0.66 | |
| 17.6 | 200 | 150 | GFRP | 0.460 | 86.0 | 2.30 | 26.8 | 0.95 | 21.35 | 0.80 | |
| Chaallal et al. (2003) [40] | 37.7 | 354 | 250 | GFRP | 0.600 | 60.0 | 1.30 | 39.6 | 0.47 | 39.61 | 1.00 |
| 22.8 | 635 | 318 | CFRP | 0.167 | 280.0 | 0.90 | 23.3 | 0.30 | 23.97 | 1.03 | |
| 22.8 | 635 | 318 | CFRP | 0.334 | 280.0 | 0.90 | 28.5 | 0.57 | 25.03 | 0.88 | |
| 24.1 | 1270 | 635 | CFRP | 3.173 | 280.0 | 0.90 | 35.2 | 1.72 | 30.92 | 0.88 | |
| Parving and Wang (2001) [41] | 46.4 | 510 | 360 | GFRP | 1.160 | 72.0 | 4.50 | 48.3 | 2.59 | 56.94 | 1.18 |
| 49.7 | 510 | 360 | GFRP | 2.900 | 72.0 | 4.50 | 53.2 | 5.42 | 71.86 | 1.35 | |
| 53.8 | 510 | 360 | GFRP | 1.200 | 77.0 | 4.40 | 64.0 | 2.73 | 65.01 | 1.02 | |
| 46.8 | 510 | 360 | GFRP | 0.960 | 80.0 | 4.20 | 52.9 | 2.23 | 55.90 | 1.06 | |
| 47.6 | 740 | 510 | GFRP | 0.960 | 80.0 | 4.20 | 48.1 | 1.60 | 54.11 | 1.13 | |
| Micelli and Modarelli (2013) [35] | 28.0 | 200 | 150 | CFRP | 0.165 | 221.0 | 1.40 | 30.3 | 0.63 | 30.50 | 1.01 |
| 28.0 | 200 | 150 | CFRP | 0.330 | 221.0 | 1.40 | 34.1 | 0.90 | 31.56 | 0.93 | |
| 28.0 | 200 | 150 | GFRP | 0.230 | 85.0 | 2.28 | 32.2 | 0.65 | 30.59 | 0.95 | |
| Ombres (2006) [37] | 27.1 | 300 | 150 | CFRP | 0.047 | 240.0 | 1.42 | 28.5 | 0.25 | 28.05 | 0.98 |
| 27.1 | 300 | 150 | CFRP | 0.047 | 240.0 | 1.42 | 28.5 | 0.25 | 28.05 | 0.98 | |
| 27.1 | 300 | 150 | CFRP | 0.094 | 240.0 | 1.42 | 30.5 | 0.49 | 29.00 | 0.95 | |
| 27.1 | 300 | 150 | CFRP | 0.094 | 240.0 | 1.42 | 30.5 | 0.49 | 29.00 | 0.95 | |
| 27.1 | 300 | 150 | CFRP | 0.141 | 240.0 | 1.42 | 34.4 | 0.72 | 29.90 | 0.87 | |
| 27.1 | 300 | 150 | CFRP | 0.141 | 240.0 | 1.42 | 33.3 | 0.72 | 29.90 | 0.90 | |
| 27.1 | 300 | 150 | CFRP | 0.141 | 240.0 | 1.42 | 32.2 | 0.72 | 29.90 | 0.93 | |
| Shehata et al. (2002) [27] | 23.7 | 188 | 94 | CFRP | 0.165 | 235.0 | 1.50 | 25.8 | 1.07 | 27.92 | 1.08 |
| 23.7 | 188 | 94 | CFRP | 0.330 | 235.0 | 1.50 | 33.2 | 1.58 | 29.95 | 0.90 | |
| 29.5 | 188 | 94 | CFRP | 0.165 | 235.0 | 1.50 | 32.0 | 1.14 | 34.05 | 1.06 | |
| 29.5 | 188 | 94 | CFRP | 0.330 | 235.0 | 1.50 | 38.7 | 1.76 | 36.52 | 0.94 |
4. Conclusions
Acknowledgments
Conflicts of Interest
References
- Di Ludovico, M.; Ceroni, F.; Lignola, G.P.; Prota, A.; Manfredi, G.; Cosenza, E. Externally Bonded Reinforced Concrete Structures. Wiley Encyclopedia of Composites, John Wiley & Sons, Inc.: Chichester, UK, 2012; pp. 1–17. [Google Scholar]
- Ozbakkaloglu, T.; Lim, J.C.; Vincent, T. FRP-confined concrete in circular sections: Review and assessment of stress–strain models. Eng. Struct. 2013, 49, 1068–1088. [Google Scholar] [CrossRef]
- Pham, T.; Hadi, M. Stress prediction model for FRP confined rectangular concrete columns with rounded corners. J. Compos. Constr. 2014. [Google Scholar] [CrossRef]
- Choi, E.; Jeon, J.; Cho, B.; Park, K. External jacket of FRP wire for confining concrete and its advantages. Eng. Struct. 2013, 56, 555–566. [Google Scholar] [CrossRef]
- Rousakis, T.C.; Tourtouras, I.S. RC columns of square section—Passive and active confinement with composite ropes. Compos. B Eng. 2014, 58, 573–581. [Google Scholar] [CrossRef]
- Richart, F.E.; Brandtzaeg, A.; Brown, R.L. A Study of the Failure of Concrete under Combined Compressive Stresses. University of Illinois Engineering Experimental Station: Champaign, IL, USA, 1928; Bulletin No. 185; Volume XXVI, No. 12. [Google Scholar]
- Elwi, A.A.; Murray, D.W. A 3D hypoelastic concrete constitutive relationship. J. Eng. Mech. Div. 1979, 105, 623–641. [Google Scholar]
- American Concrete Institute. Guide for the Design and Construction of Externally Bonded FRP Systems for Strengthening of Concrete Structure. ACI 440.2R-02; American Concrete Institute: Farmington Hill, MI, USA, 2002. [Google Scholar]
- Lignola, G.P.; Prota, A.; Manfredi, G.; Cosenza, E. Unified theory for confinement of RC solid and hollow circular columns. Compos. B Eng. 2008, 39, 1151–1160. [Google Scholar] [CrossRef]
- De Lorenzis, L.; Tepfers, R. Comparative study of models on confinement of concrete cylinders with fiber reinforced polymer composites. J. Compos. Constr. 2003, 7, 219–237. [Google Scholar] [CrossRef]
- American Concrete Institute. Guide for the Design and Construction of Externally Bonded FRP Systems for Strengthening of Concrete Structure. ACI 440.2R-08; American Concrete Institute: Farmington Hill, MI, USA, 2008. [Google Scholar]
- CEN European Standard EN 1998-3. Eurocode 8: Design of Structures for Earthquake Resistance—Part 3: Assessment and Retrofitting of Buildings. European Committee for Standardization: Brussels, Belgium, 2005. [Google Scholar]
- CNR-DT 200 R1. Guide for the Design and Construction of Externally Bonded FRP Systems for Strengthening Existing Structures. National Research Council: Rome, Italy, 2013. [Google Scholar]
- Braga, F.; Gigliotti, R.; Laterza, M. Analytical stress–strain relationship for concrete confined by steel stirrups and/or FRP jackets. J. Struct. Eng. 2006, 132, 1402–1416. [Google Scholar] [CrossRef]
- D’Amato, M.; Braga, F.; Gigliotti, R.; Kunnath, S.; Laterza, M. A numerical general-purpose confinement model for non-linear analysis of R/C members. Comput. Struct. 2012, 102–103, 64–75. [Google Scholar] [CrossRef]
- Lignola, G.P.; Prota, A.; Manfredi, G.; Cosenza, E. Performance of FRP confinement on non circular members. In Proceedings of The 3rd fib Congress 2010, Washington, DC, USA, 29 May–2 June 2010.
- Goodman, R.E. Introduction to Rock Mechanics. John Wiley & Sons: Hoboken, NJ, USA, 1989. [Google Scholar]
- Li, Y.; Lin, C.; Sung, Y. A Constitute model for concrete confined with carbon fibre reinforced plastics. Mech. Mater. 2003, 35, 603–619. [Google Scholar] [CrossRef]
- Teng, J.G.; Huang, Y.L.; Lam, L.; Ye, L.P. Theoretical model for fiber reinforced polymer-confined concrete. ASCE J. Compos. Constr. 2007, 11, 201–210. [Google Scholar] [CrossRef]
- Moran, D.A.; Pantelides, C.P. Elliptical and circular FRP-confined concrete sections: A Mohr–Coulomb analytical model. Int. J. Solids Struct. 2012, 49, 881–898. [Google Scholar] [CrossRef]
- Girgin, Z.C. Modified johnston failure criterion from rock mechanics to predict the ultimate strength of fiber reinforced polymer (FRP) confined columns. Polymers 2014, 6, 59–75. [Google Scholar] [CrossRef]
- Lignola, G.P.; Nardone, F.; Prota, A.; de Luca, A.; Nanni, A. Analysis of RC hollow columns strengthened with GFRP. ASCE J. Compos. Constr. 2011, 15, 545–556. [Google Scholar] [CrossRef]
- Campione, G. Influence of FRP wrapping techniques on the compressive behaviour of concrete prisms. Cem. Concr. Compos. 2006, 28, 497–505. [Google Scholar] [CrossRef]
- Rousakis, T.C.; Karabinis, A.I.; Kiousis, P.D. FRP-confined concrete members: Axial compression experiments and plasticity modelling. Eng. Struct. 2007, 29, 1343–1353. [Google Scholar] [CrossRef]
- Wang, L.M.; Wu, Y.F. Effect of corner radius on the performance of CFRP-confined square concrete columns: Test. Eng. Struct. 2008, 30, 493–505. [Google Scholar] [CrossRef]
- Harries, K.A.; Carey, S.A. Shape and “gap” effects on the behaviour of variably confined concrete. Cem. Concr. Res. 2003, 33, 881–890. [Google Scholar] [CrossRef]
- Shehata, I.A.E.M.; Carneinro, L.A.V.; Shehata, L.C.D. Strength of short concrete columns confined with CFRP sheet. Mater. Struct. 2002, 35, 50–58. [Google Scholar] [CrossRef]
- Lam, L.; Teng, J.G.; Cheung, C.H.; Xiao, Y. FRP-confined concrete under cyclic axial compression. Cem. Concr. Compos. 2006, 28, 949–958. [Google Scholar] [CrossRef]
- Ilki, A.; Kumbasar, N. Compressive behaviour of carbon fibre and non-circular cross-sections. J. Earthq. Eng. 2003, 7, 381–406. [Google Scholar]
- Al-Salloum, Y.A. Influence of edge sharpness on the strength of square concrete columns confined with FRP composite laminates. Compos. B Eng. 2006, 38, 640–650. [Google Scholar] [CrossRef]
- Harajli, M.H. Axial stress-strain relationship for FRP confined circular and rectangular concrete columns. Cem. Concr. Compos. 2006, 28, 938–948. [Google Scholar] [CrossRef]
- Masia, M.J.; Gale, T.N.; Shrive, N.G. Size effects in axially loaded square section concrete prisms strengthened using carbon fiber reinforced polymer wrapping. Can. J. Civil. Eng. 2004, 31, 1–13. [Google Scholar] [CrossRef]
- Mandal, S.; Hoskin, A.; Fam, A. Influence of concrete strength on confinement effectiveness of fiber-reinforced polymer jackets. ACI Struct. J. 2005, 102, 383–392. [Google Scholar]
- Tao, Z.; Yu, Q.; Zhong, Y.-Z. Compressive behaviour of CFRP-confined rectangular concrete columns. Mag. Concr. Res. 2008, 60, 735–745. [Google Scholar] [CrossRef]
- Micelli, F.; Modarelli, R. Experimental and analytical study on properties affecting the behaviour of FRP-confined concrete. Compos. B 2013, 45, 1420–1431. [Google Scholar] [CrossRef]
- Faella, C.; Realfonzo, R.; Salerno, N. Sulla resistenza e deformazione di elementi in c.a. confinati con tessuti in FRP. In Proceedings of the Atti dell’XI Congresso Nazionale “L’ingegneria sismica in Italia”, Genova, Italy, 25–29 January 2004. (In Italian)
- Ombres, L. Influenza del sistema di rinforzo sul confinamento di elementi compressi in calcestruzzo rinforzato con FRP. In Proceedings of the Atti del 16° Congresso C.T.E., Parma, Italy, 9–11 November 2006. (In Italian)
- Demers, M.; Neale, K.W. Confinement of reinforced concrete columns with fibre-reinforced composite sheets-an experimental study. Can. J. Civ. Eng. 1999, 26, 226–241. [Google Scholar] [CrossRef]
- Rochette, P.; Labossiére, P. Axial testing of rectangular column models confined with composites. J. Compos. Constr. 2000, 4, 129–136. [Google Scholar] [CrossRef]
- Chaallal, O.; Shahawy, M.; Hassa, M. Performance of axially loaded short rectangular columns strengthened with carbon FRP wrapping. J. Compos. Constr. 2003, 7, 200–208. [Google Scholar] [CrossRef]
- Parvin, A.; Wang, W. Behavior of FRP jacketed concrete columns under eccentric loading. J. Compos. Constr. 2001, 5, 146–152. [Google Scholar] [CrossRef]
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Lignola, G.P.; Prota, A.; Manfredi, G. Simplified Modeling of Rectangular Concrete Cross-Sections Confined by External FRP Wrapping. Polymers 2014, 6, 1187-1206. https://doi.org/10.3390/polym6041187
Lignola GP, Prota A, Manfredi G. Simplified Modeling of Rectangular Concrete Cross-Sections Confined by External FRP Wrapping. Polymers. 2014; 6(4):1187-1206. https://doi.org/10.3390/polym6041187
Chicago/Turabian StyleLignola, Gian Piero, Andrea Prota, and Gaetano Manfredi. 2014. "Simplified Modeling of Rectangular Concrete Cross-Sections Confined by External FRP Wrapping" Polymers 6, no. 4: 1187-1206. https://doi.org/10.3390/polym6041187
APA StyleLignola, G. P., Prota, A., & Manfredi, G. (2014). Simplified Modeling of Rectangular Concrete Cross-Sections Confined by External FRP Wrapping. Polymers, 6(4), 1187-1206. https://doi.org/10.3390/polym6041187