Mechanical Analysis of Stress Distribution in a Carbon Fiber-Reinforced Polymer Rod Bonding Anchor
Abstract
:1. Introduction

2. Mechanical Analysis of Shear Stress Distribution
- All the materials are elastic: the stress state of the anchorage system remains elastic.
- Deformation of the metal barrel is not considered, because the stiffness of the barrel is much higher than that of the adhesive. Therefore, the internal surface of the barrel is considered fixed.
- Interface slippage is ignored, so that the displacement compatibility can be founded at the interface between the barrel and adhesive (hereinafter, called the first interface) and the interface between the adhesive and CFRP rods (hereinafter, called the second interface).
2.1. Single Rod

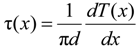
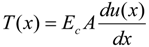
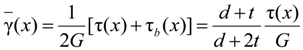
 . The general solution of Equation (6) is u(x) = C1ex + C2e−x. With boundary conditions at the free end of u(0) = 0 and the loading end T(l) = T0, the value of C1 and C2 can be calculated as below:
. The general solution of Equation (6) is u(x) = C1ex + C2e−x. With boundary conditions at the free end of u(0) = 0 and the loading end T(l) = T0, the value of C1 and C2 can be calculated as below:
2.2. Multiple Rods



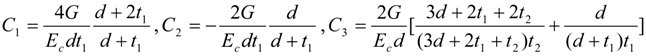
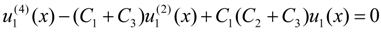
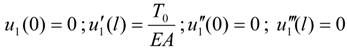
3. Finite Element Analysis of Shear Stress Distribution
3.1. Single Rod Anchor
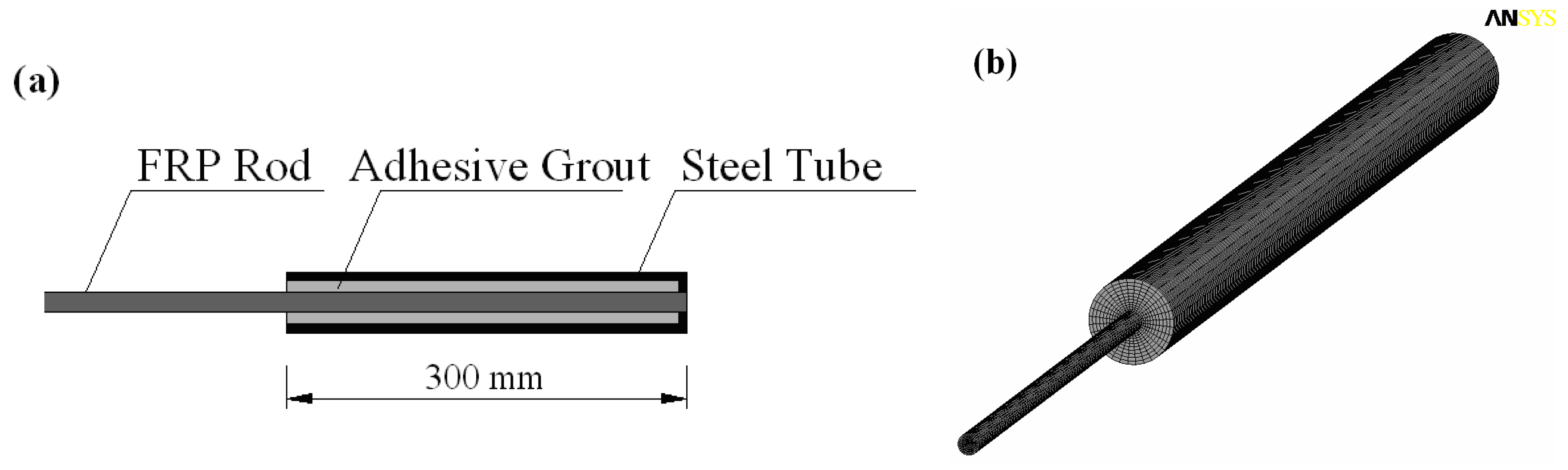
| Material | Ex | Ey, Ez | vxy, vxz | vyz | Gxy, Gxz | Gyz |
|---|---|---|---|---|---|---|
| CFRP rod | 181 | 10.05 | 0.28 | 0.3 | 7.17 | 7.17 |
| Steel | 200 | / | 0.27 | / | 78.74 | / |
| No. | 1 | 2 | 3 |
|---|---|---|---|
| Modulus of adhesive (GPa) | 5 | 5 | 2 |
| Thickness of adhesive (mm) | 2 | 5 | 5 |

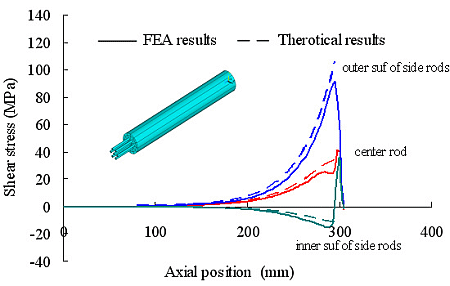
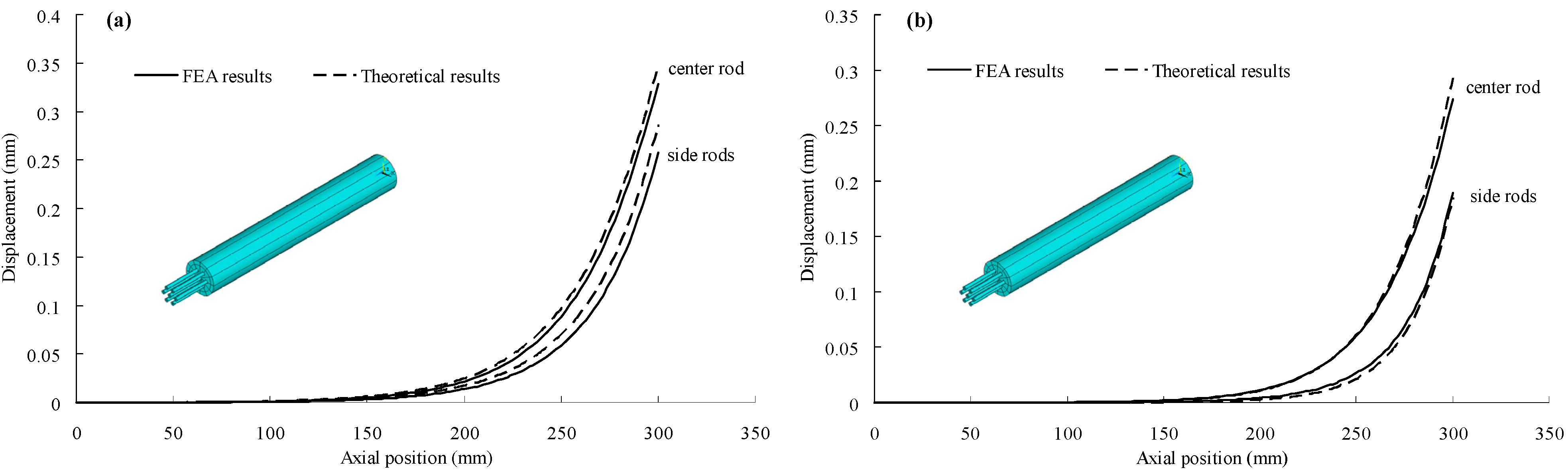
3.2. Multi-Rod Anchor
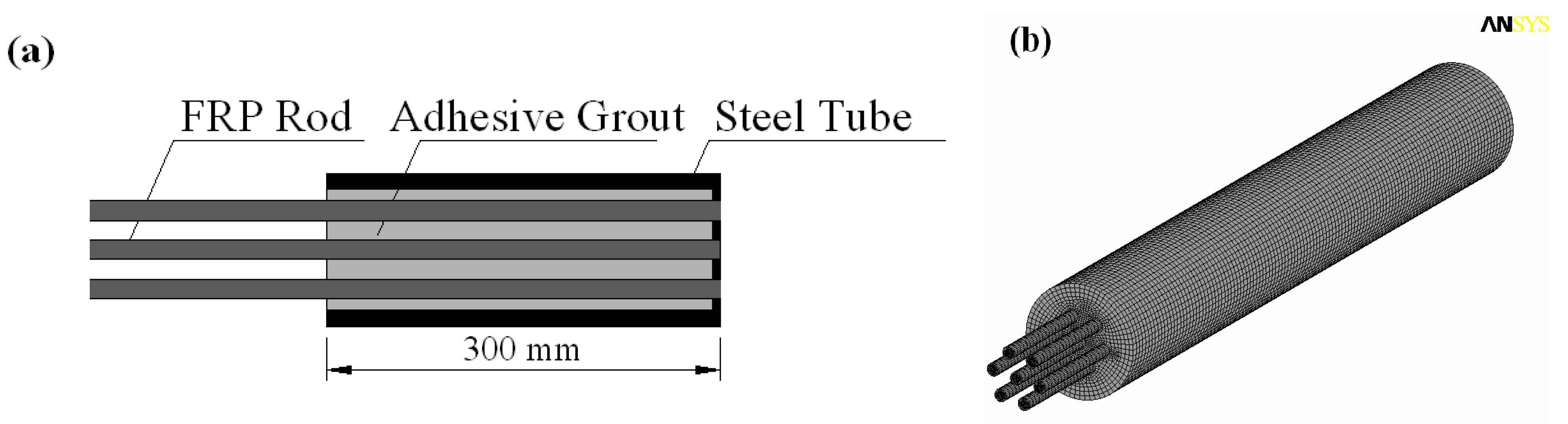
| No. | Thickness of adhesive Layer 1 (mm) | Thickness of adhesive Layer 2 (mm) |
|---|---|---|
| 1 | 5 | 5 |
| 2 | 8 | 2 |

4. Parametric Analysis of In-Cone Bonding Anchor
4.1. Design and Modeling of the Inner Cone Anchor

| Case No. | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|
| COF at the first interface | 0 | 0.05 | 0.1 | 0.2 | 0.05 | 0.05 | 0.05 |
| Inner inclined angle | 3% | 3% | 3% | 3% | 2% | 4% | Straight-parabolic |
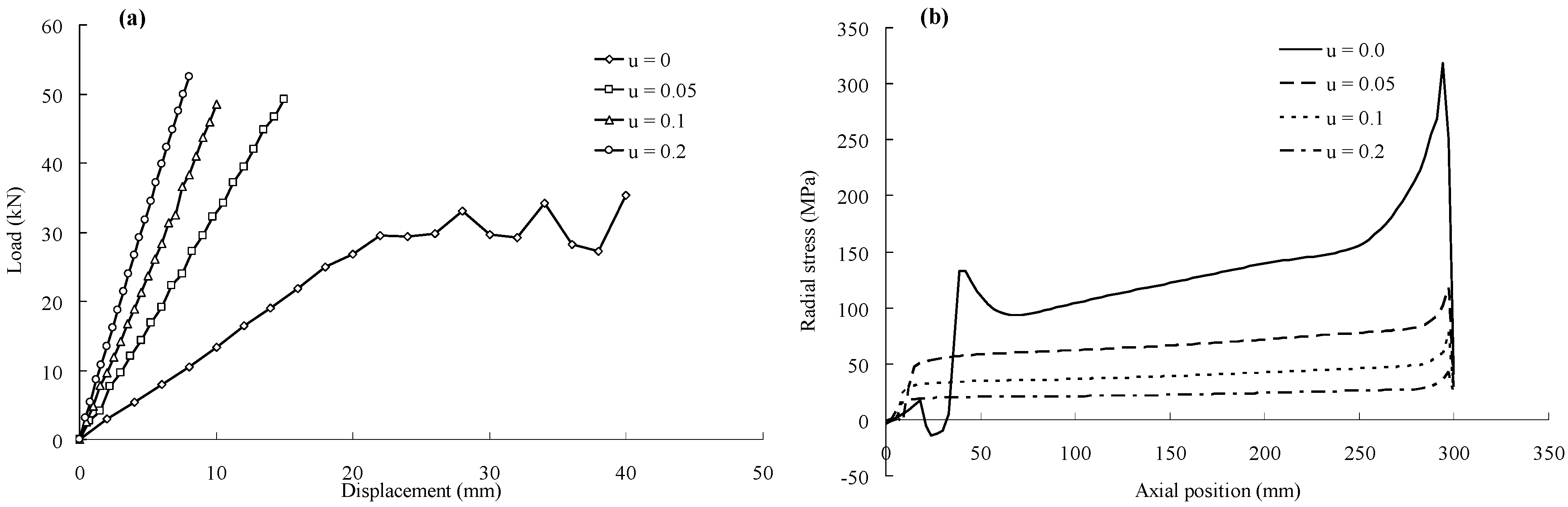
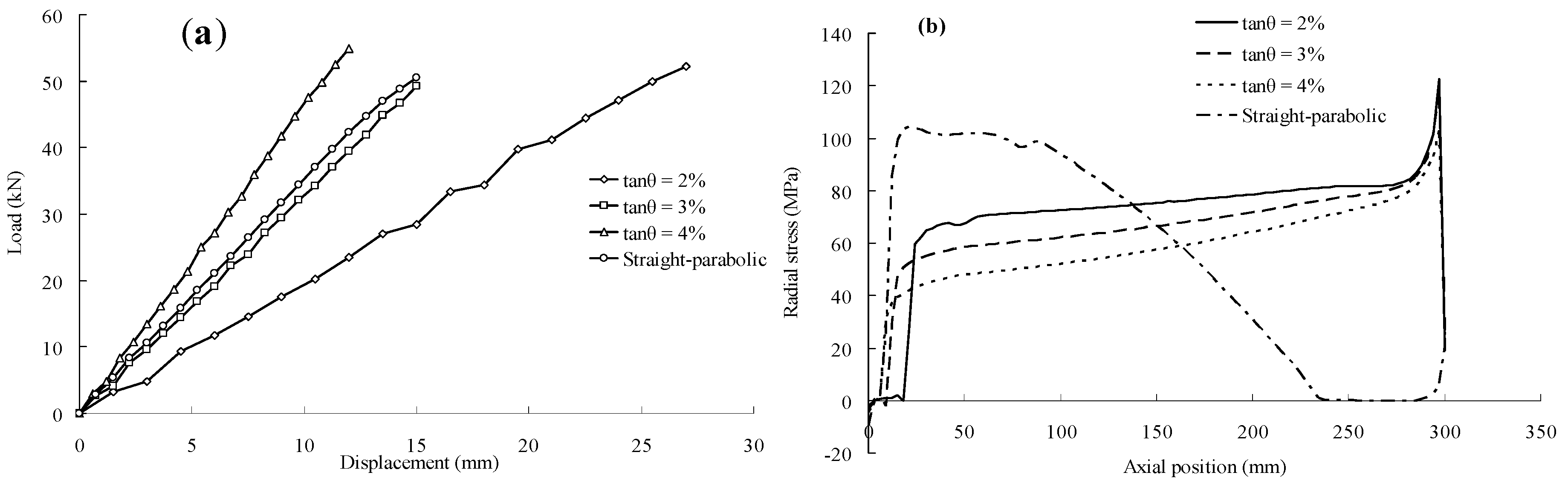
4.2. Numerical Results of Inner Cone Anchor

5. Conclusions
- With fundamental assumptions of elasticity and non-slip, a theoretical model for single and multiple rod bonding anchors is proposed by calculating the shear stress distribution on the rods. The theoretical equations are derived from the equilibrium and geometric conditions of the CFRP rods and adhesive. The theoretical model is suitable for preliminary shear stress analysis in the elastic state, and it can provide support for further study on decreasing the shear stress at the loading end cross-section of the anchorage.
- Finite element results show good agreement with the theoretical results, thus confirming the accuracy of the theory. For the single rod bonding anchor, as the modulus of the adhesive increases or the thickness of the adhesive decreases, the stiffness of the single rod and the peak value of the shear stress will increase. For multi-rod anchors, the stiffness and shear stress peak value will also increase as the space between the center rod and side rods increases. Anyway, the side rods have a complex stress state under tensile force, which may lead to premature failure. Therefore, the modulus and thickness of the adhesive, as well as the space between the rods need to be considered in the anchorage design. The modulus of the adhesive should be high enough to ensure the stiffness of the anchor, but not too high to cause shear or sliding failure. A thin adhesive layer can help to improve the anchorage performance on the condition that the bond strength is guaranteed. Small spacing between the rods is preferred in a multi-rod anchor, because the longitudinal radial stress is more uniform, and the influence on the side rods caused by asymmetry becomes smaller. The size of the anchorage can also be smaller.
- In the parametric analysis of the in-cone bonding anchor, as the coefficient of friction at the barrel-adhesive interface increases, the stiffness will increase and the radial compression will decrease, such that it will be more difficult for the steel barrel to yield under a certain load. The stiffness of the anchor also increases when the inner inclined angle increases, with the side effect that the radial pressure is more uneven. In the anchorage design, the inner inclined angle should be appropriate under the overall consideration of the stiffness and radial pressure.
- Straight-parabolic in-cone anchoring is shown to be an efficient way to reduce the concentrated shear stress and to improve the anchorage efficiency by moving the stress peak from the loading end to the free end. It can be a feasible type of anchorage for CFRP cable made up of parallel CFRP rods in engineering.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Feng, P.; Ye, L.P.; Teng, J.G. Large-span woven web structure made of fiber-reinforced polymer. J. Compos. Constr. 2007, 11, 110–119. [Google Scholar] [CrossRef]
- Qi, Y.J.; Feng, P.; Ye, L.P. Fundamental mechanical model and analysis of single layer FRP woven web structures. Eng. Mech. 2012, 29, 180–188. (In Chinese) [Google Scholar]
- Qi, Y.J.; Feng, P.; Ye, L.P.; Yang, J.Q. Model test of construction and formation of large-span FRP woven web structures. J. Build. Struct. 2012, 33, 117–126. (In Chinese) [Google Scholar]
- Qi, Y.J.; Feng, P.; Ye, L.P. Comparison of Theoretical Solutions and Ultimate Span-Length between FRP Cables and Steel Cables. J. Civ. Archit. Environ. Eng. 2011, 33, 52–59. (In Chinese) [Google Scholar]
- Wang, X.; Wu, Z.S. Integrated high-performance thousand-metre scale cable-stayed bridge with hybrid FRP cables. Compos. Part B Eng. 2010, 41, 166–175. [Google Scholar] [CrossRef]
- Nanni, A.; Bakis, C.E.; O’Neil, E.F.; Dixon, T.O. Performance of FRP tendon-anchor systems for prestressed concrete structures. PCI J. 1996, 41, 34–43. [Google Scholar]
- Sayed-Ahmed, E.Y.; Shrive, N.G. A new steel anchorage system for post-tensioning applications using carbon fiber reinforced plastic tendons. Can. J. Civ. Eng. 1998, 25, 113–127. [Google Scholar] [CrossRef]
- Campbell, T.I.; Shrive, N.G.; Soudki, K.A.; Al-Mayah, A.; Keatley, J.P.; Reda, M.M. Design and evaluation of a wedge-type anchor for fibre reinforced polymer tendons. Can. J. Civ. Eng. 2000, 27, 985–992. [Google Scholar] [CrossRef]
- Al-Mayah, A.; Soudki, K.A.; Plumtree, A. Experimental and analytical investigation of a stainless steel anchorage for CFRP prestressing tendons. PCI J. 2001, 46, 88–99. [Google Scholar]
- Al-Mayah, A.; Soudki, K.; Plumtree, A. Effect of sandblasting on interfacial contact behavior of carbon-fiber-reinforced polymer-metal couples. J. Compos. Constr. 2005, 9, 289–295. [Google Scholar] [CrossRef]
- Al-Mayah, A.; Soudki, K.; Plumtree, A. Effect of sleeve material on interfacial contact behavior of CFRP-metal couples. J. Mater. Civ. Eng. 2006, 18, 825–830. [Google Scholar] [CrossRef]
- Al-Mayah, A.; Soudki, K.; Plumtree, A. Novel anchor system for CFRP rod: Finite-element and mathematical models. J. Compos. Const. 2007, 11, 469–476. [Google Scholar] [CrossRef]
- Benmokrane, B.; Zhang, B.; Chennouf, A. Tensile properties and pullout behavior of AFRP and CFRP rods for grouted anchor applications. Constr. Build. Mater. 2000, 14, 157–170. [Google Scholar] [CrossRef]
- Zhang, B.; Benmokrane, B. Pullout bond properties of fiber-reinforced polymer tendons to grout. J. Mater. Civ. Eng. 2002, 14, 399–408. [Google Scholar] [CrossRef]
- Enomoto, T.; Ushijima, K. Use of CFCC tendons and reinforcements in concrete structures for durability. In Proceedings of Asia-Pacific Conference on FRP in Structures (APFIS) 2012, Hokkaido, Japan, 2–4 February 2012.
- Rohleder, W.J.; Tang, B.; Doe, T.A.; Grace, N.F.; Burgess, C.J. Carbon Fiber-Reinforced Polymer Strand Application on Cable-Stayed Bridge, Penobscot Narrows, Maine. Transp. Res. Rec. J. Transp. Res. Board 2008, 2050, 169–176. [Google Scholar] [CrossRef]
- Meier, U. Carbon Fiber Reinforced Polymer Cables: Why? Why Not? What If? Arab. J. Sci. Eng. 2009, 37, 399–411. [Google Scholar] [CrossRef]
- Zhang, B.; Benmokrane, B.; Chennouf, A. Prediction of tensile capacity of bond anchorages for FRP tendons. J. Compos. Constr. 2000, 4, 39–47. [Google Scholar] [CrossRef]
- Mei, K.H. Analysis of mechanical behavior of CFRP cable bonding anchors. Bridge Constr. 2007, 3, 80–83. (In Chinese) [Google Scholar]
- Zhu, G.P.; Ye, H.W.; Qiang, S.Z. Experimental investigation and mechanical behavior analysis of multiple CFRP tendons anchorage system. Eng. Mech. 2011, 28, 165–170. (In Chinese) [Google Scholar]
- Fang, Z.; Jiang, T.Y.; Liang, D. The Anchorage Behavior of CFRP Tendons in RPC. J. Hunan Univ. 2007, 34, 1–5. (In Chinese) [Google Scholar]
- Fang, Z.; Zhang, K.; Tu, B. Experimental investigation of a bond-type anchorage system for multiple FRP tendons. Eng. Struct. 2013, 57, 364–373. [Google Scholar] [CrossRef]
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Feng, P.; Zhang, P.; Meng, X.; Ye, L. Mechanical Analysis of Stress Distribution in a Carbon Fiber-Reinforced Polymer Rod Bonding Anchor. Polymers 2014, 6, 1129-1143. https://doi.org/10.3390/polym6041129
Feng P, Zhang P, Meng X, Ye L. Mechanical Analysis of Stress Distribution in a Carbon Fiber-Reinforced Polymer Rod Bonding Anchor. Polymers. 2014; 6(4):1129-1143. https://doi.org/10.3390/polym6041129
Chicago/Turabian StyleFeng, Peng, Pan Zhang, Xinmiao Meng, and Lieping Ye. 2014. "Mechanical Analysis of Stress Distribution in a Carbon Fiber-Reinforced Polymer Rod Bonding Anchor" Polymers 6, no. 4: 1129-1143. https://doi.org/10.3390/polym6041129
APA StyleFeng, P., Zhang, P., Meng, X., & Ye, L. (2014). Mechanical Analysis of Stress Distribution in a Carbon Fiber-Reinforced Polymer Rod Bonding Anchor. Polymers, 6(4), 1129-1143. https://doi.org/10.3390/polym6041129