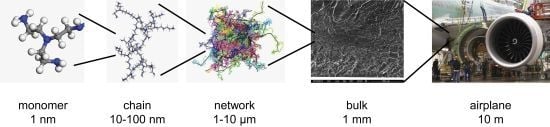
Challenges in Multiscale Modeling of Polymer Dynamics
Abstract
:1. Introduction

2. Overview of Multiscale Modeling Techniques
| Category | Method | Key references | Governing formulation |
|---|---|---|---|
| (i) | Bond-fluctuation method | [67,77] Section 3.1 | Monte Carlo |
| (i) | Finite-extensible non-linear elastic (FENE) Model | [78,79] Section 3.2 | molecular dynamics (MD) |
| (i) | Slip link model | [80,81] Section 3.3 | MD |
| (ii) | Iterative Boltzmann Inversion method | [82,83] Section 4.1 | MD |
| (ii) | Blob model | [84,85] Section 4.2 | MD |
| (ii) | Numerical super coarse-graining method | [86] Section 4.3 | MD |
| (ii) | Analytical super coarse-graining method | [87,88] Section 4.3 | MD |
| (iii) | Dynamic mapping onto tube model | [89] Section 5.1 | MD and primitive path (PP) analysis |
| (iii) | Molecularly-derived constitutive equation | [90] Section 5.2 | MD and continuum model |
| (iii) | Concurrent modeling of polymer melts | [91] Section 5.3 | MD and continuum model |
| (iii) | Hierarchical modeling of polymer rheology | [92] Section 5.4 | MD, PP analysis and continuum model |
| Category | Method | Approachable temporal and spatial scales | Predictable properties in the approachable scales | Acceleration |
|---|---|---|---|---|
| All-atomistic method | s and m | , , , , η | ||
| (i) | Bond-fluctuation model | m and no time scale | N/A | |
| (i) | FENE model | s and m | , , , , η | N/A |
| (i) | Slip link model | s and m | , , , , η | N/A |
| (ii) | Iterative Boltzmann Inversion method | s and m | ||
| (ii) | Blob model | s and m | , , , , η | |
| (ii) | Numerical super coarse-graining method | s and m | , , , , η | |
| (ii) | Analytical super coarse-graining method | s and m | ||
| (iii) | Dynamic mapping onto tube model | s and m | , , , , η | |
| (iii) | Molecularly-derived constitutive equation | s and m | , , , η | N/A |
| (iii) | Concurrent modeling of polymer melts | s and m | η | N/A |
| (iii) | Hierarchical modeling of polymer rheology | s and m | , , , , η |
3. Coarse-Graining Methods for Generic Polymers
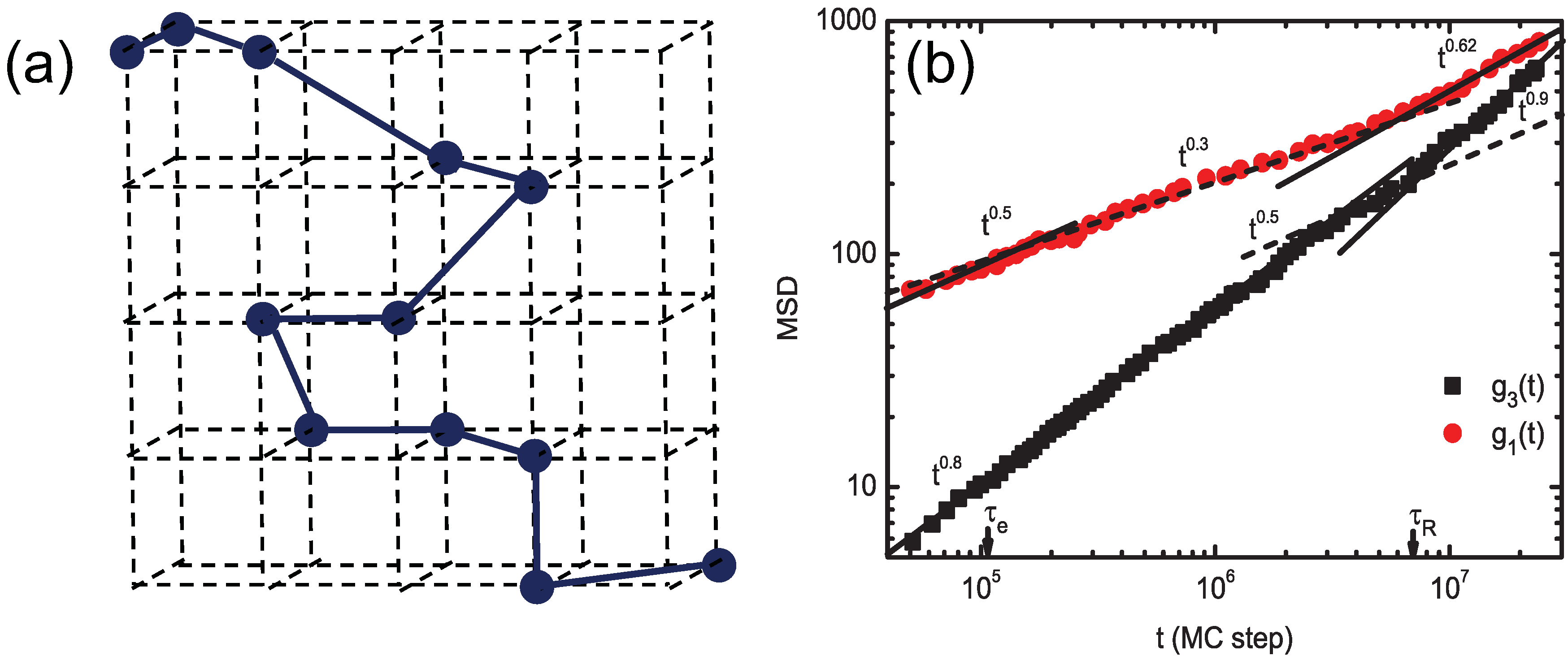
3.1. Bond-Fluctuation Method
3.2. FENE Model
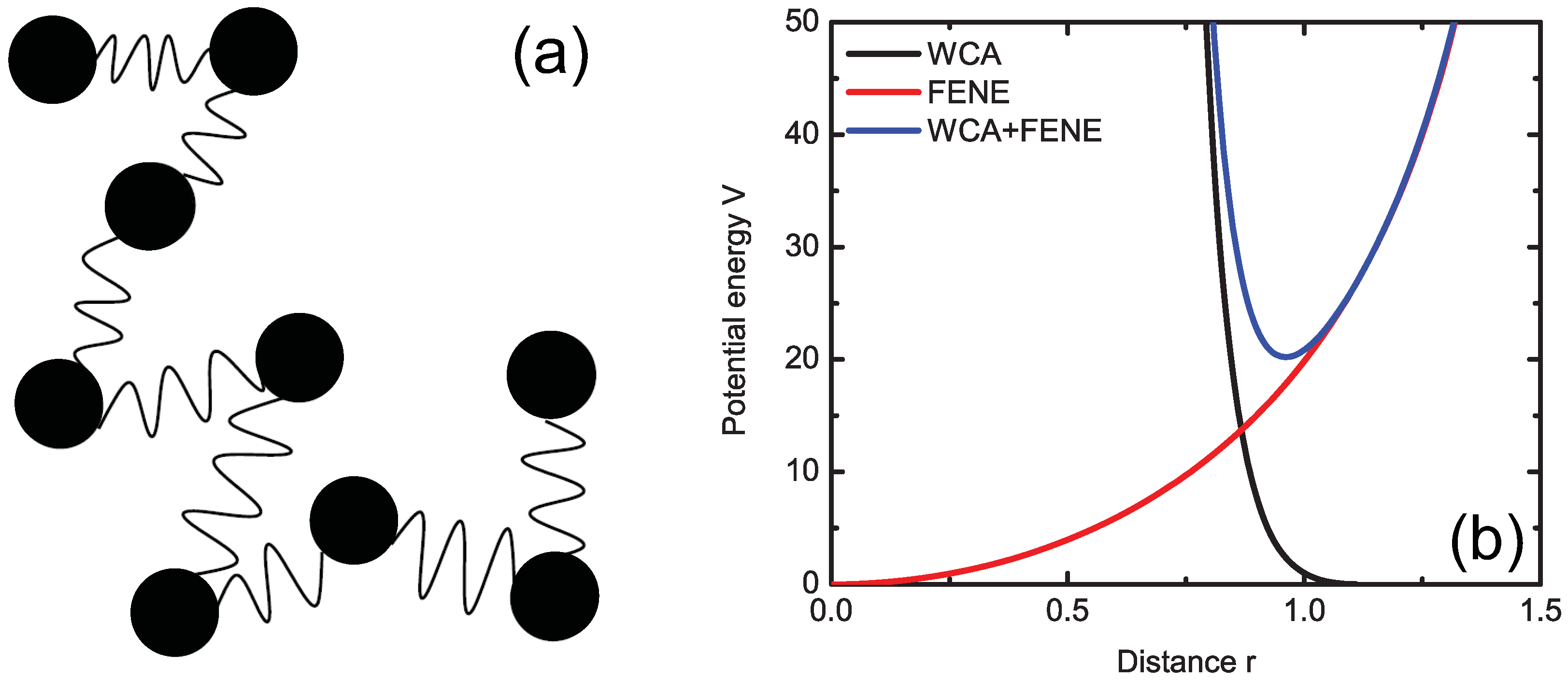
3.3. Slip-Link Model

4. Systematic Coarse-Graining Methods
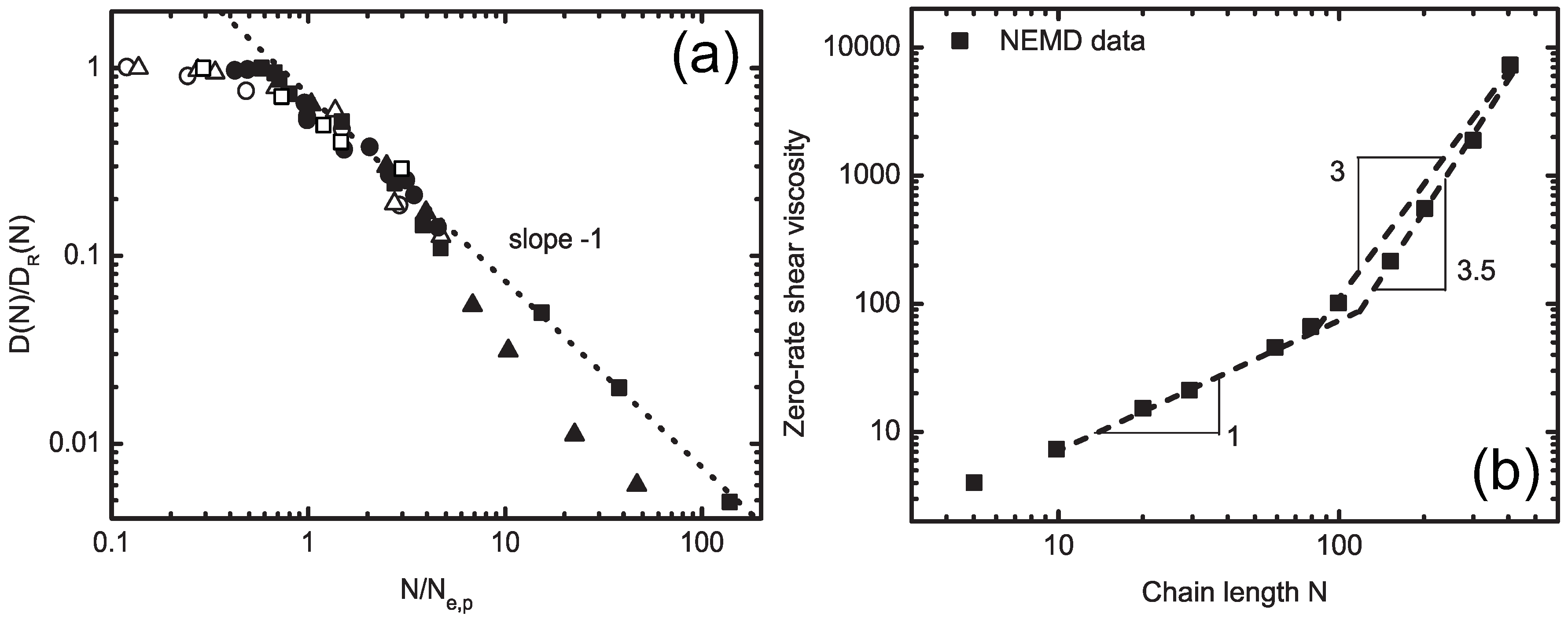
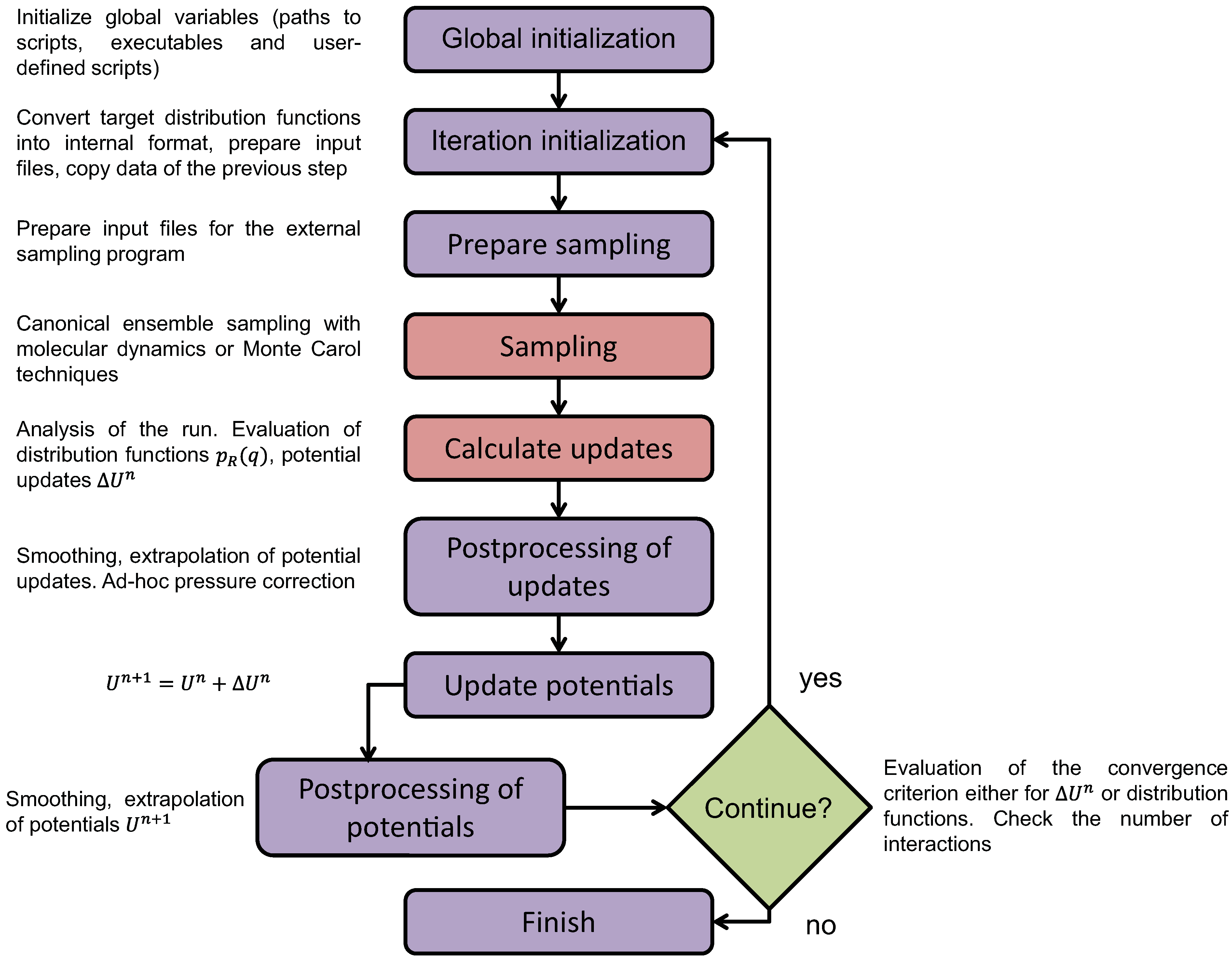
4.1. Iterative Boltzmann Inversion Method
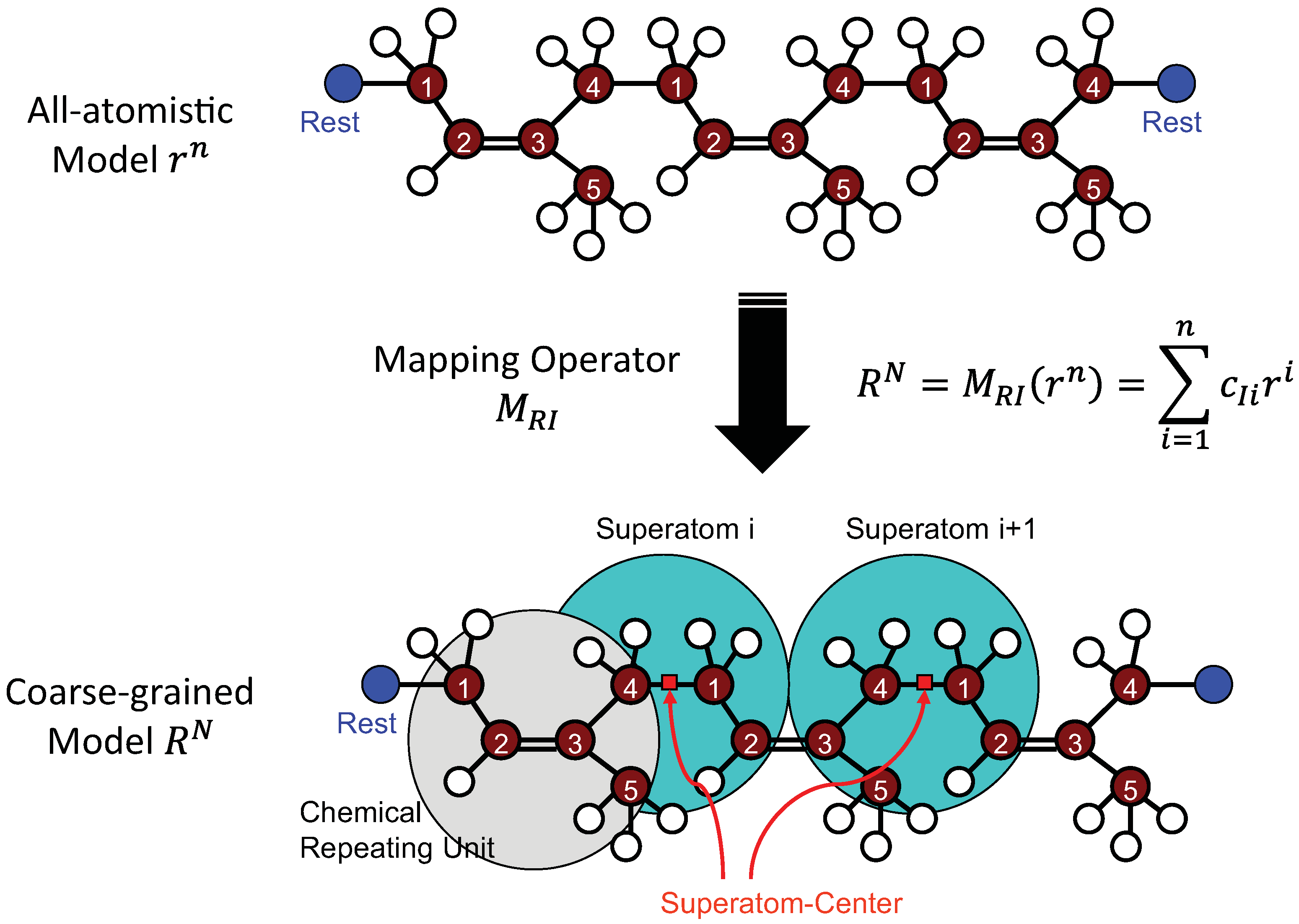
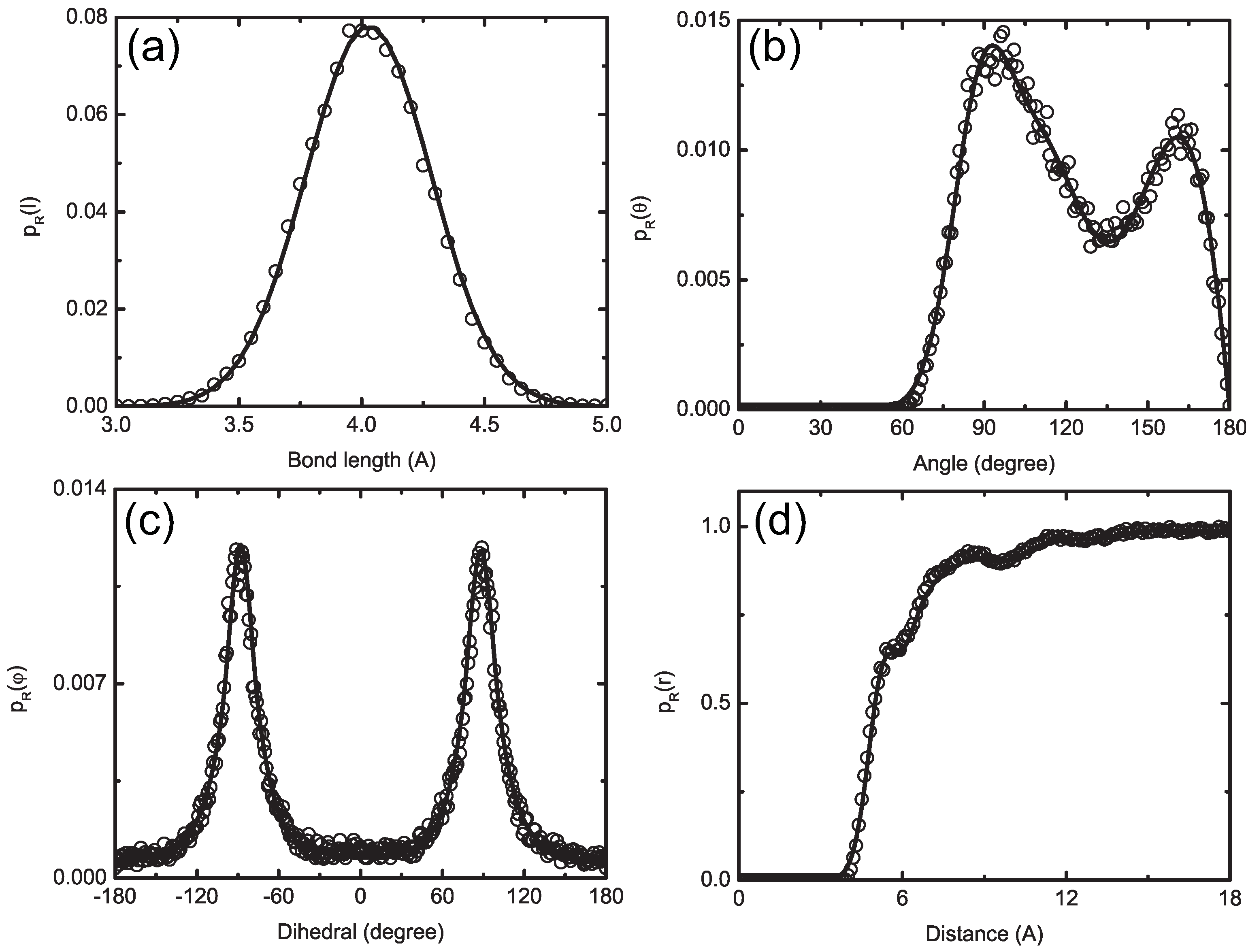
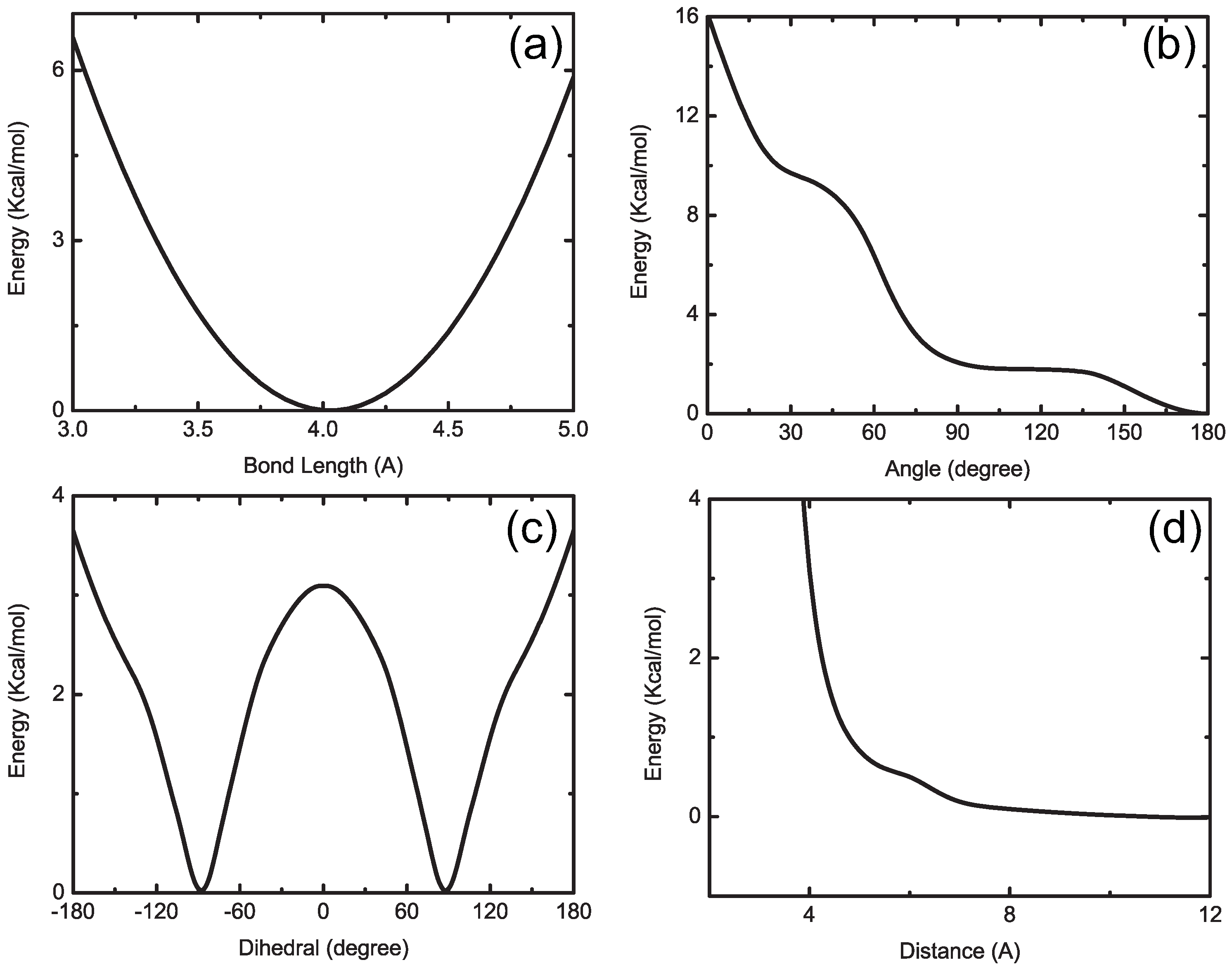
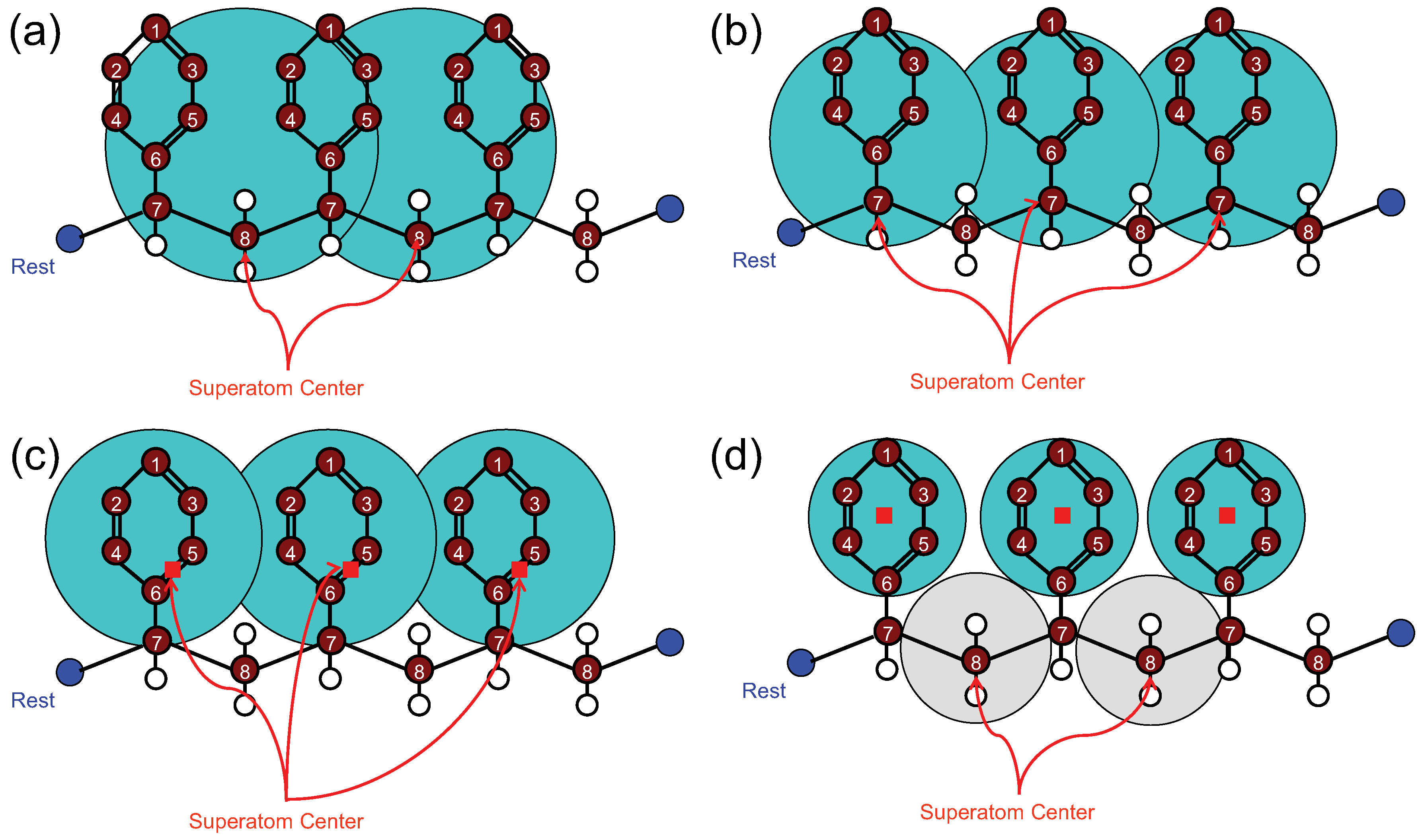
4.1.1. Definition of Super Atom
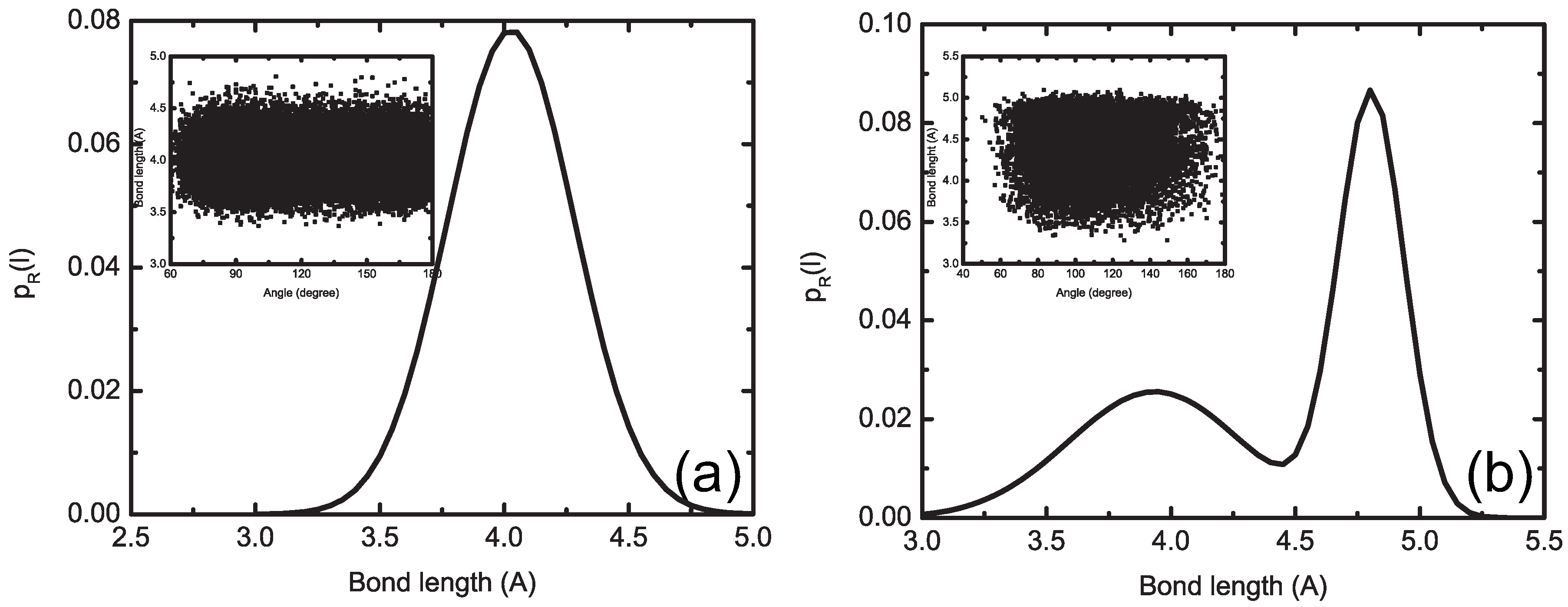
4.1.2. Smoothing, Extrapolation and Convergence
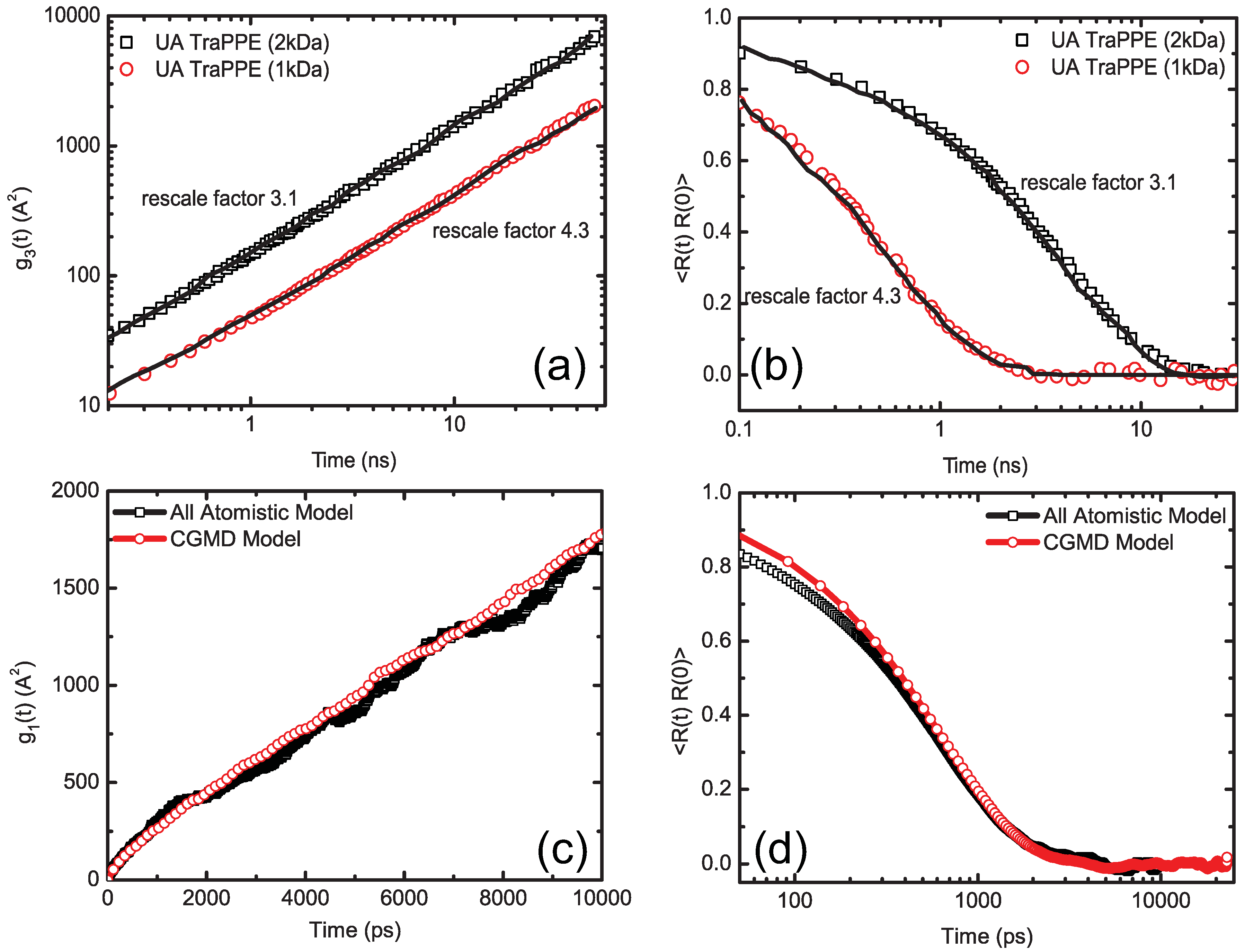
4.1.3. Dynamic Rescaling
4.1.4. Transferability and Thermodynamic Consistency
4.2. Blob Model and Uncrossability of Coarse-Grained Chains

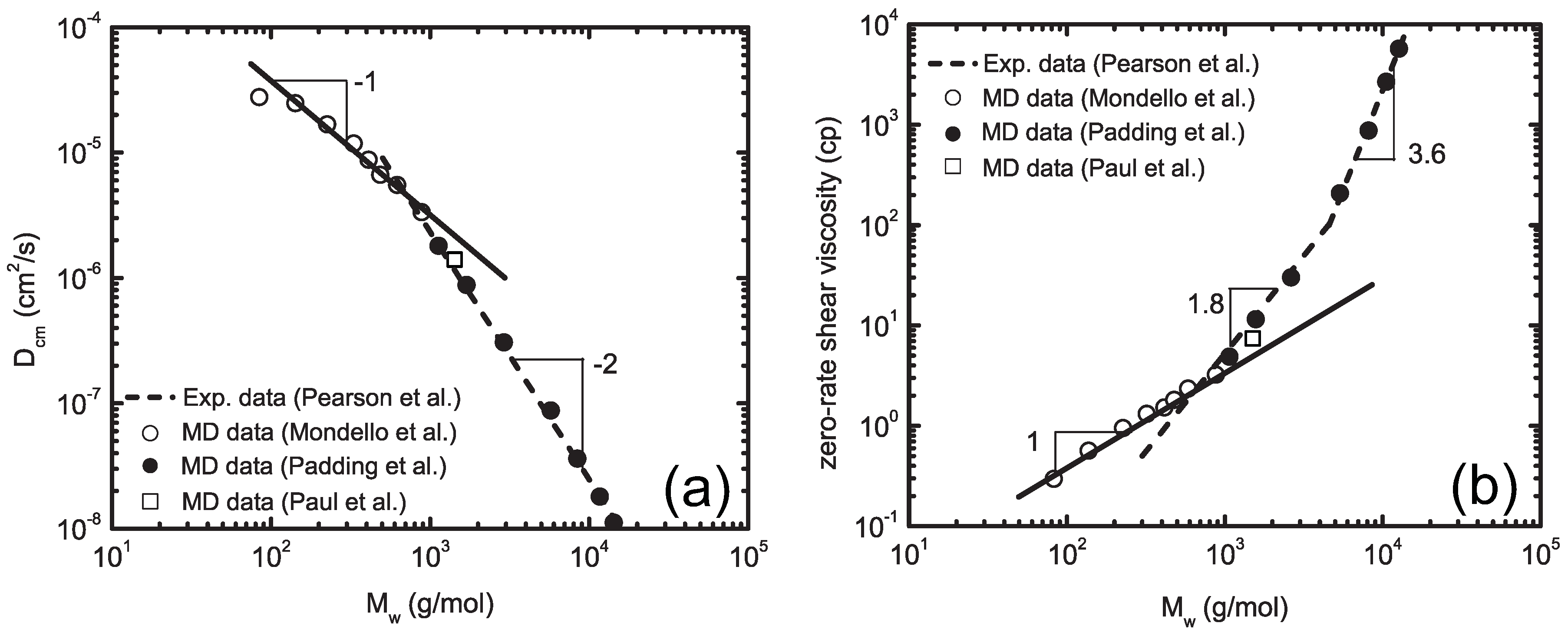
4.3. Super Coarse-Graining Method
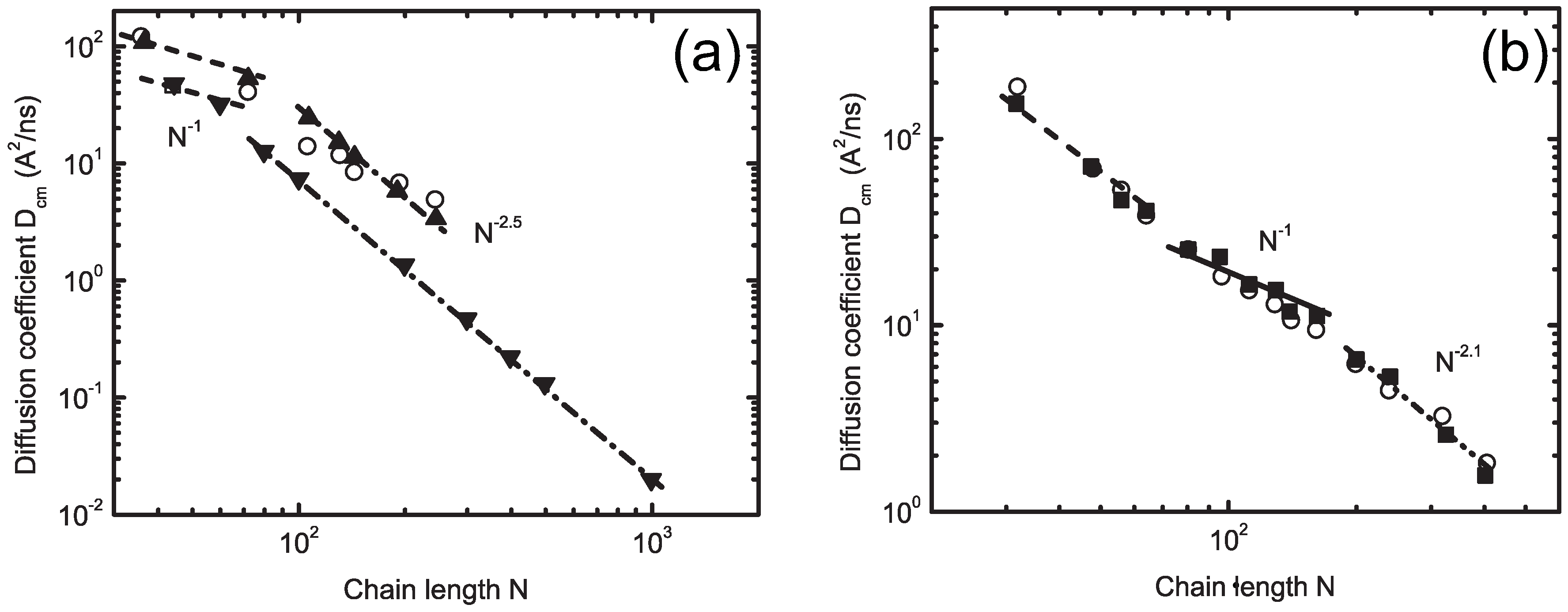
5. Multiple-Scale-Bridging Methods
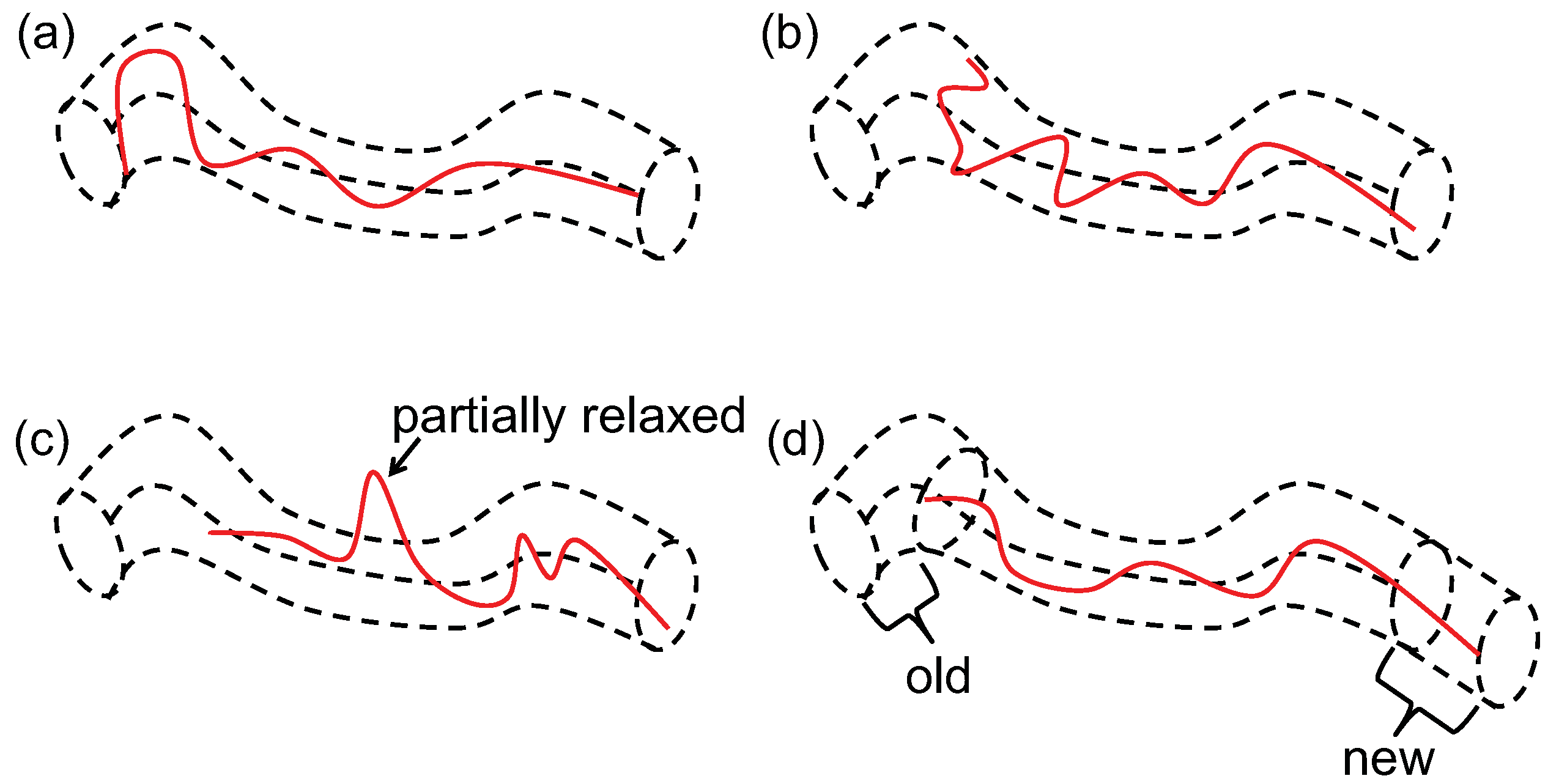
5.1. Dynamic Mapping onto Tube Model

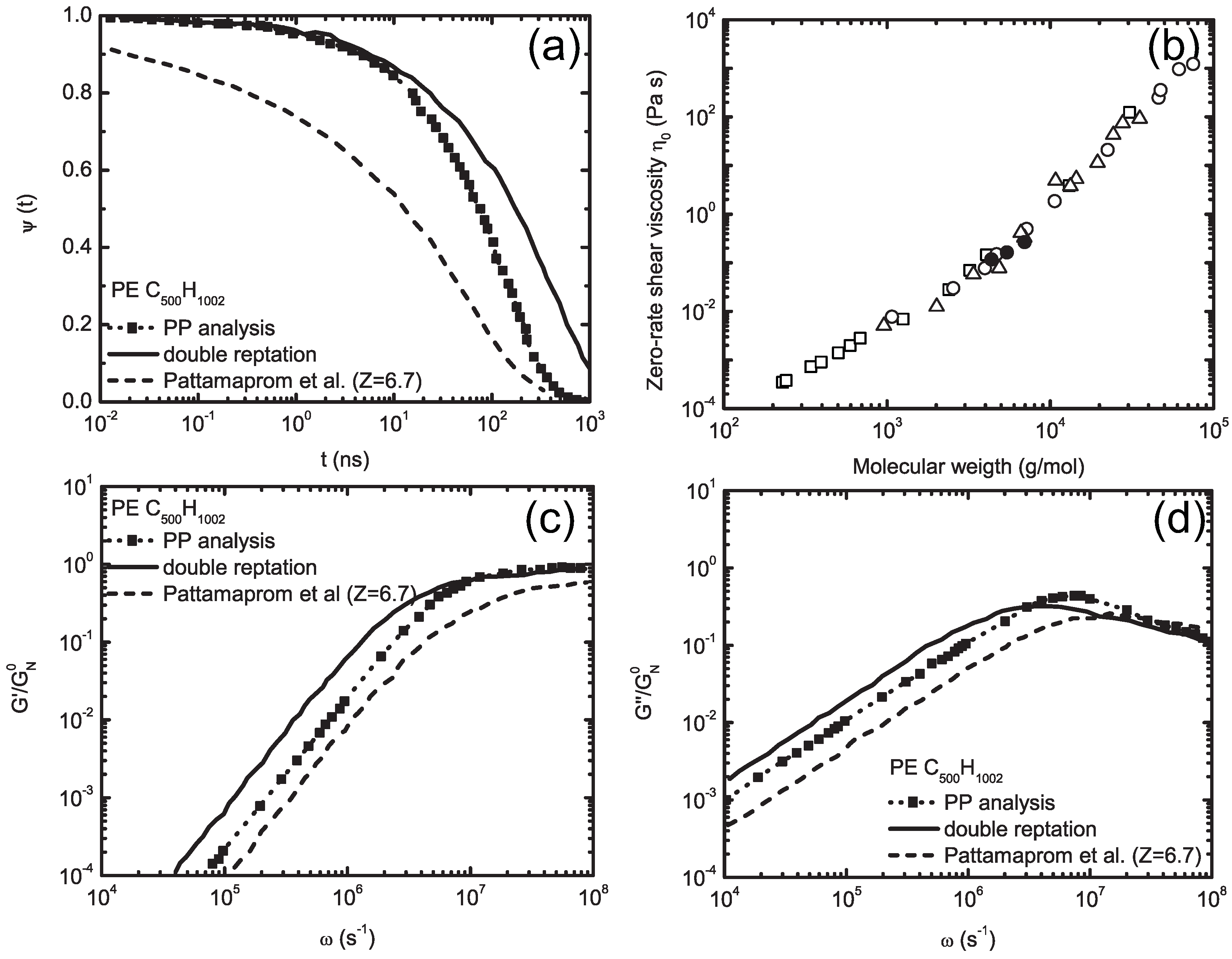
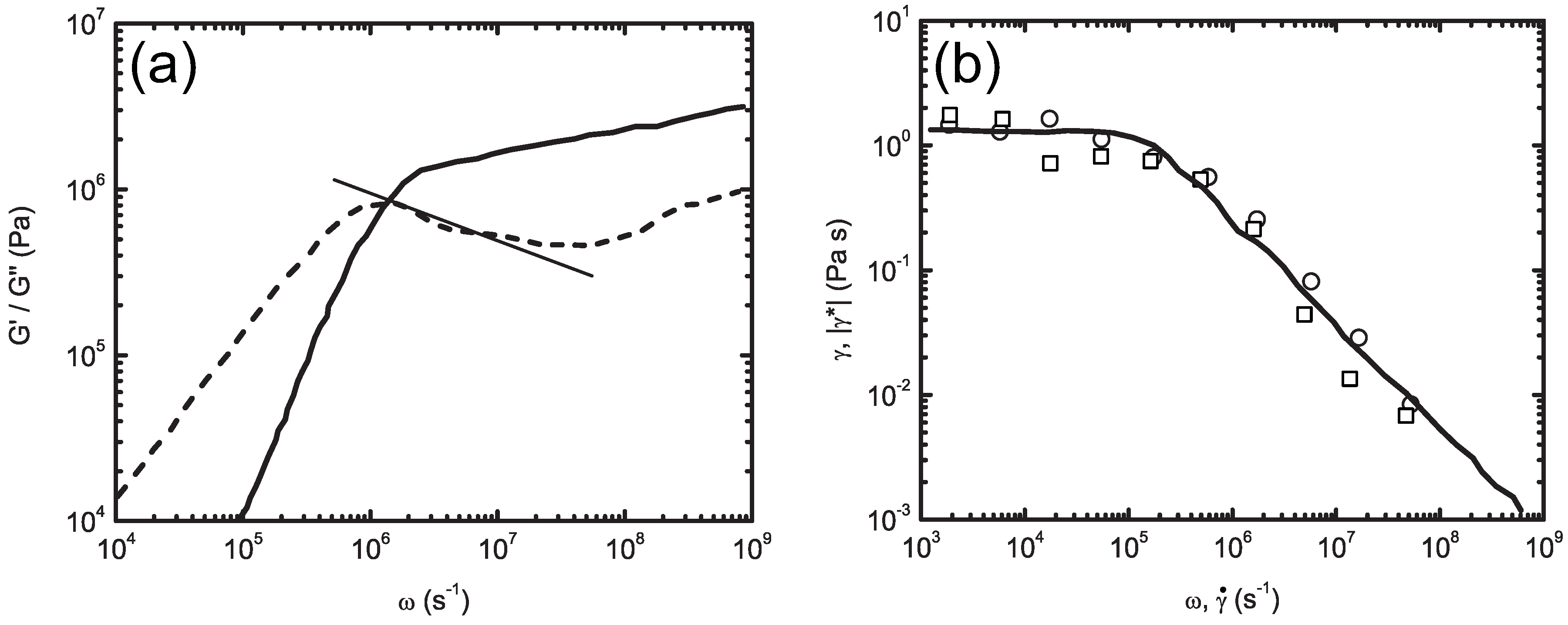
5.2. Molecularly-Derived Constitutive Equation
- Step (i): Choose initial values for the Lagrange multipliers, Λ
- Step (ii): Generate n-independent configurations distributed according to the generalized canonical ensemble in Equation (31)
- Step (iii): Solve Hamilton’s unconstrained equations of motion for all n systems during a short time interval,
- Step (iv): Calculate the friction matrix, , from Equation (33) and directly from the n trajectories produced in (iii)
- Step (v): Calculate an updated value for Λ by solving Equation (32) for Λ with (in terms of , and ; the transposed velocity gradient, , is “hidden” in )

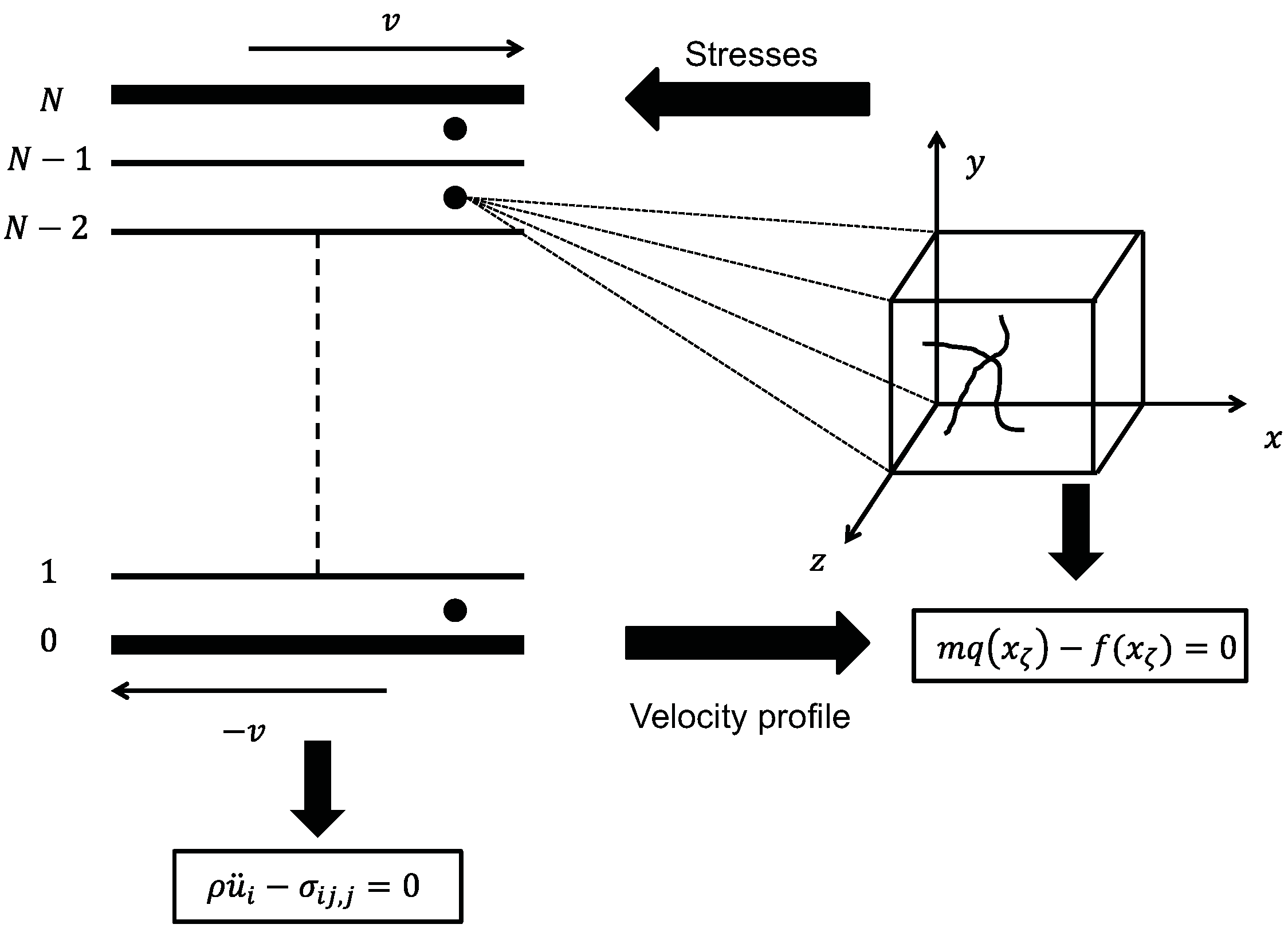
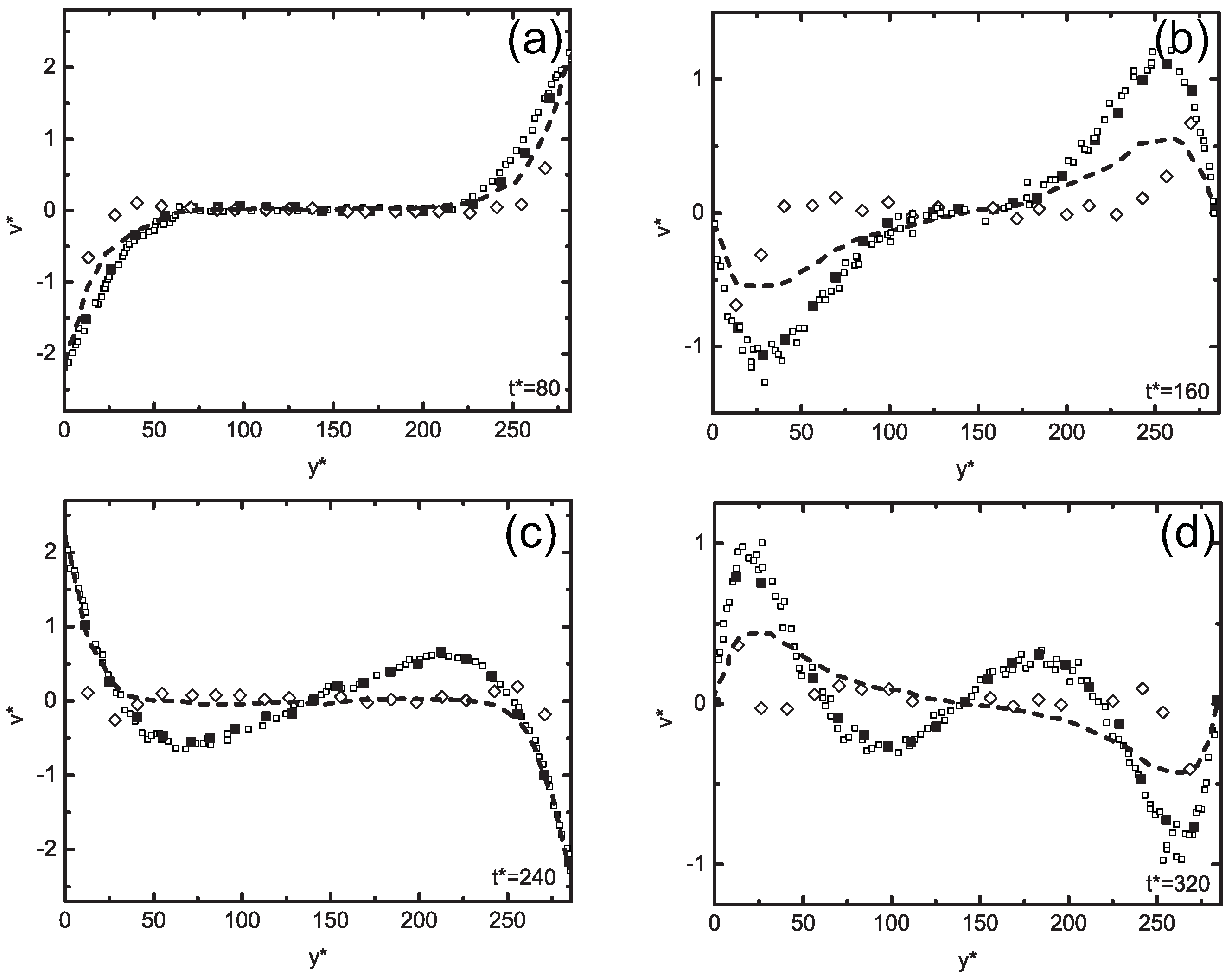
5.3. Concurrent Modeling of Polymer Melts under Shear Flow
5.4. Hierarchical Modeling of Polymer Rheology
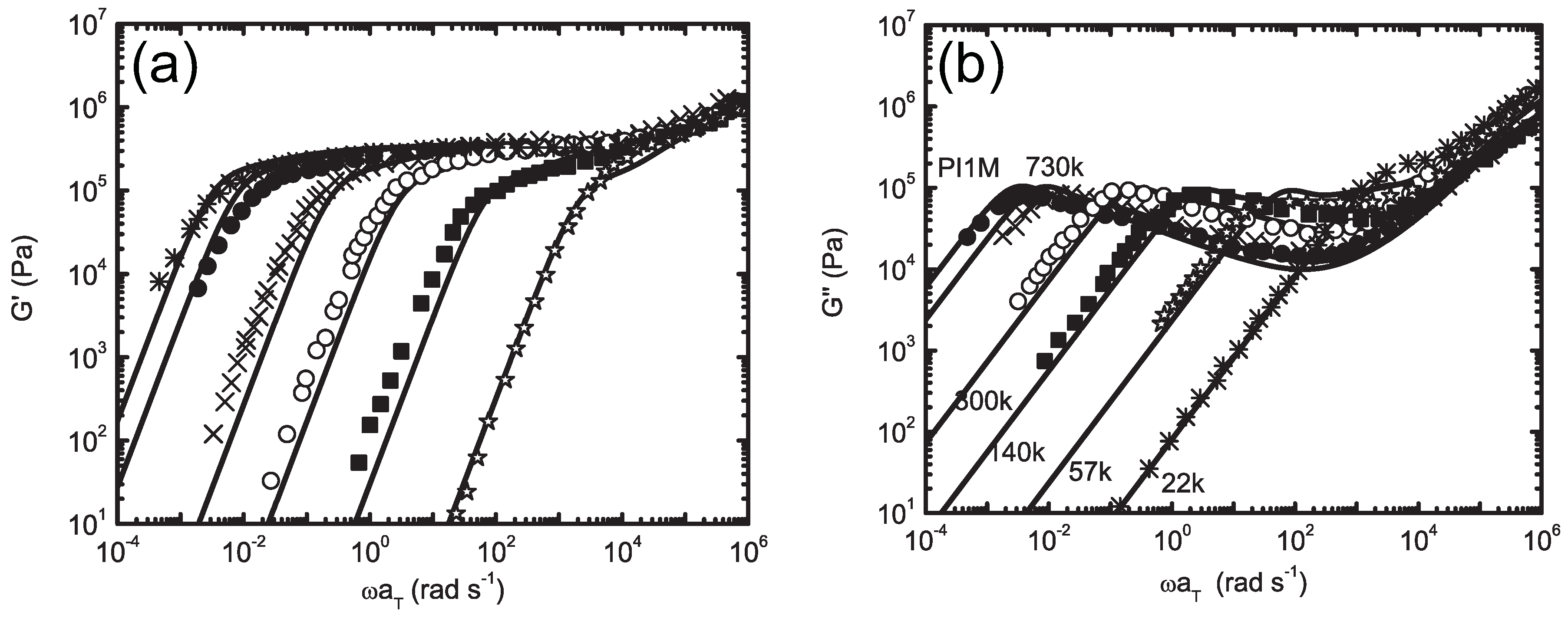
5.4.1. Mittag-Leffler Exponent α
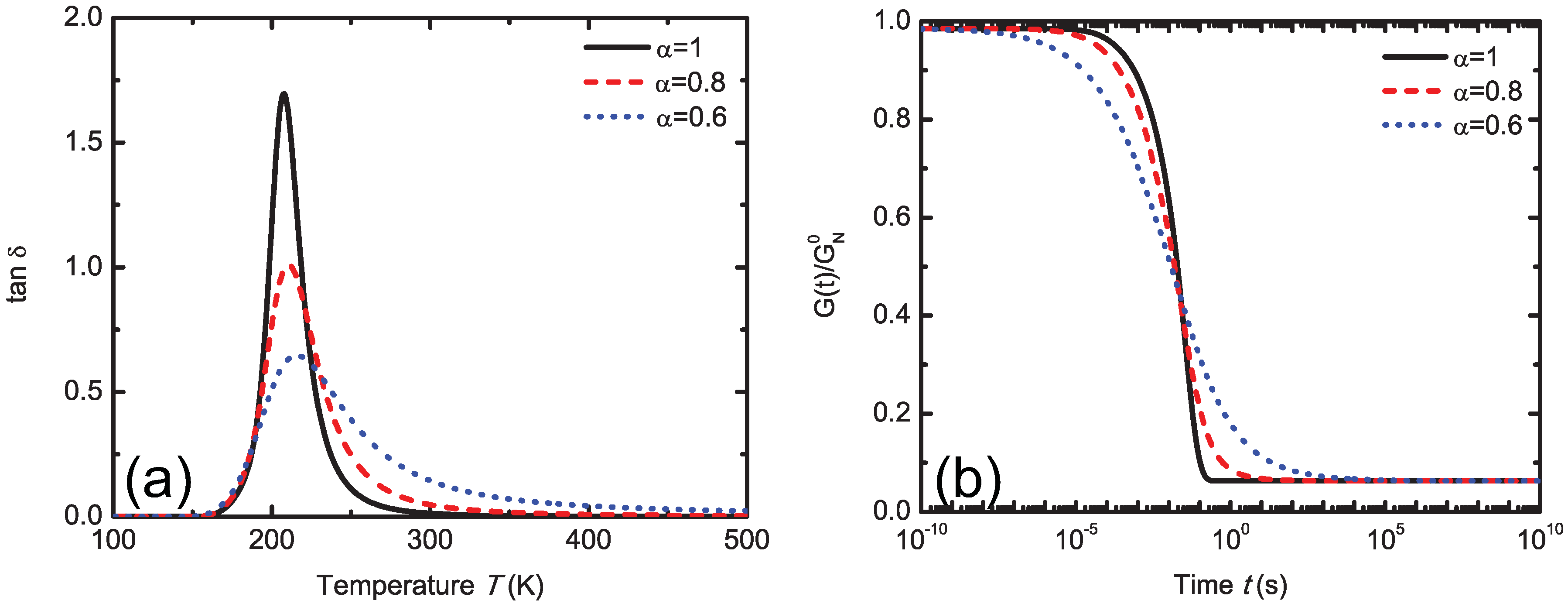
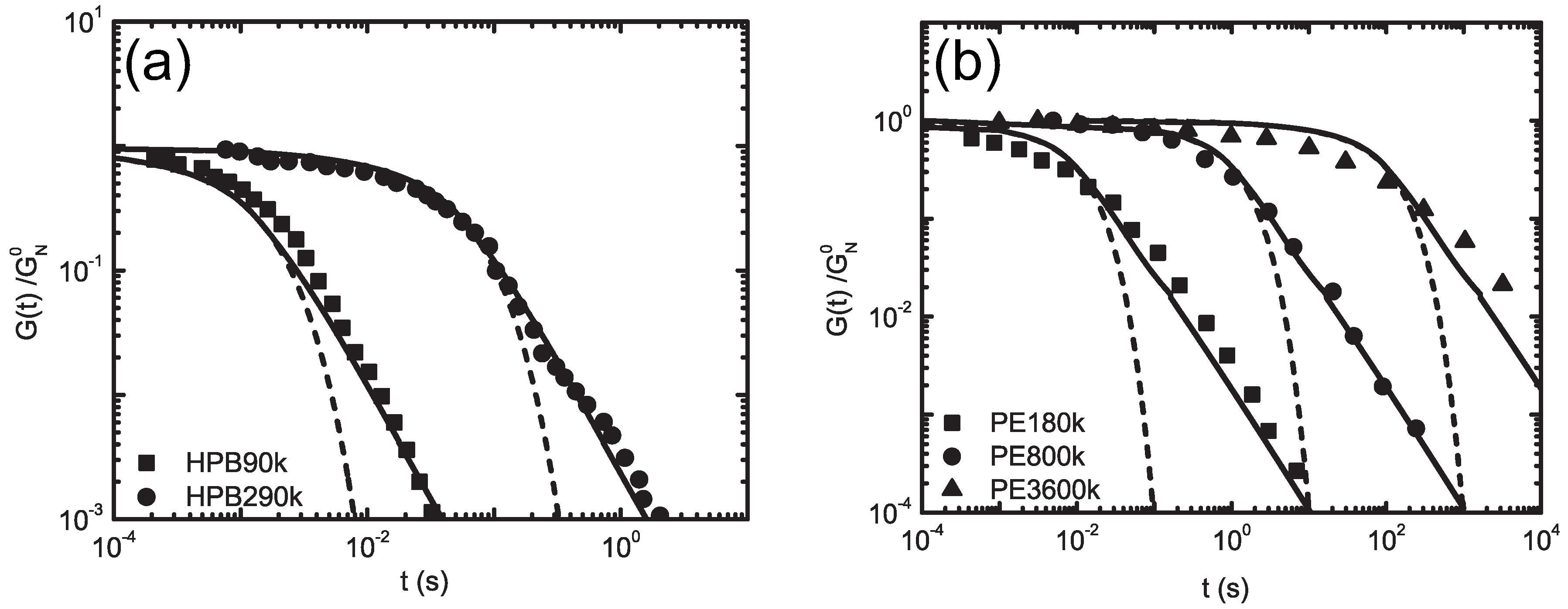
5.4.2. Finite Viscoelasticity Modeling
6. Perspectives and Challenges for Multiscale Modeling
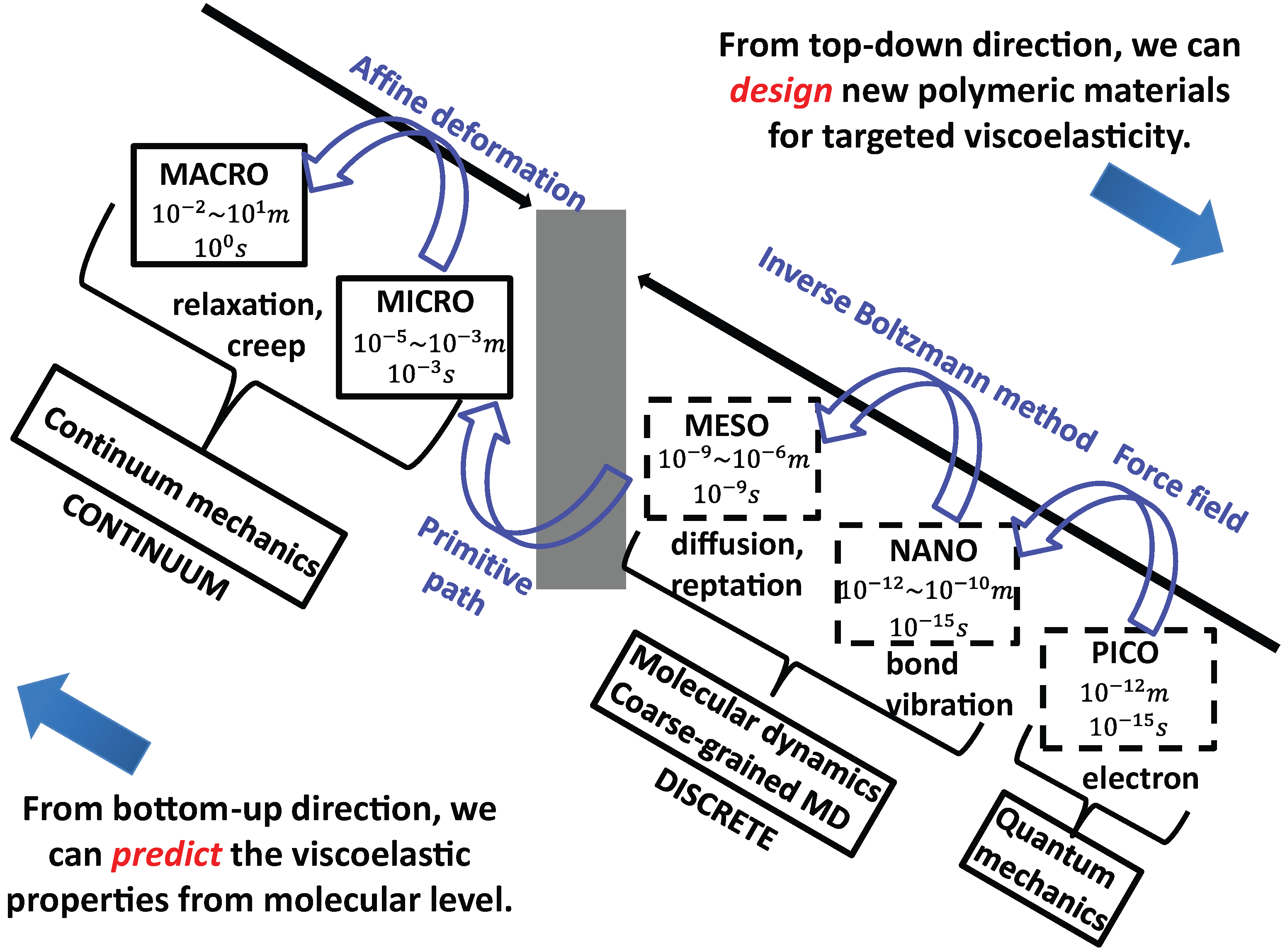
6.1. From Atomistic to Macroscopic Scales and Back
6.2. Polymer Dynamics under Flow
6.3. Polymer Dynamics at Interfaces and in Interphases
6.4. Nonlinear Viscoelasticity, Viscoplasticity and Damage
7. Summary and Conclusions
| Nomenclature | definitions are given here in the following sequence: Roman alphabetical order followed by Greek alphabetical order. Bold quantities denote vectors or tensors. |
tube diameter in reptation/tube model | |
shift factor in time-temperature superposition principle | |
| b | Kuhn length of polymer chain as |
self-diffusion coefficient of polymer chain | |
diffusion coefficient defined by the Rouse model as | |
| , | storage and loss shear moduli |
| , | plateau and relaxation shear moduli |
deformation gradient tensor | |
| L, | current and initial length of material in the direction of uniaxial tension |
primitive chain length in reptation/tube model, defined as | |
geometric mapping matrix between all-atomistic and coarse-grained models | |
| N | number of monomers per chain |
entanglement length, which is the number of monomers between two entanglements | |
number of polymer chains per unit volume | |
entanglement number (at equilibrium) between particle pairs i and j | |
| , | configurational probability distributions in all-atomistic and coarse-grained models, respectively |
end-to-end distance of polymer chain | |
radius of gyration of polymer chain | |
| s | segment index/contour length variable along primitive chain |
single chain coherent dynamic scattering function | |
| Z | number of entanglements per chain, defined as |
| α | exponent in standard Mittag-Leffler function |
elastic part of Cauchy stress | |
viscous part of Cauchy stress | |
elastic part of nominal stress | |
viscous part of nominal stress | |
viscosity and zero-rate viscosity | |
| γ, | shear strain and shear strain rate |
| λ | stretch ratio in uniaxial tension, defined as |
unit tangent vector of the primitive chain | |
| ω | circular frequency |
probability that chain segment, s, remains in the tube of reptation at time, t | |
tube survivability function, defined as | |
disentanglement time of polymer chain, defined as | |
entanglement time of polymer chain, defined as | |
Rouse time of polymer chain, defined as | |
| ζ | friction coefficient between polymer beads |
| , | friction coefficients in all-atomistic and coarse-grained models, respectively |
Acknowledgments
References
- Rouse, P.E., Jr. A theory of the linear viscoelastic properties of dilute solutions of coiling polymers. J. Chem. Phys. 1953, 21, 1272–1280. [Google Scholar] [CrossRef]
- Mondello, M.; Grest, G.S.; Webb, E.B.; Peczak, P. Dynamics of n-alkanes: Comparison to Rouse model. J. Chem. Phys. 1998, 109, 798–805. [Google Scholar] [CrossRef]
- Harmandaris, V.A.; Doxastakis, M.; Mavrantzas, V.G.; Theodorou, D.N. Detailed molecular dynamics simulation of the self-diffusion of n-alkane and cis-1, 4 polyisoprene oligomer melts. J. Chem. Phys. 2002, 116, 436–446. [Google Scholar] [CrossRef]
- Fleischer, G.; Appel, M. Chain length and temperature dependence of the self-diffusion of polyisoprene and polybutadiene in the melt. Macromolecules 1995, 28, 7281–7283. [Google Scholar] [CrossRef]
- De Gennes, P.G. Scaling Concepts in Polymer Physics; Cornell University Press: Ithaca, NY, USA, 1979. [Google Scholar]
- Doi, M.; Edwards, S.F. The Theory of Polymer Dynamics; Oxford University Press: New York, NY, USA, 1988; Volume 73. [Google Scholar]
- McLeish, T.C.B. Tube theory of entangled polymer dynamics. Adv. Phys. 2002, 51, 1379–1527. [Google Scholar] [CrossRef]
- Doi, M. Explanation for the 3. 4-power law for viscosity of polymeric liquids on the basis of the tube model. J. Polym. Sci. Polym. Lett. 1983, 21, 667–684. [Google Scholar] [CrossRef]
- Needs, R.J. Computer simulation of the effect of primitive path length fluctuations in the reptation model. Macromolecules 1984, 17, 437–441. [Google Scholar] [CrossRef]
- Watanabe, H. Viscoelasticity and dynamics of entangled polymers. Progr. Polym. Sci. 1999, 24, 1253–1403. [Google Scholar] [CrossRef]
- Schweizer, K.S.; Curro, J.G. Integral equation theories of the structure, thermodynamics, and phase transitions of polymer fluids. Adv. Chem. Phys. 1997, 98, 1–142. [Google Scholar]
- Schweizer, K.S.; Fuchs, M.; Szamel, G.; Guenza, M.; Tang, H. Polymer-mode-coupling theory of the slow dynamics of entangled macromolecular fluids. Macromol. Theory Simul. 1997, 6, 1037–1117. [Google Scholar] [CrossRef]
- Dealy, J.M.; Larson, R.G. Structure and Rheology of Molten Polymers: From Structure to Flow Behavior and Back again; Hanser Gardner Publications: Heidelberg, Germany, 2006. [Google Scholar]
- Likhtman, A.E.; McLeish, T.C.B. Quantitative theory for linear dynamics of linear entangled polymers. Macromolecules 2002, 35, 6332–6343. [Google Scholar] [CrossRef]
- Hou, J.X.; Svaneborg, C.; Everaers, R.; Grest, G.S. Stress relaxation in entangled polymer melts. Phys. Rev. Lett. 2010, 105, 068301:1–068301:4. [Google Scholar] [CrossRef]
- Kröger, M. Simple models for complex nonequilibrium fluids. Phys. Rep. 2004, 390, 453–551. [Google Scholar] [CrossRef]
- Larson, R.G.; Zhou, Q.; Shanbhag, S.; Park, S.J. Advances in modeling of polymer melt rheology. AIChE J. 2007, 53, 542–548. [Google Scholar] [CrossRef]
- Likhtman, A.E. Viscoelasticity and Molecular Rheology. In Comprehensive Polymer Science; Elsevier: Amsterdam, The Netherlands, 2011. [Google Scholar]
- Fang, J.; Kröger, M.; Öttinger, H.C. A thermodynamically admissible reptation model for fast flows of entangled polymers. II. Model predictions for shear and extensional flows. J. Rheol. 2000, 44, 1293–1317. [Google Scholar] [CrossRef]
- Shanbhag, S. Analytical rheology of polymer melts: State of the art. ISRN Mater. Sci. 2012, 2012, 732176:1–732176:24. [Google Scholar] [CrossRef]
- Edwards, S.F.; Vilgis, T.A. The tube model theory of rubber elasticity. Rep. Progr. Phys. 1999, 51, 243–297. [Google Scholar] [CrossRef]
- Edwards, S. The statistical mechanics of polymerized material. Proc. Phys. Soc. 1967, 92, 9–16. [Google Scholar] [CrossRef]
- Edwards, S. Statistical mechanics with topological constraints: I. Proc. Phys. Soc. 1967, 91, 513–519. [Google Scholar] [CrossRef]
- Edwards, S. Statistical mechanics with topological constraints: II. J. Phys. A 1968, 1, 15–28. [Google Scholar] [CrossRef]
- De Gennes, P.G. Reptation of a polymer chain in the presence of fixed obstacles. J. Chem. Phys. 1971, 55, 572–579. [Google Scholar] [CrossRef]
- Rubinstein, M.; Panyukov, S. Nonaffine deformation and elasticity of polymer networks. Macromolecules 1997, 30, 8036–8044. [Google Scholar] [CrossRef]
- Rubinstein, M.; Panyukov, S. Elasticity of polymer networks. Macromolecules 2002, 35, 6670–6686. [Google Scholar] [CrossRef]
- Arruda, E.M.; Boyce, M.C. A three-dimensional constitutive model for the large stretch behavior of rubber elastic materials. J. Mech. Phys. Solids 1993, 41, 389–412. [Google Scholar] [CrossRef]
- Miehe, C.; Göktepe, S.; Lulei, F. A micro-macro approach to rubber-like materials. Part I: The non-affine micro-sphere model of rubber elasticity. J. Mech. Phys. Solids 2004, 52, 2617–2660. [Google Scholar] [CrossRef]
- Miehe, C.; Göktepe, S. A micro–macro approach to rubber-like materials. Part II: The micro-sphere model of finite rubber viscoelasticity. J. Mech. Phys. Solids 2005, 53, 2231–2258. [Google Scholar] [CrossRef]
- Göktepe, S.; Miehe, C. A micro–macro approach to rubber-like materials. Part III: The micro-sphere model of anisotropic Mullins-type damage. J. Mech. Phys. Solids 2005, 53, 2259–2283. [Google Scholar] [CrossRef]
- Tang, S.; Greene, M.S.; Liu, W.K. Two-scale mechanism-based theory of nonlinear viscoelasticity. J. Mech. Phys. Solids 2012, 60, 199–226. [Google Scholar] [CrossRef]
- Jensen, M.K.; Khaliullin, R.; Schieber, J.D. Self-consistent modeling of entangled network strands and linear dangling structures in a single-strand mean-field slip-link model. Rheol. Acta 2012, 51, 21–35. [Google Scholar] [CrossRef]
- Gee, R.H.; Lacevic, N.; Fried, L.E. Atomistic simulations of spinodal phase separation preceding polymer crystallization. Nat. Mater. 2005, 5, 39–43. [Google Scholar] [CrossRef] [PubMed]
- Baschnagel, J.; Binder, K.; Doruker, P.; Gusev, A.; Hahn, O.; Kremer, K.; Mattice, W.; Müller-Plathe, F.; Murat, M.; Paul, W.; et al. Bridging the Gap between Atomistic and Coarse-grained Models of Polymers: Status and Perspectives. In Viscoelasticity, Atomistic Models, Statistical Chemistry; Springer: Berlin, Germany, 2000; pp. 41–156. [Google Scholar]
- Kremer, K.; Müller-Plathe, F. Multiscale simulation in polymer science. Mol. Simul. 2002, 28, 729–750. [Google Scholar] [CrossRef]
- Faller, R. Automatic coarse graining of polymers. Polymer 2004, 45, 3869–3876. [Google Scholar] [CrossRef]
- Müller-Plathe, F. Coarse-graining in polymer simulation: From the atomistic to the mesoscopic scale and back. ChemPhysChem 2002, 3, 754–769. [Google Scholar] [CrossRef]
- Müller-Plathe, F. Scale-hopping in computer simulations of polymers. Soft Mater. 2002, 1, 1–31. [Google Scholar] [CrossRef]
- Paul, W.; Smith, G.D. Structure and dynamics of amorphous polymers: Computer simulations compared to experiment and theory. Rep. Progr. Phys. 2004, 67, 1117–1185. [Google Scholar] [CrossRef]
- Padding, J.T.; Briels, W.J. Systematic coarse-graining of the dynamics of entangled polymer melts: The road from chemistry to rheology. J. Phys. Condens. Matter 2011, 23, 233101:1–233101:17. [Google Scholar] [CrossRef] [PubMed]
- Karimi-Varzaneh, H.A.; van der Vegt, N.F.A.; Müller-Plathe, F.; Carbone, P. How good are coarse-grained polymer models? A comparison for atactic polystyrene. ChemPhysChem 2012, 13, 3428–3439. [Google Scholar] [CrossRef] [PubMed]
- Brini, E.; Algaer, E.A.; Ganguly, P.; Li, C.; Rodríguez-Ropero, F.; van der Vegt, N.F. Systematic coarse-graining methods for soft matter simulations—A review. Soft Matter 2013, 9, 2108–2119. [Google Scholar] [CrossRef]
- Holm, C.; Kremer, K. Advanced computer simulation approaches for soft matter sciences I. Adv. Polym. Sci. 2005, 173, 1–275. [Google Scholar]
- Holm, C.; Kremer, K. Advanced computer simulation approaches for soft matter sciences II. Adv. Polym. Sci. 2005, 185, 1–250. [Google Scholar]
- Holm, C.; Kremer, K. Advanced computer simulation approaches for soft matter sciences III. Adv. Polym. Sci. 2009, 221, 1–237. [Google Scholar]
- Voth, G.A. Coarse-Graining of Condensed Phase and Biomolecular Systems; CRC Press: Cambridge, UK, 2009. [Google Scholar]
- Faller, R. Biomembrane Frontiers: Nanostructures, Models, and the Design of Life; Springer: Berlin, Germany, 2009; Volume 2. [Google Scholar]
- Scheutjens, J.M.H.M.; Fleer, G.J. Statistical theory of the adsorption of interactingchain molecules. 1. Partition-function, segment density distribution, and adsoprtion-isotherms. J. Phys. Chem. 1979, 83, 1619–1635. [Google Scholar] [CrossRef]
- Boris, D.; Rubinstein, M. A self-consistent mean field model of a starburst dendrimer: Dense core vs. dense shell. Macromolecules 1996, 29, 7251–7260. [Google Scholar] [CrossRef]
- Lai, P.Y.; Binder, K. Structure and dynamics of polymer brushes near the theta point-A Monte Carlo simulation. J. Chem. Phys. 1992, 97, 586–595. [Google Scholar] [CrossRef]
- Szleifer, I.; Carignano, M.A. Tethered polymer layers. Adv. Chem. Phys. 1996, 94, 165–260. [Google Scholar]
- Detcheverry, F.A.; Kang, H.M.; Daoulas, K.C.; Müller, M.; Nealey, P.F.; de Pablo, J.J. Monte Carlo simulations of a coarse grain model for block copolymers and nanocomposites. Macromolecules 2008, 41, 4989–5001. [Google Scholar] [CrossRef]
- Zhulina, E.B.; Wolterink, J.K.; Borisov, O.V. Screening effects in a polyelectrolyte brush: Self-consistent-field theory. Macromolecules 2000, 33, 4945–4953. [Google Scholar] [CrossRef]
- Müller, M. Phase diagram of a mixed polymer brush. Phys. Rev. E 2002, 65, 030802:1–030802:4. [Google Scholar] [CrossRef]
- Stuart, M.A.C.; Huck, W.T.S.; Genzer, J.; Müller, M.; Ober, C.; Stamm, M.; Sukhorukov, G.B.; Szleifer, I.; Tsukruk, V.V.; Urban, M.; et al. Emerging applications of stimuli-responsive polymer materials. Nat. Mater. 2010, 9, 101–113. [Google Scholar] [CrossRef] [PubMed]
- Halperin, A.; Kröger, M. Theoretical considerations on mechanisms of harvesting cells cultured on thermoresponsive polymer brushes. Biomaterials 2012, 33, 4975–4987. [Google Scholar] [CrossRef] [PubMed]
- Peleg, O.; Tagliazucchi, M.; Kröger, M.; Rabin, Y.; Szleifer, I. Morphology control of hairy nanopores. ACS Nano 2011, 5, 4737–4747. [Google Scholar] [CrossRef] [PubMed]
- Tagliazucchi, M.; Peleg, O.; Kröger, M.; Rabin, Y.; Szleifer, I. Effect of charge, hydrophobicity and sequence of nucleoporins on the translocation of model particles through the nuclear pore complex. Proc. Natl. Acad. Sci. USA 2013, 110, 3363–3368. [Google Scholar] [CrossRef] [PubMed]
- Csányi, G.; Albaret, T.; Payne, M.; de Vita, A. “Learn on the fly”: A hybrid classical and quantum-mechanical molecular dynamics simulation. Phys. Rev. Lett. 2004, 93, 175503:1–175503:4. [Google Scholar] [CrossRef]
- Johnston, K.; Harmandaris, V. Properties of benzene confined between two Au (111) surfaces using a combined density functional theory and classical molecular dynamics approach. J. Phys. Chem. C 2011, 115, 14707–14717. [Google Scholar] [CrossRef]
- Johnston, K.; Nieminen, R.M.; Kremer, K. A hierarchical dualscale study of bisphenol-A-polycarbonate on a silicon surface: Structure, dynamics and impurity diffusion. Soft Matter 2011, 7, 6457–6466. [Google Scholar] [CrossRef]
- Johnston, K.; Harmandaris, V. Properties of short polystyrene chains confined between two gold surfaces through a combined density functional theory and classical molecular dynamics approach. Soft Matter 2012, 8, 6320–6332. [Google Scholar] [CrossRef]
- Ilett, S.M.; Orrock, A.; Poon, W.; Pusey, P. Phase behavior of a model colloid-polymer mixture. Phys. Rev. E 1995, 51, 1344–1352. [Google Scholar] [CrossRef]
- Müller, M.; Binder, K. Computer simulation of asymmetric polymer mixtures. Macromolecules 1995, 28, 1825–1834. [Google Scholar] [CrossRef]
- Müller, M.; Schmid, F. Incorporating Fluctuations and Dynamics in Self-consistent Field Theories for Polymer Blends. In Advanced Computer Simulation Approaches for Soft Matter Sciences II; Springer: Berlin, Germany, 2005; pp. 1–58. [Google Scholar]
- Deutsch, H.P.; Binder, K. Interdiffusion and self-diffusion in polymer mixtures: A Monte Carlo study. J. Chem. Phys. 1991, 94, 2294–2304. [Google Scholar] [CrossRef]
- Faller, R. Correlation of static and dynamic inhomogeneities in polymer mixtures: A computer simulation of polyisoprene and polystyrene. Macromolecules 2004, 37, 1095–1101. [Google Scholar] [CrossRef]
- Qian, H.J.; Carbone, P.; Chen, X.; Karimi-Varzaneh, H.A.; Liew, C.C.; Müller-Plathe, F. Temperature-transferable coarse-grained potentials for ethylbenzene, polystyrene, and their mixtures. Macromolecules 2008, 41, 9919–9929. [Google Scholar] [CrossRef]
- Murat, M.; Kremer, K. From many monomers to many polymers: Soft ellipsoid model for polymer melts and mixtures. J. Chem. Phys. 1998, 108, 4340–4348. [Google Scholar] [CrossRef]
- McCarty, J.; Guenza, M.G. Multiscale modeling of binary polymer mixtures: Scale bridging in the athermal and thermal regime. J. Chem. Phys. 2010, 133, 094904:1–094904:15. [Google Scholar] [CrossRef] [PubMed]
- McCarty, J.; Lyubimov, I.Y.; Guenza, M.G. Effective soft-core potentials and mesoscopic simulations of binary polymer mixtures. Macromolecules 2010, 43, 3964–3979. [Google Scholar] [CrossRef]
- Yatsenko, G.; Sambriski, E.J.; Nemirovskaya, M.A.; Guenza, M. Analytical soft-core potentials for macromolecular fluids and mixtures. Phys. Rev. Lett. 2004, 93, 257803:1–257803:4. [Google Scholar] [CrossRef]
- Baig, C.; Stephanou, P.S.; Tsolou, G.; Mavrantzas, V.G.; Kröger, M. Understanding dynamics in binary mixtures of entangled cis-1, 4-polybutadiene melts at the level of primitive path segments by mapping atomistic simulation data onto the tube model. Macromolecules 2010, 43, 8239–8250. [Google Scholar] [CrossRef]
- Harmandaris, V.A.; Kremer, K.; Floudas, G. Dynamic heterogeneity in fully miscible blends of polystyrene with oligostyrene. Phys. Rev. Lett. 2013, 110, 165701:1–165701:5. [Google Scholar] [CrossRef]
- Harmandaris, V.A.; Mavrantzas, V.G.; Theodorou, D.N.; Kröger, M.; Ramirez, J.; Öttinger, H.C.; Vlassopoulos, D. Crossover from the Rouse to the entangled polymer melt regime: Signals from long, detailed atomistic molecular dynamics simulations, supported by rheological experiments. Macromolecules 2003, 36, 1376–1387. [Google Scholar] [CrossRef]
- Carmesin, I.; Kremer, K. The bond fluctuation method: A new effective algorithm for the dynamics of polymers in all spatial dimensions. Macromolecules 1988, 21, 2819–2823. [Google Scholar] [CrossRef]
- Grest, G.S.; Kremer, K. Molecular dynamics simulation for polymers in the presence of a heat bath. Phys. Rev. A 1986, 33, 3628–3631. [Google Scholar] [CrossRef] [PubMed]
- Kremer, K.; Grest, G.S. Dynamics of entangled linear polymer melts: A molecular-dynamics simulation. J. Chem. Phys. 1990, 92, 5057–5086. [Google Scholar] [CrossRef]
- Hua, C.C.; Schieber, J.D. Segment connectivity, chain-length breathing, segmental stretch, and constraint release in reptation models. I. Theory and single-step strain predictions. J. Chem. Phys. 1998, 109, 10018–10027. [Google Scholar] [CrossRef]
- Hua, C.C.; Schieber, J.D.; Venerus, D.C. Segment connectivity, chain-length breathing, segmental stretch, and constraint release in reptation models. II. Double-step strain predictions. J. Chem. Phys. 1998, 109, 10028–10032. [Google Scholar] [CrossRef]
- Tschöp, W.; Kremer, K.; Batoulis, J.; Bürger, T.; Hahn, O. Simulation of polymer melts. I. Coarse-graining procedure for polycarbonates. Acta Polym. 1998, 49, 61–74. [Google Scholar] [CrossRef]
- Meyer, H.; Biermann, O.; Faller, R.; Reith, D.; Müller-Plathe, F. Coarse graining of nonbonded inter-particle potentials using automatic simplex optimization to fit structural properties. J. Chem. Phys. 2000, 113, 6264–6275. [Google Scholar] [CrossRef]
- Padding, J.T.; Briels, W.J. Uncrossability constraints in mesoscopic polymer melt simulations: Non-Rouse behavior of C120H242. J. Chem. Phys. 2001, 115, 2846–2859. [Google Scholar] [CrossRef]
- Padding, J.T.; Briels, W.J. Time and length scales of polymer melts studied by coarse-grained molecular dynamics simulations. J. Chem. Phys. 2002, 117, 925–943. [Google Scholar] [CrossRef]
- Kindt, P.; Briels, W.J. A single particle model to simulate the dynamics of entangled polymer melts. J. Chem. Phys. 2007, 127, 134901:1–134901:12. [Google Scholar] [CrossRef] [PubMed]
- Guenza, M.G. Theoretical models for bridging timescales in polymer dynamics. J. Phys. Condens. Matter 2007, 20, 033101:1–033101:24. [Google Scholar] [CrossRef]
- McCarty, J.; Lyubimov, I.Y.; Guenza, M.G. Multiscale modeling of coarse-grained macromolecular liquids. J. Phys. Chem. B 2009, 113, 11876–11886. [Google Scholar] [CrossRef] [PubMed]
- Stephanou, P.S.; Baig, C.; Tsolou, G.; Mavrantzas, V.G.; Kröger, M. Quantifying chain reptation in entangled polymer melts: Topological and dynamical mapping of atomistic simulation results onto the tube model. J. Chem. Phys. 2010, 132, 124904:1–124904:16. [Google Scholar] [CrossRef] [PubMed]
- Ilg, P.; Öttinger, H.C.; Kröger, M. Systematic time-scale-bridging molecular dynamics applied to flowing polymer melts. Phys. Rev. E 2009, 79, 011802:1–011802:7. [Google Scholar] [CrossRef]
- De, S.; Fish, J.; Shephard, M.S.; Keblinski, P.; Kumar, S.K. Multiscale modeling of polymer rheology. Phys. Rev. E 2006, 74, 030801:1–030801:4. [Google Scholar] [CrossRef]
- Li, Y.; Tang, S.; Abberton, B.; Kröger, M.; Burkhart, C.; Jiang, B.; Papakonstantopoulos, G.; Poldneff, M.; Liu, W.K. A predictive multiscale computational framework for viscoelastic properties of linear polymers. Polymer 2012, 53, 5935–5952. [Google Scholar] [CrossRef]
- Wittmer, J.P.; Cavallo, A.; Xu, H.; Zabel, J.E.; Polinska, P.; Schulmann, N.; Meyer, H.; Farago, J.; Johner, A.; Obukhov, S.P.; Baschnagel, J. Scale-free static and dynamical correlations in melts of monodisperse and Flory-distributed homopolymers. A review of recent bond-fluctuation model studies. J. Statist. Phys. 2011, 145, 1017–1126. [Google Scholar] [CrossRef]
- Paul, W.; Binder, K.; Heermann, D.W.; Kremer, K. Dynamics of polymer solutions and melts. Reptation predictions and scaling of relaxation times. J. Chem. Phys. 1991, 95, 7726–7740. [Google Scholar] [CrossRef]
- Binder, K.; Paul, W. Monte Carlo simulations of polymer dynamics: Recent advances. J. Polym. Sci. B 1997, 35, 1–31. [Google Scholar] [CrossRef]
- Shaffer, J.S. Effects of chain topology on polymer dynamics: Bulk melts. J. Chem. Phys. 1994, 101, 4205–4213. [Google Scholar] [CrossRef]
- Everaers, R.; Sukumaran, S.K.; Grest, G.S.; Svaneborg, C.; Sivasubramanian, A.; Kremer, K. Rheology and microscopic topology of entangled polymeric liquids. Science 2004, 303, 823–826. [Google Scholar] [CrossRef] [PubMed]
- Doi, M.; Kuzuu, N.Y. Rheology of star polymers in concentrated solutions and melts. J. Polym. Sci. Polym. Phys. 1980, 18, 775–780. [Google Scholar] [CrossRef]
- Paul, W.; Binder, K.; Kremer, K.; Heermann, D.W. Structure-property correlation of polymers, a Monte Carlo approach. Macromolecules 1991, 24, 6332–6334. [Google Scholar] [CrossRef]
- Paul, W.; Pistoor, N. A mapping of realistic onto abstract polymer models and an application to two bisphenol polycarbonates. Macromolecules 1994, 27, 1249–1255. [Google Scholar] [CrossRef]
- Tries, V.; Paul, W.; Baschnagel, J.; Binder, K. Modeling polyethylene with the bond fluctuation model. J. Chem. Phys. 1997, 106, 738–748. [Google Scholar] [CrossRef]
- Baschnagel, J.; Binder, K.; Paul, W.; Laso, M.; Suter, U.W.; Batoulis, I.; Jilge, W.; Bürger, T. On the construction of coarse-grained models for linear flexible polymer chains: Distribution functions for groups of consecutive monomers. J. Chem. Phys. 1991, 95, 6014–6025. [Google Scholar] [CrossRef]
- Weeks, J.D.; Chandler, D.; Andersen, H.C. Role of repulsive forces in determining the equilibrium structure of simple liquids. J. Chem. Phys. 1971, 54, 5237–5247. [Google Scholar] [CrossRef]
- Hess, S.; Kröger, M.; Voigt, H. Thermo-mechanical properties of the WCA-Lennard-Jones model system in its fluid and solid states. Physica A 1998, 250, 58–82. [Google Scholar] [CrossRef]
- Pütz, M.; Kremer, K.; Grest, G.S. What is the entanglement length in a polymer melt? EPL (Europhys. Lett.) 2000, 49, 735–739. [Google Scholar] [CrossRef]
- Kröger, M.; Hess, S. Rheological evidence for a dynamical crossover in polymer melts via nonequilibrium molecular dynamics. Phys. Rev. Lett. 2000, 85, 1128–1131. [Google Scholar] [CrossRef] [PubMed]
- Kremer, K.; Binder, K. Dynamics of polymer chains confined into tubes: Scaling theory and Monte Carlo simulations. J. Chem. Phys. 1984, 81, 6381–6394. [Google Scholar] [CrossRef]
- Cifre, J.G.H.; Hess, S.; Kröger, M. Linear viscoelastic behavior of unentangled polymer melts via non-equilibrium molecular dynamics. Macromol. Theory Simul. 2004, 13, 748–753. [Google Scholar] [CrossRef]
- Ferry, J.D. Viscoelastic Properties of Polymers; Wiley: New York, NY, USA, 1980; Volume 641. [Google Scholar]
- Cox, W.P.; Merz, E.H. Correlation of dynamic and steady flow viscosities. J. Polym. Sci. Polym. Phys. 1958, 28, 619–622. [Google Scholar] [CrossRef]
- Antonietti, M.; Coutandin, J.; Sillescu, H. Diffusion of linear polystyrene molecules in matrixes of different molecular weights. Macromolecules 1986, 19, 793–798. [Google Scholar] [CrossRef]
- Higgins, J.S.; Roots, J.E. Effects of entanglements on the single-chain motion of polymer molecules in melt samples observed by neutron scattering. J. Chem. Soc. Faraday Trans. II 1985, 81, 757–767. [Google Scholar] [CrossRef]
- Pearson, D.S.; Fetters, L.J.; Graessley, W.W.; Ver Strate, G.; von Meerwall, E. Viscosity and self-diffusion coefficient of hydrogenated polybutadiene. Macromolecules 1994, 27, 711–719. [Google Scholar] [CrossRef]
- Smith, S.W.; Hall, C.K.; Freeman, B.D. Molecular dynamics study of entangled hard-chain fluids. J. Chem. Phys. 1996, 104, 5616–5637. [Google Scholar] [CrossRef]
- Faller, R. Influence of chain stiffness on structure and dynamics of polymers in the melt. Ph.D. thesis, University of Mainz, Mainz, Germany, 2000. [Google Scholar]
- Affouard, F.; Kröger, M.; Hess, S. Molecular dynamics of model liquid crystals composed of semiflexible molecules. Phys. Rev. E 1996, 54, 5178–5186. [Google Scholar] [CrossRef]
- Kröger, M.; Peleg, O.; Ding, Y.; Schlüter, A.D.; Öttinger, H.C. Formation of double helical and filamentous structures in models of physical and chemical gels. Soft Matter 2008, 4, 18–28. [Google Scholar] [CrossRef]
- Harasim, M.; Wunderlich, B.; Peleg, O.; Kröger, M.; Bausch, A. Direct observation of the dynamics of semiflexible polymers in shear flow. Phys. Rev. Lett. 2013, 110, 108302:1–108302:5. [Google Scholar] [CrossRef]
- Sukumaran, S.K.; Grest, G.S.; Kremer, K.; Everaers, R. Identifying the primitive path mesh in entangled polymer liquids. J. Polym. Sci. B 2005, 43, 917–933. [Google Scholar] [CrossRef]
- Uchida, N.; Grest, G.S.; Everaers, R. Viscoelasticity and primitive path analysis of entangled polymer liquids: From F-actin to polyethylene. J. Chem. Phys. 2008, 128, 044902:1–044902:6. [Google Scholar] [CrossRef] [PubMed]
- Hoy, R.S.; Robbins, M.O. Strain hardening of polymer glasses: Effect of entanglement density, temperature, and rate. J. Polym. Sci. B 2006, 44, 3487–3500. [Google Scholar] [CrossRef]
- Hoy, R.S.; Robbins, M.O. Strain hardening in polymer glasses: Limitations of network models. Phys. Rev. Lett. 2007, 99, 117801:1–117801:4. [Google Scholar] [CrossRef]
- Hoy, R.S. Why is understanding glassy polymer mechanics so difficult? J. Polym. Sci. B 2011, 49, 979–984. [Google Scholar] [CrossRef]
- Halverson, J.D.; Lee, W.B.; Grest, G.S.; Grosberg, A.Y.; Kremer, K. Molecular dynamics simulation study of nonconcatenated ring polymers in a melt. I. Statics. J. Chem. Phys. 2011, 134, 204904:1–204904:13. [Google Scholar] [CrossRef] [PubMed]
- Halverson, J.D.; Lee, W.B.; Grest, G.S.; Grosberg, A.Y.; Kremer, K. Molecular dynamics simulation study of nonconcatenated ring polymers in a melt. II. Dynamics. J. Chem. Phys. 2011, 134, 204905:1–204905:10. [Google Scholar] [CrossRef] [PubMed]
- Halverson, J.D.; Grest, G.S.; Grosberg, A.Y.; Kremer, K. Rheology of ring polymer melts: From linear contaminants to ring-linear blends. Phys. Rev. Lett. 2012, 108, 038301:1–038301:5. [Google Scholar] [CrossRef]
- Baljon, A.R.C.; van Weert, M.H.M.; DeGraaff, R.B.; Khare, R. Glass transition behavior of polymer films of nanoscopic dimensions. Macromolecules 2005, 38, 2391–2399. [Google Scholar] [CrossRef]
- Morita, H.; Tanaka, K.; Kajiyama, T.; Nishi, T.; Doi, M. Study of the glass transition temperature of polymer surface by coarse-grained molecular dynamics simulation. Macromolecules 2006, 39, 6233–6237. [Google Scholar] [CrossRef]
- Peter, S.; Meyer, H.; Baschnagel, J.; Seemann, R. Slow dynamics and glass transition in simulated free-standing polymer films: A possible relation between global and local glass transition temperatures. J. Phys. Condens. Matter 2007, 19, 205119:1–205119:11. [Google Scholar] [CrossRef]
- Barrat, J.L.; Baschnagel, J.; Lyulin, A. Molecular dynamics simulations of glassy polymers. Soft Matter 2010, 6, 3430–3446. [Google Scholar] [CrossRef]
- Kröger, M.; Makhloufi, R. Wormlike micelles under shear flow: A microscopic model studied by nonequilibrium molecular dynamics computer simulations. Phys. Rev. E 1996, 53, 2531–2536. [Google Scholar] [CrossRef]
- Li, S.F.; Sheng, N. On multiscale non-equilibrium molecular dynamics simulations. Int. J. Numer. Meth. Eng. 2010, 83, 998–1038. [Google Scholar] [CrossRef]
- Huang, C.C.; Ryckaert, J.P.; Xu, H. Structure and dynamics of cylindrical micelles at equilibrium and under shear flow. Phys. Rev. E 2009, 79, 041501:1–041501:13. [Google Scholar] [CrossRef]
- Padding, J.T.; Briels, W.J.; Stukan, M.R.; Boek, E.S. Review of multi-scale particulate simulation of the rheology of wormlike micellar fluids. Soft Matter 2009, 5, 4367–4375. [Google Scholar] [CrossRef]
- Lukyanov, A.; Likhtman, A. Dynamic surface tension effects from molecular dynamics simulations. Bull. Am. Phys. Soc. 2010, 55. Abstract ID: BAPS.2011.DFD.S26.9. [Google Scholar]
- Peter, S.; Napolitano, S.; Meyer, H.; Wubbenhorst, M.; Baschnagel, J. Modeling dielectric relaxation in polymer glass simulations: Dynamics in the bulk and in supported polymer films. Macromolecules 2008, 41, 7729–7743. [Google Scholar] [CrossRef]
- Yokomizo, K.; Banno, Y.; Kotaki, M. Molecular dynamics study on the effect of molecular orientation on polymer welding. Polymer 2012, 53, 4280–4286. [Google Scholar] [CrossRef]
- Ge, T.; Pierce, F.; Perahia, D.; Grest, G.S.; Robbins, M.O. Molecular dynamics simulations of polymer welding: Strength from interfacial entanglements. Phys. Rev. Lett. 2013, 110, 098301:1–098301:5. [Google Scholar] [CrossRef]
- Shanbhag, S.; Larson, R.G.; Takimoto, J.; Doi, M. Deviations from dynamic dilution in the terminal relaxation of star polymers. Phys. Rev. Lett. 2001, 87, 195502:1–195502:4. [Google Scholar] [CrossRef]
- Doi, M.; Takimoto, J.I. Molecular modelling of entanglement. Phil. Trans. R. Soc. Lond. A 2003, 361, 641–652. [Google Scholar] [CrossRef] [PubMed]
- Likhtman, A.E. Single-chain slip-link model of entangled polymers: Simultaneous description of neutron spin-echo, rheology, and diffusion. Macromolecules 2005, 38, 6128–6139. [Google Scholar] [CrossRef]
- Indei, T.; Schieber, J.D.; Takimoto, J.i. Effects of fluctuations of cross-linking points on viscoelastic properties of associating polymer networks. Rheol. Acta 2012, 51, 1021–1039. [Google Scholar] [CrossRef]
- Schieber, J.D.; Indei, T.; Steenbakkers, R.J.A. Fluctuating entanglements in single-chain mean-field models. Polymers 2013, 5, 643–678. [Google Scholar] [CrossRef]
- Masubuchi, Y.; Takimoto, J.I.; Koyama, K.; Ianniruberto, G.; Marrucci, G.; Greco, F. Brownian simulations of a network of reptating primitive chains. J. Chem. Phys. 2001, 115, 4387–4394. [Google Scholar] [CrossRef]
- Masubuchi, Y.; Ianniruberto, G.; Greco, F.; Marrucci, G. Entanglement molecular weight and frequency response of sliplink networks. J. Chem. Phys. 2003, 119, 6925–6930. [Google Scholar] [CrossRef]
- Masubuchi, Y.; Ianniruberto, G.; Greco, F.; Marrucci, G. Molecular simulations of the long-time behaviour of entangled polymeric liquids by the primitive chain network model. Model. Simul. Mater. Sci. Eng. 2004, 12, S91. [Google Scholar] [CrossRef]
- Masubuchi, Y.; Ianniruberto, G.; Greco, F.; Marrucci, G. Quantitative comparison of primitive chain network simulations with literature data of linear viscoelasticity for polymer melts. J. Non-Newtonian Fluid Mech. 2008, 149, 87–92. [Google Scholar] [CrossRef]
- Yaoita, T.; Isaki, T.; Masubuchi, Y.; Watanabe, H.; Ianniruberto, G.; Greco, F.; Marrucci, G. Highly entangled polymer primitive chain network simulations based on dynamic tube dilation. J. Chem. Phys. 2004, 121, 12650:1–12650:5. [Google Scholar] [CrossRef] [PubMed]
- Uneyama, T.; Masubuchi, Y. Multi-chain slip-spring model for entangled polymer dynamics. J. Chem. Phys. 2012, 137, 154902:1–154902:13. [Google Scholar] [CrossRef] [PubMed]
- Masubuchi, Y.; Ianniruberto, G.; Greco, F.; Marrucci, G. Primitive chain network simulations for branched polymers. Rheol. Acta 2006, 46, 297–303. [Google Scholar] [CrossRef]
- Yaoita, T.; Isaki, T.; Masubuchi, Y.; Watanabe, H.; Ianniruberto, G.; Greco, F.; Marrucci, G. Statics, linear, and nonlinear dynamics of entangled polystyrene melts simulated through the primitive chain network model. J. Chem. Phys. 2008, 128, 154901:1–154901:11. [Google Scholar] [CrossRef] [PubMed]
- Yaoita, T.; Isaki, T.; Masubuchi, Y.; Watanabe, H.; Ianniruberto, G.; Marrucci, G. Primitive chain network simulation of elongational flows of entangled linear chains: Role of finite chain extensibility. Macromolecules 2011, 44, 9675–9682. [Google Scholar] [CrossRef]
- Yaoita, T.; Isaki, T.; Masubuchi, Y.; Watanabe, H.; Ianniruberto, G.; Marrucci, G. Primitive chain network simulation of elongational flows of entangled linear chains: Stretch/orientation-induced reduction of monomeric friction. Macromolecules 2012, 45, 2773–2782. [Google Scholar] [CrossRef]
- Masubuchi, Y.; Watanabe, H.; Ianniruberto, G.; Greco, F.; Marrucci, G. Comparison among slip-link simulations of bidisperse linear polymer melts. Macromolecules 2008, 41, 8275–8280. [Google Scholar] [CrossRef]
- Lay, S.; Sommer, J.U.; Blumen, A. Monte Carlo study of the microphase separation of cross-linked polymer blends. J. Chem. Phys. 2000, 113, 11355–11363. [Google Scholar] [CrossRef]
- Masubuchi, Y.; Ianniruberto, G.; Greco, F.; Marrucci, G. Primitive chain network model for block copolymers. J. Non-Cryst. Solids 2006, 352, 5001–5007. [Google Scholar] [CrossRef]
- Okuda, S.; Inoue, Y.; Masubuchi, Y.; Uneyama, T.; Hojo, M. Wall boundary model for primitive chain network simulations. J. Chem. Phys. 2009, 130, 214907:1–214907:7. [Google Scholar] [CrossRef] [PubMed]
- Chappa, V.C.; Morse, D.C.; Zippelius, A.; Müller, M. Translationally invariant slip-spring model for entangled polymer dynamics. Phys. Rev. Lett. 2012, 109, 148302:1–148302:5. [Google Scholar] [CrossRef]
- Ramírez-Hernández, A.; Müller, M.; de Pablo, J.J. Theoretically informed entangled polymer simulations: Linear and non-linear rheology of melts. Soft Matter 2013, 9, 2030–2036. [Google Scholar] [CrossRef]
- Hess, B.; Holm, C.; van der Vegt, N. Osmotic coefficients of atomistic NaCl (aq) force fields. J. Chem. Phys. 2006, 124, 164509:1–164509:8. [Google Scholar] [CrossRef] [PubMed]
- Hess, B.; Holm, C.; van der Vegt, N. Modeling multibody effects in ionic solutions with a concentration dependent dielectric permittivity. Phys. Rev. Lett. 2006, 96, 147801:1–147801:4. [Google Scholar] [CrossRef]
- Wang, Y.; Noid, W.; Liu, P.; Voth, G.A. Effective force coarse-graining. Phys. Chem. Chem. Phys. 2009, 11, 2002–2015. [Google Scholar] [CrossRef] [PubMed]
- Brini, E.; Marcon, V.; van der Vegt, N.F. Conditional reversible work method for molecular coarse graining applications. Phys. Chem. Chem. Phys. 2011, 13, 10468–10474. [Google Scholar] [CrossRef] [PubMed]
- Ganguly, P.; Mukherji, D.; Junghans, C.; van der Vegt, N.F. Kirkwood–buff coarse-grained force fields for aqueous solutions. J. Chem. Theory Comput. 2012, 8, 1802–1807. [Google Scholar] [CrossRef]
- Lyubartsev, A.P.; Laaksonen, A. Calculation of effective interaction potentials from radial distribution functions: A reverse Monte Carlo approach. Phys. Rev. E 1995, 52, 3730–3737. [Google Scholar] [CrossRef]
- Shell, M.S. The relative entropy is fundamental to multiscale and inverse thermodynamic problems. J. Chem. Phys. 2008, 129, 144108:1–144108:7. [Google Scholar] [CrossRef] [PubMed]
- Mullinax, J.; Noid, W. Reference state for the generalized Yvon–Born–Green theory: Application for coarse-grained model of hydrophobic hydration. J. Chem. Phys. 2010, 133, 124107:1–124107:11. [Google Scholar] [CrossRef] [PubMed]
- Ercolessi, F.; Adams, J.B. Interatomic potentials from first-principles calculations: The force-matching method. EPL (Europhys. Lett.) 1994, 26, 583–588. [Google Scholar] [CrossRef]
- Izvekov, S.; Voth, G.A. A multiscale coarse-graining method for biomolecular systems. J. Phys. Chem. B 2005, 109, 2469–2473. [Google Scholar] [CrossRef] [PubMed]
- Izvekov, S.; Voth, G.A. Multiscale coarse graining of liquid-state systems. J. Chem. Phys. 2005, 123, 134105:1–134105:13. [Google Scholar] [CrossRef] [PubMed]
- Noid, W.G.; Chu, J.W.; Ayton, G.S.; Voth, G.A. Multiscale coarse-graining and structural correlations: Connections to liquid-state theory. J. Phys. Chem. B 2007, 111, 4116–4127. [Google Scholar] [CrossRef] [PubMed]
- Noid, W.G.; Chu, J.W.; Ayton, G.S.; Krishna, V.; Izvekov, S.; Voth, G.A.; Das, A.; Andersen, H.C. The multiscale coarse-graining method. I. A rigorous bridge between atomistic and coarse-grained models. J. Chem. Phys. 2008, 128, 244114:1–244114:11. [Google Scholar] [CrossRef] [PubMed]
- Noid, W.G.; Liu, P.; Wang, Y.; Chu, J.W.; Ayton, G.S.; Izvekov, S.; Andersen, H.C.; Voth, G.A. The multiscale coarse-graining method. II. Numerical implementation for coarse-grained molecular models. J. Chem. Phys. 2008, 128, 244115:1–244115:20. [Google Scholar] [CrossRef] [PubMed]
- Rühle, V.; Junghans, C.; Lukyanov, A.; Kremer, K.; Andrienko, D. Versatile object-oriented toolkit for coarse-graining applications. J. Chem. Theory Comput. 2009, 5, 3211–3223. [Google Scholar] [CrossRef]
- Hansen, J.P.; McDonald, I.R. Theory of Simple Liquids; Academic Press: Waltham, MA, USA, 2006. [Google Scholar]
- Tschöp, W.; Kremer, K.; Hahn, O.; Batoulis, J.; Bürger, T. Simulation of polymer melts. II. From coarse-grained models back to atomistic description. Acta Polym. 1998, 49, 75–79. [Google Scholar] [CrossRef]
- Tschöp, W.; Kremer, K.; Batoulis, J.; Bürger, T.; Hahn, O. Simulation of polymer melts. I. Coarse-graining procedure for polycarbonates. Acta Polym. 1999, 49, 61–74. [Google Scholar] [CrossRef]
- Li, Y.; Kröger, M.; Liu, W.K. Primitive chain network study on uncrosslinked and crosslinked cis-polyisoprene polymers. Polymer 2011, 52, 5867–5878. [Google Scholar] [CrossRef]
- Accelrys, 2012. Available online: http://accelrys.com/products/materials-studio/ (accessed on 7 June 2013).
- Sun, H. COMPASS: An ab initio force-field optimized for condensed-phase applications overview with details on alkane and benzene compounds. J. Phys. Chem. B 1998, 102, 7338–7364. [Google Scholar] [CrossRef]
- Doxastakis, M.; Mavrantzas, V.; Theodorou, D. Atomistic Monte Carlo simulation of cis-1,4 polyisoprene melts. I. Single temperature end-bridging Monte Carlo simulations. J. Chem. Phys. 2001, 115, 11339:1–11339:13. [Google Scholar] [CrossRef]
- Faller, R.; Müller-Plathe, F.; Doxastakis, M.; Theodorou, D.N. Local structure and dynamics of trans-polyisoprene oligomers. Macromolecules 2001, 34, 1436–1448. [Google Scholar] [CrossRef]
- Faller, R.; Müller-Plathe, F. Modeling of poly (isoprene) melts on different scales. Polymer 2002, 43, 621–628. [Google Scholar] [CrossRef]
- Faller, R.; Reith, D. Properties of poly (isoprene): Model building in the melt and in solution. Macromolecules 2003, 36, 5406–5414. [Google Scholar] [CrossRef]
- Sun, Q.; Faller, R. Systematic coarse-graining of atomistic models for simulation of polymeric systems. Comp. Chem. Eng. 2005, 29, 2380–2385. [Google Scholar] [CrossRef]
- Sun, Q.; Faller, R. Systematic coarse-graining of a polymer blend: Polyisoprene and polystyrene. J. Chem. Theor. Comput. 2006, 2, 607–615. [Google Scholar] [CrossRef]
- Ramachandran, G.N.; Ramakrishnan, C.; Sasisekharan, V. Stereochemistry of polypeptide chain configurations. J. Mol. Biol. 1963, 7, 95–99. [Google Scholar] [CrossRef]
- Harmandaris, V.A.; Reith, D.; van der Vegt, N.F.A.; Kremer, K. Comparison between coarse-graining models for polymer systems: Two mapping schemes for polystyrene. Macromol. Chem. Phys. 2007, 208, 2109–2120. [Google Scholar] [CrossRef]
- McCoy, J.D.; Curro, J.G. Mapping of explicit atom onto united atom potentials. Macromolecules 1998, 31, 9362–9368. [Google Scholar] [CrossRef]
- Akkermans, R.L.C.; Briels, W.J. A structure-based coarse-grained model for polymer melts. J. Chem. Phys. 2001, 114, 1020–1031. [Google Scholar] [CrossRef]
- Reith, D.; Meyer, H.; Müller-Plathe, F. Mapping atomistic to coarse-grained polymer models using automatic simplex optimization to fit structural properties. Macromolecules 2001, 34, 2335–2345. [Google Scholar] [CrossRef]
- Hahn, O.; Site, L.D.; Kremer, K. Simulation of polymer melts: From spherical to ellipsoidal beads. Macromol. Theory Simul. 2001, 10, 288–303. [Google Scholar] [CrossRef]
- Xie, G.; Zhang, Y.; Huang, S. Glass formation of n-butanol: Coarse-grained molecular dynamics simulations using Gay-Berne potential model. Chin. J. Chem. Phys. 2012, 25, 177–185. [Google Scholar] [CrossRef]
- Abrams, C.F.; Kremer, K. Combined coarse-grained and atomistic simulation of liquid bisphenol A-polycarbonate: Liquid packing and intramolecular structure. Macromolecules 2003, 36, 260–267. [Google Scholar] [CrossRef]
- Müller-Plathe, F. Local structure and dynamics in solvent-swollen polymers. Macromolecules 1996, 29, 4782–4791. [Google Scholar] [CrossRef]
- Milano, G.; Goudeau, S.; Müller-Plathe, F. Multicentered Gaussian-based potentials for coarse-grained polymer simulations: Linking atomistic and mesoscopic scales. J. Polym. Sci. B 2005, 43, 871–885. [Google Scholar] [CrossRef]
- Milano, G.; Müller-Plathe, F. Mapping atomistic simulations to mesoscopic models: A systematic coarse-graining procedure for vinyl polymer chains. J. Phys. Chem. B 2005, 109, 18609–18619. [Google Scholar] [CrossRef] [PubMed]
- Spyriouni, T.; Tzoumanekas, C.; Theodorou, D.; Müller-Plathe, F.; Milano, G. Coarse-grained and reverse-mapped united-atom simulations of long-chain atactic polystyrene melts: Structure, thermodynamic properties, chain conformation, and entanglements. Macromolecules 2007, 40, 3876–3885. [Google Scholar] [CrossRef]
- Fetters, L.J.; Lohse, D.J.; Richter, D.; Witten, T.A.; Zirkel, A. Connection between polymer molecular weight, density, chain dimensions, and melt viscoelastic properties. Macromolecules 1994, 27, 4639–4647. [Google Scholar] [CrossRef]
- Sun, Q.; Faller, R. Crossover from unentangled to entangled dynamics in a systematically coarse-grained polystyrene melt. Macromolecules 2006, 39, 812–820. [Google Scholar] [CrossRef]
- Harmandaris, V.A.; Adhikari, N.P.; van Der Vegt, N.F.A.; Kremer, K. Hierarchical modeling of polystyrene: From atomistic to coarse-grained simulations. Macromolecules 2006, 39, 6708–6719. [Google Scholar] [CrossRef]
- Mulder, T.; Harmandaris, V.A.; Lyulin, A.V.; van der Vegt, N.F.A.; Vorselaars, B.; Michels, M.A.J. Equilibration and deformation of amorphous polystyrene: Scale-jumping simulational approach. Macromol. Theory Simul. 2008, 17, 290–300. [Google Scholar] [CrossRef]
- Mulder, T.; Harmandaris, V.A.; Lyulin, A.V.; van der Vegt, N.F.A.; Kremer, K.; Michels, M.A.J. Structural properties of atactic polystyrene of different thermal history obtained from a multiscale simulation. Macromolecules 2009, 42, 384–391. [Google Scholar] [CrossRef]
- Harmandaris, V.A.; Kremer, K. Dynamics of polystyrene melts through hierarchical multiscale simulations. Macromolecules 2009, 42, 791–802. [Google Scholar] [CrossRef]
- Harmandaris, V.A.; Kremer, K. Predicting polymer dynamics at multiple length and time scales. Soft Matter 2009, 5, 3920–3926. [Google Scholar] [CrossRef]
- Varzaneh, H.A.K.; Chen, X.; Carbone, P.; Qian, H.J.; Müller-Plathe, F. 2008. Available online: http://www.theo.chemie.tu-darmstadt.de/ibisco/IBISCO.html (accessed on 7 June 2013).
- Karimi-Varzaneh, H.A.; Qian, H.J.; Chen, X.; Carbone, P.; Müller-Plathe, F. IBIsCO: A molecular dynamics simulation package for coarse-grained simulation. J. Comput. Chem. 2011, 32, 1475–1487. [Google Scholar] [CrossRef] [PubMed]
- Luo, C.; Sommer, J.U. Coding coarse grained polymer model for LAMMPS and its application to polymer crystallization. Comput. Phys. Commun. 2009, 180, 1382–1391. [Google Scholar] [CrossRef]
- Plimpton, S. Fast parallel algorithms for short-range molecular dynamics. J. Comput. Phys. 1995, 117, 1–19. [Google Scholar] [CrossRef]
- Faller, R.; Schmitz, H.; Biermann, O.; Müller-Plathe, F. Automatic parameterization of force fields for liquids by simplex optimization. J. Comput. Chem. 1999, 20, 1009–1017. [Google Scholar] [CrossRef]
- Reith, D.; Meyer, H.; Müller-Plathe, F. CG-OPT: A software package for automatic force field design. Comput. Phys. Commun. 2002, 148, 299–313. [Google Scholar] [CrossRef]
- Reith, D.; Pütz, M.; Müller-Plathe, F. Deriving effective mesoscale potentials from atomistic simulations. J. Comput. Chem. 2003, 24, 1624–1636. [Google Scholar] [CrossRef] [PubMed]
- Murtola, T.; Falck, E.; Karttunen, M.; Vattulainen, I. Coarse-grained model for phospholipid/cholesterol bilayer employing inverse Monte Carlo with thermodynamic constraints. J. Chem. Phys. 2007, 126, 075101:1–075101:14. [Google Scholar] [CrossRef] [PubMed]
- Wang, Q.; Keffer, D.J.; Nicholson, D.M.; Thomas, J.B. Use of the Ornstein-Zernike Percus-Yevick equation to extract interaction potentials from pair correlation functions. Phys. Rev. E 2010, 81, 061204:1–061204:9. [Google Scholar] [CrossRef]
- Wang, Q.; Keffer, D.J.; Nicholson, D.M.; Thomas, J.B. Coarse-grained molecular dynamics simulation of polyethylene terephthalate (PET). Macromolecules 2010, 43, 10722–10734. [Google Scholar] [CrossRef]
- Batchelor, G.K. An Introduction to Fluid Dynamics; Cambridge University Press: New York, NY, USA, 2000. [Google Scholar]
- Lyubimov, I.Y.; McCarty, J.; Clark, A.; Guenza, M.G. Analytical rescaling of polymer dynamics from mesoscale simulations. J. Chem. Phys. 2010, 132, 224903:1–224903:5. [Google Scholar] [CrossRef] [PubMed]
- Lyubimov, I.; Guenza, M.G. First-principle approach to rescale the dynamics of simulated coarse-grained macromolecular liquids. Phys. Rev. E 2011, 84, 031801:1–031801:19. [Google Scholar] [CrossRef]
- Harmandaris, V.A.; Floudas, G.; Kremer, K. Temperature and pressure dependence of polystyrene dynamics through molecular dynamics simulations and experiments. Macromolecules 2010, 44, 393–402. [Google Scholar] [CrossRef]
- Fritz, D.; Harmandaris, V.A.; Kremer, K.; van Der Vegt, N.F.A. Coarse-grained polymer melts based on isolated atomistic chains: Simulation of polystyrene of different tacticities. Macromolecules 2009, 42, 7579–7588. [Google Scholar] [CrossRef]
- Leon, S.; van Der Vegt, N.; Delle Site, L.; Kremer, K. Bisphenol A polycarbonate: Entanglement analysis from coarse-grained MD simulations. Macromolecules 2005, 38, 8078–8092. [Google Scholar] [CrossRef]
- Depa, P.K.; Maranas, J.K. Speed up of dynamic observables in coarse-grained molecular-dynamics simulations of unentangled polymers. J. Chem. Phys. 2005, 123, 094901:1–094901:7. [Google Scholar] [CrossRef] [PubMed]
- Depa, P.K.; Maranas, J.K. Dynamic evolution in coarse-grained molecular dynamics simulations of polyethylene melts. J. Chem. Phys. 2007, 126, 054903:1–054903:8. [Google Scholar] [CrossRef] [PubMed]
- Chen, C.; Depa, P.; Sakai, V.G.; Maranas, J.K.; Lynn, J.W.; Peral, I.; Copley, J.R.D. A comparison of united atom, explicit atom, and coarse-grained simulation models for poly (ethylene oxide). J. Chem. Phys. 2006, 124, 234901:1–234901:11. [Google Scholar] [CrossRef] [PubMed]
- Chen, C.; Depa, P.; Maranas, J.K.; Garcia Sakai, V. Comparison of explicit atom, united atom, and coarse-grained simulations of poly (methyl methacrylate). J. Chem. Phys. 2008, 128, 124906:1–124906:12. [Google Scholar] [CrossRef] [PubMed]
- Strauch, T.; Yelash, L.; Paul, W. A coarse-graining procedure for polymer melts applied to 1, 4-polybutadiene. Phys. Chem. Chem. Phys. 2009, 11, 1942–1948. [Google Scholar] [CrossRef] [PubMed]
- Karimi-Varzaneh, H.; Müller-Plathe, F. Coarse-Grained Modeling for Macromolecular Chemistry. In Multiscale Molecular Methods in Applied Chemistry; Springer: New York, NY, USA, 2012; pp. 295–321. [Google Scholar]
- Colmenero, J.; Arbe, A. Segmental dynamics in miscible polymer blends: Recent results and open questions. Soft Matter 2007, 3, 1474–1485. [Google Scholar] [CrossRef]
- Roland, C.; Ngai, K. Dynamical heterogeneity in a miscible polymer blend. Macromolecules 1991, 24, 2261–2265. [Google Scholar] [CrossRef]
- Louis, A.A. Beware of density dependent pair potentials. J. Phys. Condens. Matter 2002, 14, 9187–9206. [Google Scholar] [CrossRef]
- Fukunaga, H.; Takimoto, J.; Doi, M. A coarse-graining procedure for flexible polymer chains with bonded and nonbonded interactions. J. Chem. Phys. 2002, 116, 8183–8190. [Google Scholar] [CrossRef]
- Carbone, P.; Varzaneh, H.A.K.; Chen, X.; Müller-Plathe, F. Transferability of coarse-grained force fields: The polymer case. J. Chem. Phys. 2008, 128, 064904:1–064904:11. [Google Scholar] [CrossRef] [PubMed]
- Marrink, S.J.; de Vries, A.H.; Mark, A.E. Coarse grained model for semiquantitative lipid simulations. J. Phys. Chem. B 2004, 108, 750–760. [Google Scholar] [CrossRef]
- Harmandaris, V.A.; Adhikari, N.P.; van der Vegt, N.F.A.; Kremer, K.; Mann, B.A.; Voelkel, R.; Weiss, H.; Liew, C.C. Ethylbenzene diffusion in polystyrene: United atom atomistic/coarse grained simulations and experiments. Macromolecules 2007, 40, 7026–7035. [Google Scholar] [CrossRef]
- Hess, B.; León, S.; van Der Vegt, N.; Kremer, K. Long time atomistic polymer trajectories from coarse grained simulations: Bisphenol-A polycarbonate. Soft Matter 2006, 2, 409–414. [Google Scholar] [CrossRef]
- Öttinger, H.C. Systematic coarse graining: Four lessons and a caveat from nonequilibrium statistical mechanics. MRS Bull. 2007, 32, 936–940. [Google Scholar] [CrossRef]
- Vettorel, T.; Meyer, H. Coarse graining of short polythylene chains for studying polymer crystallization. J. Chem. Theory Comput. 2006, 2, 616–629. [Google Scholar] [CrossRef]
- Yelash, L.; Müller, M.; Paul, W.; Binder, K. How well can coarse-grained models of real polymers describe their structure? the case of polybutadiene. J. Chem. Theory Comput. 2006, 2, 588–597. [Google Scholar] [CrossRef]
- Eslami, H.; Karimi-Varzaneh, H.A.; Müller-Plathe, F. Coarse-grained computer simulation of nanoconfined polyamide-6, 6. Macromolecules 2011, 44, 3117–3128. [Google Scholar] [CrossRef]
- Bayramoglu, B.; Faller, R. Coarse-grained modeling of polystyrene in various environments by iterative Boltzmann inversion. Macromolecules 2012, 45, 9205–9219. [Google Scholar] [CrossRef]
- Pérez-Aparicio, R.; Colmenero, J.; Alvarez, F.; Padding, J.T.; Briels, W.J. Chain dynamics of poly (ethylene-alt-propylene) melts by means of coarse-grained simulations based on atomistic molecular dynamics. J. Chem. Phys. 2010, 132, 024904:1–024904:11. [Google Scholar] [CrossRef] [PubMed]
- Hoy, R.; Foteinopoulou, K.; Kröger, M. Topological analysis of polymeric melts: Chain-length effects and fast-converging estimators for entanglement length. Phys. Rev. E 2009, 80, 031803:1–031803:13. [Google Scholar] [CrossRef]
- Padding, J.T.; Briels, W.J. Zero-shear stress relaxation and long time dynamics of a linear polyethylene melt: A test of Rouse theory. J. Chem. Phys. 2001, 114, 8685–8693. [Google Scholar] [CrossRef]
- Malkin, A.; Semakov, A.; Kulichikhin, V. Macroscopic modeling of a single entanglement at high deformation rates of polymer melts. Appl. Rheol. 2012, 22, 32575:1–32575:9. [Google Scholar]
- Padding, J.T.; Briels, W.J. TWENTANGLEMENT User’s Manual; Twente University: Enschede, the Netherlands, 2000. [Google Scholar]
- Nikunen, P.; Vattulainen, I.; Karttunen, M. Reptational dynamics in dissipative particle dynamics simulations of polymer melts. Phys. Rev. E 2007, 75, 036713:1–036713:7. [Google Scholar] [CrossRef]
- Karatrantos, A.; Clarke, N.; Composto, R.J.; Winey, K.I. Topological entanglement length in polymer melts and nanocomposites by a DPD polymer model. Soft Matter 2013, 9, 3877–3884. [Google Scholar] [CrossRef]
- Karatrantos, A.; Composto, R.J.; Winey, K.I.; Kröger, M.; Clarke, N. Entanglements and dynamics of polymer melts near a SWCNT. Macromolecules 2012, 45, 7274–7281. [Google Scholar] [CrossRef]
- Goujon, F.; Malfreyt, P.; Tildesley, D.J. Mesoscopic simulation of entanglements using dissipative particle dynamics: Application to polymer brushes. J. Chem. Phys. 2008, 129, 034902. [Google Scholar] [CrossRef] [PubMed]
- Kumar, S.; Larson, R.G. Brownian dynamics simulations of flexible polymers with spring–spring repulsions. J. Chem. Phys. 2001, 114, 6937–6941. [Google Scholar] [CrossRef]
- Pearson, D.S.; Ver Strate, G.; von Meerwall, E.; Schilling, F.C. Viscosity and self-diffusion coefficient of linear polyethylene. Macromolecules 1987, 20, 1133–1141. [Google Scholar] [CrossRef]
- Paul, W.; Smith, G.D.; Yoon, D.Y. Static and dynamic properties of an-C100H202 melt from molecular dynamics simulations. Macromolecules 1997, 30, 7772–7780. [Google Scholar] [CrossRef]
- D’Adamo, G.; Pelissetto, A.; Pierleoni, C. Coarse-graining strategies in polymer solutions. Soft Matter 2012, 8, 5151–5167. [Google Scholar] [CrossRef]
- D’Adamo, G.; Pelissetto, A.; Pierleoni, C. Polymers as compressible soft spheres. J. Chem. Phys. 2012, 136, 224905:1–224905:9. [Google Scholar] [CrossRef] [PubMed]
- Vettorel, T.; Besold, G.; Kremer, K. Fluctuating soft-sphere approach to coarse-graining of polymer models. Soft Matter 2010, 6, 2282–2292. [Google Scholar] [CrossRef]
- Zhang, G.; Daoulas, K.C.; Kremer, K. A new coarse grained particle-to-mesh scheme for modeling soft matter. Macromol. Chem. Phys. 2013, 214, 214–224. [Google Scholar] [CrossRef]
- Briels, W.J. Theory of Polymer Dynamics. In Lecture Notes; Uppsala University: Uppsala, Sweden, 1994. [Google Scholar]
- Zhu, Y.L.; Liu, H.; Lu, Z.Y. A highly coarse-grained model to simulate entangled polymer melts. J. Chem. Phys. 2012, 136, 144903:1–144903:7. [Google Scholar] [CrossRef] [PubMed]
- Briels, W.J. Transient forces in flowing soft matter. Soft Matter 2009, 5, 4401–4411. [Google Scholar] [CrossRef]
- Kröger, M.; Ramirez, R.; Öttinger, H.C. Projection from an atomistic chain contour to its primitive path. Polymer 2002, 43, 477–487. [Google Scholar] [CrossRef]
- Sprakel, J.; Padding, J.T.; Briels, W.J. Transient forces and non-equilibrium states in sheared polymer networks. EPL (Europhys. Lett.) 2011, 93, 58003:1–58003:6. [Google Scholar] [CrossRef]
- Savin, T.; Briels, W.J.; Öttinger, H.C. Thermodynamic formulation of flowing soft matter with transient forces. Rheol. Acta 2013, 52, 23–32. [Google Scholar] [CrossRef]
- Sprakel, J.; Spruijt, E.; van der Gucht, J.; Padding, J.T.; Briels, W.J. Failure-mode transition in transient polymer networks with particle-based simulations. Soft Matter 2009, 5, 4748–4756. [Google Scholar] [CrossRef]
- Padding, J.T.; van Ruymbeke, E.; Vlassopoulos, D.; Briels, W.J. Computer simulation of the rheology of concentrated star polymer suspensions. Rheol. Acta 2010, 49, 473–484. [Google Scholar] [CrossRef]
- Padding, J.T.; Mohite, L.V.; Auhl, D.; Briels, W.J.; Bailly, C. Mesoscale modeling of the rheology of pressure sensitive adhesives through inclusion of transient forces. Soft Matter 2011, 7, 5036–5046. [Google Scholar] [CrossRef]
- Padding, J.T.; Mohite, L.V.; Auhl, D.; Schweizer, T.; Briels, W.J.; Bailly, C. Quantitative mesoscale modeling of the oscillatory and transient shear rheology and the extensional rheology of pressure sensitive adhesives. Soft Matter 2012, 8, 7967–7981. [Google Scholar] [CrossRef]
- Savin, T.; Briels, W.J.; Öttinger, H.C. Thermodynamic formulation of flowing soft matter with transient forces. Rheol. Acta 2013, 52, 23–32. [Google Scholar] [CrossRef]
- Clark, A.J.; Guenza, M.G. Mapping of polymer melts onto liquids of soft-colloidal chains. J. Chem. Phys. 2010, 132, 044902:1–044902:12. [Google Scholar] [CrossRef] [PubMed]
- McCarty, J.; Guenza, M. How reliable are soft potentials? Ensuring thermodynamic consistency between hierarchical models of polymer melts. Bull. Am. Phys. Soc. 2012, 57. Abstract ID: BAPS.2012.MAR.W48.2. [Google Scholar]
- McCarty, J.; Clark, A.J.; Lyubimov, I.Y.; Guenza, M.G. Thermodynamic consistency between analytic integral equation theory and coarse-grained molecular dynamics simulations of homopolymer melts. Macromolecules 2012, 45, 8482–8493. [Google Scholar] [CrossRef]
- Clark, A.J.; McCarty, J.; Lyubimov, I.Y.; Guenza, M.G. Thermodynamic consistency in variable-level coarse graining of polymeric liquids. Phys. Rev. Lett. 2012, 109, 168301:1–168301:5. [Google Scholar] [CrossRef]
- Lyubimov, I.Y.; Guenza, M.G. Theoretical reconstruction of realistic dynamics of highly coarse-grained cis-1,4-polybutadiene melts. J. Chem. Phys 2013, 138, 12A546:1–12A546:13. [Google Scholar] [CrossRef] [PubMed]
- Krakoviack, V.; Hansen, J.P.; Louis, A.A. Relating monomer to centre-of-mass distribution functions in polymer solutions. EPL (Europhys. Lett.) 2007, 58, 53–59. [Google Scholar] [CrossRef]
- Sambriski, E.J.; Yatsenko, G.; Nemirovskaya, M.A.; Guenza, M.G. Bridging length scales in polymer melt relaxation for macromolecules with specific local structures. J. Phys. Condens. Matter 2007, 19, 205115:1–205115:11. [Google Scholar] [CrossRef]
- Kröger, M.; Ramïrez, J.; Christian Öttinger, H. Projection from an atomistic chain contour to its primitive path. Polymer 2002, 43, 477–487. [Google Scholar] [CrossRef]
- Zhou, Q.; Larson, R.G. Primitive path identification and statistics in molecular dynamics simulations of entangled polymer melts. Macromolecules 2005, 38, 5761–5765. [Google Scholar] [CrossRef]
- Foteinopoulou, K.; Karayiannis, N.C.; Mavrantzas, V.G.; Kröger, M. Primitive path identification and entanglement statistics in polymer melts: Results from direct topological analysis on atomistic polyethylene models. Macromolecules 2006, 39, 4207–4216. [Google Scholar] [CrossRef]
- Alemán, C.; Karayiannis, N.C.; Curcó, D.; Foteinopoulou, K.; Laso, M. Computer simulations of amorphous polymers: From quantum mechanical calculations to mesoscopic models. J. Mol. Struct. 2009, 898, 62–72. [Google Scholar] [CrossRef]
- Karayiannis, N.C.; Kröger, M. Combined molecular algorithms for the generation, equilibration and topological analysis of entangled polymers: Methodology and performance. Int. J. Mol. Sci. 2009, 10, 5054–5089. [Google Scholar] [CrossRef] [PubMed]
- Kremer, K.; Sukumaran, S.K.; Everaers, R.; Grest, G.S. Entangled polymer systems. Comput. Phys. Commun. 2005, 169, 75–81. [Google Scholar] [CrossRef]
- Kröger, M. Shortest multiple disconnected path for the analysis of entanglements in two-and three-dimensional polymeric systems. Comput. Phys. Commun. 2005, 168, 209–232. [Google Scholar] [CrossRef]
- Tzoumanekas, C.; Theodorou, D.N. From atomistic simulations to slip-link models of entangled polymer melts: Hierarchical strategies for the prediction of rheological properties. Curr. Opin. Solid State Mater. Sci. 2006, 10, 61–72. [Google Scholar] [CrossRef]
- Tzoumanekas, C.; Theodorou, D.N. Topological analysis of linear polymer melts: A statistical approach. Macromolecules 2006, 39, 4592–4604. [Google Scholar] [CrossRef]
- Tzoumanekas, C.; Lahmar, F.; Rousseau, B.; Theodorou, D.N. Onset of entanglements revisited. Topological analysis. Macromolecules 2009, 42, 7474–7484. [Google Scholar] [CrossRef]
- Anogiannakis, S.D.; Tzoumanekas, C.; Theodorou, D.N. Microscopic description of entanglements in polyethylene networks and melts: Strong, weak, pairwise, and collective attributes. Macromolecules 2012, 45, 9475–9492. [Google Scholar] [CrossRef]
- Everaers, R. Topological versus rheological entanglement length in primitive-path analysis protocols, tube models, and slip-link models. Phys. Rev. E 2012, 86, 022801:1–022801:5. [Google Scholar] [CrossRef]
- Shanbhag, S.; Kröger, M. Primitive path networks generated by annealing and geometrical methods: Insights into differences. Macromolecules 2007, 40, 2897–2903. [Google Scholar] [CrossRef]
- Khaliullin, R.N.; Schieber, J.D. Analytic expressions for the statistics of the primitive-path length in entangled polymers. Phys. Rev. Lett. 2008, 100, 188302:1–188302:4. [Google Scholar] [CrossRef]
- Steenbakkers, R.J.; Schieber, J.D. Derivation of free energy expressions for tube models from coarse-grained slip-link models. J. Chem. Phys. 2012, 137, 034901:1–034901:19. [Google Scholar] [CrossRef] [PubMed]
- Steenbakkers, R.J.; Li, Y.; Liu, W.K.; Kröger, M.; Schieber, J.D. Primitive-path statistics of entangled polymers: Mapping multi-chain simulations onto single-chain mean-field models. New J. Phys. 2013. submitted for publication. [Google Scholar] [CrossRef]
- Baig, C.; Mavrantzas, V.G. From atomistic trajectories to primitive paths to tube models: Linking atomistic simulations with the reptation theory of polymer dynamics. Soft Matter 2010, 6, 4603–4612. [Google Scholar] [CrossRef]
- Stephanou, P.S.; Baig, C.; Mavrantzas, V.G. Projection of atomistic simulation data for the dynamics of entangled polymers onto the tube theory: Calculation of the segment survival probability function and comparison with modern tube models. Soft Matter 2011, 7, 380–395. [Google Scholar] [CrossRef]
- Stephanou, P.S.; Baig, C.; Mavrantzas, V.G. Toward an improved description of constraint release and contour length fluctuations in tube models for entangled polymer melts guided by atomistic simulations. Macromol. Theory Simul. 2011, 20, 752–768. [Google Scholar] [CrossRef]
- Lodge, T.P. Reconciliation of the molecular weight dependence of diffusion and viscosity in entangled polymers. Phys. Rev. Lett. 1999, 83, 3218–3221. [Google Scholar] [CrossRef]
- Viovy, J.L. Constraint release in the slip-link model and the viscoelastic properties of polymers. J. Phys. 1985, 46, 847–853. [Google Scholar] [CrossRef]
- Marrucci, G. Relaxation by reptation and tube enlargement: A model for polydisperse polymers. J. Polym. Sci. Polym. Phys. 1985, 23, 159–177. [Google Scholar] [CrossRef]
- Pattamaprom, C.; Larson, R.G.; Sirivat, A. Determining polymer molecular weight distributions from rheological properties using the dual-constraint model. Rheol. Acta 2008, 47, 689–700. [Google Scholar] [CrossRef]
- Pattamaprom, C.; Larson, R.G.; Van Dyke, T.J. Quantitative predictions of linear viscoelastic rheological properties of entangled polymers. Rheol. Acta 2000, 39, 517–531. [Google Scholar] [CrossRef]
- Ilg, P.; Kröger, M. Molecularly derived constitutive equation for low-molecular polymer melts from thermodynamically guided simulation. J. Rheol. 2010, 55, 69–93. [Google Scholar] [CrossRef]
- Ilg, P. Thermodynamically consistent coarse graining the non-equilibrium dynamics of unentangled polymer melts. J. Non-Newtonian Fluid Mech. 2010, 165, 973–979. [Google Scholar] [CrossRef]
- Ilg, P.; Mavrantzas, V.G.; Öttinger, H.C. Multiscale Modeling and Coarse Graining of Polymer Dynamics: Simulations Guided by Statistical Beyond-equilibrium Thermodynamics. In Modeling and Simulations in Polymers; Wiley-VCH: Weinheim, Germany, 2010. [Google Scholar]
- Jelić, A.; Ilg, P.; Öttinger, H.C. Bridging length and time scales in sheared demixing systems: From the Cahn-Hilliard to the Doi-Ohta model. Phys. Rev. E 2010, 81, 011131:1–011131:13. [Google Scholar] [CrossRef]
- Ilg, P. Enhanced Landau–de Gennes potential for nematic liquid crystals from a systematic coarse-graining procedure. Phys. Rev. E 2012, 85, 061709:1–061709:9. [Google Scholar] [CrossRef]
- Ilg, P.; Hütter, M.; Kröger, M. Ideal contribution to the macroscopic, quasiequilibrium entropy of anisotropic fluids. Phys. Rev. E 2011, 83, 061713:1–061713:7. [Google Scholar] [CrossRef]
- Ilg, P.; Karlin, I.V.; Kröger, M.; Hess, S. Canonical distribution functions in polymer dynamics: II Liquid-crystalline polymers. Physica A 2003, 319, 134–150. [Google Scholar] [CrossRef]
- Gupta, B.; Ilg, P. Energetic and entropic contributions to the Landau–de Gennes Potential for Gay–Berne Models of Liquid Crystals. Polymers 2013, 5, 328–343. [Google Scholar] [CrossRef]
- Ilg, P.; Kröger, M.; Hess, S. Magnetoviscosity of semi-dilute ferrofluids and the role of dipolar interactions: Comparison of molecular simulation and dynamical mean-field theory. Phys. Rev. E 2005, 71, 031205:1–031205:11. [Google Scholar] [CrossRef]
- Kröger, M.; Ilg, P.; Hess, S. Magnetoviscous model fluids. J. Phys. Condens. Matter 2003, 15, S1403–S1423. [Google Scholar] [CrossRef]
- Öttinger, H.C. Beyond Equilibrium Thermodynamics; Wiley-Interscience: Hoboken, NJ, USA, 2005. [Google Scholar]
- Kröger, M.; Hütter, M. Automated symbolic calculations in nonequilibrium thermodynamics. Comput. Phys. Commun. 2010, 181, 2149–2157. [Google Scholar] [CrossRef]
- Larson, R.G. The structure and Rheology of Complex Fluids; Oxford University Press: New York, NY, USA, 1999. [Google Scholar]
- Öttinger, H.C. General projection operator formalism for the dynamics and thermodynamics of complex fluids. Phys. Rev. E 1998, 57, 1416–1420. [Google Scholar] [CrossRef]
- Ilg, P. Macroscopic thermodynamics of flowing polymers derived from systematic coarse-graining procedure. Physica A 2008, 387, 6484–6496. [Google Scholar] [CrossRef]
- Hu, Y.; Wang, S.Q.; Jamieson, A.M. Rheological and flow birefringence studies of a shear-thickening complex fluid—A surfactant model system. J. Rheol. 1993, 37, 531–546. [Google Scholar] [CrossRef]
- Tapadia, P.; Wang, S.Q. Yieldlike constitutive transition in shear flow of entangled polymeric fluids. Phys. Rev. Lett. 2003, 91, 198301:1–198301:4. [Google Scholar] [CrossRef]
- Larson, R.G. Constitutive Equations for Polymer Melts and Solutions; Butterworths: London, UK, 1988; p. 364. [Google Scholar]
- Bird, R.B.; Curtiss, C.F.; Armstrong, R.C.; Hassager, O. Dynamics of Polymeric Liquids. Volume 2: Kinetic Theory; Wiley-Interscience: New York, NY, USA, 1987; p. 450. [Google Scholar]
- Baig, C.; Mavrantzas, V.G. Multiscale simulation of polymer melt viscoelasticity: Expanded-ensemble Monte Carlo coupled with atomistic nonequilibrium molecular dynamics. Phys. Rev. B 2009, 79, 144302:1–144302:17. [Google Scholar] [CrossRef]
- Baig, C.; Edwards, B.J. Analysis of the configurational temperature of polymeric liquids under shear and elongational flows using nonequilibrium molecular dynamics and Monte Carlo simulations. J. Chem. Phys. 2010, 132, 184906:1–184906:19. [Google Scholar] [CrossRef]
- Lees, A.W.; Edwards, S.F. The computer study of transport processes under extreme conditions. J. Phys. C 1972, 5, 1921–1929. [Google Scholar] [CrossRef]
- Zhou, M. A new look at the atomic level virial stress: On continuum-molecular system equivalence. Proc. R. Soc. Lond. A 2003, 459, 2347–2392. [Google Scholar] [CrossRef]
- Chen, W.; Fish, J. A mathematical homogenization perspective of virial stress. Int. J. Numer. Math. Eng. 2006, 67, 189–207. [Google Scholar] [CrossRef]
- Fish, J.; Chen, W.; Li, R. Generalized mathematical homogenization of atomistic media at finite temperatures in three dimensions. Comput. Meth. Appl. Mech. Eng. 2007, 196, 908–922. [Google Scholar] [CrossRef]
- Kröger, M.; Loose, W.; Hess, S. Rheology and structural changes of polymer melts via nonequilibrium molecular dynamics. J. Rheol. 1993, 37, 1057–1079. [Google Scholar] [CrossRef]
- Bergström, J.S.; Boyce, M.C. Constitutive modeling of the large strain time-dependent behavior of elastomers. J. Mech. Phys. Solids 1998, 46, 931–954. [Google Scholar] [CrossRef]
- Bergström, J.S.; Boyce, M.C. Large strain time-dependent behavior of filled elastomers. Mech. Mater. 2000, 32, 627–644. [Google Scholar] [CrossRef]
- Belytschko, T.; Liu, W.K.; Moran, B. Nonlinear Finite Elements for Continua and Structures; Wiley: New York, NY, USA, 2000; Volume 26. [Google Scholar]
- Li, Y.; Kröger, M.; Liu, W.K. Nanoparticle geometrical effect on structure, dynamics and anisotropic viscosity of polyethylene nanocomposites. Macromolecules 2012, 45, 2099–2112. [Google Scholar] [CrossRef]
- Li, Y.; Kröger, M.; Liu, W.K. Nanoparticle effect on the dynamics of polymer chains and their entanglement network. Phys. Rev. Lett. 2012, 109, 118001:1–118001:5. [Google Scholar] [CrossRef]
- Foteinopoulou, K.; Karayiannis, N.C.; Laso, M.; Kröger, M. Structure, dimensions, and entanglement statistics of long linear polyethylene chains. J. Phys. Chem. B 2009, 113, 442–455. [Google Scholar] [CrossRef] [PubMed]
- Milner, S.T.; McLeish, T.C.B. Reptation and contour-length fluctuations in melts of linear polymers. Phys. Rev. Lett. 1998, 81, 725–728. [Google Scholar] [CrossRef]
- Abdel-Goad, M.; Pyckhout-Hintzen, W.; Kahle, S.; Allgaier, J.; Richter, D.; Fetters, L.J. Rheological properties of 1, 4-polyisoprene over a large molecular weight range. Macromolecules 2004, 37, 8135–8144. [Google Scholar] [CrossRef]
- Lion, A.; Kardelky, C. The Payne effect in finite viscoelasticity: Constitutive modelling based on fractional derivatives and intrinsic time scales. Int. J. Plast. 2004, 20, 1313–1345. [Google Scholar] [CrossRef]
- Ramos, J.; Vega, J.F.; Theodorou, D.N.; Martinez-Salazar, J. Entanglement relaxation time in polyethylene: Simulation versus experimental data. Macromolecules 2008, 41, 2959–2962. [Google Scholar] [CrossRef]
- Vega, J.F.; Rastogi, S.; Peters, G.W.M.; Meijer, H.E.H. Rheology and reptation of linear polymers. Ultrahigh molecular weight chain dynamics in the melt. J. Rheol. 2004, 48, 663–678. [Google Scholar] [CrossRef]
- Qin, J.; So, J.; Milner, S.T. Tube diameter of stretched and compressed permanently entangled polymers. Macromolecules 2012, 45, 9816–9822. [Google Scholar] [CrossRef]
- Wen, Q.; Basu, A.; Janmey, P.A.; Yodh, A.G. Non-affine deformations in polymer hydrogels. Soft Matter 2012, 8, 8039–8049. [Google Scholar] [CrossRef] [PubMed]
- Sommer, J.U.; Lay, S. Topological structure and nonaffine swelling of bimodal polymer networks. Macromolecules 2002, 35, 9832–9843. [Google Scholar] [CrossRef]
- Basu, A.; Wen, Q.; Mao, X.M.; Lubensky, T.C.; Janmey, P.A.; Yodh, A.G. Nonaffine displacements in flexible polymer networks. Macromolecules 2011, 44, 1671–1679. [Google Scholar] [CrossRef]
- Peter, C.; Kremer, K. Multiscale simulation of soft matter systems–from the atomistic to the coarse-grained level and back. Soft Matter 2009, 5, 4357–4366. [Google Scholar] [CrossRef]
- Tschöp, W.; Kremer, K.; Hahn, O.; Batoulis, J.; Bürger, T. Simulation of polymer melts. II. From coarse-grained models back to atomistic description. Acta Polym. 1999, 49, 75–79. [Google Scholar] [CrossRef]
- Santangelo, G.; Di Matteo, A.; Müller-Plathe, F.; Milano, G. From mesoscale back to atomistic models: A fast reverse-mapping procedure for vinyl polymer chains. J. Phys. Chem. B 2007, 111, 2765–2773. [Google Scholar] [CrossRef] [PubMed]
- Chen, X.; Carbone, P.; Santangelo, G.; di Matteo, A.; Milano, G.; Müller-Plathe, F. Backmapping coarse-grained polymer models under sheared nonequilibrium conditions. Phys. Chem. Chem. Phys. 2009, 11, 1977–1988. [Google Scholar] [CrossRef] [PubMed]
- Wagner, G.J.; Liu, W.K. Coupling of atomistic and continuum simulations using a bridging scale decomposition. J. Comput. Phys. 2003, 190, 249–274. [Google Scholar] [CrossRef]
- Xiao, S.P.; Belytschko, T. A bridging domain method for coupling continua with molecular dynamics. Comput. Meth. Appl. Mech. Eng. 2004, 193, 1645–1669. [Google Scholar]
- Liu, W.K.; Karpov, E.G.; Zhang, S.; Park, H.S. An introduction to computational nanomechanics and materials. Comput. Meth. Appl. Mech. Eng. 2004, 193, 1529–1578. [Google Scholar] [CrossRef]
- Liu, W.K.; Karpov, E.G.; Park, H.S. Nano Mechanics and Materials: Theory, Multiscale Methods and Applications; John Wiley: Chichester, UK, 2006. [Google Scholar]
- Park, H.S.; Liu, W.K. An introduction and tutorial on multiple-scale analysis in solids. Comput. Meth. Appl. Mech. Eng. 2004, 193, 1733–1772. [Google Scholar] [CrossRef]
- Park, H.S.; Karpov, E.G.; Liu, W.K.; Klein, P.A. The bridging scale for two-dimensional atomistic/continuum coupling. Phil. Mag. 2005, 85, 79–113. [Google Scholar] [CrossRef]
- Liu, W.K.; Park, H.S.; Qian, D.; Karpov, E.G.; Kadowaki, H.; Wagner, G.J. Bridging scale methods for nanomechanics and materials. Comput. Meth. Appl. Mech. Eng. 2006, 195, 1407–1421. [Google Scholar] [CrossRef]
- Qian, D.; Wagner, G.J.; Liu, W.K. A multiscale projection method for the analysis of carbon nanotubes. Comput. Meth. Appl. Mech. Eng. 2004, 193, 1603–1632. [Google Scholar] [CrossRef]
- Xu, M.; Tabarraei, A.; Paci, J.T.; Oswald, J.; Belytschko, T. A coupled quantum/continuum mechanics study of graphene fracture. Int. J. Fract. 2012, 173, 1–11. [Google Scholar] [CrossRef]
- Moseley, P.; Oswald, J.; Belytschko, T. Adaptive atomistic-to-continuum modeling of propagating defects. Int. J. Numer. Math. Eng. 2012, 92, 835–856. [Google Scholar] [CrossRef]
- Xu, M.; Paci, J.T.; Oswald, J.; Belytschko, T. A constitutive equation for graphene based on density functional theory. Int. J. Solids Struct. 2012, 49, 2582–2589. [Google Scholar] [CrossRef]
- Boukany, P.E.; Wang, S.Q.; Wang, X. Step shear of entangled linear polymer melts: New experimental evidence for elastic yielding. Macromolecules 2009, 42, 6261–6269. [Google Scholar] [CrossRef]
- Liu, G.; Sun, H.; Rangou, S.; Ntetsikas, K.; Avgeropoulos, A.; Wang, S.Q. Studying the origin of strain hardening: Basic difference between extension and shear. J. Rheol. 2013, 57, 89–104. [Google Scholar] [CrossRef]
- Cheng, S.; Wang, S.Q. Is shear banding a metastable property of well-entangled polymer solutions? J. Rheol. 2012, 56, 1413–1428. [Google Scholar] [CrossRef]
- Cao, J.; Likhtman, A.E. Shear banding in molecular dynamics of polymer melts. Phys. Rev. Lett. 2012, 108, 28302:1–28302:5. [Google Scholar] [CrossRef]
- Baig, C.; Harmandaris, V.A. Quantitative analysis on the validity of a coarse-grained model for nonequilibrium polymeric liquids under flow. Macromolecules 2010, 43, 3156–3160. [Google Scholar] [CrossRef]
- Malkin, A.Y. The state of the art in the rheology of polymers: Achievements and challenges. Polym. Sci. A 2009, 51, 80–102. [Google Scholar] [CrossRef]
- Ahlrichs, P.; Everaers, R.; Dünweg, B. Screening of hydrodynamic interactions in semidilute polymer solutions: A computer simulation study. Phys. Rev. E 2001, 64, 040501:1–040501:4. [Google Scholar] [CrossRef]
- Hoogerbrugge, P.J.; Koelman, J.M.V.A. Simulating microscopic hydrodynamic phenomena with dissipative particle dynamics. EPL (Europhys. Lett.) 1992, 19, 155–160. [Google Scholar] [CrossRef]
- Winkler, R.G.; Mussawisade, K.; Ripoll, M.; Gompper, G. Rod-like colloids and polymers in shear flow: A multi-particle-collision dynamics study. J. Phys. Condens. Matter 2004, 16, S3941–S3954. [Google Scholar] [CrossRef]
- Gompper, G.; Ihle, T.; Kroll, D.; Winkler, R.G. Multi-particle Collision Dynamics: A Particle-based Mesoscale Simulation Approach to the Hydrodynamics of Complex Fluids. In Advanced Computer Simulation Approaches for Soft Matter Sciences; Springer: London, UK, 2009; Volume III, pp. 1–87. [Google Scholar]
- Succi, S. The Lattice Boltzmann Equation for Fluid Dynamics and Beyond. In Numerical Mathematics and Scientific Computation; Oxford University Press: New York, NY, USA, 2001. [Google Scholar]
- Dünweg, B.; Ladd, A. Lattice Boltzmann Simulations of Soft Matter Systems. In Advanced Computer Simulation Approaches for Soft Matter Sciences III; Springer: London, UK, 2009; Volume 221, pp. 89–166. [Google Scholar]
- Kopacz, A.M.; Patankar, N.A.; Liu, W.K. The immersed molecular finite element method. Comput. Meth. Appl. Mech. Eng. 2012, 233–236, 28–39. [Google Scholar] [CrossRef]
- Atzberger, P.J. Stochastic eulerian-lagrangian methods for fluid-structure interactions with thermal fluctuations and shear boundary conditions. J. Comput. Phys. 2011, 230, 282–2837. [Google Scholar] [CrossRef]
- Toth, R.; Voom, D.J.; Handgraaf, J.W.; Fraaje, J.G.E.M.; Fermeglia, M.; Pricl, S.; Posocco, P. Multiscale computer simulation studies of water-based montmorillonite/poly(ethylene oxide). Macromolecules 2009, 42, 8250–8270. [Google Scholar] [CrossRef]
- Montes, H.; Lequeux, F.; Berriot, J. Influence of the glass transition temperature gradient on the nonlinear viscoelastic behavior in reinforced elastomers. Macromolecules 2003, 36, 8107–8118. [Google Scholar] [CrossRef]
- Ellison, C.J.; Torkelson, J.M. The distribution of glass-transition temperatures in nanoscopically confined glass formers. Nat. Mater. 2003, 2, 695–700. [Google Scholar] [CrossRef] [PubMed]
- Yang, Z.; Fujii, Y.; Lee, F.K.; Lam, C.H.; Tsui, O.K.C. Glass transition dynamics and surface layer mobility in unentangled polystyrene films. Science 2010, 328, 1676–1679. [Google Scholar] [CrossRef] [PubMed]
- Martin, J.; Krutyeva, M.; Monkenbusch, M.; Arbe, A.; Allgaier, J.; Radulescu, A.; Falus, P.; Maiz, J.; Mijangos, C.; Colmenero, J.; et al. Direct observation of confined single chain dynamics by neutron scattering. Phys. Rev. Lett. 2010, 104, 197801:1–197801:4. [Google Scholar] [CrossRef]
- Nusser, K.; Schneider, G.J.; Richter, D. Microscopic origin of the terminal relaxation time in polymer nanocomposites: An experimental precedent. Soft Matter 2011, 7, 7988–7991. [Google Scholar] [CrossRef]
- Schneider, G.J.; Nusser, K.; Willner, L.; Falus, P.; Richter, D. Dynamics of entangled chains in polymer nanocomposites. Macromolecules 2011, 44, 5857–5860. [Google Scholar] [CrossRef]
- Papon, A.; Saalwächter, K.; Schäler, K.; Guy, L.; Lequeux, F.; Montes, H. Low-field NMR investigations of nanocomposites: Polymer dynamics and network effects. Macromolecules 2011, 44, 913–922. [Google Scholar] [CrossRef]
- Starr, F.W.; Schrøder, T.B.; Glotzer, S.C. Molecular dynamics simulation of a polymer melt with a nanoscopic particle. Macromolecules 2002, 35, 4481–4492. [Google Scholar] [CrossRef]
- Colmenero, J.; Arbe, A. Recent progress on polymer dynamics by neutron scattering: From simple polymers to complex materials. J. Polym. Sci. B 2013, 51, 87–113. [Google Scholar] [CrossRef]
- Harmandaris, V.A.; Daoulas, K.C.; Mavrantzas, V.G. Molecular dynamics simulation of a polymer melt/solid interface: Local dynamics and chain mobility in a thin film of polyethylene melt adsorbed on graphite. Macromolecules 2005, 38, 5796–5809. [Google Scholar] [CrossRef]
- Harmandaris, V.A.; Daoulas, K.C.; Mavrantzas, V.G. Molecular dynamics simulation of a polymer melt/solid interface: Local dynamics and chain mobility in a thin film of polyethylene melt adsorbed on graphite. Macromolecules 2005, 38, 5796–5809. [Google Scholar] [CrossRef]
- Hooper, J.B.; Schweizer, K.S. Theory of phase separation in polymer nanocomposites. Macromolecules 2006, 39, 5133–5142. [Google Scholar] [CrossRef]
- Cordeiro, R.M.; Zschunke, F.; Muller-Plathe, F. Mesoscale molecular dynamics simulations of the force between surfaces with grafted poly (ethylene oxide) chains derived from atomistic simulations. Macromolecules 2010, 43, 1583–1591. [Google Scholar] [CrossRef]
- Bogoslovov, R.B.; Roland, C.M.; Ellis, A.R.; Randall, A.M.; Robertson, C.G. Effect of silica nanoparticles on the local segmental dynamics in poly (vinyl acetate). Macromolecules 2008, 41, 1289–1296. [Google Scholar] [CrossRef]
- Krutyeva, M.; Wischnewski, A.; Monkenbusch, M.; Willner, L.; Maiz, J.; Mijangos, C.; Arbe, A.; Colmenero, J.; Radulescu, A.; Holderer, O.; Ohl, M.; Richter, D. Effect of nanoconfinement on polymer dynamics: Surface layers and interphases. Phys. Rev. Lett. 2013, 110, 108303:1–108303:5. [Google Scholar] [CrossRef]
- Eslami, H.; Müller-Plathe, F. How thick is the interphase in an ultrathin polymer film? Coarse grained molecular dynamics simulations of polyamide-6, 6 on graphene. J. Phys. Chem. C 2013, 117, 5249–5257. [Google Scholar] [CrossRef]
- Hooper, J.; Schweizer, K.; Desai, T.; Koshy, R.; Keblinski, P. Structure, surface excess and effective interactions in polymer nanocomposite melts and concentrated solutions. J. Chem. Phys. 2004, 121, 6986–6997. [Google Scholar] [CrossRef] [PubMed]
- Hooper, J.B.; Schweizer, K.S. Contact aggregation, bridging, and steric stabilization in dense polymer-particle mixtures. Macromolecules 2005, 38, 8858–8869. [Google Scholar] [CrossRef]
- Hooper, J.B.; Schweizer, K.S. Real space structure and scattering patterns of model polymer nanocomposites. Macromolecules 2007, 40, 6998–7008. [Google Scholar] [CrossRef]
- Jayaraman, A.; Schweizer, K.S. Effective interactions, structure, and phase behavior of lightly tethered nanoparticles in polymer melts. Macromolecules 2008, 41, 9430–9438. [Google Scholar] [CrossRef]
- Jayaraman, A.; Schweizer, K.S. Effective interactions and self-assembly of hybrid polymer grafted nanoparticles in a homopolymer matrix. Macromolecules 2009, 42, 8423–8434. [Google Scholar] [CrossRef]
- Hall, L.M.; Jayaraman, A.; Schweizer, K.S. Molecular theories of polymer nanocomposites. Curr. Opin. Solid State Mater. Sci. 2010, 14, 38–48. [Google Scholar] [CrossRef]
- Payne, A.R. The dynamic properties of carbon black-loaded natural rubber vulcanizates. Part I. J. Appl. Polym. Sci. 2003, 6, 57–63. [Google Scholar] [CrossRef]
- Payne, A.R. The dynamic properties of carbon black loaded natural rubber vulcanizates. Part II. J. Appl. Polym. Sci. 2003, 6, 368–372. [Google Scholar]
- Lion, A.; Kardelky, C.; Haupt, P. On the frequency and amplitude dependence of the Payne effect: Theory and experiments. Rubber Chem. Technol. 2003, 76, 533–547. [Google Scholar]
- Greene, M.S. Mechanics and Physics of Solids, Uncertainy, and the Archetype-Genome Exemplar. Ph.D. thesis, Northwestern University, Evanston, IL, USA, 2012. [Google Scholar]
- Haward, R.N.; Thackray, G.; Haward, R.N.; Thackray, G. The use of a mathematical model to describe isothermal stress-strain curves in glassy thermoplastics. Proc. R. Soc. Lond. A 1968, 302, 453–472. [Google Scholar]
- Arruda, E.M.; Boyce, M.C. Evolution of plastic anisotropy in amorphous polymers during finite straining. Int. J. Plast. 1993, 9, 697–720. [Google Scholar] [CrossRef]
- Akutagawa, K.; Yamaguchi, K.; Yamamoto, A.; Heguri, H.; Jinnai, H.; Shinbori, Y. Mesoscopic mechanical analysis of filled elastomer with 3D-finite element analysis and transmission electron microtomography. Rubber Chem. Technol. 2008, 81, 182–189. [Google Scholar] [CrossRef]
- Gonzalez, J.; Knauss, W.G. Strain inhomogeneity and discontinuous crack growth in a particulate composite. J. Mech. Phys. Solids 1998, 46, 1981–1995. [Google Scholar] [CrossRef]
- Simo, J.C. On a fully three-dimensional finite-strain viscoelastic damage model: Formulation and computational aspects. Comput. Meth. Appl. Mech. Eng. 1987, 60, 153–173. [Google Scholar] [CrossRef]
- Lion, A. On the large deformation behaviour of reinforced rubber at different temperatures. J. Mech. Phys. Solids 1997, 45, 1805–1834. [Google Scholar] [CrossRef]
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license ( http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Li, Y.; Abberton, B.C.; Kröger, M.; Liu, W.K. Challenges in Multiscale Modeling of Polymer Dynamics. Polymers 2013, 5, 751-832. https://doi.org/10.3390/polym5020751
Li Y, Abberton BC, Kröger M, Liu WK. Challenges in Multiscale Modeling of Polymer Dynamics. Polymers. 2013; 5(2):751-832. https://doi.org/10.3390/polym5020751
Chicago/Turabian StyleLi, Ying, Brendan C. Abberton, Martin Kröger, and Wing Kam Liu. 2013. "Challenges in Multiscale Modeling of Polymer Dynamics" Polymers 5, no. 2: 751-832. https://doi.org/10.3390/polym5020751
APA StyleLi, Y., Abberton, B. C., Kröger, M., & Liu, W. K. (2013). Challenges in Multiscale Modeling of Polymer Dynamics. Polymers, 5(2), 751-832. https://doi.org/10.3390/polym5020751