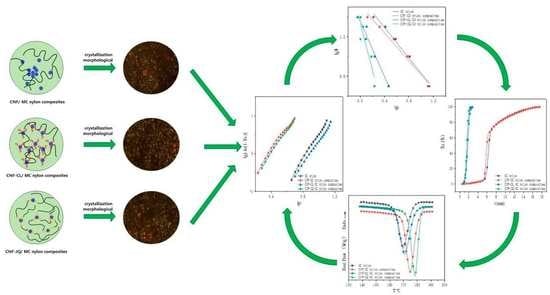
Crystallization Kinetics of Modified Nanocellulose/Monomer Casting Nylon Composites
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Sample Preparation
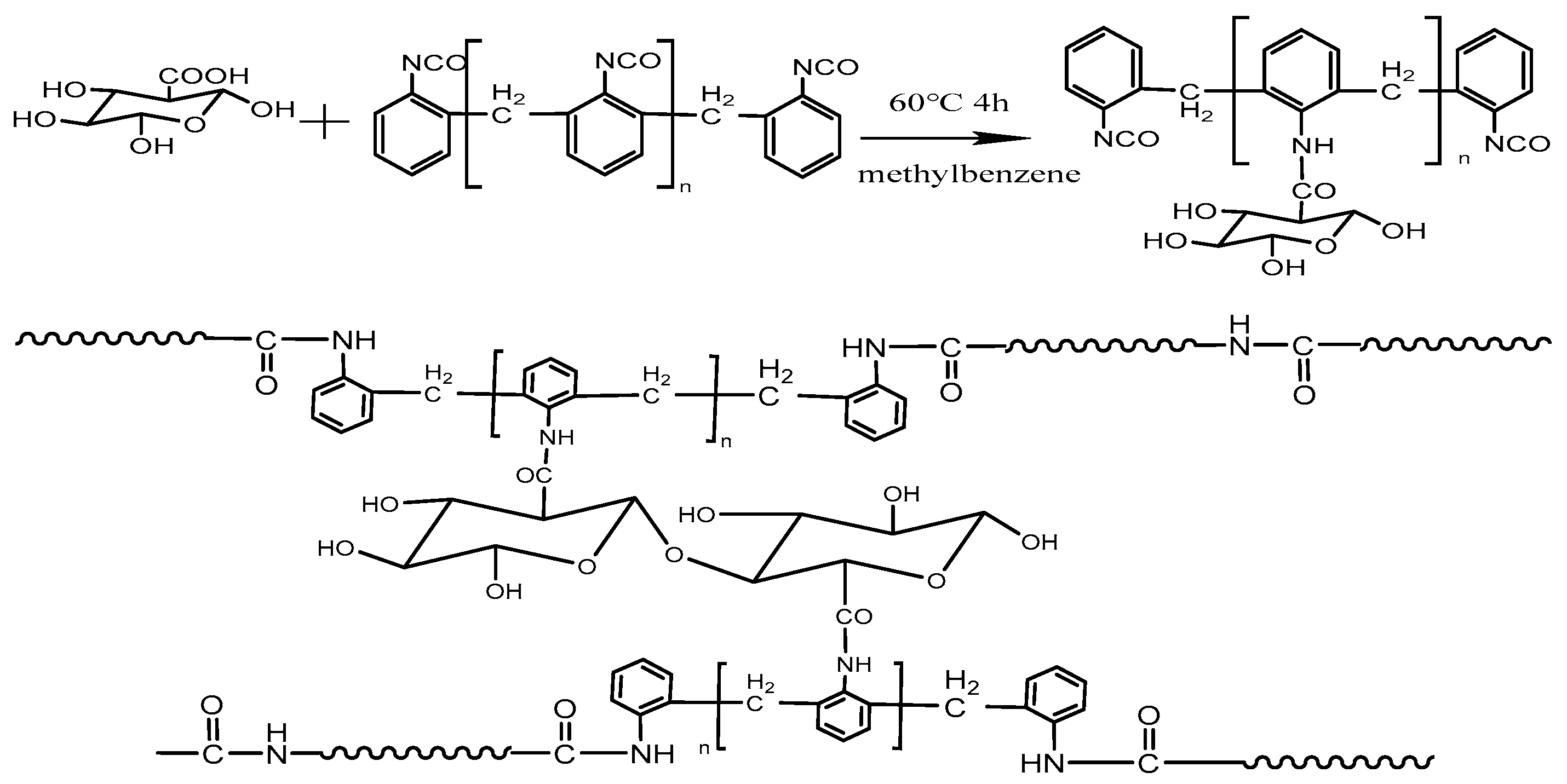
2.2.1. Preparation of Polyisocyanate Modified CNF
2.2.2. Preparation of ε-Caprolactam-Modified CNF
2.2.3. Synthesis of pure MC nylon
2.2.4. Preparation of Modified CNF/MC Nylon Composites
2.3. Characterization
- (1)
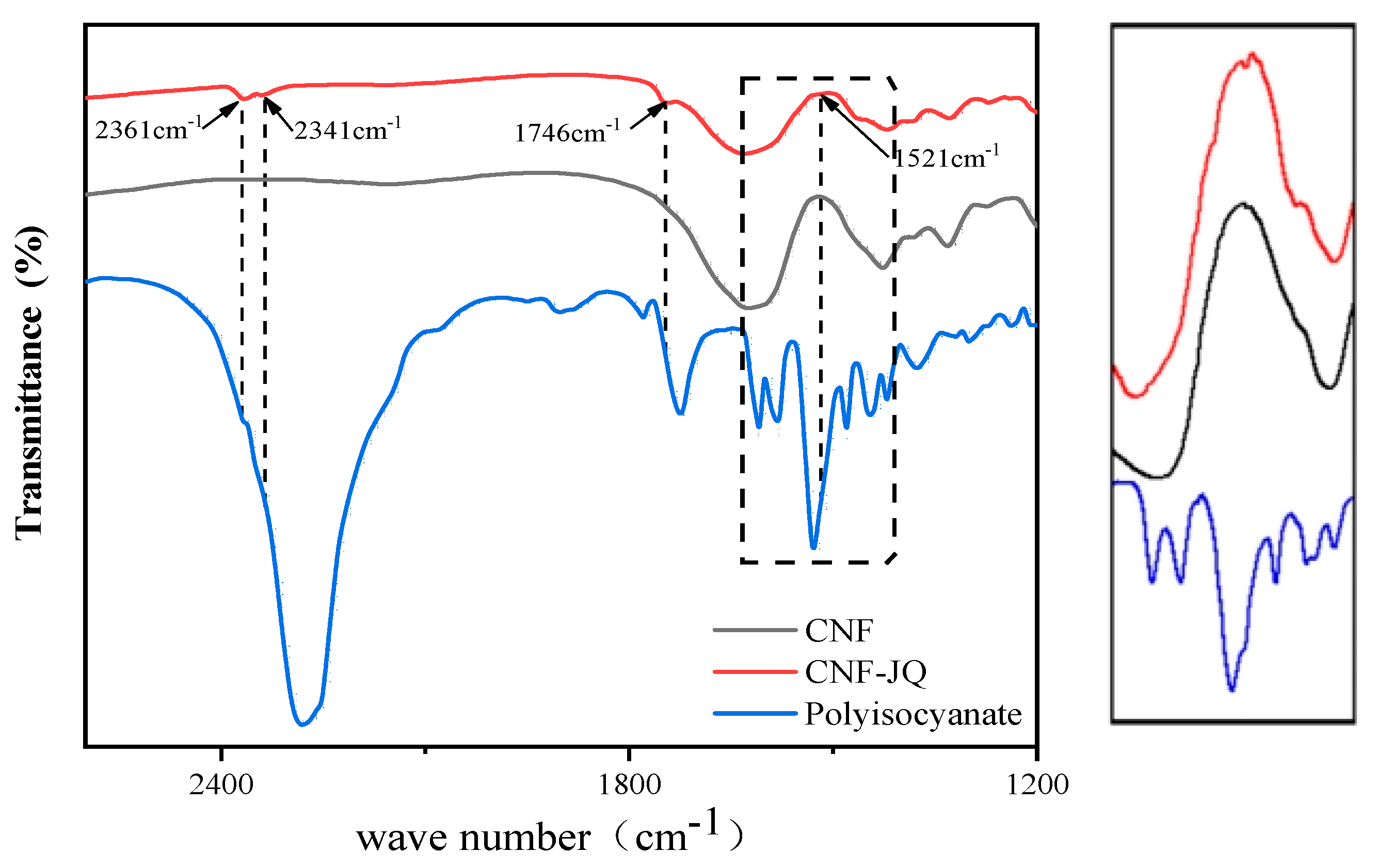
- Fourier Transform Infrared (FT-IR)
- (2)
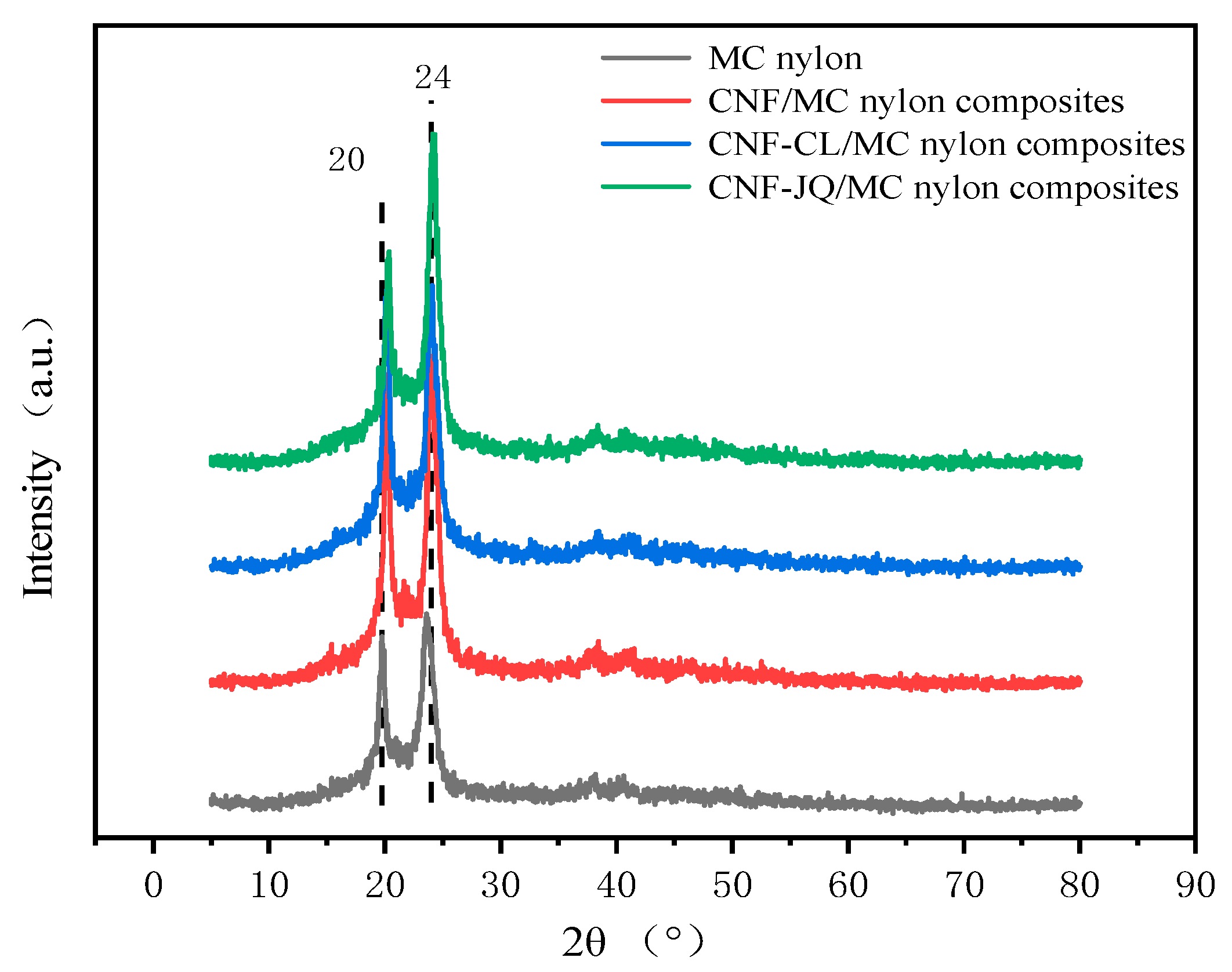
- Wide-angle X-ray diffraction (WAXD)
- (3)
- Polarized optical microscopy (POM)
- (4)
- Differential scanning calorimetry (DSC)
3. Results and Discussion
3.1. Structural Analysis of Modified CNF
3.2. Crystal Structure Analysis
3.3. Morphological Study of Crystallization
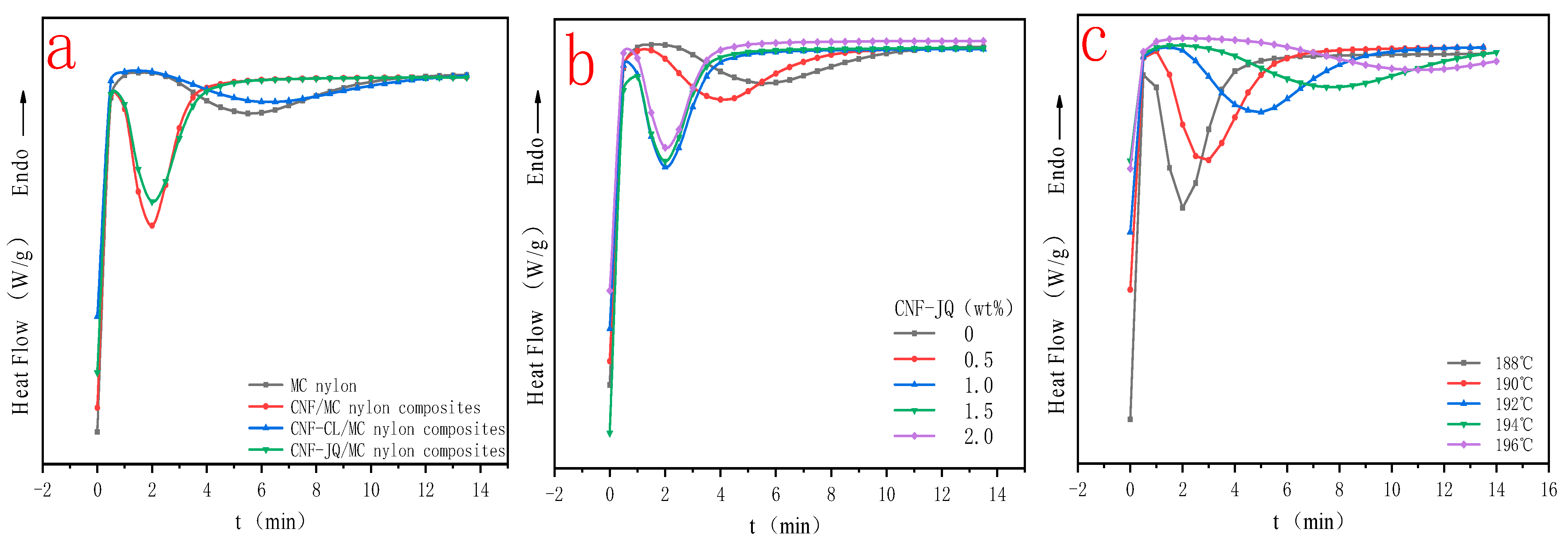
3.4. Isothermal Crystallization Kinetics
3.5. Non Isothermal Crystallization Kinetics
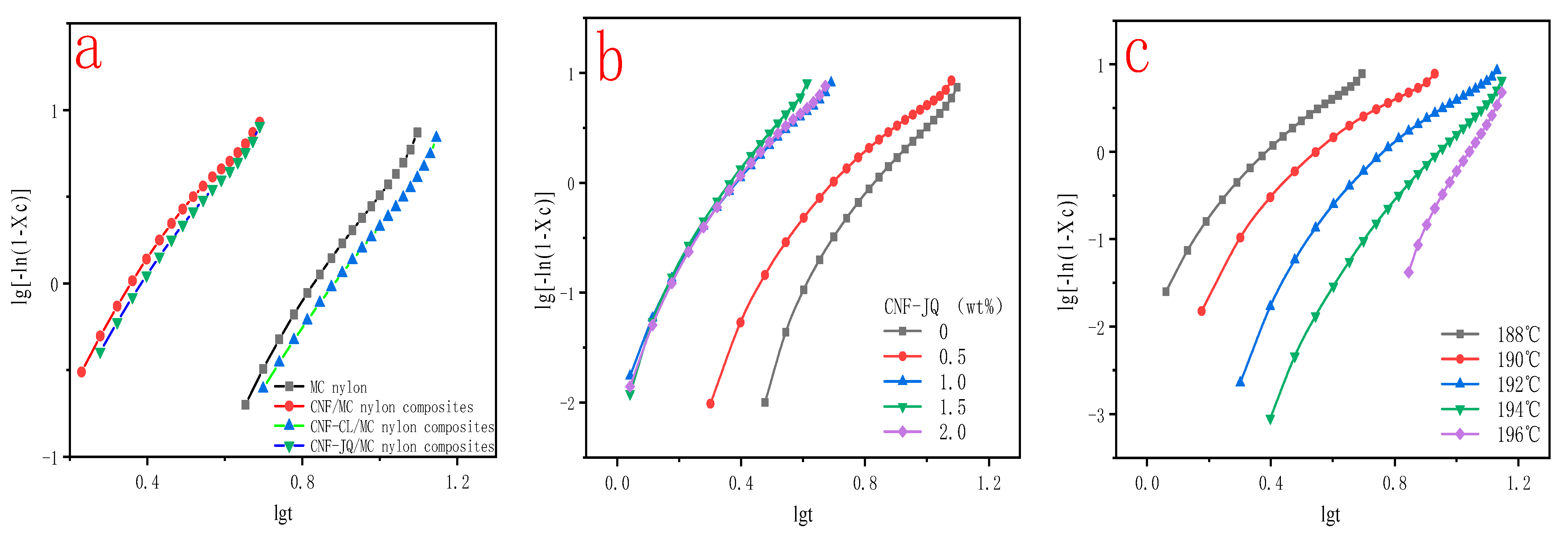
3.5.1. Jeziorny Method
3.5.2. Mo Method
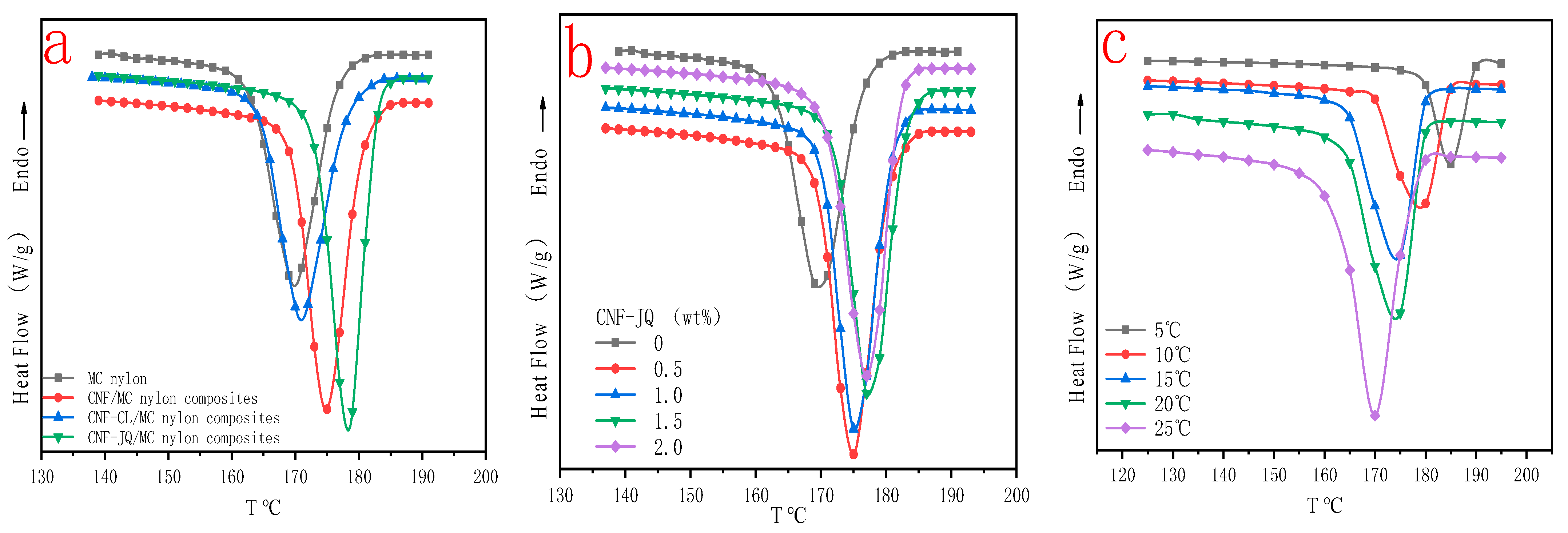
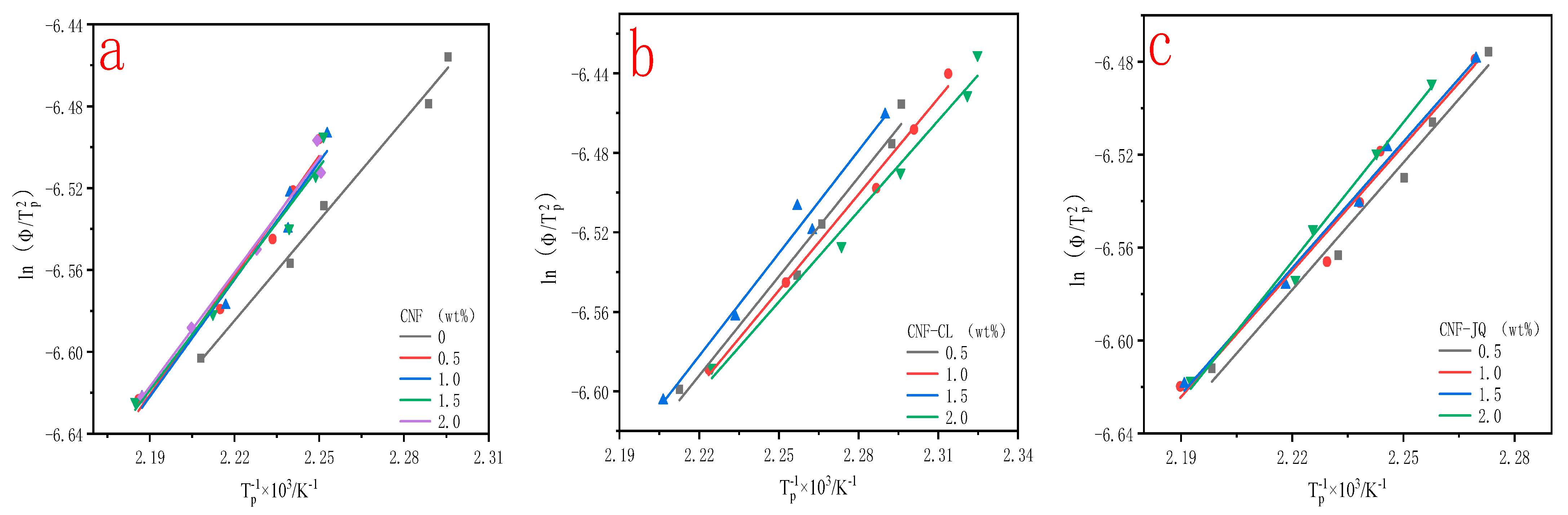
3.6. Activation Energy of Non-Isothermal Crystallization
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Gigli, M.; Negroni, A.; Zanaroli, G.; Lotti, N.; Fava, F.; Munari, A. Environmentally friendly PBS-based copolyesters containing PEG-like subunit: Effect of block length on solid-state properties and enzymatic degradation. React. Funct. Polym. 2013, 73, 764–771. [Google Scholar] [CrossRef]
- He, M.J.; Xiao, W.X.; Xie, H.; Fan, C.J.; Du, L.; Deng, X.Y.; Yang, K.K.; Wang, Y.Z. Facile fabrication of ternary nanocomposites with selective dispersion of multi-walled carbon nanotubes to access multi-stimuli-responsive shape-memory effects. Mater. Chem. Front. 2017, 1, 343–353. [Google Scholar] [CrossRef]
- Prime, R.B. Thermal Characterization of Polymeric Materials; Academic Press: Cambridge, MA, USA, 1997. [Google Scholar]
- Lim, J.Y.; Kim, J.; Kim, S.; Kwak, S.; Lee, Y.; Seo, Y. Nonisothermal crystallization behaviors of nanocomposites of poly(vinylidene fluoride) and multiwalled carbon nanotubes. Polymer 2015, 62, 11–18. [Google Scholar] [CrossRef]
- Kim, J.; Hong, S.M.; Kwak, S.; Seo, Y. Nonisothermal Crystallization Behaviors of Nanocomposites Prepared by In Situ Polymerization of High-Density Polyethylene on Multiwalled Carbon Nanotubes. Phys. Chem. Chem. Phys. 2009, 11, 10851–10859. [Google Scholar] [CrossRef] [PubMed]
- Wurm, A.; Lellinger, D.; Minakov, A.A.; Skipa, T.; Potschke, P.; Nicula, R.; Alig, I.; Schick, C. Crystallization of poly(ε-caprolactone)/MWCNT composites: A combined SAXS/WAXS, electrical and thermal conductivity study. Polymer 2014, 55, 2220–2232. [Google Scholar] [CrossRef]
- Yao, H.M.; Lin, Z.Y.; Li, B.X.; Tong, C.Q. Effect of Interaction between PPES and MC nylon 6 on MC nylon 6 Crystallization and Melting Behavior of PPES/MC Nylon6 Blends. Chem. Eng. Equip. 2008, 143, 37–40. [Google Scholar]
- Kim, H.B.; Han, J.W.; Cha, S.W. Mechanical Properties of injection molded part using rice bran. Polym. Eng. Sci. 2013, 53, 1809–1822. [Google Scholar]
- Qiu, S.C.; Zheng, Y.Y.; Zeng, A.R. Effect of Carbon Nanotubes on the Crystallization Behaviors of MC Nylon 6. Spectrosc. Spectr. Anal. 2011, 31, 2491–2494. [Google Scholar]
- Qu, X.; Ding, H.; Lu, J.; Wang, Y.; Zhang, L. Isothermal and nonisothermal crystallization kinetics of MC nylon and polyazomethine/MC nylon composites. J. Appl. Polym. Sci. 2010, 93, 2844–2855. [Google Scholar] [CrossRef]
- Habibi, Y.; Aouadi, S.; Raquez, J.-M.; Dubois, P. Effects of interfacial stereocomplexation in cellulose nanocrystal-filled polylactide nanocomposites. Cellulose 2013, 20, 2877–2885. [Google Scholar] [CrossRef]
- Diaz, J.A.; Ye, Z.; Wu, X.; Moore, A.L.; Moon, R.J.; Martini, A.; Boday, D.J.; Youngblood, J.P. Thermal Conductivity in Nanostructured Films: From Single Cellulose Nanocrystals to Bulk Films. Biomacromolecules 2014, 15, 4096–4101. [Google Scholar] [CrossRef] [PubMed]
- Diaz, J.A.; Wu, X.; Martini, A.; Youngblood, J.P.; Moon, R.J. Thermal Expansion of Self-Organized and Shear-Oriented Cellulose Nanocrystal Films. Biomacromolecules 2013, 14, 2900–2908. [Google Scholar] [CrossRef] [PubMed]
- Chowdhury, R.; Nuruddin, M.; Clarkson, C.; Montes, F.; Howarter, J.A.; Youngblood, J.P. Cellulose Nanocrystal (CNC) Coatings with Controlled Anisotropy as High-Performance Gas Barrier Films. ACS Appl. Mater. Interfaces 2018, 11, 1376–1383. [Google Scholar] [CrossRef] [PubMed]
- Peng, S.X.C.; Kumar, H.; Moon, S.; Youngblood, R.J.; Jeffrey, P. A comparative guide to controlled hydrophobization of cellulose nanocrystals via surface esterification. Cellulose 2016, 23, 1825–1846. [Google Scholar] [CrossRef]
- Yoo, Y.; Youngblood, J.P. Green One-Pot Synthesis of Surface Hydrophobized Cellulose Nanocrystals in Aqueous Medium. ACS Sustain. Chem. Eng. 2016, 4, 3927–3938. [Google Scholar] [CrossRef]
- Lorenzo, A.T.; Arnal, M.L.; Albuerne, J.; Müller, A. DSC isothermal polymer crystallization kinetics measurements and the use of the Avrami equation to fit the data: Guidelines to avoid common problems. Polym. Test. 2007, 26, 222–231. [Google Scholar] [CrossRef]
- Hoffman, J.D.; Weeks, J.J. Melting process and the euilibrium melting temperature of polychlorotrifluoroethylene. J. Res. Natl. Bur. Stand. Sect. A Phys. Chem. 1962, 66, 13–28. [Google Scholar] [CrossRef]
- Wang, Q.; Zhang, Q.; Wang, F.; Zhao, Y.; Wang, Y. Chemically functionalized SiO2 to improve mechanical properties of oil-impregnated monomer casting nylon. J. Appl. Polym. Ence 2018, 136, 46994. [Google Scholar] [CrossRef]
- Carlsson, L.; Ingverud, T.; Blomberg, H.; Carlmark, A.; Larsson, P.T.; Malmstrom, E. Surface characteristics of cellulose nanoparticles grafted by surface-initiated ring-opening polymerization of epsilon-caprolactone. Cellulose 2015, 22, 1063–1074. [Google Scholar] [CrossRef]
- Tseng, C.-H.; Tsai, P.-S. Biobased Copolyamides 56/66: Synthesis, Characterization and Crystallization Kinetics. Polymers 2022, 14, 3879. [Google Scholar] [CrossRef]
- Choi, J.; Shin, T.; Song, K.; Seo, Y.P.; Seo, Y. Nonisothermal Crystallization Behaviors of Structure-Modified Polyamides (Nylon 6s). ACS Omega 2020, 5, 29325–29332. [Google Scholar] [CrossRef]
- Rwei, S.P.; Ranganathan, P.; Lee, Y.H. Isothermal Crystallization Kinetics Study of Fully Aliphatic PA6 Copolyamides: Effect of Novel Long-Chain Polyamide Salt as a Comonomer. Polymers 2019, 11, 472. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hwang, J.J.; Huang, S.M.; Liu, H.J.; Chu, H.C.; Lin, L.H.; Chung, C.S. Crystallization kinetics of poly (L-lactic acid)/montmorillonite nanocomposites under isothermal crystallization condition. J. Appl. Polym. Sci. 2012, 124, 2216–2226. [Google Scholar] [CrossRef]
- Chen, E.C.; Wu, T.M. Isothermal and nonisothermal crystallization kinetics of nylon 6/functionalized multi-walled carbon nanotube composites. J. Polym. Sci. Part B Polym. Phys. 2008, 46, 158–169. [Google Scholar] [CrossRef]
- Kang, J.; Chen, Z.; Zhou, T.; Yang, F.; Chen, J.; Cao, Y.; Xiang, M. Dynamic crystallization and melting behavior of β-nucleated isotactic polypropylene with different melt structures. J. Polym. Res. 2014, 21, 384. [Google Scholar] [CrossRef]
- Chen, Z.; Wang, B.; Jian, K.; Peng, H.; Ming, X. Crystallization behavior and morphology of β-nucleated isotactic polypropylene with different stereo-defect distribution. Polym. Adv. Technol. 2014, 25, 353–363. [Google Scholar] [CrossRef]
- Kang, J.; Yang, F.; Wu, T.; Li, H.; Liu, D.; Cao, Y.; Xiang, M. Investigation of the stereodefect distribution and conformational behavior of isotactic polypropylene polymerized with different Ziegler-Natta catalysts. J. Appl. Polym. Sci. 2012, 125, 3076–3083. [Google Scholar] [CrossRef]
- Avrami, M. Kinetics of Phase Change. I General Theory. J. Chem. Phy. 1939, 7, 1103–1112. [Google Scholar] [CrossRef]
- Avrami, M. Kinetics of Phase Change. II Transformation-Time Relations for Random Distribution of Nuclei. J. Chem. Phys. 1940, 8, 212–224. [Google Scholar] [CrossRef]
- Zhang, C.; Lan, Q.; Zhai, T.; Nie, S.; Luo, J.; Yan, W. Melt Crystallization Behavior and Crystalline Morphology of Polylactide/Poly(ε-caprolactone) Blends Compatibilized by Lactide-Caprolactone Copolymer. Polymers 2018, 10, 1181. [Google Scholar] [CrossRef] [Green Version]
- Hao, Z.; Li, L.; Yang, B.; Sheng, X.; Liao, X. Influences of Hyperbranched Polyester Modification on the Crystallization Kinetics of Isotactic Polypropylene/Graphene Oxide Composites. Polymers 2019, 11, 433. [Google Scholar] [CrossRef] [Green Version]
- Wang, R.Y.; Zou, S.F.; Jiang, B.Y.; Fan, B.; Hou, M.F.; Zuo, B.; Wang, X.P.; Xu, J.T.; Fan, Z. A Generalized Avrami Equation for Crystallization Kinetics of Polymers with Concomitant Double Crystallization Processes. Cryst. Growth Des. 2017, 17, 5908–5917. [Google Scholar] [CrossRef]
- Raimo, M.; Lotti, E. Rebuilding growth mechanisms through visual observations. ChemTexts 2016, 2. [Google Scholar] [CrossRef]
- He, Y.; Asakawa, N.; Li, J.; Inoue, Y. Effects of low molecular weight compounds with hydroxyl groups on properties of poly(L-lactic acid). J. Appl. Polym. Sci. 2001, 82, 640–649. [Google Scholar] [CrossRef]
- He, Y.; Asakawa, N.; Inoue, Y. Blends of Poly(3-hydroxybutyrate)/4,4’-thiodiphenol and Poly(3-hydroxybutyrate-co-3-hydroxyvalerate)/4,4’-thiodiphenol: The Specific Interaction and Properties. J. Polym. Sci. Part B Polym. Phys. 2000, 38, 2891–2900. [Google Scholar] [CrossRef]
- Si, P.; Luo, F. Hydrogen bonding interaction and crystallization behavior of poly (butylene succinate-co-butylene adipate)/thiodiphenol complexes. Polym. Adv. Technol. 2016, 27, 1413–1421. [Google Scholar] [CrossRef]
- Tao, Y.; Mai, K. Non-isothermal crystallization and melting behavior of compatibilized polypropylene/recycled poly(ethylene terephthalate) blends. Eur. Polym. J. 2007, 43, 3538–3549. [Google Scholar] [CrossRef]
- Ye, X.; Hu, Z.; Li, X.; Wang, S.; Ding, J.; Li, M.; Zhao, Y. Non-Isothermal Crystallization Kinetics of Polyether-Ether-Ketone Nanocomposites and Analysis of the Mechanical and Electrical Conductivity Performance. Polymers 2022, 14, 4623. [Google Scholar] [CrossRef]
- Chen, S.; Xie, S.; Guang, S.; Bao, J.; Chen, W. Crystallization and Thermal Behaviors of Poly(ethylene terephthalate)/Bisphenols Complexes through Melt Post-Polycondensation. Polymers 2020, 12, 3053. [Google Scholar] [CrossRef] [PubMed]
- Qiu, Z.; Yang, W. Nonisothermal melt and cold crystallization kinetics of poly(aryl ether ether ketone ketone). Polym. Eng. Sci. 2010, 37, 568–575. [Google Scholar] [CrossRef]
- Supaphol, P.; Dangseeyun, N.; Srimoaon, P.; Nithitanakul, M. Nonisothermal melt-crystallization kinetics for three linear aromatic polyesters. Thermochim. Acta 2003, 406, 207–220. [Google Scholar] [CrossRef] [Green Version]
- Tong, X.; Wang, Z.; Zhang, M.L.; Wang, X.J.; Yang, J. Synthesis, Characterization and Non-Isothermal Crystallization Kinetics of a New Family of Poly (Ether-Block-Amide)s Based on Nylon 10T/10I. Polymers 2021, 13, 72. [Google Scholar] [CrossRef] [PubMed]
- Vyazovkin, S. Is the Kissinger Equation Applicable to the Processes that Occur on Cooling? Macromol. Rapid Commun. 2002, 23, 771–775. [Google Scholar] [CrossRef]
- El-Taweel, S.H.; Al-Ahmadi, A.O. Isothermal Crystallization Kinetics of Poly (3-hydroxybutyrate/Poly(ethylene-co-vinyl acetate) Blends Enhanced by NH 4 Cl as a Nucleating Agent. J. Macromol. Sci. Part B 2019, 58, 518–534. [Google Scholar] [CrossRef]


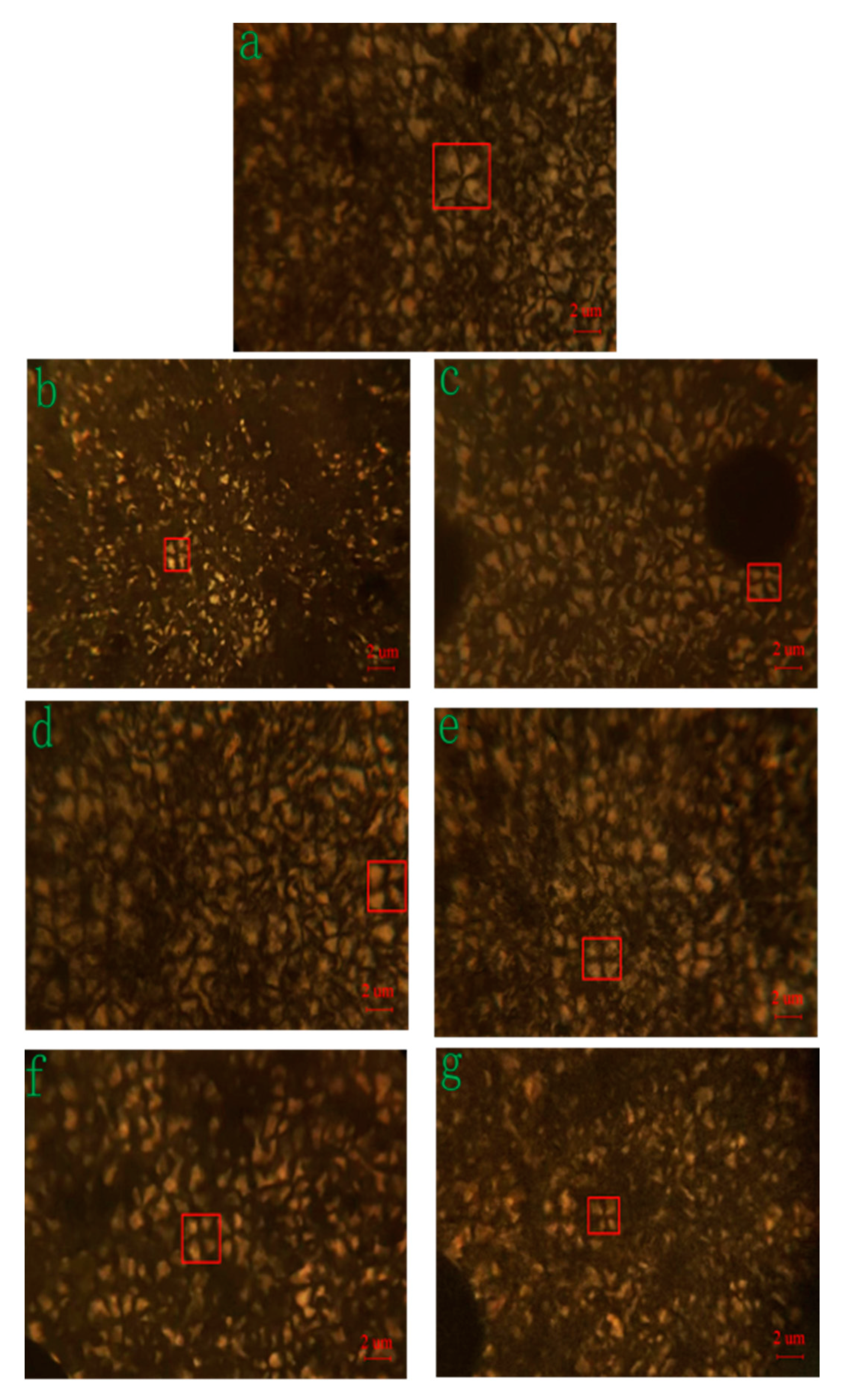





| MC Nylon (a) | CNF (wt%) | CNF–CL (wt%) | CNF–JQ (wt%) | ||||
|---|---|---|---|---|---|---|---|
| 0.5 (b) | 1.0 (c) | 0.5 (d) | 1.0 (e) | 0.5 (f) | 1.0 (g) | ||
| Number of Crystals | 452 | 554 | 511 | 463 | 594 | 620 | 626 |
| Diameter size (nm) | 3.78 | 2.22 | 2.35 | 2.95 | 2.50 | 2.33 | 2.19 |
| n | K (×10−3) | t1/2/min | G | ||
|---|---|---|---|---|---|
| Modified CNF | MC nylon | 4.255 | 0.252 | 1.268 | 0.788 |
| CNF | 2.962 | 8.312 | 0.432 | 2.313 | |
| CNF–CL | 3.023 | 2.572 | 0.648 | 1.543 | |
| CNF–JQ | 2.992 | 19.50 | 0.328 | 3.050 | |
| Content of CNF–JQ/wt% (cooling rate 188 °C) | 0 | 4.255 | 0.252 | 1.268 | 0.788 |
| 0.5 | 3.597 | 1.294 | 0.841 | 1.189 | |
| 1.0 | 2.996 | 19.50 | 0.328 | 3.046 | |
| 1.5 | 3.613 | 15.12 | 0.426 | 2.347 | |
| 2.0 | 3.104 | 15.53 | 0.367 | 2.723 | |
| Cooling rate/°C (CNF–JQ 1.0 wt%) | 188 | 2.994 | 19.50 | 0.328 | 3.048 |
| 190 | 3.192 | 11.75 | 0.412 | 2.427 | |
| 192 | 3.657 | 0.955 | 0.916 | 1.092 | |
| 194 | 4.625 | 0.039 | 1.863 | 0.537 | |
| 196 | 6.314 | 0.003 | 2.368 | 0.422 |
| n | Zt | Zc | ||
|---|---|---|---|---|
| Modified CNF | MC nylon | 3.628 | 0.344 | 0.899 |
| CNF | 3.847 | 0.280 | 0.880 | |
| CNF–CL | 3.340 | 0.471 | 0.927 | |
| CNF–JQ | 3.587 | 0.679 | 0.962 | |
| Content of CNF–JQ/wt% (15 °C/min) | 0 | 5.082 | 0.646 | 0.971 |
| 0.5 | 5.534 | 0.692 | 0.976 | |
| 1.0 | 4.945 | 0.692 | 0.976 | |
| 1.5 | 3.786 | 0.741 | 0.980 | |
| 2.0 | 4.833 | 4.571 | 1.107 | |
| Φ (CNF–JQ 1.0 wt%) | 5 | 6.412 | 0.481 × 10−3 | 0.217 |
| 10 | 5.614 | 0.039 | 0.724 | |
| 15 | 4.945 | 0.692 | 0.976 | |
| 20 | 3.645 | 0.295 | 0.941 | |
| 25 | 5.557 | 0.054 | 0.890 |
| Relative Crystallinity (%) | F(T) (°C × min−1) | ||
|---|---|---|---|
| Modified CNF (1.0 wt%) | MC nylon | 40 | 39.72 |
| CNF | 40 | 33.04 | |
| CNF–CL | 40 | 22.86 | |
| CNF–JQ | 40 | 21.78 | |
| Content of CNF–JQ (wt%) | 0 | 40 | 25.70 |
| 0.5 | 40 | 21.78 | |
| 1.0 | 40 | 17.14 | |
| 1.5 | 40 | 18.20 | |
| 2.0 | 40 | 25.70 | |
| Content of CNF–JQ (wt%) | 1.0 | 20 | 16.22 |
| 1.0 | 40 | 17.14 | |
| 1.0 | 60 | 21.38 | |
| 1.0 | 80 | 25.70 |
| ΔEa (kJ/mol) | ||
|---|---|---|
| MC nylon | 13.58 | |
| Content of CNF (wt%) | 0.5 | 15.90 |
| 1.0 | 15.12 | |
| Content of CNF–CL (wt%) | 0.5 | 13.40 |
| 1.0 | 12.65 | |
| Content of CNF–JQ (wt%) | 0.5 | 15.16 |
| 1.0 | 14.98 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, X.; Guo, F.; Tang, K.; Ge, T. Crystallization Kinetics of Modified Nanocellulose/Monomer Casting Nylon Composites. Polymers 2023, 15, 719. https://doi.org/10.3390/polym15030719
He X, Guo F, Tang K, Ge T. Crystallization Kinetics of Modified Nanocellulose/Monomer Casting Nylon Composites. Polymers. 2023; 15(3):719. https://doi.org/10.3390/polym15030719
Chicago/Turabian StyleHe, Xiaofeng, Fuqiang Guo, Kaihong Tang, and Tiejun Ge. 2023. "Crystallization Kinetics of Modified Nanocellulose/Monomer Casting Nylon Composites" Polymers 15, no. 3: 719. https://doi.org/10.3390/polym15030719
APA StyleHe, X., Guo, F., Tang, K., & Ge, T. (2023). Crystallization Kinetics of Modified Nanocellulose/Monomer Casting Nylon Composites. Polymers, 15(3), 719. https://doi.org/10.3390/polym15030719