Kinetics of Micellization and Liquid–Liquid Phase Separation in Dilute Block Copolymer Solutions
Abstract
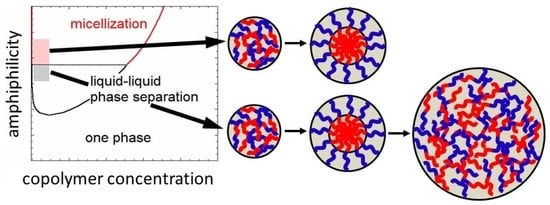
:1. Introduction
2. Thermodynamics
2.1. Models and Mixing Gibbs Energy Densities [27]
2.2. Phase Diagram
3. Kinetics of Micellization and Liquid–Liquid Phase Separation
3.1. Growth of the Concentrated-Phase Droplet and Spherical Micelle in the Early Stage
3.2. Modification of the Lifshitz–Slyosov Theory in the Late Stage of the Phase Separation
4. Concluding Remarks
Funding
Conflicts of Interest
Appendix A. Interfacial Tension and Interfacial Thickness

References
- Honda, C.; Hasegawa, Y.; Hirunuma, R.; Nose, T. Micellization Kinetics of Block Copolymers in Selective Solvent. Macromolecules 1994, 27, 7660–7668. [Google Scholar] [CrossRef]
- Hecht, E.; Hoffmann, H. Kinetic and Calorimetric Investigations on Micelle Formation of Block Copolymers of the Poloxamer Type. Colloid Surf. A Physicochem. Eng. Asp. 1995, 96, 181–197. [Google Scholar] [CrossRef]
- Goldmints, I.; Holzwarth, J.F.; Smith, K.A.; Hatton, T.A. Micellar Dynamics in Aqueous Solutions of PEO-PPO-PEO Block Copolymers. Langmuir 1997, 13, 6130–6134. [Google Scholar] [CrossRef]
- Kositza, M.J.; Bohne, C.; Alexandridis, P.; Hatton, T.A.; Holzwarth, J.F. Micellization Dynamics and Impurity Solubilization of the Block-Copolymer L64 in an Aqueous Solution. Langmuir 1999, 15, 322–325. [Google Scholar] [CrossRef]
- Kositza, M.J.; Bohne, C.; Alexandridis, P.; Hatton, T.A.; Holzwarth, J.F. Dynamics of Micro- and Macrophase Separation of Amphiphilic Block-Copolymers in Aqueous Solution. Macromolecules 1999, 32, 5539–5551. [Google Scholar] [CrossRef]
- Waton, G.; Michels, B.; Zana, R. Dynamics of Block Copolymer Micelles in Aqueous Solution. Macromolecules 2001, 34, 907–910. [Google Scholar] [CrossRef]
- Bednář, B.; Edwards, K.; Almgren, M.; Tormod, S.; Tuzar, Z. Rates of Association and Dissociation of Block Copolymer Micelles: Light-Scattering Stopped-Flow Measurements. Makromol. Chem. Rapid Commun. 1988, 9, 785–790. [Google Scholar] [CrossRef]
- Zhu, Z.; Armes, S.P.; Liu, S. pH-Induced Micellization Kinetics of ABC Triblock Copolymers Measured by Stopped-Flow Light Scattering. Macromolecules 2005, 38, 9803–9812. [Google Scholar] [CrossRef]
- Wang, D.; Yin, J.; Zhu, Z.; Ge, Z.; Liu, H.; Armes, S.P.; Liu, S. Micelle Formation and Inversion Kinetics of a Schizophrenic Diblock Copolymer. Macromolecules 2006, 39, 7378–7385. [Google Scholar] [CrossRef]
- Zhu, Z.; Xu, J.; Zhou, S.; Jiang, X.; Armes, S.P.; Liu, S. Effect of Salt on the Micellization Kinetics of pH-Responsive ABC Triblock Copolymers. Macromolecules 2007, 40, 6393–6400. [Google Scholar] [CrossRef]
- Ge, Z.; Cai, Y.; Yin, J.; Zhu, Z.; Rao, J.; Liu, S. Synthesis and ‘Schizophrenic’ Micellization of Double Hydrophilic AB4 Miktoarm Star and AB Diblock Copolymers: Structure and Kinetics of Micellization. Langmuir 2007, 23, 1114–1122. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Wu, T.; Liu, S. Micellization Kinetics of a Novel Multi-Responsive Double Hydrophilic Diblock Copolymer Studied by Stopped-Flow pH and Temperature Jump. Macromol. Chem. Phys. 2007, 208, 2492–2501. [Google Scholar] [CrossRef]
- Zhang, J.; Li, Y.; Armes, S.P.; Liu, S. Probing the Micellization Kinetics of Pyrene End-Labeled Diblock Copolymer via a Combination of Stopped-Flow Light-Scattering and Fluorescence Techniques. J. Phys. Chem. B 2007, 111, 12111–12118. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Xu, J.; Liu, S. Chain-Length Dependence of Diblock Copolymer Micellization Kinetics Studied by Stopped-Flow pH-Jump. J. Phys. Chem. B 2008, 112, 11284–11291. [Google Scholar] [CrossRef] [PubMed]
- Lund, R.; Willner, L.; Monkenbusch, M.; Panine, P.; Narayanan, T.; Colmenero, J.; Richter, D. Structural Observation and Kinetic Pathway in the Formation of Polymeric Micelles. Phys. Rev. Lett. 2009, 102, 188301. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lund, R.; Willner, L.; Richter, D. Kinetics of Block Copolymer Micelles Studied by Small-Angle Scattering Methods. Adv. Polym. Sci. 2013, 259, 51–158. [Google Scholar]
- Aniansson, E.A.G.; Wall, S.N. On the Kinetics of Step-Wise Micelle Association. J. Phys. Chem. 1974, 78, 1024–1030. [Google Scholar] [CrossRef]
- Aniansson, E.A.G.; Wall, S.N.; Almgren, M.; Hoffmann, H.; Kielmann, I.; Ulbrlcht, W.; Zana, R.; Lang, J.; Tondre, C. Theory of the Kinetics of Micellar Equilibria and Quantitative Interpretation of Chemical Relaxation Studies of Micellar Solutions of Ionic Surfactants. J. Phys. Chem. 1976, 80, 905–922. [Google Scholar] [CrossRef]
- Dormidontova, E.E. Micellization Kinetics in Block Copolymer Solutions: Scaling Model. Macromolecules 1999, 32, 7630–7644. [Google Scholar] [CrossRef]
- Neu, J.C.; Cañizo, J.A.; Bonilla, L.L. Three Eras of Micellization. Phy. Rev. E 2002, 66, 061406. [Google Scholar] [CrossRef] [Green Version]
- Shchekin, A.K.; Kuni, F.M.; Grinin, A.P.; Rusanov, A.I. Nucleation in Micellization Processes; Schmelzer, J.W.P., Ed.; WILEY-VCH: Weinheim, Germany, 2005; pp. 312–374. [Google Scholar]
- Takahashi, R.; Sato, T.; Terao, K.; Qiu, X.-P.; Winnik, F.M. Self-Association of a Thermosensitive Poly(alkyl-2-oxazoline) Block Copolymer in Aqueous Solution. Macromolecules 2012, 45, 6111–6119. [Google Scholar] [CrossRef]
- Sato, T.; Tanaka, K.; Toyokura, A.; Mori, R.; Takahashi, R.; Terao, K.; Yusa, S. Self-Association of a Thermosensitive Amphiphilic Block Copolymer Poly(N-isopropylacrylamide)-b-poly(N-vinyl-2-pyrrolidone) in Aqueous Solution upon Heating. Macromolecules 2013, 46, 226–235. [Google Scholar] [CrossRef]
- Takahashi, R.; Qiu, X.-P.; Xue, N.; Sato, T.; Terao, K.; Winnik, F.M. Self-Association of the Thermosensitive Block Copolymer Poly(2-isopropyl-2-oxazoline)-b-poly(N-isopropylacrylamide) in Water−Methanol Mixtures. Macromolecules 2014, 47, 6900–6910. [Google Scholar] [CrossRef]
- Takahashi, R.; Sato, T.; Terao, K.; Yusa, S. Intermolecular Interactions and Self-Assembly in Aqueous Solution of a Mixture of Anionic−Neutral and Cationic−Neutral Block Copolymers. Macromolecules 2015, 48, 7222–7229. [Google Scholar] [CrossRef]
- Kuang, C.; Yusa, S.; Sato, T. Micellization and Phase Separation in Aqueous Solutions of Thermosensitive Block Copolymer Poly(N-isopropylacrylamide)-b-poly(N-vinyl-2-pyrrolidone) upon Heating. Macromolecules 2019, 52, 4812–4819. [Google Scholar] [CrossRef]
- Sato, T.; Takahashi, R. Competition between the Micellization and the Liquid–Liquid Phase Separation in Amphiphilic Block Copolymer Solutions. Polym. J. 2017, 49, 273–277. [Google Scholar] [CrossRef]
- Leibler, L.; Orland, H.; Wheeler, J.C. Theory of Critical Micelle Concentration for Solutions of Block Copolymers. J. Chem. Phys. 1983, 79, 3550–3557. [Google Scholar] [CrossRef]
- Flory, P.J. Principle of Polymer Chemistry; Cornell University Press: Ithaca, NY, USA, 1953; Chapter 12. [Google Scholar]
- Noolandi, J.; Hong, K.M. Theory of Block Copolymer Micelles in Solution. Macromolecules 1983, 16, 1443–1448. [Google Scholar] [CrossRef]
- Lifshitz, I.M.; Slyozov, V.V. The Kinetics of Precipitation from Supersaturated Solid Solutions. J. Phys. Chem. Solids 1961, 19, 35–50. [Google Scholar] [CrossRef]
- Gunton, J.D.; San Miguel, M.; Sahni, P.S. The Dynamics of First-Order Phase Transitions. In Phase Transition and Critical Phenomena; Domb, C., Lebowitz, J.L., Eds.; Academic: New York, NY, USA, 1983; Volume 8, Chapter 3. [Google Scholar]
- Narang, N.; Sato, T. Unique Phase Behaviour and Self-Assembly of a Lysine Derivative, Fmoc-Homoarginine, in Water–DMSO Mixtures. Soft Matter 2022, 18, 7968–7974. [Google Scholar] [CrossRef]





Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sato, T. Kinetics of Micellization and Liquid–Liquid Phase Separation in Dilute Block Copolymer Solutions. Polymers 2023, 15, 708. https://doi.org/10.3390/polym15030708
Sato T. Kinetics of Micellization and Liquid–Liquid Phase Separation in Dilute Block Copolymer Solutions. Polymers. 2023; 15(3):708. https://doi.org/10.3390/polym15030708
Chicago/Turabian StyleSato, Takahiro. 2023. "Kinetics of Micellization and Liquid–Liquid Phase Separation in Dilute Block Copolymer Solutions" Polymers 15, no. 3: 708. https://doi.org/10.3390/polym15030708