Simulation of the Particle Transport Behaviors in Nanoporous Matter
Abstract
:1. Introduction
2. Materials and Methods
2.1. Simulation Codes
2.2. Proton Irradiation
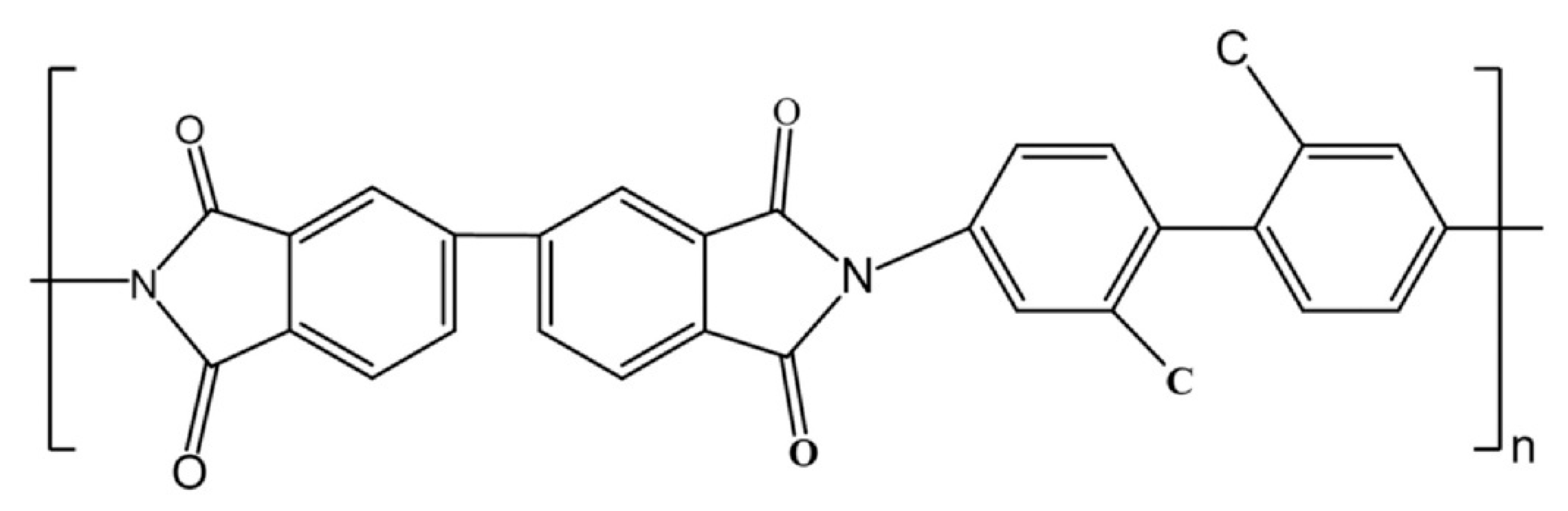
2.3. Materials and Testing
3. Results and Discussion
3.1. Simulation Part
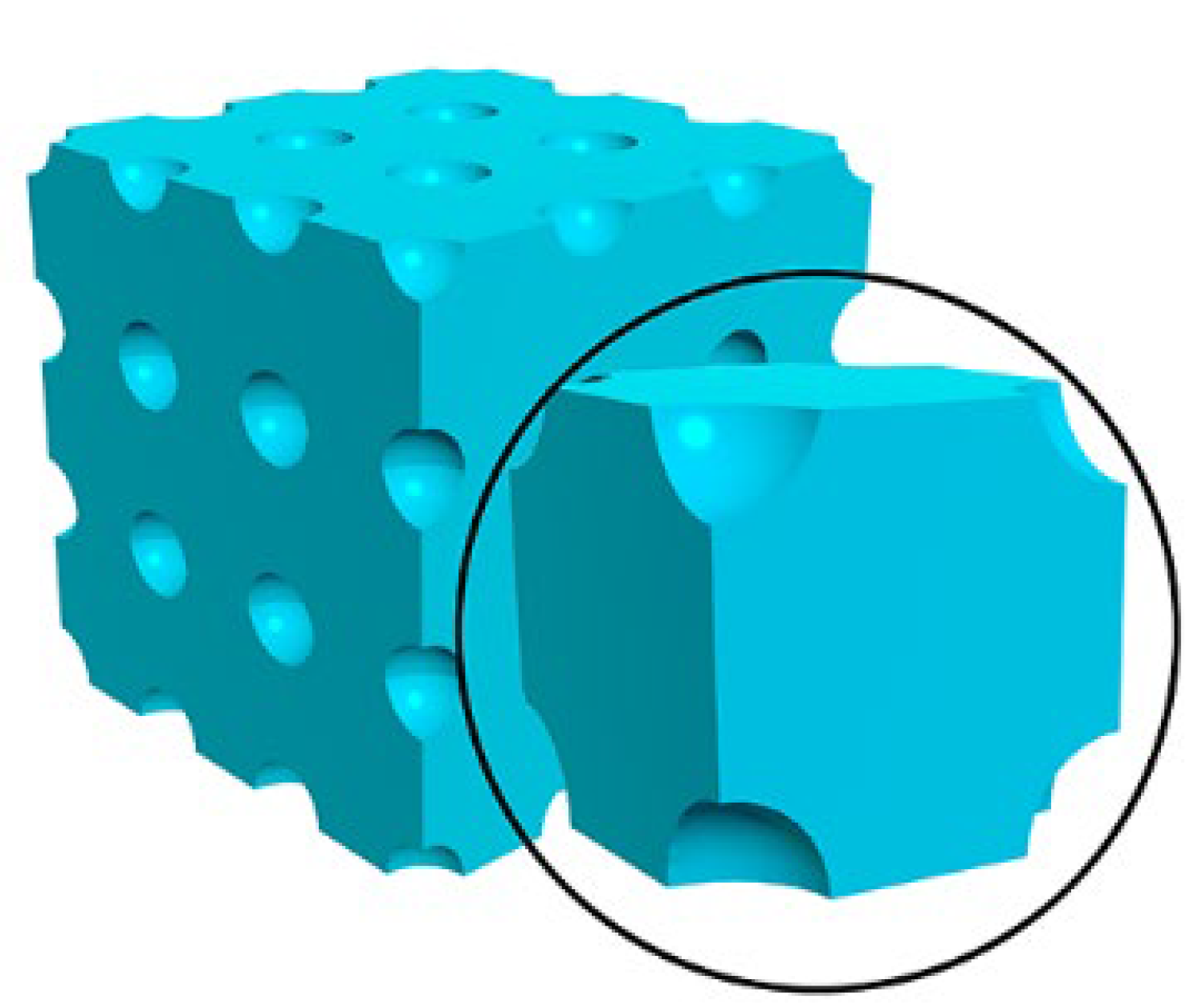
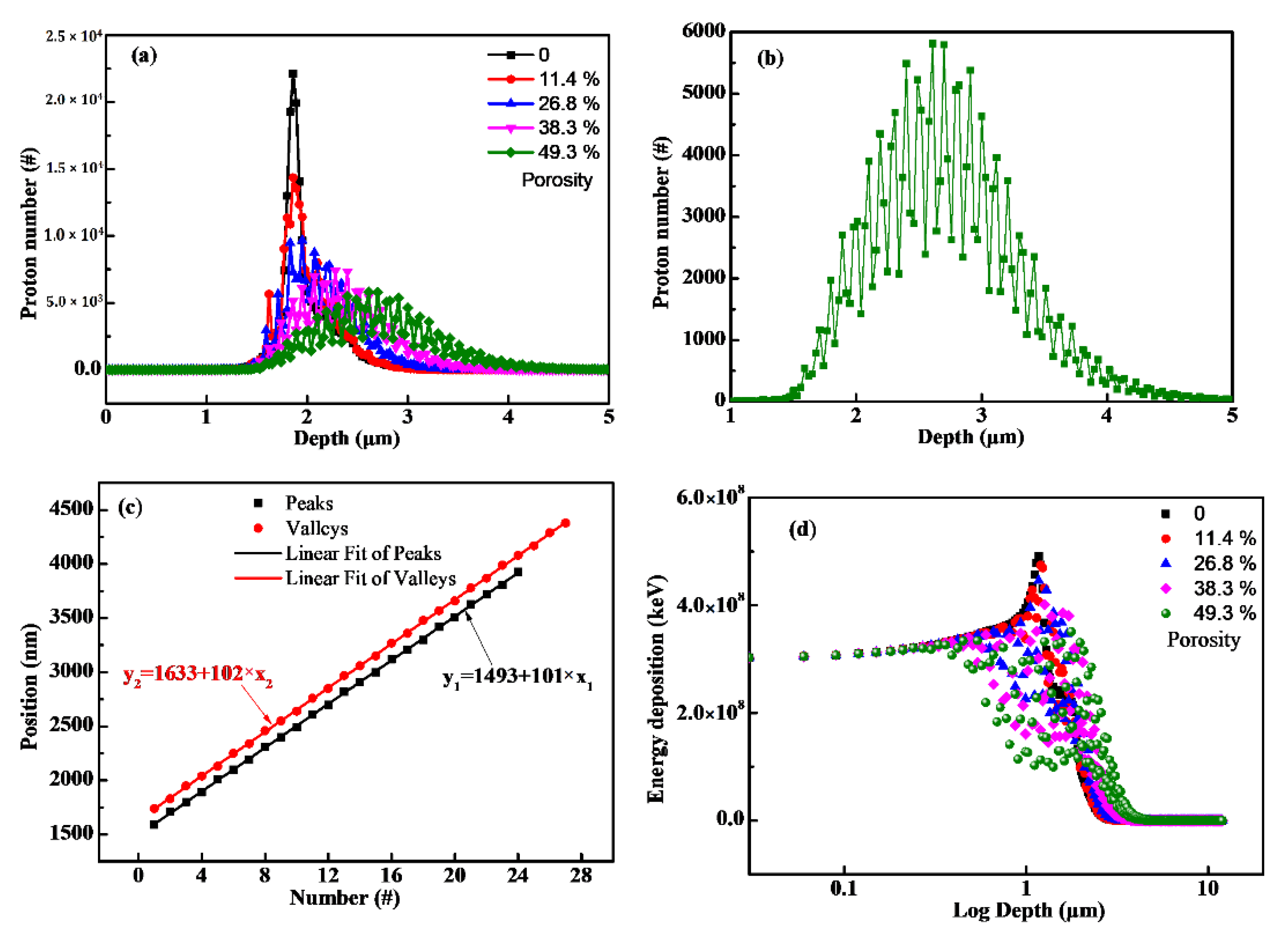
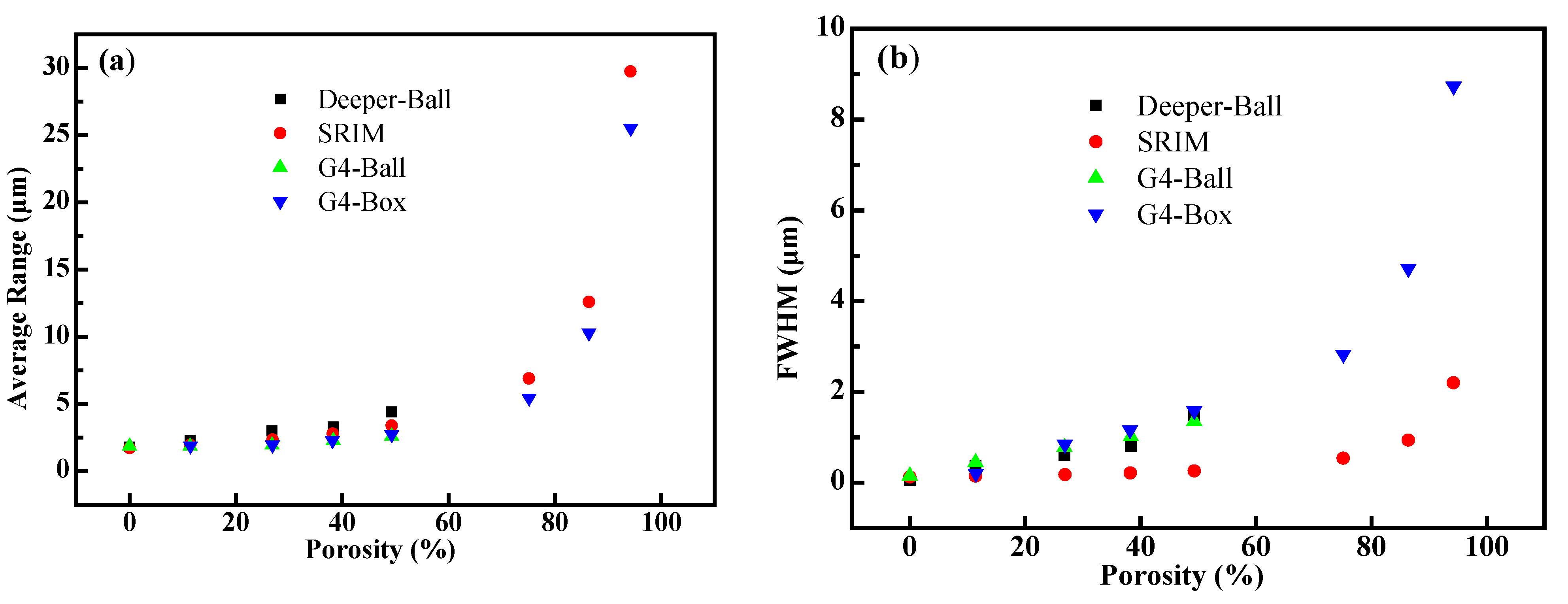
3.1.1. Porosity Effects
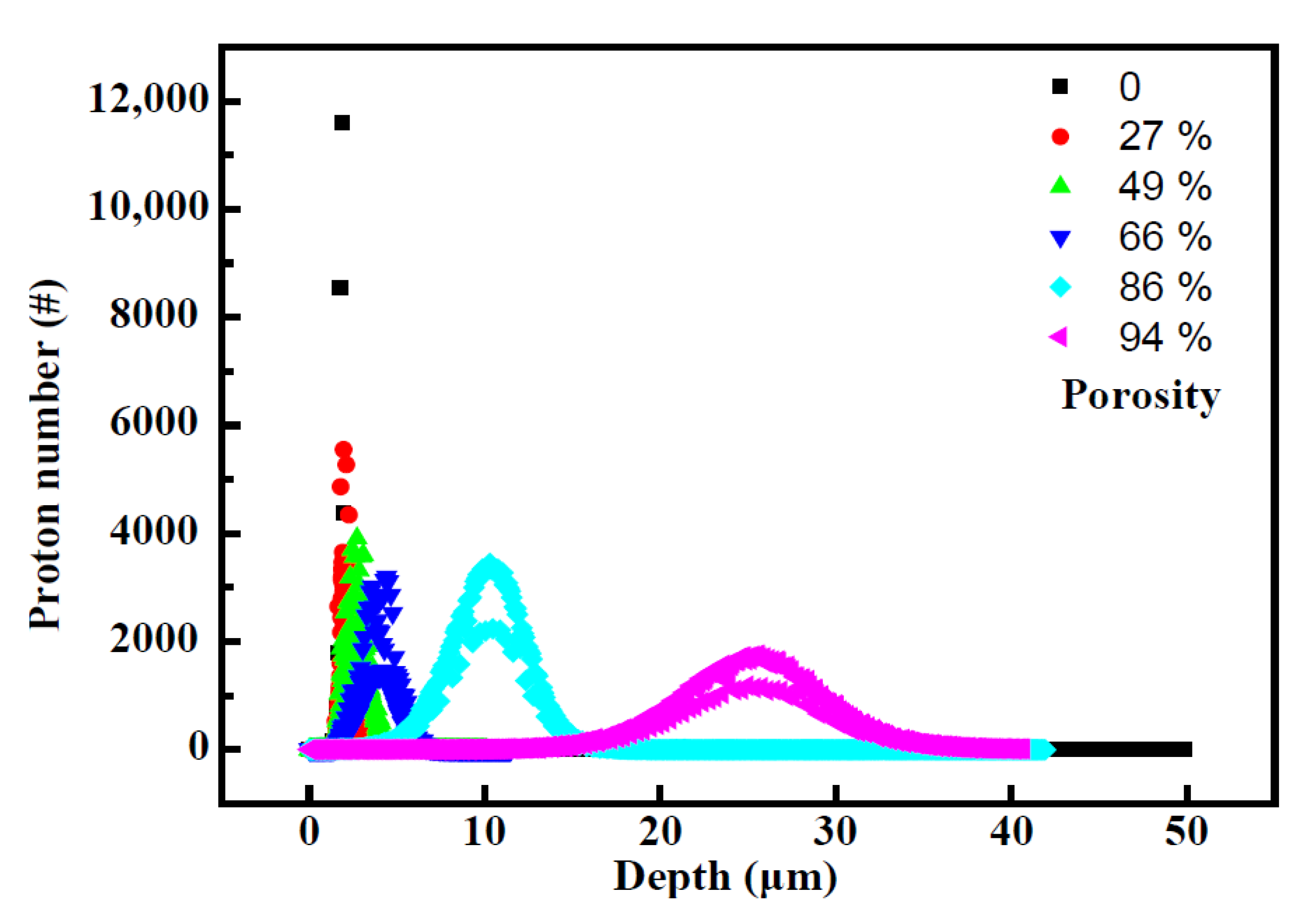
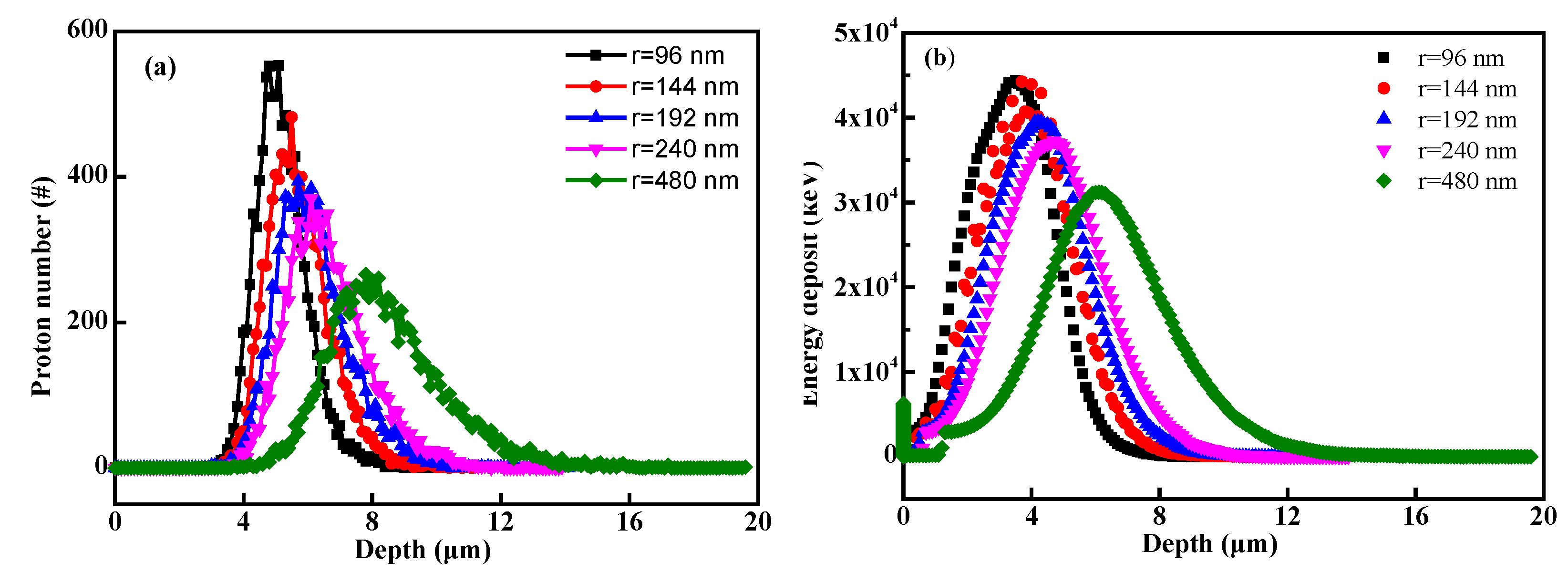
3.1.2. Voids Size Effect
3.2. Experiments Part
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Beyerlein, I.J.; Caro, A.; Demkowicz, M.J.; Mara, N.A.; Misra, A.; Uberuaga, B.P. Radiation damage tolerant nanomaterials. Mater. Today 2013, 16, 443–449. [Google Scholar] [CrossRef]
- Li, J.; Wang, H.; Zhang, X. A Review on the Radiation Response of Nanoporous Metallic Materials. JOM 2018, 70, 2753–2764. [Google Scholar] [CrossRef]
- Caro, M.; Mook, W.M.; Fu, E.G.; Wang, Y.Q.; Sheehan, C.; Martinez, E.; Baldwin, J.K.; Caro, A. Radiation induced effects on mechanical properties of nanoporous gold foams. Appl. Phys. Lett. 2014, 104, 233109. [Google Scholar] [CrossRef]
- Cheng, Y.; Yao, H.; Duan, J.; Xu, L.; Zhai, P.; Lyu, S.; Chen, Y.; Maaz, K.; Mo, D.; Sun, Y.; et al. Surface Modification and Damage of MeV-Energy Heavy Ion Irradiation on Gold Nanowires. Nanomaterials 2017, 7, 108. [Google Scholar] [CrossRef]
- Fu, E.G.; Caro, M.; Zepeda-Ruiz, L.A.; Wang, Y.Q.; Baldwin, K.; Bringa, E.; Nastasi, M.; Caro, A. Surface effects on the radiation response of nanoporous Au foams. Appl. Phys. Lett. 2012, 101, 191607. [Google Scholar] [CrossRef]
- Li, N.; Fu, E.G.; Wang, H.; Carter, J.J.; Shao, L.; Maloy, S.A.; Misra, A.; Zhang, X. He ion irradiation damage in Fe/W nanolayer films. J. Nucl. Mater. 2009, 389, 233–238. [Google Scholar] [CrossRef]
- Sun, C.; Bufford, D.; Chen, Y.; Kirk, M.A.; Wang, Y.Q.; Li, M.; Wang, H.; Maloy, S.A.; Zhang, X. In situ study of defect migration kinetics in nanoporous Ag with enhanced radiation tolerance. Sci. Rep. 2014, 4, 3737. [Google Scholar] [CrossRef]
- Hu, Z.Y.; Chen, H.Q.; Zhao, Y.B.; Wang, P.P.; Yang, K.J.; Zhang, J.; Liu, Z.L.; Wang, X.J.; Fu, E.G. Abundant free surface in nanoporous copper films enhancing tolerance against helium ion irradiation. J. Alloy. Compd. 2020, 843, 155829. [Google Scholar] [CrossRef]
- Bringa, E.M.; Monk, J.D.; Caro, A.; Misra, A.; Zepeda-Ruiz, L.; Duchaineau, M.; Abraham, F.; Nastasi, M.; Picraux, S.T.; Wang, Y.Q.; et al. Are nanoporous materials radiation resistant? Nano Lett. 2012, 12, 3351–3355. [Google Scholar] [CrossRef]
- Li, J.; Fan, C.; Ding, J.; Xue, S.; Chen, Y.; Li, Q.; Wang, H.; Zhang, X. In situ heavy ion irradiation studies of nanopore shrinkage and enhanced radiation tolerance of nanoporous Au. Sci. Rep. 2017, 7, 39484. [Google Scholar] [CrossRef] [Green Version]
- Yang, T.; Huang, X.; Wang, C.; Zhang, Y.; Xue, J.; Yan, S.; Wang, Y. Enhanced structural stability of nanoporous zirconia under irradiation of He. J. Nucl. Mater. 2012, 427, 225–232. [Google Scholar] [CrossRef]
- Chen, Y.; Liu, Y.; Fu, E.G.; Sun, C.; Yu, K.Y.; Song, M.; Li, J.; Wang, Y.Q.; Wang, H.; Zhang, X. Unusual size-dependent strengthening mechanisms in helium ion-irradiated immiscible coherent Cu/Co nanolayers. Acta Mater. 2015, 84, 393–404. [Google Scholar] [CrossRef]
- Li, J.; Chen, Y.; Wang, H.; Zhang, X. In situ study on enhanced heavy ion irradiation tolerance of porous Mg. Scr. Mater. 2018, 144, 13–17. [Google Scholar] [CrossRef]
- Li, J.; Fan, C.; Li, Q.; Wang, H.; Zhang, X. In situ studies on irradiation resistance of nanoporous Au through temperature-jump tests. Acta Mater. 2018, 143, 30–42. [Google Scholar] [CrossRef]
- Zhou, K.; Li, W.; Patel, B.B.; Tao, R.; Chang, Y.; Fan, S.; Diao, Y.; Cai, L. Three-Dimensional Printable Nanoporous Polymer Matrix Composites for Daytime Radiative Cooling. Nano Lett. 2021, 21, 1493–1499. [Google Scholar] [CrossRef]
- Rathilal, S. Adsorption and Photocatalytic Mineralization of Bromophenol Blue Dye with TiO2 Modified with Clinoptilolite/Activated Carbon. Catalysts 2020, 11, 7. [Google Scholar]
- Sibiya, N.P.; Rathilal, S.; Tetteh, E.K. Coagulation Treatment of Wastewater: Kinetics and Natural Coagulant Evaluation. Molecules 2021, 26, 698. [Google Scholar] [CrossRef]
- Tetteh, E.K.; Rathilal, S. Evaluation of different polymeric coagulants for the treatment of oil refinery wastewater. Cogent. Eng. 2020, 7, 1785756. [Google Scholar] [CrossRef]
- Tetteh, E.K.; Rathilal, S. Application of organic coagulants in water and wastewater treatment. In Organic Polymers; IntechOpen: London, UK, 2019. [Google Scholar] [CrossRef]
- Li, M.; Gan, F.; Dong, J.; Fang, Y.; Zhao, X.; Zhang, Q. Facile Preparation of Continuous and Porous Polyimide Aerogel Fibers for Multifunctional Applications. ACS Appl. Mater. Interfaces 2021, 13, 10416–10427. [Google Scholar] [CrossRef]
- Yamagishi, A.; Yokobori, S.I.; Kobayashi, K.; Mita, H.; Yabuta, H.; Tabata, M.; Higashide, M.; Yano, H. Scientific Targets of Tanpopo: Astrobiology Exposure and Micrometeoroid Capture Experiments at the Japanese Experiment Module Exposed Facility of the International Space Station. Astrobiology 2021, 21, 1451–1460. [Google Scholar] [CrossRef]
- Ziegler, J.F.; Ziegler, M.D.; Biersack, J.P. SRIM—The stopping and range of ions in matter. Nucl. Instrum. Methods Phys. Res. Sect. B Beam Interact. Mater. At. 2010, 268, 1818–1823. [Google Scholar] [CrossRef]
- Yan, Q.; Shao, L. A Monte Carlo simulation code for calculating damage and particle transport in solids: The case for electron-bombarded solids for electron energies up to 900 MeV. J. Nucl. Mater. 2017, 485, 98–104. [Google Scholar] [CrossRef]
- Agostinelli, S.; Allison, J.; Amako, K.; Apostolakis, J.; Araujo, H.; Arce, P.; Asai, M.; Axen, D.; Banerjee, S.; Barrand, G.; et al. GEANT4—A simulation toolkit. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 2003, 506, 250–303. [Google Scholar] [CrossRef]
- Wu, Y.; Sun, C.; Wu, Y.; Xing, Y.; Xiao, J.; Guo, B.; Wang, Y.; Sui, Y. The degradation behavior and mechanism of polytetrafluoroethylene under low energy proton irradiation. Nucl. Instrum. Methods Phys. Res. 2018, 430, 47–53. [Google Scholar] [CrossRef]
- Fang, G.; Li, H.; Liu, J.; Ni, H.; Yang, H.; Wang, G. Intrinsically Atomic-oxygen Resistant POSS-containing Polyimide Aerogels: Synthesis and Characterization. Chem. Lett. 2015, 44, 1083–1085. [Google Scholar] [CrossRef]
- Xie, T.; Xu, K.; Yang, B.; He, Y. Effect of pore size and porosity distribution on radiation absorption and thermal performance of porous solar energy absorber. Sci. China Technol. Sci. 2019, 62, 2213–2225. [Google Scholar] [CrossRef]
- Wu, Y.; Ju, D.; Wang, H.; Zhao, H.; Sun, C.; Wu, Y.; Guo, B.; Wang, Y. Modification of surface structure and mechanical properties in polyimide aerogel by low-energy proton implantation. Surf. Coat. Technol. 2020, 403, 126364. [Google Scholar] [CrossRef]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, Y.; Ju, D.; Wang, H.; Sun, C.; Wu, Y.; Cao, Z.; Tolochko, O.V. Simulation of the Particle Transport Behaviors in Nanoporous Matter. Polymers 2022, 14, 3563. https://doi.org/10.3390/polym14173563
Wu Y, Ju D, Wang H, Sun C, Wu Y, Cao Z, Tolochko OV. Simulation of the Particle Transport Behaviors in Nanoporous Matter. Polymers. 2022; 14(17):3563. https://doi.org/10.3390/polym14173563
Chicago/Turabian StyleWu, You, Dandan Ju, Hao Wang, Chengyue Sun, Yiyong Wu, Zhengli Cao, and Oleg V Tolochko. 2022. "Simulation of the Particle Transport Behaviors in Nanoporous Matter" Polymers 14, no. 17: 3563. https://doi.org/10.3390/polym14173563





