Pyrolysis Study of Mixed Polymers for Non-Isothermal TGA: Artificial Neural Networks Application
Abstract
:1. Introduction
2. Materials and Methods
2.1. Thermal Decomposition
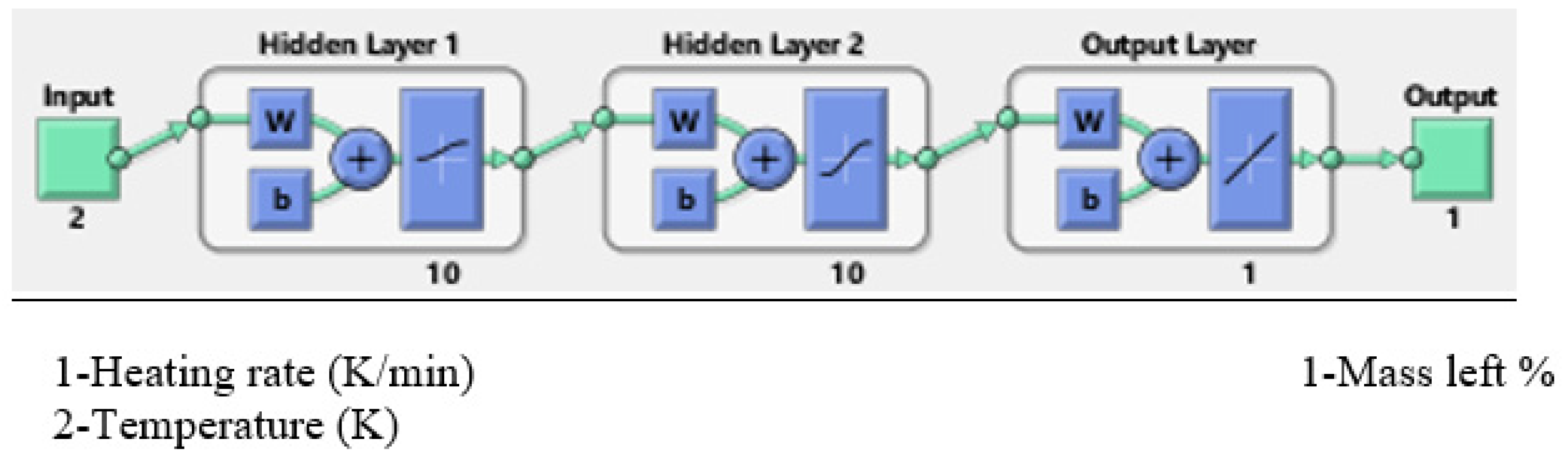
2.2. Structure of ANNs
- (W %)est: is the estimated value of the weight left % by ANN model;
- (W %)exp, is the experimental value of the weight left %; and
- : is the average values of weight left %.
3. Results and Discussion
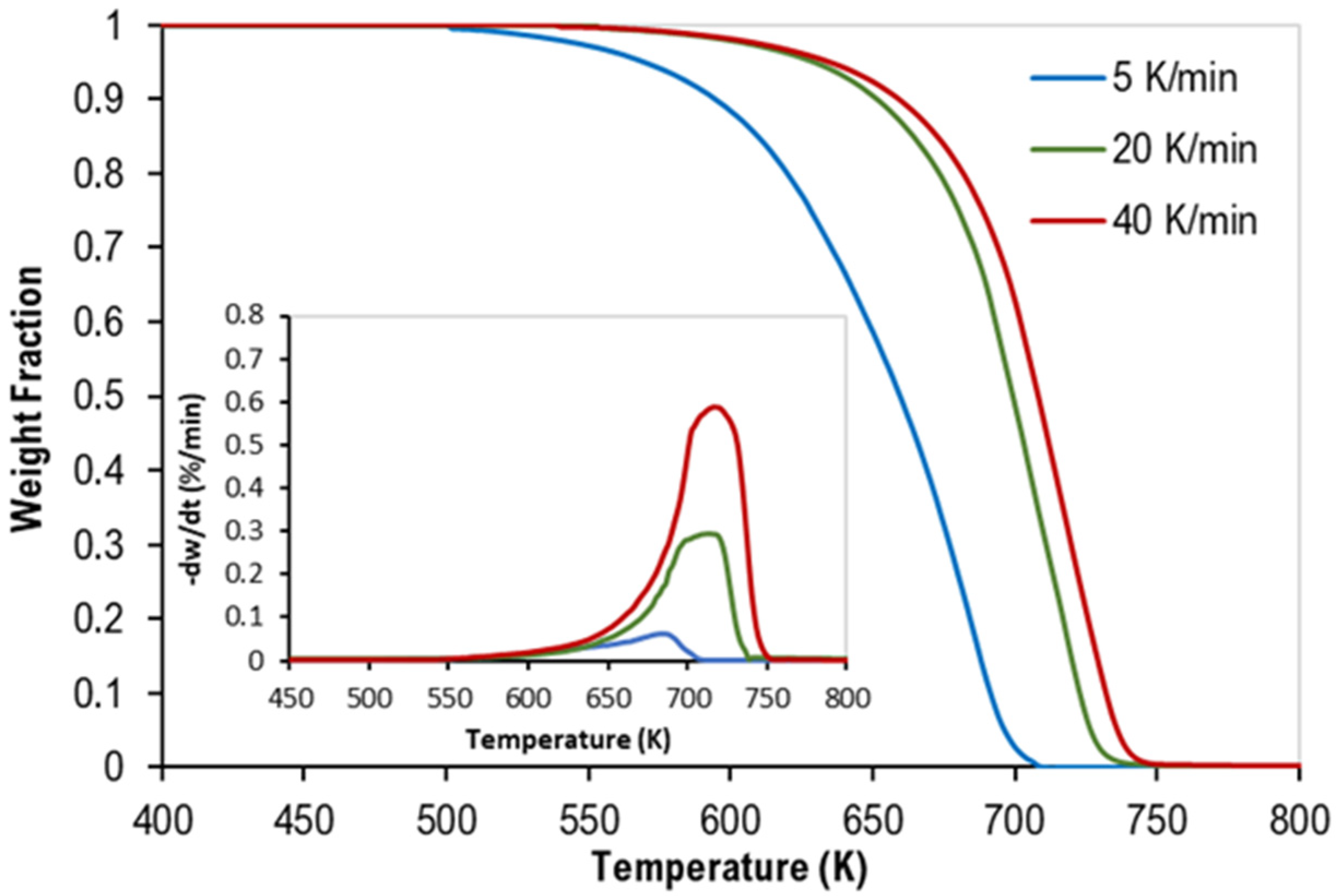
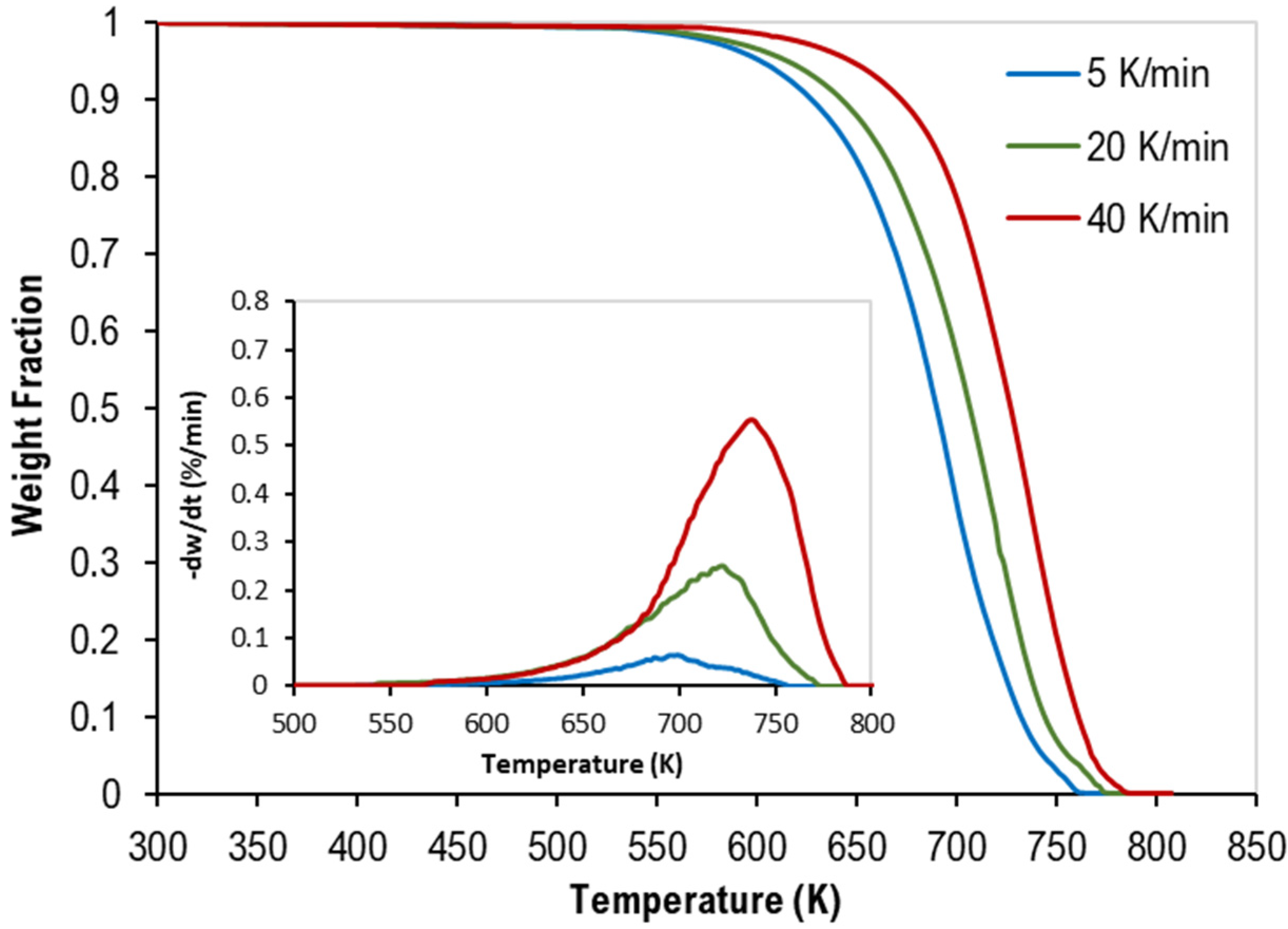
3.1. TGA of Mixed Polymers
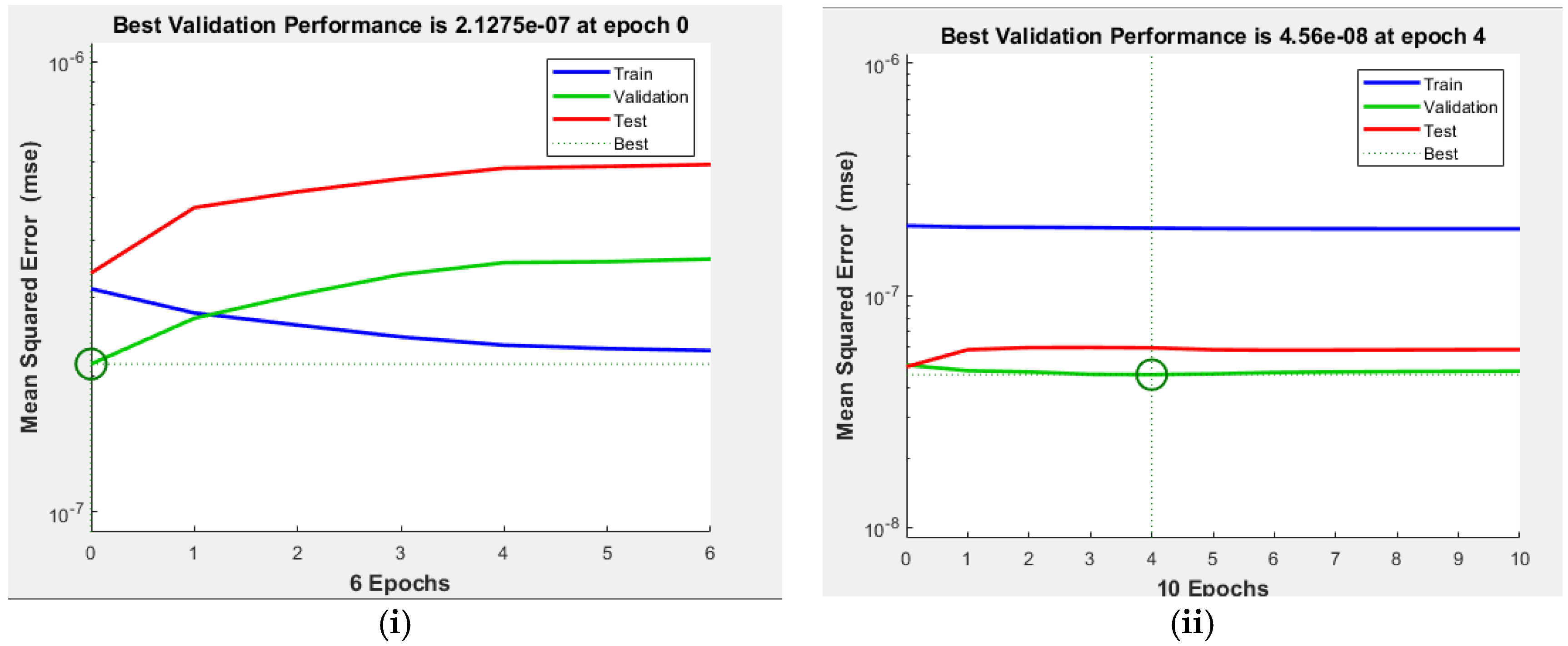
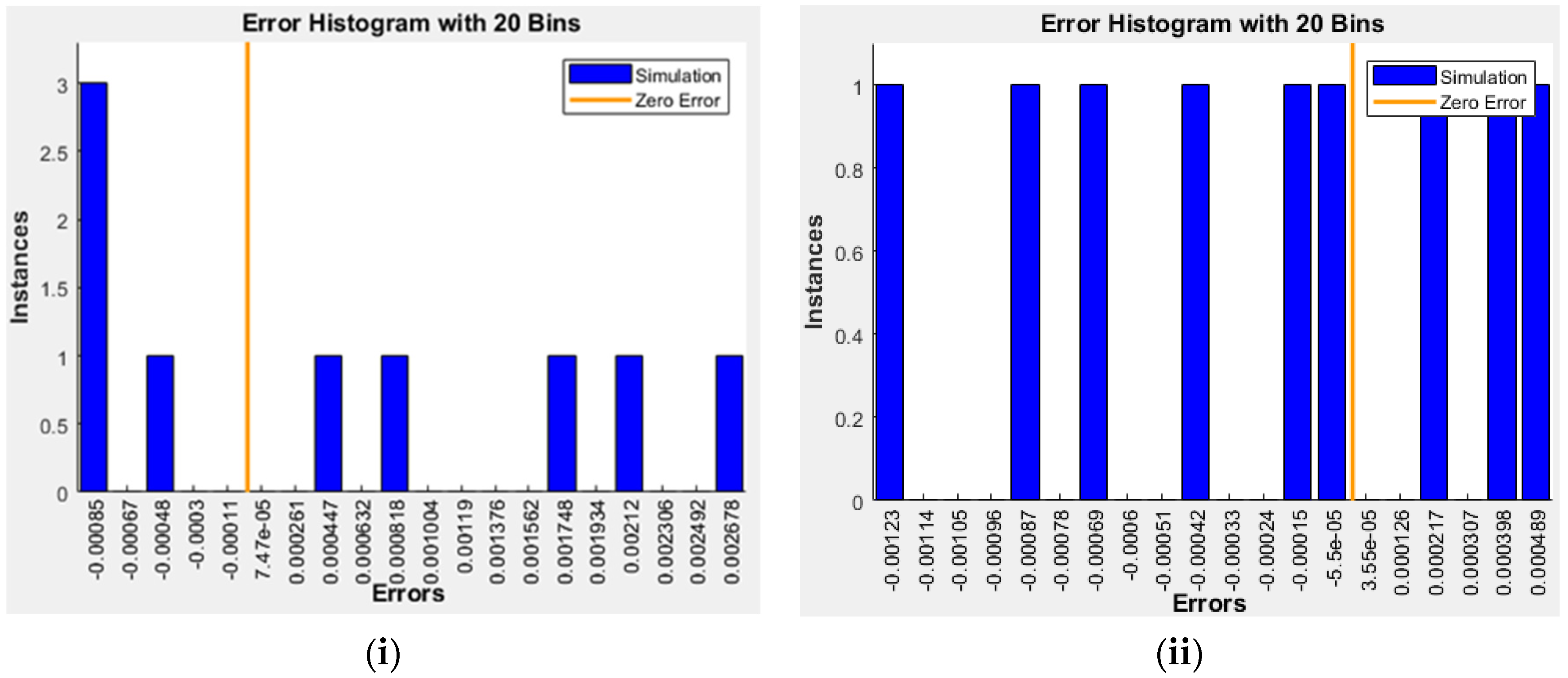
3.2. Pyrolysis Prediction by ANN Model
4. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Conesa, J.A.; Caballero, J.A.; Labarta, J.A. Artificial neural network for modelling thermal decompositions. J. Anal. Appl. Pyrolysis 2004, 71, 343–352. [Google Scholar] [CrossRef]
- Bezerra, E.; Bento, M.; Rocco, J.; Iha, K.; Lourenço, V.; Pardini, L. Artificial neural network (ANN) prediction of kinetic parameters of (CRFC) composites. Comput. Mater. Sci. 2008, 44, 656–663. [Google Scholar] [CrossRef]
- Yıldız, Z.; Uzun, H.; Ceylan, S.; Topcu, Y. Application of artificial neural networks to co-combustion of hazelnut husk–lignite coal blends. Bioresour. Technol. 2016, 200, 42–47. [Google Scholar] [CrossRef] [PubMed]
- Çepelioğullar, Ö.; Mutlu, I.; Yaman, S.; Haykiri-Acma, H. A study to predict pyrolytic behaviors of refuse-derived fuel (RDF): Artificial neural network application. J. Anal. Appl. Pyrolysis 2016, 122, 84–94. [Google Scholar] [CrossRef]
- Ahmad, M.S.; Mehmood, M.A.; Taqvi, S.T.H.; Elkamel, A.; Liu, C.-G.; Xu, J.; Rahimuddin, S.A.; Gull, M. Pyrolysis, kinetics analysis, thermodynamics parameters and reaction mechanism of Typha latifolia to evaluate its bioenergy potential. Bioresour. Technol. 2017, 245, 491–501. [Google Scholar] [CrossRef] [Green Version]
- Çepelioğullar, Ö.; Mutlu, I.; Yaman, S.; Haykiri-Acma, H. Activation energy prediction of biomass wastes based on different neural network topologies. Fuel 2018, 220, 535–545. [Google Scholar] [CrossRef]
- Chen, J.; Xie, C.; Liu, J.; He, Y.; Xie, W.; Zhang, X.; Chang, K.; Kuo, J.; Sun, J.; Zheng, L.; et al. Co-combustion of sewage sludge and coffee grounds under increased O2/CO2 atmospheres: Thermodynamic characteristics, kinetics and artificial neural network modeling. Bioresour. Technol. 2018, 250, 230–238. [Google Scholar] [CrossRef]
- Naqvi, S.R.; Tariq, R.; Hameed, Z.; Ali, I.; Taqvi, S.A.; Naqvi, M.; Niazi, M.B.; Noor, T.; Farooq, W. Pyrolysis of high-ash sewage sludge: Thermo-kinetic study using TGA and artificial neural networks. Fuel 2018, 233, 529–538. [Google Scholar] [CrossRef]
- Ahmad, M.S.; Liu, H.; Alhumade, H.; Tahir, M.H.; Çakman, G.; Yıldız, A.; Ceylan, S.; Elkamel, A.; Shen, B. A modified DAEM: To study the bioenergy potential of invasive Staghorn Sumac through pyrolysis, ANN, TGA, kinetic modeling, FTIR and GC–MS analysis. Energy Convers. Manag. 2020, 221, 113173. [Google Scholar] [CrossRef]
- Bi, H.; Wang, C.; Lin, Q.; Jiang, X.; Jiang, C.; Bao, L. Combustion behavior, kinetics, gas emission characteristics and artificial neural network modeling of coal gangue and biomass via TG-FTIR. Energy 2020, 213, 118790. [Google Scholar] [CrossRef]
- Bong, J.T.; Loy, A.C.M.; Chin, B.L.F.; Lam, M.K.; Tang, D.K.H.; Lim, H.Y.; Chai, Y.H.; Yusup, S. Artificial neural network approach for co-pyrolysis of Chlorella vulgaris and peanut shell binary mixtures using microalgae ash catalyst. Energy 2020, 207, 118289. [Google Scholar] [CrossRef]
- Bi, H.; Wang, C.; Lin, Q.; Jiang, X.; Jiang, C.; Bao, L. Pyrolysis characteristics, artificial neural network modeling and environmental impact of coal gangue and biomass by TG-FTIR. Sci. Total Environ. 2020, 751, 142293. [Google Scholar] [CrossRef] [PubMed]
- Liew, J.X.; Loy, A.C.M.; Chin, B.L.F.; AlNouss, A.; Shahbaz, M.; Al-Ansari, T.; Govindan, R.; Chai, Y.H. Synergistic effects of catalytic co-pyrolysis of corn cob and HDPE waste mixtures using weight average global process model. Renew. Energy 2021, 170, 948–963. [Google Scholar] [CrossRef]
- Zaker, A.; Chen, Z.; Zaheer-Uddin, M. Catalytic pyrolysis of sewage sludge with HZSM5 and sludge-derived activated char: A comparative study using TGA-MS and artificial neural networks. J. Environ. Chem. Eng. 2021, 9, 105891. [Google Scholar] [CrossRef]
- Dubdub, I.; Al-Yaari, M. Pyrolysis of Low Density Polyethylene: Kinetic Study Using TGA Data and ANN Prediction. Polymers 2020, 12, 891. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Dubdub, I.; Al-Yaari, M. Thermal Behavior of Mixed Plastics at Different Heating Rates: I. Pyrolysis Kinetics. Polymers 2021, 13, 3413. [Google Scholar] [CrossRef]
- Al-Yaari, M.; Dubdub, I. Application of Artificial Neural Networks to Predict the Catalytic Pyrolysis of HDPE Using Non-Isothermal TGA Data. Polymers 2020, 12, 1813. [Google Scholar] [CrossRef]
- Al-Yaari, M.; Dubdub, I. Pyrolytic Behavior of Polyvinyl Chloride: Kinetics, Mechanisms, Thermodynamics, and Artificial Neural Network Application. Polymers 2021, 13, 4359. [Google Scholar] [CrossRef]
- Quantrille, T.E.; Liu, Y.A. Artificial Intelligence in Chemical Engineering; Elsevier Science: Amsterdam, The Netherlands, 1992. [Google Scholar]
- Halali, M.A.; Azari, V.; Arabloo, M.; Mohammadi, A.H.; Bahadori, A. Application of a radial basis function neural network to estimate pressure gradient in water–oil pipelines. J. Taiwan Inst. Chem. Eng. 2016, 58, 189–202. [Google Scholar] [CrossRef]
- Govindan, B.; Jakka, S.C.B.; Radhakrishnan, T.K.; Tiwari, A.K.; Sudhakar, T.M.; Shanmugavelu, P.; Kalburgi, A.K.; Sanyal, A.; Sarkar, S. Investigation on Kinetic Parameters of Combustion and Oxy-Combustion of Calcined Pet Coke Employing Thermogravimetric Analysis Coupled to Artificial Neural Network Modeling. Energy Fuels 2018, 32, 3995–4007. [Google Scholar] [CrossRef]
- Bar, N.; Bandyopadhyay, T.K.; Biswas, M.N.; Das, S.K. Prediction of pressure drop using artificial neural network for non-Newtonian liquid flow through piping components. J. Pet. Sci. Eng. 2010, 71, 187–194. [Google Scholar] [CrossRef]
- Al-Wahaibi, T.; Mjalli, F.S. Prediction of Horizontal Oil-Water Flow Pressure Gradient Using Artificial Intelligence Techniques. Chem. Eng. Commun. 2013, 201, 209–224. [Google Scholar] [CrossRef]
- Osman, E.-S.A.; Aggour, M.A. Artificial Neural Network Model for Accurate Prediction of Pressure Drop in Horizontal and Near-Horizontal-Multiphase Flow. Pet. Sci. Technol. 2002, 20, 1–15. [Google Scholar] [CrossRef]
- Qinghua, W.; Honglan, Z.; Wei, L.; Junzheng, Y.; Xiaohong, W.; Yan, W. Experimental Study of Horizontal Gas-liquid Two-phase Flow in Two Medium-diameter Pipes and Prediction of Pressure Drop through BP Neural Networks. Int. J. Fluid Mach. Syst. 2018, 11, 255–264. [Google Scholar] [CrossRef]
- Beale, M.H.; Hagan, M.T.; Demuth, H.B. Neural Network Toolbox TM User’s Guide; MathWorks: Natick, MA, USA, 2018. [Google Scholar]

| Author | Input Variables | Output Variables | Architecture Model | No. of Hidden Layers | Transfer Function for Hidden Layers | Data Points | ||
|---|---|---|---|---|---|---|---|---|
| Bezerra et al. [2] | temperature | heating rate | - | mass retained | 2-21-21-1 | 2 | 1941 | |
| Yıldız et al. [3] | temperature | heating rate | blend ratio | Mass loss % | 3-5-15-1 | 2 | tangsig-tansig | |
| Ahmad et al. [5] | temperature | Heating rate | - | weight loss | 2 | 1021 | ||
| Çepelioĝullar et al. [6] Individual | temperature | heating rate | - | weight loss | 2-20–20-1 (LFR)2-19–16-1 (OOR) | 2 | tangsig-logsig | 4000 |
| Çepelioĝullar et al. [6] Combined | 2-7–6-1 | 2 | 8000 | |||||
| Chen et al. [7] | temperature | heating rate | mixing ratio | mass loss % | 3-3-19-1 | 2 | tansig-tansig | |
| Naqvi et al. [8] | temperature | heating rate | - | weight loss | 2-5-1 | 1 | tansig | 1400 |
| Ahmad et al. [9] | temperature | Heating rate | - | weight loss | 2-10-1 | 1 | 1155 | |
| Bi et al. [10] (combustion), (pyrolysis) | temperature | mixing ratio | - | residual mass | 2-3-18-1 2-3-15-1 | 2 | tangsig-tangsig | |
| Bong et al. [11] | temperature | heating rate | - | weight loss % | 2-(9-12)-(9-12)-1 | 2 | tansig-tansig and logsig-tansig | |
| Bi et al. [12] | temperature | heating rate | mixing ratio | remaining mass % | 3-5-10-1 | 2 | tangsig-tangsig | 5000 |
| Zaker et al. [14] | temperature | heating rate | - | weight loss (%) | 2-7-1 | 1 | tansig | |
| Al-Yaari and Dubdub [17] | temperature | heating rate | mass ratio | mass left % | 3-10-10-1 | 2 | tansig-logsig | 900 |
| Set No. | Test No. | Heating Rate (K/min) | Weight % | Comment | ||
|---|---|---|---|---|---|---|
| PP | PS | LDPE | ||||
| 1 | 1 | 5 | 50 | 50 | 0 | mixture of PS, and PP |
| 2 | 20 | 50 | 50 | 0 | ||
| 3 | 40 | 50 | 50 | 0 | ||
| 2 | 4 | 5 | 33.3 | 33.3 | 33.3 | mixture of PS, LDPE, and PP |
| 5 | 20 | 33.3 | 33.3 | 33.3 | ||
| 6 | 40 | 33.3 | 33.3 | 33.3 | ||
| Set No. | Test No. | Heating Rate (K/min) | Data Set Number | Total |
|---|---|---|---|---|
| 1 | 1 | 5 | 126 | 358 |
| 2 | 20 | 101 | ||
| 3 | 40 | 131 | ||
| 2 | 4 | 5 | 251 | 752 |
| 5 | 20 | 251 | ||
| 6 | 40 | 250 |
| Number of inputs | 2 (Temperature (K), Heating rate (K/min) |
| Number of output | 1 (Mass left %) |
| Number of hidden layers | 1-2 |
| Transfer function of hidden layers | logsig-tansig |
| Number of neurons of hidden layers Transfer function of out layer | 10-10 purelin |
| Data division function | Dividerand |
| Learning algorithm | Levenberg-Marquardt (TRAINLM) |
| Data division (Training-Validation-Testing) | 70%-15%-15% |
| Data number (Training-Validation-Testing) | 250-54-54 = 358 526-113-113 = 752 |
| Data number (Simulation) | 9-9 |
| Performance function | MSE |
| Validation checks | 6 |
| Model | Network Topology (no. of Neurons) 2 Input-Hidden Layers (1 or 2 Layers)-1 Output | Hidden Layers | R | |
|---|---|---|---|---|
| 1st Transfer Function | 2nd Transfer Function | |||
| i | ||||
| AN1-A | 2-5-1 | tansig | - | 0.99881 |
| AN2-A | 2-5-1 | logsig | - | 0.99972 |
| AN3-A | 2-10-1 | tansig | - | 0.99995 |
| AN4-A | 2-10-1 | logsig | - | 0.99997 |
| AN5-A | 2-15-1 | tansig | - | 0.99997 |
| AN6-A | 2-15-1 | logsig | - | 0.99999 |
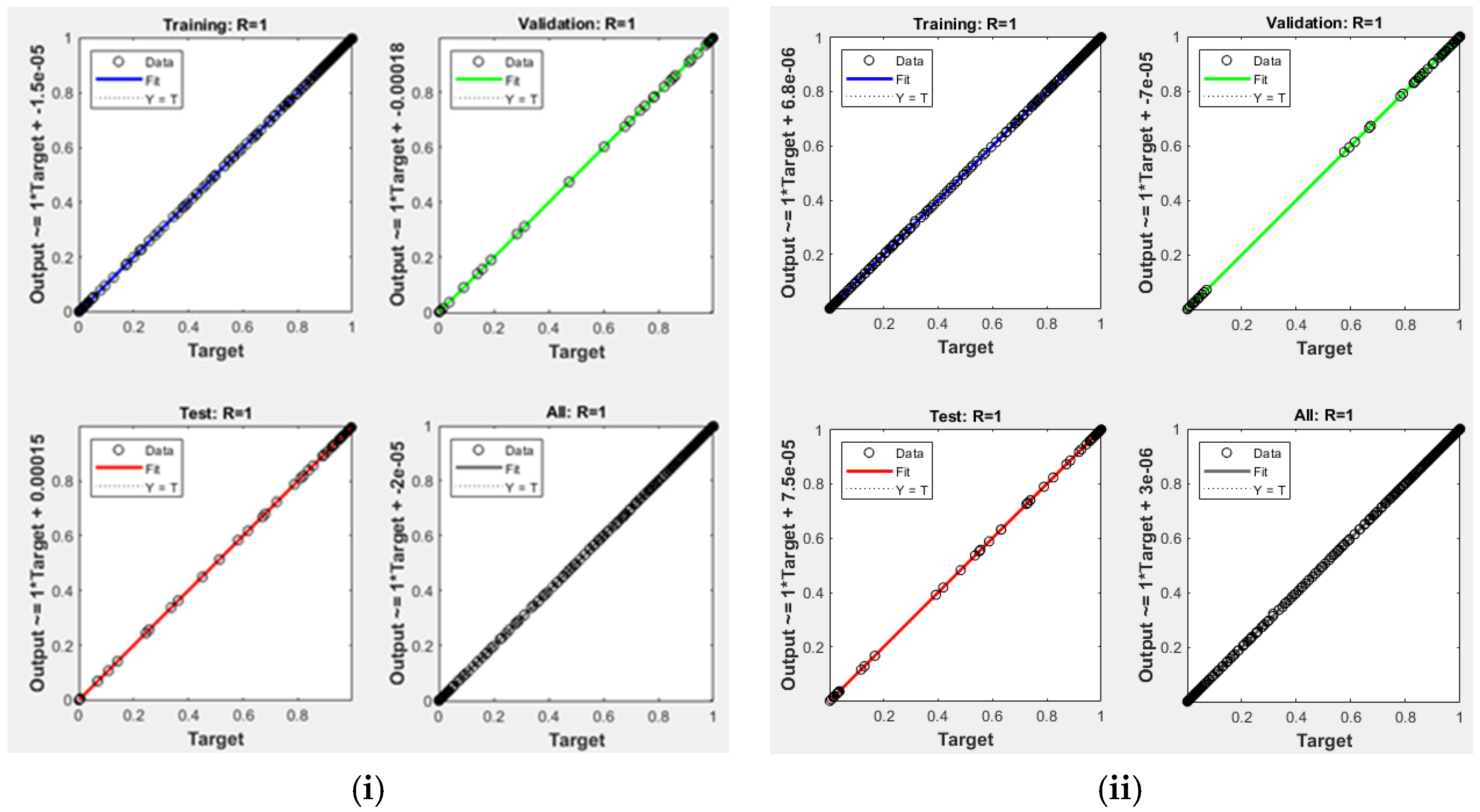
| AN7-A | 2-10-10-1 | logsig | tansig | 1.00000 |
| ii | ||||
| AN1-B | 2-5-1 | tansig | - | 0.99976 |
| AN2-B | 2-5-1 | logsig | - | 0.99997 |
| AN3-B | 2-10-1 | tansig | - | 0.99999 |
| AN4-B | 2-10-1 | logsig | - | 0.99999 |
| AN5-B | 2-15-1 | tansig | - | 0.99999 |
| AN6-B | 2-15-1 | logsig | - | 0.99999 |
| AN7-B | 2-10-10-1 | logsig | tansig | 1.00000 |
| Set | AN7-A | AN7-B | ||||||
|---|---|---|---|---|---|---|---|---|
| Statistical Parameters | Statistical Parameters | |||||||
| R2 | RMSE | MAE | MBE | R2 | RMSE | MAE | MBE | |
| Training | 1.0 | 0.00055 | 0.00030 | −0.00001 | 1.0 | 0.00044 | 0.00016 | 1.49 × 10−6 |
| Validation | 1.0 | 0.00046 | 0.00029 | −0.00001 | 1.0 | 0.00021 | 0.00012 | −1.74 × 10−6 |
| Test | 1.0 | 0.00058 | 0.00032 | 0.000018 | 1.0 | 0.00024 | 0.00014 | 0.000034 |
| All | 1.0 | 0.00054 | 0.00030 | −0.000012 | 1.0 | 0.000389 | 0.000154 | 6.018 × 10−6 |
| No. | Mixture of PS and PP for AN7-A | Mixture of PS, LDPE, and PP for AN7-B | ||||
|---|---|---|---|---|---|---|
| Input Data | Output Data | Input Data | Output Data | |||
| Heating Rate (K/min) | Temperature (K) | Weight Fraction | Heating Rate (K/min) | Temperature (K) | Weight Fraction | |
| 1 | 5 | 690 | 0.11471 | 5 | 731 | 0.10335 |
| 2 | 5 | 668 | 0.41012 | 5 | 697 | 0.40892 |
| 3 | 5 | 634 | 0.70892 | 5 | 669 | 0.70090 |
| 4 | 20 | 716 | 0.21154 | 20 | 731 | 0.20736 |
| 5 | 20 | 698 | 0.51639 | 20 | 705 | 0.51387 |
| 6 | 20 | 672 | 0.80757 | 20 | 669 | 0.80014 |
| 7 | 40 | 718 | 0.32648 | 40 | 741 | 0.30962 |
| 8 | 40 | 700 | 0.62535 | 40 | 717 | 0.60931 |
| 9 | 40 | 658 | 0.90289 | 40 | 671 | 0.90323 |
| AN7-A | AN7-B | ||||||
|---|---|---|---|---|---|---|---|
| Statistical Parameters | Statistical Parameters | ||||||
| R2 | RMSE | MAE | MBE | R2 | RMSE | MAE | MBE |
| 0.99999 | 0.00144 | 0.00123 | −0.00052 | 0.99999 | 0.00062 | 0.00049 | 0.00026 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dubdub, I. Pyrolysis Study of Mixed Polymers for Non-Isothermal TGA: Artificial Neural Networks Application. Polymers 2022, 14, 2638. https://doi.org/10.3390/polym14132638
Dubdub I. Pyrolysis Study of Mixed Polymers for Non-Isothermal TGA: Artificial Neural Networks Application. Polymers. 2022; 14(13):2638. https://doi.org/10.3390/polym14132638
Chicago/Turabian StyleDubdub, Ibrahim. 2022. "Pyrolysis Study of Mixed Polymers for Non-Isothermal TGA: Artificial Neural Networks Application" Polymers 14, no. 13: 2638. https://doi.org/10.3390/polym14132638






