Analysis of Leaky Modes in Photonic Crystal Fibers Using the Surface Integral Equation Method
Abstract
:1. Introduction
2. Surface Integral Equation Formulation
3. Numerical Result
4. Conclusions
Acknowledgments
Conflicts of Interest
References
- Snyder, A.W.; Love, J.D. Optical Waveguide Theory; Kluwer Academic Publishers: Norwell, MA, USA, 1983. [Google Scholar]
- Marcuvitz, N. On field representations in terms of leaky modes or eigenmodes. IRE Trans. Antennas Propag. 1956, 4, 192–194. [Google Scholar] [CrossRef]
- Hu, J.; Menyuk, C.R. Understanding leaky modes: Slab waveguide revisited. Adv. Opt. Photonics 2009, 1, 58–106. [Google Scholar] [CrossRef]
- Cassedy, E.S.; Cohn, M. On the existence of leaky waves due to a line source above a grounded dielectric slab. IRE Trans. Microw. Theory Tech. 1961, 9, 243–247. [Google Scholar] [CrossRef]
- Maeda, M.; Yamada, S. Leaky modes on W-fibers: Mode structure and attenuation. Appl. Opt. 1977, 16, 2198–2203. [Google Scholar] [CrossRef] [PubMed]
- Renner, H. Leaky-mode loss in coated depressed-cladding fibers. IEEE Photonics Technol. Lett. 1991, 3, 31–32. [Google Scholar] [CrossRef]
- Chou, C.C.; Sun, N.H. Analysis of leaky-mode losses for optical fibers. J. Opt. Soc. Am. B 2008, 25, 545–554. [Google Scholar] [CrossRef]
- Harris, J.; Lu, P.; Larocque, H.; Chen, L.; Bao, X. In-fiber Mach–Zehnder interferometric refractive index sensors with guided and leaky modes. Sens. Actuators B Chem. 2015, 206, 246–251. [Google Scholar] [CrossRef]
- Liu, Q.; Li, S.; Chen, H.; Fan, Z.; Li, J. Photonic crystal fiber temperature sensor based on coupling between liquid-core mode and defect mode. IEEE Photonics J. 2015, 7, 1–9. [Google Scholar] [CrossRef]
- Gao, R.; Lu, D.F.; Cheng, J.; Jiang, Y.; Jiang, L.; Qi, Z.M. Humidity sensor based on power leakage at resonance wavelengths of a hollow core fiber coated with reduced graphene oxide. Sens. Actuators B Chem. 2016, 222, 618–624. [Google Scholar] [CrossRef]
- Wang, P.; Semenova, Y.; Wu, Q.; Farrell, G.; Ti, Y.; Zheng, J. Macrobending single-mode fiber-based refractometer. Appl. Opt. 2009, 48, 6044–6049. [Google Scholar] [CrossRef] [PubMed]
- Lu, P.; Chen, Q. Femtosecond laser microfabricated fiber Mach–Zehnder interferometer for sensing applications. Opt. Lett. 2011, 36, 268–270. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.; Peng, W. Fiber optic refractometer based on leaky-mode interference of bent fiber. IEEE Photonics Technol. Lett. 2015, 27, 11–14. [Google Scholar] [CrossRef]
- Knight, J.C.; Birks, T.A.; Russell, P.S.J.; Atkin, D.M. All-silica single-mode optical fiber with photonic crystal cladding. Opt. Lett. 1996, 21, 1547–1549. [Google Scholar] [CrossRef] [PubMed]
- Broeng, J.; Mogilevstev, D.; Barkou, S.E.; Bjarklev, A. Photonic crystal fibers: A new class of optical waveguides. Opt. Fiber Technol. 1999, 5, 305–330. [Google Scholar] [CrossRef]
- Chiang, J.S.; Wu, T.L. Analysis of propagation characteristics for an octagonal photonic crystal fiber (O-PCF). Opt. Commun. 2006, 258, 170–176. [Google Scholar] [CrossRef]
- Ferrando, A.; Silvestre, E.; Miret, J.J.; Andres, P.; Andres, M.V. Vector description of higher-order modes in photonic crystal fibers. J. Opt. Soc. Am. A 2000, 17, 1333–1340. [Google Scholar] [CrossRef]
- Birks, T.A.; Knight, J.C.; Russell, P.S.J. Endlessly single-mode photonic crystal fiber. Opt. Lett. 1997, 22, 961–963. [Google Scholar] [CrossRef] [PubMed]
- Broderick, N.G.R.; Monro, T.M.; Bennett, P.J.; Richardson, D.J. Nonlinearity in holey optical fibers: Measurement and future opportunities. Opt. Lett. 1999, 24, 1395–1397. [Google Scholar] [CrossRef] [PubMed]
- Knight, J.C. Photonic crystal fibres. Nature 2003, 424, 847–851. [Google Scholar] [CrossRef] [PubMed]
- Cregan, R.F.; Mangan, B.J.; Knight, J.C.; Birks, T.A.; Russell, P.S.J.; Roberts, P.J.; Allan, D.C. Single-mode photonic bandgap guidance of light in air. Science 1999, 285, 1537–1539. [Google Scholar] [CrossRef] [PubMed]
- Zolla, F.; Renversez, G.; Nicolet, A.; Kuhlmey, B.; Guenneau, S.; Felbacq, D. Foundations of Photonic Crystal Fibres; Imperial College Press: London, UK, 2005. [Google Scholar]
- Su, C.C. A surface integral equations method for homogeneous optical fibers and coupled image lines of arbitrary cross sections. IEEE Trans. Microw. Theory Tech. 1985, 33, 1114–1119. [Google Scholar]
- Yang, W.; Gopinath, A. A boundary integral method for propagation problems in integrated optical structures. IEEE Photonics Technol. Lett. 1995, 7, 777–779. [Google Scholar] [CrossRef]
- Wu, T.L.; Chiang, J.S.; Chao, C.H. A novel approach for calculating the dispersions of photonic crystal fibers. IEEE Photonics Technol. Lett. 2004, 16, 1492–1494. [Google Scholar] [CrossRef]
- Chiang, J.S.; Wu, T.L. Analysis of an ultrashort PCF-based polarization splitter. J. Light. Technol. 2010, 28, 707–713. [Google Scholar] [CrossRef]
- White, T.P.; McPhedran, R.C.; de Sterke, C.M.; Botten, L.C.; Steel, M.J. Confinement loss in microstructured optical fibers. Opt. Lett. 2001, 26, 1660–1662. [Google Scholar] [CrossRef] [PubMed]
- Ferrarini, D.; Vincetti, L.; Zoboli, M.; Cucinotta, A.; Selleri, S. Leakage properties of photonic crystal fibers. Opt. Express 2002, 10, 1314–1319. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Z.; Shi, Y.; Bian, B.; Lu, J. Dependence of leaky mode coupling on loss in photonic crystal fiber with hybrid cladding. Opt. Express 2008, 16, 1915–1922. [Google Scholar] [CrossRef] [PubMed]
- Gu, G.; Kong, F.; Hawkins, T.W.; Foy, P.; Wei, K.; Samson, B.; Dong, L. Impact of fiber outer boundaries on leaky mode losses in leakage channel fibers. Opt. Express 2013, 21, 24039–24048. [Google Scholar] [CrossRef] [PubMed]
- Steel, M.J.; Osgood, R.M., Jr. Polarization and dispersive properties of elliptical-hole photonic crystal fibers. J. Light. Technol. 2001, 19, 495–503. [Google Scholar] [CrossRef]
- Finazzi, V.; Monro, T.M.; Richardson, D.J. Small-core silica holey fibers: Nonlinearity and confinement loss trade-offs. J. Opt. Soc. Am. B 2003, 20, 1427–1436. [Google Scholar] [CrossRef]
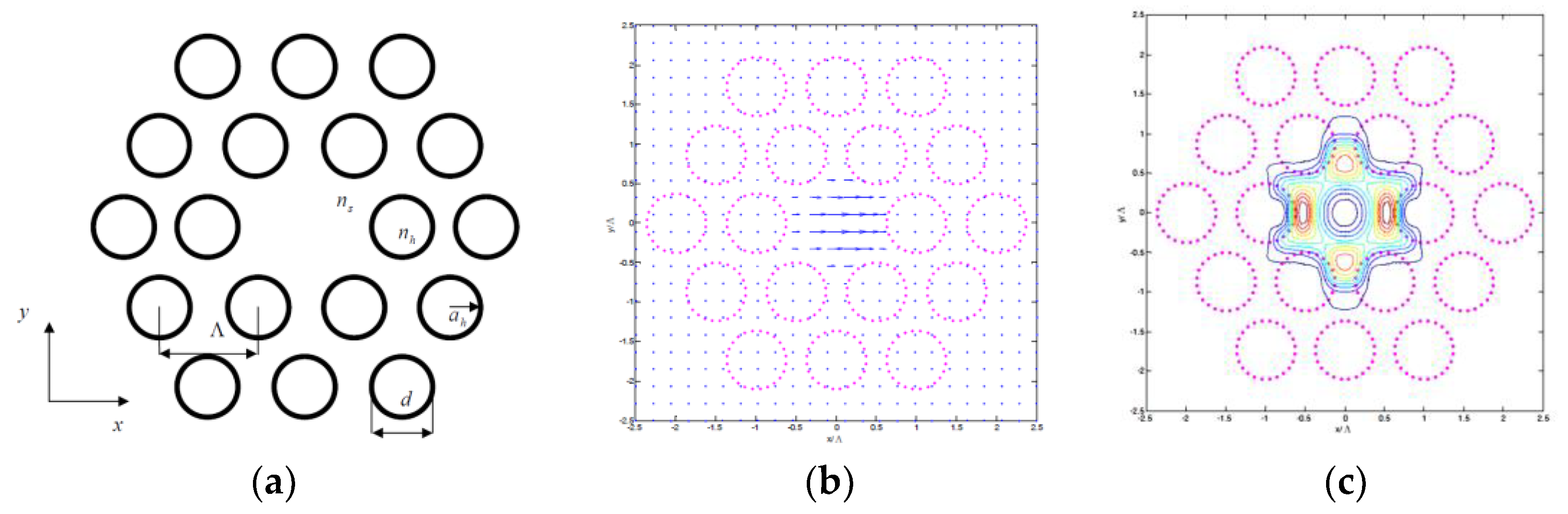
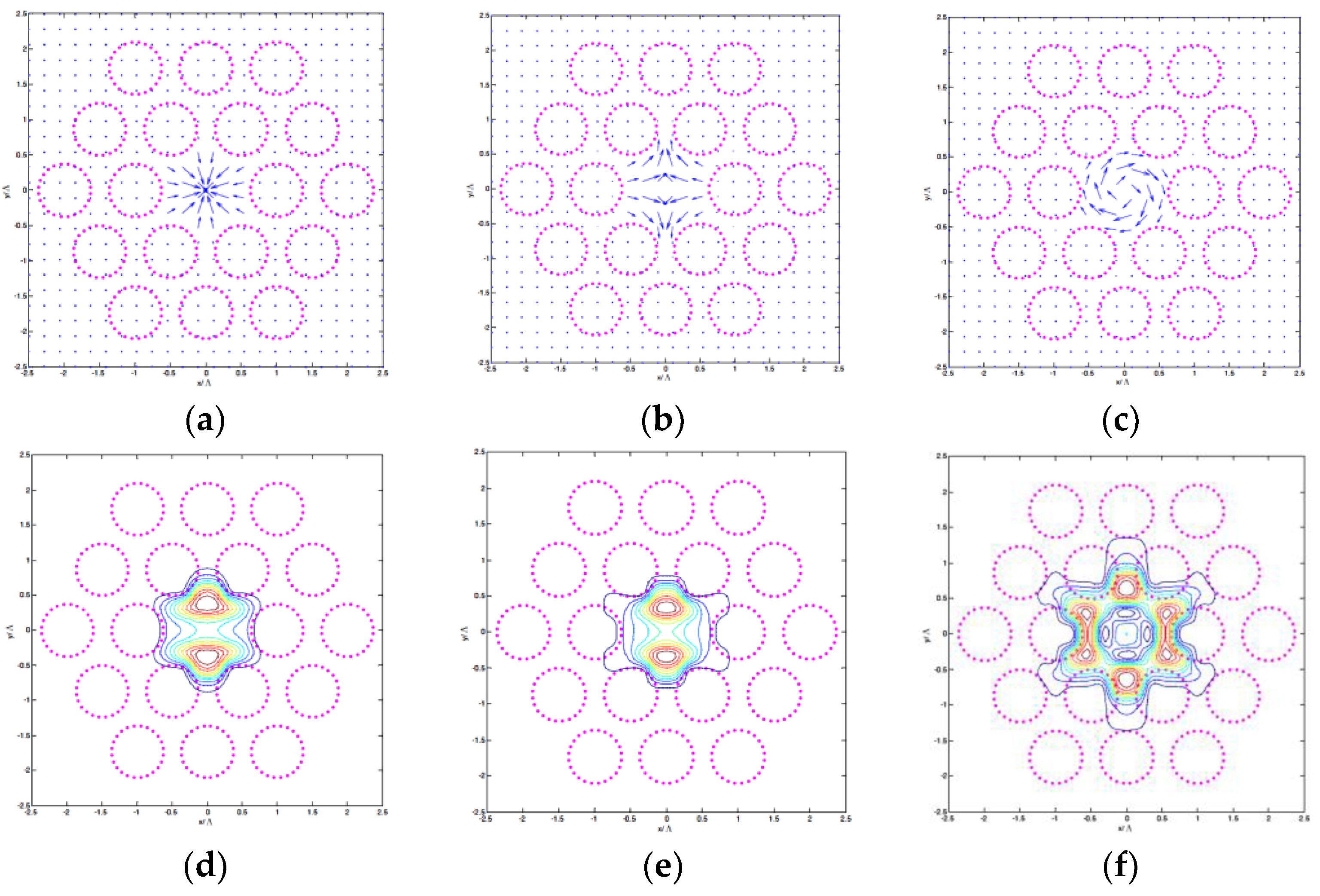
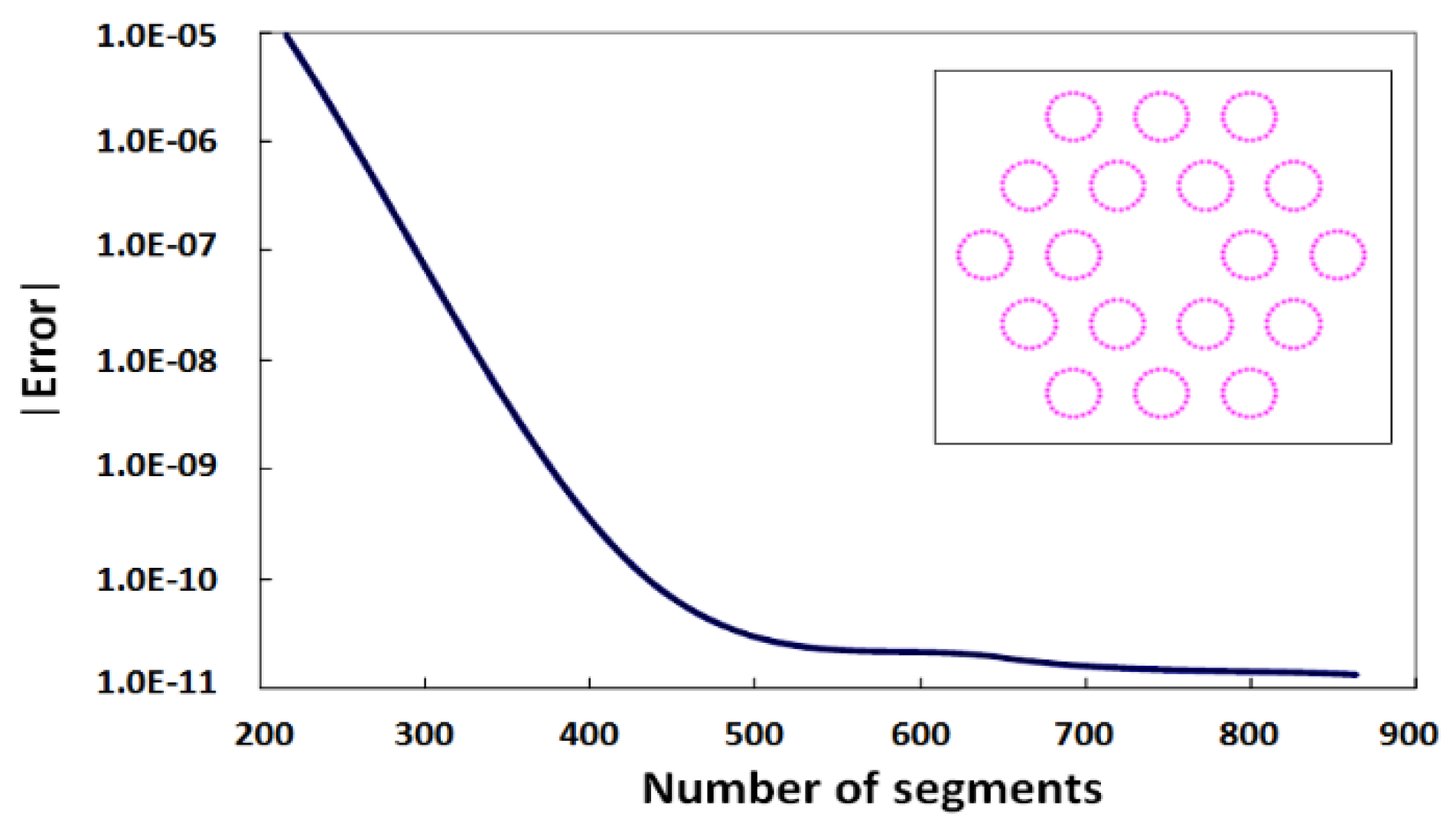
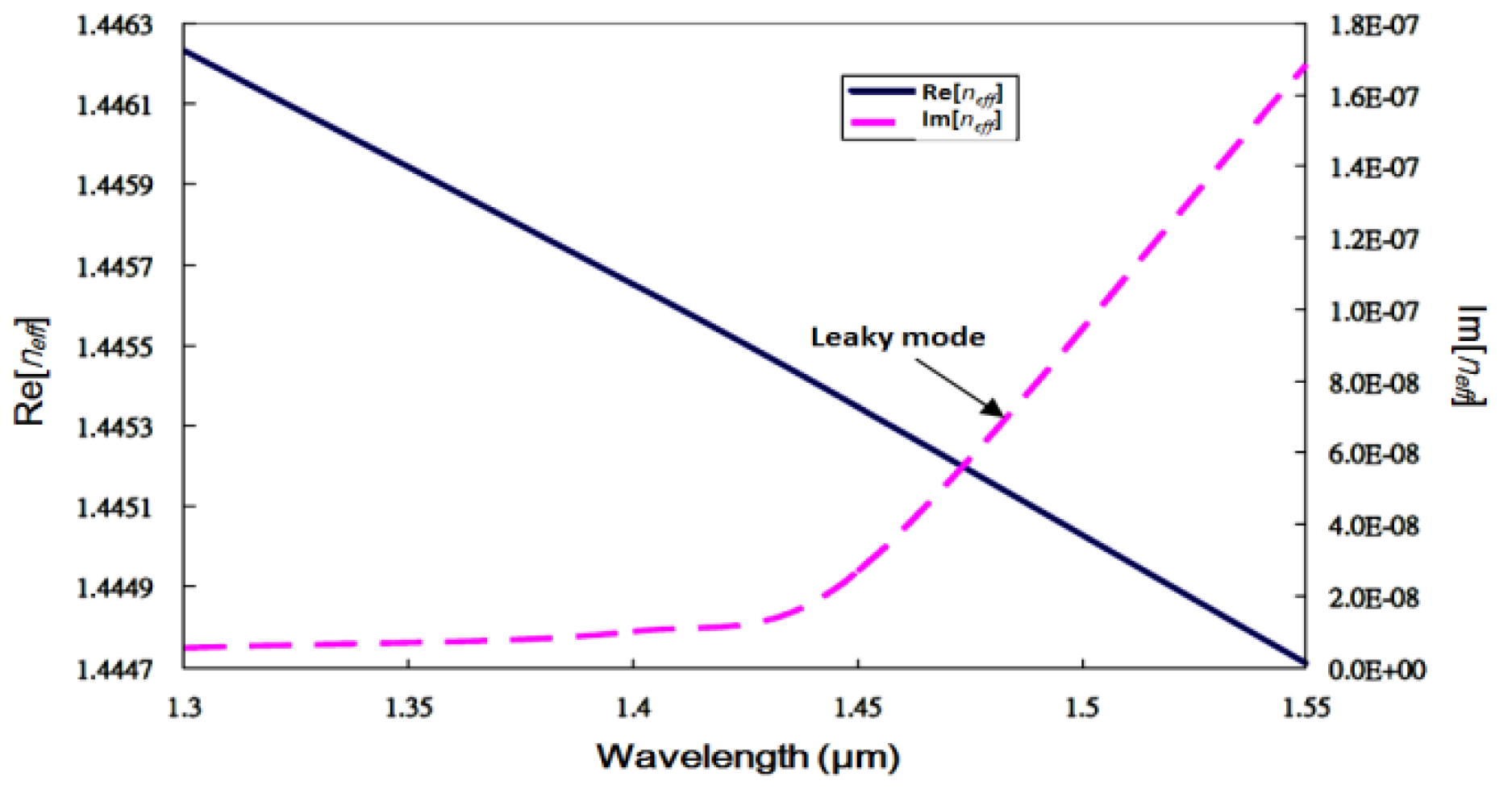
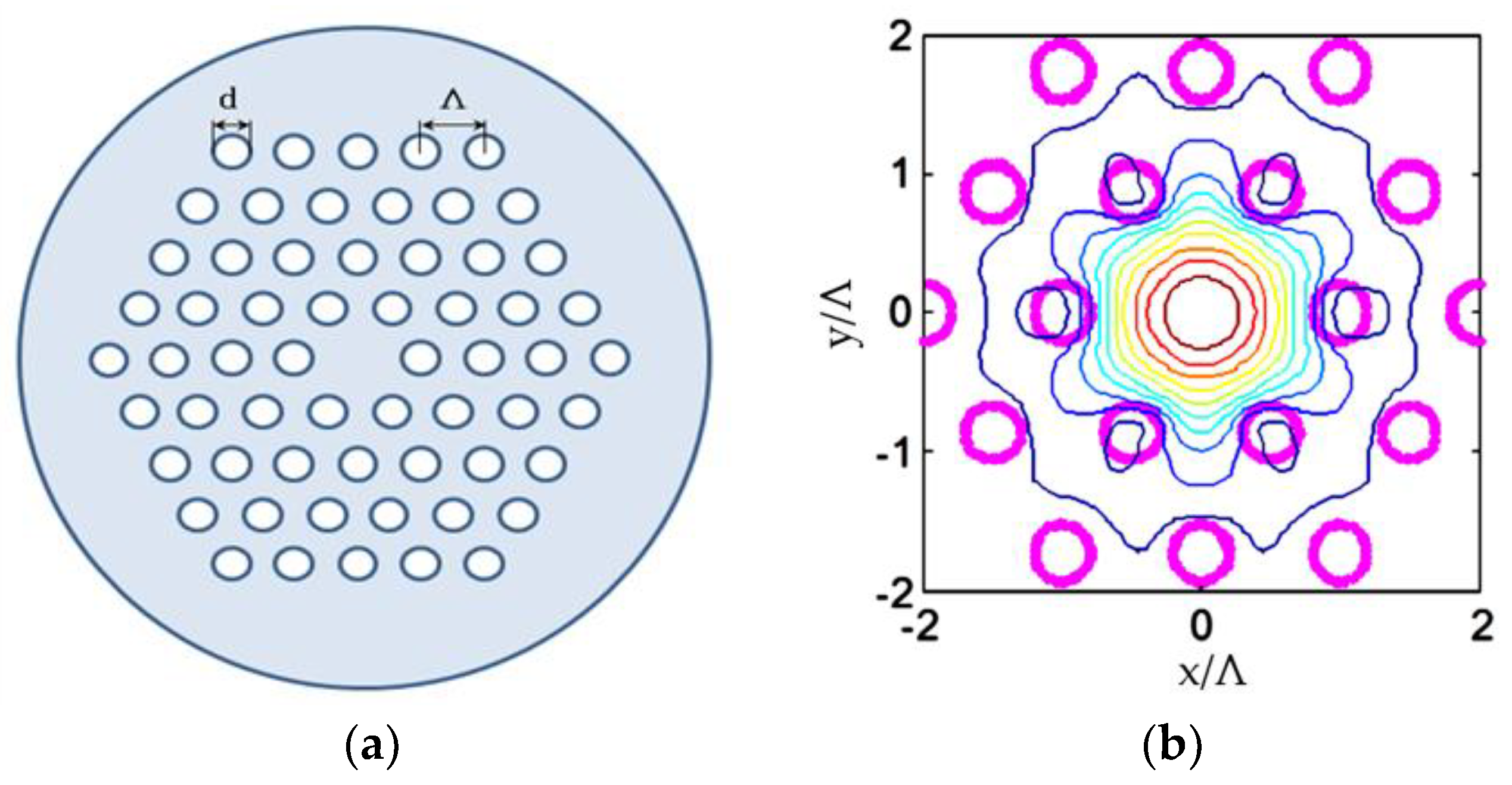
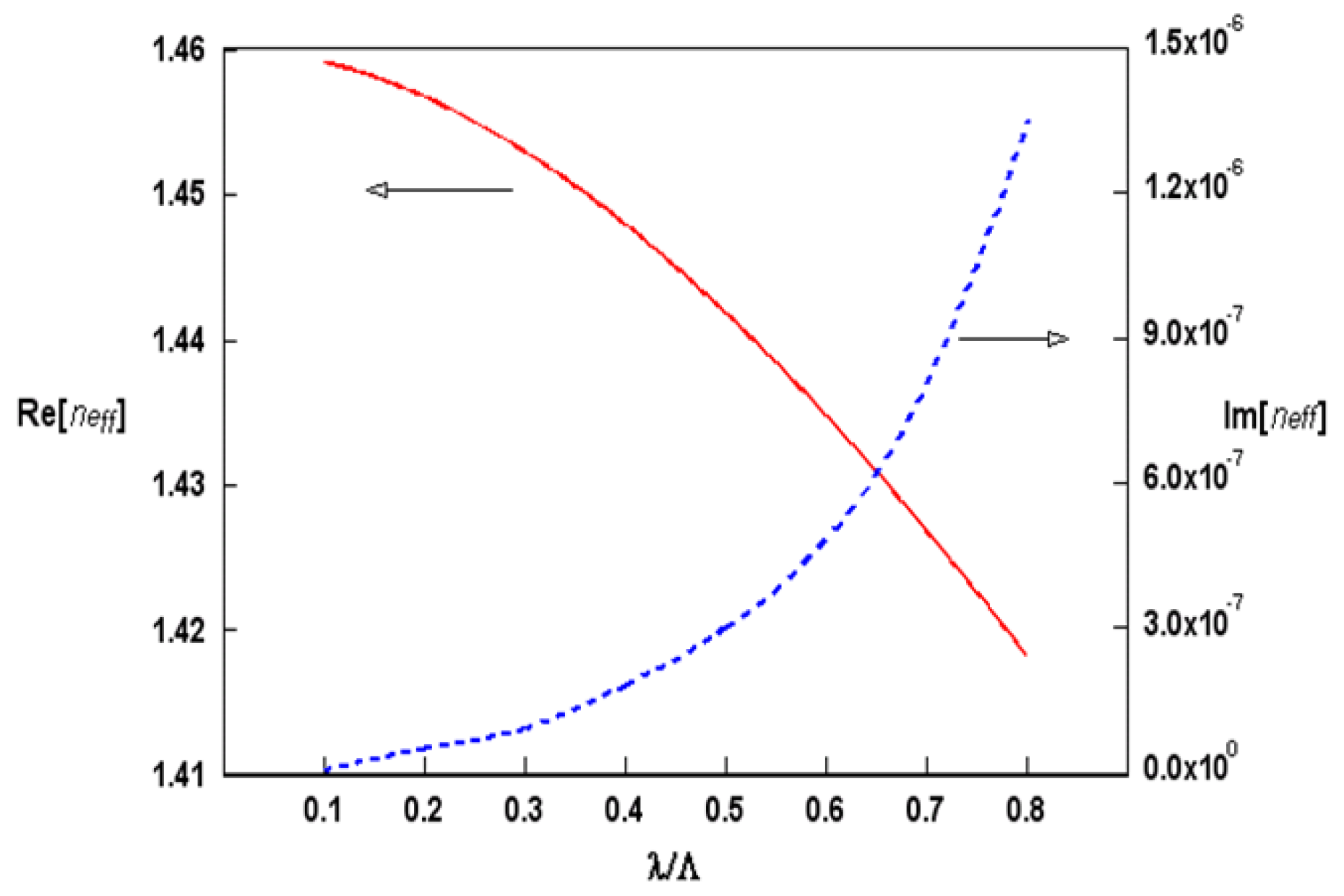
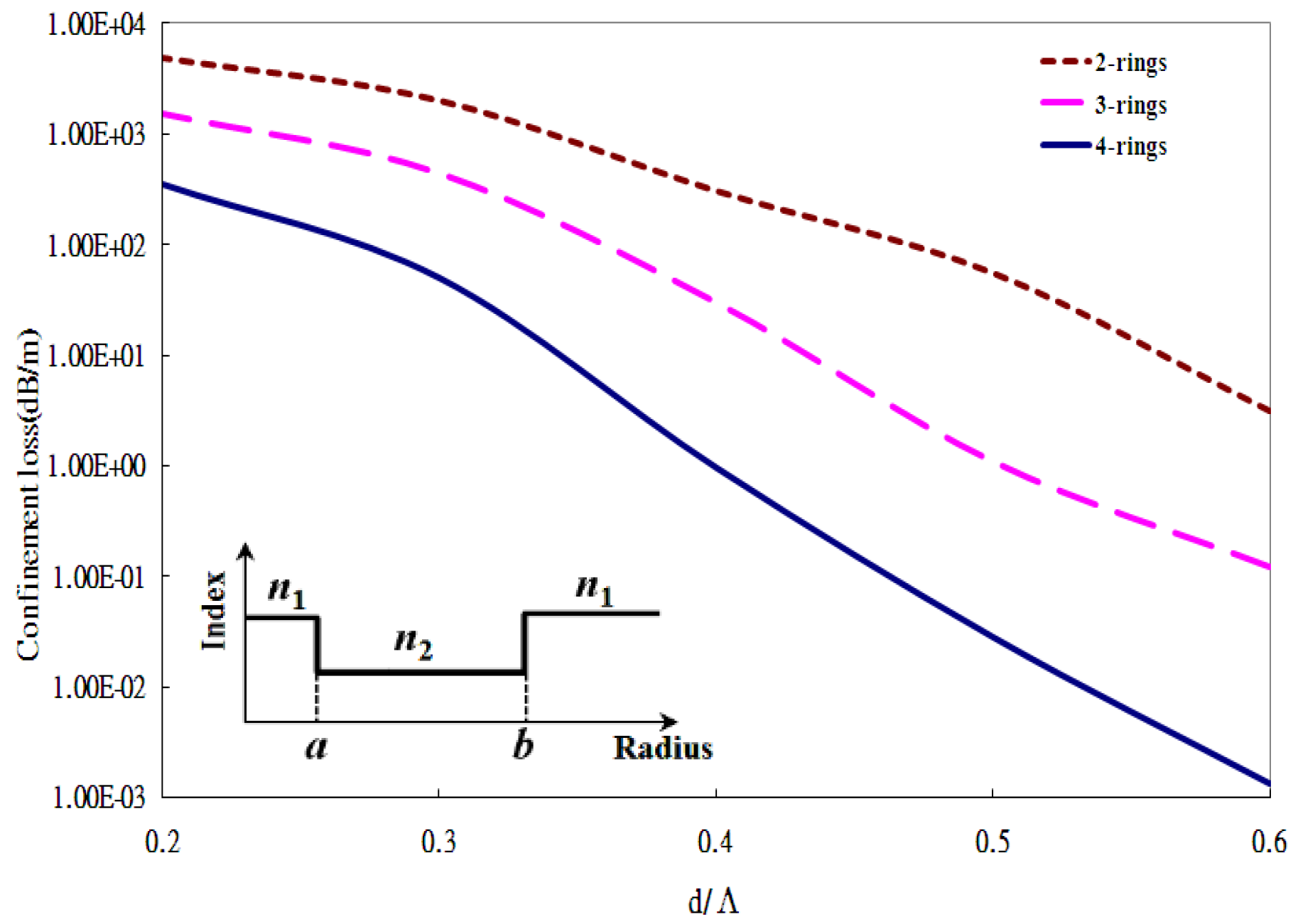

| Mode Class | SIEM neff | Loss (dB/m) | Multipole Method neff |
|---|---|---|---|
| HE11 | 1.4453471152 + i2.684 × 10−8 | 1.01 | 1.4453471163 + i2.578 × 10−8 |
| TE01 | 1.4384402631 + i4.062 × 10−7 | 15.29 | 1.4384402675 + i4.101 × 10−7 |
| HE21 | 1.4383130349 + i6.974 × 10−7 | 26.25 | 1.4383130373 + i6.898 × 10−7 |
| TM01 | 1.4382295027 + i1.256 × 10−6 | 47.28 | 1.4382295029 + i1.268 × 10−6 |
© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chiang, J.-S. Analysis of Leaky Modes in Photonic Crystal Fibers Using the Surface Integral Equation Method. Crystals 2018, 8, 177. https://doi.org/10.3390/cryst8040177
Chiang J-S. Analysis of Leaky Modes in Photonic Crystal Fibers Using the Surface Integral Equation Method. Crystals. 2018; 8(4):177. https://doi.org/10.3390/cryst8040177
Chicago/Turabian StyleChiang, Jung-Sheng. 2018. "Analysis of Leaky Modes in Photonic Crystal Fibers Using the Surface Integral Equation Method" Crystals 8, no. 4: 177. https://doi.org/10.3390/cryst8040177





