Microstructure Evolution of Ag-Alloyed PbTe-Based Compounds and Implications for Thermoelectric Performance
Abstract
:1. Introduction
2. Experimental Procedure
2.1. Materials Synthesis
2.2. Characterization Methods
2.2.1. Microstructure Analysis
2.2.2. Thermoelectric Property Measurements
3. Results
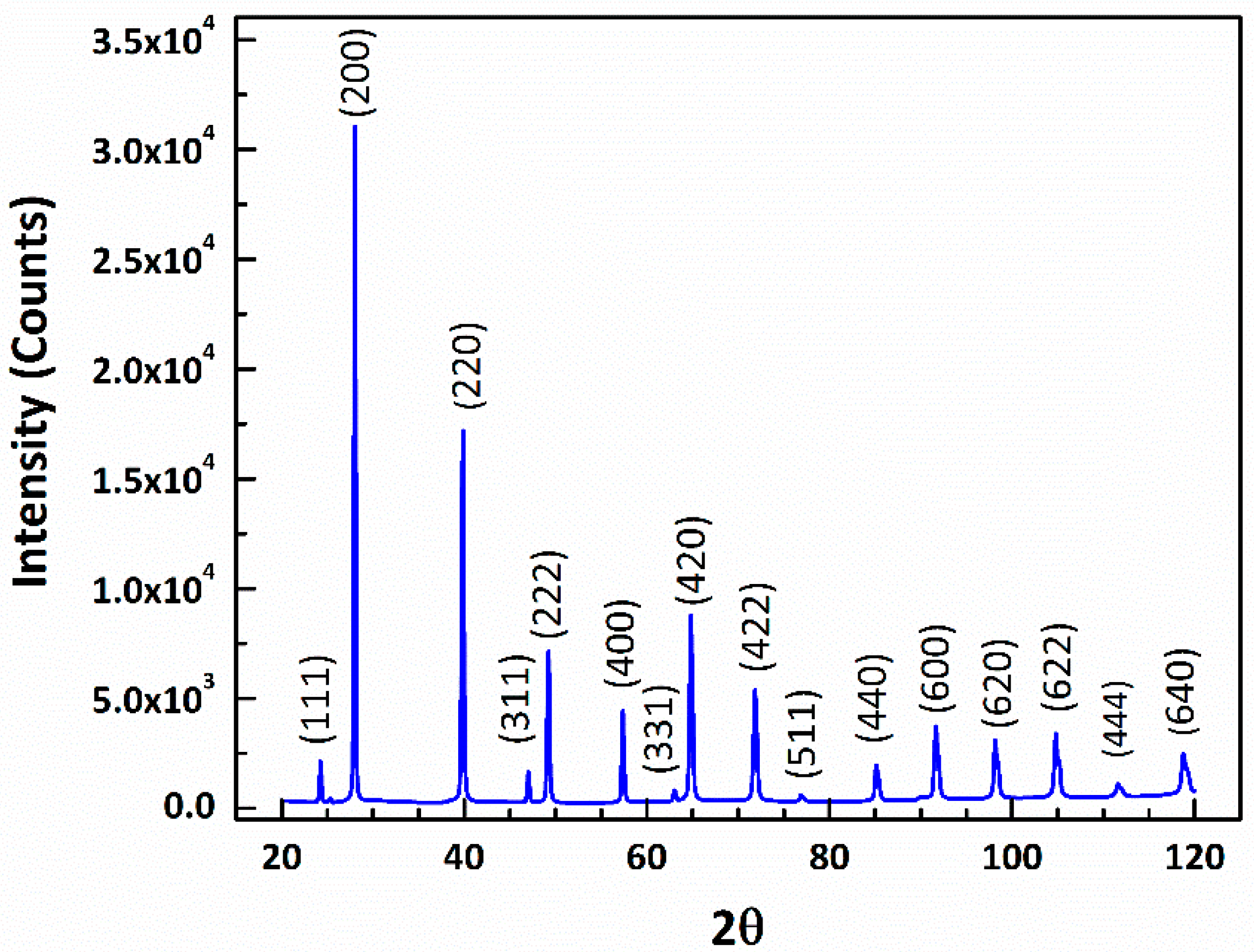
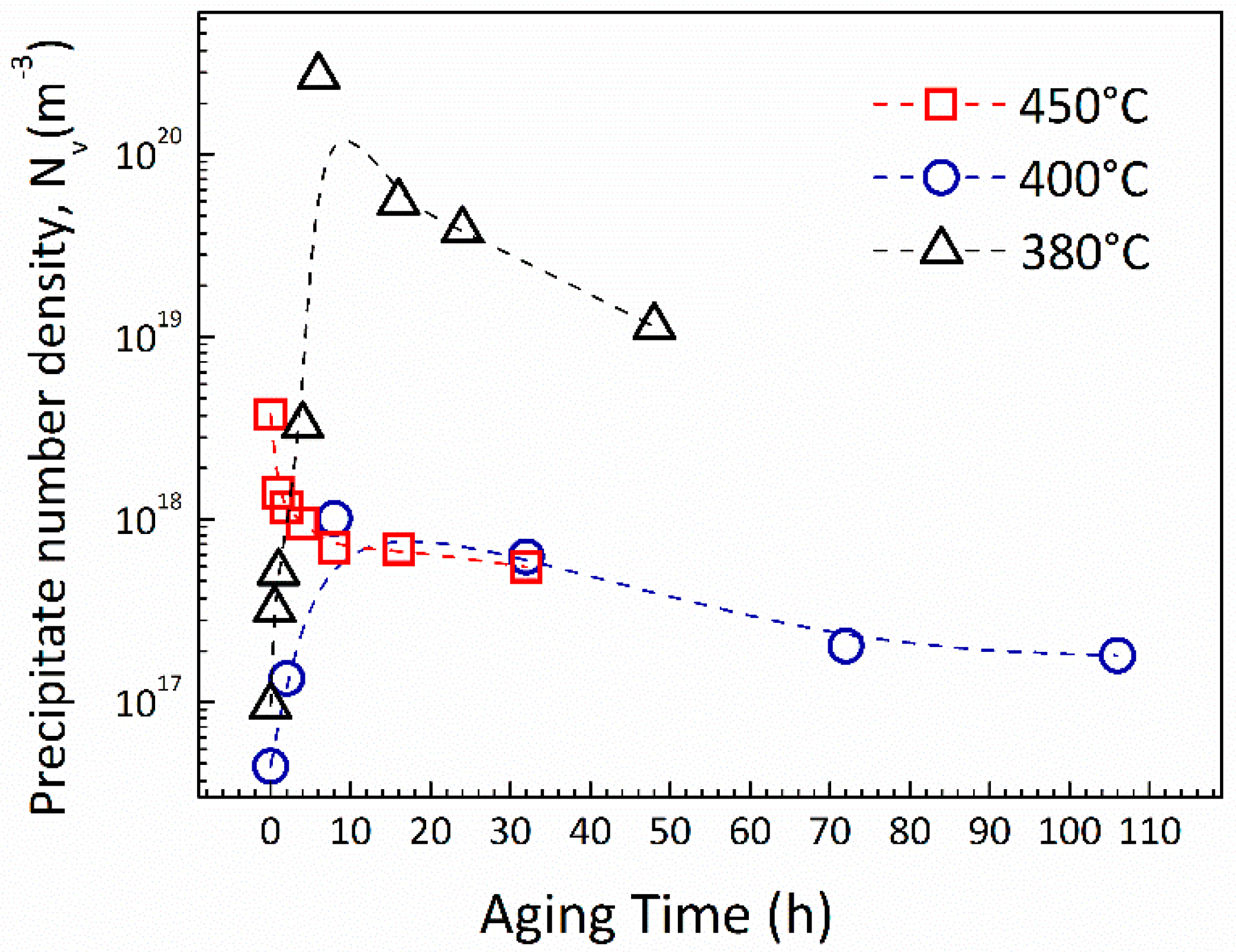
3.1. Microstructure Characterization
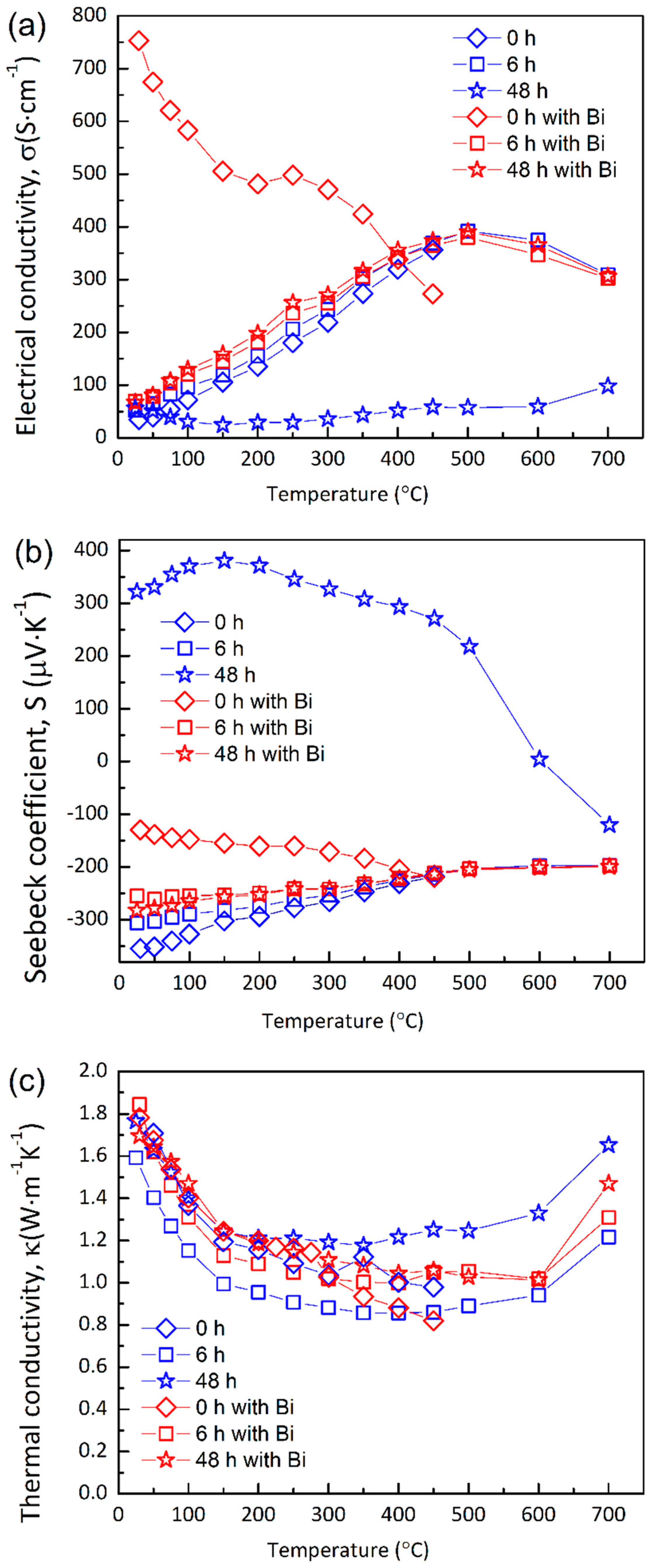
3.2. Thermoelectric Transport Properties
4. Discussion
4.1. Materials Processing and Microstructure Evolution
4.2. Electronic Transport Properties
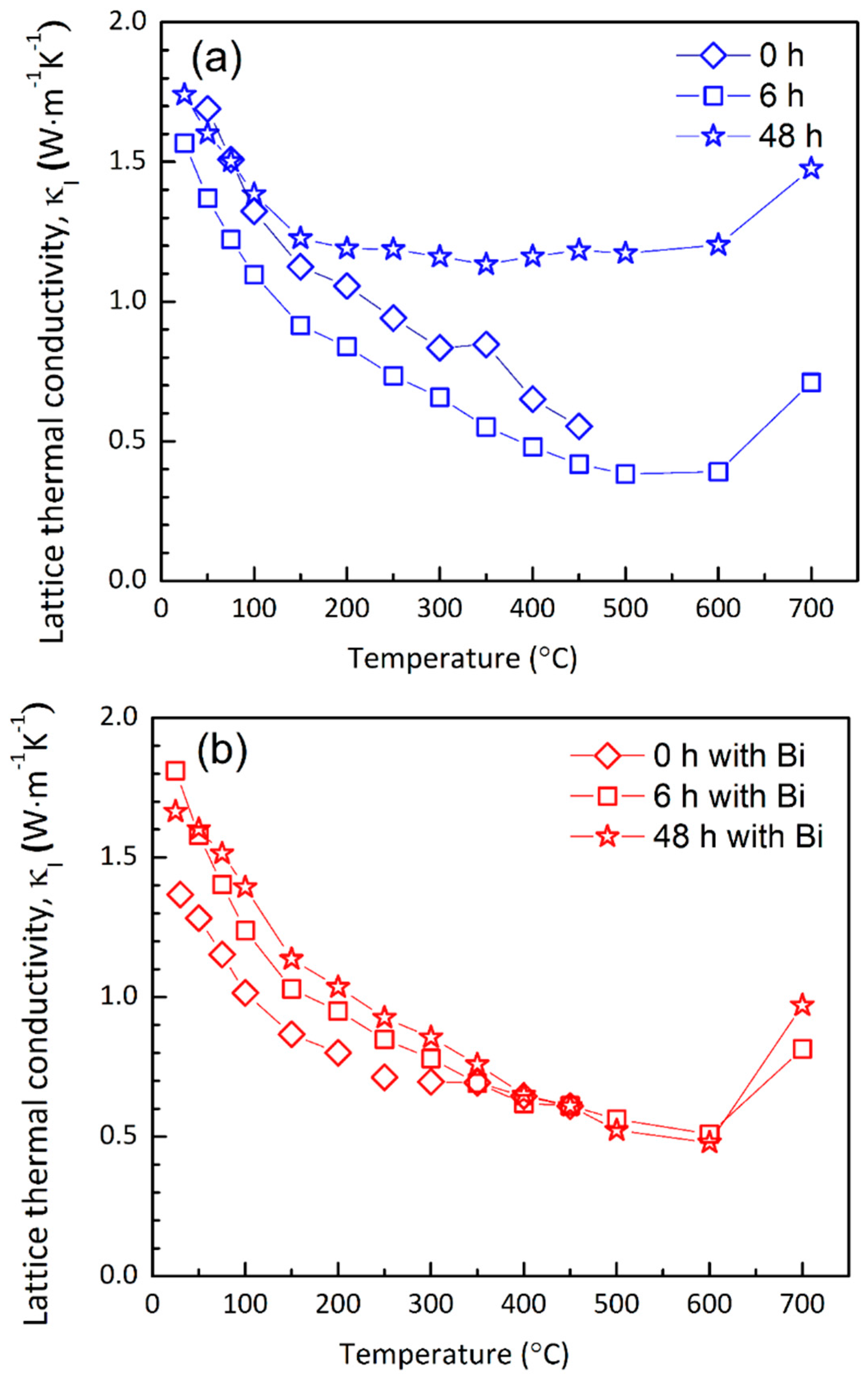
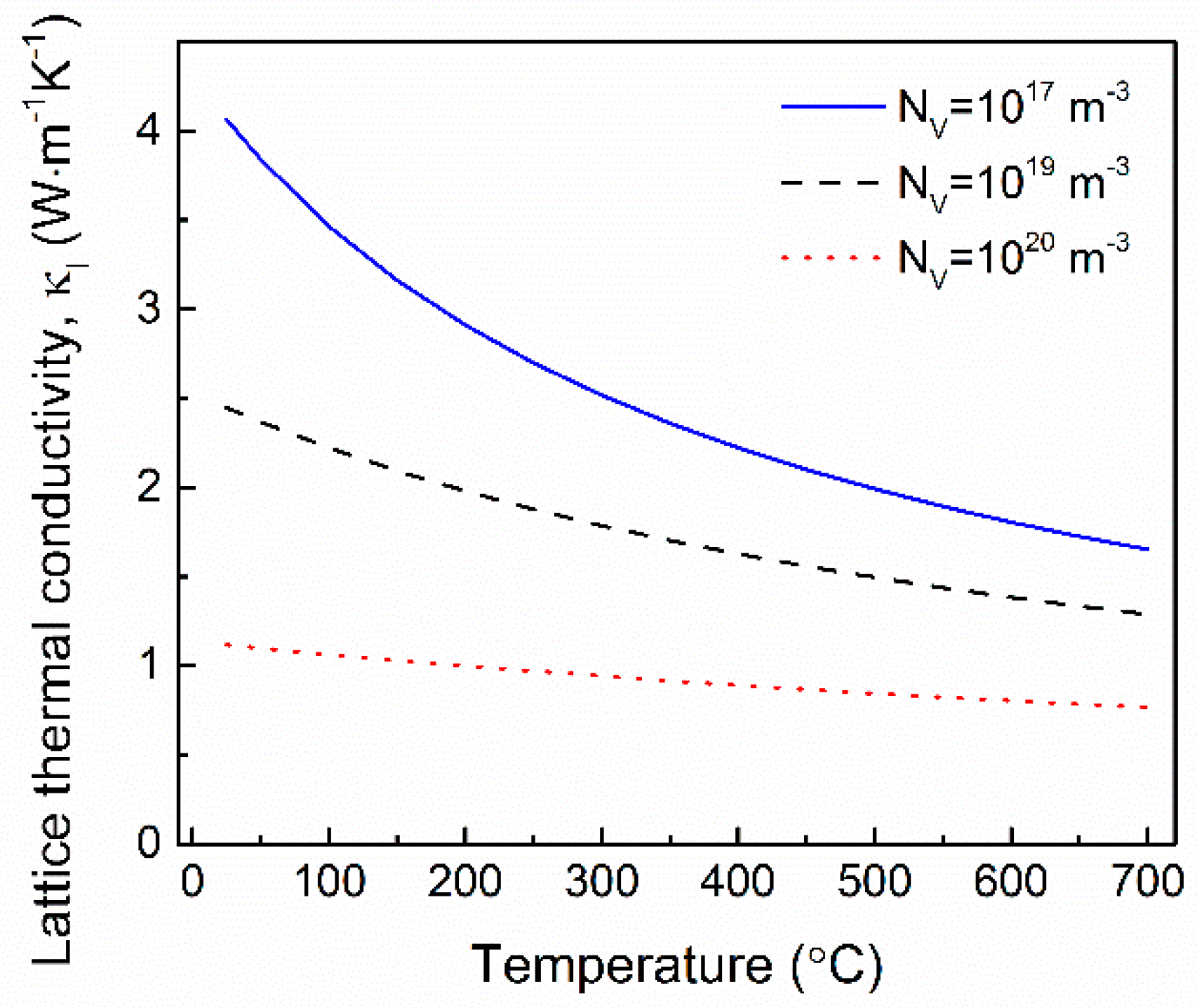
4.3. Thermal Transport Properties
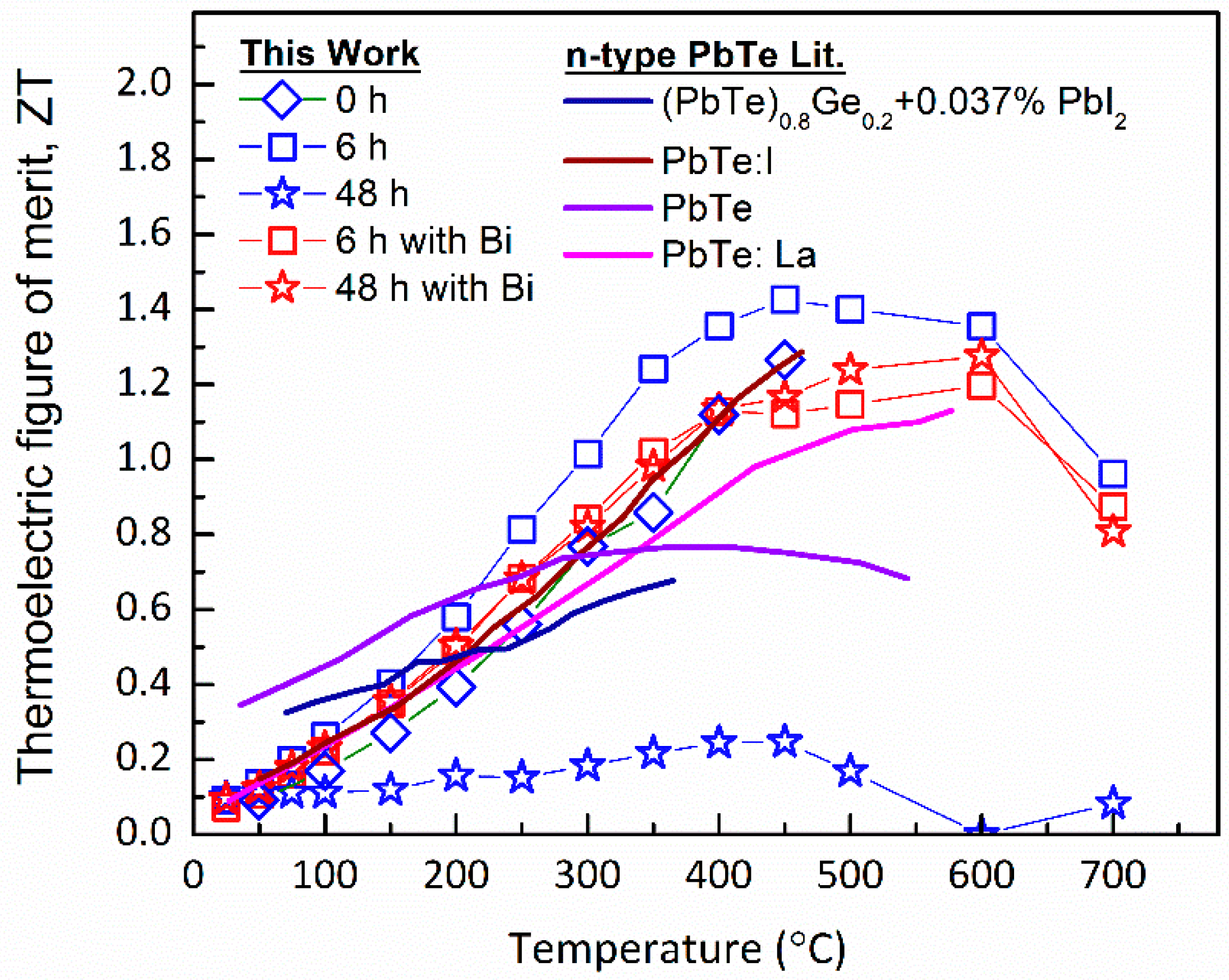
4.4. Thermoelectric Performance
5. Summary and Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- LaLonde, A.D.; Pei, Y.; Wang, H.; Snyder, G.J. Lead telluride alloy thermoelectrics. Mater. Today 2011, 14, 526–532. [Google Scholar] [CrossRef]
- Snyder, G.J.; Toberer, E.S. Complex thermoelectric materials. Nat. Mater. 2008, 7, 105–114. [Google Scholar] [CrossRef] [PubMed]
- Dughaish, Z.H. Lead telluride as a thermoelectric material for thermoelectric power generation. Phys. B Condens. Matter 2002, 322, 205–223. [Google Scholar] [CrossRef]
- Tan, G.; Shi, F.; Hao, S.; Zhao, L.D.; Chi, H.; Zhang, X.; Uher, C.; Wolverton, C.; Dravid, V.P.; Kanatzidis, M.G. Non-equilibrium processing leads to record high thermoelectric figure of merit in PbTe-SrTe. Nat. Commun. 2016, 7, 12167. [Google Scholar] [CrossRef] [PubMed]
- Korkosz, R.J.; Chasapis, T.C.; Lo, S.h.; Doak, J.W.; Kim, Y.J.; Wu, C.I.; Hatzikraniotis, E.; Hogan, T.P.; Seidman, D.N.; Wolverton, C.; et al. High ZT in p-type (PbTe)1–2x(PbSe)x(PbS)x thermoelectric materials. J. Am. Chem. Soc. 2014, 136, 3225–3237. [Google Scholar] [CrossRef] [PubMed]
- Rawat, P.K.; Paul, B.; Banerji, P. Exploration of Zn resonance levels and thermoelectric properties in I-doped PbTe with ZnTe nanostructures. ACS Appl. Mater. Interfaces 2014, 6, 3995–4004. [Google Scholar] [CrossRef] [PubMed]
- Tan, G.; Kanatzidis, M.G. Chapter 4 All-Scale Hierarchical PbTe. In Materials Aspect of Thermoelectricity; CRC Press: Boca Raton, FL, USA, 2016; pp. 125–158. [Google Scholar]
- Tritt, T.M. Thermal Conductivity: Theory, Properties, and Applications; Springer: Berlin, Germany, 2004. [Google Scholar]
- Rowe, D.M. Thermoelectrics Handbook: Macro to Nano; CRC Press: Boca Raton, FL, USA, 2006. [Google Scholar]
- Wu, D.; Zhao, L.-D.; Zheng, F.; Jin, L.; Kanatzidis, M.G.; He, J. Understanding nanostructuring processes in thermoelectrics and their effects on lattice thermal conductivity. Adv. Mater. 2016, 28, 2737–2743. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Zhang, X.; Lin, S.; Chen, Z.; Pei, Y. Realizing the high thermoelectric performance of GeTe by Sb-doping and Se-alloying. Chem. Mater. 2017, 29, 605–611. [Google Scholar] [CrossRef]
- He, J.Q.; Sootsman, J.R.; Girard, S.N.; Zheng, J.C.; Wen, J.G.; Zhu, Y.M.; Kanatzidis, M.G.; Dravid, V.P. On the origin of increased phonon scattering in nanostructured PbTe based thermoelectric materials. J. Am. Chem. Soc. 2010, 132, 8669–8675. [Google Scholar] [CrossRef] [PubMed]
- Medlin, D.L.; Snyder, G.J. Interfaces in bulk thermoelectric materials a review for current opinion in colloid and interface science. Curr. Opin. Colloid Interface Sci. 2009, 14, 226–235. [Google Scholar] [CrossRef]
- Ikeda, T.; Collins, L.A.; Ravi, V.A.; Gascoin, F.S.; Haile, S.M.; Snyder, G.J. Self-assembled nanometer lamellae of thermoelectric PbTe and Sb2Te3 with epitaxy-like interfaces. Chem. Mater. 2007, 19, 763–767. [Google Scholar] [CrossRef]
- Ikeda, T.; Haile, S.M.; Ravi, V.A.; Azizgolshani, H.; Gascoin, F.; Snyder, G.J. Solidification processing of alloys in the pseudo-binary PbTe- Sb2Te3 system. Acta Mater. 2007, 55, 1227–1239. [Google Scholar] [CrossRef]
- Ikeda, T.; Iwanaga, S.; Wu, H.J.; Marolf, N.J.; Chen, S.W.; Snyder, G.J. A combinatorial approach to microstructure and thermopower of bulk thermoelectric materials: The pseudo-ternary PbTe-Ag2Te-Sb2Te3 system. J. Mater. Chem. 2012, 24335–24347. [Google Scholar] [CrossRef]
- Ikeda, T.; Marolf, N.J.; Bergum, K.; Toussaint, M.B.; Heinz, N.A.; Ravi, V.A.; Jeffrey Snyder, G. Size control of Sb2Te3 Widmanstätten precipitates in thermoelectric PbTe. Acta Mater. 2011, 59, 2679–2692. [Google Scholar] [CrossRef]
- Ikeda, T.; Ravi, V.; Jeffrey Snyder, G. Microstructure size control through cooling rate in thermoelectric PbTe-Sb2Te3 composites. Metall. Mater. Trans. A 2010, 41, 641–650. [Google Scholar] [CrossRef]
- Ikeda, T.; Ravi, V.A.; Snyder, G.J. Formation of Sb2Te3 Widmanstätten precipitates in thermoelectric PbTe. Acta Mater. 2009, 57, 666–672. [Google Scholar] [CrossRef]
- Ikeda, T.; Toberer, E.S.; Ravi, V.A.; Snyder, G.J.; Aoyagi, S.; Nishibori, E.; Sakata, M. In situ observation of eutectoid reaction forming a PbTe-Sb2Te3 thermoelectric nanocomposite by synchrotron X-ray diffraction. Scr. Mater. 2009, 60, 321–324. [Google Scholar] [CrossRef]
- Ikeda, T.; Toussaint, M.; Bergum, K.; Iwanaga, S.; Jeffrey Snyder, G. Solubility and formation of ternary Widmanstätten precipitates in PbTe in the pseudo-binary PbTe–Bi2Te3 system. J. Mater. Sci. 2011, 46, 3846–3854. [Google Scholar] [CrossRef]
- Pei, Y.; Heinz, N.A.; LaLonde, A.; Snyder, G.J. Combination of large nanostructures and complex band structure for high performance thermoelectric lead telluride. Energy Environ. Sci. 2011, 4, 3640–3645. [Google Scholar] [CrossRef]
- Pei, Y.; Lensch-Falk, J.; Toberer, E.S.; Medlin, D.L.; Snyder, G.J. High thermoelectric performance in PbTe due to large nanoscale Ag2Te precipitates and La doping. Adv. Funct. Mater. 2011, 21, 241–249. [Google Scholar] [CrossRef]
- Pei, Y.; May, A.F.; Snyder, G.J. Self-tuning the carrier concentration of PbTe/Ag2Te composites with excess Ag for high thermoelectric performance. Adv. Energy Mater. 2011, 1, 291–296. [Google Scholar] [CrossRef]
- Lensch-Falk, J.L.; Sugar, J.D.; Hekmaty, M.A.; Medlin, D.L. Morphological evolution of Ag2Te precipitates in thermoelectric PbTe. J. Alloys Compd. 2010, 504, 37–44. [Google Scholar] [CrossRef]
- Bergum, K.; Ikeda, T.; Jeffrey Snyder, G. Solubility and microstructure in the pseudo-binary PbTe-Ag2Te system. J. Solid State Chem. 2011, 184, 2543–2552. [Google Scholar] [CrossRef]
- Porter, D.A.; Easterling, K.E. Phase Transformations in Metals and Alloys, 2nd ed.; Chapman & Hall: London, UK, 1992. [Google Scholar]
- Koresh, I.; Amouyal, Y. Effects of microstructure evolution on transport properties of thermoelectric nickel-doped zinc oxide. J. Eur. Ceram. Soc. 2017, 37, 3541–3550. [Google Scholar] [CrossRef]
- Goldsmid, H.J. Introduction to Thermoelectricity; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Kim, H.-S.; Gibbs, Z.M.; Tang, Y.; Wang, H.; Snyder, G.J. Characterization of Lorenz number with Seebeck coefficient measurement. APL Mater. 2015, 3, 041506. [Google Scholar] [CrossRef]
- Pei, Y.-L.; Liu, Y. Electrical and thermal transport properties of Pb-based chalcogenides: PbTe, PbSe, and PbS. J. Alloys Compd. 2012, 514, 40–44. [Google Scholar] [CrossRef]
- Amouyal, Y. Reducing lattice thermal conductivity of the thermoelectric compound AgSbTe2 (P4/mmm) by lanthanum substitution: Computational and experimental approaches. J. Electron. Mater. 2014, 43, 3772–3779. [Google Scholar] [CrossRef]
- Amouyal, Y. A practical approach to evaluate lattice thermal conductivity in two-phase thermoelectric alloys for energy applications. Materials 2017, 10, 386. [Google Scholar] [CrossRef] [PubMed]
- He, J.; Blum, I.D.; Wang, H.Q.; Girard, S.N.; Doak, J.; Zhao, L.D.; Zheng, J.C.; Casillas, G.; Wolverton, C.; Jose-Yacaman, M.; et al. Morphology control of nanostructures: Na-doped PbTe–PbS system. Nano Lett. 2012, 12, 5979–5984. [Google Scholar] [CrossRef] [PubMed]
- Strauss, A.J. Effect of Pb- and Te-saturation on carrier concentrations in impurity-doped PbTe. J. Electron. Mater. 1973, 2, 553–569. [Google Scholar] [CrossRef]
- Grossfeld, T. Microstructure Evolution and Enhancement of the Thermoelectric Conversion Efficiency of PbTe-Based Compounds for Renewable Energy Applications. Mater’s Thesis, Technion—Israel Institute of Technology, Haifa, Israel, 2015. [Google Scholar]
- Cojocaru-Mirédin, O.; Abdellaoui, L.; Nagli, M.; Zhang, S.; Yu, Y.; Scheu, C.; Raabe, D.; Wuttig, M.; Amouyal, Y. Role of nanostructuring and microstructuring in silver antimony telluride compounds for thermoelectric applications. ACS Appl. Mater. Interfaces 2017, 9, 14779–14790. [Google Scholar] [CrossRef] [PubMed]
- Pei, Y.; LaLonde, A.; Iwanaga, S.; Snyder, G.J. High thermoelectric figure of merit in heavy hole dominated PbTe. Energy Environ. Sci. 2011, 4, 2085–2089. [Google Scholar] [CrossRef]
- Pei, Y.; Wang, H.; Snyder, G.J. Band engineering of thermoelectric materials. Adv. Mater. 2012, 24, 6125–6135. [Google Scholar] [CrossRef] [PubMed]
- Pei, Y.; Shi, X.; LaLonde, A.; Wang, H.; Chen, L.; Snyder, G.J. Convergence of electronic bands for high performance bulk thermoelectrics. Nature 2011, 473, 66–69. [Google Scholar] [CrossRef] [PubMed]
- Wang, H.; Pei, Y.; LaLonde, A.D.; Snyder, G.J. Weak electron–phonon coupling contributing to high thermoelectric performance in n-type PbSe. Proc. Natl. Acad. Sci. USA 2012, 109, 9705–9709. [Google Scholar] [CrossRef] [PubMed]
- Wang, H.; Pei, Y.; LaLonde, A.D.; Snyder, G.J. Heavily doped p-type PbSe with high thermoelectric performance: An alternative for PbTe. Adv. Mater. 2011, 23, 1366–1370. [Google Scholar] [CrossRef] [PubMed]
- Pei, Y.; LaLonde, A.D.; Wang, H.; Snyder, G.J. Low effective mass leading to high thermoelectric performance. Energy Environ. Sci. 2012, 5, 7963–7969. [Google Scholar] [CrossRef]

| Material | Aging Temperature [°C] | Aging Times [h] |
|---|---|---|
| As-cast (AC) (PbTe)0.95(Ag2Te)0.05 | 400 | 0, 2, 8, 32, 72, 106 |
| 450 | 0, 1, 2, 4, 8, 16, 32 | |
| Hot-pressed (HP) (PbTe)0.97(Ag2Te)0.03 | 380 | 0, 0.5, 1, 2, 4, 6, 8, 16, 24, 48 |
| Hot-pressed (HP) 0.04 at. % Bi + (PbTe)0.97(Ag2Te)0.03 | 380 | 0, 2, 6, 48 |
| Aging Time (h) | Bulk Density (g·cm−3) | |
|---|---|---|
| Bi-Free | Bi-Alloyed | |
| 0 | 8.00 | 7.86 |
| 1 | 7.65 | 7.42 |
| 2 | 7.82 | 7.45 |
| 6 | 7.97 | 7.37 |
| 18 | 7.85 | 7.38 |
| 48 | 7.97 | 7.58 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Grossfeld, T.; Sheskin, A.; Gelbstein, Y.; Amouyal, Y. Microstructure Evolution of Ag-Alloyed PbTe-Based Compounds and Implications for Thermoelectric Performance. Crystals 2017, 7, 281. https://doi.org/10.3390/cryst7090281
Grossfeld T, Sheskin A, Gelbstein Y, Amouyal Y. Microstructure Evolution of Ag-Alloyed PbTe-Based Compounds and Implications for Thermoelectric Performance. Crystals. 2017; 7(9):281. https://doi.org/10.3390/cryst7090281
Chicago/Turabian StyleGrossfeld, Tom, Ariel Sheskin, Yaniv Gelbstein, and Yaron Amouyal. 2017. "Microstructure Evolution of Ag-Alloyed PbTe-Based Compounds and Implications for Thermoelectric Performance" Crystals 7, no. 9: 281. https://doi.org/10.3390/cryst7090281
APA StyleGrossfeld, T., Sheskin, A., Gelbstein, Y., & Amouyal, Y. (2017). Microstructure Evolution of Ag-Alloyed PbTe-Based Compounds and Implications for Thermoelectric Performance. Crystals, 7(9), 281. https://doi.org/10.3390/cryst7090281






