Next Article in Journal
Graphene Coated Nanoprobes: A Review
Next Article in Special Issue
Halogen and Hydrogen Bonding in Multicomponent Crystals of Tetrabromo-1H-Benzotriazole
Previous Article in Journal
Spark Plasma Sintering of Tungsten Oxides WOx (2.50 ≤ x ≤ 3): Phase Analysis and Thermoelectric Properties
Previous Article in Special Issue
Electrostatic Potential and a Simple Extended Electric Dipole Model of Hydrogen Fluoride as Probes of Non-Bonding Electron Pairs in the Cyclic Ethers 2,5-Dihydrofuran, Oxetane and Oxirane
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Crystals
Volume 7
Issue 9
10.3390/cryst7090273
crystals-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Strength and Character of R–X···π Interactions Involving Aromatic Amino Acid Sidechains in Protein-Ligand Complexes Derived from Crystal Structures in the Protein Data Bank

by
Kevin E. Riley
* and
Khanh-An Tran
Department of Chemistry, Xavier University of Louisiana, New Orleans, LA 70125, USA
*
Author to whom correspondence should be addressed.
Crystals 2017, 7(9), 273; https://doi.org/10.3390/cryst7090273
Submission received: 1 July 2017 / Revised: 18 August 2017 / Accepted: 30 August 2017 / Published: 8 September 2017
(This article belongs to the Special Issue Analysis of Halogen and Other σ-Hole Bonds in Crystals)
Browse Figures
Versions Notes

Abstract

:
Here, we investigate the strengths of R–X···π interactions, involving both chlorine and bromine, in model systems derived from protein-ligand complexes found in the PDB. We find that the strengths of these interactions can vary significantly, with binding energies ranging from −2.01 to −3.60 kcal/mol. Symmetry adapted perturbation theory (SAPT) analysis shows that, as would be expected, dispersion plays the largest role in stabilizing these R–X···π interactions, generally accounting for about 50% to 80% of attraction. R–Br···π interactions are, for the most part, found to be stronger than R–Cl···π interactions, although the relative geometries of the interacting pair and the halogen’s chemical environment can also have a strong impact. The two factors that have the strongest impact on the strength of these R–X···π interactions is the distance between the halogen and the phenyl plane as well as the size of the halogen σ-hole.

1. Introduction

In the past several years, halogen bonding has been recognized as an important contributor to the stability of supramolecular structures [1,2,3], crystals [3,4,5], protein-ligand complexes [6,7,8,9,10,11], as well as other chemical and biomolecular structures [12,13,14,15,16]. These noncovalent interactions have properties that are similar to those of hydrogen bonds, most notably their strong directionality and electrostatic character [12,13]. However, because of the involvement of large polarizable halogens, halogen bonds depend more strongly on the contributions from dispersion forces [15], making their solubilities and binding free energy properties distinctly different from those of hydrogen bonds [17,18]. Traditionally, electronegative Lewis bases have been considered the primary halogen bond accepting group, as is true in hydrogen bonding [12,13,14,15,16]. More recently, π-bonding and aromatic moieties have been shown to be effective halogen bond acceptors, leading to a subclass of interactions, sometimes called R–X···π (or C–X···π) interactions [19,20,21,22,23,24,25].
Halogen bonds have been found to be of particular interest in the stabilization of protein-ligand complexes and in the field of drug design, where these interactions are being actively explored as a means to modify binding free energies [6,7,8,9,10,11]. In recent protein database (PDB) survey studies seeking to identify halogen bonds existing in protein-ligand complexes, R–X···π interactions have been found to be one of the most common types of halogen bonding motifs [9,26,27,28]. Examples of R-X···π interactions that contribute to the stabilization of protein-ligand complexes are given in Figure 1. In one study, Zhu and coworkers found that 33% of halogen bonds in the PDB are of the R–X···π type, the second most common halogen bonding motif identified, with the most common motif being of the R–X···O type (53%) [9]. Matter and coworkers identify R–X···π interactions in several different types of protein-ligand complexes, and find that the introduction of R–Cl···π and R–Br···π interactions in complexes involving inhibitors of serine protease factor (fXa) results in the dramatic enhancement of ligand binding affinity [26]. Imai and coworkers identified 59 Cl···π contacts within the PDB (2007 release), with 21, 15, 15, and 8 contacts involving phenylalanine, tyrosine, tryptophan, and histidine, respectively [27]. Sirimulla and coworkers examine the propensities for each of the amino acids to form halogen bonds, carefully distinguishing between the interactions involving protein sidechains and those involving the backbone [28]. Among all sidechain interactions, it is found that halogen contacts with the aromatic amino acids phenylalanine and tyrosine are among the most frequent, while interactions involving tryptophan and histidine, while still significant, occur less frequently.
One of the main sources of attraction in an R–X···Y halogen bond is an electrostatic interaction that occurs between the σ-hole, a region of positive potential (electron deficiency), located along the extension of the R–X bond and an electronegative Lewis base (Y) [12,13,14,15]. Because of the large size and polarizability of halogens, dispersion also plays a significant role in stabilizing halogen bonds [15]. The σ-hole is responsible for halogen bond directionality, although the nature of this directionality is not as straightforward as might be presumed [12,13,14,29,30,31]. Several recent computational studies based on symmetry adapted perturbation theory (SAPT), a method that provides interaction energies that are divided into contributions from electrostatics, dispersion, induction, and exchange, indicate that it is exchange-repulsion, and not electrostatics, as might be assumed, that are responsible for R–X···Y directionality [29,30,31]. In a phenomenon known as polar flattening [32], the electron density envelope in the region of the σ-hole exhibits a flat character in a plane perpendicular to the R–X bond. As this flat region rotates away from the optimal R–X···Y angle of 180°, there is an increase in the electron density overlap of the halogen and the Lewis base, resulting in an increasingly larger exchange-repulsion contribution, thus destabilizing the R–X···Y complex [30].
R–X···π interactions are generally slightly weaker than their R–X···Y counterparts, with binding energies whose magnitudes are typically 10–25% lower [20,25,29]. The SAPT characteristics of R–X···π interactions are similar to those of R–X···Y interactions, however, the former tend to have larger relative contributions from dispersion, which is to be expected given the large size and polarizabilities of both halogens and phenyl groups [25,29]. The geometric properties of R–X···π interactions are inherently different than those of standard halogen bonds because of the diffuse nature of the region of negative potential in an aromatic system.
In a recent computational study, utilizing the accurate CCSD(T)/aug-cc-pVQZ and SAPT2+3δMP2/aug-cc-pVTZ methods on model complexes involving a benzene R–X···π acceptor, the ways in which the strengths of R–X···π interaction depends on the relative orientation of the interacting pair that were investigated [25]. It was seen that the strength of an R–X···π interaction depends strongly on the distance between the halogen and the benzene ring, a distance that is described by both R(R–X···π) and the α angle (as defined in Figure 2, and first introduced by Glaser et al.) [33], while being only mildly dependent on the R–X···π angle (θ). Another useful geometric parameter, R⫫, derived from both R(R–X···π) and α, describes the distance between the halogen and the benzene plane (not the benzene centroid). With this definition, we can say that the strength of an R–X···π interaction depends strongly on R⫫. It is also found in this study that the C6V (T-shaped) structure of the complex, in which the bromine is directly above the benzene center with the C-Br bond perpendicular to the benzene plane, is not the global minimum for this complex. The global potential energy minimum was not found in that study, however, it is shown that shifting the R–X···π donor across the benzene plane results in interactions energies that are slightly more attractive (by about 0.05 kcal/mol) at shift distances of 0.50–0.75 Å. The rotation of the R–X···π donor away from perpendicularity with the benzene plane (i.e., decreasing the θ angle) results in a weaker interaction, however this destabilization is a weaker function of this rotation than has been observed for R–X···Y interactions. In terms of SAPT contributions to the interaction energy, the chief reason for R–X···π destabilization upon rotation away from perpendicularity is an increase in the (repulsive) exchange term, with the dispersion term becoming slightly more attractive as the a(R–X···π) angle decreases, as has been observed for “standard” R–X···Y type interactions [30]. The electrostatic and induction terms are essentially flat throughout the rotation (whose minimum angle is 140°).
There are two main factors that control the size and charge of a halogen’s σ-hole, thus modulating the strength of a R–X···π or R–X···Y interaction. The identity of the halogen has a large impact on interaction strength, with larger halogens generally forming stronger interactions (I > Br > Cl), both because larger halogens have larger σ-holes and because larger halogens have higher polarizabilities, which leads to stronger dispersion interactions [12,13]. The chemical environment in which the halogen is found also has a large impact on the σ-hole size, with the electronegativity of neighboring atoms having the largest impact on the σ-hole size. Thus, it is observed that a halogen bound to an electron withdrawing group will generally have a larger, more positive, σ-hole than one bound to an electropositive or electroneutral group. The size of a σ-hole correlates strongly with the strength of the halogen bonding, or R–X···π, interaction in which the halogen participates [24,25,34,35].
Although R–X···π contacts appear to be quite common in protein-ligand complexes, these interactions have not been the subject of intensive study until recently, and their characteristics are not understood nearly as well as those of their R–X···Y counterparts. Here we seek to investigate the strength and character of R–X···π interactions found within protein-ligand complexes obtained from the PDB. Several model complexes, derived from these protein-ligand structures are considered, including six R–Cl···π complexes and five R–Br···π complexes. This study is not intended to be a comprehensive survey of R–X…π interactions in protein-ligand complexes, but is aimed at elucidating the strengths and properties of these interactions that can be expected to be observed within the context of the protein binding pocket. As such, we have chosen the 11 systems studied here to have varying near-halogen chemical environments (i.e., differing σ-hole magnitudes) as well as variable R–X···π geometries.

2. Results and Discussion

Before computational results are discussed, it is important to clearly state here that, although we have gone to a good deal of effort to exclude secondary (i.e., non-R–X···π) interactions from consideration in our model systems to as great an extent as possible, there are several systems for which this task was not possible. Thus, some of the interaction energies reported here do not purely reflect the strength of the R–X···π interaction in question alone, but may also include some other non-negligible contribution to intermolecular attraction that either stabilizes or destabilizes the overall complex. A large number of complexes were excluded from our study because of the large contributions to binding made by secondary interactions. It will be further noted that R–X···π complexes whose geometric arrangements are far from the C6v configuration are the most likely to include secondary interactions, as these structures often include interactions between aromatic hydrogens (or other aromatic substituents) on the R–X···π donor and the aromatic amino acid R–X···π acceptor. Model systems in which secondary interactions clearly play a role in complex stabilization will be indicated throughout the text. The difficulty in finding R–X···π interactions that are not significantly affected by secondary interaction highlights the fact that a particular noncovalent interaction motif often does not exist “in a vacuum” within a protein-ligand complex, meaning that it is difficult to separate contributions to overall protein-ligand complex stability that are made by the various noncovalent contacts between the ligand and the surrounding amino acids.
Figure 3 gives electrostatic potential maps for benzene, ethylbenzene (phenylalanine model), and 4-ethylphenol (tyrosine model). Here, it is seen that the area of minimum charge near the aromatic centroid is of similar size and charge for all three molecules, although slightly smaller for 4-ethylphenol. In the case of 4-ethylphenol, this region of negative charge extends towards the electronegative hydroxyl oxygen with only a small barrier of less negative potential. The main point to be made about the electrostatic potentials of these three molecules is that they all have negative regions with potentials of roughly the same magnitude (~−100 kcal/mol) and size, although it can be seen that the central negative region in 4-ethylphenol is slightly smaller than that of the other two molecules. Thus, at least in terms of electrostatics, it can be expected that the interactions involving ethylbenzene and 4-ethylphenol as R–X···π acceptors can be expected to have properties that are similar to those having benzene as the R–X···π acceptor.
Table 1 illustrates model complex geometries, geometric parameters, SAPT2+ interaction energies, and interaction terms, R–Cl···π donor electrostatic potentials, and VS,max values for all R–Cl···π model complexes considered here. The VS,max value represents the most positive potential on a σ-hole and reflects the size and charge of that σ-hole. One of the most outstanding features of the depicted data is the relatively low variability of the interaction strengths, with all of the complexes having binding energies falling within the range from −2.10 kcal/mol to −2.66 kcal/mol. This finding is consistent with the results of previous studies in which it was found that the strength of an R–X···π interaction does not strongly depend on geometric factors other than the R–X···π distance. It will be noted here that the most stable complex in this group (−2.66 kcal/mol), 1T4V, contains a strong C–H···O contact in addition to the R–Cl···π interaction. Neglecting this system, the next most stable complex (−2.56 kcal/mol), 1IQE, can be seen to have the most favorable C–Cl···π distance (3.47 Å, R⫫ = 3.36 Å) and the second highest VS,max value (53 kcal/mol) within the group. This result is consistent with previous studies showing that the two factors most strongly affecting the strength of an R–X···π interaction are the R–X···π distance and the size/charge of the halogen σ-hole (i.e., VS,max value).
In terms of SAPT interaction contributions, it is clearly seen that dispersion is the largest attractive force for all interactions considered here, with electrostatics also playing a significant role in attraction. This is consistent with previous SAPT results on model R–X···benzene complexes [24,25] and with the results of Imai and coworkers [27], who used Morokuma decomposition and comparison of Hartree-Fock and MP2 results to investigate the origins of attraction in R–Cl···benzene complexes. SAPT dispersion components fall in the range between −3.35 kcal/mol and −4.29 kcal/mol, while the electrostatic term ranges from −1.05 kcal/mol and −1.86 kcal/mol. In terms of the relative role that each attractive term plays in stabilizing these complexes, reflected in the % attraction quantity, it is seen that dispersion is responsible for 64% to 72% of attraction in the R–Cl···π complexes considered here. Large dispersion contributions to attraction are expected here, as both the R–X···π donor and acceptor are large polarizable groups, and the size of each of these leads to a high degree of overlap between the two electron density envelopes. This high degree of overlap also leads to strong exchange-repulsion components, with the SAPT values varying between 2.01 kcal/mol and 4.47 kcal/mol. In previous studies it has been seen that the strengths of the dispersion and exchange interaction contributions depend strongly on the R⫫ distance, but are affected relatively little by the R–X···π angle (θ) and by the R–X···π donor VS,max value. The electrostatic and induction SAPT terms are also relatively insensitive to the variations in θ angles, but depend strongly on both R⫫ and on the donor VS,max value. Thus, as is the case for standard R–X···Y type halogen bonds, the tuning of the strength of an R–X···π interaction is mediated primarily through the electrostatic and, to a much lesser extent, induction contributions to attraction.
Looking at the SAPT binding energy terms as a function of geometric parameters, it can be seen that the electrostatic, dispersion, and exchange terms exhibit a degree of correlation with the R⫫ distance; the electrostatic and dispersion terms become more attractive, and the exchange term becomes more repulsive as the R⫫ decreases. For example, the three complexes having R⫫ distances of at least 3.40 Å (1T4V, 1NFY, and 2BMG) have electrostatic terms ranging from −1.05 to −1.19 kcal/mol, dispersion terms ranging from −3.35 to −3.41 kcal/mol, and exchange terms ranging from 2.01 to 2.75 kcal/mol while the complexes having R⫫ distances of less than 3.36 Å (1IQE, 1NFU, and 2BQW) have electrostatic terms ranging from −1.75 to −1.86 kcal/mol, dispersion terms ranging from −4.09 to −4.29 kcal/mol, and exchange terms ranging from 3.80 to 4.47 kcal/mol. Conversely, there is no strong correlation seen here between the SAPT interaction terms and the θ angle.
Table 2 gives model complex geometries, geometric parameters, SAPT2+ interaction energies and interaction terms, R–Cl···π donor electrostatic potentials, and VS,max values for all R–Br···π model complexes considered here. The most salient aspect of the data depicted here is the fact that, as expected, R–X···π interactions involving bromine are generally stronger than those involving chlorine, with R–Br···π interactions having binding energies that fall in the range from −2.01 to −3.60 kcal/mol. There are two principal reasons for the enhanced strength of R–Br···π interactions relative to R–Cl···π interactions, both related to the larger size of bromine: larger halogens tend to form larger, more positive, σ-holes, and larger halogens are more polarizable and, thus, tend to form stronger dispersion interactions. The first of these points (increased σ-hole size) is reflected in VS,max values, which range from 57 to 118 kcal/mol for R–Br···π donors, and from 25 to 54 kcal/mol for R–Cl···π donors.
In terms of geometric parameters, it is seen that R–Br···π distances are generally greater than R–Cl···π distances, as would be expected because of the larger size of bromine, with an average difference of 0.20 Å. It should be noted here that, in comparison to the R–Cl···π complexes, a wider range of R–X···π angles, both α and θ, is represented in the set of five R–Br···π structures, with α angles ranging from 16.3 to 30.3° and θ angles in the range from 127.5 to 174.8°. The result of the larger variation in the three principal geometric parameters is a larger variation of the R⫫ distance, which varies from 3.18 to 3.82 Å (∆R⫫ = 0.64 Å) for R–Br···π structures, as compared to varying from 3.29 to 3.68 Å (∆R⫫ = 0.39Å) for R–Cl···π complexes. The 1P5E complex, which exhibits the shortest R–Br···π distance and the most positive σ-hole, represents the strongest interaction among all complexes considered here, with an interaction energy of −3.60 kcal/mol. The strength of this interaction is principally attributable to the large size and charge of the bromine σ-hole (VS,max = 118 kcal/mol) and the very short distance between the halogen and the benzene ring (R⫫ = 3.18 Å). The short R⫫ distance results in SAPT terms that are all large relative to structures with shorter intermolecular separations. This is not a surprising result, as it has been seen that the magnitude of all SAPT terms tend to increase sharply with decreasing intermolecular separation within the region of the interaction energy potential energy minimum for R–X···π interactions, traditional halogen bonds, and other noncovalently bound complexes. It should also be noted that 1P5E has the largest relative contribution from electrostatics, with a % attraction value of 35.6%, which is attributable to both the short R⫫ distance and the large VS,max value. Comparing the 1ZOE complex, representing the second strongest interaction in this study, to 1P5E, it is seen that 1ZOE has a bromine σ-hole that is significantly smaller (VS,max = 86 kcal/mol) and an R⫫ distance that is much higher, resulting in a R–Br···π interaction that is weaker by 0.50 kcal/mol. The relative contribution of electrostatics in stabilizing this complex is smaller than in 1P5E (% attraction = 30.5%), but is higher than in all of the other complexes considered here, which is again attributable to a short R⫫ distance and large VS,max value. The low binding energy (−2.01 kcal/mol) of the weakest complex in this group, 1O27, is chiefly attributable to a large R⫫ distance of 3.82 Å. This complex is seen to be largely dispersion-bound, with dispersion accounting for 78.4% of attraction.

3. Conclusions

In this work, we have found that the strengths of R–X···π interactions in protein-ligand complexes vary a great deal, with binding energies ranging from −2.01 to −3.60 kcal/mol. SAPT analysis has shown that dispersion plays the largest role in stabilizing these R–X···π interactions, generally accounting for about 50% to 80% of attraction. Electrostatics are also important, accounting for roughly 20% to 35% of attraction. Generally, R–Br···π interactions are stronger than R–Cl···π interactions, however, geometric factors, as well as the halogen’s chemical environment play a large role in determining this strength, meaning that the strongest R–Cl···π interactions can be stronger than the weakest R–Br···π interactions. It will be noted here that it is reasonable to expect that the R–X···π interactions involving iodine, which is larger and generally has a larger σ-hole than bromine (for an equivalent chemical environment), would tend to be stronger than those involving bromine or chlorine. Interactions involving iodine are not included here, as the influence of relativistic effects in these interactions is strong and we are not able to include these effects in our SAPT calculations.
In previous studies on smaller model systems involving benzene as the R–X···π donor, it was found that the two factors most strongly affecting the strength of these interactions is the distance between the halogen, the phenyl plane, and the size of the halogen’s σ-hole. The R–X···π angle (θ) has a much weaker influence on binding energies. The results of this investigation largely confirm these findings, with interactions that generally increase with increasing VS,max values and decreasing R⫫ distances.
For both R–Cl···π and R–Br···π interactions, it is seen that the SAPT electrostatic, dispersion, and exchange terms are strongly correlated with the R⫫ distance, with E(elec) and E(disp) increasing, and E(exch) decreasing as R⫫ becomes larger. In the case of R–Br···π interactions, it is also clearly seen that interaction energies, which depend both on geometric factors and σ-hole size, generally decrease (become more stable) with a decreasing R⫫.

4. Computational Methods

As noted above, the interaction energies are computed for R–X···π complexes derived from the PDB. In all cases, the R–X···π donor is derived from the ligand and the R–X···π acceptor is derived from a protein tyrosine or phenylalanine residue.
These complexes are prepared in such a way that the critical aspects of the halogen’s chemical environment are included, while the size of the R–X···π donor is kept as small as possible. There are two critical reasons for minimizing the size of the R–X···π donating system: firstly, this limits the computational expense for dimer calculations, and secondly (and perhaps more importantly), this helps limit the possibility for secondary (non-R–X···π) interactions from being present in the complexes. As our primary aim is to study the strengths of R–X···π interactions, it is important to limit the role that other interactions within the system may play in stabilizing the complexes under investigation.
For all 11 ligands investigated here, the halogen on the R–X···π donating group is bound to an aromatic carbon, which is the most common situation for these types of interactions, as has been shown through PDB survey studies [9]. In all of the cases, with the exceptions of the 1P5E and 1ZOE R–Br···π structures, the entire ligand is not retained for model calculations, but only the aromatic moiety on which the halogen is located along with relevant functional groups that are also bound to that aromatic moiety (see figures in Table 1 and Table 2). Phenylalanine is modeled as ethylbenzene, and tyrosine is modeled as 4-ethylphenol. Heavy (non-hydrogen) atoms remain fixed in their crystal structure geometries while the positions of hydrogens, which are not determined experimentally, are determined by optimization at the BLYP/def2-TZVP level of theory.
The main tool used here to investigate the strength and character of R–X···π interactions is the symmetry adapted perturbation theory, SAPT2+/aug-cc-pVDZ [36,37,38], method, which has been shown to provide the binding energies that are at least semi-quantitatively accurate [38]. For example, for the S22 database of hydrogen bonded and dispersion bound complexes, this method consistently yields binding energies that are more accurate (mean unsigned error of 0.22 kcal/mol) than the, very commonly used, MP2/cc-pVTZ method (mean unsigned error of 0.70 kcal/mol) [38,39]. An additional feature of SAPT methods is that the interaction energy is divided into physically meaningful components corresponding to electrostatics, induction, dispersion, and exchange-repulsion. These terms give insight into the nature of a noncovalent interaction, and indicate the dominant stabilizing (and/or destabilizing) forces in an interacting pair. All SAPT calculations are performed using the PSI4 suite of molecular electronic structure programs [40].
Electrostatic potential maps are produced on the molecular ‘surface’, taken to be the 0.001 electron/bohr contour of the molecule’s electron density. Molecular electronic densities are computed at the B3LYP/6-311G* level of theory [41]. Electrostatic potentials are computed using the Spartan molecular electronic structure program [42]. The VS,max value, which represents the maximum potential value on the halogen, is a convenient measure of the magnitude of the size of a σ-hole, and is used extensively throughout this work [41].

Acknowledgments

The authors gratefully acknowledge support from the NSF HBCU-UP program (HRD-1505219), the NIH R15 program (1R15GM113193-01), the NIH RISE program (5R25GM060926-10), and the NSF BUILD program (5RL5GM118966-03).

Author Contributions

K.E.R. and K.-A.T. conceived and designed the experiments; K.-A.T. performed the experiments; K.E.R. and K.-A.T. analyzed the data; K.E.R. wrote the~paper.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Gilday, L.C.; Robinson, S.W.; Barendt, T.A.; Langton, M.J.; Mullaney, B.R.; Beer, P.D. Halogen Bonding in Supramolecular Chemistry. Chem. Rev. 2015, 115, 7118–7195. [Google Scholar] [CrossRef] [PubMed]
  2. Aackeröy, C.B.; Hurley, D.P.; Desper, J. Modulating Supramolecular Reactivity Using Covalent “Switches” on a Pyrazole Platform. Cryst. Growth Des. 2012, 12, 5806–5814. [Google Scholar] [CrossRef]
  3. Cavallo, G.; Metrangolo, P.; Milani, R.; Pilati, T.; Priimagi, A.; Resnati, G.; Terraneo, G. The Halogen Bond. Chem. Rev. 2016, 116, 2478–2601. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  4. Aackeröy, C.B.; Wijethunga, T.K.; Desper, J.; Đaković, M. Crystal Engineering with Iodoethynylmitrobenzenes: A Group of Highly Effective Halogen Bond Donors. Cryst. Growth Des. 2015, 15, 3853–3861. [Google Scholar] [CrossRef]
  5. Mukherjee, A.; Tothadi, S.; Desiraju, G.R. Halogen Bonds in Crystal Engineering: Like Hydrogen Bonds Yet Different. Acc. Chem. Res. 2014, 47, 2514–2524. [Google Scholar] [CrossRef] [PubMed]
  6. Riley, K.E.; Hobza, P. Strength and Character of Halogen Bonds in Protein-Ligand Complexes. Cryst. Growth Des. 2011, 11, 4272–4278. [Google Scholar] [CrossRef]
  7. Parisini, E.; Metrangolo, P.; Pilati, T.; Resnati, G.; Terraneo, G. Halogen Bonding in Halocarbon-Protein Complexes: A Structural Survey. Chem. Soc. Rev. 2011, 40, 2267–2278. [Google Scholar] [CrossRef] [PubMed]
  8. Scholfield, M.R.; Van der Zanden, C.M.; Carter, M.; Ho, P.S. Halogen Bonding (X-Bonding): A Biological Perspective. Protein Sci. 2013, 22, 139–152. [Google Scholar] [CrossRef] [PubMed]
  9. Lu, Y.; Wang, Y.; Zhu, W. Nonbonding Interactions of Organic Halogens in Biological Systems: Implications for Drug Discovery and Biomolecular Design. Phys. Chem. Chem. Phys. 2010, 12, 4543–4551. [Google Scholar] [CrossRef] [PubMed]
  10. Wilcken, R.; Zimmermann, M.O.; Lange, A.; Joerger, A.C.; Boeckler, F.M. Principles and Applications of Halogen Bonding in Medicinal Chemistry and Chemical Biology. J. Med. Chem. 2013, 56, 1363–1388. [Google Scholar] [CrossRef] [PubMed]
  11. Ho, P.S. Halogen Bonding in Medicinal Chemistry: From Observation to Prediction. Future Sci. 2017, 9, 637–640. [Google Scholar] [CrossRef] [PubMed]
  12. Politzer, P.; Lane, P.; Concha, M.C.; Ma, Y.; Murray, J.S. An Overview of Halogen Bonding. J. Mol. Model. 2007, 13, 305–311. [Google Scholar] [CrossRef] [PubMed]
  13. Politzer, P.; Murray, J.S.; Clark, T. Halogen Bonding and other σ-Hole Interactions: A Perspective. Phys. Chem. Chem. Phys. 2013, 15, 11178–11189. [Google Scholar] [CrossRef] [PubMed]
  14. Murray, J.S.; Riley, K.E.; Politzer, P.; Clark, T. Directional Weak Intermolecular Interactions: σ-Hole Bonding. Aust. J. Chem. 2010, 63, 1598–1607. [Google Scholar] [CrossRef]
  15. Riley, K.E.; Hobza, P. Investigations into the Nature of Halogen Bonding Including Symmetry Adapted Perturbation Theory Analyses. J. Chem. Theory Comput. 2008, 4, 232–242. [Google Scholar] [CrossRef] [PubMed]
  16. Kolář, M.H.; Hobza, P. Computer Modeling of Halogen Bonding and other σ-Hole Interactions. Chem. Rev. 2016, 116, 5155–5187. [Google Scholar] [CrossRef] [PubMed]
  17. Lu, Y.; Li, H.; Zhu, X.; Zhu, W.; Liu, H. How Does Halogen Bonding Behave in Solution? A Theoretical Study Using Implicit Solvation Model. J. Phys. Chem. A 2011, 115, 4467–4475. [Google Scholar] [CrossRef] [PubMed]
  18. Robertson, C.C.; Perutz, R.N.; Brammer, L.; Hunber, C. A Solvent-Resistant Halogen Bond. Chem. Sci. 2014, 5, 4179–4183. [Google Scholar] [CrossRef]
  19. Lu, Y.X.; Zou, J.W.; Wang, Y.H.; Yu, Q.S. Theoretical Investigations of the C–X/π Interactions between Benzene and Some Model Halocarbons. Chem. Phys. 2006, 334, 1–7. [Google Scholar] [CrossRef]
  20. Forni, A.; Pieraccini, S.; Rendine, S.; Gabas, F.; Sironi, M. Halogen-Bonding Interactions with π Systems: CCSD(T), MP2, and DFT Calculations. ChemPhysChem 2012, 13, 4224–4234. [Google Scholar] [CrossRef] [PubMed]
  21. Forni, A.; Pieraccini, S.; Rendine, S.; Sironi, M. Halogen Bonds with Benzene: An Assessment of DFT Functionals. J. Comput. Chem. 2014, 35, 386–394. [Google Scholar] [CrossRef] [PubMed]
  22. Nagels, N.; Hauchecorne, D.; Herrebout, W.A. Exploring the C–X···π Halogen Bonding Motif: An Infrared and Raman Study of the Complexes of CF3X (X = Cl, Br, and I) with the Aromatic Model Compounds Benzene and Toluene. Molecules 2013, 18, 6829–6851. [Google Scholar] [CrossRef] [PubMed]
  23. Tsuzuki, S.; Uchimaru, T.; Wakisaka, A.; Ono, T. Magnitude and Directionality of Halogen Bond of Benzene with C6F5X, C6H5X, and CF3X (X = I, Br, Cl, and F). J. Phys. Chem. A 2016, 120, 7020–7029. [Google Scholar] [CrossRef] [PubMed]
  24. Riley, K.E.; Ford, C.L.; Demouchet, K. Comparison of Hydrogen Bonds, Halogen Bonds, C–H···π Interactions, and C–X···π Interactions using High-Level Ab Initio Methods. Chem. Phys. Lett. 2015, 621, 165–170. [Google Scholar] [CrossRef]
  25. Riley, K.E.; Vazquez, M.; Umemura, C.; Miller, C.; Tran, K.-A. Exploring the (Very Flat) Potential Energy Landscape of R–Br···π Interactions with Accurate CCSD(T) and SAPT Techniques. Chem. Eur. J. 2016, 22, 17690–17695. [Google Scholar] [CrossRef] [PubMed]
  26. Matter, H.; Nazaré, M.; Güssregen, S.; Will, D.S.; Schreuder, H.; Bauer, A.; Urmann, M.; Ritter, K.; Wagner, M.; Wehner, V. Evidence for C–Cl/C–Br···π Interactions as an Important Contribution to Protein-Ligand Binding Affinity. Ang. Chem. Int. Ed. 2009, 48, 2911–2916. [Google Scholar] [CrossRef] [PubMed]
  27. Imai, Y.N.; Inoue, Y.; Nakanishi, I.; Kitaura, K. Cl-π Interactions in Protein-Ligand Complexes. Protein Sci. 2008, 17, 1129–1137. [Google Scholar] [CrossRef] [PubMed]
  28. Sirimulla, S.; Bailey, J.B.; Vegesna, R.; Narayan, M. Halogen Interactions in Protein-Ligand Complexes: Implications of Halogen Bonding for Rational Drug Design. J. Chem. Inf. Model. 2013, 53, 2781–2791. [Google Scholar] [CrossRef] [PubMed]
  29. Scheiner, S. Sensitivity of Noncovalent Bonds to Intermolecular Separation: Hydrogen, Halogen, Chalcogen, and Pnicogen Bonds. CrystEngComm 2013, 15, 3119–3124. [Google Scholar] [CrossRef]
  30. Stone, A.J. Are Halogen Bonded Structures Electrostatically Driven. J. Am. Chem. Soc. 2013, 135, 7005–7009. [Google Scholar] [CrossRef] [PubMed]
  31. Adhikari, U.; Scheiner, S. Sensitivity of Pnicogen, Chalcogen, Halogen, and H-Bonds to Angular Distortions. Chem. Phys. Lett. 2012, 532, 31–35. [Google Scholar] [CrossRef]
  32. Sedlák, R.; Kolář, M.H.; Hobza, P. Polar Flattening and the Strength of Halogen Bonding. J. Chem. Theory Comput. 2015, 11, 4727–4732. [Google Scholar] [CrossRef] [PubMed]
  33. Glaser, R.; Murphy, R.F.; Sui, Y.; Barnesab, C.L.; Kim, H.S. Multifurcated Halogen Bonding involving Ph–Cl···H–CPhLN-R9 Interactions and its Relation to Idiotelamphiphile Layer Architecture. CrystEngComm 2006, 8, 372–376. [Google Scholar] [CrossRef]
  34. Riley, K.E.; Murray, J.S.; Fanfrlik, J.; Řezáč, J.; Solá, R.J.; Concha, M.C.; Ramos, F.M.; Politzer, P. Halogen Bond Tunability I: The Effects of Aromatic Fluorine Substitution on the Strengths of Halogen-Bonding Interactions Involving Chlorine, Bromine, and Iodone. J. Mol. Model. 2011, 17, 3309–3318. [Google Scholar] [CrossRef] [PubMed]
  35. Riley, K.E.; Murray, J.S.; Fanfrlik, J.; Řezáč, J.; Solá, R.J.; Concha, M.C.; Ramos, F.M.; Politzer, P. Halogen Bond Tunability II: The Varying Roles of Electrostatics and Dispersion to Attraction in Halogen Bonds. J. Mol. Model. 2013, 19, 4651–4659. [Google Scholar] [CrossRef] [PubMed]
  36. Jeziorski, B.; Moszynski, R.; Szalewicz, K. Perturbation Theory Approach to Intermolecular Potential Energy Surfaces of Van Der Waals Complexes. Chem. Rev. 1994, 94, 1887–1930. [Google Scholar] [CrossRef]
  37. Hohenstein, E.G.; Sherrill, C.D. Wavefunction Methods for Noncovalent Interactions. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2012, 2, 304–326. [Google Scholar] [CrossRef]
  38. Parker, T.M.; Burns, L.A.; Parrish, R.M.; Ryno, A.G.; Sherrill, C.D. Levels of Symmetry Adapted Perturbation Theory (SAPT) I. Efficiency and Performance for Interaction Energies. J. Chem. Phys. 2014, 140, 094106. [Google Scholar] [CrossRef] [PubMed]
  39. Riley, K.E.; Hobza, P. Assessment of the MP2 Method, Along with Several Basis Sets, for the Computational of Interaction Energies of Biologically Relevant Hydrogen Bonded and Dispersion Bound Complexes. J. Phys. Chem. A 2007, 111, 8257–8263. [Google Scholar] [CrossRef] [PubMed]
  40. Turney, J.M.; Simmonett, A.C.; Parrish, R.M.; Hohenstein, E.G.; Evangelista, F.; Fermann, J.T.; Mintz, B.J.; Burns, L.A.; Wilke, J.J.; Abrams, M.L.; et al. PSI4: An Open-Source Ab Initio Electronic Structure Program. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2012, 2, 556. [Google Scholar] [CrossRef]
  41. Riley, K.E.; Tran, K.A.; Lane, P.; Murray, J.S.; Politzer, P. Comparative Analysis of Electrostatic Potential Maxima and Minima on Molecular Surfaces, As Determined by Three Methods and a Variety of Basis Sets. J. Comput. Sci. 2016, 17, 273–284. [Google Scholar] [CrossRef]
  42. Shao, Y.; Molnar, L.F.; Jung, Y.; Kussmann, J.; Ochsenfeld, C.; Brown, S.T.; Gilbert, A.T.B.; Slipchenko, L.V.; Levchenko, S.V.; O’Neill, D.P.; et al. Advances in Methods and Algorithms in a Modern Quantum Chemistry Program Package. Phys. Chem. Chem. Phys. 2006, 8, 3172–3191. [Google Scholar] [CrossRef] [PubMed]
Crystals 07 00273 g001 550
Figure 1. R–X···π interactions in 1IQE (a) and 1P5E (b) structures. Bromine shown in dark red, and chlorine shown in green. 1IQE is a factor Xa inhibitor bound to the blood coagulation factor Xa protein. 1P5E is a kinase inhibitor complexed with the cyclin dependent kinase 2 protein.
Figure 1. R–X···π interactions in 1IQE (a) and 1P5E (b) structures. Bromine shown in dark red, and chlorine shown in green. 1IQE is a factor Xa inhibitor bound to the blood coagulation factor Xa protein. 1P5E is a kinase inhibitor complexed with the cyclin dependent kinase 2 protein.
Crystals 07 00273 g001
Crystals 07 00273 g002 550
Figure 2. Geometric parameters used to describe R–X···π interactions investigated in this work. R⫫, a parameter describing the distance between the halogen and the benzene plane, is also used extensively throughout this work.
Figure 2. Geometric parameters used to describe R–X···π interactions investigated in this work. R⫫, a parameter describing the distance between the halogen and the benzene plane, is also used extensively throughout this work.
Crystals 07 00273 g002
Crystals 07 00273 g003 550
Figure 3. Electrostatic potentials of R–X···π benzene (left), ethylbenzene (middle), and 4-ethylphenol (right).
Figure 3. Electrostatic potentials of R–X···π benzene (left), ethylbenzene (middle), and 4-ethylphenol (right).
Crystals 07 00273 g003
Table
Table 1. Geometric parameters, VS,max values, symmetry adapted perturbation theory (SAPT) interaction energy terms, SAPT % attraction terms a, model complex geometries, and donor electrostatic potentials for all R–Cl···π complexes considered in this study.
Table 1. Geometric parameters, VS,max values, symmetry adapted perturbation theory (SAPT) interaction energy terms, SAPT % attraction terms a, model complex geometries, and donor electrostatic potentials for all R–Cl···π complexes considered in this study.
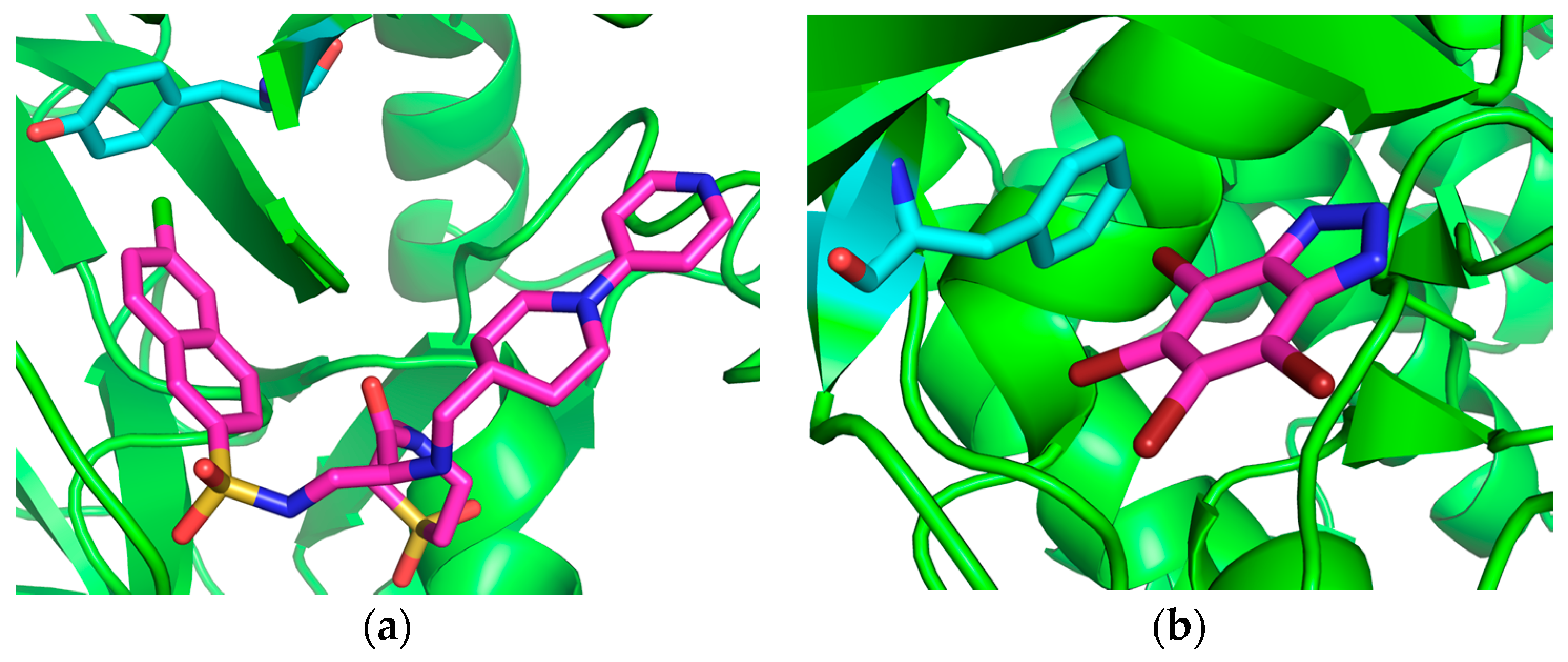
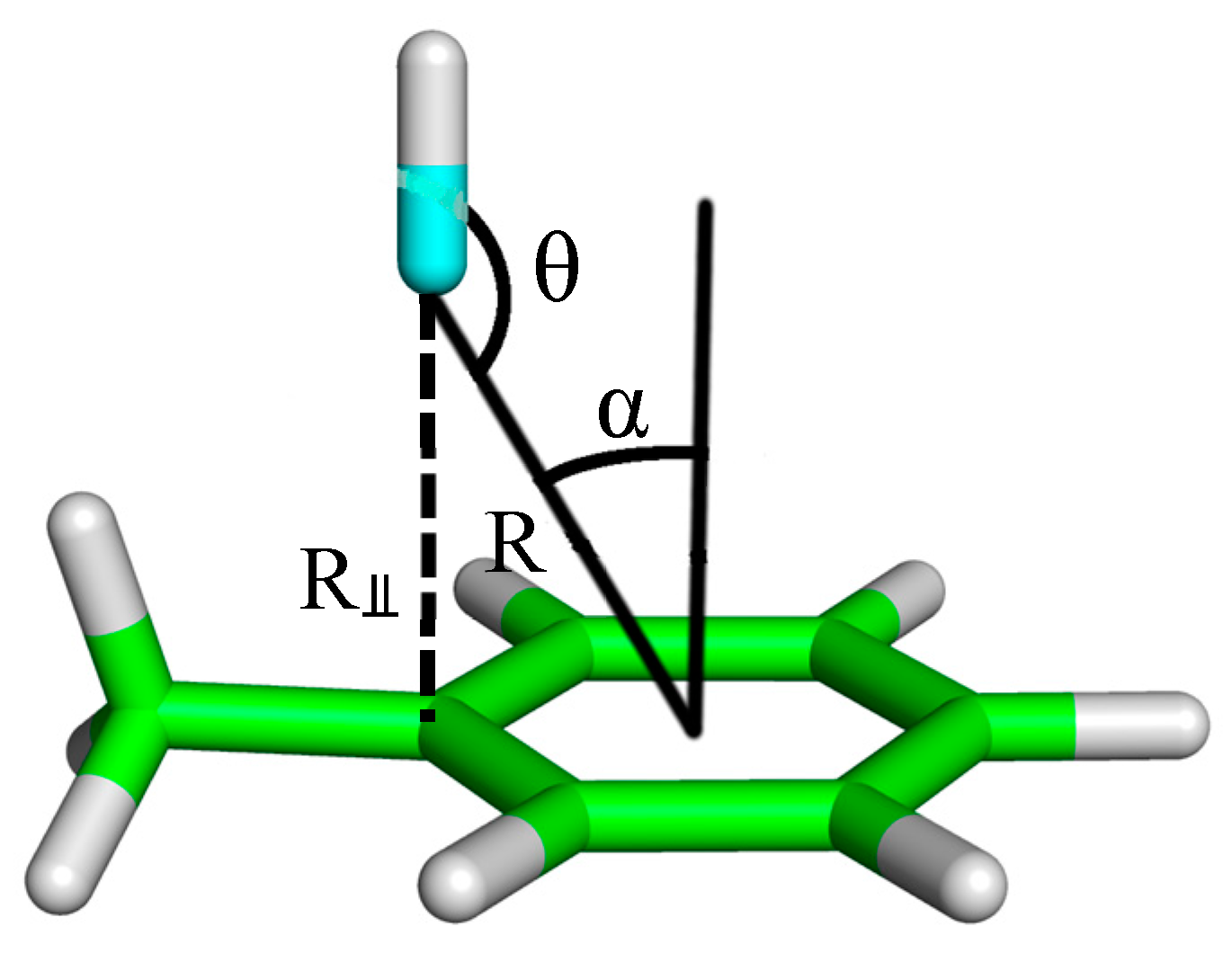
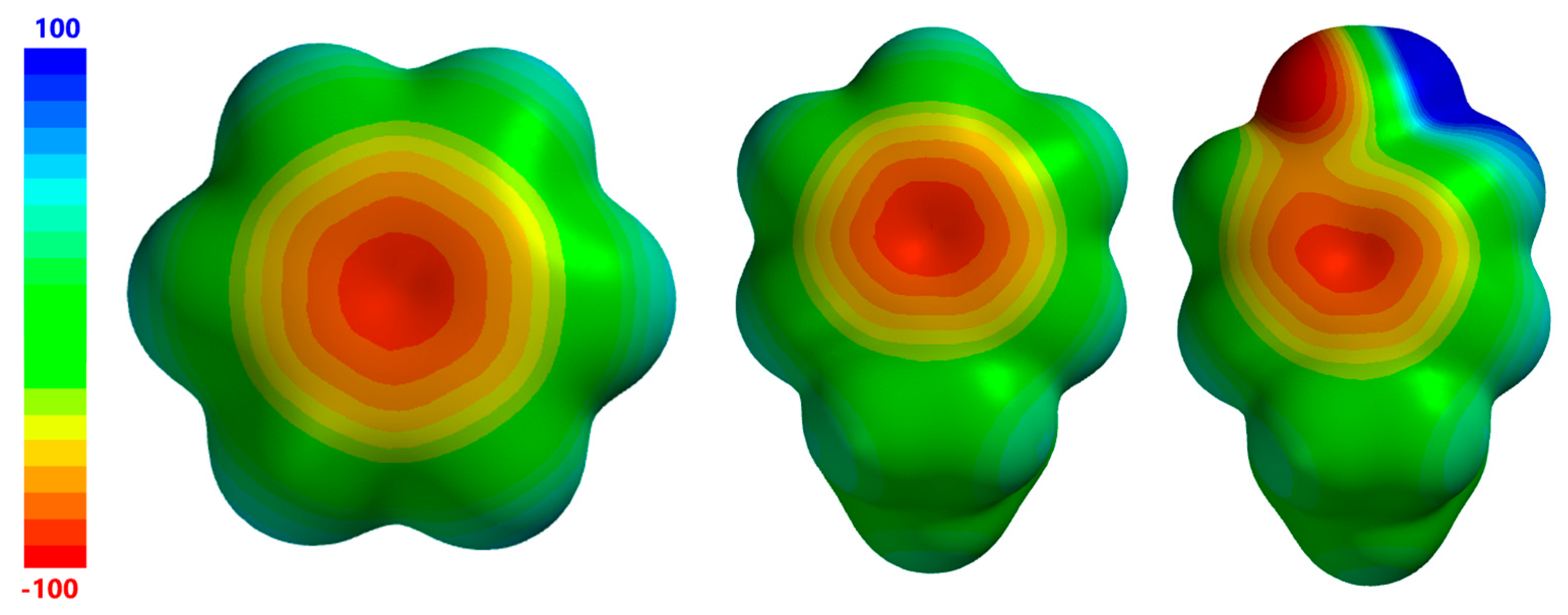
Complex
Geometry
VS,max (kcal/mol)		SAPT Interaction
Energy Terms (kcal/mol)
(% attraction)		Model ComplexR–Cl···π Donor ESP
Crystals 07 00273 i001
1T4V Crystals 07 00273 i002 Crystals 07 00273 i003
R = 3.78 ÅE(elec): −1.05 (22.6)
α = 13.4°E(disp): −3.35 (71.9)
θ = 137.1°E(ind): −0.26 (5.5)
R⫫ = 3.68 ÅE(exch): 2.01
VS,max = 32∆E(int): −2.66
1IQE Crystals 07 00273 i004 Crystals 07 00273 i005
R = 3.47 ÅE(elec): −1.73 (27.3)
α = 14.7°E(disp): −4.15 (65.3)
θ = 169.1°E(ind): −0.47 (7.4)
R⫫ = 3.36 ÅE(exch): 3.80
VS,max = 53∆E(int): −2.56
1NFY Crystals 07 00273 i006 Crystals 07 00273 i007
R = 3.70 ÅE(elec): −1.19 (24.2)
α = 21.9°E(disp): −3.36 (68.5)
θ = 177.0°E(ind): −0.36 (7.3)
R⫫ = 3.43 ÅE(exch): 2.57
VS,max = 53∆E(int): −2.34
1NFU Crystals 07 00273 i008 Crystals 07 00273 i009
R = 3.57 ÅE(elec): −1.78 (27.9)
α = 22.4°E(disp): −4.09 (63.9)
θ = 173.9°E(ind): −0.52 (8.2)
R⫫ = 3.30 ÅE(exch): 4.09
VS,max = 54∆E(int): −2.30
2BQW Crystals 07 00273 i010 Crystals 07 00273 i011
R = 3.50 ÅE(elec): −1.86 (27.9)
α = 19.9°E(disp): −4.29 (64.3)
θ = 174.6°E(ind): −0.52 (7.8)
R⫫ = 3.29 ÅE(exch): 4.47
VS,max = 25∆E(int): −2.20
2BMG Crystals 07 00273 i012 Crystals 07 00273 i013
R = 3.71 ÅE(elec): −1.06 (21.9)
α = 22.4°E(disp): −3.41 (70.4)
θ = 167.5°E(ind): −0.37 (7.7)
R⫫ = 3.43 ÅE(exch): 2.75
VS,max = 37∆E(int): −2.10
a % attraction is computed for electrostatic, dispersion, and induction terms as a fraction of all three attractive terms (e.g., %E(elec) = 100 × E(elec)/(E(elec) + E(disp) + E(ind))).
Table
Table 2. Geometric parameters, VS,max values, SAPT interaction energy terms, SAPT % attraction terms, model complex geometries, and donor electrostatic potentials for all R–Cl···π complexes considered in this study.
Table 2. Geometric parameters, VS,max values, SAPT interaction energy terms, SAPT % attraction terms, model complex geometries, and donor electrostatic potentials for all R–Cl···π complexes considered in this study.
Complex
Geometry
VS,max (kcal/mol)		SAPT Interaction
Energy Terms (kcal/mol)
(% attraction)		Model ComplexR–Br···π Donor ESP
Crystals 07 00273 i014
1P5E Crystals 07 00273 i015 Crystals 07 00273 i016
R = 3.68 ÅE(elec): −4.35 (35.6)
α = 30.3°E(disp): −6.57 (53.8)
θ = 174.8°E(ind): −1.28 (10.5)
R⫫ = 3.18 ÅE(exch): 8.60
VS,max = 118∆E(int): −3.60
1ZOE Crystals 07 00273 i017 Crystals 07 00273 i018
R = 3.93 ÅE(elec): −2.18 (30.5)
α = 28.7°E(disp): −4.36 (61.1)
θ = 163.0°E(ind): −0.60 (8.4)
R⫫ = 3.45 ÅE(exch): 4.04
VS,max = 86∆E(int): −3.10
3JTK Crystals 07 00273 i019 Crystals 07 00273 i020
R = 3.82 ÅE(elec): −1.57 (23.4)
α = 20.3°E(disp): −4.71 (70.3)
θ = 127.5°E(ind): −0.42 (6.3)
R⫫ = 3.58 ÅE(exch): 4.21
VS,max = 61∆E(int): −2.49
2AF6 Crystals 07 00273 i021 Crystals 07 00273 i022
R = 3.80 ÅE(elec): −1.70 (28.7)
α = 23.1°E(disp): −3.70 (62.4)
θ = 164.7°E(ind): −0.53 (8.9)
R⫫ = 3.50 ÅE(exch): 3.80
VS,max = 57∆E(int): −2.12
1O27 Crystals 07 00273 i023 Crystals 07 00273 i024
R = 3.98 ÅE(elec): −0.45 (13.7)
α = 16.3°E(disp): −2.61 (78.4)
θ = 162.4°E(ind): −0.27 (8.0)
R⫫ = 3.82 ÅE(exch): 1.32
VS,max = 71∆E(int): −2.01

Share and Cite

MDPI and ACS Style

Riley, K.E.; Tran, K.-A. Strength and Character of R–X···π Interactions Involving Aromatic Amino Acid Sidechains in Protein-Ligand Complexes Derived from Crystal Structures in the Protein Data Bank. Crystals 2017, 7, 273. https://doi.org/10.3390/cryst7090273

AMA Style

Riley KE, Tran K-A. Strength and Character of R–X···π Interactions Involving Aromatic Amino Acid Sidechains in Protein-Ligand Complexes Derived from Crystal Structures in the Protein Data Bank. Crystals. 2017; 7(9):273. https://doi.org/10.3390/cryst7090273

Chicago/Turabian Style

Riley, Kevin E., and Khanh-An Tran. 2017. "Strength and Character of R–X···π Interactions Involving Aromatic Amino Acid Sidechains in Protein-Ligand Complexes Derived from Crystal Structures in the Protein Data Bank" Crystals 7, no. 9: 273. https://doi.org/10.3390/cryst7090273

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop