Strength of Alkane–Fluid Attraction Determines the Interfacial Orientation of Liquid Alkanes and Their Crystallization through Heterogeneous or Homogeneous Mechanisms
Abstract
:1. Introduction
2. Methods
3. Results and Discussion
3.1. Thermodynamic Properties of the Models
3.1.1. Thermodynamics of Pure Alkanes
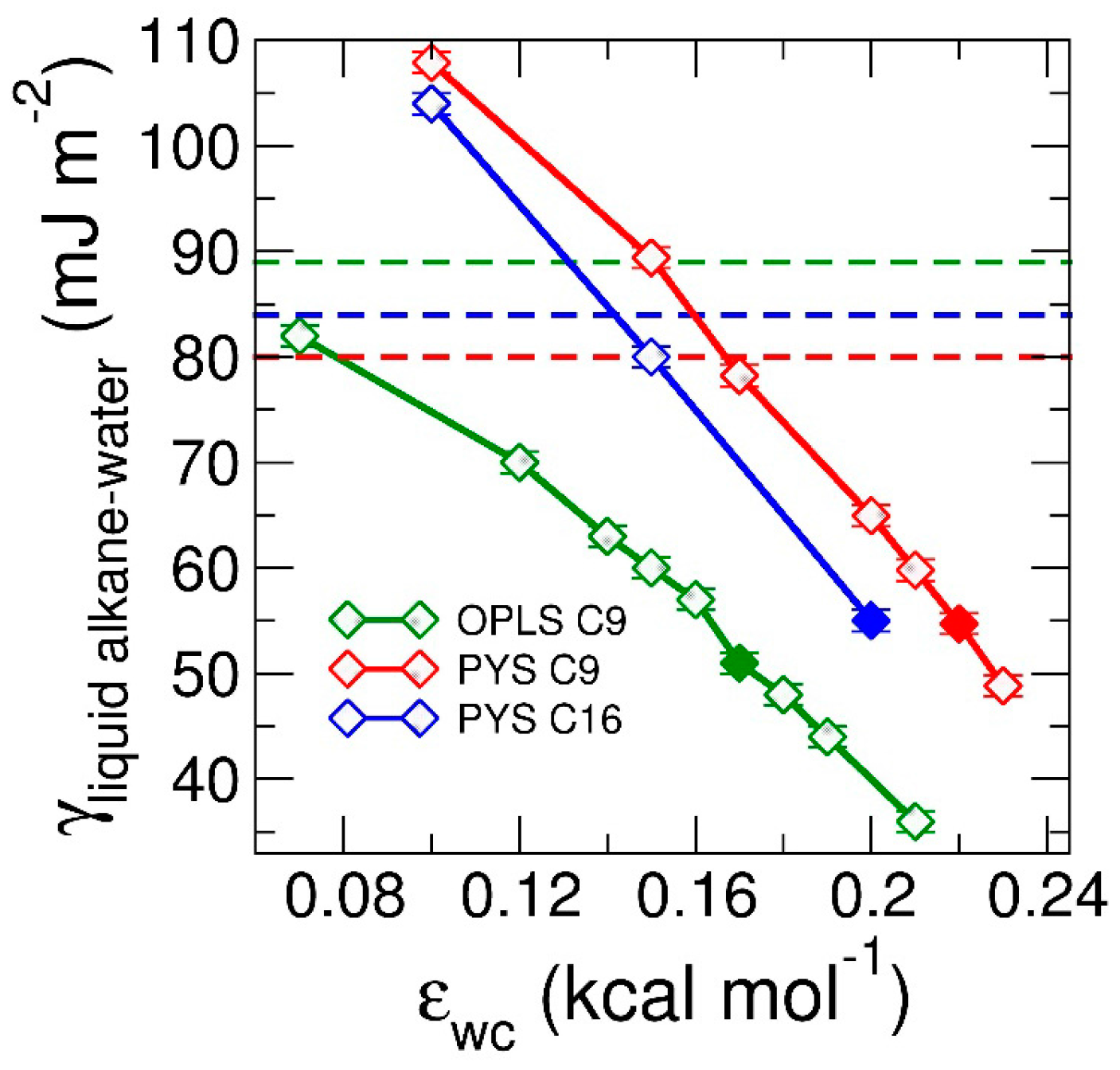
3.1.2. Thermodynamics of Alkane–Water Systems
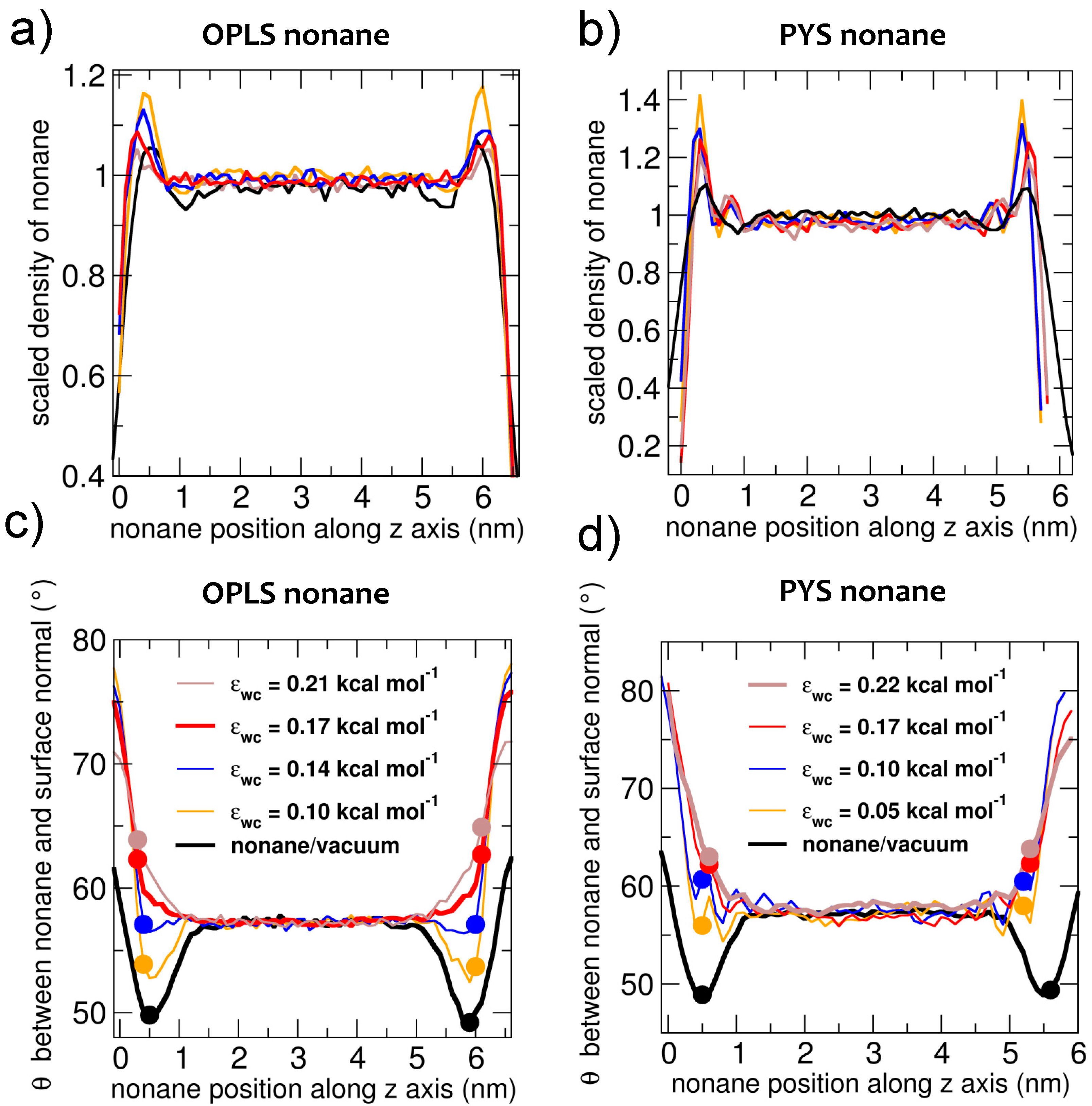
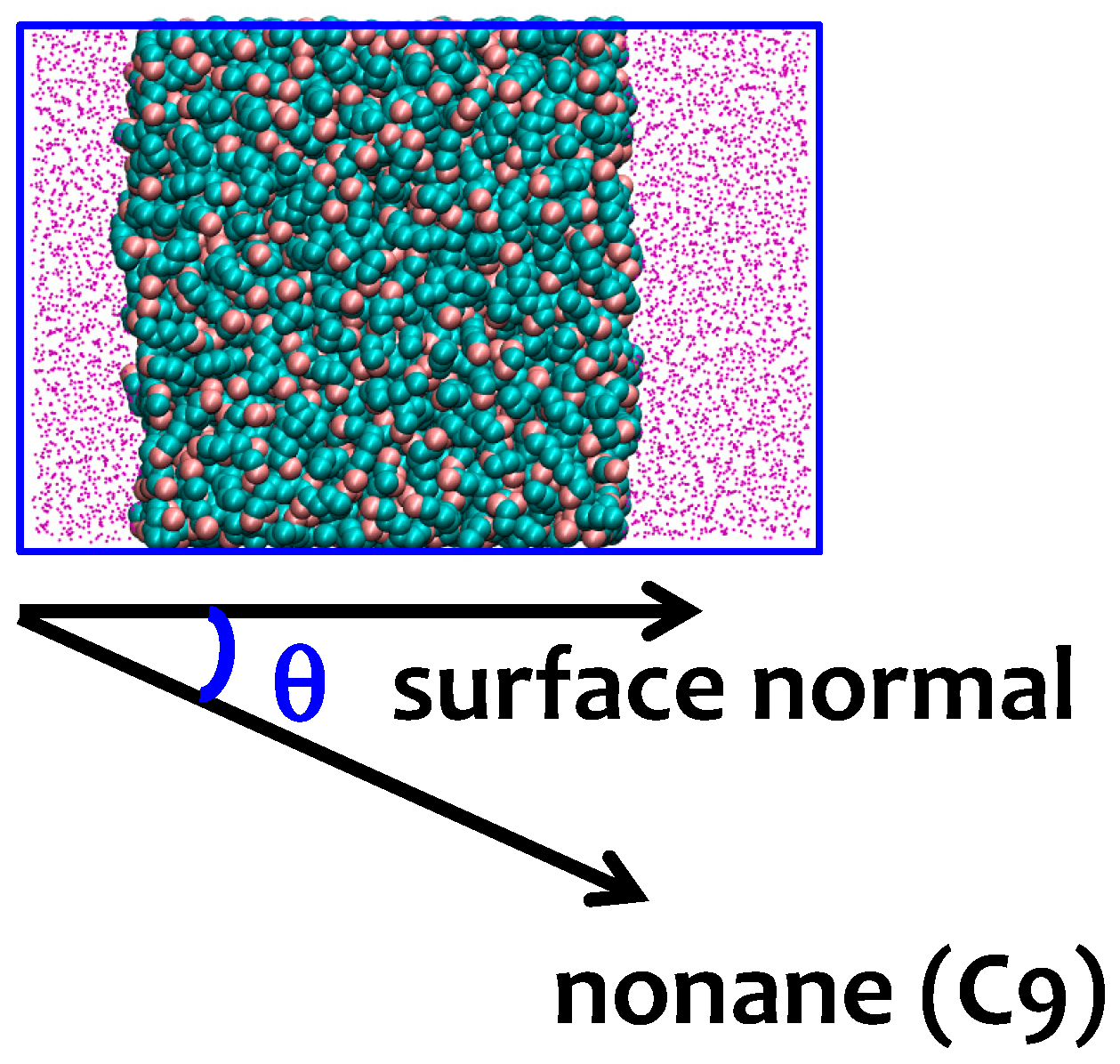
3.2. Interfacial Orientation of Liquid Alkanes is Controlled by the Strength of Attraction to the Other Phase
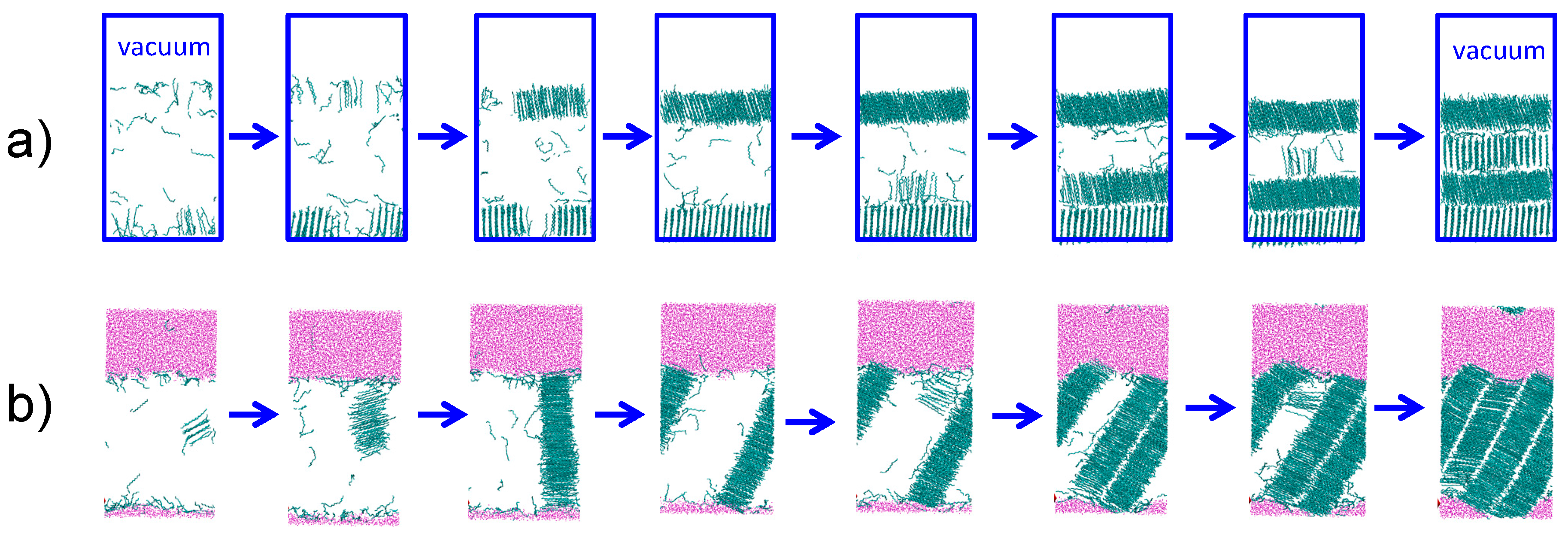
3.3. Strength of the Alkane–Solvent Attraction Determines Whether Alkanes Crystallize through Heterogeneous or Homogeneous Nucleation
3.4. The Sign and Magnitude of the Binding Free Energy of the Alkane Crystal to the Surface Determine Whether the Crystal Nucleation is Homogeneous, Heterogeneous, or There Is Surface Freezing
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Wu, X.; Sirota, E.; Sinha, S.; Ocko, B.; Deutsch, M. Surface crystallization of liquid normal-alkanes. Phys. Rev. Lett. 1993, 70, 958–961. [Google Scholar] [CrossRef] [PubMed]
- Ocko, B.M.; Wu, X.Z.; Sirota, E.B.; Sinha, S.K.; Gang, O.; Deutsch, M. Surface freezing in chain molecules: Normal alkanes. Phys. Rev. E 1997, 55, 3164–3182. [Google Scholar] [CrossRef]
- Tkachenko, A.V.; Rabin, Y. Fluctuation-Stabilized Surface Freezing of Chain Molecules. Phys. Rev. Lett. 1996, 76, 2527–2530. [Google Scholar] [CrossRef] [PubMed]
- Modak, V.P.; Pathak, H.; Thayer, M.; Singer, S.J.; Wyslouzil, B.E. Experimental evidence for surface freezing in supercooled n-alkane nanodroplets. Phys. Chem. Chem. Phys. 2013, 15, 6783–6795. [Google Scholar] [CrossRef] [PubMed]
- Tikhonov, A.M.; Mitrinovic, D.M.; Li, M.; Huang, Z.; Schlossman, M.L. An X-ray reflectivity study of the water-docosane interface. J. Phys. Chem. B 2000, 104, 6336–6339. [Google Scholar] [CrossRef]
- Conboy, J.; Daschbach, J.; Richmond, G. Studies of Alkane/Water Interfaces by Total Internal Reflection Second Harmonic Generation. J. Phys. Chem. 1994, 98, 9688–9692. [Google Scholar] [CrossRef]
- Conboy, J.C.; Daschbach, J.L.; Richmond, G.L. Total internal reflection second-harmonic generation: Probing the alkane water interface. Appl. Phys. A 1994, 59, 623–629. [Google Scholar] [CrossRef]
- Mitrinović, D.M.; Tikhonov, A.M.; Li, M.; Huang, Z.; Schlossman, M.L. Noncapillary-Wave Structure at the Water-Alkane Interface. Phys. Rev. Lett. 2000, 85, 582–585. [Google Scholar] [CrossRef] [PubMed]
- Vácha, R.; Roke, S. Sodium Dodecyl Sulfate at Water–Hydrophobic Interfaces: A Simulation Study. J. Phys. Chem. B 2012, 116, 11936–11942. [Google Scholar] [CrossRef] [PubMed]
- Van Buuren, A.R.; Marrink, S.J.; Berendsen, H.J.C. A molecular dynamics study of the decane/water interface. J. Phys. Chem. 1993, 97, 9206–9212. [Google Scholar] [CrossRef]
- Xiao, H.; Zhen, Z.; Sun, H.; Cao, X.; Li, Z.; Song, X.; Cui, X.; Liu, X. Molecular dynamics study of the water/n-alkane interface. Sci. China Chem. 2010, 53, 945–949. [Google Scholar] [CrossRef]
- Bourque, A.J.; Locker, C.R.; Rutledge, G.C. Heterogeneous Nucleation of an n-Alkane on Tetrahedrally Coordinated Crystals. J. Phys. Chem. B 2017, 121, 904–911. [Google Scholar] [CrossRef] [PubMed]
- Qiu, Y.; Odendahl, N.; Hudait, A.; Mason, R.H.; Bertram, A.K.; Paesani, F.; de Mott, P.J.; Molinero, V. Ice nucleation efficiency of hydroxylated organic surfaces is controlled by their structural fluctuations and mismatch to ice. J. Am. Chem. Soc. 2017, 139, 3052–3064. [Google Scholar] [CrossRef] [PubMed]
- Waheed, N.; Ko, M.J.; Rutledge, G.C. Molecular simulation of crystal growth in long alkanes. Polymer 2005, 46, 8689–8702. [Google Scholar] [CrossRef]
- Waheed, N.; Lavine, M.S.; Rutledge, G.C. Molecular simulation of crystal growth in n-eicosane. J. Chem. Phys. 2002, 116, 2301–2309. [Google Scholar] [CrossRef]
- Paul, W.; Yoon, D.Y.; Smith, G.D. An optimized united atom model for simulations of polymethylene melts. J. Chem. Phys 1995, 103, 1702–1709. [Google Scholar] [CrossRef]
- Jorgensen, W.L.; Tirado-Rives, J. The OPLS [optimized potentials for liquid simulations] potential functions for proteins, energy minimizations for crystals of cyclic peptides and crambin. J. Am. Chem. Soc. 1988, 110, 1657–1666. [Google Scholar] [CrossRef] [PubMed]
- Jorgensen, W.L.; Madura, J.D.; Swenson, C.J. Optimized intermolecular potential functions for liquid hydrocarbons. J. Am. Chem. Soc. 1984, 106, 6638–6646. [Google Scholar] [CrossRef]
- Bourque, A.J.; Rutledge, G.C. Kinetic Model for Layer-by-Layer Crystal Growth in Chain Molecules. Macromolecules 2016, 49, 3956–3964. [Google Scholar] [CrossRef]
- Bourque, A.; Locker, C.R.; Rutledge, G.C. Molecular Dynamics Simulation of Surface Nucleation during Growth of an Alkane Crystal. Macromolecules 2016, 49, 3619–3629. [Google Scholar] [CrossRef]
- Anwar, M.; Turci, F.; Schilling, T. Crystallization mechanism in melts of short n-alkane chains. J. Chem. Phys. 2013, 139, 214904. [Google Scholar] [CrossRef] [PubMed]
- Yi, P.; Rutledge, G.C. Molecular simulation of crystal nucleation in n-octane melts. J. Chem. Phys. 2009, 131, 134902. [Google Scholar] [PubMed]
- Yi, P.; Rutledge, G.C. Molecular simulation of bundle-like crystal nucleation from n-eicosane melts. J. Chem. Phys 2011, 135, 024903. [Google Scholar] [PubMed]
- Hrahsheh, F.; Wilemski, G. Fluctuating structure of aqueous organic nanodroplets. AIP Conf. Proc. 2013, 1527, 63–66. [Google Scholar]
- Yang, H.; Zhao, X.J.; Sun, M. Induced crystallization of single-chain polyethylene on a graphite surface: Molecular dynamics simulation. Phys. Rev. B 2011, 84, 011803. [Google Scholar] [CrossRef] [PubMed]
- Kaner, P.; Ruiz-Orta, C.; Boz, E.; Wagener, K.B.; Tasaki, M.; Tashiro, K.; Alamo, R.G. Kinetic control of chlorine packing in crystals of a precisely substituted polyethylene. Toward advanced polyolefin materials. Macromolecules 2013, 47, 236–245. [Google Scholar] [CrossRef]
- Wang, J.; Zhu, X.; Lu, X.; Zhou, Z.; Wang, G. On structures and properties of polyethylene during heating and cooling processes based on molecular dynamics simulations. Comp. Theor. Chem. 2015, 1052, 26–34. [Google Scholar] [CrossRef]
- Yamamoto, T. Molecular dynamics of crystallization in n-alkane mixtures; texture, compatibility, and diffusion in crystals. Polymer 2016, 99, 721–733. [Google Scholar] [CrossRef]
- Yi, P.; Locker, C.R.; Rutledge, G.C. Molecular dynamics simulation of homogeneous crystal nucleation in polyethylene. Macromolecules 2013, 46, 4723–4733. [Google Scholar] [CrossRef]
- Modak, V.P.; Wyslouzil, B.E.; Singer, S.J. On the determination of the crystal-vapor surface free energy, and why a Gaussian expression can be accurate for a system far from Gaussian. J. Chem. Phys. 2016, 145, 054710. [Google Scholar] [CrossRef] [PubMed]
- Obeidat, A.; Hrahsheh, F.; Wilemski, G. Scattering Form Factors for Russian Doll Aerosol Droplet Models. J. Phys. Chem. B 2014, 119, 9304–9311. [Google Scholar] [CrossRef] [PubMed]
- Anwar, M.; Schilling, T. Crystallization of polyethylene: A molecular dynamics simulation study of the nucleation and growth mechanisms. Polymer 2015, 76, 307–312. [Google Scholar] [CrossRef]
- Wang, E.; Escobedo, F.A. Mechanical Properties of Tetrapolyethylene and Tetrapoly (Ethylene Oxide) Diamond Networks Via Molecular Dynamics Simulations. Macromolecules 2016, 49, 2375–2386. [Google Scholar] [CrossRef]
- Romanos, N.A.; Theodorou, D.N. Crystallization and melting simulations of oligomeric α1 isotactic polypropylene. Macromolecules 2010, 43, 5455–5469. [Google Scholar] [CrossRef]
- Lee, S.; Rutledge, G.C. Plastic deformation of semicrystalline polyethylene by molecular simulation. Macromolecules 2011, 44, 3096–3108. [Google Scholar] [CrossRef]
- Yi, P.; Rutledge, G.C. Molecular origins of homogeneous crystal nucleation. Annu. Rev. Chem. Biomol. Eng. 2012, 3, 157–182. [Google Scholar] [CrossRef] [PubMed]
- Qiu, Y.; Molinero, V. Morphology of Liquid–Liquid Phase Separated Aerosols. J. Am. Chem. Soc. 2015, 137, 10642–10651. [Google Scholar] [CrossRef] [PubMed]
- Molinero, V.; Moore, E.B. Water modeled as an intermediate element between carbon and silicon. J. Phys. Chem. B 2009, 113, 4008–4016. [Google Scholar] [CrossRef] [PubMed]
- Malkin, T.L.; Murray, B.J.; Salzmann, C.G.; Molinero, V.; Pickering, S.J.; Whale, T.F. Stacking disorder in ice I. Phys. Chem. Chem. Phys. 2015, 17, 60–76. [Google Scholar] [CrossRef] [PubMed]
- Moore, E.B.; Molinero, V. Is it cubic? Ice crystallization from deeply supercooled water. Phys. Chem. Chem. Phys. 2011, 13, 20008–20016. [Google Scholar] [CrossRef] [PubMed]
- Moore, E.B.; de la Llave, E.; Welke, K.; Scherlis, D.A.; Molinero, V. Freezing, melting and structure of ice in a hydrophilic nanopore. Phys. Chem. Chem. Phys. 2010, 12, 4124–4134. [Google Scholar] [CrossRef] [PubMed]
- Solveyra, E.G.; Llave, E.D.L.; Molinero, V.; Soler-Illia, G.J. A.A.; Scherlis, D.A. Structure, Dynamics, and Phase Behavior of Water in TiO2 Nanopores. J. Phys. Chem. C 2013, 117, 3330–3342. [Google Scholar] [CrossRef]
- Hudait, A.; Molinero, V. Ice crystallization in ultrafine water-salt aerosols: Nucleation, ice-solution equilibrium, and internal structure. J. Am. Chem. Soc. 2014, 136, 8081–8093. [Google Scholar] [CrossRef] [PubMed]
- Johnston, J.C.; Molinero, V. Crystallization, melting, and structure of water nanoparticles at atmospherically relevant temperatures. J. Am. Chem. Soc. 2012, 134, 6650–6659. [Google Scholar] [CrossRef] [PubMed]
- Lu, J.; Qiu, Y.; Baron, R.; Molinero, V. Coarse-Graining of TIP4P/2005, TIP4P-Ew, SPC/E, and TIP3P to Monatomic Anisotropic Water Models Using Relative Entropy Minimization. J. Chem. Theory Comput. 2014, 10, 4104–4120. [Google Scholar] [CrossRef] [PubMed]
- Lupi, L.; Hudait, A.; Molinero, V. Heterogeneous nucleation of ice on carbon surfaces. J. Am. Chem. Soc. 2014, 136, 3156–3164. [Google Scholar] [CrossRef] [PubMed]
- Moore, E.B.; Molinero, V. Structural transformation in supercooled water controls the crystallization rate of ice. Nature 2011, 479, 506–508. [Google Scholar] [CrossRef] [PubMed]
- Moore, E.B.; Allen, J.T.; Molinero, V. Liquid-ice coexistence below the melting temperature for water confined in hydrophilic and hydrophobic nanopores. J. Phys. Chem. C 2012, 116, 7507–7514. [Google Scholar] [CrossRef]
- Moore, E.B.; Molinero, V. Ice crystallization in water’s “no-man’s land”. J. Chem. Phys. 2010, 132, 244504. [Google Scholar] [CrossRef] [PubMed]
- Moore, E.B.; Molinero, V. Growing correlation length in supercooled water. J. Chem. Phys. 2009, 130, 244505. [Google Scholar] [CrossRef] [PubMed]
- Hujo, W.; Shadrack Jabes, B.; Rana, V.K.; Chakravarty, C.; Molinero, V. The Rise and Fall of Anomalies in Tetrahedral Liquids. J. Stat. Phys. 2011, 145, 293–312. [Google Scholar] [CrossRef]
- Kastelowitz, N.; Johnston, J.C.; Molinero, V. The anomalously high melting temperature of bilayer ice. J. Chem. Phys. 2010, 132, 124511. [Google Scholar] [CrossRef] [PubMed]
- Xu, L.; Molinero, V. Is There a Liquid–Liquid Transition in Confined Water? J. Phys. Chem. B 2011, 115, 14210–14216. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, A.H.; Molinero, V. Identification of Clathrate Hydrates, Hexagonal Ice, Cubic Ice, and Liquid Water in Simulations: The CHILL+ Algorithm. J. Phys. Chem. B 2015, 119, 9369–9376. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, A.H.; Koc, M.A.; Shepherd, T.D.; Molinero, V. Structure of the Ice–Clathrate Interface. J. Phys. Chem. C 2015, 119, 4104–4117. [Google Scholar] [CrossRef]
- Holten, V.; Limmer, D.T.; Molinero, V.; Anisimov, M.A. Nature of the anomalies in the supercooled liquid state of the mW model of water. J. Chem. Phys. 2013, 138, 174501. [Google Scholar] [CrossRef] [PubMed]
- Bullock, G.; Molinero, V. Low-density liquid water is the mother of ice: On the relation between mesostructure, thermodynamics and ice crystallization in solutions. Faraday Discuss. 2013, 167, 371–388. [Google Scholar] [CrossRef] [PubMed]
- González Solveyra, E.A.; de la Llave, E.; Scherlis, D.A.; Molinero, V. Melting and crystallization of ice in partially filled nanopores. J. Phys. Chem. B 2011, 115, 14196–14204. [Google Scholar] [CrossRef] [PubMed]
- Reinhardt, A.; Doye, J.P.K. Effects of surface interactions on heterogeneous ice nucleation for a monatomic water model. J. Chem. Phys. 2014, 141, 084501. [Google Scholar] [CrossRef] [PubMed]
- Factorovich, M.H.; Molinero, V.; Scherlis, D.A. A simple grand canonical approach to compute the vapor pressure of bulk and finite size systems. J. Chem. Phys. 2014, 140, 064111. [Google Scholar] [CrossRef] [PubMed]
- Factorovich, M.H.; Molinero, V.; Scherlis, D.A. Vapor pressure of water nanodroplets. J. Am. Chem. Soc. 2014, 136, 4508–4514. [Google Scholar] [CrossRef] [PubMed]
- Limmer, D.T.; Chandler, D. The putative liquid-liquid transition is a liquid-solid transition in atomistic models of water. J. Chem. Phys. 2011, 135, 134503. [Google Scholar] [CrossRef] [PubMed]
- Limmer, D.T.; Chandler, D. The putative liquid-liquid transition is a liquid-solid transition in atomistic models of water. II. J. Chem. Phys. 2013, 138, 214504. [Google Scholar] [CrossRef] [PubMed]
- Espinosa, J.R.; Vega, C.; Valeriani, C.; Sanz, E. Seeding approach to crystal nucleation. J. Chem. Phys. 2016, 144, 034501. [Google Scholar] [CrossRef] [PubMed]
- Zaragoza, A.; Conde, M.M.; Espinosa, J.R.; Valeriani, C.; Vega, C.; Sanz, E. Competition between ices Ih and Ic in homogeneous water freezing. J. Chem. Phys. 2015, 143, 134504. [Google Scholar] [CrossRef] [PubMed]
- Espinosa, J.R.; Sanz, E.; Valeriani, C.; Vega, C. Homogeneous ice nucleation evaluated for several water models. J. Chem. Phys. 2014, 141, 18C529. [Google Scholar] [CrossRef] [PubMed]
- Bi, Y.; Cabriolu, R.; Li, T. Heterogeneous Ice Nucleation Controlled by the Coupling of Surface Crystallinity and Surface Hydrophilicity. J. Phys. Chem. B 2016, 120, 1507–1514. [Google Scholar] [CrossRef]
- Cabriolu, R.; Li, T. Ice nucleation on carbon surface supports the classical theory for heterogeneous nucleation. Phys. Rev. E 2015, 91, 052402. [Google Scholar] [CrossRef] [PubMed]
- Li, T.; Donadio, D.; Russo, G.; Galli, G. Homogeneous ice nucleation from supercooled water. Phys. Chem. Chem. Phys. 2011, 13, 19807–19813. [Google Scholar] [CrossRef] [PubMed]
- Jacobson, L.C.; Molinero, V. A Methane−Water Model for Coarse-Grained Simulations of Solutions and Clathrate Hydrates. J. Phys. Chem. B 2010, 114, 7302–7311. [Google Scholar] [CrossRef] [PubMed]
- Dhabal, D.; Nguyen, A.H.; Singh, M.; Khatua, P.; Molinero, V.; Bandyopadhyay, S.; Chakravarty, C. Excess entropy and crystallization in Stillinger-Weber and Lennard-Jones fluids. J. Chem. Phys. 2015, 143, 164512. [Google Scholar] [CrossRef] [PubMed]
- Singh, M.; Dhabal, D.; Nguyen, A.H.; Molinero, V.; Chakravarty, C. Triplet Correlations Dominate the Transition from Simple to Tetrahedral Liquids. Phys. Rev. Lett. 2014, 112, 147801. [Google Scholar] [CrossRef] [PubMed]
- Hudait, A.; Qiu, S.; Lupi, L.; Molinero, V. Free energy contributions and structural characterization of stacking disordered ices. Phys. Chem. Chem. Phys. 2016, 18, 9544–9553. [Google Scholar] [CrossRef] [PubMed]
- Cox, S.J.; Kathmann, S.M.; Slater, B.; Michaelides, A. Molecular simulations of heterogeneous ice nucleation. I. Controlling ice nucleation through surface hydrophilicity. J. Chem. Phys. 2015, 142, 184704. [Google Scholar] [CrossRef] [PubMed]
- Cox, S.J.; Kathmann, S.M.; Slater, B.; Michaelides, A. Molecular simulations of heterogeneous ice nucleation. II. Peeling back the layers. J. Chem. Phys. 2015, 142, 184705. [Google Scholar] [CrossRef] [PubMed]
- Lupi, L.; Kastelowitz, N.; Molinero, V. Vapor deposition of water on graphitic surfaces: Formation of amorphous ice, bilayer ice, ice I, and liquid water. J. Chem. Phys. 2014, 141, 18C508. [Google Scholar] [CrossRef] [PubMed]
- Fitzner, M.; Sosso, G.C.; Cox, S.J.; Michaelides, A. The Many Faces of Heterogeneous Ice Nucleation: Interplay Between Surface Morphology and Hydrophobicity. J. Am. Chem. Soc. 2015, 137, 13658–13669. [Google Scholar] [CrossRef] [PubMed]
- Li, T.; Donadio, D.; Galli, G. Ice nucleation at the nanoscale probes no man’s land of water. Nat. Commun. 2013, 4, 1887. [Google Scholar] [CrossRef] [PubMed]
- Lu, J.; Chakravarty, C.; Molinero, V. Relationship between the line of density anomaly and the lines of melting, crystallization, cavitation, and liquid spinodal in coarse-grained water models. J. Chem. Phys. 2016, 144, 234507. [Google Scholar] [CrossRef] [PubMed]
- Jabes, B.S.; Nayar, D.; Dhabal, D.; Molinero, V.; Chakravarty, C. Water and other tetrahedral liquids: Order, anomalies and solvation. J. Phys. Condens. Matter 2012, 24, 284116. [Google Scholar] [CrossRef] [PubMed]
- Factorovich, M.H.; Gonzalez Solveyra, E.; Molinero, V.; Scherlis, D.A. Sorption Isotherms of Water in Nanopores: Relationship Between Hydropohobicity, Adsorption Pressure, and Hysteresis. J. Phys. Chem. C 2014, 118, 16290–16300. [Google Scholar] [CrossRef]
- Limmer, D.T.; Chandler, D. Phase diagram of supercooled water confined to hydrophilic nanopores. J. Chem. Phys. 2012, 137, 044509. [Google Scholar] [CrossRef] [PubMed]
- Haji-Akbari, A.; de Fever, R.S.; Sarupria, S.; Debenedetti, P.G. Suppression of sub-surface freezing in free-standing thin films of a coarse-grained model of water. Phys. Chem. Chem. Phys. 2014, 16, 25916–25927. [Google Scholar] [CrossRef] [PubMed]
- Sun, H. COMPASS: An ab initio force-field optimized for condensed-phase applications overview with details on alkane and benzene compounds. J. Phys. Chem. B 1998, 102, 7338–7364. [Google Scholar] [CrossRef]
- Plimpton, S. Fast Parallel Algorithms for Short-Range Molecular Dynamics. J. Comput. Phys. 1995, 117, 1–19. [Google Scholar] [CrossRef]
- Berendsen, H.J.C.; Grigera, J.R.; Straatsma, T.P. The missing term in effective pair potentials. J. Phys. Chem. 1987, 91, 6269–6271. [Google Scholar] [CrossRef]
- Goebel, A.; Lunkenheimer, K. Interfacial tension of the water/n-alkane interface. Langmuir 1997, 13, 369–372. [Google Scholar] [CrossRef]
- Zeppieri, S.; Rodríguez, J.; López de Ramos, A.L. Interfacial Tension of Alkane + Water Systems. J. Chem. Eng. Data 2001, 46, 1086–1088. [Google Scholar] [CrossRef]
- Nosé, S. A unified formulation of the constant temperature molecular dynamics methods. J. Chem. Phys. 1984, 81, 511–519. [Google Scholar] [CrossRef]
- Hoover, W.G. Canonical dynamics: Equilibrium phase-space distributions. Phys. Rev. A 1985, 31, 1695–1697. [Google Scholar] [CrossRef]
- Groom, C.R.; Bruno, I.J.; Lightfoot, M.P.; Ward, S.C. The Cambridge Structural Database. Acta Crystallogr. Sect. B 2016, 72, 171–179. [Google Scholar] [CrossRef] [PubMed]
- Schneider, T.; Stoll, E. Molecular-dynamics study of a three-dimensional one-component model for distortive phase transitions. Phys. Rev. B 1978, 17, 1302–1322. [Google Scholar] [CrossRef]
- Gloor, G.J.; Jackson, G.; Blas, F.J.; de Miguel, E. Test-area simulation method for the direct determination of the interfacial tension of systems with continuous or discontinuous potentials. J. Chem. Phys. 2005, 123, 134703. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Steinhardt, P.; Nelson, D.; Ronchetti, M. Bond-orientational order in liquids and glasses. Phys. Rev. B 1983, 28, 784–805. [Google Scholar] [CrossRef]
- Rozmanov, D.; Kusalik, P.G. Anisotropy in the crystal growth of hexagonal ice, I(h). J. Chem. Phys 2012, 137, 094702. [Google Scholar] [CrossRef] [PubMed]
- Acree, W.E.; Chickos, J.S. Phase Transition Enthalpy Measurements of Organic and Organometallic Compounds. In NIST Chemistry WebBook, NIST Standard Reference Database Number 69; Linstrom, P.J., Mallard, W.G., Eds.; National Institute of Standards and Technology: Gaithersburg MD, USA, 2016. [Google Scholar]
- Rolo, L.I.; Caço, A.I.; Queimada, A.J.; Marrucho, I.M.; Coutinho, J.A.P. Surface tension of heptane, decane, hexadecane, eicosane, and some of their binary mixtures. J. Chem. Eng. Data 2002, 47, 1442–1445. [Google Scholar] [CrossRef]
- Viton, C.; Chavret, M.; Jose, J. Enthalpies of Vaporization of Normal Alkanes from Nonane to Pentadecane at Temperatures from 298 to 359 K. ELDATA Int. Electron. J. Phys. Chem. Data 1996, 2, 103. [Google Scholar]
- Mondieig, D.; Rajabalee, F.; Metivaud, V.; Oonk, H.; Cuevas-Diarte, M. n-Alkane binary molecular alloys. Chem. Mater. 2004, 16, 786–798. [Google Scholar] [CrossRef]
- Benet, J.; MacDowell, L.G.; Menduiña, C. Liquid-vapor phase equilibria and surface tension of ethane as predicted by the TraPPE and OPLS models. J. Chem. Eng. Data 2010, 55, 5465–5470. [Google Scholar] [CrossRef]
- Wick, C.D.; Siepmann, J.I.; Schure, M.R. Molecular Simulation of Concurrent Gas−Liquid Interfacial Adsorption and Partitioning in Gas−Liquid Chromatography. Anal. Chem. 2002, 74, 3518–3524. [Google Scholar] [CrossRef] [PubMed]
- Haji-Akbari, A.; Debenedetti, P.G. Thermodynamic and kinetic anisotropies in octane thin films. J. Chem. Phys. 2015, 143, 214501. [Google Scholar] [CrossRef] [PubMed]
- Harris, J.G. Liquid-vapor interfaces of alkane oligomers: Structure and thermodynamics from molecular dynamics simulations of chemically realistic models. J. Phys. Chem. 1992, 96, 5077–5086. [Google Scholar] [CrossRef]
- Kawamata, M.; Yamamoto, T. Molecular dynamics simulation of surface ordering in liquid n-alkanes. J. Phys. Soc. Jpn. 1997, 66, 2350–2354. [Google Scholar] [CrossRef]
- Baron, R.; Molinero, V. Water-driven cavity-ligand binding: Comparison of thermodynamic signatures from coarse-grained and atomic-level simulations. J. Chem. Theory Comput. 2012, 8, 3696–3704. [Google Scholar] [CrossRef] [PubMed]
- Yamamoto, T.; Nozaki, K.; Yamaguchi, A.; Urakami, N. Molecular simulation of crystallization in n-alkane ultrathin films: Effects of film thickness and substrate attraction. J. Chem. Phys. 2007, 127, 154704. [Google Scholar] [CrossRef] [PubMed]
- Turnbull, D.; Fisher, J.C. Rate of nucleation in condensed systems. J. Chem. Phys. 1949, 17, 71–73. [Google Scholar] [CrossRef]
- Young, T. An essay on the cohesion of fluids. Philos. Trans. R. Soc. Lond. 1805, 95, 65–87. [Google Scholar] [CrossRef]
- Iwamatsu, M. Heterogeneous Nucleation on a Completely Wettable Substrate. In Advances in Contact Angle, Wettability and Adhesion; John Wiley & Sons, Inc.: Salem, MA, USA, 2013; pp. 49–72. [Google Scholar]
- Auer, S.; Frenkel, D. Line tension controls wall-induced crystal nucleation in hard-sphere colloids. Phys. Rev. Lett. 2003, 91, 015703. [Google Scholar] [CrossRef] [PubMed]
- Sirota, E.; Wu, X.; Ocko, B.; Deutsch, M. What Drives the Surface Freezing in Alkanes? Phys. Rev. Lett. 1997, 79, 531. [Google Scholar] [CrossRef]
- Merkl, C.; Pfohl, T.; Riegler, H. Influence of the molecular ordering on the wetting of SiO2/air interfaces by alkanes. Phys. Rev. Lett. 1997, 79, 4625. [Google Scholar] [CrossRef]
- Volkmann, U.G.; Pino, M.; Altamirano, L.; Taub, H.; Hansen, F.Y. High-resolution ellipsometric study of an n-alkane film, dotriacontane, adsorbed on a SiO2 surface. J. Chem. Phys. 2002, 116, 2107–2115. [Google Scholar] [CrossRef] [Green Version]
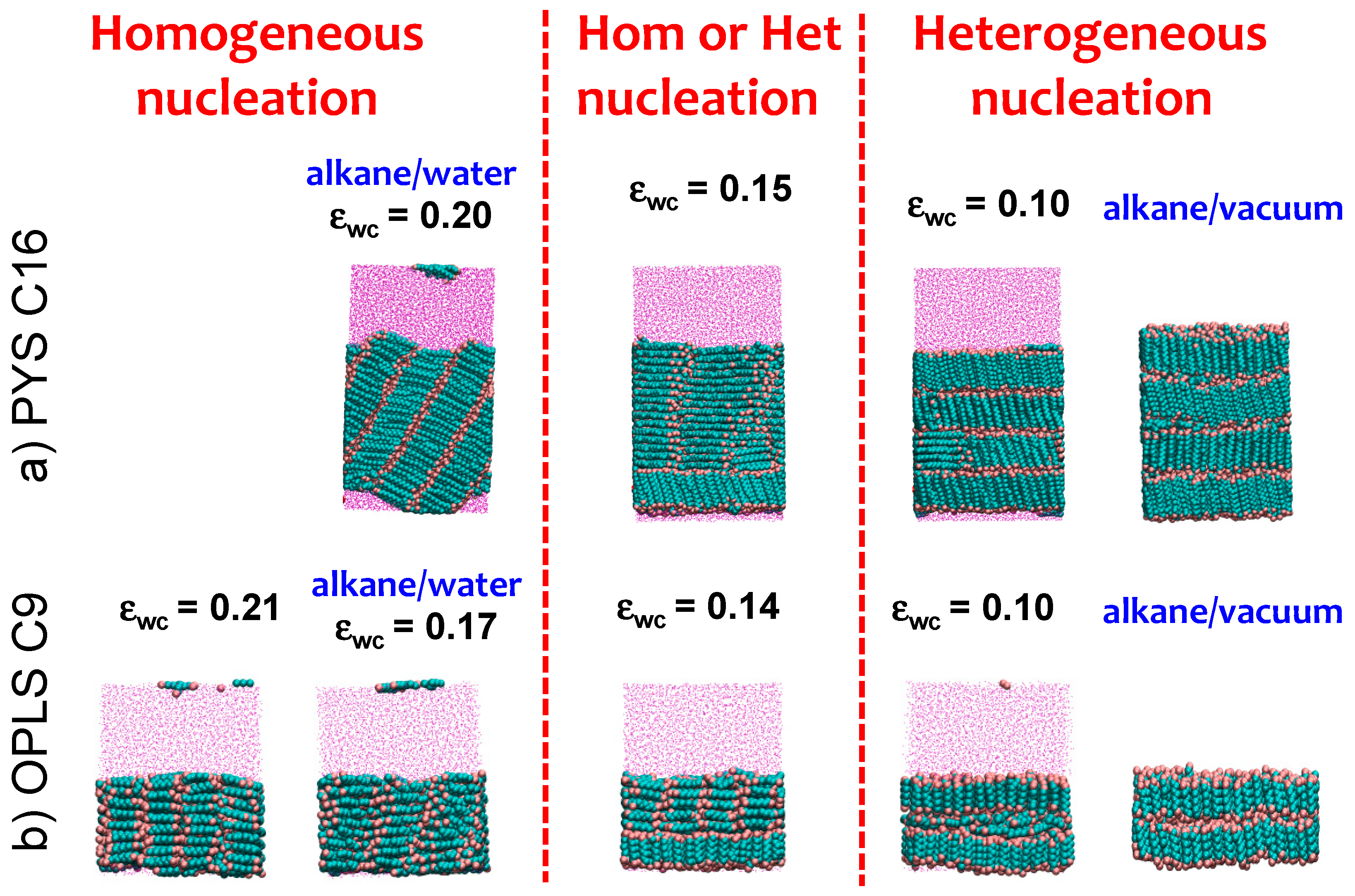
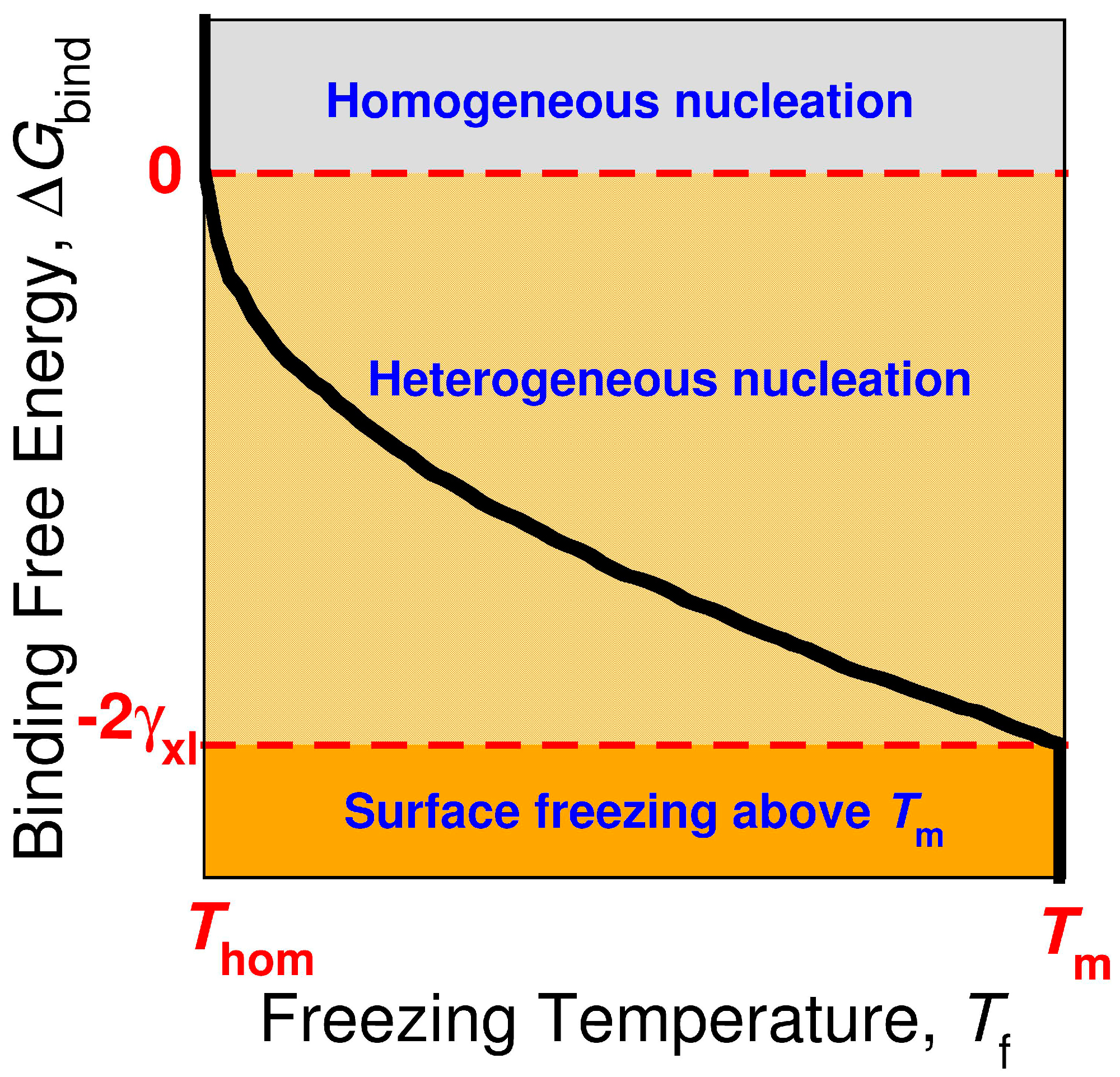
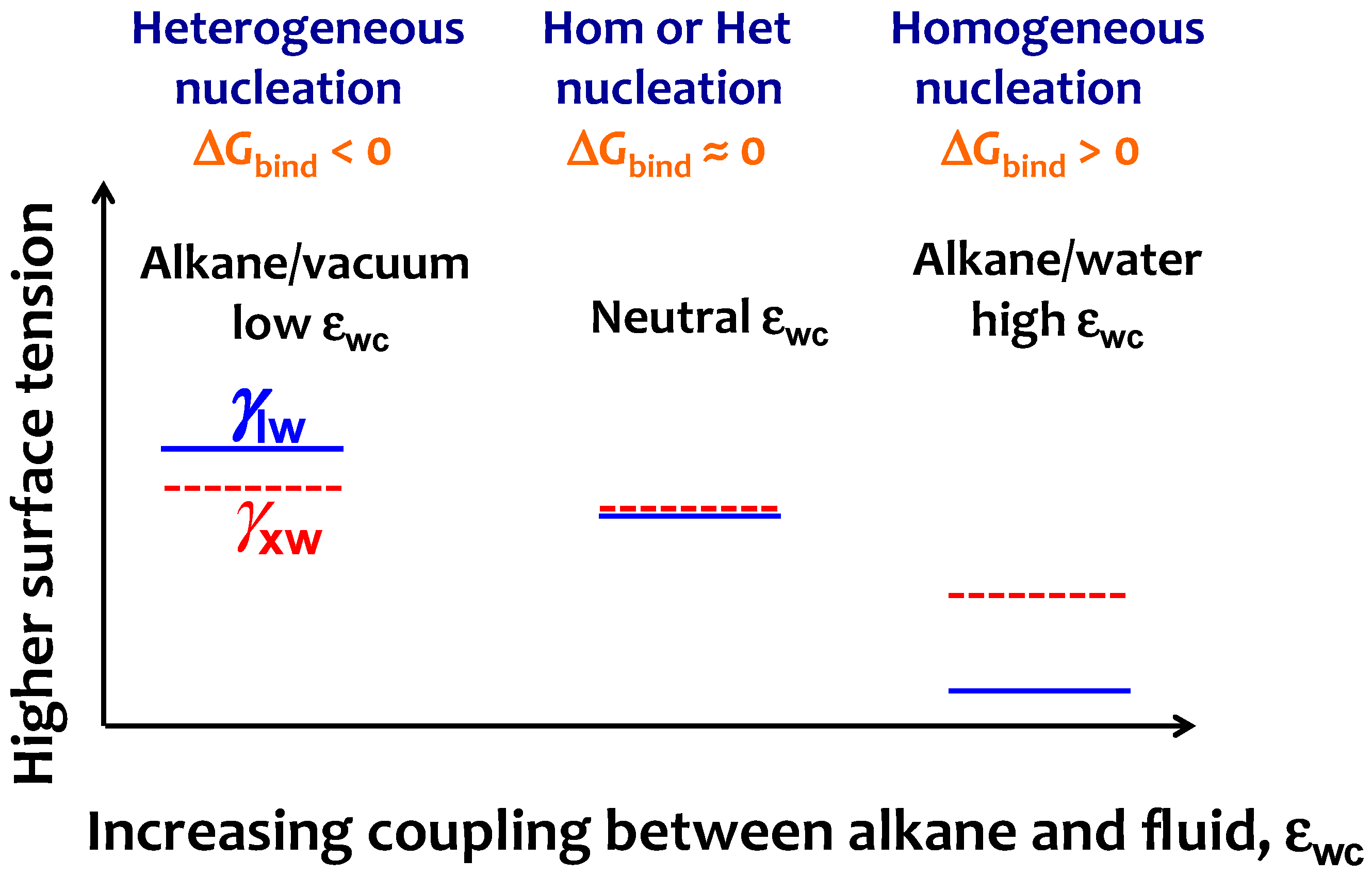
| Alkane | Tm (K) a | Exp. Tm (K) | γlv (mJ·m−2) | Exp. γlv (mJ·m−2) | γlw (mJ·m−2) | Exp. γlw (mJ·m−2) |
|---|---|---|---|---|---|---|
| Nonane | 219 ± 2 | 219.5 ± 0.5 b | 14 ± 1 c | 22.70 e | 54 ± 1 c | 52.4 e |
| Hexadecane | 289 ± 2 | 291 ± 1 b | 18 ± 1 d | 26.26 f | 55 ± 1 c | 55.2 e |
| Eicosane | 309 ± 2 | 310 ± 1 b | 19 ± 1 d | 27.62 f | 58 ± 1 c | 56.7 g |
| Nonane Model | Tm (K) | γlv (mJ·m−2) | ΔHvap (kcal·mol−1) | ΔHm (kcal·mol−1) | ΔSm (cal K−1·mol−1) |
|---|---|---|---|---|---|
| OPLS | 307 ± 2 a | 23 ± 1 c | 12.70 e | 4.25 g | 13.9 |
| PYS | 219 ± 2 a | 14 ± 1 c | 11.19 e | 3.50 h | 15.9 |
| Experiment | 219.5 ± 0.5 b | 22.7 d | 11.16 f | 3.59 i | 16.4 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qiu, Y.; Molinero, V. Strength of Alkane–Fluid Attraction Determines the Interfacial Orientation of Liquid Alkanes and Their Crystallization through Heterogeneous or Homogeneous Mechanisms. Crystals 2017, 7, 86. https://doi.org/10.3390/cryst7030086
Qiu Y, Molinero V. Strength of Alkane–Fluid Attraction Determines the Interfacial Orientation of Liquid Alkanes and Their Crystallization through Heterogeneous or Homogeneous Mechanisms. Crystals. 2017; 7(3):86. https://doi.org/10.3390/cryst7030086
Chicago/Turabian StyleQiu, Yuqing, and Valeria Molinero. 2017. "Strength of Alkane–Fluid Attraction Determines the Interfacial Orientation of Liquid Alkanes and Their Crystallization through Heterogeneous or Homogeneous Mechanisms" Crystals 7, no. 3: 86. https://doi.org/10.3390/cryst7030086
APA StyleQiu, Y., & Molinero, V. (2017). Strength of Alkane–Fluid Attraction Determines the Interfacial Orientation of Liquid Alkanes and Their Crystallization through Heterogeneous or Homogeneous Mechanisms. Crystals, 7(3), 86. https://doi.org/10.3390/cryst7030086





