In Silico Prediction of Growth and Dissolution Rates for Organic Molecular Crystals: A Multiscale Approach
Abstract
:1. Introduction
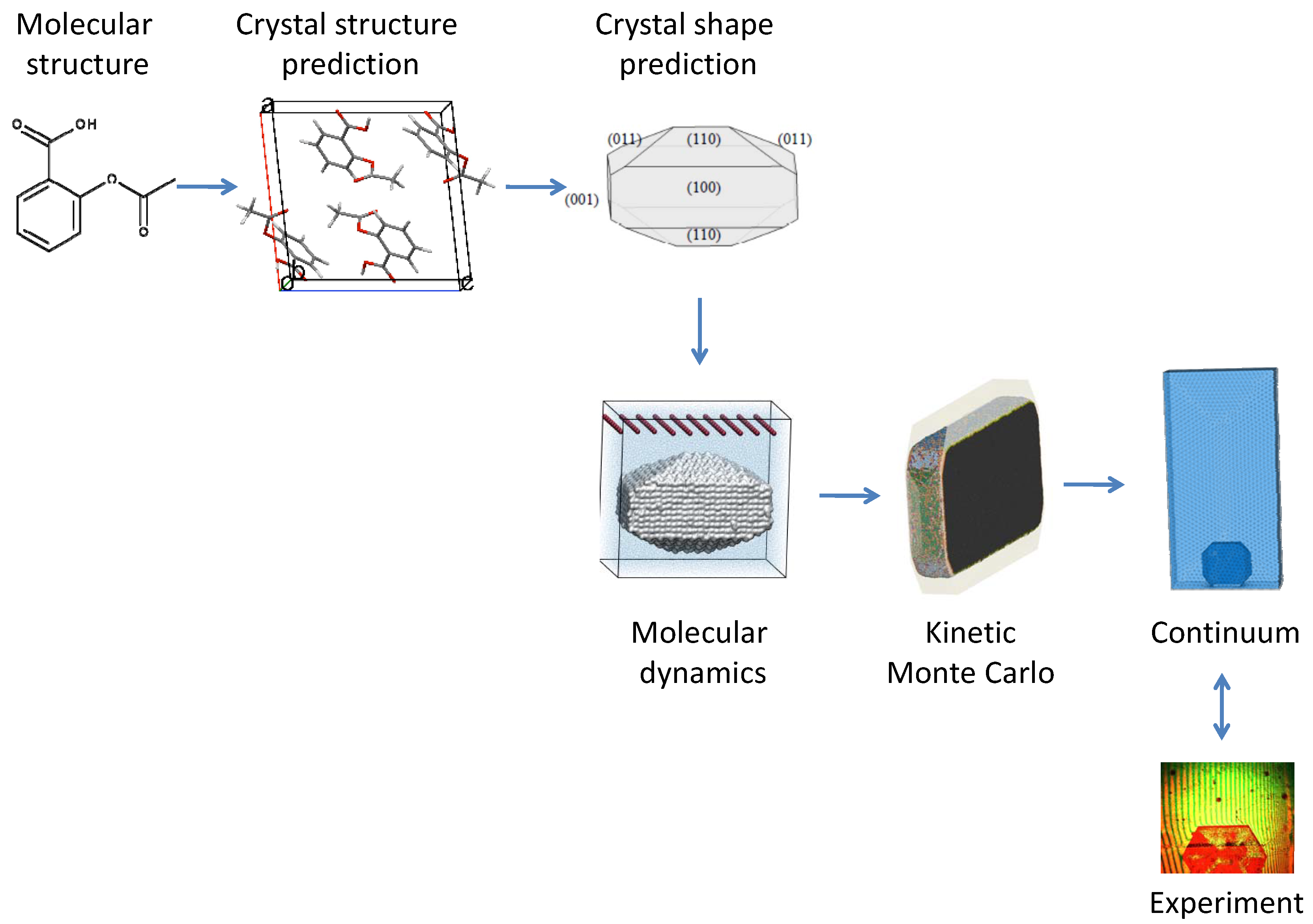
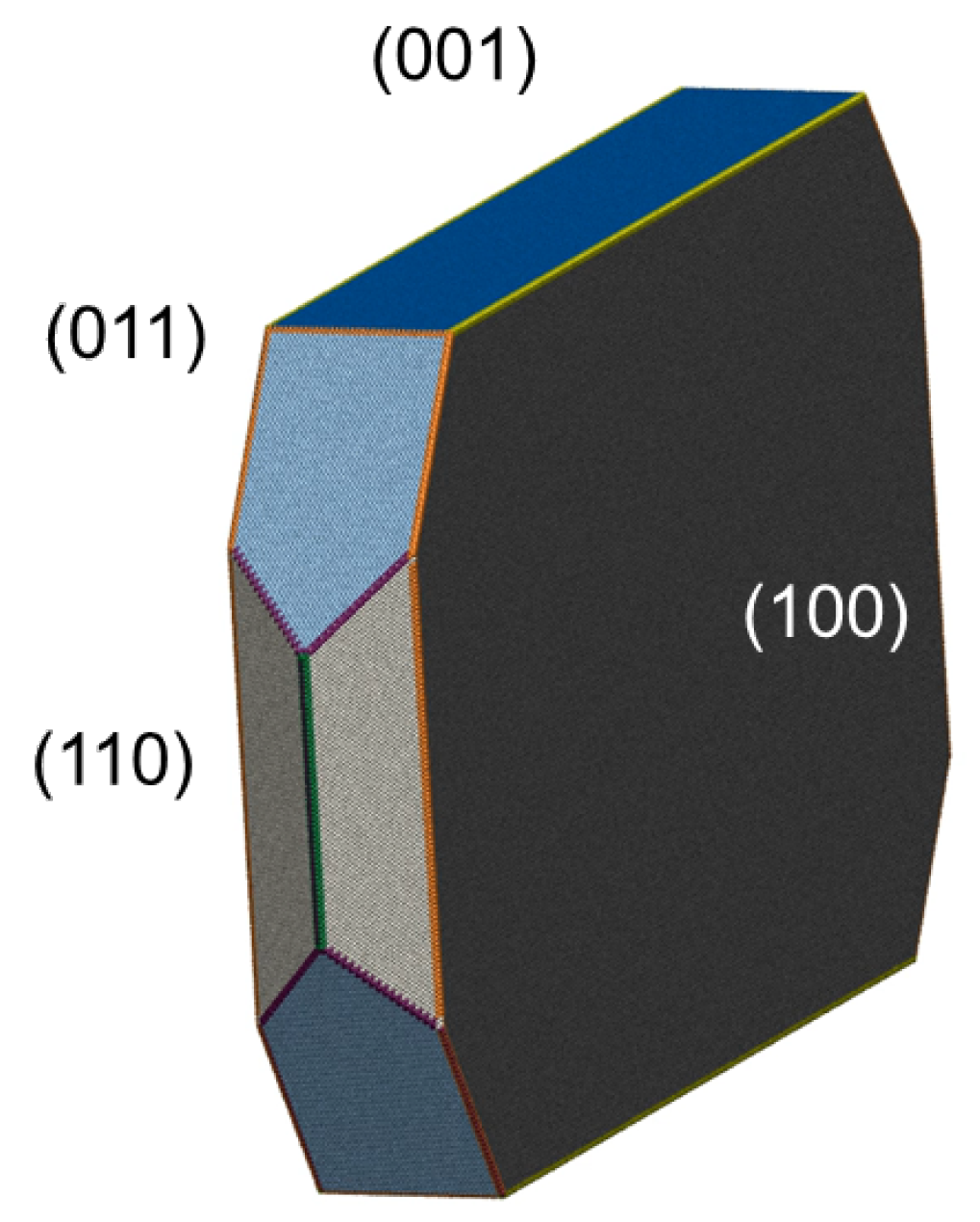
2. Crystal Structure and Shape Prediction
3. MD Simulations
3.1. Choosing the Force Field
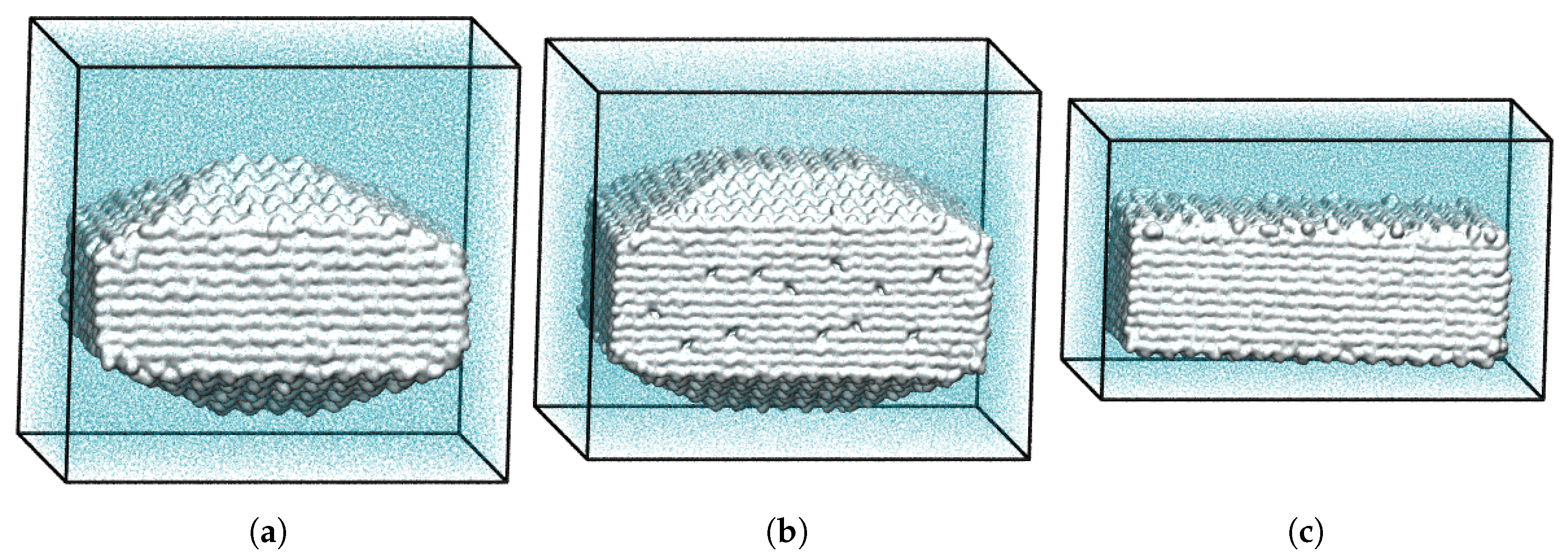
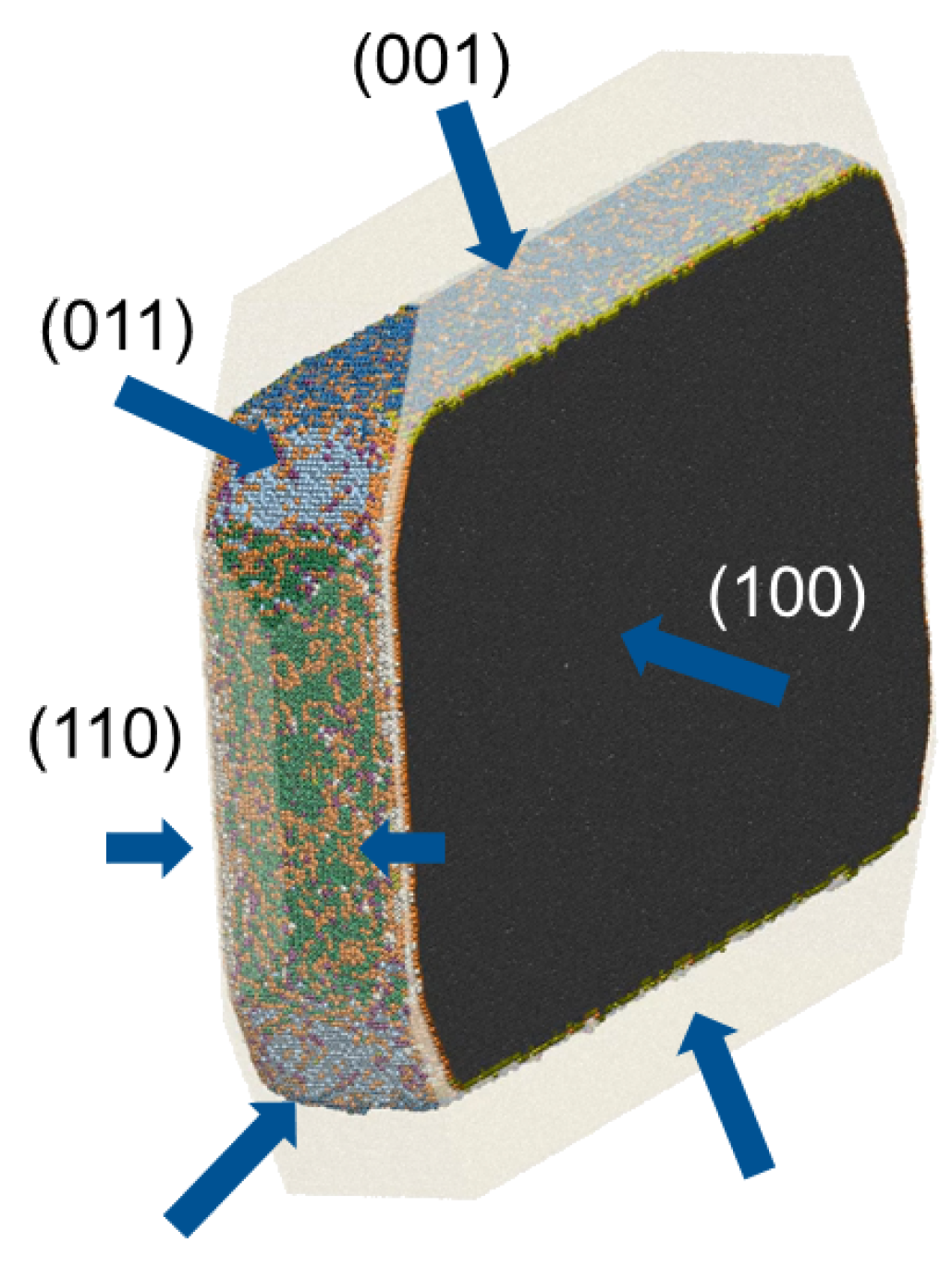
3.2. Superiority of Three-Dimensional over Two-Dimensional Dissolution Simulations
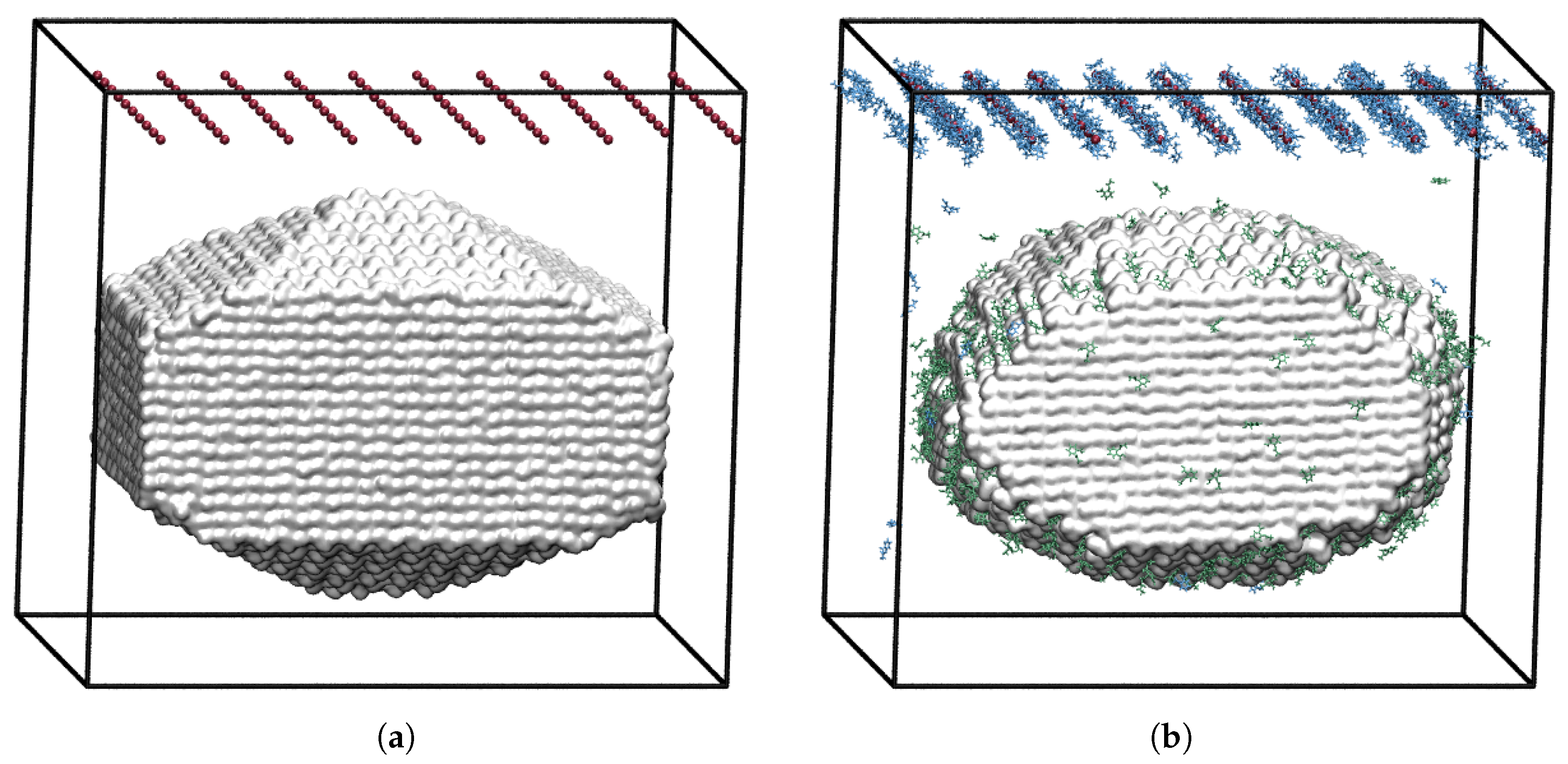
3.3. Constant Chemical Potential
4. Linking Nanoscale and Microscale
5. Kinetic Monte Carlo Simulations
6. Coupling Molecular and Continuum Domains
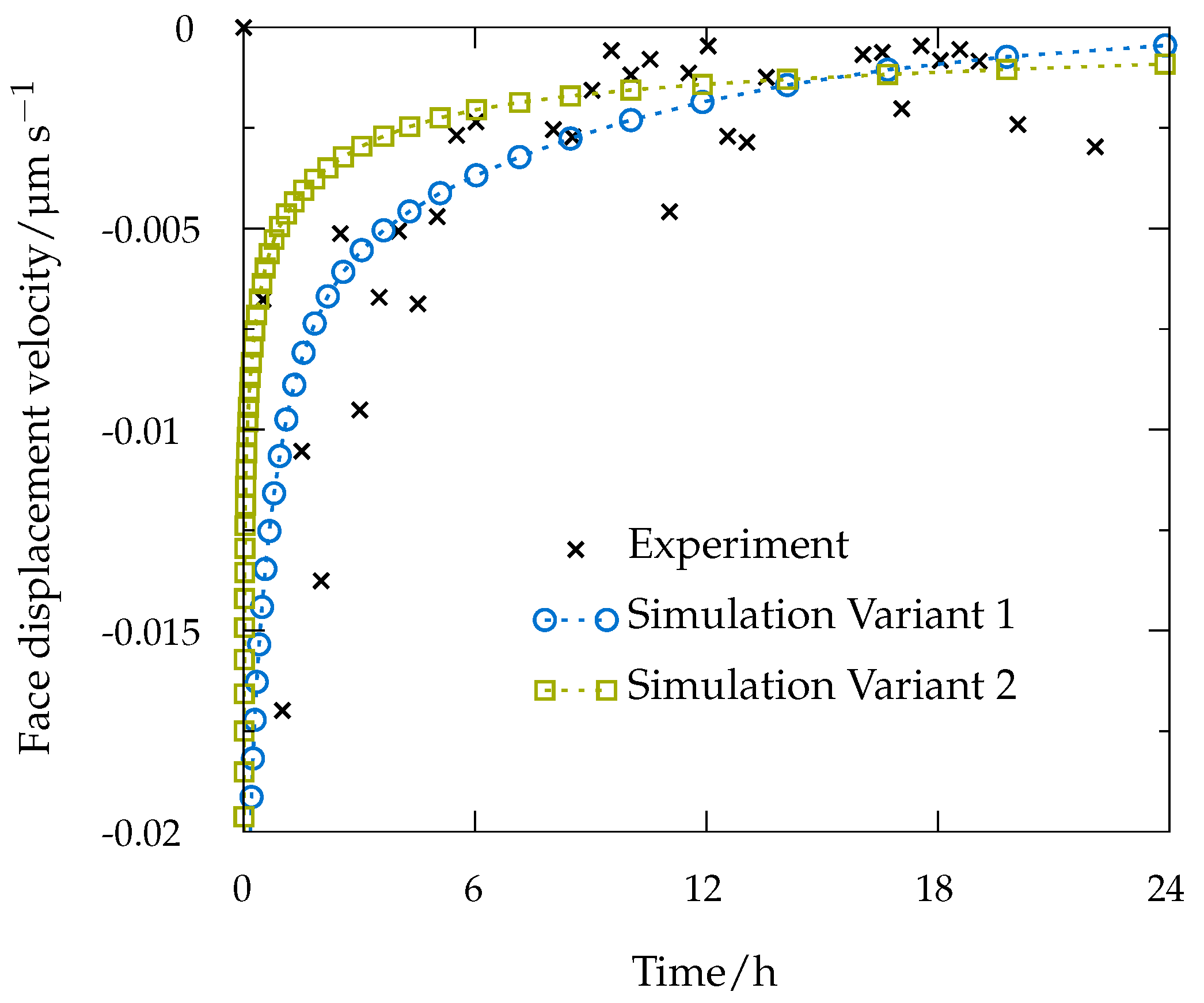
7. Continuum Simulations and Results
8. Conclusions and Outlook
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Weeks, J.; Gilmer, G.H. Advances in Chemical Physics; Chapter Dynamics of Crystal Growth; John Wiley and Sons, Inc.: Hoboken, NJ, USA, 2007; Volume 40, pp. 157–228. [Google Scholar]
- Dhanaraj, G.; Byrappa, K.; Prasad, V.; Dudley, M. (Eds.) Springer Handbook of Crystal Growth; Springer: Heidelberg, Germany, 2010. [Google Scholar]
- Nishinaga, T. (Ed.) Handbook of Crystal Growth. Fundamentals: Thermodynamics and Kinetics; Elsevier: Amsterdam, The Netherland, 2014. [Google Scholar]
- Mullin, J. Crystallization: Third Edition; Butterworth-Heinemann: London, UK, 1997. [Google Scholar]
- Hurle, D. (Ed.) Handbook of Crystal Growth; Fundamentals. (a): Thermodynamics and Kinetics; (b): Transport and Stability; North Holland Elsevier Science Publishers: Amsterdam, The Netherlands, 1993; Volume 1. [Google Scholar]
- Dove, P.; Han, N. Kinetics of Mineral Dissolution and Growth as Reciprocal Microscopic Surface Processes Across Chemical Driving Force. Perspectives on Inorganic, Organic and Biological Crystal Growth: From Fundamentals to Applications Directions. Am. Inst. Phys. Conf. Ser. 2007, 916, 215–234. [Google Scholar]
- Clark, J.N.; Ihli, J.; Schenk, A.S.; Kim, Y.Y.; Kulak, A.N.; Campbell, J.M.; Nisbet, G.; Meldrum, F.C.; Robinson, I.K. Three-Dimensional Imaging of Dislocation Propagation During Crystal Growth and Dissolution. Nat. Mater. 2015, 14, 780–784. [Google Scholar] [CrossRef] [PubMed]
- Veesler, S.; Puel, F. Handbook of Crystal Growth. Fundamentals: Thermodynamics and Kinetics; Part A, Chapter Crystallization of Pharmaceutical Crystals; Elsevier: Amsterdam, The Netherland, 2014; Volume I, pp. 915–951. [Google Scholar]
- Derby, J.J.; Chelikowsky, J.R.; Sinno, T.; Dai, B.; Kwon, Y.I.; Lun, L.; Pandy, A.; Yeckel, A. Large-Scale Numerical Modeling of Melt and Solution Crystal Growth. AIP Conf. Proc. 2007, 916, 139–158. [Google Scholar]
- Allen, M.P.; Tildesley, D.J. Computer Simulation of Liquids; Oxford University Press Inc.: New York, NY, USA, 1989. [Google Scholar]
- Piana, S.; Gale, J.D. Understanding the Barriers to Crystal Growth: Dynamical Simulation of the Dissolution and Growth of Urea from Aqueous Solution. J. Am. Chem. Soc. 2005, 127, 1975–1982. [Google Scholar] [CrossRef] [PubMed]
- Salvalaglio, M.; Vetter, T.; Giberti, F.; Mazzotti, M.; Parrinello, M. Uncovering Molecular Details of Urea Crystal Growth in the Presence of Additives. J. Am. Chem. Soc. 2012, 134, 17221–17233. [Google Scholar] [CrossRef] [PubMed]
- Salvalaglio, M.; Vetter, T.; Mazzotti, M.; Parrinello, M. Controlling and Predicting Crystal Shapes: The Case of Urea. Angew. Chem. Int. Ed. 2013, 52, 13369–13372. [Google Scholar] [CrossRef] [PubMed]
- Banerjee, S.; Briesen, H. Molecular dynamics simulations of glycine crystal-solution interface. J. Chem. Phys. 2009, 131, 184705. [Google Scholar] [CrossRef] [PubMed]
- Gnanasambandam, S.; Rajagopalan, R. Growth Morphology of α-Glycine Crystals in Solution Environments: An Extended Interface Structure Analysis. CrystEngComm 2010, 12, 1740–1749. [Google Scholar] [CrossRef]
- Cheong, D.W.; Boon, Y.D. Comparative Study of Force Fields for Molecular Dynamics Simulations of α-Glycine Crystal Growth from Solution. Cryst. Growth Des. 2010, 10, 5146–5158. [Google Scholar] [CrossRef]
- Parks, C.; Koswara, A.; Tung, H.H.; Nere, N.K.; Bordawekar, S.; Nagy, Z.K.; Ramkrishna, D. Nanocrystal Dissolution Kinetics and Solubility Increase Prediction from Molecular Dynamics: The Case of α-, β-, and γ-Glycine. Mol. Pharm. 2017, 14, 1023–1032. [Google Scholar] [CrossRef] [PubMed]
- Volkov, I.; Cieplak, M.; Koplik, J.; Banavar, J.R. Molecular Dynamics Simulations of Crystallization of Hard Spheres. Phys. Rev. E 2002, 66, 061401. [Google Scholar] [CrossRef] [PubMed]
- Lemarchand, C.A. Molecular dynamics simulations of a hard sphere crystal and reaction-like mechanism for homogeneous melting. J. Chem. Phys. 2012, 136, 234505. [Google Scholar] [CrossRef] [PubMed]
- Reilly, A.; Briesen, H. Modeling crystal growth from solution with molecular dynamics simulations: Approaches to transition rate constants. J. Chem. Phys. 2012, 136, 034704. [Google Scholar] [CrossRef] [PubMed]
- Gruhn, T.; Monson, P.A. Molecular dynamics simulations of hard sphere solidification at constant pressure. Phys. Rev. E 2001, 64, 061703. [Google Scholar] [CrossRef] [PubMed]
- Mandal, T.; Huang, W.; Mecca, J.M.; Getchell, A.; Porter, W.W.; Larson, R.G. A framework for multi-scale simulation of crystal growth in the presence of polymers. Soft Matter 2017, 13, 1904–1913. [Google Scholar] [CrossRef] [PubMed]
- Mandal, T.; Marson, R.L.; Larson, R.G. Coarse-grained modeling of crystal growth and polymorphism of a model pharmaceutical molecule. Soft Matter 2016, 12, 8246–8255. [Google Scholar] [CrossRef] [PubMed]
- Ingólfsson, H.I.; Lopez, C.A.; Uusitalo, J.J.; de Jong, D.H.; Gopal, S.M.; Periole, X.; Marrink, S.J. The power of coarse graining in biomolecular simulations. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2014, 4, 225–248. [Google Scholar] [CrossRef] [PubMed]
- Kästner, J. Umbrella sampling. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2011, 1, 932–942. [Google Scholar] [CrossRef]
- Quigley, D.; Rodger, P. A metadynamics-based approach to sampling crystallisation events. Mol. Simul. 2009, 35, 613–623. [Google Scholar] [CrossRef]
- Allen, R.J.; Valeriani, C.; ten Wolde, P.R. Forward flux sampling for rare event simulations. J. Phys. Condens. Matter 2009, 21, 463102. [Google Scholar] [CrossRef] [PubMed]
- Sosso, G.C.; Chen, J.; Cox, S.J.; Fitzner, M.; Pedevilla, P.; Zen, A.; Michaelides, A. Crystal Nucleation in Liquids: Open Questions and Future Challenges in Molecular Dynamics Simulations. Chem. Rev. 2016, 116, 7078–7116. [Google Scholar] [CrossRef] [PubMed]
- Dogan, B.; Schneider, J.; Reuter, K. In Silico Prediction of Dissolution Rates of Pharmaceutical Ingredients. Chem. Phys. Lett. 2016, 662, 52–55. [Google Scholar] [CrossRef]
- Schneider, J.; Zheng, C.; Reuter, K. Thermodynamics of Surface Defects at the Aspirin/Water Interface. J. Chem. Phys. 2014, 141, 124702. [Google Scholar] [CrossRef] [PubMed]
- Schneider, J.; Reuter, K. Efficient Calculation of Microscopic Dissolution Rate Constants: The Aspirin-Water Interface. J. Phys. Chem. Lett. 2014, 5, 3859–3862. [Google Scholar] [CrossRef] [PubMed]
- Burton, W.K.; Cabrera, N.; Frank, F.C. The Growth of Crystals and the Equilibrium Structure of their Surfaces. Philos. Trans. R. Soc. 1951, 243, 299–358. [Google Scholar] [CrossRef]
- Piana, S.; Reyhani, M.; Gale, J.D. Simulating micrometre-scale crystal growth from solution. Nature 2005, 483, 70–73. [Google Scholar] [CrossRef] [PubMed]
- Reilly, A.; Briesen, H. A detailed kinetic Monte Carlo study of growth from solution using MD-derived rate constants. J. Cryst. Growth 2012, 354, 34–43. [Google Scholar] [CrossRef]
- Piana, S.; Gale, J.D. Three-dimensional kinetic Monte Carlo simulation of crystal growth from solution. J. Cryst. Growth 2006, 294, 46–52. [Google Scholar] [CrossRef]
- Kurganskaya, I.; Luttge, A. Kinetic Monte Carlo Simulations of Silicate Dissolution: Model Complexity and Parametrization. J. Phys. Chem. C 2013, 117, 24894–24906. [Google Scholar] [CrossRef]
- Stack, A.G.; Raiteri, P.; Gale, J.D. Accurate Rates of the Complex Mechanisms for Growth and Dissolution of Minerals Using a Combination of Rare-Event Theories. J. Am. Chem. Soc. 2012, 134, 11–14. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.C.; Reischl, B.; Spijker, P.; Holmberg, N.; Laasonen, K.; Foster, A.S. Ab initio Kinetic Monte Carlo simulations of dissolution at the NaCl-water interface. Phys. Chem. Chem. Phys. 2014, 16, 22545–22554. [Google Scholar] [CrossRef] [PubMed]
- Dkhissi, A.; Estéve, A.; Mastail, C.; Olivier, S.; Mazaleyrat, G.; Jeloaica, L.; Rouhani, M.D. Multiscale Modeling of the Atomic Layer Deposition of HfO2 Thin Film Grown on Silicon: How to Deal with a Kinetic Monte Carlo Procedure. J. Chem. Theory Comput. 2008, 4, 1915–1927. [Google Scholar] [CrossRef] [PubMed]
- Elts, E.; Greiner, M.; Briesen, H. Predicting Dissolution Kinetics for Active Pharmaceutical Ingredients on the Basis of Their Molecular Structures. Cryst. Growth Des. 2016, 16, 4154–4164. [Google Scholar] [CrossRef]
- Boetker, J.P.; Rantanen, J.; Rades, T.; Müllertz, A.; Østergaard, J.; Jensen, H. A New Approach to Dissolution Testing by UV Imaging and Finite Element Simulations. Pharm. Res. 2013, 30, 1328–1337. [Google Scholar] [CrossRef] [PubMed]
- Haddish-Berhane, N.; Nyquist, C.; Haghighi, K.; Corvalan, C.; Keshavarzian, A.; Campanella, O.; Rickus, J.; Farhadi, A. A multi-scale stochastic drug release model for polymer-coated targeted drug delivery systems. J. Control. Release 2006, 110, 314–322. [Google Scholar] [CrossRef] [PubMed]
- Bai, G.; Armenante, P.M. Hydrodynamic, mass transfer, and dissolution effects induced by tablet location during dissolution testing. J. Pharm. Sci. 2009, 98, 1511–1531. [Google Scholar] [CrossRef] [PubMed]
- Lamberti, G.; Galdi, I.; Barba, A.A. Controlled release from hydrogel-based solid matrices. A model accounting for water up-take, swelling and erosion. Int. J. Pharm. 2011, 407, 78–86. [Google Scholar] [CrossRef] [PubMed]
- D’Arcy, D.M.; Healy, A.M.; Corrigan, O.I. Towards determining appropriate hydrodynamic conditions for in vitro in vivo correlations using computational fluid dynamics. Eur. J. Pharm. Sci. 2009, 37, 291–299. [Google Scholar] [CrossRef] [PubMed]
- Boetker, J.; Raijada, D.; Aho, J.; Khorasani, M.; Søgaard, S.V.; Arnfast, L.; Bohr, A.; Edinger, M.; Water, J.J.; Rantanen, J. In silico product design of pharmaceuticals. Asian J. Pharm. Sci. 2016, 11, 492–499. [Google Scholar] [CrossRef]
- Kindgen, S.; Rach, R.; Nawroth, T.; Abrahamsson, B.; Langguth, P. A Novel Disintegration Tester for Solid Dosage Forms Enabling Adjustable Hydrodynamics. J. Pharm. Sci. 2016, 105, 2402–2409. [Google Scholar] [CrossRef] [PubMed]
- Haddish-Berhane, N.; Rickus, J.L.; Haghighi, K. The role of multiscale computational approaches for rational design of conventional and nanoparticle oral drug delivery systems. Int. J. Nanomed. 2007, 2, 315–331. [Google Scholar]
- Greiner, M.; Elts, E.; Schneider, J.; Reuter, K.; Briesen, H. Dissolution study of active pharmaceutical ingredients using molecular dynamics simulations with classical force fields. J. Cryst. Growth 2014, 405, 122–130. [Google Scholar] [CrossRef]
- Greiner, M.; Elts, E.; Briesen, H. Insights into Pharmaceutical Nanocrystal Dissolution: A Molecular Dynamics Simulation Study on Aspirin. Mol. Pharm. 2014, 11, 3009–3016. [Google Scholar] [CrossRef] [PubMed]
- Elts, E.; Greiner, M.; Briesen, H. Data Filtering for Effective Analysis of Crystal-Solution Interface Molecular Dynamics Simulations. J. Chem. Theory Comput. 2014, 10, 1686–1697. [Google Scholar] [CrossRef] [PubMed]
- Greiner, M.; Choscz, C.; Eder, C.; Elts, E.; Briesen, H. Multiscale modeling of aspirin dissolution: From molecular resolution to experimental scales of time and size. CrystEngComm 2016, 18, 5302–5312. [Google Scholar] [CrossRef]
- Eder, C.; Choscz, C.; Müller, V.; Briesen, H. Jamin-interferometer-setup for the determination of concentration and temperature dependent face-specific crystal growth rates from a single experiment. J. Cryst. Growth 2015, 426, 255–264. [Google Scholar] [CrossRef]
- Sundaralingam, M.; Jensen, L.H. Refinement of the structure of salicylic acid. Acta Crystallogr. 1965, 18, 1053–1058. [Google Scholar] [CrossRef] [PubMed]
- Payne, R.S.; Rowe, R.C.; Roberts, R.J.; Charlton, M.H.; Docherty, R. Potential polymorphs of aspirin. J. Comput. Chem. 1999, 20, 262–273. [Google Scholar] [CrossRef]
- Bond, A.; Boese, R.; Desiraju, G. On the Polymorphism of Aspirin: Crystalline Aspirin as Intergrowths of Two “Polymorphic” Domains. Angew. Chem. Int. Ed. 2007, 46, 618–622. [Google Scholar] [CrossRef] [PubMed]
- Hammond, R.B.; Pencheva, K.; Ramachandran, V.; Roberts, K.J. Application of Grid-Based Molecular Methods for Modeling Solvent-Dependent Crystal Growth Morphology: Aspirin Crystallized from Aqueous Ethanolic Solution. Cryst. Growth Des. 2007, 7, 1571–1574. [Google Scholar] [CrossRef]
- Hammond, R.B.; Pencheva, K.; Roberts, K.J. A Structural-Kinetic Approach to Model Face-Specific Solution/Crystal Surface Energy Associated with the Crystallization of Acetyl Salicylic Acid from Supersaturated Aqueous/Ethanol Solution. Cryst. Growth Des. 2006, 6, 1324–1334. [Google Scholar] [CrossRef]
- Kim, Y.; Matsumoto, M.; Machida, K. Specific Surface Energies and Dissolution Behavior of Aspirin Crystal. Chem. Pharm. Bull. 1985, 33, 4125–4131. [Google Scholar] [CrossRef]
- Danesh, A.; Connell, S.D.; Davies, M.C.; Roberts, C.J.; Tendler, S.J.B.; Williams, P.M.; Wilkins, M.J. An in situ dissolution study of aspirin crystal planes (100) and (001) by atomic force microscopy. Pharm. Res. 2001, 18, 299–303. [Google Scholar] [CrossRef] [PubMed]
- Woodley, S.M.; Catlow, R. Crystal structure prediction from first principles. Nat. Mater. 2008, 7, 937–946. [Google Scholar] [CrossRef] [PubMed]
- Day, G. Computational Pharmaceutical Solid State Chemistry; Chapter Advances in Crystal Structure Prediction and Applications to Pharmaceutical Materials; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2016; pp. 87–115. ISBN 978-1-11-870068-6. [Google Scholar]
- Price, S. Predicting crystal structures of organic compounds. Chem. Soc. Rev. 2014, 43, 2098–2111. [Google Scholar] [CrossRef] [PubMed]
- Reilly, A.M.; Cooper, R.I.; Adjiman, C.S.; Bhattacharya, S.; Boese, A.D.; Brandenburg, J.G.; Bygrave, P.J.; Bylsma, R.; Campbell, J.E.; Car, R.; et al. Report on the Sixth Blind Test of Organic Crystal-Structure Prediction Methods. Acta Crystallogr. Sect. B 2016, 72, 439–459. [Google Scholar] [CrossRef] [PubMed]
- Thompson, H.P.; Day, G.M. Which conformations make stable crystal structures? Mapping crystalline molecular geometries to the conformational energy landscape. Chem. Sci. 2014, 5, 3173–3182. [Google Scholar] [CrossRef]
- Nývlt, J.; Ulrich, J. Addmixtures in Crystallization; VCH: Weinheim, Germany, 1995. [Google Scholar]
- Wulff, G. Velocity of growth and dissolution of crystal faces. Z. Kristallogr. 1901, 34, 449–530. [Google Scholar]
- Rogal, J.; Reuter, K.; Scheffler, M. Thermodynamic stability of PdO surfaces. Phys. Rev. B 2004, 69, 075421. [Google Scholar] [CrossRef]
- Ouyang, R.; Liu, J.X.; Li, W.X. Atomistic Theory of Ostwald Ripening and Disintegration of Supported Metal Particles under Reaction Conditions. J. Am. Chem. Soc. 2013, 135, 1760–1771. [Google Scholar] [CrossRef] [PubMed]
- Garcia-Mota, M.; Rieger, M.; Reuter, K. Ab Initio Prediction of the Equilibrium Shape of Supported Ag Nanoparticles on α-Al2O3(0001). J. Catal. 2015, 321, 1–6. [Google Scholar] [CrossRef]
- Lovette, M.A.; Robben Browning, A.; Griffin, D.W.; Sizemore, J.P.; Snyder, R.C.; Doherty, M.F. Crystal Shape Engineering. Ind. Eng. Chem. Res. 2008, 47, 9812–9833. [Google Scholar] [CrossRef]
- Kuvadia, Z.B.; Doherty, M.F. Spiral growth model for faceted crystals of non-centrosymmetric organic molecules grown from solution. Cryst. Growth Des. 2011, 11, 2780–2802. [Google Scholar] [CrossRef]
- Mayerson, A.S. (Ed.) Handbook of industrial Crystallization; Butterworth-Heinemann: Newton, MA, USA, 2002. [Google Scholar]
- Bravais, A. Etudes Crystallographiques; Academie des Sciences: Paris, France, 1913. [Google Scholar]
- Friedel, G. Etudes sur la loi de Bravais. Bull. Soc. Fr. Miner. 1907, 30, 326–455. [Google Scholar]
- Donnay, J.D.H.; Harker, D. A new law of crystal morphology extending the law of Bravais. Am. Miner. 1937, 22, 446–467. [Google Scholar]
- Hartman, P.; Bennema, P. The attachment energy as a habit controlling factor. I. Theoretical considerations. J. Cryst. Growth 1980, 49, 145–156. [Google Scholar] [CrossRef]
- Rai, B. (Ed.) Molecular Modeling for the Design of Novel Performance Chemicals and Materials; CRC Press: Boca Raton, FL, USA, 2012. [Google Scholar]
- Li, J.; Doherty, M.F. Steady State Morphologies of Paracetamol Crystal from Different Solvents. Cryst. Growth Des. 2017, 17, 659–670. [Google Scholar] [CrossRef]
- Tilbury, C.J.; Green, D.A.; Marshall, W.J.; Doherty, M.F. Predicting the Effect of Solvent on the Crystal Habit of Small Organic Molecules. Cryst. Growth Des. 2016, 16, 2590–2604. [Google Scholar] [CrossRef]
- Shim, H.M.; Koo, K.K. Prediction of Growth Habit of β-Cyclotetramethylene-tetranitramine Crystals by the First-Principles Models. Cryst. Growth Des. 2015, 15, 3983–3991. [Google Scholar] [CrossRef]
- Zhang, C.; Ji, C.; Li, H.; Zhou, Y.; Xu, J.; Xu, R.; Li, J.; Luo, Y. Occupancy Model for Predicting the Crystal Morphologies Influenced by Solvents and Temperature, and Its Application to Nitroamine Explosives. Cryst. Growth. Des. 2013, 13, 282–290. [Google Scholar] [CrossRef]
- Yang, X.; Qian, G.; Zhang, X.; Duan, X.; Zhou, X. Effects of Solvent and Impurities on Crystal Morphology of Zinc Lactate Trihydrate. Chin. J. Chem. Eng. 2014, 22, 221–226. [Google Scholar] [CrossRef]
- Wilson, C.C. Interesting proton behaviour in molecular structures. Variable temperature neutron diffraction and ab initio study of acetylsalicylic acid: Characterising librational motions and comparing protons in different hydrogen bonding potentials. New J. Chem. 2002, 26, 1733–1739. [Google Scholar] [CrossRef]
- MacKerell, A.D.; Bashford, D.; Bellott, M.; Dunbrack, R.; Evanseck, J.D.; Field, M.J.; Fischer, S.; Gao, J.; Guo, H.; Ha, S.; et al. All-atom empirical potential for molecular modeling and dynamics studies of proteins. J. Phys. Chem. B 1998, 102, 3586–3616. [Google Scholar] [CrossRef] [PubMed]
- Hornak, V.; Abel, R.; Okur, A.; Strockbine, B.; Roitberg, A.; Simmerling, C. Comparison of Multiple Amber Force Fields and Development of Improved Protein Backbone Parameters. Proteins Struct. Funct. Bioinf. 2006, 65, 712–725. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.M.; Wolf, R.M.; Caldwell, J.W.; Kollman, P.A.; Case, D.A. Development and testing of a general AMBER force field. J. Comput. Chem. 2004, 25, 1157–1174. [Google Scholar] [CrossRef] [PubMed]
- Jorgensen, W.L.; Maxwell, D.S.; Tirado-Rives, J. Development and testing of the OPLS all-atom force field on conformational energetics and properties of organic liquids. J. Am. Chem. Soc. 1996, 118, 11225–11236. [Google Scholar] [CrossRef]
- Zoete, V.; Cuendet, M.A.; Grosdidier, A.; Michielin, O. SwissParam, a Fast Force Field Generation Tool For Small Organic Molecules. J. Comput. Chem. 2011, 32, 2359–2368. [Google Scholar] [CrossRef] [PubMed]
- Halgren, T.A. Merck molecular force field. I. Basis, form, scope, parameterization, and performance of MMFF94. J. Comput. Chem. 1996, 17, 490–519. [Google Scholar] [CrossRef]
- Da Silva Sousa, A.; Alan, W.; Vranken, W.F. ACPYPE—AnteChamber PYthon Parser interfacE. BMC Res. Notes 2012, 5, 367. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Wang, W.; Kollman, P.A.; Case, D.A. Automatic atom type and bond type perception in molecular mechanical calculations. J. Mol. Graph. Model. 2006, 25, 247–260. [Google Scholar] [CrossRef] [PubMed]
- Schüttelkopf, A.W.; van Aalten, D.M.F. PRODRG: A tool for high-throughput crystallography of protein-ligand complexes. Acta Crystallogr. 2004, 60, 1355–1363. [Google Scholar] [CrossRef] [PubMed]
- Oostenbrink, C.; Villa, A.; Mark, A.E.; van Gunsteren, W.F. A biomolecular force field based on the free enthalpy of hydration and solvation: The GROMOS force-field parameter sets 53A5 and 53A6. J. Comput. Chem. 2004, 25, 1656–1676. [Google Scholar] [CrossRef] [PubMed]
- Lemkul, J.A.; Allen, W.J.; Bevan, D.R. Practical Considerations for Building GROMOS-Compatible Small-Molecule Topologies. J. Chem. Inf. Model. 2010, 50, 2221–2235. [Google Scholar] [CrossRef] [PubMed]
- Hawtin, R.; Quigley, D.; Rodger, P. Gas hydrate nucleation and cage formation at a water/methane interface. Phys. Chem. Chem. Phys. 2008, 10, 4853–4864. [Google Scholar] [CrossRef] [PubMed]
- Liang, S.; Kusalik, P.G. Explorations of gas hydrate crystal growth by molecular simulations. Chem. Phys. Lett. 2010, 494, 123–133. [Google Scholar] [CrossRef]
- Jacobson, L.C.; Matsumoto, M.; Molinero, V. Order parameters for the multistep crystallization of clathrate hydrates. J. Chem. Phys. 2011, 135, 074501. [Google Scholar] [CrossRef] [PubMed]
- Gao, Y.; Olsen, K.W. Molecular Dynamics of Drug Crystal Dissolution: Simulation of Acetaminophen Form I in Water. Mol. Pharm. 2013, 10, 905–917. [Google Scholar] [CrossRef] [PubMed]
- Humphrey, W.; Dalke, A.; Schulten, K. VMD: Visual molecular dynamics. J. Mol. Graph. 1996, 14, 33–38. [Google Scholar] [CrossRef]
- Wen, H.; Li, T.; Morris, K.R.; Park, K. Dissolution Study on Aspirin and α-Glycine Crystals. J. Phys. Chem. B 2004, 108, 11219–11227. [Google Scholar] [CrossRef]
- Wedelkind, J.; Reguera, D.; Strey, R. Finite-size effects in simulations of nucleation. J. Chem. Phys. 2006, 125, 214505. [Google Scholar] [CrossRef] [PubMed]
- Salvalaglio, M.; Mazzotti, M.; Parrinello, M. Urea homogeneous nucleation mechanism is solvent dependent. Faraday Discuss. 2015, 179, 291–307. [Google Scholar] [CrossRef] [PubMed]
- Grossier, R.; Veesler, S. Reaching One Single and Stable Critical Cluster through Finite-Sized Systems. Cryst. Growth Des. 2009, 9, 1917–1922. [Google Scholar] [CrossRef]
- Perego, C.; Salvalaglio, M.; Parrinello, M. Molecular dynamics simulations of solutions at constant chemical potential. J. Chem. Phys. 2015, 142, 144113. [Google Scholar] [CrossRef] [PubMed]
- Zimmermann, N.E.R.; Vorselaars, B.; Quigley, D.; Peters, B. Nucleation of NaCl from Aqueous Solution: Critical Sizes, Ion-Attachment Kinetics, and Rates. J. Am. Chem. Soc. 2015, 137, 13352–13361. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Anwar, J.; Zahn, D. Uncovering Molecular Processes in Crystal Nucleation and Growth by Using Molecular Simulation. Angew. Chem. Int. Ed. 2011, 50, 1996–2013. [Google Scholar] [CrossRef] [PubMed]
- Steinhardt, P.J.; Nelson, D.R.; Ronchetti, M. Bond-orientational order in liquids and glasses. Phys. Rev. B 1983, 28, 784–805. [Google Scholar] [CrossRef]
- Lechner, W.; Dellago, C. Accurate determination of crystal structures based on averaged local bond order parameters. J. Chem. Phys. 2008, 129, 114707. [Google Scholar] [CrossRef] [PubMed]
- Radhakrishnan, R.; Trout, B.L. Nucleation of Hexagonal Ice (Ih) in Liquid Water. J. Am. Chem. Soc. 2003, 125, 7743–7747. [Google Scholar] [CrossRef] [PubMed]
- Brukhno, A.; Anwar, J.; Davidchack, R.; Handel, R. Challenges in molecular simulation of homogeneous ice nucleation. J. Phys. Condens. Matter 2008, 20, 494243. [Google Scholar] [CrossRef]
- Leyssale, J.M.; Delhommelle, J.; Millot, C. Reorganization and Growth of Metastable α-N2 Critical Nuclei into Stable β-N2 Crystals. J. Am. Chem. Soc. 2004, 126, 12286–12287. [Google Scholar] [CrossRef] [PubMed]
- Mettes, J.A.; Keith, J.B.; McClurg, R.B. Molecular crystal global phase diagrams. I. Method of construction. Acta Crystallogr. Sect. A Found. Crystallogr. 2004, 60, 621–636. [Google Scholar] [CrossRef] [PubMed]
- Zahn, D. Atomistic Mechanisms of Phase Separation and Formation of Solid Solutions: Model Studies of NaCl, NaCl-NaF, and Na(Cl1−xBrx) Crystallization from Melt. J. Phys. Chem. B 2007, 111, 5249–5253. [Google Scholar] [CrossRef] [PubMed]
- Xu, S.; Bartell, L. Analysis of Orientational Order in Molecular Clusters. A Molecular Dynamics Study. J. Phys. Chem. 1993, 97, 13544–13549. [Google Scholar] [CrossRef]
- Kinney, K.E.; Xu, S.; Bartell, L.S. Molecular Dynamics Study of the Freezing of Clusters of Chalcogen Hexafluorides. J. Phys. Chem. 1996, 100, 6935–6941. [Google Scholar] [CrossRef]
- Santiso, E.E.; Trout, B.L. A general set of order parameters for molecular crystals. J. Chem. Phys. 2011, 134, 064109. [Google Scholar] [CrossRef] [PubMed]
- Reuter, K. First-Principles Kinetic Monte Carlo Simulations for Heterogeneous Catalysis: Concepts, Status, and Frontiers. In Modeling and Simulation of Heterogeneous Catalytic Reactions: From the Molecular Process to the Technical System; Deutschmann, O., Ed.; Wiley-VCH: Weinheim, Germany, 2011; pp. 71–111. [Google Scholar]
- Kalman, R.E. A New Approach to Linear Filtering and Prediction Problems. J. Basic Eng. 1960, 82, 35–45. [Google Scholar] [CrossRef]
- Bortz, A.B.; Kalos, M.H.; Lebowitz, J.L. A new algorithm for Monte Carlo simulation of Ising spin systems. J. Comput. Phys. 1975, 17, 10–18. [Google Scholar] [CrossRef]
- Chatterjee, A.; Vlachos, D. An overview of spatial microscopic and accelerated kinetic Monte Carlo methods. J. Comput. Aided Mater. Des. 2007, 14, 253–308. [Google Scholar] [CrossRef]
- Burghaus, U.; Stephan, J.; Vattuone, L.; Rogowska, J. A Practical Guide to Kinetic Monte Carlo Simulations and Classical Molecular Dynamics Simulations; Nova Science Publishers, Inc.: New York, NY, USA, 2006. [Google Scholar]
- Comsol AB. COMSOL Multiphysics User’S Guide; Comsol AB: Stockholm, Sweden, 2014. [Google Scholar]
- Edwards, L.J. The Dissolution and Diffusion of Aspirin In Aqueous Media. Trans. Faraday Soc. 1951, 47, 1191–1210. [Google Scholar] [CrossRef]
- Klamt, A. Conductor-like Screening Model for Real Solvent: A New Approach to the Quantitative Calculation of Solvation Phenomena. J. Phys. Chem. A 1995, 99, 2224–2235. [Google Scholar] [CrossRef]
- Espinosa, J.R.; Young, J.M.; Jiang, H.; Gupta, D.; Vega, C.; Sanz, E.; Debenedetti, P.G.; Panagiotopoulos, A.Z. On the calculation of solubilities via direct coexistence simulations: Investigation of NaCl aqueous solutions and Lennard-Jones binary mixtures. J. Chem. Phys. 2016, 145, 154111. [Google Scholar] [CrossRef] [PubMed]
- Sugano, K. Theoretical comparison of hydrodynamic diffusion layer models used for dissolution simulation in drug discovery and development. Int. J. Pharm. 2008, 363, 73–77. [Google Scholar] [CrossRef] [PubMed]
- Chakrabarti, S.; Southard, M. Control of Poorly Soluble Drug Dissolution in Conditions Simulating the Gastrointestinal Tract Flow. 1. Effect of Tablet Geometry in Buffered Medium. J. Pharm. Sci. 1996, 85, 313–319. [Google Scholar] [CrossRef] [PubMed]
- Chakrabarti, S.; Southard, M.Z. Control of Poorly Soluble Drug Dissolution in Conditions Simulating the Gastrointestinal Tract Flow. 2. Cocompression of Drugs with Buffers. J. Pharm. Sci. 1997, 86, 465–469. [Google Scholar] [CrossRef] [PubMed]
- Sikarra, D.; Shukla, V.; Kharia, A.; Chatterjee, D. Techniques for solubility enhancement of poorly soluble drugs: An overview. J. Med. Pharm. Allied Sci. 2012, 1, 1–22. [Google Scholar]
- Tiwle, R.; Ajazuddin; Giri, T.; Tripathi, D.; Jain, V.; Alexander, A. An exhaustive review on solubility enhancement for hydrophobic compounds by possible applications of novel techniques. Trends Appl. Sci. Res. 2012, 7, 596–619. [Google Scholar]


© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Elts, E.; Greiner, M.; Briesen, H. In Silico Prediction of Growth and Dissolution Rates for Organic Molecular Crystals: A Multiscale Approach. Crystals 2017, 7, 288. https://doi.org/10.3390/cryst7100288
Elts E, Greiner M, Briesen H. In Silico Prediction of Growth and Dissolution Rates for Organic Molecular Crystals: A Multiscale Approach. Crystals. 2017; 7(10):288. https://doi.org/10.3390/cryst7100288
Chicago/Turabian StyleElts, Ekaterina, Maximilian Greiner, and Heiko Briesen. 2017. "In Silico Prediction of Growth and Dissolution Rates for Organic Molecular Crystals: A Multiscale Approach" Crystals 7, no. 10: 288. https://doi.org/10.3390/cryst7100288





