Epitaxial Graphene and Graphene–Based Devices Studied by Electrical Scanning Probe Microscopy
Abstract
:1. Introduction
2. Results and Discussion
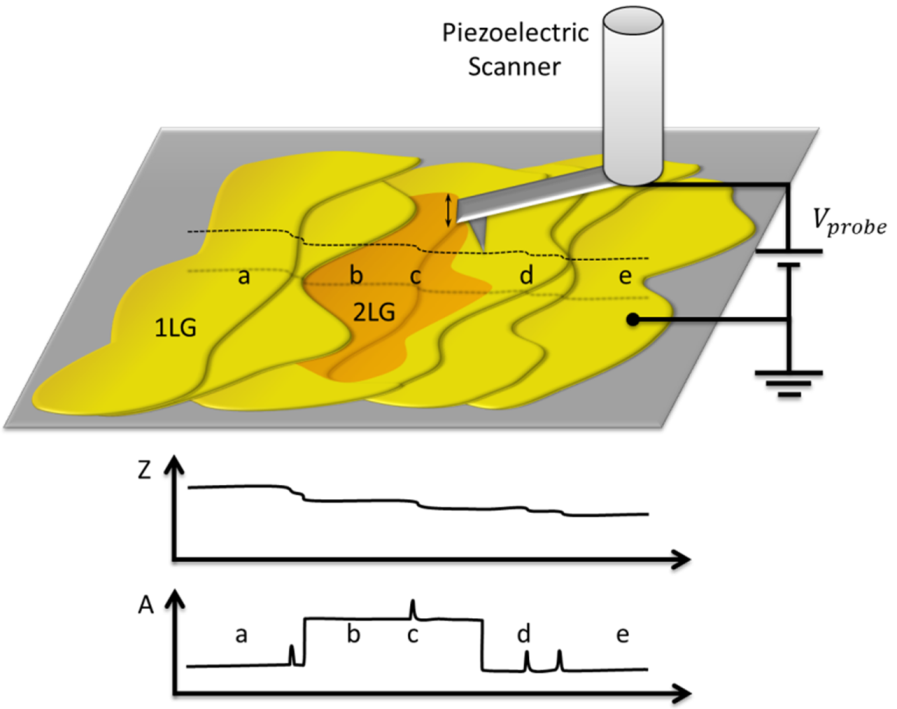
2.1. Identification of Epitaxial Graphene Domains Using Quantified Topography Images
2.1.1. Models and Method
| Graphene layers | Model used | Step height (nm) |
|---|---|---|
| 1 LG−2 LG | Filleter et al. [22] | −0.915, −0.665, −0.415, −0.165, +0.085, +0.335, +0.585, +0.835, +1.085 |
| 1 LG−2 LG | Hass et al. [52] | −0.925, −0.673, −0.421, −0.169, +0.083, +0.335, +0.587, +0.839, +1.092 |
| 1 LG + 0.400 nm−2 LG | Burnett et al. [54] | −1.065, −0.815, −0.565, −0.315, −0.065, +0.185, +0.435, +0.685, +0.935 |
2.1.2. Experimental Results
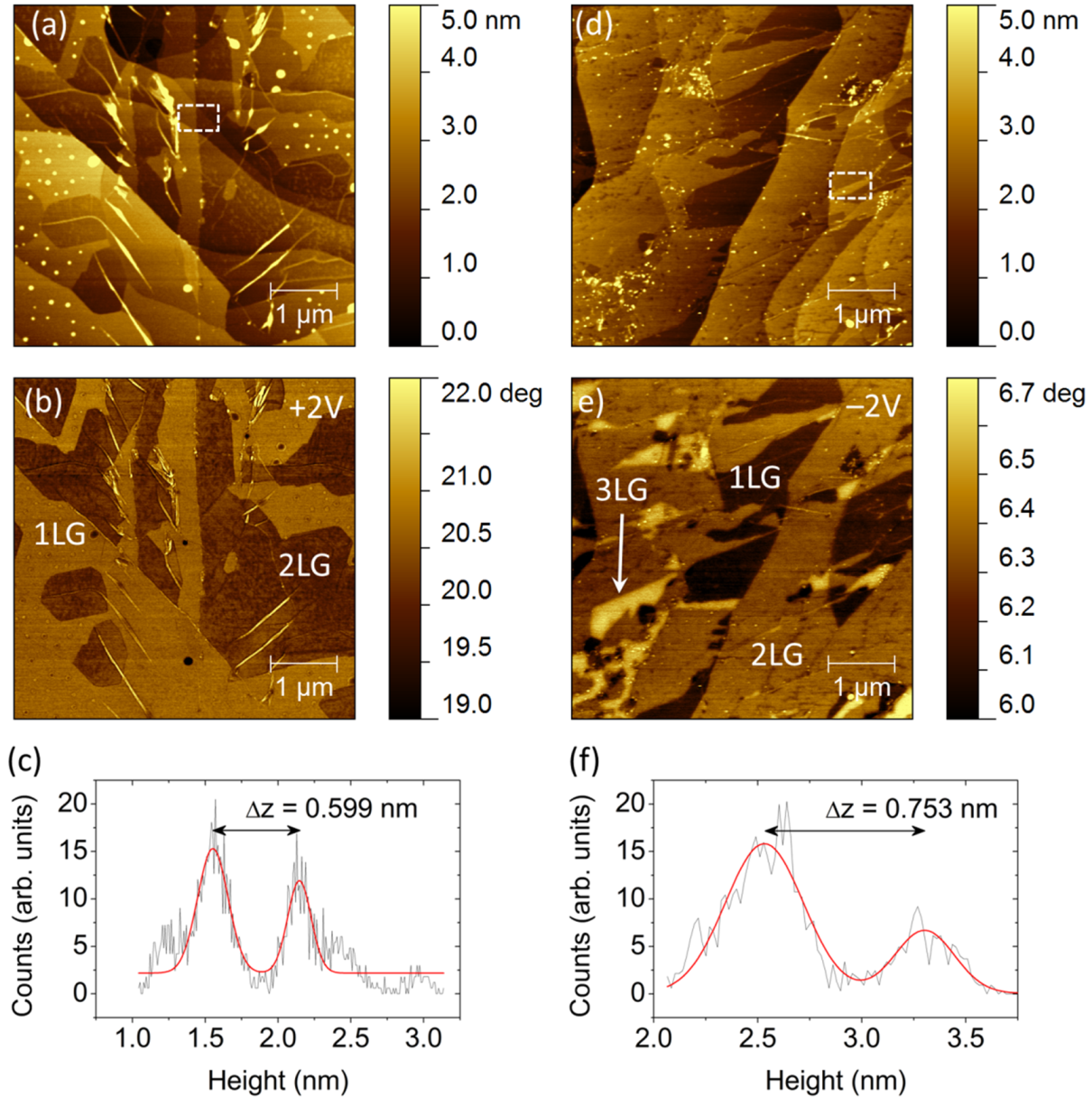
2.2. Mapping of Local Electrical Properties in Epitaxial Graphene
2.2.1. Experimental Results

2.2.2. Discussion
2.2.2.1. Effect of the Substrate on the Electronic Properties of Epitaxial Graphene
2.2.2.2. Effects of Structural Defects and Strain
2.2.2.3. Influence of Adsorbates
2.3. Wettability of Epitaxial Graphene and Effect of Atmospheric Water
2.3.1. Case of Epitaxial Graphene on Si-Face SiC
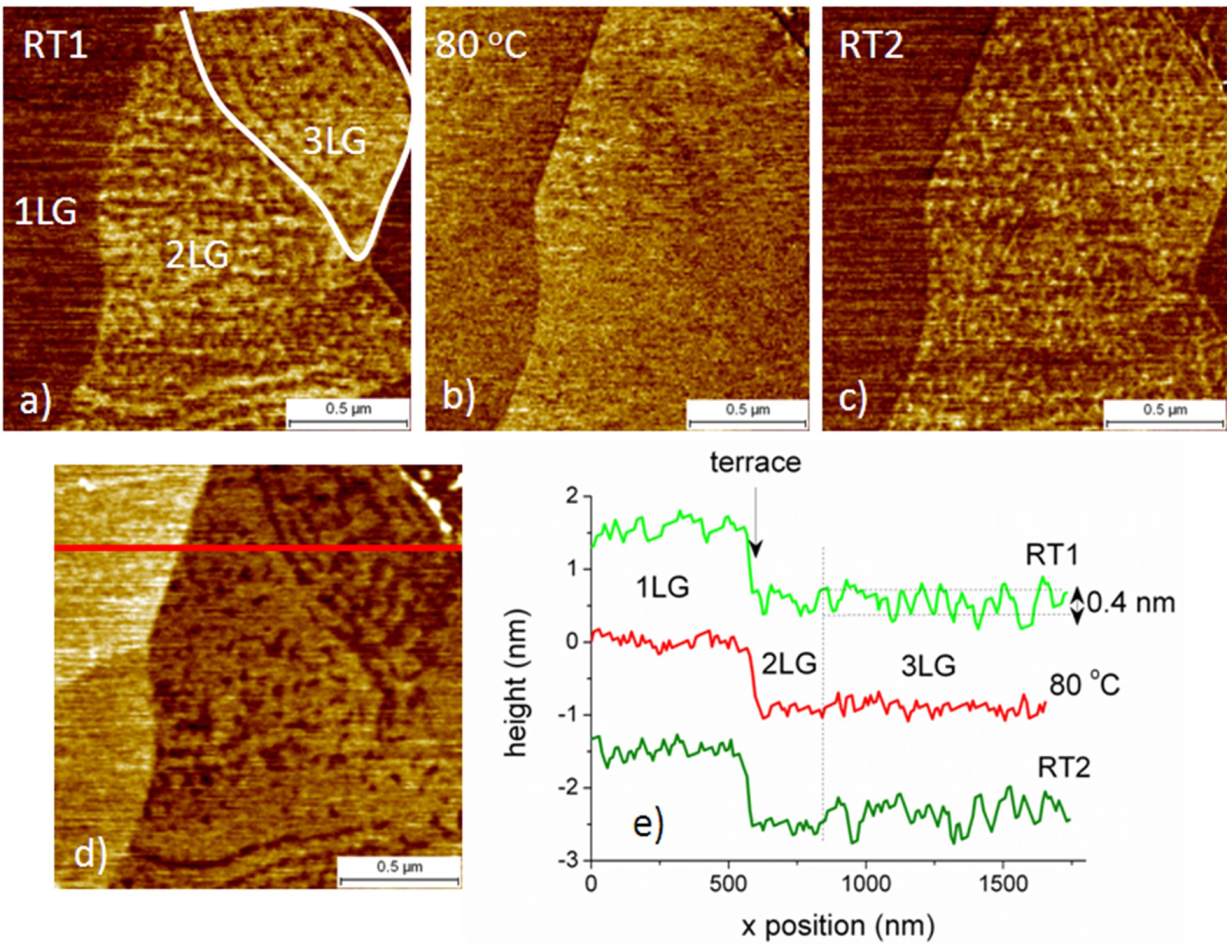

2.3.2. Case of Epitaxial Graphene on C-Face SiC
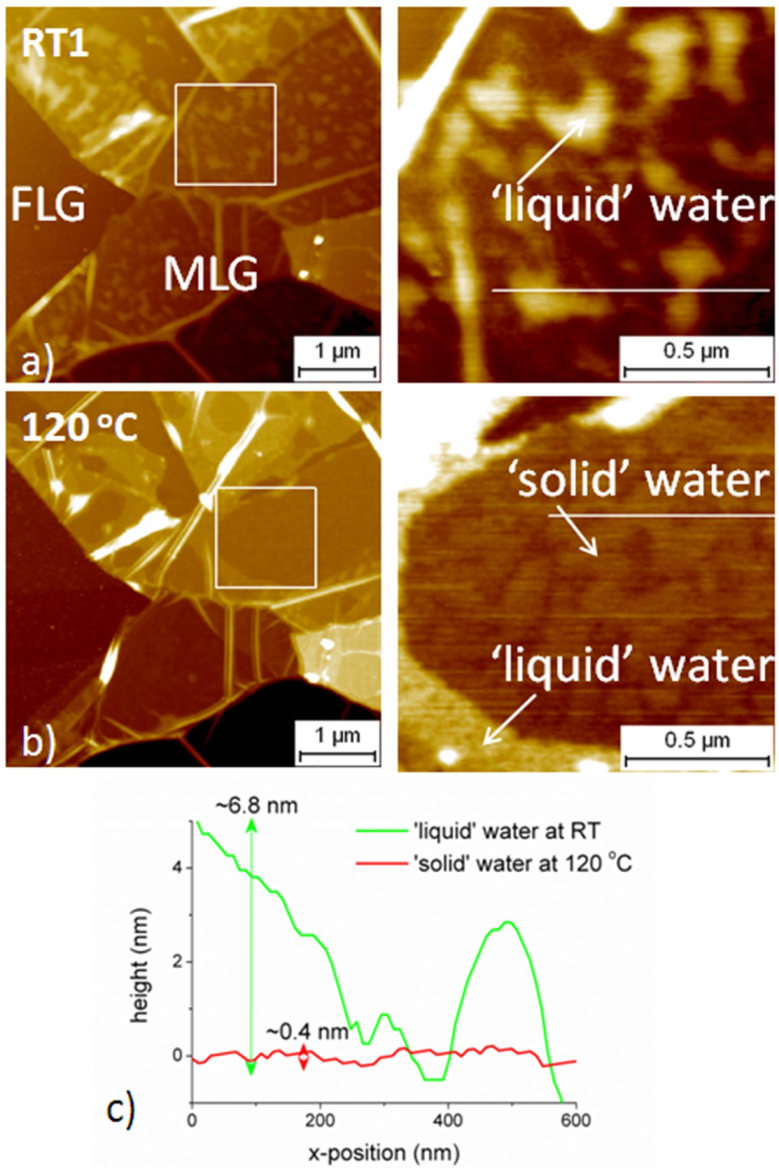


2.3.3. Discussion
2.4. Electrical SPM for Studies of Graphene Devices

2.4.1. Influence of External Conditions

| State of Device #3a | R4 (kΩ) | RH (Ω T−1) | n (cm−2) | μ (cm2 V−1 s−1) |
|---|---|---|---|---|
| With residue | 26 | –945 | nh = 6.61 × 1011 | μh = 1449 |
| Cleaned | 6 | +250 | ne = 2.55 × 1012 | μe = 1673 |
| Cleaned + 5 days | 33 | +1332 | ne = 4.71 × 1011 | μe = 1616 |
2.4.2. Calibrated Work Functions of p-n Junction
| Device #3b | Carriers | RH (Ω T−1) | n (cm−2) | EF (eV) | Φ (eV) |
|---|---|---|---|---|---|
| Cross 1 (resist residue) | Holes | −250 | nh = 2.50 × 1012 | 0.148 | 4.68 ± 0.05 |
| Cross 2 (cleaned) | Electrons | +535 | ne = 1.17 × 1012 | 0.101 | 4.35 ± 0.05 |
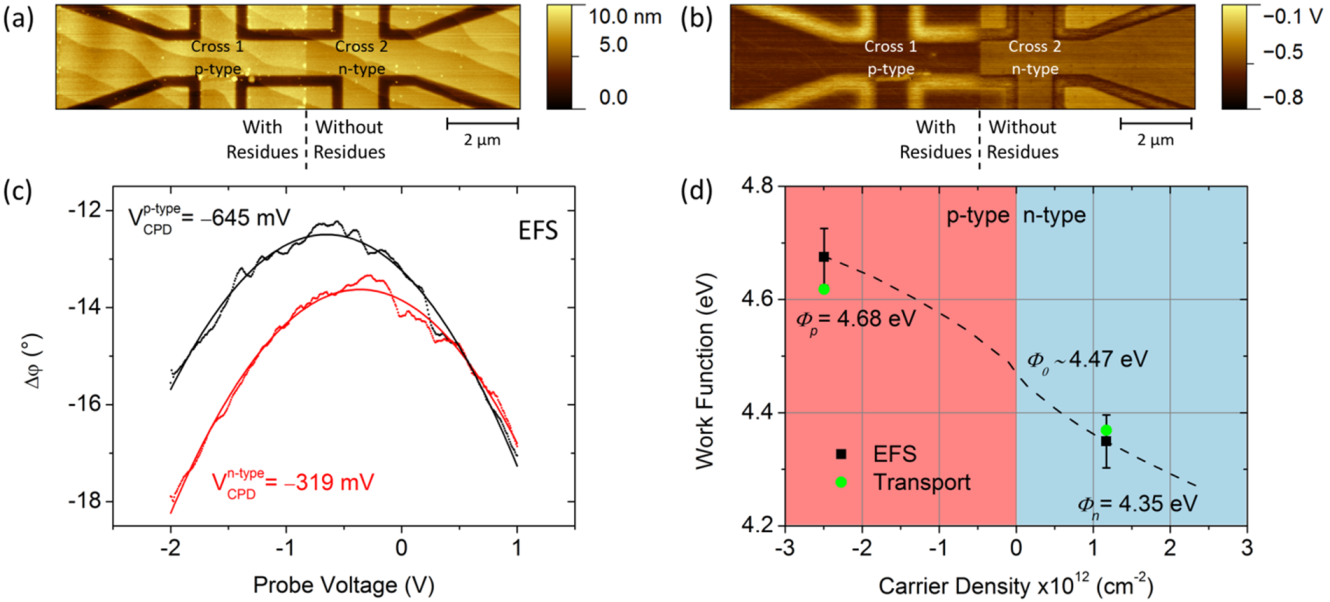
2.4.3. Calibrated Work Functions of Single- and Double-Layer Graphene
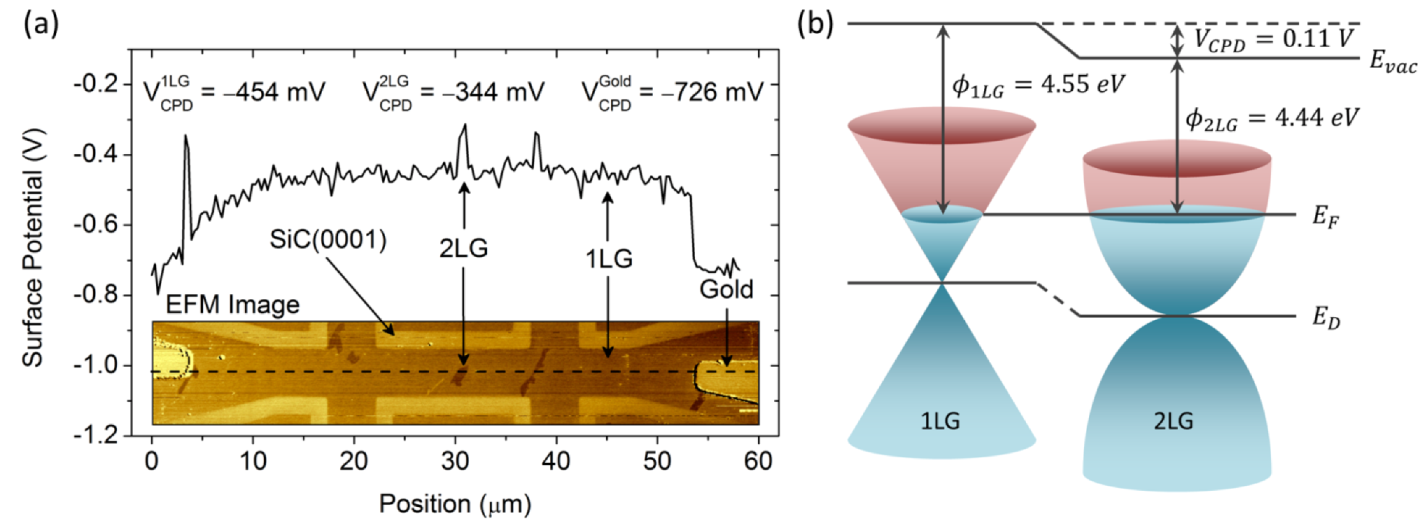
| Substrate | Φ1 LG (eV) | Φ2 LG (eV) | ΔΦ1-2 LG (meV) | Technique | Reference |
|---|---|---|---|---|---|
| 4H-SiC | 4.55 ± 0.02 | 4.44 ± 0.02 | 110 ± 21 | FM-KPFM | Device #4 |
| 4H-SiC | – | – | 15−50 (1) | AM-KPFM | Sample #1 |
| 6H-SiC | – | – | 135 ± 9 | FM-KPFM | [22] |
| 4H-SiC | – | – | 35 | AM-KPFM | [107] |
| Flakes on SiO2 | 4.57 ± 0.05 | 4.69 ± 0.05 | 120 ± 50 | FM-KPFM | [106] |
| Flakes on SiO2 | – | – | 68 | AM-KPFM | [21] |
| Flakes on SrTiO3 | 4.409 ± 0.039 | 4.516 ± 0.035 | 107 ± 36 (2) | FM-KPFM | [108] |
3. Experimental Section
3.1. Atomic Force Microscopy (AFM)
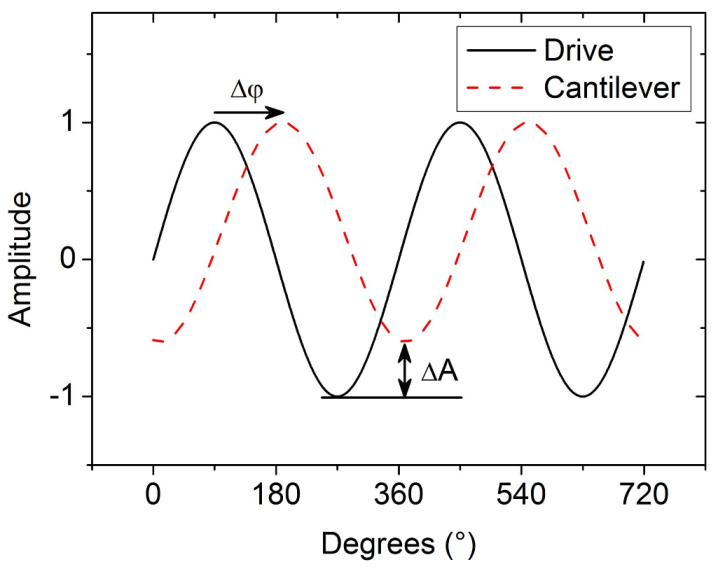
3.2. Electrostatic Force Microscopy (EFM)
 , where C and z are probe-sample capacitance and probe-sample distance [16,111,112]. The voltage V is composed of the contact potential difference (VCPD), the applied DC voltage (Vprobe) and any other externally induced DC voltages related to an operating device (Vinduced), i.e., VCPD + Vprobe + Vinduced. The force related to the DC bias, which deflects the cantilever, is given by
, where C and z are probe-sample capacitance and probe-sample distance [16,111,112]. The voltage V is composed of the contact potential difference (VCPD), the applied DC voltage (Vprobe) and any other externally induced DC voltages related to an operating device (Vinduced), i.e., VCPD + Vprobe + Vinduced. The force related to the DC bias, which deflects the cantilever, is given by
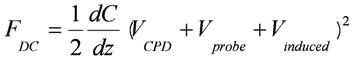
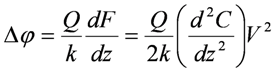
3.3. Electrostatic Force Spectroscopy (EFS)
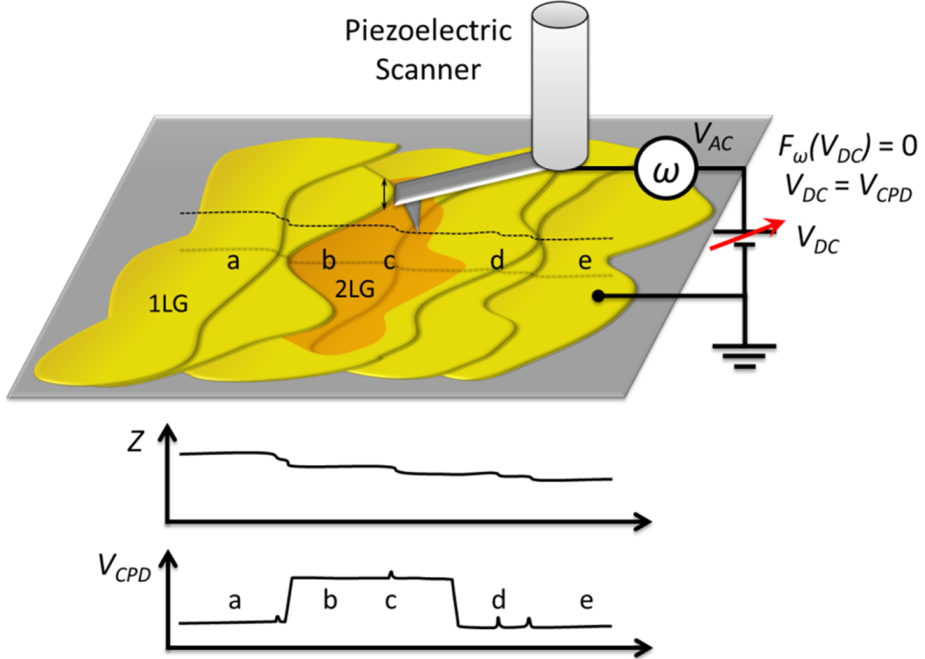
 (i.e., 2 LG is brighter than 1 LG in KPFM images), the Φ1 LG > Φ2 LG.
(i.e., 2 LG is brighter than 1 LG in KPFM images), the Φ1 LG > Φ2 LG.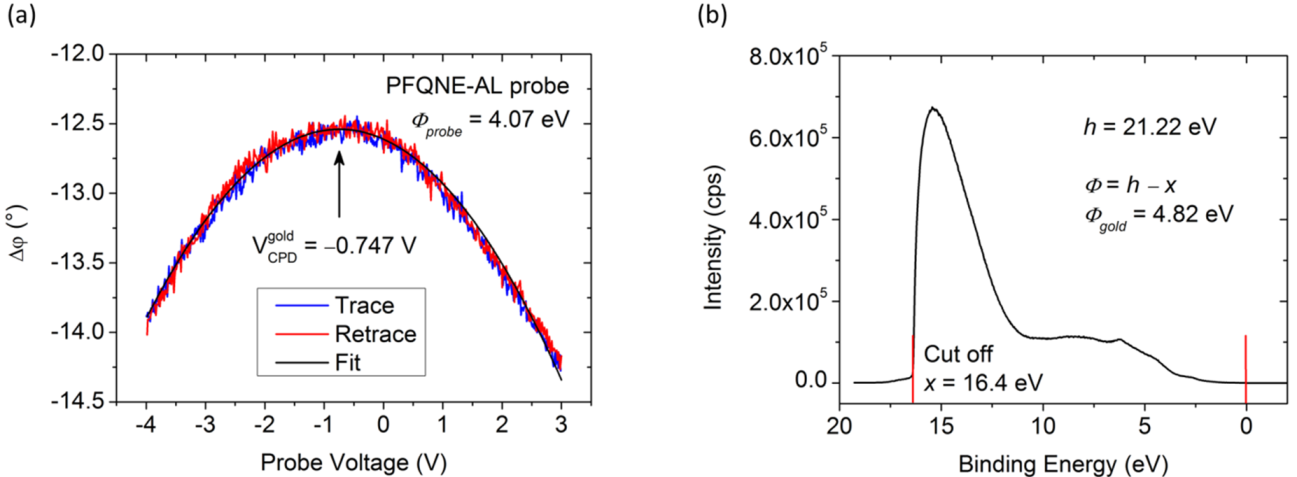
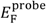 and
and 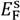 are Fermi energy levels of the probe and gold, respectively. Note: in the case of ground connected to the sample, negative Vprobe is applied to nullify VCPD. Figure is adapted from [114].
are Fermi energy levels of the probe and gold, respectively. Note: in the case of ground connected to the sample, negative Vprobe is applied to nullify VCPD. Figure is adapted from [114].
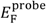 and
and 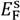 are Fermi energy levels of the probe and gold, respectively. Note: in the case of ground connected to the sample, negative Vprobe is applied to nullify VCPD. Figure is adapted from [114].
are Fermi energy levels of the probe and gold, respectively. Note: in the case of ground connected to the sample, negative Vprobe is applied to nullify VCPD. Figure is adapted from [114]. 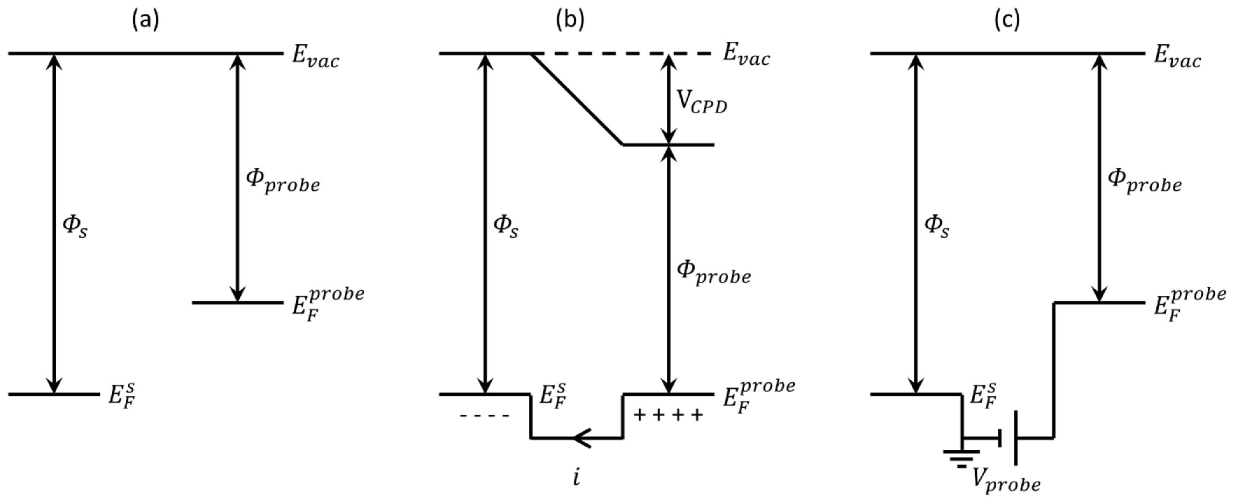
3.4. Amplitude-Modulated Kelvin Probe Force Microscopy (AM-KPFM)
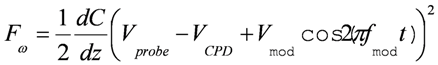
3.5. Frequency-Modulated Kelvin Probe Force Microscopy (FM-KPFM)
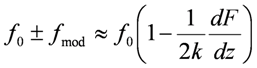

3.6. Environmental Conditions
3.7. Growth of Graphene Films and Raman Spectroscopy Characterization


3.8. Layer Identification
3.9. Device Fabrication
- (1)
- Bonding pads: PMMA/MMA (250 nm) and ZEP520 (200 nm) resist was spin coated and baked on the epitaxial graphene sample followed by EBL to define the bonding pads. The sample was developed in o-Xylene (96%) and H2O/IPA (7:93 ratio) followed by oxygen plasma to etch the graphene. Cr/Au (5/100 nm) was thermally evaporated followed by lift-off in acetone, forming the bonding pads with excellent adhesion to the substrate.
- (2)
- Leads: The leads were defined in similar fashion to step 1, however with the crucial absence of oxygen plasma etching step to ensure good electrical contact to the graphene.
- (3)
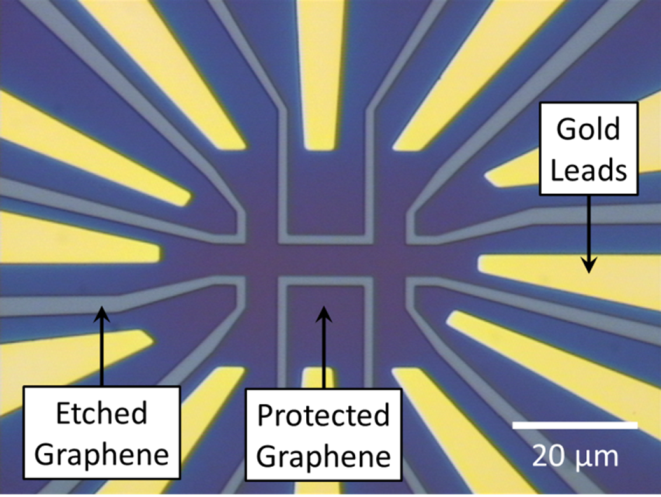
- Hall bars: PMMA/MMA (250 nm) and ZEP520 (200 nm) resist was spin coated and baked on the sample followed by EBL to write the Hall bar pattern in the resist. Developing the sample in o-Xylene (96%) and H2O/IPA (7:93 ratio) exposed the unwanted regions of the graphene while leaving behind the resist in the shape of Hall bars and leads (Figure 20). Oxygen plasma was used to etch away the unwanted graphene, leaving behind only the protected graphene to form devices with the cross width ranging from 0.5 to 5 µm. The remaining resist was exposed to deep UV light (250 nm) and dissolved, leaving behind 1–2 nm thick layers of resist residues.
4. Conclusions
Acknowledgements
Conflict of Interest
References and Notes
- Novoselov, K. Nobel lecture: Graphene: Materials in the flatland. Rev. Mod. Phys. 2011, 83, 837–849. [Google Scholar] [CrossRef]
- Novoselov, K.S.; Fal’ko, V.I.; Colombo, L.; Gellert, P.R.; Schwab, M.G.; Kim, K. A roadmap for graphene. Nature 2012, 490, 192–200. [Google Scholar]
- Tzalenchuk, A.; Lara-Avila, S.; Kalaboukhov, A.; Paolillo, S.; Syväjärvi, M.; Yakimova, R.; Kazakova, O.; Janssen, T.J.B.M.; Fal’ko, V.; Kubatkin, S. Towards a quantum resistance standard based on epitaxial graphene. Nat. Nanotechnol. 2010, 5, 186–189. [Google Scholar]
- Virojanadara, C.; Syväjarvi, M.; Yakimova, R.; Johansson, L.; Zakharov, A.; Balasubramanian, T. Homogeneous large-area graphene layer growth on 6H-SiC(0001). Phys. Rev. B 2008, 78, 245403:1–245403:6. [Google Scholar]
- Lin, Y.-M.; Valdes-Garcia, A.; Han, S.-J.; Farmer, D.B.; Meric, I.; Sun, Y.; Wu, Y.; Dimitrakopoulos, C.; Grill, A.; Avouris, P.; Jenkins, K.A. Wafer-scale graphene integrated circuit. Science 2011, 332, 1294–1297. [Google Scholar] [CrossRef]
- Dimitrakopoulos, C.; Lin, Y.-M.; Grill, A.; Farmer, D.B.; Freitag, M.; Sun, Y.; Han, S.-J.; Chen, Z.; Jenkins, K.A.; Zhu, Y.; Liu, Z.; McArdle, T.J.; Ott, J.A.; Wisnieff, R.; Avouris, P. Wafer-scale epitaxial graphene growth on the Si-face of hexagonal SiC(0001) for high frequency transistors. J. Vac. Sci. Technol. B Microelectron. Nanometer. Struct. 2010, 28, 985–992. [Google Scholar] [CrossRef]
- Moser, J.; Verdaguer, A.; Jiménez, D.; Barreiro, A.; Bachtold, A. The environment of graphene probed by electrostatic force microscopy. Appl. Phys. Lett. 2008, 92, 123507:1–123507:3. [Google Scholar]
- Verdaguer, A.; Cardellach, M.; Segura, J.J.; Sacha, G.M.; Moser, J.; Zdrojek, M.; Bachtold, A.; Fraxedas, J. Charging and discharging of graphene in ambient conditions studied with scanning probe microscopy. Appl. Phys. Lett. 2009, 94, 233105:1–233105:3. [Google Scholar]
- Burnett, T.L.; Patten, J.; Kazakova, O. Water desorption and re-adsorption on epitaxial graphene studied by SPM. Available online: http://arxiv.org/abs/1204.3323 (accessed on 26 February 2013).
- Emtsev, K.V.; Bostwick, A.; Horn, K.; Jobst, J.; Kellogg, G.L.; Ley, L.; McChesney, J.L.; Ohta, T.; Reshanov, S.A.; Röhrl, J.; Rotenberg, E.; Schmid, A.K.; Waldmann, D.; Weber, H.B.; Seyller, T. Towards wafer-size graphene layers by atmospheric pressure graphitization of silicon carbide. Nat. Mater. 2009, 8, 203–207. [Google Scholar] [CrossRef]
- Bolen, M.; Harrison, S.; Biedermann, L.; Capano, M. Graphene formation mechanisms on 4H-SiC(0001). Phys. Rev. B 2009, 80. [Google Scholar]
- Ferrer, F.J.; Moreau, E.; Vignaud, D.; Deresmes, D.; Godey, S.; Wallart, X. Initial stages of graphitization on SiC(000-1), as studied by phase atomic force microscopy. J. Appl. Phys. 2011, 109, 054307:1–054307:6. [Google Scholar]
- Camara, N.; Tiberj, A.; Jouault, B.; Caboni, A.; Jabakhanji, B.; Mestres, N.; Godignon, P.; Camassel, J. Current status of self-organized epitaxial graphene ribbons on the C face of 6H-SiC substrates. J. Phys. D Appl. Phys. 2010, 43, 374011:1–374011:13. [Google Scholar]
- Nonnenmacher, M.; O’Boyle, M.P.; Wickramasinghe, H.K. Kelvin probe force microscopy. Appl. Phys. Lett. 1991, 58, 2921:1–2921:3. [Google Scholar]
- Zerweck, U.; Loppacher, C.; Otto, T.; Grafström, S.; Eng, L. Accuracy and resolution limits of Kelvin probe force microscopy. Phys. Rev. B 2005, 71, 125424:1–125424:9. [Google Scholar]
- Girard, P. Electrostatic force microscopy: Principles and some applications to semiconductors. Nanotechnology 2001, 12, 485–490. [Google Scholar] [CrossRef]
- Panchal, V.; Burnett, T.L.; Pearce, R.; Cedergren, K.; Yakimova, R.; Tzalenchuk, A.; Kazakova, O. Surface potential variations in epitaxial graphene devices investigated by Electrostatic Force Spectroscopy. In Proceeding of12th IEEE Conference on Nanotechnology (IEEE-NANO), Birmingham, UK, 20-23 August 2012.
- Lu, Y.; Muñoz, M.; Steplecaru, C.; Hao, C.; Bai, M.; Garcia, N.; Schindler, K.; Esquinazi, P. Electrostatic Force Microscopy on oriented graphite surfaces: Coexistence of insulating and conducting behaviors. Phys. Rev. Lett. 2006, 97, 076805:1–076805:4. [Google Scholar]
- Datta, S.S.; Strachan, D.R.; Mele, E.J.; Johnson, A.T.C. Surface potentials and layer charge distributions in few-layer graphene films. Nano Lett. 2009, 9, 7–11. [Google Scholar] [CrossRef]
- Burnett, T.; Yakimova, R.; Kazakova, O. Mapping of local electrical properties in epitaxial graphene using electrostatic force microscopy. Nano Lett. 2011, 11, 2324–2328. [Google Scholar] [CrossRef]
- Ziegler, D.; Gava, P.; Güttinger, J.; Molitor, F.; Wirtz, L.; Lazzeri, M.; Saitta, A.; Stemmer, A.; Mauri, F.; Stampfer, C. Variations in the work function of doped single- and few-layer graphene assessed by Kelvin probe force microscopy and density functional theory. Phys. Rev. B 2011, 83, 235434:1–235434:7. [Google Scholar]
- Filleter, T.; Emtsev, K.V.; Seyller, T.; Bennewitz, R. Local work function measurements of epitaxial graphene. Appl. Phys. Lett. 2008, 93, 133117:1–133117:3. [Google Scholar]
- Filleter, T.; McChesney, J.; Bostwick, A.; Rotenberg, E.; Emtsev, K.; Seyller, T.; Horn, K.; Bennewitz, R. Friction and dissipation in epitaxial graphene films. Phys. Rev. Lett. 2009, 102, 086102:1–086102:4. [Google Scholar]
- Curtin, A.E.; Fuhrer, M.S.; Tedesco, J.L.; Myers-Ward, R.L.; Eddy, C.R.; Gaskill, D.K. Kelvin probe microscopy and electronic transport in graphene on SiC(0001) in the minimum conductivity regime. Appl. Phys. Lett. 2011, 98, 243111:1–243111:3. [Google Scholar]
- Xu, K.; Cao, P.; Heath, J.R. Graphene visualizes the first water adlayers on mica at ambient conditions. Science 2010, 329, 1188–1191. [Google Scholar] [CrossRef]
- Shin, Y.J.; Wang, Y.; Huang, H.; Kalon, G.; Wee, A.T.S.; Shen, Z.; Bhatia, C.S.; Yang, H. Surface-energy engineering of graphene. Langmuir 2010, 26, 3798–3802. [Google Scholar]
- Wang, S.; Zhang, Y.; Abidi, N.; Cabrales, L. Wettability and surface free energy of graphene films. Langmuir 2009, 25, 11078–11081. [Google Scholar] [CrossRef]
- Zhou, H.; Ganesh, P.; Presser, V.; Wander, M.; Fenter, P.; Kent, P.; Jiang, D.; Chialvo, A.; McDonough, J.; Shuford, K.; Gogotsi, Y. Understanding controls on interfacial wetting at epitaxial graphene: Experiment and theory. Phys. Rev. B 2012, 85, 035406:1–035406:11. [Google Scholar]
- Rafiee, J.; Mi, X.; Gullapalli, H.; Thomas, A.V.; Yavari, F.; Shi, Y.; Ajayan, P.M.; Koratkar, N.A. Wetting transparency of graphene. Nat. Mater. 2012, 11, 217–222. [Google Scholar] [CrossRef]
- Ferrari, A.C.; Meyer, J.C.; Scardaci, V.; Casiraghi, C.; Lazzeri, M.; Mauri, F.; Piscanec, S.; Jiang, D.; Novoselov, K.S.; Roth, S.; Geim, A.K. Raman spectrum of graphene and graphene layers. Phys. Rev. Lett. 2006, 97, 187401:1–187401:4. [Google Scholar]
- Graf, D.; Molitor, F.; Ensslin, K.; Stampfer, C.; Jungen, A.; Hierold, C.; Wirtz, L. Spatially resolved Raman spectroscopy of single- and few-layer graphene. Nano Lett. 2007, 7, 238–242. [Google Scholar]
- Wang, Y.; Ni, Z.H.; Yu, T.; Shen, Z.X.; Wang, H.M.; Wu, Y.H.; Chen, W.; Shen Wee, A.T. Raman studies of monolayer graphene: The Substrate effect. J. Phys. Chem. C 2008, 112, 10637–10640. [Google Scholar]
- Lazzeri, M.; Attaccalite, C.; Wirtz, L.; Mauri, F. Impact of the electron-electron correlation on phonon dispersion: Failure of LDA and GGA DFT functionals in graphene and graphite. Phys. Rev. B 2008, 78, 081403:1–081403:4. [Google Scholar]
- Casiraghi, C.; Pisana, S.; Novoselov, K.S.; Geim, A.K.; Ferrari, A.C. Raman fingerprint of charged impurities in graphene. Appl. Phys. Lett. 2007, 91, 233108:1–233108:3. [Google Scholar]
- Podila, R.; Rao, R.; Tsuchikawa, R.; Ishigami, M.; Rao, A.M. Raman spectroscopy of folded and scrolled graphene. ACS Nano 2012, 6, 5784–5790. [Google Scholar] [CrossRef]
- Faugeras, C.; Nerrière, A.; Potemski, M.; Mahmood, A.; Dujardin, E.; Berger, C.; de Heer, W.A. Few-layer graphene on SiC, pyrolitic graphite, and graphene: A Raman scattering study. Appl. Phys. Lett. 2008, 92, 011914:1–011914:3. [Google Scholar]
- Malard, L.M.; Pimenta, M.A.; Dresselhaus, G.; Dresselhaus, M.S. Raman spectroscopy in graphene. Phys. Rep. 2009, 473, 51–87. [Google Scholar]
- Röhrl, J.; Hundhausen, M.; Emtsev, K.V.; Seyller, T.; Graupner, R.; Ley, L. Raman spectra of epitaxial graphene on SiC(0001). Appl. Phys. Lett. 2008, 92, 201918:1–201918:3. [Google Scholar]
- Hibino, H.; Kageshima, H.; Maeda, F.; Nagase, M.; Kobayashi, Y.; Yamaguchi, H. Microscopic thickness determination of thin graphite films formed on SiC from quantized oscillation in reflectivity of low-energy electrons. Phys. Rev. B 2008, 77, 075413:1–075413:7. [Google Scholar]
- Man, K.L.; Altman, M.S. Low energy electron microscopy and photoemission electron microscopy investigation of graphene. J. Phys. Condens. Matter 2012, 24, 314209:1–314209:20. [Google Scholar]
- Ohta, T.; El Gabaly, F.; Bostwick, A.; McChesney, J.L.; Emtsev, K.V.; Schmid, A.K.; Seyller, T.; Horn, K.; Rotenberg, E. Morphology of graphene thin film growth on SiC(0001). New J. Phys. 2008, 10, 023034:1–023034:7. [Google Scholar]
- Khokhar, F.S.; Hlawacek, G.; van Gastel, R.; Zandvliet, H.J.W.; Teichert, C.; Poelsema, B. The influence of substrate temperature on growth of para-sexiphenyl thin films on Ir{111} supported graphene studied by LEEM. Surf. Sci. 2012, 606, 475–480. [Google Scholar] [CrossRef]
- Osaklung, J.; Euaruksakul, C.; Meevasana, W.; Songsiriritthigul, P. Spatial variation of the number of graphene layers formed on the scratched 6H-SiC(0001) surface. Appl. Surf. Sci. 2012, 258, 4672–4677. [Google Scholar] [CrossRef]
- Jin, L.; Fu, Q.; Zhang, H.; Mu, R.; Zhang, Y.; Tan, D.; Bao, X. Tailoring the growth of graphene on Ru(0001) via engineering of the substrate surface. J. Phys. Chem. C 2012, 116, 2988–2993. [Google Scholar]
- Mathieu, C.; Lalmi, B.; Menteş, T.O.; Pallecchi, E.; Locatelli, A.; Latil, S.; Belkhou, R.; Ouerghi, A. Effect of oxygen adsorption on the local properties of epitaxial graphene on SiC(0001). Phys. Rev. B 2012, 86, 035435:1–035435:5. [Google Scholar]
- Matey, J.R.; Blanc, J. Scanning capacitance microscopy. J. Appl. Phys. 1985, 57, 1437:1–1437:8. [Google Scholar]
- Isenbart, J.; Born, A.; Wiesendanger, R. The physical principles of scanning capacitance spectroscopy. Appl. Phys. A Mater. Sci. Proc. 2001, 72, S243–S251. [Google Scholar] [CrossRef]
- Naitou, Y.; Ogiso, H. Capacitive Imaging of Graphene Flakes on SiO2 Substrate. Jpn. J. Appl. Phys. 2011, 50, 066602:1–066602:4. [Google Scholar]
- Zhao, S.; Lv, Y.; Yang, X. Layer-dependent nanoscale electrical properties of graphene studied by conductive scanning probe microscopy. Nanoscale Res. Lett. 2011, 6, 498:1–498:6. [Google Scholar]
- Giannazzo, F.; Sonde, S.; Nigro, R.; Rimini, E. Mapping the density of scattering centers limiting the electron mean free path in graphene. Nano Lett. 2011, 4612–4618. [Google Scholar] [CrossRef]
- Lee, J.E.; Ahn, G.; Shim, J.; Lee, Y.S.; Ryu, S. Optical separation of mechanical strain from charge doping in graphene. Nat. Commun. 2012, 3, 1024:1–1024:8. [Google Scholar]
- Hass, J.; Millán-Otoya, J.; First, P.; Conrad, E. Interface structure of epitaxial graphene grown on 4H-SiC(0001). Phys. Rev. B 2008, 78, 205424:1–205424:10. [Google Scholar]
- Park, J.H.; Mitchel, W.C.; Smith, H.E.; Grazulis, L.; Eyink, K.G. Studies of interfacial layers between 4H-SiC (0001) and graphene. Carbon 2010, 48, 1670–1673. [Google Scholar] [CrossRef]
- Burnett, T.L.; Yakimova, R.; Kazakova, O. Identification of epitaxial graphene domains and adsorbed species in ambient conditions using quantified topography measurements. J. Appl. Phys. 2012, 112, 054308:1–054308:7. [Google Scholar]
- Nemes-Incze, P.; Osváth, Z.; Kamarás, K.; Biró, L.P. Anomalies in thickness measurements of graphene and few layer graphite crystals by tapping mode atomic force microscopy. Carbon 2008, 46, 1435–1442. [Google Scholar] [CrossRef]
- Lauffer, P.; Emtsev, K.V.; Graupner, R.; Seyller, T.; Ley, L. Atomic and electronic structure of few-layer graphene on SiC(0001) studied with scanning tunneling microscopy and spectroscopy. Phys. Rev. B 2008, 77, 155426:1–155426:10. [Google Scholar]
- Eriksson, J.; Pearce, R.; Iakimov, T.; Virojanadara, C.; Gogova, D.; Andersson, M.; Syväjärvi, M.; Lloyd Spetz, A.; Yakimova, R. The influence of substrate morphology on thickness uniformity and unintentional doping of epitaxial graphene on SiC. Appl. Phys. Lett. 2012, 100, 241607:1–241607:5. [Google Scholar]
- Dimitrakopoulos, C.; Grill, A.; McArdle, T.J.; Liu, Z.; Wisnieff, R.; Antoniadis, D.A. Effect of SiC wafer miscut angle on the morphology and Hall mobility of epitaxially grown graphene. Appl. Phys. Lett. 2011, 98, 222105:1–222105:3. [Google Scholar]
- Low, T.; Perebeinos, V.; Tersoff, J.; Avouris, P. Deformation and scattering in graphene over substrate steps. Phys. Rev. Lett. 2012, 108, 096601:1–096601:4. [Google Scholar]
- Robinson, J.; Weng, X.; Trumbull, K.; Cavalero, R.; Wetherington, M.; Frantz, E.; Labella, M.; Hughes, Z.; Fanton, M.; Snyder, D. Nucleation of epitaxial graphene on SiC(0001). ACS Nano 2010, 4, 153–158. [Google Scholar] [CrossRef]
- Vecchio, C.; Sonde, S.; Bongiorno, C.; Rambach, M.; Yakimova, R.; Raineri, V.; Giannazzo, F. Nanoscale structural characterization of epitaxial graphene grown on off-axis 4H-SiC (0001). Nanoscale Res. Lett. 2011, 6, 269:1–269:7. [Google Scholar]
- Zhu, W.; Low, T.; Perebeinos, V.; Bol, A.A.; Zhu, Y.; Yan, H.; Tersoff, J.; Avouris, P. Structure and electronic transport in graphene wrinkles. Nano Lett. 2012, 12, 3431–3436. [Google Scholar]
- Schmidt, D.; Ohta, T.; Beechem, T. Strain and charge carrier coupling in epitaxial graphene. Phys. Rev. B 2011, 84, 235422:1–235422:8. [Google Scholar]
- Haigh, S.J.; Gholinia, A.; Jalil, R.; Romani, S.; Britnell, L.; Elias, D.C.; Novoselov, K.S.; Ponomarenko, L.A.; Geim, A.K.; Gorbachev, R. Cross-sectional imaging of individual layers and buried interfaces of graphene-based heterostructures and superlattices. Nat. Mater. 2012, 11, 764–767. [Google Scholar] [CrossRef]
- Koutsos, V.; Haschke, H.; Miles, M.J.; Madani, F. Pulling single chains out of a collapsed polymer monolayer in bad-solvent conditions. MRS Proc. 2011, 734, 49–53. [Google Scholar]
- Madani-Grasset, F.; Pham, N.T.; Glynos, E.; Koutsos, V. Imaging thin and ultrathin organic films by scanning white light interferometry. Mater. Sci. Eng. B 2008, 152, 125–131. [Google Scholar] [CrossRef]
- Yavari, F.; Kritzinger, C.; Gaire, C.; Song, L.; Gulapalli, H.; Borca-Tasciuc, T.; Ajayan, P.M.; Koratkar, N. Tunable bandgap in graphene by the controlled adsorption of water molecules. Small 2010, 6, 2535–2538. [Google Scholar] [CrossRef]
- Kalon, G.; Shin, Y.J.; Yang, H. Tunable metal-insulator transitions in bilayer graphene by thermal annealing. Appl. Phys. Lett. 2011, 98, 233108:1–233108:3. [Google Scholar]
- Yang, Y.; Brenner, K.; Murali, R. The influence of atmosphere on electrical transport in graphene. Carbon 2012, 50, 1727–1733. [Google Scholar] [CrossRef]
- Riedl, C.; Coletti, C.; Starke, U. Structural and electronic properties of epitaxial graphene on SiC(0001): A review of growth, characterization, transfer doping and hydrogen intercalation. J. Phys. D Appl. Phys. 2010, 43, 374009:1–374009:17. [Google Scholar]
- Chung, M.G.; Kim, D.H.; Lee, H.M.; Kim, T.; Choi, J.H.; Seo, D.K.; Yoo, J.-B.; Hong, S.-H.; Kang, T.J.; Kim, Y.H. Highly sensitive NO2 gas sensor based on ozone treated graphene. Sens. Actuators B Chem. 2012, 166-167, 172–176. [Google Scholar]
- Yoon, H.J.; Jun, D.H.; Yang, J.H.; Zhou, Z.; Yang, S.S.; Cheng, M.M.-C. Carbon dioxide gas sensor using a graphene sheet. Sens. Actuators B Chem. 2011, 157, 310–313. [Google Scholar] [CrossRef]
- Schedin, F.; Geim, A.K.; Morozov, S.V.; Hill, E.W.; Blake, P.; Katsnelson, M.I.; Novoselov, K.S. Detection of individual gas molecules adsorbed on graphene. Nat. Mater. 2007, 6, 652–655. [Google Scholar] [CrossRef]
- Wehling, T.O.; Novoselov, K.S.; Morozov, S.V.; Vdovin, E.E.; Katsnelson, M.I.; Geim, A.K.; Lichtenstein, A.I. Molecular doping of graphene. Nano Lett. 2008, 8, 173–177. [Google Scholar] [CrossRef]
- Zhou, S.; Siegel, D.; Fedorov, A.; Lanzara, A. Metal to insulator transition in epitaxial graphene induced by molecular doping. Phys. Rev. Lett. 2008, 101, 086402:1–086402:4. [Google Scholar]
- Sojoudi, H.; Baltazar, J.; Henderson, C.; Graham, S. Impact of post-growth thermal annealing and environmental exposure on the unintentional doping of CVD graphene films. J. Vac. Sci. Technol. B Microelectron. Nanometer. Struct. 2012, 30, 041213:1–041213:6. [Google Scholar]
- Llobet, E. Gas sensors using carbon nanomaterials: A review. Sens. Actuators B Chem. 2013, in press. [Google Scholar]
- Verdaguer, A.; Sacha, G.M.; Bluhm, H.; Salmeron, M. Molecular structure of water at interfaces: Wetting at the nanometer scale. Chem. Rev. 2006, 106, 1478–510. [Google Scholar] [CrossRef]
- Kazakova, O.; Burnett, T.L.; Patten, J.; Yang, L.; Yakimova, R. Epitaxial graphene on SiC(000-1): Electrical functional microscopy studies and effect of atmosphere. Nanotechnology 2012. submitted for publication. [Google Scholar]
- Cao, P.; Xu, K.; Varghese, J.O.; Heath, J.R. The microscopic structure of adsorbed water on hydrophobic surfaces under ambient conditions. Nano Lett. 2011, 11, 5581–5586. [Google Scholar] [CrossRef]
- Kimmel, G.A.; Matthiesen, J.; Baer, M.; Mundy, C.J.; Petrik, N.G.; Smith, R.S.; Dohnálek, Z.; Kay, B.D. No confinement needed: Observation of a metastable hydrophobic wetting two-layer ice on graphene. J. Am. Chem. Soc. 2009, 131, 12838–12844. [Google Scholar] [CrossRef]
- Yang, D.-S.; Zewail, A.H. Ordered water structure at hydrophobic graphite interfaces observed by 4D, ultrafast electron crystallography. Proc. Natl. Acad. Sci. USA 2009, 106, 4122–4126. [Google Scholar] [CrossRef]
- Hibino, H.; Tanabe, S.; Mizuno, S.; Kageshima, H. Growth and electronic transport properties of epitaxial graphene on SiC. J. Phys. D Appl. Phys. 2012, 45, 154008:1–154008:12. [Google Scholar]
- Srivastava, N.; He, G.; Mende, P.C.; Feenstra, R.M.; Sun, Y. Graphene formed on SiC under various environments: Comparison of Si-face and C-face. J. Phys. D Appl. Phys. 2012, 45, 154001:1–154001:12. [Google Scholar]
- Sun, D.; Divin, C.; Berger, C.; de Heer, W.A.; First, P.N.; Norris, T.B. Spectroscopic measurement of interlayer screening in multilayer epitaxial graphene. Phys. Rev. Lett. 2010, 104, 136802:1–036802:4. [Google Scholar]
- Johansson, L.; Watcharinyanon, S.; Zakharov, A.; Iakimov, T.; Yakimova, R.; Virojanadara, C. Stacking of adjacent graphene layers grown on C-face SiC. Phys. Rev. B 2011, 84, 125405:1–125405:8. [Google Scholar]
- Nomani, M.W.K.; Shields, V.; Tompa, G.; Sbrockey, N.; Spencer, M.G.; Webb, R.A.; Koley, G. Correlated conductivity and work function changes in epitaxial graphene. Appl. Phys. Lett. 2012, 100, 092113:1–092113:4. [Google Scholar]
- Lin, Y.-M.; Dimitrakopoulos, C.; Farmer, D.B.; Han, S.-J.; Wu, Y.; Zhu, W.; Gaskill, D.K.; Tedesco, J.L.; Myers-Ward, R.L.; Eddy, C.R.; Grill, A.; Avouris, P. Multicarrier transport in epitaxial multilayer graphene. Appl. Phys. Lett. 2010, 97, 112107:1–112107:3. [Google Scholar]
- Ryu, S.; Liu, L.; Berciaud, S.; Yu, Y.-J.; Liu, H.; Kim, P.; Flynn, G.W.; Brus, L.E. Atmospheric oxygen binding and hole doping in deformed graphene on a SiO2 substrate. Nano Lett. 2010, 4944–4951. [Google Scholar]
- Leenaerts, O.; Partoens, B.; Peeters, F. Adsorption of H2O, NH3, CO, NO2, and NO on graphene: A first-principles study. Phys. Rev. B 2008, 77, 125416:1–125416:6. [Google Scholar]
- Zhao, J.; Xiao, B.; Ding, Y. Theoretical prediction of the N−H and O−H bonds cleavage catalyzed by the single-walled silicon carbide nanotube. J. Phys. Chem. C 2009, 113, 16736–16740. [Google Scholar] [CrossRef]
- Li, H.; Zeng, X.C. Wetting and interfacial properties of water nanodroplets in contact with graphene and monolayer boron-nitride sheets. ACS Nano 2012, 6, 2401–2409. [Google Scholar] [CrossRef]
- Gordillo, M.C.; Martí, J. Effect of surface roughness on the static and dynamic properties of water adsorbed on graphene. J. Phys. Chem. B 2010, 114, 4583–4589. [Google Scholar] [CrossRef]
- Rosso, M.; Arafat, A.; Schroën, K.; Giesbers, M.; Roper, C.S.; Maboudian, R.; Zuilhof, H. Covalent attachment of organic monolayers to silicon carbide surfaces. Langmuir 2008, 24, 4007–4012. [Google Scholar]
- Zhuang, H.; Song, B.; Srikanth, V.V.S.S.; Jiang, X.; Schönherr, H. Controlled wettability of diamond/β-SiC composite thin films for biosensoric applications. J. Phys. Chem. C 2010, 114, 20207–20212. [Google Scholar]
- Panchal, V.; Cox, D.; Yakimova, R.; Kazakova, O. Epitaxial graphene sensors for detection of small magnetic moments. IEEE Trans. Mag. 2013, 49, 97–100. [Google Scholar]
- Panchal, V.; Cedergren, K.; Yakimova, R.; Tzalenchuk, A.; Kubatkin, S.; Kazakova, O. Small epitaxial graphene devices for magnetosensing applications. J. Appl. Phys. 2012, 111, 07E509:1–07E509:3. [Google Scholar]
- Goossens, A.M.; Calado, V.E.; Barreiro, A.; Watanabe, K.; Taniguchi, T.; Vandersypen, L.M.K. Mechanical cleaning of graphene. Appl. Phys. Lett. 2012, 100, 073110:1–073110:3. [Google Scholar]
- Moser, J.; Barreiro, A.; Bachtold, A. Current-induced cleaning of graphene. Appl. Phys. Lett. 2007, 91, 163513:1–163513:3. [Google Scholar]
- Bryan, S.E.; Yang, Y.; Murali, R. Conductance of epitaxial graphene nanoribbons: Influence of size effects and substrate morphology. J. Phys. Chem. C 2011, 115, 10230–10235. [Google Scholar] [CrossRef]
- Lara-Avila, S.; Moth-Poulsen, K.; Yakimova, R.; Bjørnholm, T.; Fal’ko, V.; Tzalenchuk, A.; Kubatkin, S. Non-volatile photochemical gating of an epitaxial graphene/polymer heterostructure. Adv. Mater. 2011, 23, 878–882. [Google Scholar]
- Kopylov, S.; Tzalenchuk, A.; Kubatkin, S.; Fal’ko, V.I. Charge transfer between epitaxial graphene and silicon carbide. Appl. Phys. Lett. 2010, 97, 112109:1–112109:3. [Google Scholar]
- Sonde, S.; Giannazzo, F.; Raineri, V.; Yakimova, R.; Huntzinger, J.-R.; Tiberj, A.; Camassel, J. Electrical properties of the graphene/4H-SiC (0001) interface probed by scanning current spectroscopy. Phys. Rev. B 2009, 80, 241406:1–241406:4. [Google Scholar]
- Okudaira, K.K.; Morikawa, E.; Hasegawa, S.; Sprunger, P.T.; Saile, V.; Seki, K.; Harada, Y.; Ueno, N. Radiation damage of poly(methylmethacrylate) thin films analyzed by UPS. J. Electron SpectrosC. Relat. Phenom. 1998, 88-91, 913–917. [Google Scholar] [CrossRef]
- Ikeura-Sekiguchi, H.; Sekiguchi, T.; Koike, M. Characterization and degradation of ZEP520 resist film by TOF-PSID and NEXAFS. J. Electron Spectrosc. Relat. Phenom. 2005, 144-147, 453–455. [Google Scholar] [CrossRef]
- Yu, Y.-J.; Zhao, Y.; Ryu, S.; Brus, L.E.; Kim, K.S.; Kim, P. Tuning the graphene work function by electric field effect. Nano Lett. 2009, 9, 3430–3434. [Google Scholar]
- Pearce, R. On the differing sensitivity to chemical gating of single and double layer epitaxial graphene explored using Scanning Kelvin Probe Microscopy. ACS Nano 2012. submitted for publication. [Google Scholar]
- Bussmann, B.K.; Ochedowski, O.; Schleberger, M. Doping of graphene exfoliated on SrTiO3. Nanotechnology 2011, 22, 265703:1–265703:5. [Google Scholar]
- Bruker Cooperation Home Page. Available online: http://www.bruker.com/ (accessed on 27 February 2013).
- Bruker AFM Probe. Available online: http://www.brukerafmprobes.com/ (accessed on 27 February 2013).
- Oliver, R.A. Advances in AFM for the electrical characterization of semiconductors. Rep. Prog. Phys. 2008, 71, 076501:1–076501:37. [Google Scholar]
- Hao, G.L.; Qi, X.; Li, J.; Yang, L.W.; Yin, J.J.; Lu, F.; Zhong, J.X. Surface potentials of few-layer graphene films in high vacuum and ambient conditions. Solid State Commun. 2011, 151, 818–821. [Google Scholar]
- Takagi, A.; Yamada, F.; Matsumoto, T.; Kawai, T. Electrostatic force spectroscopy on insulating surfaces: the effect of capacitive interaction. Nanotechnology 2009, 20, 365501:1–0365501:7. [Google Scholar]
- Melitz, W.; Shen, J.; Kummel, A.C.; Lee, S. Kelvin probe force microscopy and its application. Surf. Sci. Rep. 2011, 66, 1–27. [Google Scholar]
- Glatzel, T.; Sadewasser, S.; Lux-Steiner, M.C. Amplitude or frequency modulation-detection in Kelvin probe force microscopy. Appl. Surf. Sci. 2003, 210, 84–89. [Google Scholar]
- Ziegler, D.; Stemmer, A. Force gradient sensitive detection in lift-mode Kelvin probe force microscopy. Nanotechnology 2011, 22, 075501:1–075501:9. [Google Scholar]
- Krok, F.; Sajewicz, K.; Konior, J.; Goryl, M.; Piatkowski, P.; Szymonski, M. Lateral resolution and potential sensitivity in Kelvin probe force microscopy: Towards understanding of the sub-nanometer resolution. Phys. Rev. B 2008, 77, 235427:1–235427:9. [Google Scholar]
- Yakimova, R.; Virojanadara, C.; Gogova, D.; Syväjärvi, M.; Siche, D.; Larsson, K.; Johansson, L.I. Analysis of the Formation Conditions for Large Area Epitaxial Graphene on SiC Substrates. Mater. Sci. Forum 2010, 645-648, 565–568. [Google Scholar] [CrossRef]
- Yakimova, R.; Iakimova, T.; Syväjärvi, M. Process for growth of graphene 2012. WIPO Patent WO2012036608, International Application No. PCT/SE2011/050328 23 March 2011. [Google Scholar]
- Yannopoulos, S.N.; Siokou, A.; Nasikas, N.K.; Dracopoulos, V.; Ravani, F.; Papatheodorou, G.N. CO2-laser-induced growth of epitaxial graphene on 6H-SiC(0001). Adv. Funct. Mater. 2012, 22, 113–120. [Google Scholar] [CrossRef]
- Luo, Z.; Cong, C.; Zhang, J.; Xiong, Q.; Yu, T. Direct observation of inner and outer G' band double-resonance Raman scattering in free standing graphene. Appl. Phys. Lett. 2012, 100, 243107:1–243107:4. [Google Scholar]
- Tiberj, A.; Camara, N.; Godignon, P.; Camassel, J. Micro-Raman and micro-transmission imaging of epitaxial graphene grown on the Si and C faces of 6H-SiC. Nanoscale Res. Lett. 2011, 6, 478:1–478:9. [Google Scholar]
- Lee, D.S.; Riedl, C.; Krauss, B.; von Klitzing, K.; Starke, U.; Smet, J.H. Raman spectra of epitaxial graphene on SiC and of epitaxial graphene transferred to SiO2. Nano Lett. 2008, 8, 4320–4325. [Google Scholar] [CrossRef]
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Kazakova, O.; Panchal, V.; Burnett, T.L. Epitaxial Graphene and Graphene–Based Devices Studied by Electrical Scanning Probe Microscopy. Crystals 2013, 3, 191-233. https://doi.org/10.3390/cryst3010191
Kazakova O, Panchal V, Burnett TL. Epitaxial Graphene and Graphene–Based Devices Studied by Electrical Scanning Probe Microscopy. Crystals. 2013; 3(1):191-233. https://doi.org/10.3390/cryst3010191
Chicago/Turabian StyleKazakova, Olga, Vishal Panchal, and Tim L. Burnett. 2013. "Epitaxial Graphene and Graphene–Based Devices Studied by Electrical Scanning Probe Microscopy" Crystals 3, no. 1: 191-233. https://doi.org/10.3390/cryst3010191
APA StyleKazakova, O., Panchal, V., & Burnett, T. L. (2013). Epitaxial Graphene and Graphene–Based Devices Studied by Electrical Scanning Probe Microscopy. Crystals, 3(1), 191-233. https://doi.org/10.3390/cryst3010191