Pressure Effect on Organic Conductors
Abstract
:1. Introduction
2. Method of Pressure in Organic Conductors
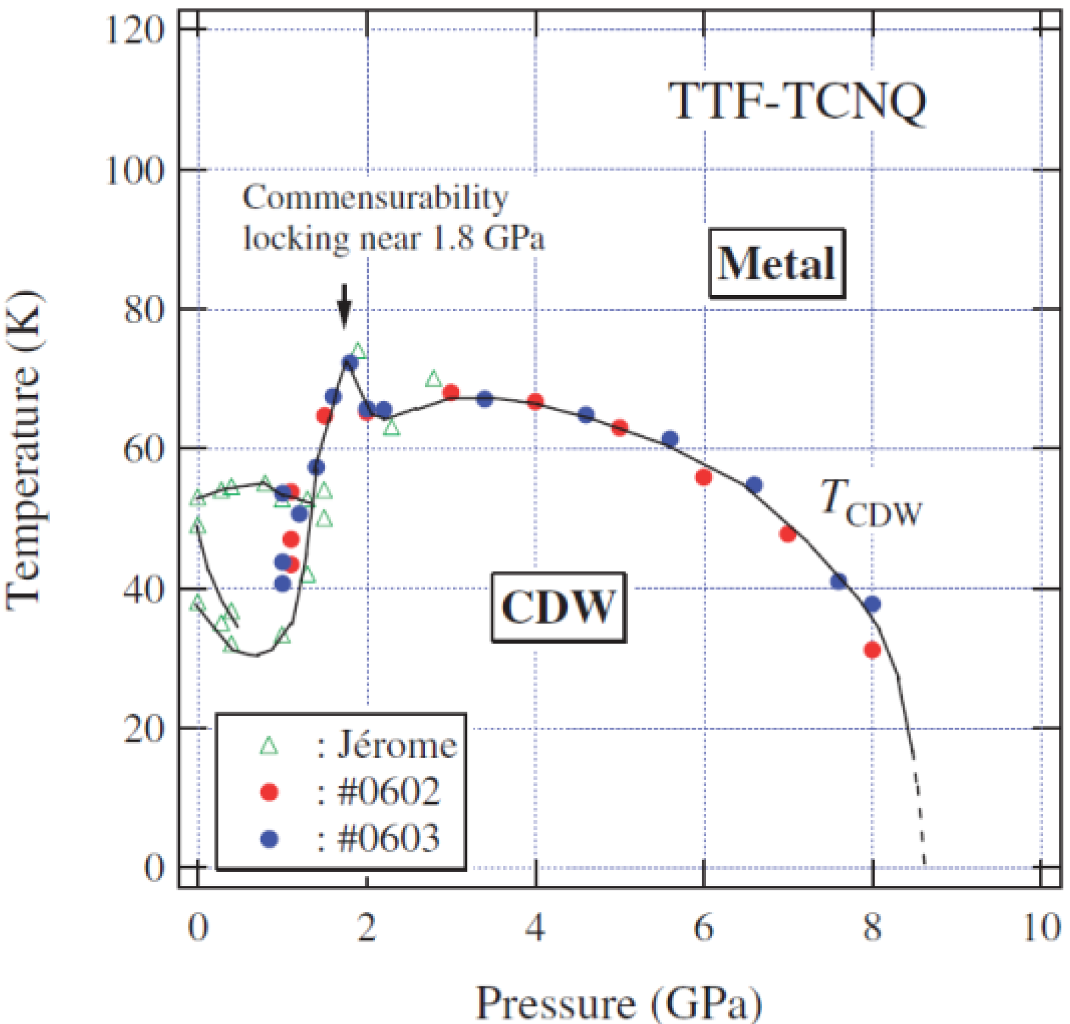
3. TTF-TCNQ and TSeF-TCNQ
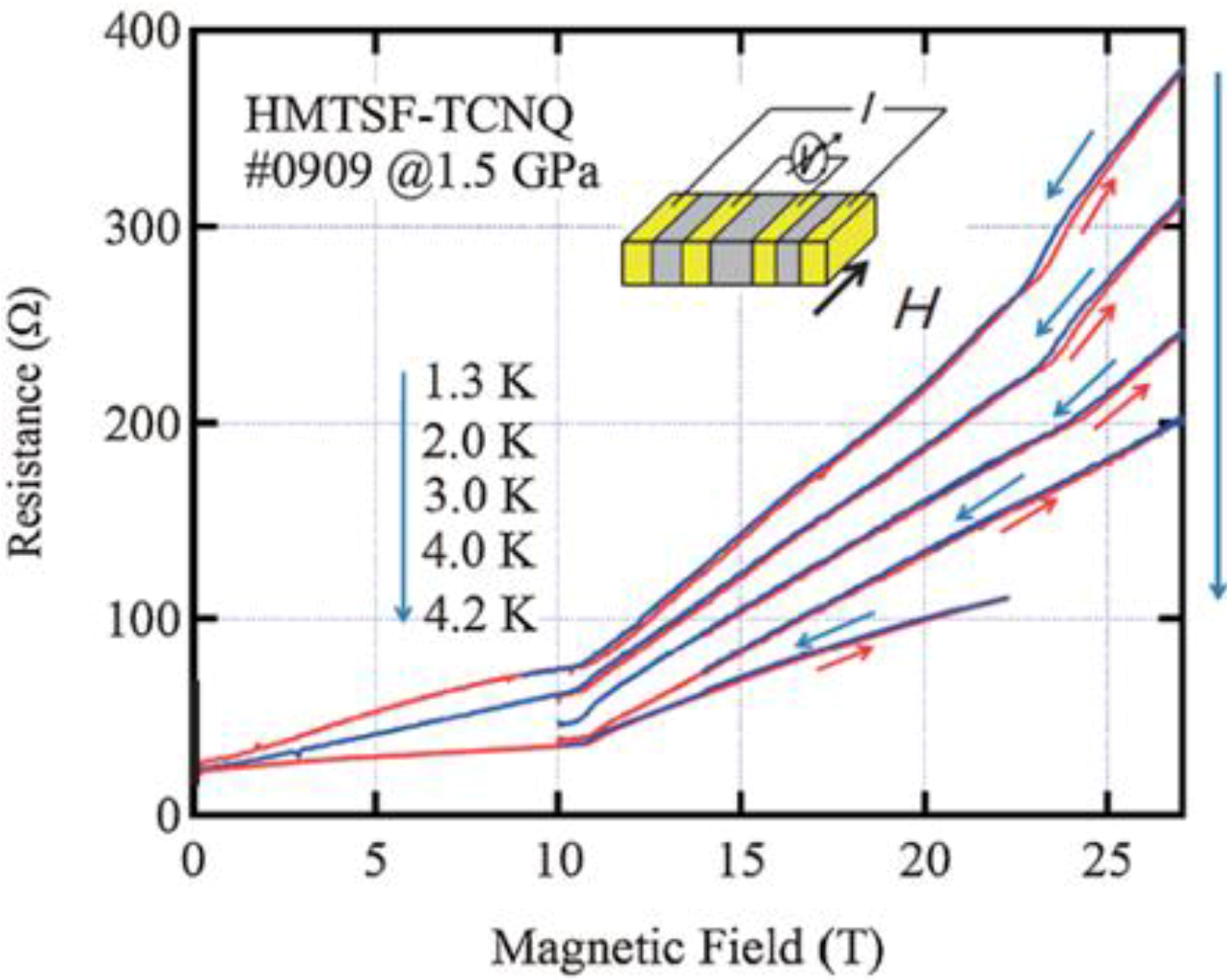
4. HMTSF-TCNQ
| Stacking pattern (viewed along 1D) | Super-Structure | Charge transfer | PCDW | |
|---|---|---|---|---|
| TTF-TCNQ | F F F F | 2kF & 4kF | 0.59 | 9 GPa |
| Q Q Q Q | ||||
| F F F F | ||||
| Q Q Q Q | ||||
| TSeF-TCNQ | F F F F | 2kF only | 0.63 | 7 GPa |
| Q Q Q Q | ||||
| F F F F | ||||
| Q Q Q Q | ||||
| HMTTF-TCNQ | F Q F Q | 2kF & 4kF | 0.72 | |
| Q F Q F | ||||
| F Q F Q | ||||
| Q F Q F | ||||
| HMTSF-TCNQ | F Q F Q | 2kF only | 0.74 | 1 GPa |
| Q F Q F | ||||
| F Q F Q | ||||
| Q F Q F |
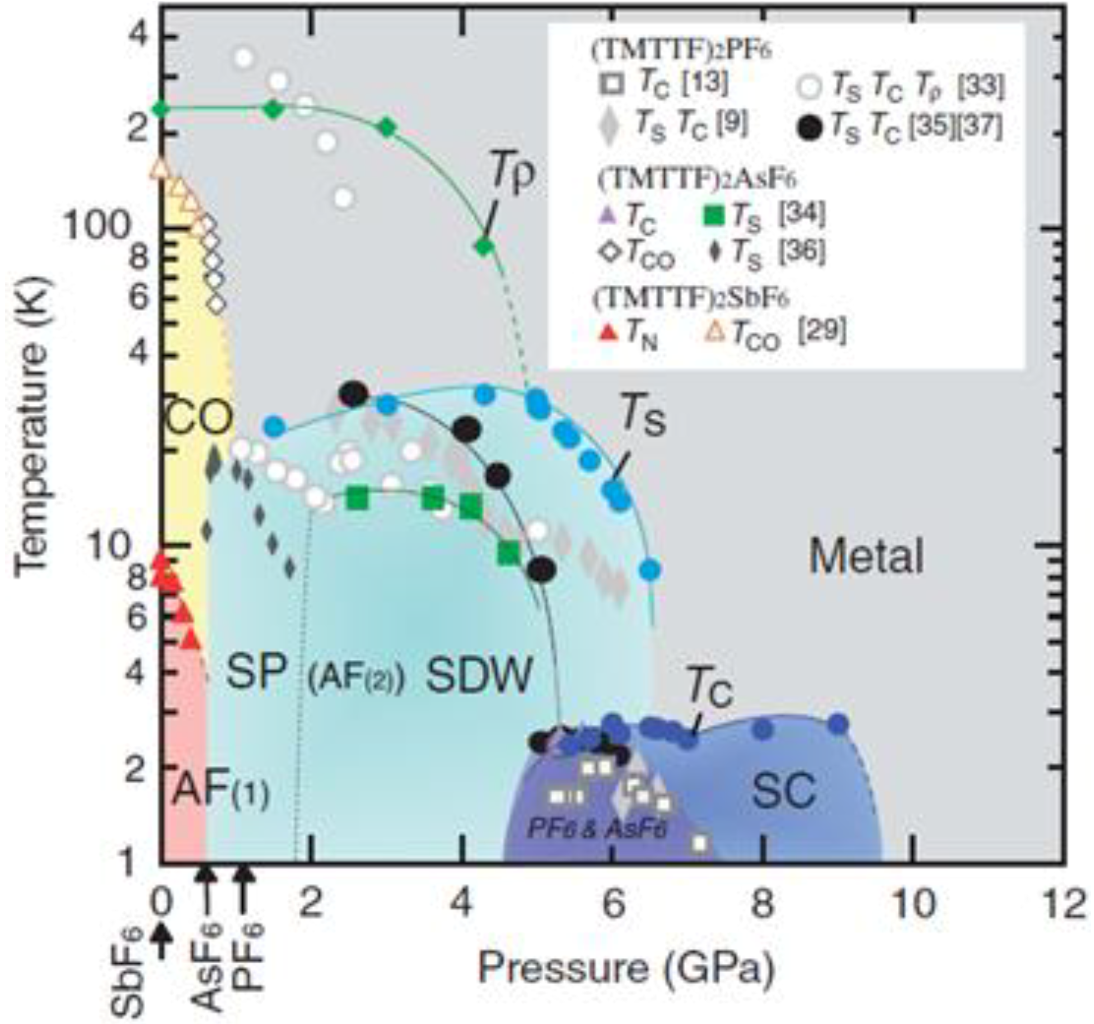
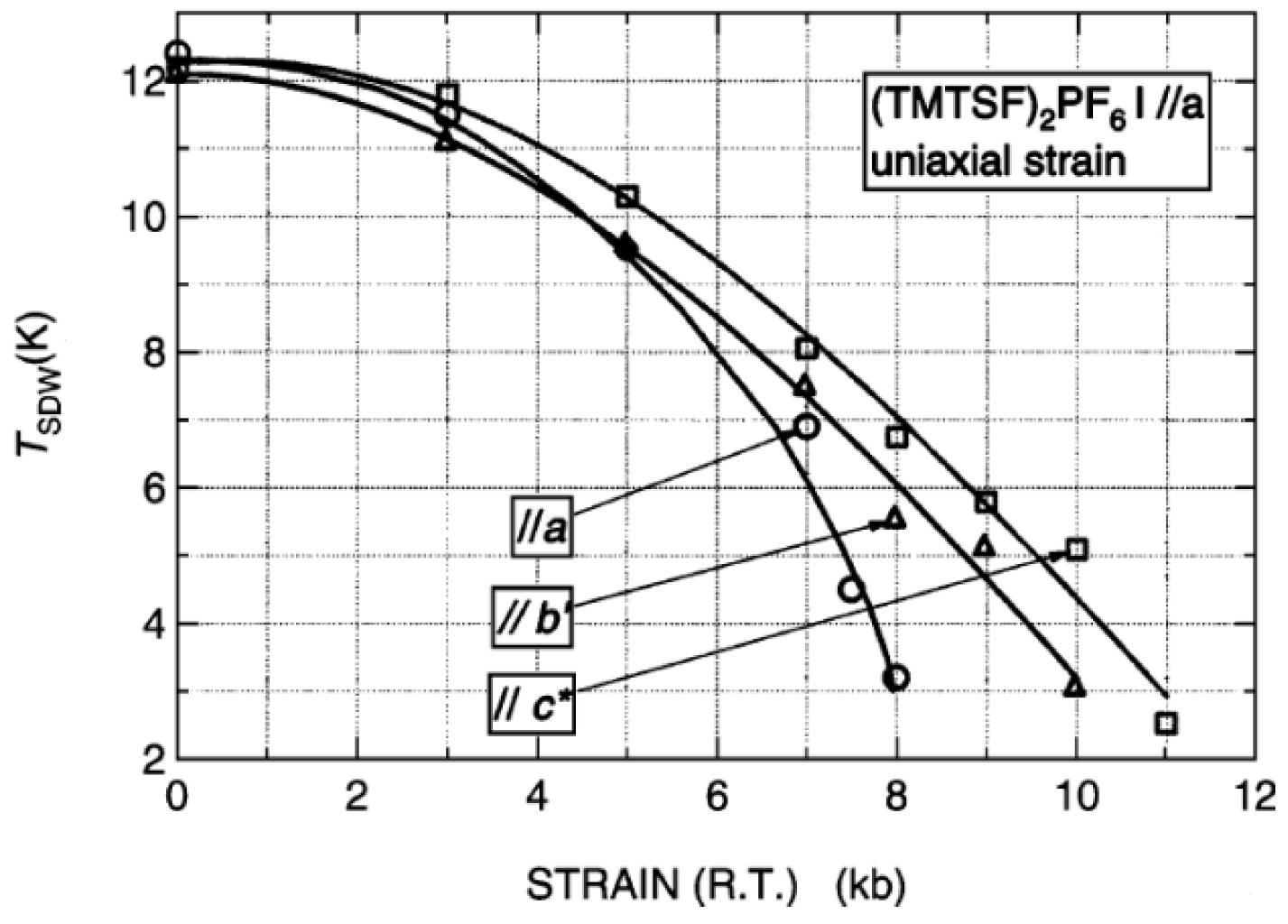
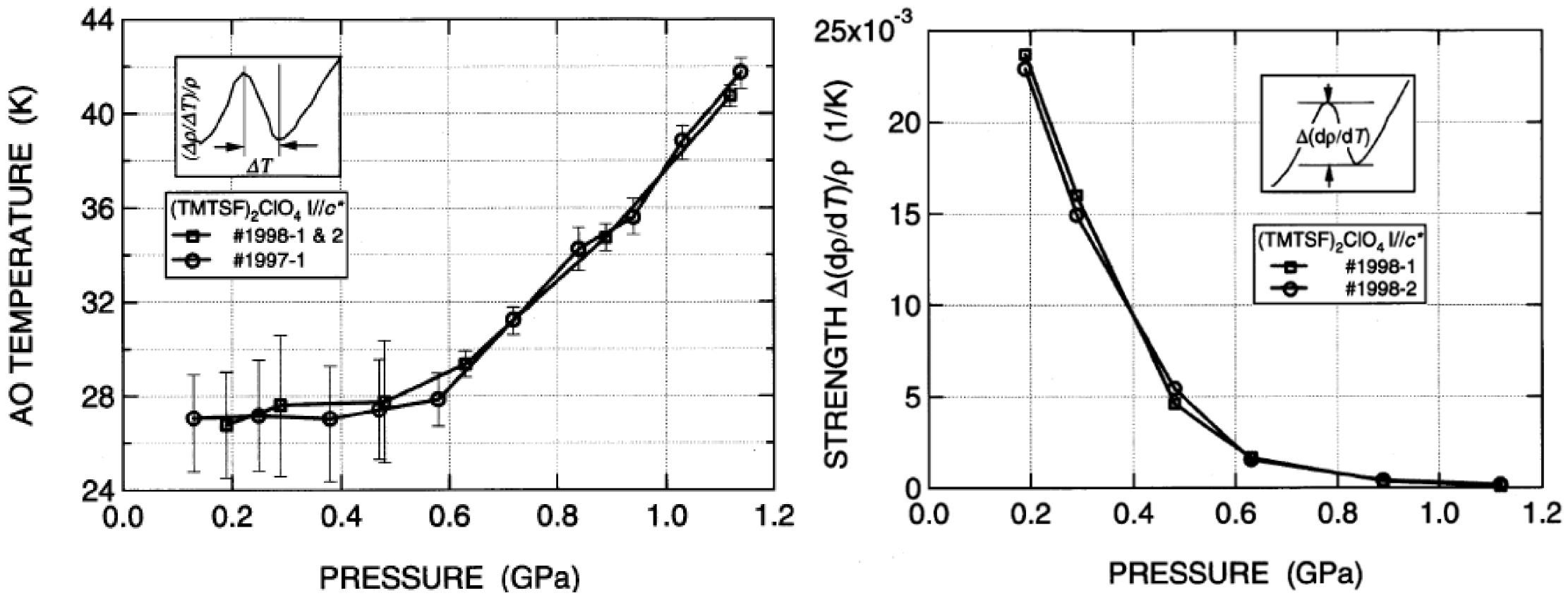
5. (TMTTF)2X and (TMTSF)2X
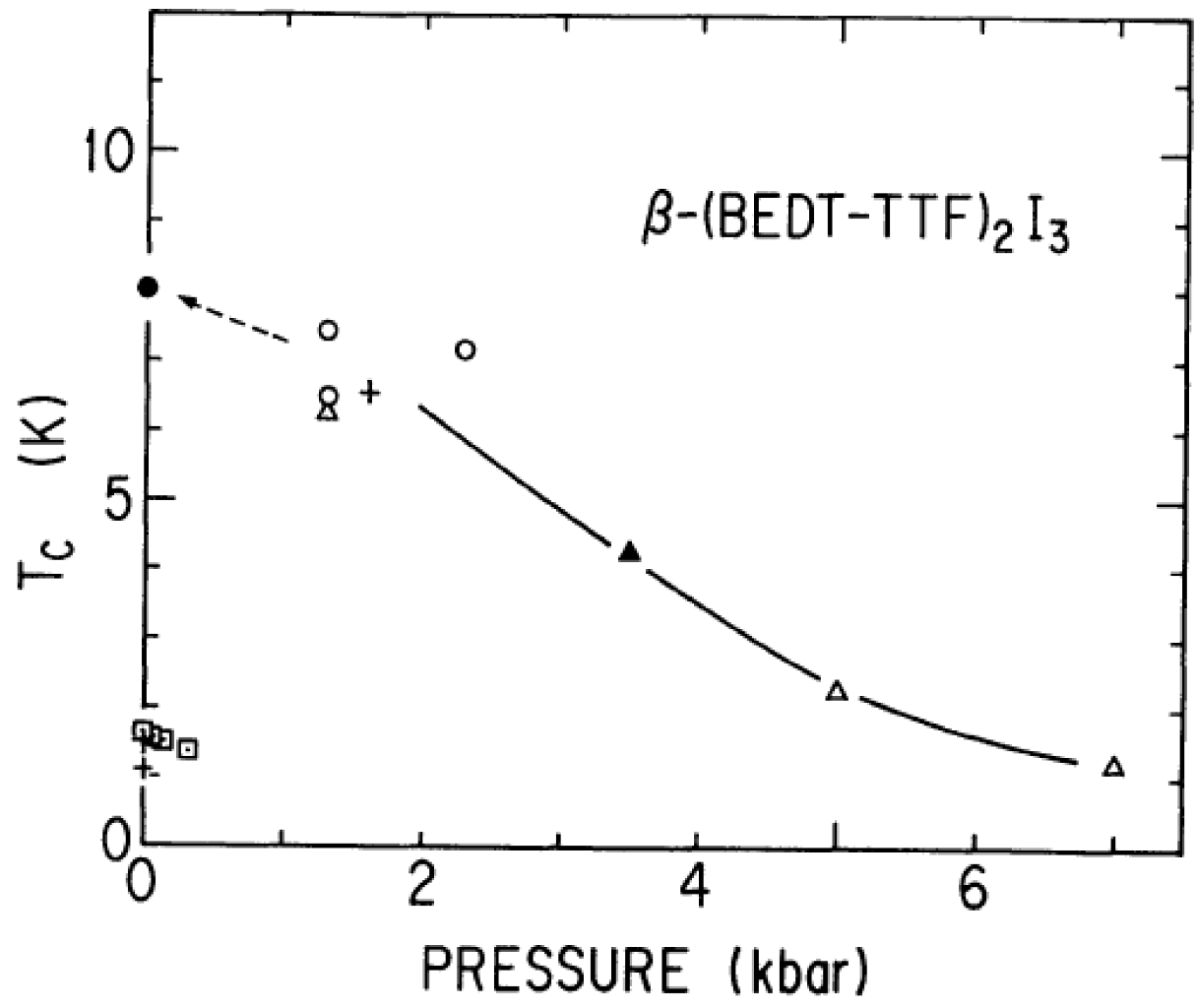
6. β-(BEDT-TTF)2I3
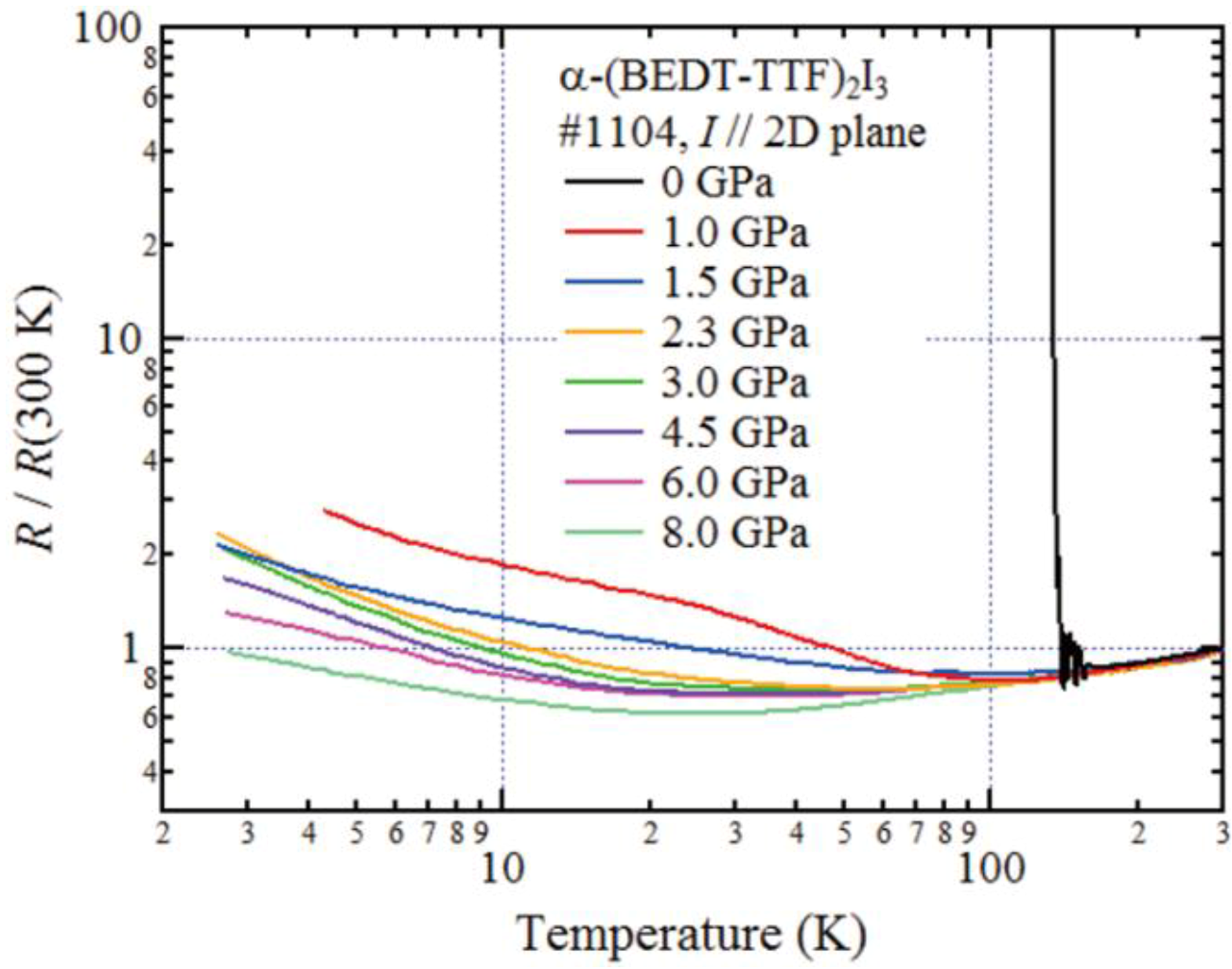
7. α-(BEDT-TTF)2I3

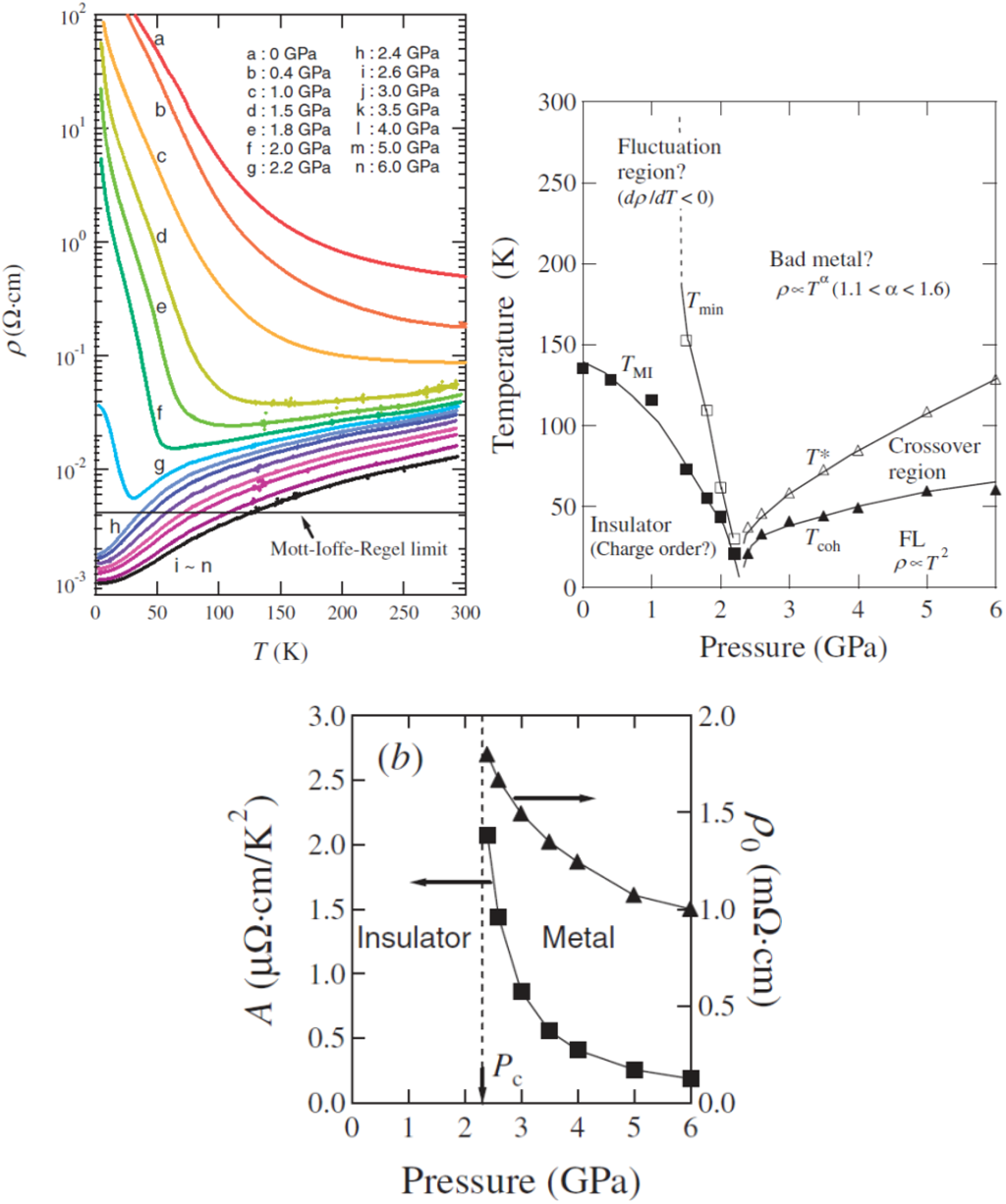
8. κ-(MeDH-TTP)2AsF6
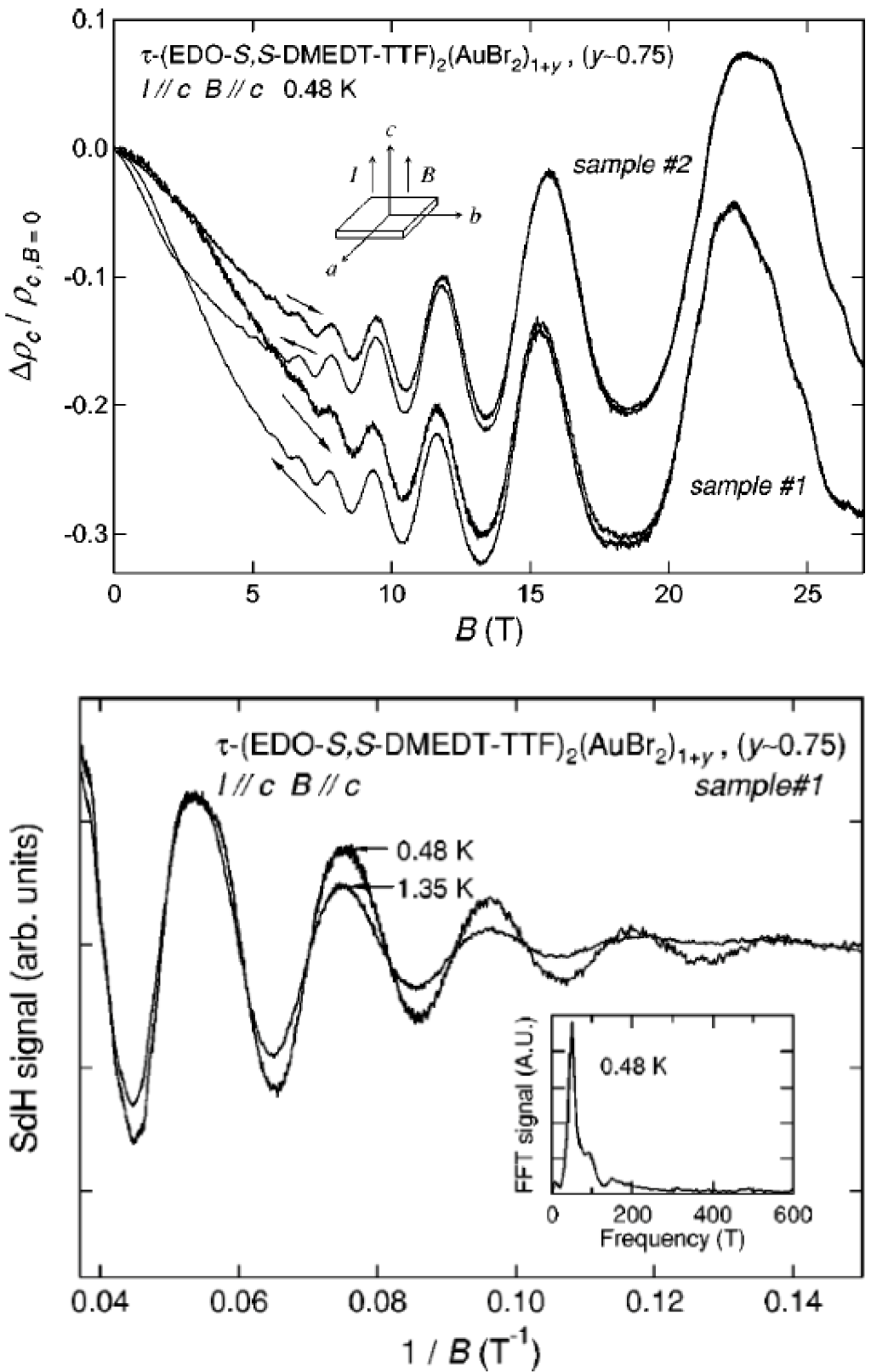
9. τ-type Conductors
10. Conclusion
Acknowledgements
References
- Andrieux, A.; Schulz, H.J.; Jérome, D. Conductivity of the one-dimensional conductor tetrathiafulvalene-tetracyanoquinodimethane (TTF-TCNQ) near commensurability. Phys. Rev. Lett. 1979, 43, 227–230. [Google Scholar] [CrossRef]
- Jérome, D.; Mazaud, A.; Ribault, M.; Bechgaard, K. Superconductivity in a synthetic organic conductor (TMTSF)2PF6. J. Phys. Lett. 1980, 41, L95–L98. [Google Scholar] [CrossRef]
- Chaikin, P.M. Field Induced Spin density waves. J. Phys. I France 1996, 6, 1875–1898. [Google Scholar] [CrossRef]
- Wu, M.K.; Ashburn, J.R.; Torng, C.J.; Hor, P.H.; Meng, R.L.; Gao, L.; Huang, Z.J.; Wang, Y.Q.; Chu, C.W. Superconductivity at 93 K in a new mixed-phase Y-Ba-Cu-0 compound system at ambient pressure. Phys. Rev. Lett. 1987, 58, 908–910. [Google Scholar] [CrossRef]
- Murata, K.; Yoshino, H.; Yadav, H.O.; Honda, Y.; Shirakawa, N. Pt resistor thermometry and pressure calibration in a clamped pressure cell with the medium, Daphne 7373. Rev. Sci. Instrum. 1997, 68, 2490–2493. [Google Scholar] [CrossRef]
- Yokogawa, K.; Murata, K.; Yoshino, H.; Aoyama, S. Solidification of high pressure medium Daphne 7373. Jpn. J. Appl. Phys. 2007, 46, 3636–3639. [Google Scholar] [CrossRef]
- Shishido, H.; Ueda, T.; Hashimoto, S.; Kubo, T.; Settai, R.; Harima, H.; Onuki, Y. A de Haas–van Alphen experiment under pressure on CeCoIn5, deviation from the quantum critical region. J. Phys. Condens. Matter 2003, 15, L499–L504. [Google Scholar] [CrossRef]
- Takashima, M.; Aoki, H.; Haworth, C.J.; Matsumoto, T.; Terashima, T.; Uji, S.; Terakura, C.; Miura, T.; Uesawa, A.; Suzuki, T. De Haas-van Alphen effect of CeSb under pressure. J. Phys. Soc. Jpn. 1998, 167, 3859–3866. [Google Scholar]
- Taniguchi, H.; Miyashita, M.; Uchiyama, K.; Satoh, K.; Mori, N.; Okamoto, H.; Miyagawa, K.; Kanoda, K.; Hedo, M.; Uwatoko, Y. Superconductivity at 14.2 K in layered organic under extreme pressure. J. Phys. Soc. Jpn. 2003, 72, 468–471. [Google Scholar] [CrossRef]
- Itoi, M.; Araki, C.; Hedo, M.; Uwatoko, Y.; Nakamura, T. Anomalously wide superconducting phase of one-dimensional organic conductor (TMTTF)2SbF6. J. Phys. Soc. Jpn. 2008, 77, 1–4. [Google Scholar]
- Murata, K.; Yokogawa, K.; Yoshino, H.; Klotz, S.; Munsch, P.; Irizawa, A.; Nishiyama, M.; Iizuka, K.; Nanba, T.; Okada, T.; Shiraga, Y.; Aoyama, S. Pressure transmitting medium Daphne 7474 solidifying at 3.7 GPa at room temperature. Rev. Sci. Instrum. 2008, 79, 1–8. [Google Scholar]
- Kotegawa, H.; Kawazoe, T.; Sugawara, H.; Murata, K.; Tou, H. Effect of uniaxial stress for pressure-induced superconductor, SrFe2As2. J. Phys. Soc. Jpn. 2009, 78, 1–4. [Google Scholar] [CrossRef]
- Yamazaki, T.; Takeshita, N.; Kobayashi, R.; Fukazawa, H.; Kohori, Y.; Kihou, K.; Lee, C.H.; Kito, H.; Iyo, A.; Eisaki, H. Appearance of pressure-induced superconductivity in BaFe2As2 under hydrostatic conditions and its extremely high sensitivity to uniaxial stress. Phys. Rev. B 2010, 81, 1–5. [Google Scholar]
- Campos, C.E.; Brooks, J.S.; van Bentum, P.J.M.; Perenboom, J.A.A.J.; Rook, J.; Klepper, S.J.; Tokumoto, M. Uniaxial stress method for delicate crystals: Application to Shubnikov-de Haas and superconductivity studies in organic conductors. Rev. Sci. Instrum. 1995, 66, 1061–1064. [Google Scholar] [CrossRef]
- Maesato, M.; Kaga, Y.; Kondo, R.; Kagoshima, S. Uniaxial strain method for soft crystals: Application to the control of the electronic properties of organic conductors. Rev. Sci. Instrum. 2000, 71, 176–181. [Google Scholar] [CrossRef]
- Kondo, R.; Kagoshima, S.; Harada, J. Crystal structure analysis under uniaxial strain at low temperature using a unique design of four-axis X-ray diffractometer with a fixed sample. Rev. Sci. Instrum. 2005, 76, 1–7. [Google Scholar]
- Campos, C.E.; Brooks, J.S.; van Bentum, P.J.M.; Perenboom, J.A.A.J.; Klepper, S.J.; Sandhu, P.S.; Valfells, S.; Tanaka, Y.; Kinoshita, T.; Kinoshita, N.; Tokumoto, M.; Anzai, H. Uniaxial-Stress-Induced superconductivity in organic conductors. Phys. Rev. B 1995, 52, R7014–R7017. [Google Scholar]
- Tajima, N.; Ebina-Tajima, A.; Tamura, M.; Nishio, Y.; Kajita, K. Effects of uniaxial strain on transport properties of organic conductor alpha-(BEDT-TTF)2I3 and discovery of superconductivity. J. Phys. Soc. Jpn. 2002, 71, 1832–1835. [Google Scholar] [CrossRef]
- Maesato, M.; Shimizu, Y.; Saito, G.; Miyagawa, K.; Kanoda, K. Spin-Liquid behavior and superconductivity in κ-(BEDT-TTF)2X: The role of uniaxial strain. J. Phys. IV France 2004, 114, 227–231. [Google Scholar] [CrossRef]
- Mori, H.; Tanaka, S.; Mori, T. Systematic study of the electronic state in θ-type BEDT-TTF organic conductors by changing the electronic correlation. Phys. Rev. B 1998, 57, 12023–12029. [Google Scholar] [CrossRef]
- Shimizu, Y.; Miyagawa, K.; Kanoda, K.; Maesato, M.; Saito, G. Spin liquid state in an organic Mott insulator with a triangular lattice. Phys. Rev. Lett. 2003, 91, 1–4. [Google Scholar]
- Andrieux, A.; Schulz, H.J.; Jérome, D.; Bechgaard, K. Fluctuation conductivity in 1-D conductor tetrathiafulvalene-tetracyanoquinodimethane (TTF-TCNQ). J. Phys. Lett. 1979, 40, L385–L389. [Google Scholar] [CrossRef]
- Jérome, D.; Schulz, H.J. Organic conductors and superconductors. Adv. Phys. 1982, 31, 299–490. [Google Scholar]
- Pouget, J.-P. X-Ray diffuse scattering as precursor of incommensurate Peierls transitions in one-dimensional organic charge transfer conductors. Z. Kristallogr. (Munich) 2004, 219, 711–718. [Google Scholar] [CrossRef]
- Khanna, S.K.; Pouget, J.P.; Comes, R.; Garito, A.F.; Heeger, A.J. X-Ray studies of 2kF and 4kF anomalies in tetrathiafulvalene-tetracyanoquinodimethane (TTF-TCNQ). Phys. Rev. B 1977, 16, 1468–1479. [Google Scholar] [CrossRef]
- Pouget, J.-P.; Khanna, S.K.; Denoyer, F.; Comes, R.; Garito, A.F.; Heeger, A.J. X-Ray observation of 2kF and 4kF scatterings in tetrathiafulvalene-tetracyanoquinodimethane (TTF-TCNQ). Phys. Rev. Lett. 1976, 37, 437–440. [Google Scholar] [CrossRef]
- Kagoshima, S.; Ishiguro, T.; Anzai, H. X-Ray scattering study of phonon anomalies and superstructures in TTF-TCNQ. J. Phys. Soc. Jpn. 1976, 41, 2061–2071. [Google Scholar] [CrossRef]
- Jérome, D. Organic conductors: From charge density wave TTF-TCNQ to superconducting (TMTSF)2PF6. Chem. Rev. 2004, 104, 5565–5591. [Google Scholar] [CrossRef]
- Yasuzuka, S.; Murata, K.; Arimoto, T.; Kato, R. Temperature-Pressure phase diagram in TTF-TCNQ: Strong suppression of charge-density-wave state under extremely high pressure. J. Phys. Soc. Jpn. 2007, 76, 1–4. [Google Scholar] [CrossRef]
- Ishibashi, S.; Kohyama, M. Ab initio pseudopotential calculation for TTF-TCNQ and TSeF-TCNQ. Phys. Rev. B 2000, 62, 7839–7844. [Google Scholar] [CrossRef]
- Friend, R.H.; Miljak, M.; Jérome, D. Pressure dependence of the phase transitions in tetrathiafulvalene-tetracyanoquinodimethane (TTF-TCNQ): Evidence for a longitudinal lock-in at 20 kbar. Phys. Rev. Lett. 1978, 40, 1048–1051. [Google Scholar] [CrossRef]
- Murata, K. Temperature-Pressure phase diagram of TSeF-TCNQ. Osaka City University: Osaka, Japan, Unpublished work. 2006. [Google Scholar]
- Soda, G.; Jérome, D.; Weger, M.; Fabre, J.M.; Giral, L. Interchain coupling and nuclear magnetic relaxation in the organic conductor tetrathiafulvalene-tetracyanoquinodimethane TTF-TCNQ. Solid State Commun. 1976, 18, 1417–1421. [Google Scholar] [CrossRef]
- Murata, K.; Weng, Y.; Seno, Y.; Tamilselvan, N.R.; Kobayashi, K.; Arumugam, S.; Takashima, Y.; Yoshino, H.; Kato, R. Fluctuation of the charge density wave in TTF-TCNQ under high pressure. Phys. B Phys. Condens. Matter 2009, 404, 373–375. [Google Scholar] [CrossRef]
- Weger, M. A model for the electronic band structure of HMTSeF-TCNQ. Solid State Commun. 1976, 19, 1149–1155. [Google Scholar] [CrossRef]
- Ishibashi, S. Electronic band structure calculation under pressure of TTF-TCNQ. Private Communication, Agency of Industrial Science and Technology: Tsukuba, Japan, 2008. [Google Scholar]
- Murata, K.; Yokogawa, K.; Kobayashi, K.; Masuda, K.; Sasaki, T.; Seno, Y.; Tamilselvan, N.R.; Yoshino, H.; Brooks, J.S.; Jérome, D.; et al. Field-Induced successive phase transitions in the CDW organic conductor HMTSF-TCNQ. J. Phys. Soc. Jpn. 2010, 79, 1–4. [Google Scholar]
- Murata, K.; Kang, W.; Masuda, K.; Kuse, T.; Sasaki, T.; Yokogawa, K.; Yoshino, H.; Brooks, J.S.; Choi, E.S.; Kiswandhi, A.; Kato, R. Field-Induced CDW in HMTSF-TCNQ. Phys. B 2012, 407, 1927–1929. [Google Scholar] [CrossRef]
- Mortensen, K.; Tomkiewicz, Y.; Bechgaard, K. Antiferromagnetism in the organic conductor, bis-tetramethyltetraselenafulvalene hexafluoroarsenate, [(TMTSF)2AsF6]: Static magnetic susceptibility. Phys. Rev. B 1982, 25, 3319–3325. [Google Scholar] [CrossRef]
- Takahashi, T.; Maniwa, Y.; Kawamura, H.; Saito, G. Determination of SDW characteristics in (TMTSF)2PF6 by 1H-NMR analysis. Phys. B + C 1986, 143, 417–421. [Google Scholar] [CrossRef]
- Delrieu, J.M.; Roger, M.; Toffano, Z.; Moradpour, A.; Bechgaard, K. NMR proton lineshape in (TMTSF)2X: Incommensurability of nesting vector and order parameter. J. Phys. France 1986, 47, 839–861. [Google Scholar] [CrossRef]
- Murata, K.; Anzai, H.; Ukachi, T.; Ishiguro, T. Metal-Insulator transition in (TMTTF)2BF4 under pressure. J. Phys. Soc. Jpn. 1984, 53, 491–494. [Google Scholar] [CrossRef]
- Chow, D.S.; Zamborszky, F.; Alavi, B.; Tantillo, D.J.; Baur, A.; Merlic, C.; Brown, S.E. Charge ordering in the TMTTF Family of molecular conductors. Phys. Rev. Lett. 2000, 85, 1698–1701. [Google Scholar] [CrossRef]
- Zamborszky, F.; Raas, W.Y.W.; Brown, S.E.; Alavi, B.; Merlic, C.A.; Baur, A. Competition and coexistence of bond and charge orders in (TMTTF)2AsF6. Phys. Rev. B 2002, 66, 1–4. [Google Scholar]
- Takahashi, T.; Nogami, Y.; Yakushi, K. Charge ordering in organic conductors. J. Phys. Soc. Jpn. 2006, 75, 1–17. [Google Scholar]
- Jérome, D. The physics of organic superconductors. Science 1991, 252, 1509–1514. [Google Scholar]
- Adachi, T.; Ojima, E.; Kato, K.; Kobayashi, H.; Miyazaki, T.; Tokumoto, M.; Kobayashi, A. Superconducting transition of (TMTTF)2PF6 above 50 kbar [TMTTF = Tetramethyltetra-thiafulvalene. J. Am. Chem. Soc. 2000, 122, 3238–3239. [Google Scholar] [CrossRef]
- Jaccard, D.; Wilhelm, H.; Jérome, D.; Moser, J.; Carcel, C.; Fabre, J.M. From spin-Peierls to superconductivity: (TMTTF)2PF6 under high pressure. J. Phys. Condens. Matter 2001, 13, L89–L95. [Google Scholar] [CrossRef]
- Guo, F.Z.; Murata, K.; Oda, A.; Mizuno, Y.; Yoshino, H. Spin density wave transition in (TMTSF)2PF6 under uniaxial strain. J. Phys. Soc. Jpn. 2000, 69, 2164–2169. [Google Scholar] [CrossRef]
- Murata, K.; Mizuno, Y.; Guo, FZ.; Shodai, S.; Iwashita, K.; Yoshino, H. Spin density wave in a reduced anisotropy in (TMTSF)2PF6. Mol. Cryst. Liq. Cryst. 2002, 380, 85–92. [Google Scholar]
- Grant, P.M. Electronic structure of the 2:1 charge transfer salts of TMTCF. J. Phys. Colloques 1983, 44, 847–857. [Google Scholar]
- Guo, F.Z.; Murata, K.; Yoshino, H.; Maki, S.; Tanaka, S.; Yamada, J.; Nakatsuji, S.; Anzai, H. Anion-Ordering transition in (TMTSF)2ClO4 under pressure. J. Phys. Soc. Jpn. 1998, 67, 3000–3002. [Google Scholar] [CrossRef]
- Yagubskii, E.B.; Shchegolev, I.F.; Laukhin, V.N.; Kononovich, P.A.; Karatsovnik, M.V.; Zvarykina, A.V.; Buravov, L.I. Normal-Pressure superconductivity in an organic metal (BEDT-TTF)2I3. JETP Lett. 1984, 39, 12–16. [Google Scholar]
- Murata, K.; Tokumoto, M.; Anzai, H.; Bando, H.; Saito, G.; Kajimura, K.; Ishiguro, T. Superconductivity with the onset at 8 K in β-(BEDT-TTF)2I3 under pressure. J. Phys. Soc. Jpn. 1985, 54, 1236–1239. [Google Scholar] [CrossRef]
- Murata, K.; Tokumoto, M.; Anzai, H.; Bando, H.; Saito, G.; Kajimura, K.; Ishiguro, T. Pressure phase diagram of the organic superconductor β-(BEDT-TTF)2I3. J. Phys. Soc. Jpn. 1985, 54, 2084–2087. [Google Scholar] [CrossRef]
- Laukhin, V.N.; Kostyuchenko, E.E.; Sushko, V.Y.; Shchegolev, I.F.; Yagubskii, E.B. Effect of pressure on the superconductivity of beta-(BEDT-TTF)2I3. JETP Lett. 1985, 41, 81–84. [Google Scholar]
- Lacoe, R.C.; Wolf, S.A.; Chaikin, P.M.; Wudl, F.; Aharon-Shalom, E. Metal-Insulator transitions and superconductivity in ditetramethyltetraselenafulvalenium fluorosulfonate [(TMTSF)2FSO3]. Phys. Rev. B 1983, 27, 1947–1950. [Google Scholar]
- Fisher, R.A.; Kim, S.; Woodfield, B.F.; Phillips, N.E.; Taillefer, L.; Hasselbach, K.; Flouquet, J.; Giorgi, A.L.; Smith, J.L. Specific heat of UPt3: Evidence for unconventional superconductivity. Phys. Rev. Lett. 1989, 62, 1411–1414. [Google Scholar]
- Leung, P.C.W.; Emge, T.J.; Beno, M.A.; Wang, H.H.; Williams, J.M.; Petricek, V.; Coppens, P. Novel structural modulation in the ambient-pressure sulfur-based organic superconductor β-(BEDT-TTF)2I3: Origin and effects on its electrical conductivity. J. Am. Chem. Soc. 1985, 107, 6184–6191. [Google Scholar] [CrossRef]
- Ravy, S.; Moret, R.; Pouget, J.P. Explanation of the phase diagram of beta-di[bis(ethylene-dithio)tetrathiafulvalene] triiodide based on the two configurations of the organic molecule. Phys. Rev. B 1988, 38, 4469–4480. [Google Scholar] [CrossRef]
- Ginodman, V.B.; Gudenko, A.V.; Kononovich, P.A.; Laukhin, V.N.; Shchegolev, I.F. Direct detection of the beta-1.5 beta-8 phase transition in beta-(ET)2I3. JETP Lett. 1986, 44, 673–677. [Google Scholar]
- Tokumoto, M.; Anzai, H.; Murata, K.; Kajimura, K.; Ishiguro, T. Effect of Alloying on the superconductivity in organic metals β-(BEDT-TTF)2 trihalides. Synthet. Metal. 1988, 27, A251–A256. [Google Scholar] [CrossRef]
- Murata, K.; Tokumoto, M.; Anzai, H.; Honda, Y.; Kinoshita, N.; Ishiguro, T.; Toyota, N.; Sasaki, T.; Muto, Y. Superconductivity of BEDT-TTF salts; (I) effect of pressure and alloying and (II) Shubnikov de Haas Effect. Synthet. Metal. 1988, 27, A263–A270. [Google Scholar] [CrossRef]
- Murata, K.; Toyota, N.; Tokumoto, M.; Anzai, H.; Saito, G.; Kajimura, K.; Morita, S.; Muto, Y.; Ishiguro, T. Upper critical field of β-(BEDT-TTF)2I3 in the High Tc superconducting state. Phys. B 1986, 143, 366–368. [Google Scholar]
- Laukhin, V.N.; Pesotskii, S.I.; Yagubskii, E.B. Exceeding the paramagnetic limit of Hc2 in an organic superconductor beta-(ET)2I3 with Tc = 7.1 K. JETP Lett. 1987, 45, 501–504. [Google Scholar]
- Murata, K.; Toyota, N.; Honda, Y.; Sasaki, T.; Tokumoto, M.; Bando, H.; Anzai, H.; Muto, Y.; Ishiguro, T. Magnetoresistance in β-(BEDT-TTF)2I3 and β-(BEDT-TTF)2IBr2, Shubnikov de Haas effect. J. Phys. Soc. Jpn. 1988, 57, 1540–1543. [Google Scholar] [CrossRef]
- Toyota, N.; Sasaki, T.; Murata, K.; Honda, Y.; Tokumoto, M.; Bando, H.; Anzai, H.; Ishiguro, T.; Muto, Y. Cyclotron mass and Dingle temperature of conduction electrons moving in a layered plane of organic superconductors β-(BEDT-TTF)2IBr2, β-(BEDT-TTF)2I3 and κ-(BEDT-TTF)2Cu(NCS)2. J. Phys. Soc. Jpn. 1988, 57, 2616–2619. [Google Scholar]
- Kang, W.; Montambaux, G.; Cooper, J.R.; Jérome, D.; Batail, P.; Lenoir, C. Observation of giant magnetoresistance oscillation in the high-Tc phase of the two-dimensional organic conductor beta-(BEDT-TTF)2I3. Phys. Rev. Lett. 1989, 62, 2559–2562. [Google Scholar] [CrossRef]
- Oshima, K.; Mori, T.; Inokuchi, H.; Urayama, H.; Yamochi, H.; Saito, G. Shubnikov-de Haas effect and Fermi surface in an ambient pressure organic superconductor (BEDT-TTF)2Cu(NCS)2. Phys. Rev. B 1988, 38, 938–941. [Google Scholar]
- Kajita, K.; Nishio, Y.; Takahashi, T.; Sasaki, W.; Kato, R.; Kobayashi, H.; Kobayashi, A.; Iye, Y. A new type oscillatory phenomenon in the magnetotransport of θ-(BEDT-TTF)2I3. Solid State Commun. 1989, 70, 1189–1193. [Google Scholar] [CrossRef]
- Yamaji, K. On the angle dependence of the magnetoresistance in quasi-two-dimensional organic superconductors. J. Phys. Soc. Jpn. 1989, 58, 1520–1523. [Google Scholar] [CrossRef]
- Kartsovnik, M.V.; Kononovich, P.A.; Laukhin, V.N.; Schegolev, I.F. Anisotropy of magnetoresistance and the Shubnikov-de Haas oscillations in the organic metal beta-(ET)2IBr2. Pis’ma Zh. Eksp. Teor. Fiz. 1988, 48, 498–501. [Google Scholar]
- Hennig, I.; Bender, K.; Schweitzer, D.; Dietz, K.; Endres, H.; Keller, H.J.; Gleitz, A.; Helberg, H.W. Alpha- and beta-(BEDT-TTF)2+I3− two dimensional organic metals. Mol. Cryst. Liq. Cryst. 1985, 11, 337–441. [Google Scholar]
- Kinoshita, N.; Tokumoto, M.; Anzai, H.; Saito, G. Anisotropy in ESR 9 Factors and Linewidths for α-and β-(BEDT-TTF)2I3. J. Phys. Soc. Jpn. 1985, 54, 4498–4501. [Google Scholar] [CrossRef]
- Sugano, T.; Saito, G.; Kinoshita, M. Spin relaxation and diffusion in quasi-two-dimensional organic metals: The bis(ethylenedithiolo)tetrathiafulvalene compounds β-(BEDT-TTF)2X (X = I3 and IBr2). Phys. Rev. B 1987, 35, 6554–6559. [Google Scholar] [CrossRef]
- Sugano, T.; Saito, G.; Kinoshita, M. Conduction-Electron-Spin resonance in organic conductors: α and β phases of di[bis(ethylenedithiolo)tetrathiafulvalene]triiodide [(BEDT-TTF)2I3]. Phys. Rev. B 1986, 34, 117–125. [Google Scholar]
- Kajita, K.; Ojiro, T.; Fujii, H.; Nishio, Y.; Kobayashi, H.; Kobayashi, A.; Kato, R. Magnetotransport phenomena of α-Type (BEDT-TTF)2I3 under high pressures. J. Phys. Soc. Jpn. 1992, 61, 23–26. [Google Scholar] [CrossRef]
- Katayama, S.; Kobayashi, A.; Suzumura, Y. Pressure-Induced zero-gap semiconducting state in organic conductor α-(BEDT-TTF)2I3 salt. J. Phys. Soc. Jpn. 2006, 75, 1–6. [Google Scholar]
- Takahashi, T.; Nogami, Y.; Yakushi, K. Charge ordering in organic conductors. J. Phys. Soc. Jpn. 2006, 75. [Google Scholar]
- Takano, Y.; Hiraki, K.; Takada, Y.; Yamamoto, H.M.; Takahashi, T. Local spin susceptibility characteristic of zero-gap state of α-(BEDT-TTF)2I3 under pressure. J. Phys. Soc. Jpn. 2010, 79, 1–7. [Google Scholar]
- Montambaux, G.; Piéchon, F.; Fuchs, J.-N.; Goerbig, M.O. Merging of Dirac points in a two-dimensional crystal. Phys. Rev. B 2009, 80, 1–4. [Google Scholar]
- Kino, H. Theoretical electronic band structure of alpha-(BEDT-TTF)2I3. Private Communication, National Research Institute for Metals: Tsukuba, Japan, 2012. [Google Scholar]
- Nishikawa, H.; Sekiya, H.; Fujiwara, A.; Kodama, T.; Ikemoto, I.; Kikuchi, K.; Yamada, J.; Oshio, H.; Kobayashi, K.; Yasuzuka, S.; Murata, K. Molecular conductor based on reduced π-system donor: Insulating state of (MeDH-TTP)2AsF6. Chem. Lett. 2006, 35, 912–913. [Google Scholar]
- Yasuzuka, S.; Kobayashi, K.; Nishiwaka, H.; Yoshino, H.; Murata, K. Quantum criticality in reduced pi-donor system (MeDH-TTP)2AsF6. J. Phys. Soc. Jpn. 2006, 75, 1–4. [Google Scholar]
- Zambounis, J.S.; Pfeiffer, J.; Papavassiliou, G.C.; Lagouvardos, D.J.; Terzis, A.; Raptoupoulou, C.P.; Delhaes, P.; Ducasse, L.; Fortune, N.A.; Murata, K. Structural and physical properties of τ-(P-(S,S)-DMEDT-TTF)2(AuBr2)1(AuBr2)0.75. Solid State Commun. 1995, 95, 211–215. [Google Scholar] [CrossRef]
- Papavassiliou, G.C.; Lagouvardos, D.J.; Zambounis, J.S.; Terzis, A.; Raptopoulou, C.R.; Murata, K.; Shirakawa, N.; Ducasse, L.; Delhaes, P. Structural and physical properties of τ-(EDO-S,S-DMEDT-TTF)2(AuBr2)1(AuBr2)y. Mol. Cryst. Liq. Cryst. 1996, 285, 83–88. [Google Scholar] [CrossRef]
- Murata, K.; Yoshino, H.; Tsubaki, Y.; Papavassiliou, G.C. Hysteretic magnetic state in the organic τ-phase conductors. Synthet. Metal. 1998, 94, 69–72. [Google Scholar] [CrossRef]
- Konoike, T.; Iwashita, K.; Nakano, I.; Yoshino, H.; Sasaki, T.; Takahashi, T.; Nogami, Y.; Brooks, J.S.; Graf, D.; Mielke, C.H.; Papavassiliou, G.C.; Murata, K. Shubnikov-de Haas oscillations and low temperature electric structure in τ-phase conductors. Synthet. Metal. 2003, 615-616, 135–136. [Google Scholar]
- Konoike, T.; Iwashita, K.; Yoshino, H.; Murata, K.; Sasaki, T.; Papavassiliou, G.C. Shubnikov de Haas oscillations in a 2D organic conductor tau-(EDO-S,S-DMEDT-TTF)2(AuBr2)1+y (y ~ 0.75). Phys. Rev. B 2002, 66, 1–5. [Google Scholar]
- Storr, K.; Balicas, L.; Brooks, J.S.; Graf, D.; Papavassiliou, G.C. Magnetic-Field-Dependent interplay between incoherent and Fermi liquid transport mechanisms in low-dimensional τ-phase organic conductors. Phys. Rev. B 2001, 64, 1–9. [Google Scholar]
- Murata, K.; Yoshino, H.; Nakanishi, T.; Konoike, T.; Brooks, J.; Graf, D.; Mielke, C.; Papavassiliou, G.C. A new quantum hall effect in the two-dimensional organic conductor, tau-(EDO-S,S-DMEDT-TTF)2(AuBr2)1+y. Curr. Appl. Phys. 2004, 4, 488–490. [Google Scholar] [CrossRef]
- Brooks, J.S.; Graf, D.; Choi, E.S.; Balicas, L.; Storr, K.; Mielk, C.H.; Papavassiliou, G.C. High magnetic field-induced insulating phase in an organic conductor. 2002, arXiv:cond-mat/0209592v1. Available online: http://arxiv.org/abs/physics/0402096 (accessed on 9 October 2012).
- Yoshino, H.; Aizawa, H.; Kuroki, K.; Anyfantis, G.C.; Papavassiliou, G.C.; Murata, K. Thermoelectric figure of merit of τ-type conductors of several donors. Physica B 2010, 405, S79–S81. [Google Scholar]
- Kikuchi, K.; Isono, T.; Kojima, M.; Yoshimoto, H.; Kodama, T.; Fujita, W.; Yokogawa, K.; Yoshino, H.; Murata, K.; Kaihatsu, T.; Akutsu, H.; Yamada, J. Uniaxial strain orientation dependence of superconducting transition temperature (Tc) and critical superconducting pressure (Pc) in β-(BDA-TTP)2I3. J. Am. Chem. Soc. 2011, 133, 19590–19593. [Google Scholar]
- Nuruzzaman, M.; Yokogawa, K.; Yoshino, H.; Yoshimoto, H.; Kikuchi, K.; Kaihatsu, T.; Yamada, J.; Murata, K. Uniaxial-Strain-Orientation dependence of the competition between Mott and charge ordered phases and their corresponding superconductivity of β-(BDA-TTP)2I3. J. Phys. Soc. Jpn. 2012, in press. [Google Scholar]
© 2012 by the authors; licensee MDPI, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Murata, K.; Yokogawa, K.; Arumugam, S.; Yoshino, H. Pressure Effect on Organic Conductors. Crystals 2012, 2, 1460-1482. https://doi.org/10.3390/cryst2041460
Murata K, Yokogawa K, Arumugam S, Yoshino H. Pressure Effect on Organic Conductors. Crystals. 2012; 2(4):1460-1482. https://doi.org/10.3390/cryst2041460
Chicago/Turabian StyleMurata, Keizo, Keiichi Yokogawa, Sonachalam Arumugam, and Harukazu Yoshino. 2012. "Pressure Effect on Organic Conductors" Crystals 2, no. 4: 1460-1482. https://doi.org/10.3390/cryst2041460
APA StyleMurata, K., Yokogawa, K., Arumugam, S., & Yoshino, H. (2012). Pressure Effect on Organic Conductors. Crystals, 2(4), 1460-1482. https://doi.org/10.3390/cryst2041460





