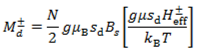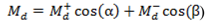2.1. Large 3d Spin Degrees of Freedom
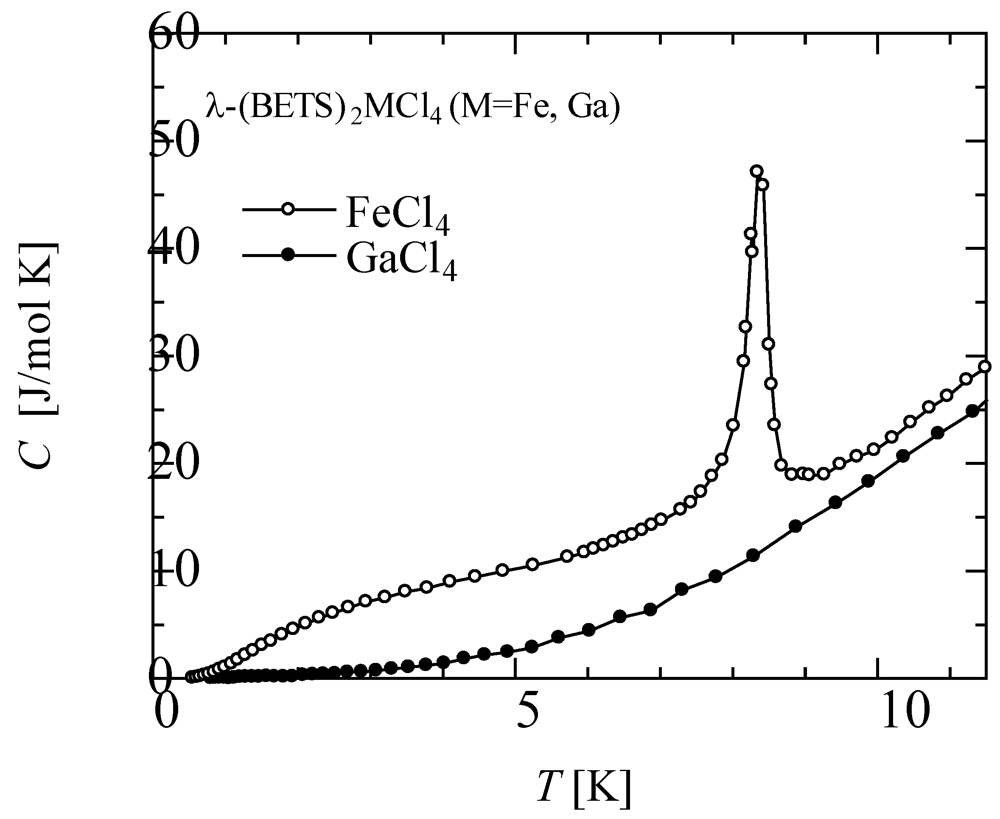
We measured the specific heat of λ-BETS
2FeCl
4 and nonmagnetic λ-BETS
2GaCl
4 by the thermal relaxation method. The specific heat of FeCl
4 and GaCl
4salts are indicated by open and closed circles in
Figure 1, respectively. The specific heat of FeCl
4 salt shows a sharp peak at the MI transition temperature (
TMI ~ 8.3 K) and has a larger value than that of GaCl
4 salt at the entire temperature region. In order to study the excess components of the FeCl
4 salt in detail, we first estimated its lattice and electronic specific heat. We assumed that the specific heat of isostructural GaCl
4 salt was equivalent to the lattice specific heat of FeCl
4 salt.
Figure 1.
Temperature dependencies of the specific heat of λ-BETS
2FeCl
4 (○) and λ-BETS
2GaCl
4 (●). Reproduced with permission from JPSJ [
11].
Figure 1.
Temperature dependencies of the specific heat of λ-BETS
2FeCl
4 (○) and λ-BETS
2GaCl
4 (●). Reproduced with permission from JPSJ [
11].
The electronic specific heats of these two salts were clearly different since the GaCl
4 salt exhibited superconductivity at 5.5 K, while the FeCl
4 salt underwent an MI transition at 8.3 K. Around 5.5 K, the GaCl
4 salt exhibited superconductivity of the BCS type and showed the specific heat jump 1.43 γ
T J/mol·K [
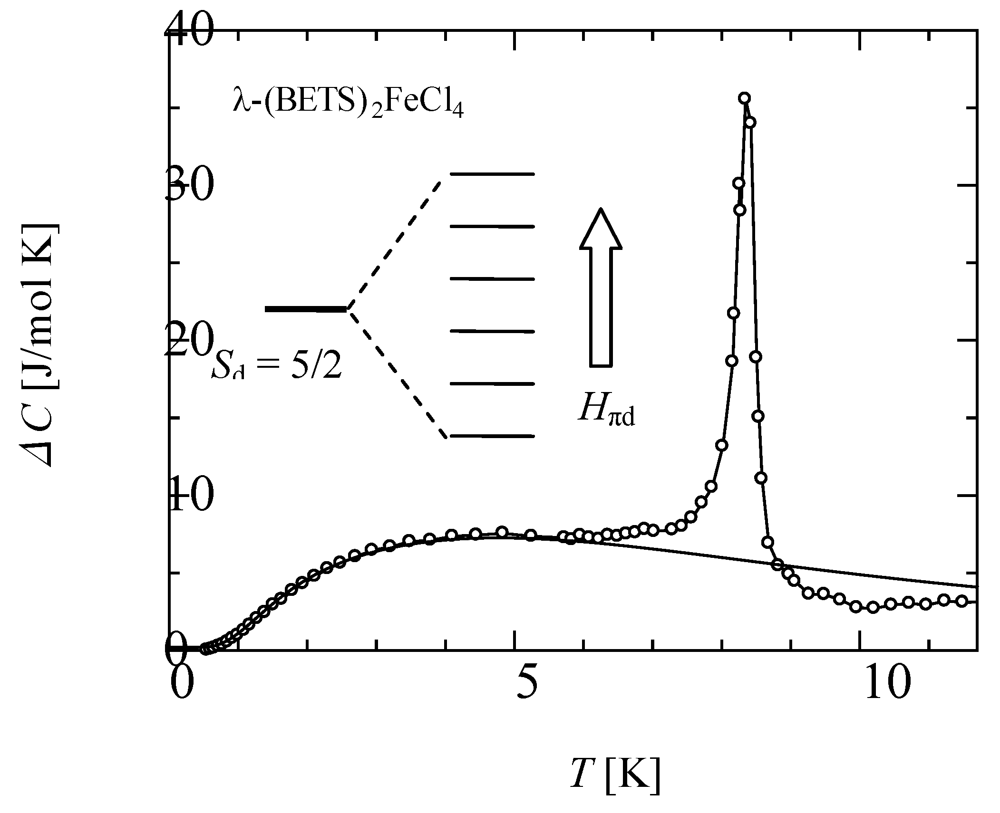
12]. Considering the difference in these electronic specific heats, we obtained the excess specific heats Δ
C (shown in
Figure 2) by subtracting the lattice and electronic specific heats in the PM phase, and subtracting the lattice contribution in the AFI phase, respectively.
Figure 2.
Excess specific heat Δ
C of λ-BETS
2FeCl
4 by subtracting the lattice and the electric specific heat estimated for λ-BETS
2GaCl
4. The solid curve shows the calculated specific heat based on the paramagnetic 3
d spin (Fe
3+sd= 5/2) system under the internal magnetic field
Hπd = 4.0 T. The inset shows the energy levels of
sd = 5/2 caused by Zeeman splitting. Reproduced with permission from JPSJ [
11].
Figure 2.
Excess specific heat Δ
C of λ-BETS
2FeCl
4 by subtracting the lattice and the electric specific heat estimated for λ-BETS
2GaCl
4. The solid curve shows the calculated specific heat based on the paramagnetic 3
d spin (Fe
3+sd= 5/2) system under the internal magnetic field
Hπd = 4.0 T. The inset shows the energy levels of
sd = 5/2 caused by Zeeman splitting. Reproduced with permission from JPSJ [
11].
The open circles in
Figure 2 show the excess specific heat Δ
C obtained by subtraction of the lattice and electronic specific heat estimated for the GaCl
4 salt from the total specific heat of the FeCl
4 salt. A sharp peak was observed at 8.3 K. It should be noted that a broad hump that appears to be a Schottky-type anomaly was found in a lower temperature side of the sharp peak. If the π and 3
d spins cooperatively align antiferromagnetically below
TMI, as was expected for the present system, the larger peak of the specific heat would only exist at
TMI, followed by a rapid reduction without the formation of the hump. This behavior is completely different from that of Δ
C in
Figure 2. We can speculate that the Schottky-type specific heat is derived from the paramagnetic 3
d spin under the internal magnetic field induced by the π-
d interaction.
Since the Schottky-type anomaly occurs for 3
d or π spin systems only under the influence of a magnetic field, we calculated the temperature dependence of the specific heat of the 3
d spin
sd = 5/2 and π spin
sπ = 1/2 systems for paramagnetic states and obtained the best fit for the excess specific heat Δ
C in the case of the Fe
3+ 3
d spin. The energies at
sd = 5/2 were split into six levels by the Zeeman splitting under an internal magnetic field
Hπd ascribed to the π-
d interactions, as shown in the inset of
Figure 2. On the basis of the results of the energy splitting, we estimated the internal magnetic field
Hπd from the π spin to the 3
d spin as 4.0 T, while the internal magnetic field
Hdπ caused by the 3
d spin to the π electron was estimated as
Hdπ = 33 T from the experimental results of the field-induced superconductivity [
4,
13]. We consider that this disagreement is mainly due to the different origins (
sπ and
sd) of
Hπd and
Hdπ.
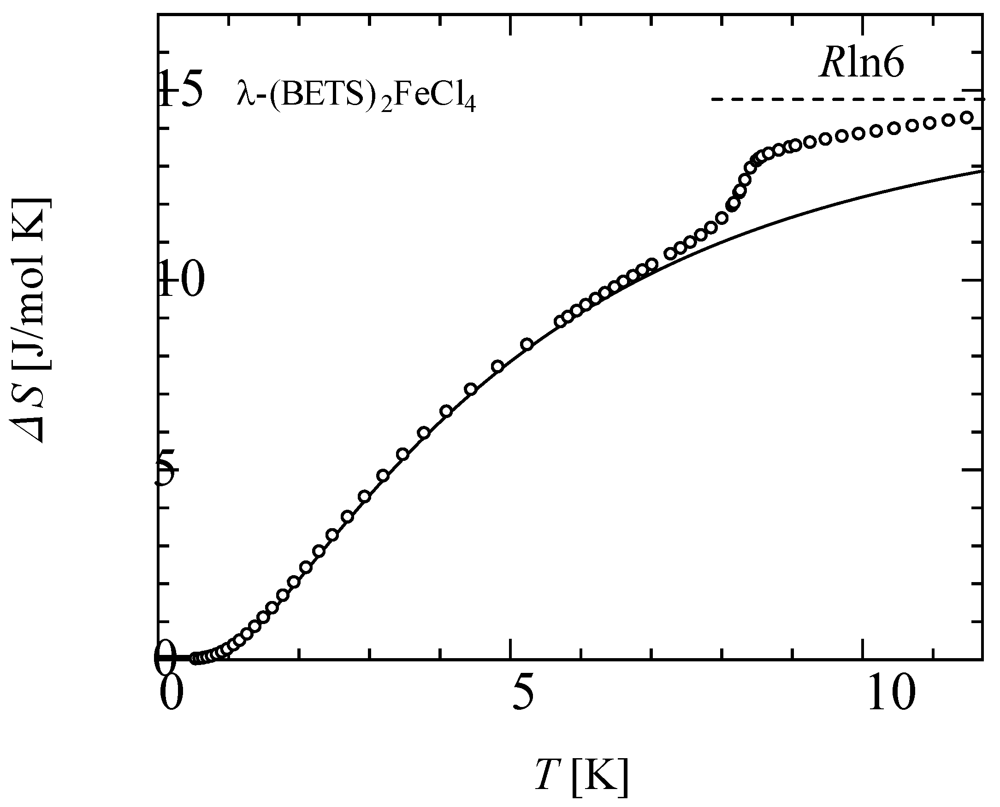
The integration of Δ
C/
T was performed to estimate the entropy
S, which derives information about the degrees of freedom, as shown in
Figure 3. The resulting entropy was close to a value of
Rln6 (
Rln6 = 14.9 J/mol·K),
i.e., the spin degrees of freedom for the 3
d spin (
Rln(2
sd + 1),
sd = 5/2). These experimental results suggest that the 3
d spin degrees of freedom give a large contribution to the sharp peak as well as the Schottky-type hump. It should be noted that about 80% of the 3
d spin degrees of freedom is sustained just below
TMI.
Figure 3.
Temperature dependencies of spin entropy of λ-BETS
2FeCl
4 calculated from Δ
C (○), calculated from specific heat of Schottky-type (solid curves). The dashed line shows the degrees of freedom for 3
d spins. Reproduced with permission from JPSJ [
11].
Figure 3.
Temperature dependencies of spin entropy of λ-BETS
2FeCl
4 calculated from Δ
C (○), calculated from specific heat of Schottky-type (solid curves). The dashed line shows the degrees of freedom for 3
d spins. Reproduced with permission from JPSJ [
11].
At MI transition, π electron system transfers from the Pauli paramagnetic metal state having the entropy of π electron
Sπ = γ
T to the antiferromagnetic insulator with
Sπ = 0 because of the strong π-π exchange interaction
Jππ/
kB = 448 K, which is much larger than the metal-insulator transition temperature
TMI [
14]. The entropy difference Δ
Sπ in both phases corresponds to the γ
TMI = 0.014 × 8.3 = 0.17 J/mol·K by assuming that the electronic density of the states at Fermi level is the same with that of GaCl
4 salt [
12]. Its value is much smaller than the observed 3
d contribution
Rln6. From this result of entropy, we could not detect the large reductions of
Rln2 ~ 5.7 J/mol·K accompanied with the AF ordering of π spin (
sπ = 1/2). Combining the metal-insulator transition is a remarkable feature of this novel AF spin alignment.
2.2. Magnetic and Thermal Properties in AFI Phase
The magnetic susceptibility provides information about the direction and magnitude of the internal magnetic field
Hπd. To clarify the origin of the splitting of the 3
d spin state, we examined the magnetic susceptibility.
Figure 4 illustrates the magnetic susceptibility observed under application of an external field
H of 0.1 T along the
c-axis. Above
TMI, the magnetic susceptibility
M/
H shows Curie-Weiss-type behavior for
sd = 5/2. At
TMI, it shows a sharp step down, and subsequently,
M/
H reduces with decreasing temperature. We also find that
M/
H has a shoulder-shaped anomaly below
TMI. This characteristic shoulder is observed in the curve at low temperatures, corresponding to the region where the Schottky-type specific heat anomaly is also observed. These findings suggest a common origin of the shoulder in the magnetic susceptibility curve and the Schottky-type specific heat.
Figure 4.
Magnetic susceptibility
M/
H of λ-BETS
2FeCl
4 under an external magnetic field parallel to the
c-axis. The solid and dashed curves show the magnetic susceptibility calculated on the basis of the paramagnetic 3
d spin model and Curie–Weiss law, respectively. Reproduced with permission from JPSJ [
15].
Figure 4.
Magnetic susceptibility
M/
H of λ-BETS
2FeCl
4 under an external magnetic field parallel to the
c-axis. The solid and dashed curves show the magnetic susceptibility calculated on the basis of the paramagnetic 3
d spin model and Curie–Weiss law, respectively. Reproduced with permission from JPSJ [
15].
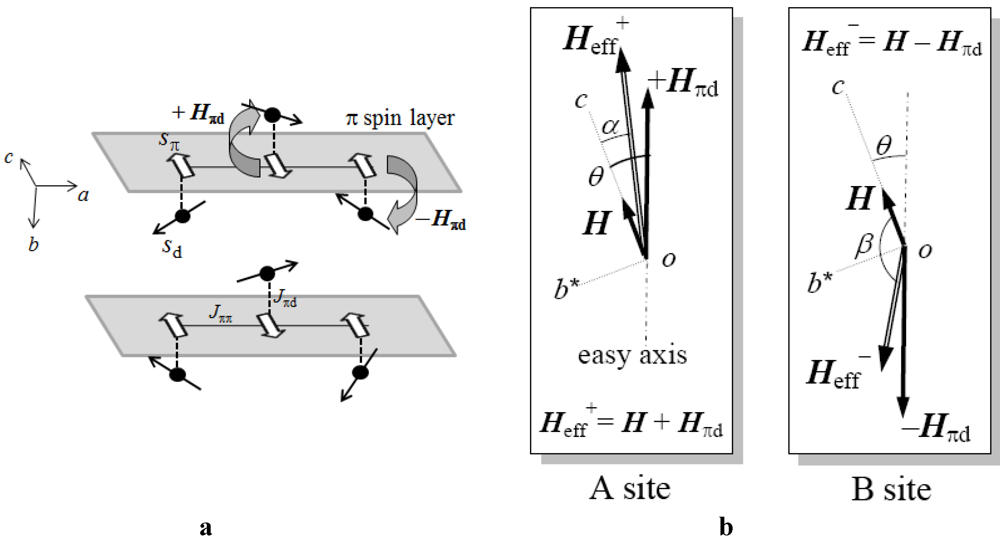
This internal magnetic field
Hπd is generated by the exchange interaction
Jπd with the AF-ordered π spin system. The π-
d interaction having the shortest contact was found to be the strongest coupling between several π-
d couplings [
14]. Assuming that this coupling dominates the internal magnetic field
Hπd, we may ignore the other weak couplings and propose a possible spin structure in the AFI phase, as shown in
Figure 5a. In this case, the internal magnetic field on the 3
d spin induced by the nearest neighbor π spin is alternately oriented in the opposite direction. Since the alternating internal magnetic field begins to align the 3
d spins as the temperature decreases, the magnetization of the 3
d spin system will be canceled out, and so will gradually decrease in the AFI phase.
Figure 5.
(
a) Schematic view of the π and 3
d spin structure in the AFI phase. The open and closed arrows represent π spin
sπ = 1/2 localized at the BETS dimer and Fe 3
d spin
sd = 5/2, respectively. After the AF ordering of π spin, the internal fields +
Hπd and −
Hπd are expected at the Fe sites. (
b) Effective magnetic field
Heff+ (
Heff−) at the Fe A (B) site with the external field
H parallel to the
c-axis and the internal field +
Hπd (−
Hπd). The AF easy axis is confined to the
b*
c plane and makes an angle θ with respect to the
c-axis [
16].
Figure 5.
(
a) Schematic view of the π and 3
d spin structure in the AFI phase. The open and closed arrows represent π spin
sπ = 1/2 localized at the BETS dimer and Fe 3
d spin
sd = 5/2, respectively. After the AF ordering of π spin, the internal fields +
Hπd and −
Hπd are expected at the Fe sites. (
b) Effective magnetic field
Heff+ (
Heff−) at the Fe A (B) site with the external field
H parallel to the
c-axis and the internal field +
Hπd (−
Hπd). The AF easy axis is confined to the
b*
c plane and makes an angle θ with respect to the
c-axis [
16].
Next, we tried to reproduce the characteristic shoulder in the magnetic susceptibility on the basis of this spin model. Under the weak external field
H = 0.1 T (<< spin-flop field
HSF ~ 1 T [
6]), the π spin system forms AF alignment along the easy axis and produces the internal magnetic fields +
Hπd and −
Hπd on the Fe 3
d spin at sites A and B, respectively, where the effective magnetic field
Heff± becomes
Heff± =
H ±
Hπd, as shown in
Figure 5b. We calculated the magnetizations
Md+ and
Md− at sites A and B, respectively, using the Brillouin function
Bs(
x) as
In this study, the external magnetic field is applied along the
c-axis. According to the torque measurement by Sasaki
et al. [
16], the
c-axis is tilted by about θ = 30° from the easy axis. Considering the tilt angle θ, the total magnetization component
Md parallel to
H can be obtained as
where the angles α between
H and
Heff+ and β between
H and
Heff− can be determined from θ,
Hπd, and
H (see
Figure 6b). The calculated magnetic susceptibility
Md/
H can well reproduce the resulting data, as shown by the solid curve in
Figure 4, using the following parameter values:
H = 0.1 T, θ = 25°, and
Hπd = 4 T. The strength of this internal field is in good agreement with the value estimated from the Schottky specific heat. In addition, Waerenborgh
et al. observed sextet Fe Mössbauer signals generated by an internal magnetic field
Hπd, which supports the paramagnetic model of the Fe 3
d spin [
17].
Figure 6.
(a) Temperature dependence of specific heat for mixed crystals λ-BETS2FexGa1−xCl4 (○) and λ-BETS2GaCl4 (●). (b) Excess specific heat ΔC of λ-BETS2FexGa1−xCl4 obtained by subtracting lattice and electric specific heats estimated for λ-BETS2GaCl4.
Figure 6.
(a) Temperature dependence of specific heat for mixed crystals λ-BETS2FexGa1−xCl4 (○) and λ-BETS2GaCl4 (●). (b) Excess specific heat ΔC of λ-BETS2FexGa1−xCl4 obtained by subtracting lattice and electric specific heats estimated for λ-BETS2GaCl4.
In the high-temperature metallic phase, the magnetic susceptibility follows the Curie-Weiss law with 3
d spin
sd = 5/2, as shown by the dashed curve in
Figure 4. It is notable that over the entire temperature range studied, the Fe 3
d spin paramagnetic states dominate the magnetic susceptibility and specific heat. Because we can expect that for the π spin system, the temperature-independent Pauli paramagnetic susceptibility
χPauli is approximately 3 × 10
−4 emu, which is three orders of magnitude smaller than that for Fe 3
d predicted by the Curie-Weiss law, assuming that the electronic density of states at the Fermi level is the same as that for λ-BETS
2GaCl
4 [
12].
At
TMI, the paramagnetic metal PM-AFI transition causes a sharp step down. In the metallic region, the interaction working on the 3
d spins is of the Ruderman-Kittel-Kasuya-Yoshida (RKKY) type via the conduction π electrons [
18]. Across the MI transition, this spin network will be cut off by the localization of π electrons. Therefore, the magnetic susceptibility curve of 3
d spin changes from following the Curie-Weiss law (dashed curve in
Figure 4) to the present paramagnetic model (solid curve in
Figure 4). The 3
d spin dominates the step down at
TMI and the slow reduction in the AFI phase.
2.3. Role of Fe 3d Spin in PM-AFI Transition
Figure 6a shows the specific heats of mixed crystals λ-BETS
2Fe
xGa
1−xCl
4 (0.4 <
x ≤ 1) and λ-BETS
2GaCl
4. The specific heats of λ-BETS
2Fe
xGa
1−xCl
4 show sharp peaks at
TMI or SC-AFI transition temperature
TSCI and broad humps below these sharp peaks, while non-magnetic λ-BETS
2GaCl
4 does not exhibit these anomalies. Because the specific heat of λ-BETS
2Fe
xGa
1−xCl
4 in the metallic phase was close to that of λ-BETS
2GaCl
4 in the metallic phase, we assumed that the lattice and electronic specific heats of isostructural λ-BETS
2GaCl
4 were equivalent to those of λ-BETS
2Fe
xGa
1−xCl
4. We obtained the excess specific heats Δ
C (shown in
Figure 6b) by subtracting the estimated lattice and electronic specific heat in the metal phase, and subtracting the lattice contribution in the AFI phase, respectively. In
Figure 6a, broad humps are found below sharp peaks for all mixed crystals. This large value for Δ
C in the low-temperature AFI phase suggests that a majority of the spin degrees of freedom in this system were maintained even after transition to the AFI phase was achieved. These anomalies in the AFI ground state of the mixed crystals contrast the critical behavior that in π-
d system κ-BETS
2FeBr
4, Fe 3
d spin (
sd = 5/2) takes place at AF transition at Neel temperature [
19,
20].
Figure 7 shows the excess entropies obtained by integrating Δ
C/
T over temperature. The resulting total entropies were close to the values of
xR ln6 (dashed line in
Figure 7) expected for the degrees of freedom of 3
d high spins (
sd = 5/2) per molecular formula. These experimental results suggest that the 3
d spin degrees of freedom contributed substantially to the sharp peaks as well as the Schottky-type humps for all mixed crystals. During transition, π spin resulted in AF ordering and produced a strong internal magnetic field at the nearest neighboring Fe sites. At the transition temperature, an increase in the intensity of the internal magnetic field at the Fe sites caused a rapid reduction in 3
d spin entropy, indicated by sharp peaks in the specific heats.
Figure 7.
Temperature dependencies of spin entropy of λ-BETS2FexGa1−xCl4 calculated from ΔC. The dashed lines show the degrees of freedom for 3d spins for values of xRln6.
Figure 7.
Temperature dependencies of spin entropy of λ-BETS2FexGa1−xCl4 calculated from ΔC. The dashed lines show the degrees of freedom for 3d spins for values of xRln6.
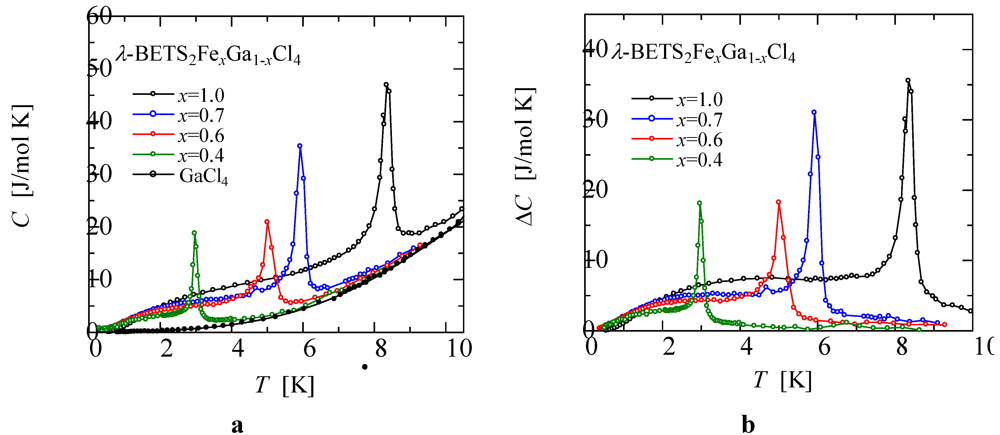
To discuss the origin of this transition, we investigated the dependence of excess specific heat on Fe content.
Figure 8a indicates excess specific heats normalized by Fe content Δ
C/
x. The maximum of these broad humps gradually shifts to a lower temperature with decreasing
x. The broad humps of all mixed crystals could be fitted to the calculated Schottky specific heats of
sd = 5/2 (solid curves in
Figure 8a).
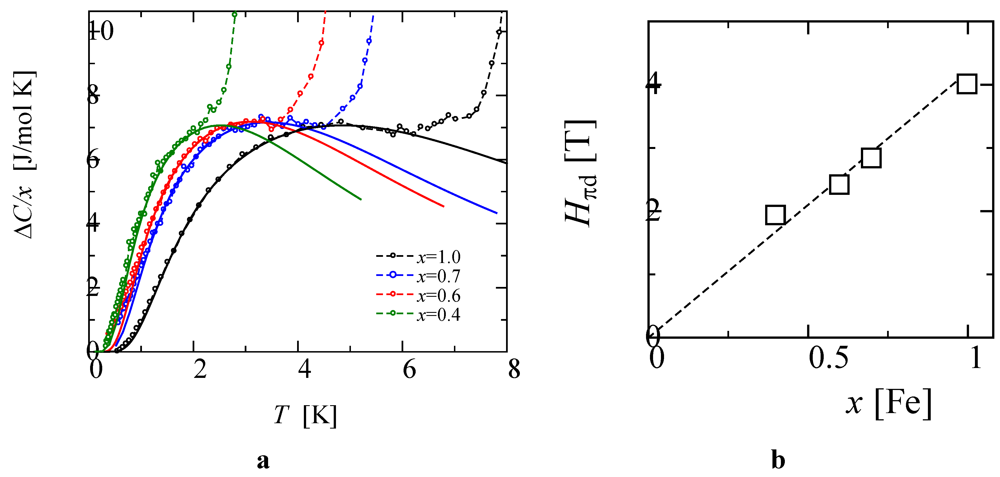
Figure 8.
(a) Temperature dependencies of excess specific heat divided by Fe content ΔC/x. The solid curves show the 6-level Schottky specific heats, which are based on the paramagnetic 3d spin (s = 5/2) system under the internal magnetic field Hπd. The broad maximum of the Schottky specific heat shifts to lower temperature with decreasing Hπd. (b) Fe density dependence of Hπd.
Figure 8.
(a) Temperature dependencies of excess specific heat divided by Fe content ΔC/x. The solid curves show the 6-level Schottky specific heats, which are based on the paramagnetic 3d spin (s = 5/2) system under the internal magnetic field Hπd. The broad maximum of the Schottky specific heat shifts to lower temperature with decreasing Hπd. (b) Fe density dependence of Hπd.
As we approach the transition temperature, the experimental data deviate from the solid curves because of the formation of sharp peaks. The sharp peaks are attributed to the rapid enhancement of the internal magnetic field at the Fe sites accompanied with the development of spontaneous magnetization in the π spin system. When the π magnetization reaches saturation, Δ
C follows the calculated Schottky curves under fixed internal magnetic fields
Hπd. The intensity of
Hπd estimated from the agreement between the Δ
C data and the calculated curves were proportional to the
x values, as shown in
Figure 8b. However, these experimental results are very puzzling because the high density of
paramagnetic Fe 3
d spin increased the internal magnetic field
Hπd, owing to the saturation magnetization of the AF ordered π spin and increased the PM-AFI transition temperature. These results clarify that the Fe 3
d spin plays a crucial role in stabilizing AF ordering in the π spin system. Further analysis of the sharp peaks enables a measurement of the strong temperature dependence of the internal magnetic field in the vicinity of the transition temperature and gives information about a characteristic critical behavior of the spontaneous magnetization in the low-dimensional π spin system. The detailed studies of this critical behavior will be reported in our next paper.
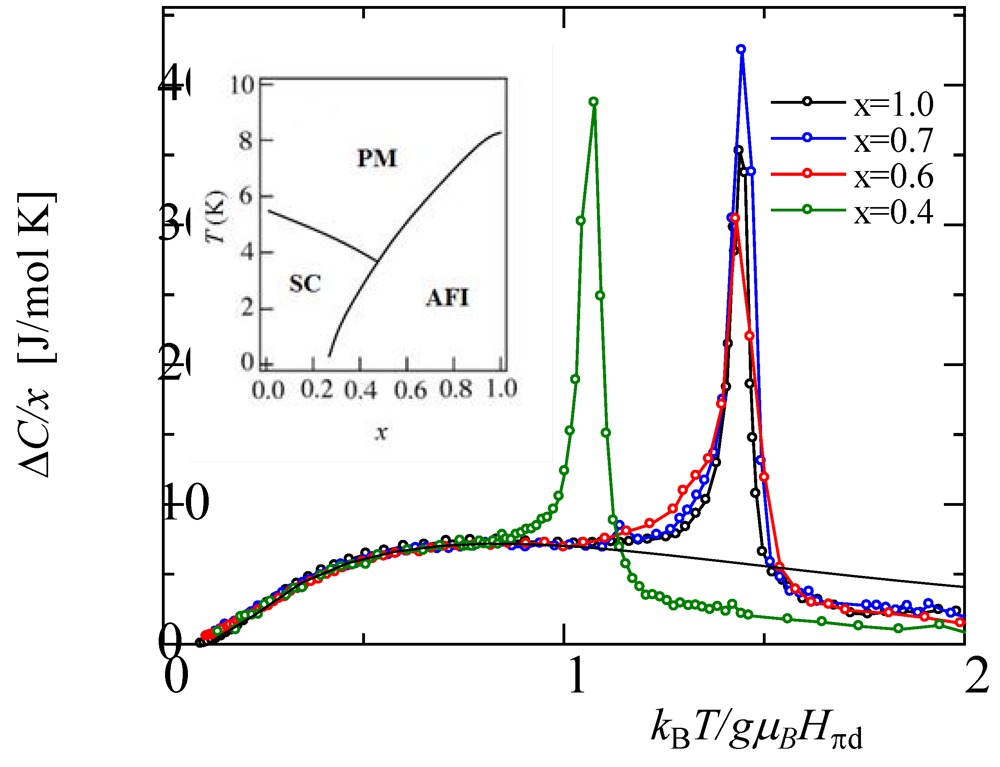
Figure 9 shows a plot of Δ
C/
x versus the temperature normalized by each internal magnetic field
kBT/
gμBHπd. These normalized data fit to one of the curves obtained at the temperatures studied. The sharp peaks as well as the Schottky-type broad humps could be normalized in the high Fe-content region of
x > 0.5, where the PM-AFI transition occurs [
9]. In the low Fe-content region (0.3 <
x < 0.5), the Schottky term could be reduced to the same universal curve; however, the sharp peak at the phase transition could not be normalized, because at peak temperatures, the SC-AFI transition occurred instead of the PM-AFI transition (see the inset of
Figure 9). It should be noted that at the PM-AFI transition, the phase transition temperatures as well as the Schottky specific heats could be scaled by internal magnetic field
Hπd. These scaling rules clarify that the internal magnetic field drove the PM-AFI transition.
Figure 9.
Δ
C/
x versus the temperature normalized by the internal magnetic field
kBT/
gμBHπd. The inset is
T-
x phase diagram of
λ-BETS
2Fe
xGa
1−xCl
4 [
9].
Figure 9.
Δ
C/
x versus the temperature normalized by the internal magnetic field
kBT/
gμBHπd. The inset is
T-
x phase diagram of
λ-BETS
2Fe
xGa
1−xCl
4 [
9].
We have a possible explanation for the role of Fe 3
d spins in PM-AFI transitions and propose a mechanism for this peculiar phase transition, in which the fluctuation of the π spin system is suppressed by magnetic anisotropy introduced by Fe 3
d spin via the π-
d interaction. Magnetic susceptibility measurements suggested that the π spin system, which exhibits isotropic magnetic properties in ordinary organic conductors, has finite anisotropy in λ-BETS
2FeCl
4 [
5]. A decrease in Fe content weakens the anisotropic magnetic properties,
i.e., the spin-flop fields
HSF in magnetization [
21]. These results suggest that the magnetic anisotropy of the π spin system originates from the anisotropic crystal field surrounding the Fe 3
d spin system through the π-
d interaction; this Fe-induced anisotropy suppresses two-dimensional fluctuation in the present π spin system and increases the PM-AFI transition temperature.
We have studied the critical behavior of the PM-AFI transition for the λ-BETS2FeCl4 system, measuring the excess magnetic specific heat. We estimated the critical process of the spontaneous magnetization of π spin in the vicinity of the transition temperature. We could observe the low dimensional criticality of the magnetization of π spin. We considered that the magnetic anisotropy induced by π-d interactions transfer the π spin from the two-dimensional (2D) Heisenberg spin system to the 2D Ising one having the easy axis. Antiferromagnetic order cannot be established in 2D Heisenberg spin systems. In contrast, 2D Ising spin system exhibits long-range magnetic order. To find unambiguous evidence for 2D long-range ordering in the AFI phase, a more detailed study on the criticality of this phase transition is now in progress.