Vibrational Spectra of β″-Type BEDT-TTF Salts: Relationship between Conducting Property, Time-Averaged Site Charge and Inter-Molecular Distance
Abstract
:1. Introduction
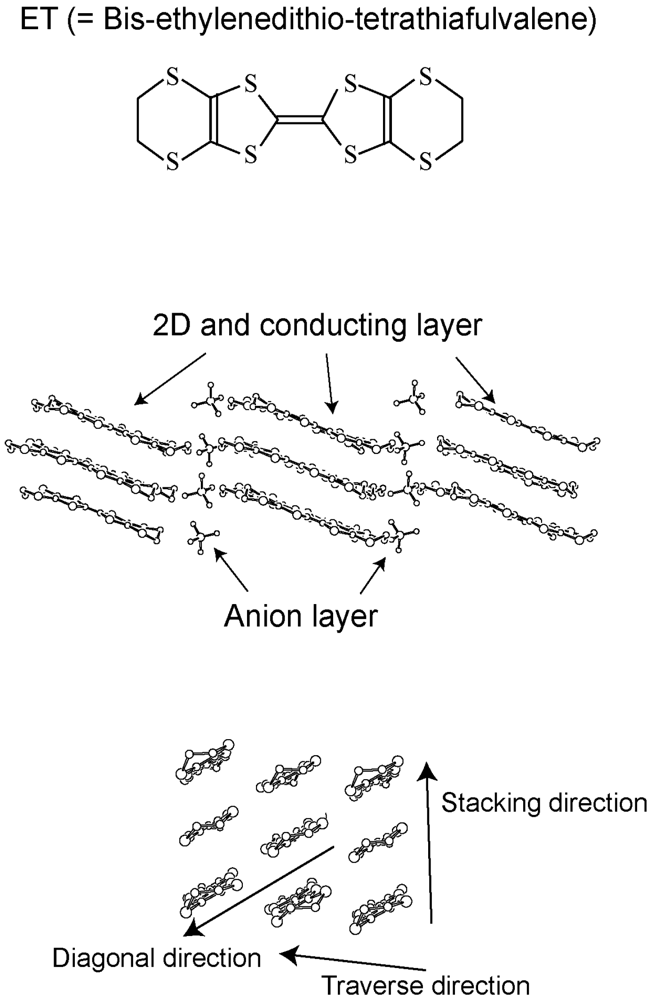
2. Requirements for the Model Compounds

| 2/3-Filled | Group | Resistivity | M:H | Reference |
| (ET)3(ClO4)2 | (b4) | TMI ~ 170 K | 3:2 | [41] |
| (ET)3(HSO4)2 | (b4) | TMI = 127 K | 3:2 | [42] |
| (ET)3(ReO4)2 | (b4) | TMI = 80 K | 3:2 | [43,44] |
| (ET)3Cl2·2H2O | (b5) | TMI = 170~100 K, | 6:4 a | [39,40,45] |
| TSC = 2-6 K (1.6-1.2 kbar) | ||||
| 3/4-Filled | Group | Resistivity | M:H | Reference |
| (ET)4Ni(CN)4·H2O | (b4) | TMI ~100 K | 4:2 | [38] |
| (ET)4Pd(CN)4·H2O | (b3) | TMI ~ 100 K, | 4:2 | [5] |
| TSC = 1.2 K (7 kbar) | ||||
| (ET)4Pt(CN)4·H2O | (b3) | TMI ~ 100 K, TSC = 2 K (6.5 kbar) | 4:2 | [38] |
| (ET)4[(H3O)Ga(C2O4)3]PhNO2 | (b2) | TMI ~ 100 K, TSC = 7.5 K | 4:2 b | [35] |
| (ET)4[(H3O)Ga(C2O4)3]Pyridine | (b1) | Metal | 4:2 b | [35] |
| (ET)4[(H3O)Ga(C2O4)3]CH2Cl2 | (b1) | Metal | 4:2 b | [46] |
| (ET)2Cl(C2I2) | (b1) | Metal | 2:1 | [33] |
| (ET)2Br(C2I2) | (b1) | Metal | 2:1 | [33] |
| (ET)2AuBr2 | (b1) | Metal | 2:1 | [47] |
3. The Properties of the C=C Stretching Modes and the Methodology for Observing the C=C Stretching Modes
3.1. C=C Stretching Mode of Isolated Molecules
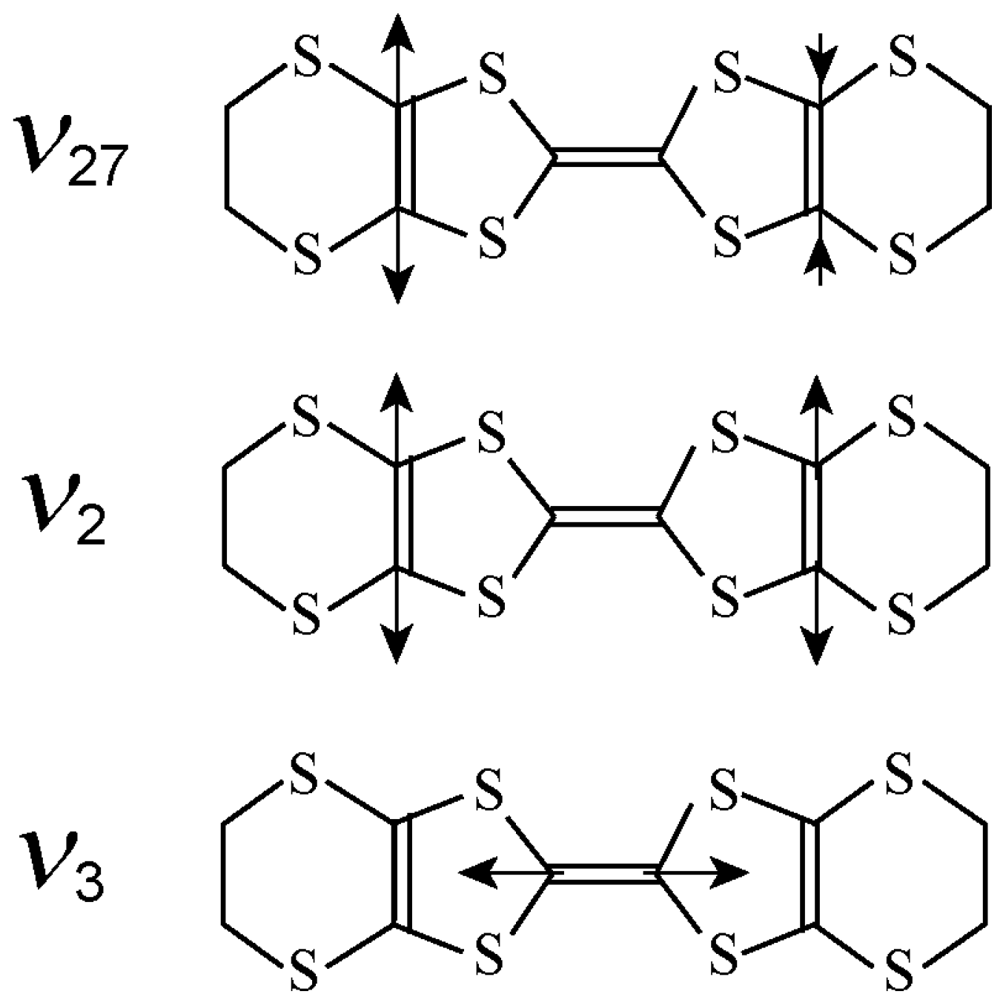
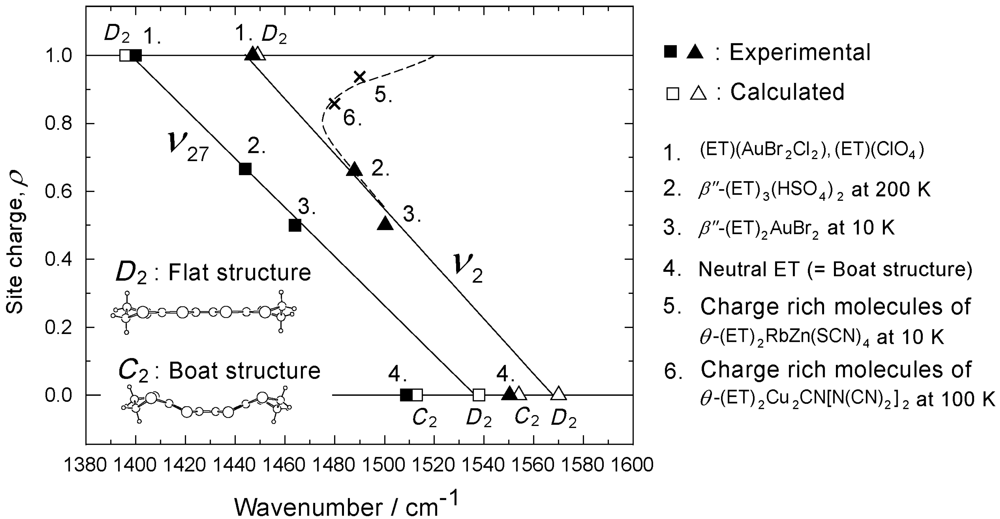
3.2. Relationship Between the Molecular Charge and the Frequency of the Charge Sensitive Mode
 (1)
(1) (2)
(2) (3)
(3)
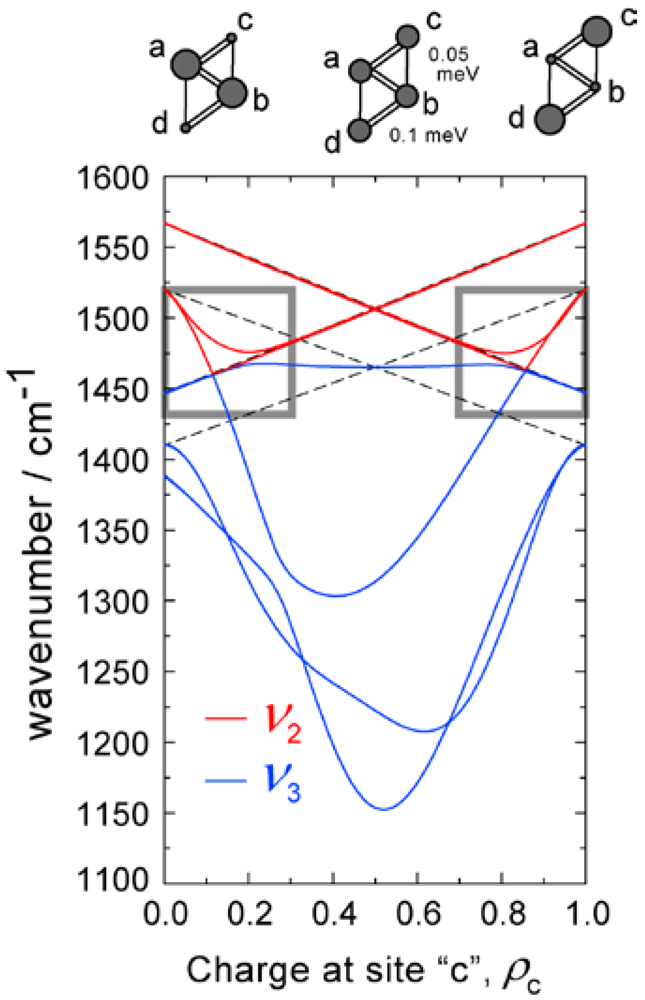
3.3. Factor Group Splitting in ν3 Mode

3.4. Experimental Method
4. Results of Vibrational Spectra and Degree of Charge Fluctuation
4.1. 2/3-Filled and 3:2-Salts
4.1.1. β″-(ET)3(ClO4)2 and β″-(ET)3(HSO4)2

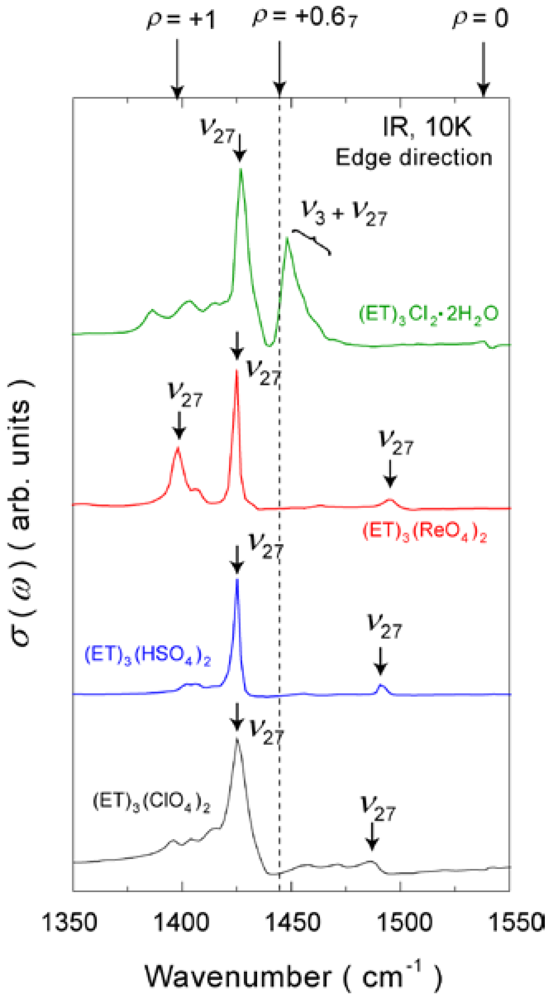
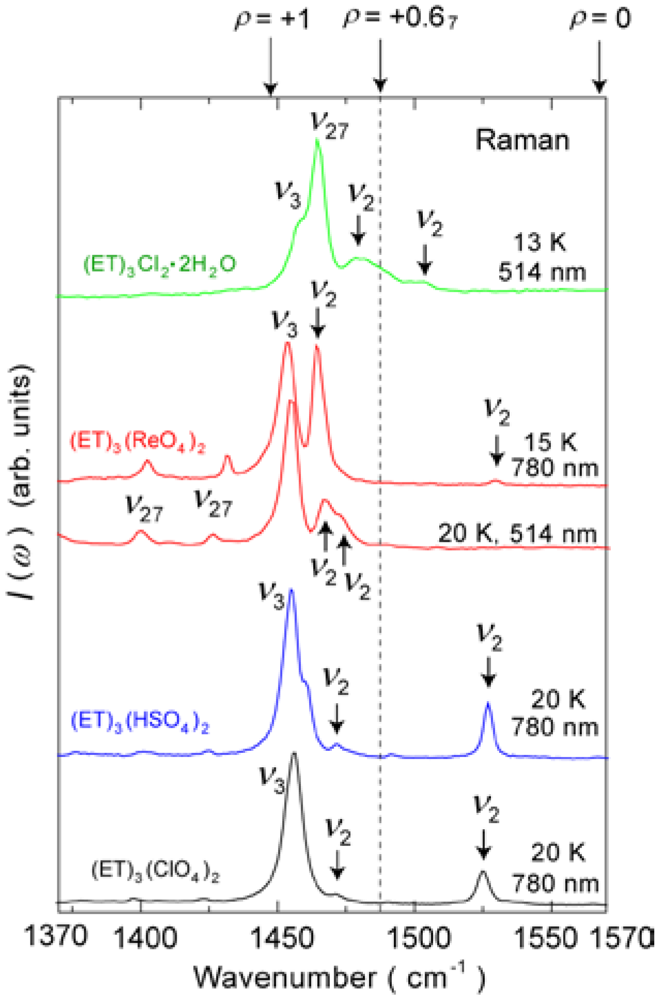
4.1.2. β″-(ET)3(ReO4)2

| 2/3-Filled | M:H | ND | NSD | NAD | ∆ρ |
| (ET)3(ClO4)2 | 3:2 | 3 | 1 | — | 0.5 |
| (ET)3(HSO4)2 | 3:2 | 3 | 1 | — | 0.4 |
| (ET)3(ReO4)2 | 3:2 | 3 | 1 a | — | 0.7 |
| (ET)3Cl2·2H2O | 6:4 | 9 | 1 | (4) b | 0.25 |
| 3/4-Filled | M:H | ND | NSD | NAD | ∆ρ |
| (d8-ET)4Pt(CN)4·H2O c | 4:2 | 6 | 1 | — | 0.6 |
| (ET)4Ni(CN)4·H2O | 4:2 | 6 | 1 | — | 0.3 |
| (ET)4Pd(CN)4·H2O | 4:2 | 6 | 1 | (4) b | 0.3 |
| (ET)4Pt(CN)4·H2O | 4:2 | 6 | (1) d | (4) b | 0.15 |
| (ET)4[(H3O)Ga(C2O4)3]PhNO2 | 4:2e | 6 | 1< | 5 | 0.13 |
| (ET)4[(H3O)Ga(C2O4)3]Pyridine | 4:2e | 6 | (1<) f | 5≤ f | 0.08 |
| (ET)4[(H3O)Ga(C2O4)3]CH2Cl2 | 4:2e | 6 | (1<) f | 5≤ f | 0.05 |
| (ET)2Cl(C2I2) | 2:1 | 2 | 2 | — | 0.03 |
| (ET)2Br(C2I2) | 2:1 | 2 | 2 | — | 0.03 |
| (ET)2AuBr2 | 2:1 | 2 | 2 | — | < 0.03 g |
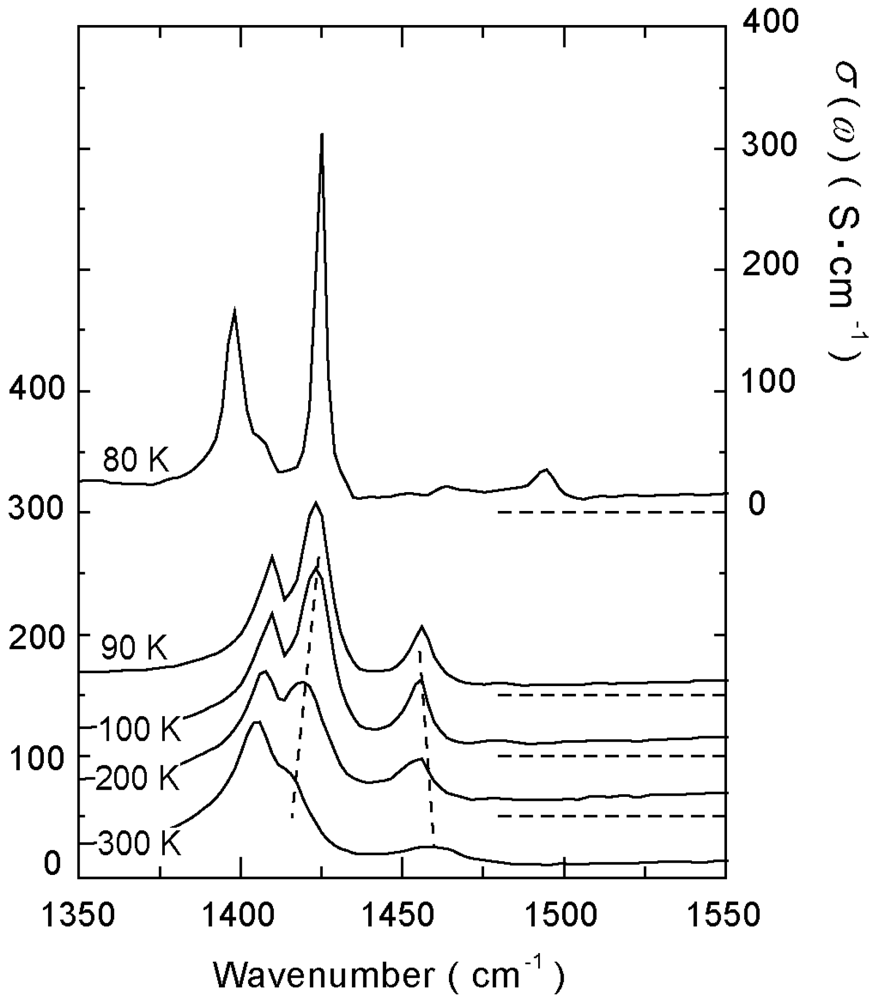
4.2. 2/3-Filled and 6:4-Salt: β″-(ET)3Cl2·2H2O
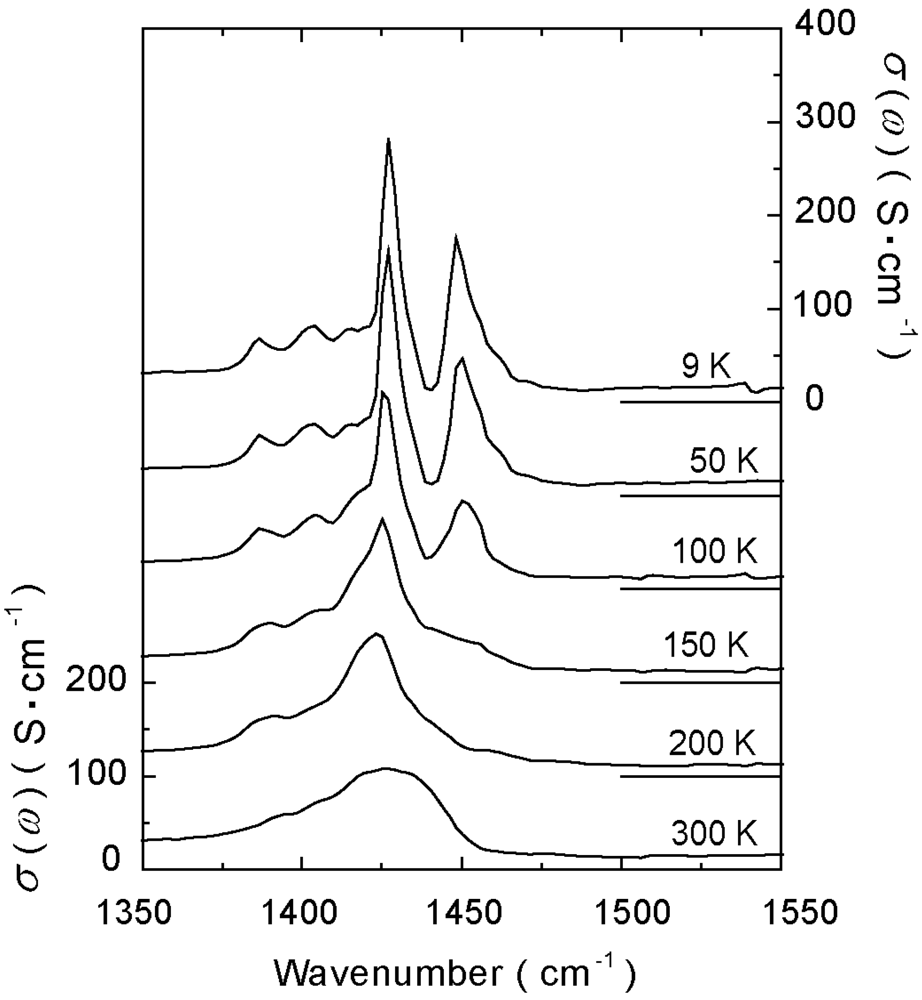
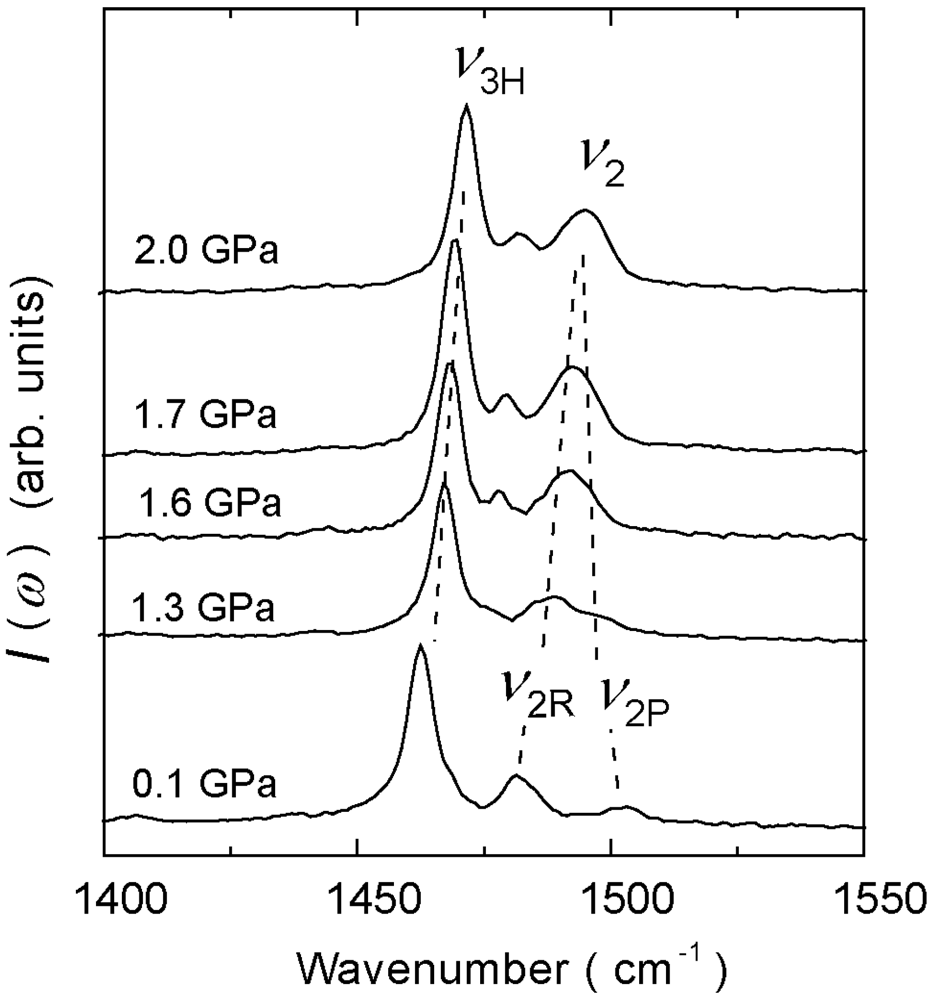
4.3. 3/4-Filled and 2:1-Salts
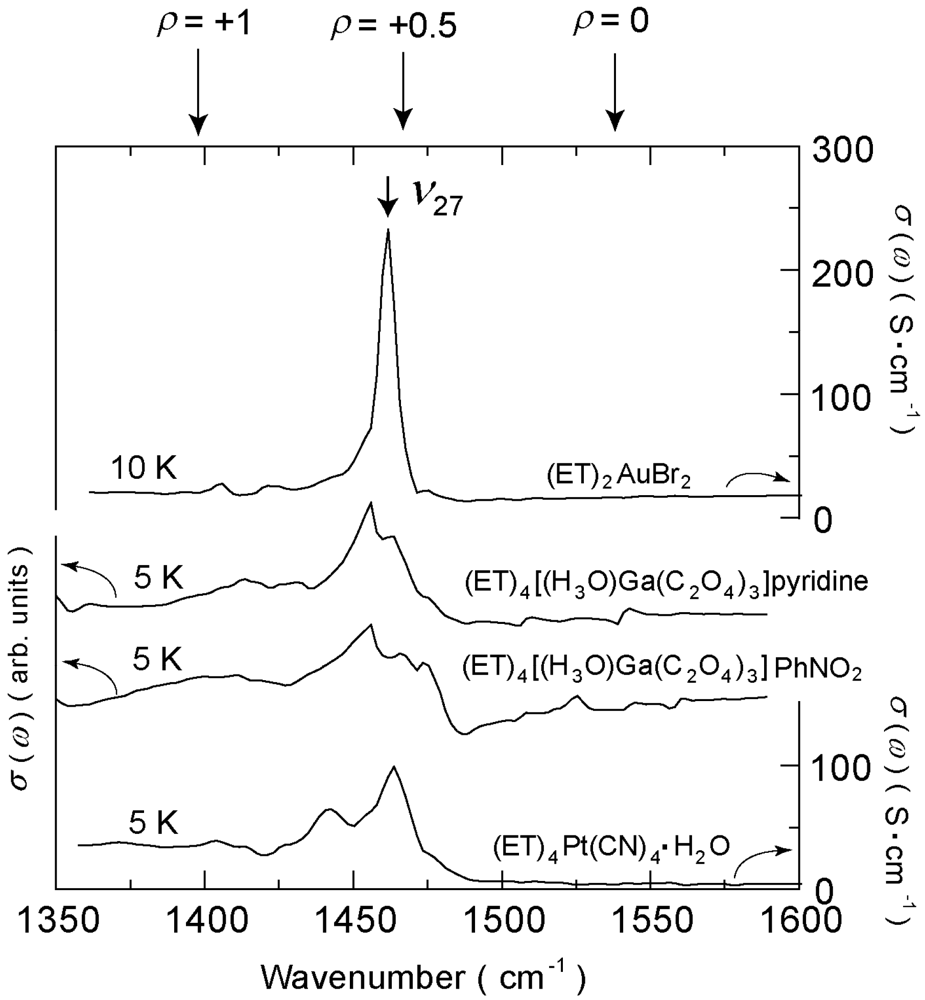
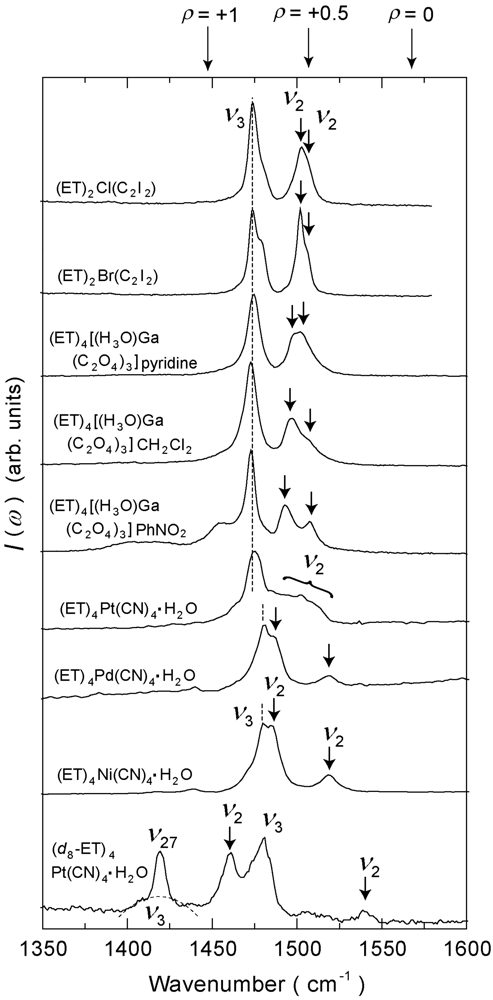
4.4. 3/4-Filled and 4:2-Salts
4.4.1. β″-(ET)4M(CN)4·H2O [M = Ni, Pd, Pt]

4.4.2. Deuterium Effect on the Molecular Charges in β″-(ET)4Pt(CN)4·H2O
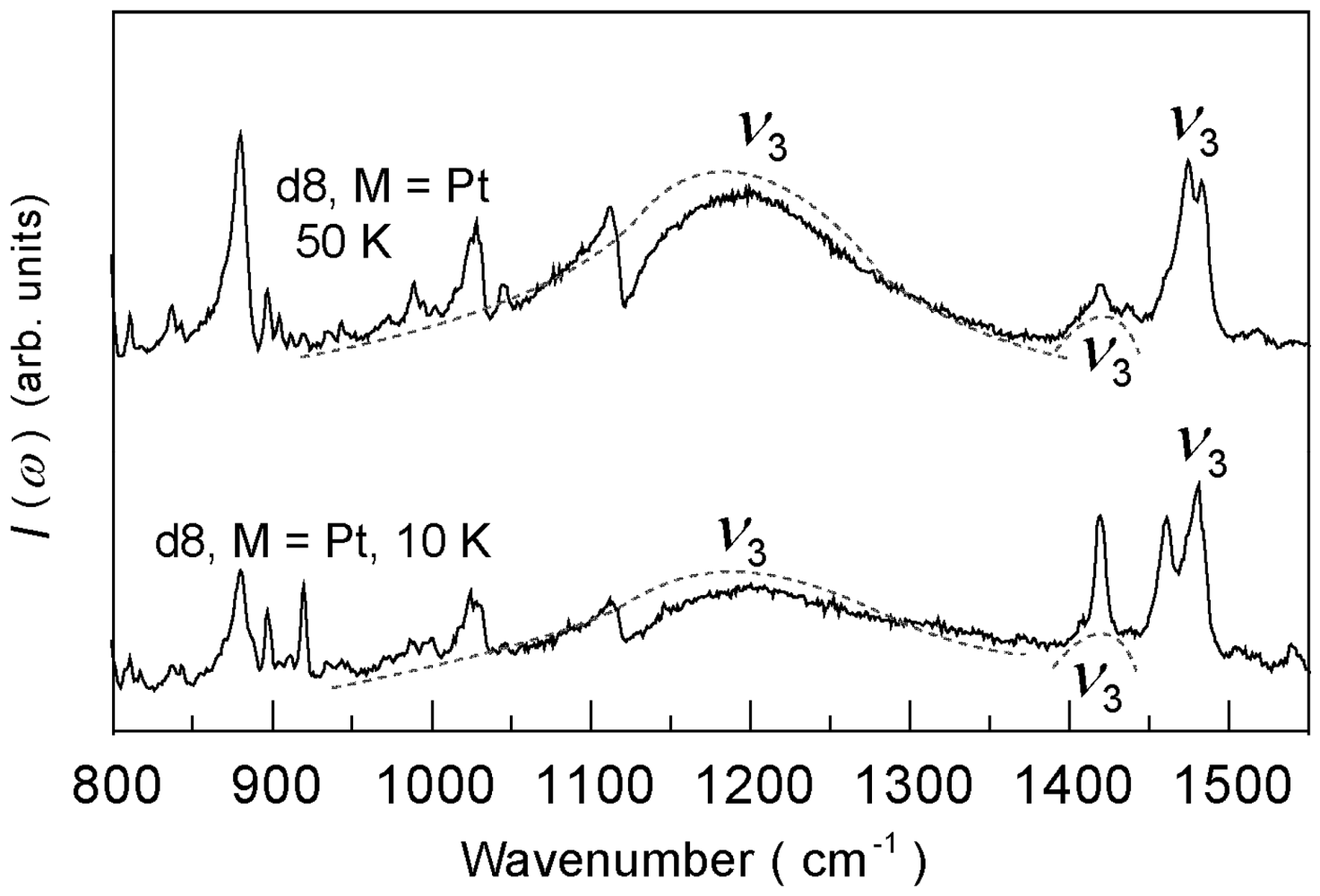
4.4.3. β″-(ET)4[Ga(ox)3H3O]X [ox = Oxalate Anion, X = PhNO2, CH2Cl2, Pyridine]
5. Phase Diagram and Degree of Charge Fluctuation in Other β″-Type ET Salts
Acknowledgments
References and Notes
- Mori, T. Structural Genealogy of BEDT-TTF-Based Organic Conductors II. Inclined Molecules: θ, α, and κ Phases. Bull. Chem. Soc. Jpn. 1999, 72, 179–197. [Google Scholar] [CrossRef]
- Mori, T. Structural Genealogy of BEDT-TTF-Based Organic Conductors I. Parallel Molecules: β and β″ Phases. Bull. Chem. Soc. Jpn. 1998, 71, 2509–2526. [Google Scholar] [CrossRef]
- Obertelli, S.D.; Marsden, I.R.; Friend, R.H.; Kurmoo, M.; Rosseinsky, M.J.; Day, P.; Pratt, F.L.; Hayes, W. Electronic properties of (BEDT-TTF)3Cl·2H2O. Phys. Chem. Org. Supercondut. 1990, 51, 181–184. [Google Scholar]
- Carneiro, K.; Scott, J.C.; Engler, E.M. Comparative ESR study of three (BEDT-TTF): ReO4 salts: An organic superconductor, a peierls metal and a semiconductor. Solid State Commun. 1984, 50, 477–481. [Google Scholar] [CrossRef]
- Mori, T.; Kato, K.; Maruyama, Y.; Inokuchi, H.; Mori, H.; Hirabayashi, I.; Tanaka, S. Structural and physical properties of a new organic superconductor, (BEDT-TTF)4Pd(CN)4H2O. Solid State Commun. 1992, 82, 177–181. [Google Scholar] [CrossRef]
- Parkin, S.S.P.; Engler, E.M.; Schumaker, R.R.; Lagier, R.; Lee, V.Y.; Scott, J.C.; Greene, R.L. Superconductivity in a new family of organic conductors. Phys. Rev. Lett. 1983, 50, 270–273. [Google Scholar]
- Merino, J.; McKenzie, R.H. Superconductivity mediated by charge fluctuations in layered molecular crystals. Phys. Rev. Lett. 2001, 87, 237002:1–237002:4. [Google Scholar]
- Powell, B.J. Mixed order parameters, accidental nodes and broken time reversal symmetry in organic superconductors: a group theoretical analysis. J. Phys. Condens. Matter 2006, 18, L575–L584. [Google Scholar] [CrossRef]
- Greco, A.; Merino, J.; Foussats, A.; McKenzie, R.H. Spin exchange and superconductivity in a t-J′-V model for two-dimensional quarter-filled systems. Phys. Rev. B 2005, 71, 144502:1–144502:8. [Google Scholar]
- Mazumdar, S.; Clay, R.T. Quantum critical transition from charge-ordered to superconducting state in the negative- U extended Hubbard model on a triangular lattice. Phys. Rev. B 2008, 77, 180515:1–180515:4. [Google Scholar]
- Kobayashi, A.; Suzumura, Y.; Higa, M.; Kondo, R.; Kagoshima, S.; Nishikawa, H. Charge ordered metal and pressure-induced superconductivity in the two-dimensional organic conductor β''-(DODHT)2PF6. J. Phys. Condens. Matter 2008, 20, 125205:1–125205:6. [Google Scholar]
- Watanabe, H.; Ogata, M. Novel charge order and superconductivity in two-dimensional frustrated lattice at quarter filling. J. Phys. Soc. Jpn. 2006, 75, 063702:1–063702:4. [Google Scholar]
- Kuroki, K. The origin of the charge ordering and its relevance to superconductivity in θ-(BEDT-TTF)2X: The effect of the Fermi surface nesting and the distant electron–electron interactions. J. Phys. Soc. Jpn. 2006, 75, 114716:1–114716:14. [Google Scholar]
- Tanaka, Y.; Yanase, Y.; Ogata, M. Superconductivity due to charge fluctuation in θ-type organic conductors. J. Phys. Soc. Jpn. 2004, 73, 2053–2056. [Google Scholar] [CrossRef]
- Note that the transfer integral network of β″–(DODHT)2PF6 in [11] belongs to those of the θ- and α-type salts. Detailed discussions are described in Section 5.
- Yamamoto, T.; Uruichi, M.; Yamamoto, K.; Yakushi, K.; Kawamoto, A.; Taniguchi, H. Examination of the charge-sensitive vibrational modes in Bis(ethylenedithio)tetrathiafulvalene. J. Phys. Chem. B 2005, 109, 15226–15235. [Google Scholar]
- Ymamoto, T.; Uruichi, M.; Yakushi, K.; Yamaura, J.I.; Tajima, H. Infrared and Raman evidence for the charge-ordering in β ″-(BEDT-TTF)3(ReO4)2. Phys. Rev. B 2004, 70, 125102:1–125102:11. [Google Scholar]
- Yamamoto, T.; Uruichi, M.; Yakushi, K.; Kawamoto, A. Charge ordering state of β″-(ET)3(HSO4)2 and β″-(ET)3(ClO4)2 by temperature-dependent infrared and Raman spectroscopy. Phys. Rev. B 2006, 73, 125116:1–125116:12. [Google Scholar]
- Yamamoto, T.; Yamamoto, H.M.; Kato, R.; Uruichi, M.; Yakushi, K.; Akutsu, H.; Sato-Akutsu, A.; Kawamoto, A.; Turner, S.S.; Day, P. Inhomogeneous site charges at the boundary between the insulating, superconducting, and metallic phases of β″-type bis-ethylenedithio-tetrathiafulvalene molecular charge-transfer salts. Phys. Rev. B 2008, 77, 205120:1–12520:14. [Google Scholar]
- Yamamoto, T.; Nakazawa, Y.; Tamura, M.; Nakao, A.; Ikemoto, Y.; Moriwaki, T.; Fukaya, A.; Kato, R.; Yakushi, K. Intradimer Charge Disproportionation in Triclinic-EtMe3P[Pd(dmit)2]2 (dmit: 1,3-Dithiole-2-thione-4,5-dithiolate). J. Phys. Soc. Jpn. 2011, 80, 123709:1–123709:4. [Google Scholar]
- Canadell, E.; Rachidi, I.E.-I.; Ravy, S.; Pouget, J.-P.; Brossard, L.; Legnos, J.P. On the band electronic structure of X [M (dmit)2]2 (X = TTF, (CH3)4N ; M = Ni, Pd) molecular conductors and superconductors. J. Phys. (France) 1989, 50, 2967–2981. [Google Scholar] [CrossRef]
- Canadell, E.; Ravy, S.; Pouget, J.P.; Brossard, L. Concerning the band structure of D(M(dmit)2)2 (D = TTF, Cs, NMe4); M = Ni, Pd) molecular conductors and superconductors: Role of the M(dmit)2 Homo and Lumo. Solid State Commun. 1990, 75, 633–638. [Google Scholar] [CrossRef]
- Tamura, M.; Takenaka, K.; Takagi, H.; Sugai, S.; Tajima, A.; Kato, R. Spectroscopic evidence for the low-temperature charge-separated state of [Pd(dmit)2] salts. Chem. Phys. Lett. 2005, 411, 133–137. [Google Scholar] [CrossRef]
- Nakao, A.; Kato, R. Structural Study of Low Temperature Charge-Separated Phases of Pd(dmit)2-Based Molecular Conductors. J. Phys. Soc. Jpn. 2005, 74, 2754–2763. [Google Scholar] [CrossRef]
- M:H = 1:0.5 corresponds to the uniform columnar structure. In such case, the number of the charge distribution can be defined as 2, which is the same as that of M:H = 2:1. β″-(ET)(TCNQ) belongs to M:H=1:0.5 [26]. The homogeneous time-averaged charge distribution is confirmed in the low temperature phase [26]
- Uruichi, M.; Yakushi, K.; Yamamoto, H.M.; Kato, R. Infrared and Raman studies of the charge-ordering phase transition at −170 K in the quarter-filled organic conductor, β''-(ET)(TCNQ). J. Phys. Soc. Jpn. 2006, 75, 074720:1–074720:10. [Google Scholar]
- Yamamoto, K.; Yakushi, K.; Miyagawa, K.; Kanoda, K.; Kawamoto, A. Charge ordering in θ-(BEDT-TTF)2RbZn(SCN)4 studied by vibrational spectroscopy. Phys. Rev. B 2002, 65, 085110:1–085110:8. [Google Scholar]
- Pratt, F.L.; Fisher, A.J.; Hayes, W.; Singleton, J.; Spermon, S.J.R.M.; Kurmoo, M.; Day, P. Quantum oscillations and negative magnetoresistance in the organic metal β’’(BEDT-TTF)2AuBr2. Phys. Rev. Lett. 1988, 61, 2721–2724. [Google Scholar] [CrossRef]
- Kajita, K.; Nishio, Y.; Moriyama, S.; Sasaki, W.; Koto, R.; Kobayashi, H.; Kobayashi, A. Transport property of a newly synthesized organic conductor, β″-(BEDT-TTF)2AuBr2. Solid State Commun. 1986, 60, 811–815. [Google Scholar] [CrossRef]
- Bangura, A.F.; Coldea, A.I.; Singleton, J.; Ardavan, A.; Akutsu-Sato, A.; Akutsu, H.; Turner, S.S.; Day, P.; Yamamoto, T.; Yakushi, K. Robust superconducting state in the low-quasiparticle-density organic metals β″-(BEDT-TTF)4[(H3O)M(C2O4)3]∙Y: Superconductivity due to proximity to a charge-ordered state. Phys. Rev. B 2005, 72, 014543:1–104543:13. [Google Scholar]
- Coldea, A.I.; Bangura, A.; Singleton, J.; Akutsu-Sato, A.; Akutsu, H.; Day, P. Fermi-surface topology and the effects of intrinsic disorder in a class of charge-transfer salts containing magnetic ions: β″-(BEDT-TTF)4[(H3O)M(C2O4)3]Y (M=Fe, Cr, Ga; Y=C5H5N). Phys. Rev. B 2004, 69, 085112:1–085112:11. [Google Scholar]
- Yasuzuka, S.; Terakura, C.; Terashima, T.; Yakabe, T.; Terai, Y.; Yamamoto, H.M.; Kato, R.; Uji, S. Fermi surface and resistance anomalies in ET-TCNQ. Syn. Met. 2003, 135, 647–648. [Google Scholar] [CrossRef]
- Yamamoto, H.M.; Yamaura, J.; Kato, R. Structural and electrical properties of (BEDT-TTF)2X(diiodoacetylene) (X=Cl, Br): the novel self-assembly of neutral Lewis-acidic molecules and halide anions in a molecular metal. J. Mater. Chem. 1998, 8, 15–16. [Google Scholar] [CrossRef]
- Geiser, U.; Schlueter, J.A.; Wang, H.H.; Kini, A.N.; Willliams, J.M.; She, P.P.; Zakowicz, H.I.; VanZile, M.L.; Dudek, J.D.; Nixson, P.G.; et al. Superconductivity at 5.2 K in an Electron donor radical salt of Bis(ethylenedithio)tetrathiafulvalene (BEDT-TTF) with the novel polyfluorinated organic anion SF5CH2CF2SO3−. J. Am. Chem. Soc. 1996, 118, 9996–9997. [Google Scholar]
- Akutsu, H.; Akutsu-Sato, A.; Turner, S.S.; Pevelen, D.L.; Day, P.; Laukhin, V.; Klehe, A.K.; Singleton, J.; Tocher, D.A.; Probert, M.R.; Howard, J.A. Effect of included guest molecules on the normal state conductivity and superconductivity of β"-(ET)4[(H3O)Ga(C2O4)3]·G (G = Pyridine, Nitrobenzene). J. Am. Chem. Soc. 2002, 124, 12430–12431. [Google Scholar]
- Kurmoo, M.; Graham, A.W.; Day, P.; Coles, S.J.; Hursthouse, M.B.; Caulfield, J.L.; Singleton, J.; Pratt, F.L.; Hayes, W. Superconducting and semiconducting magnetic charge transfer salts: (BEDT-TTF)4AFe(C2O4)3·C6H5CN (A = H2O, K, NH4). J. Am. Chem. Soc. 1995, 117, 12209–12217. [Google Scholar]
- Prokhorova, T.G.; Buravov, L.I.; Yagubskii, E.B.; Zorina, L.V.; Khasanov, S.S.; Simonov, S.V.; Shibaeva, R.P.; Korobenko, A.V.; Zverev, V.N. Effect of electrocrystallization medium on quality, structural features, and conducting properties of single crystals of the (BEDT-TTF)4AI[FeIII(C2O4)3]·G family. Cryst. Eng. Commun. 2011, 13, 537–545. [Google Scholar]
- Mori, H.; Hirabayashi, I.; Tanaka, S.; Mori, T.; Maruyama, Y.; Inokuchi, H. Superconductivity in (BEDT-TTF)4Pt(CN) 4H2O. Solid State Commun. 1991, 80, 411–415. [Google Scholar] [CrossRef]
- Mori, T.; Inokuchi, H. Superconductivity in (BEDT-TTF)3Cl2·2H2O. Solid State Commun. 1987, 64, 335–337. [Google Scholar] [CrossRef]
- Lubczynski, W.; Demishev, S.V.; Singleton, J.; Caulfield, J.M.; du Croo de Jongh, L.; Kepert, C.J.; Blundell, S.J.; Hayes, W.; Kurmoo, M.; Day, P. A study of the magnetoresistance of the charge-transfer salt(BEDT-TTF)3Cl2·2H2O at hydrostatic pressures of up to 20 kbar: evidence for a charge-density-wave ground state and the observation of pressure-induced superconductivity. J. Phys. Condens. Matter 1996, 8, 6005–6017. [Google Scholar]
- Kobayashi, H.; Kato, R.; Mori, T.; Kobayashi, A.; Sasaki, Y.; Saito, G.; Enoki, T.; Inokuchi, H. The crystal structures and electrical resistivities of (BEDT-TTF)3(ClO4)2 and (BEDT-TTF)2ClO4(C4H8O2). Chem. Lett. 1984, 1984, 179–182. [Google Scholar]
- Miyazaki, A.; Enoki, T.; Uekusa, H.; Ohashi, Y.; Saito, G. Phase transition of (BEDT-TTF)3(HSO4)2. Phys. Rev. B 1997, 55, 6847–6855. [Google Scholar]
- Parkin, S.S.P.; Engler, E.M.; Lee, V.Y.; Schumaker, R.R. The many faces of ET. Mol. Cryst. Liq. Cryst. 1985, 119, 375–387. [Google Scholar] [CrossRef]
- Yakushi, K.; Kanbara, H.; Tajima, H.; Kuroda, H.; Saito, G.; Mori, T. Temperature dependence of the reflectance spectra of the single crystals of Bis(ethylenedithio)tetrathiafulvalenium salts. α-(BEDT–TTF)3(ReO4)2 and α-(BEDT–TTF)2I3. Bull. Chem. Soc. Jpn 1987, 60, 4251–4257. [Google Scholar] [CrossRef]
- Gaultier, J.; Bracchetti, S.H.; Guionneau, P.; Kepert, C.J.; Chasseau, D.; Ducasse, L.; Barrans, Y.; Kurmoo, M.; Day, P. Structural properties of the superconducting salt (BEDT-TTF)3Cl2·(H2O)2 at low temperatures. J. Solid State Chem. 1999, 145, 496–502. [Google Scholar] [CrossRef]
- Akutsu-Sato, A.; Kobayashi, A.; Mori, T.; Akutsu, H.; Yamada, J.; Nakatsuji, S.; Turner, S.S.; Day, P.; Tocher, D.A.; Light, M.E.; Hursthouse, M.B. Structures and physical properties of new β"-BEDT-TTF tris-oxalato-metallate (III) salts containing chlorobenzene and halomethane guest molecules. Synth. Met. 2005, 152, 373–376. [Google Scholar] [CrossRef]
- Mori, T.; Sakai, F.; Saito, G.; Inokuchi, H. Crystalandband structures of an organic conductor β″-(BEDT-TTF)2AuBr2. Chem. Lett. 1986, 15, 1037–1040. [Google Scholar]
- Kozlov, M.E.; Pokohodnia, K.I.; Yurchenko, A.A. The assignment of fundamental vibrations of BEDT-TTF and BEDT-TTF-d8. Spectrochim. Acta Part A 1987, 43, 323–329. [Google Scholar] [CrossRef]
- Kozlov, M.E.; Pokohodnia, K.I.; Yurchenko, A.A. Electron molecular vibration coupling in vibrational spectra of BEDT-TTF based radical cation salts. Spectrochim. Acta Part A 1989, 45, 437–444. [Google Scholar] [CrossRef]
- Eldridge, J.E.; Homes, C.C.; Williams, J.M.; Kini, A.M.; Wang, H.H. The assignment of the normal modes of the BEDT-TTF electron-donor molecule using the infrared and Raman spectra of several isotopic analogs. Spectrochim. Acta Part A 1995, 51, 947–960. [Google Scholar] [CrossRef]
- Demiralp, E.; Dasgupta, S.; Goddard, W.A. MSX force field and vibrational frequencies for BEDT-TTF (neutral and cation). J. Phys. Chem. A 1997, 101, 1975–1981. [Google Scholar]
- Yartsev, V.M.; Świetlik, R. Infrared properties of quasi-one-dimensional organic semiconductors. Rev. Solid State Sci. 1990, 4, 69–117. [Google Scholar]
- Painelli, A.; Pecile, C.; Girlando, A. Cs2TCNQ3 revisited: A detailed description of its ground state through a reinterpretation of the optical spectra. Mol. Cryst. Liq. Cryst. 1986, 134, 1–19. [Google Scholar] [CrossRef]
- Bozio, R.; Feis, A.; Pedron, D.; Zanon, I.; Pelile, C. Structural properties of molecular charge-transfer conductors and semiconductors from infrared and Raman spectroscopy. In Low Dimensional Systems and Molecular Electronics; Metzger, R.M., Day, P., Papavassiliou, G.C., Eds.; Plenum Press: New York, NY, USA, 1991; pp. 23–41. [Google Scholar]
- Bozio, R.; Meneghetti, D.; Pedron, D.; Pelile, C. Optical studies of the interplay between electron-lattice and electron-electron interactions in organic conductors and superconductors. In Low Dimensional Systems and Molecular Electronics; Metzger, R.M., Day, P., Papavassiliou, G.C., Eds.; Plenum Press: New York, NY, USA, 1991; pp. 129–142. [Google Scholar]
- Yartsev, V.M. Charge transfer and electron-molecular vibration coupling in tetramerized quasi-lD semiconductors. Phys. Status Solidi B 1984, 126, 501–510. [Google Scholar] [CrossRef]
- Painelli, A.; Girlando, A. Electron–molecular vibration (e–mv) coupling in charge-transfer compounds and its consequences on the optical spectra: A theoretical framework. J. Chem. Phys. 1986, 84, 5655–5671. [Google Scholar] [CrossRef]
- Yamamoto, T.; Yakushi, K.; Shimizu, Y.; Saito, G. Infrared and Raman study of the charge-ordered state of θ-(ET)2Cu2CN[N(CN)2]2. J. Phys. Soc. Jpn. 2004, 73, 2326–2332. [Google Scholar] [CrossRef]
- Suzuki, K.; Yamamoto, K.; Yakushi, K. Charge-ordering transition in orthorhombic and monoclinic single-crystals of θ-(BEDT-TTF)2TlZn(SCN)4 studied by vibrational spectroscopy. Phys. Rev. B 2004, 69, 085114:1–085114:11. [Google Scholar]
- wietlik, R.; Kushch, N.D.; Kushch, L.A.; Yagubskii, E.B. Spectral studies of isostructural organic metals (BEDT-TTF)3(HSO4)2 and [Ni(dddt)2]3(HSO4)2. Phys. Status Solidi B 1994, 181, 499–507. [Google Scholar] [CrossRef]
- Świetlik, R.; Garrigou-Lagrange, C. Charge transfer coupling to B1u modes in BEDT-TTF salts. Synth. Met. 1993, 55–57, 2217–2221. [Google Scholar]
- Enoki, T.; Tsujikawa, K.; Suzuki, K.; Uchida, A.; Ohashi, Y.; Yamakado, H.; Yakushi, K.; Saito, G. Metal-semiconductor transition and structural change in (BEDT-TTF)3(ClO4)2. Phys. Rev. B 1994, 50, 16287–16294. [Google Scholar]
- The line-width of the ν2 mode in κ-(ET)2Cu[N(CN)2]Cl at 5 K is ~6 cm−1, which is significantly smaller than that of κ-(ET)2Cu[N(CN)2]Br, ~14 cm−1. This observation indicates that the difference in the line-width is ascribed to the difference in the degree of dimerization.
- On the other hand, the frequencies of the three ν3 modes are reproduced by assuming the pseudo-symmetric trimer. This consistency is ascribed to the fact that the frequencies depend on the molecular charge and the transfer integrals.
- Sugano, T.; Hayashi, H.; Kinoshita, M.; Nishikida, K. Infrared conductivity and electron–molecular-vibration coupling in the organic superconductor di[bis(ethylenedithio)tetrathiafulvalene] bis(isothiocyanato)cuprate(I), κ-(BEDT-TTF)2 [Cu(NCS)2]: Protonated and deuterated salts. Phys. Rev. B 1989, 39, 11387–11397. [Google Scholar]
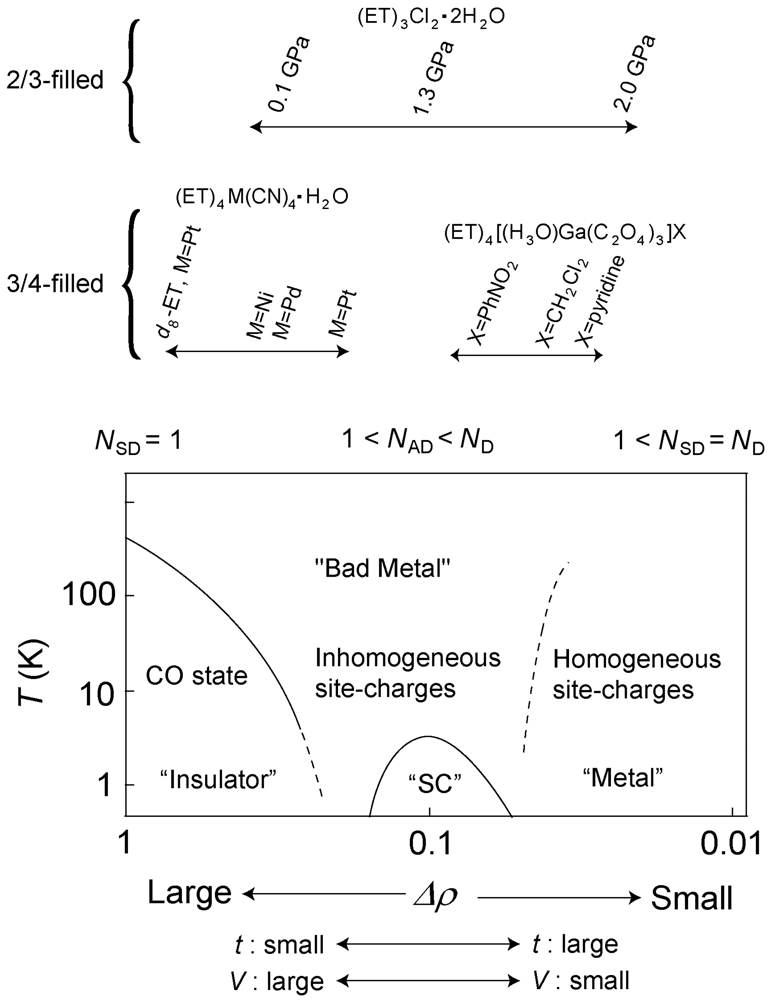
- The fused line-shape in the charge sensitive mode suggests the spatial fluctuation along with the dynamical fluctuation. Recently, the author’s group has observed the spatial dependence in the reflectance spectra (to be published). The spatial fluctuation indicates that the domains of the CO state and the fluctuated state are coexisted in the low temperature. From the viewpoint of the number of the charge distributions, each domains correspond to the conditions of NSD = 1 and 1< NAD < ND, respectively.
- Kanoda, K. Electron correlation, metal-insulator transition and superconductivity in quasi-2D organic system, (ET)2X. Physica C 1997, 282–287, 299–302. [Google Scholar] [CrossRef]
- Kawamoto, A.; Miyagawa, K.; Kanoda, K. Deuterated κ-(BEDT-TTF)2Cu[N(CN)2]Br: A system on the borderof the superconductor–magnetic-insulator transition. Phys. Bev. B 1997, 55, 14140–14143. [Google Scholar]
- Schlueter, J.A.; Kini, A.N.; Ward, B.H.; Geiser, U.; Wang, H.H.; Mohtasham, J.; Winter, R.W.; Gard, G. Universal inverse deuterium isotope effect on the Tc of BEDT-TTF-based molecular superconductors. Physica C 2001, 351, 261–273. [Google Scholar] [CrossRef]
- Aonuma, S.; Sawa, H.; Okano, Y.; Kato, R.; Kobayashi, H. Synthesis of DMe-DCNQI-d7 and deuterium-induced metal-insulator transition of (DMe-DCNQI-d7)2Cu. Synth. Met. 1993, 58, 29–37. [Google Scholar] [CrossRef]
- Tajima, N.; Eda, J. RIKEN, Wakō, Japan. Private communication. 2007. [Google Scholar]
- Schlueter, J.A.; Ward, B.H.; Geiser, U.; Wang, H.H.; Kini, A.M.; Parakka, J.; Morales, E.; Koo, H.-J.; Whangbo, M.-H.; Winter, R.H.; Mohtasham, J.; Gard, G.L. Crystal structure, physical properties and electronic structure of a new organic conductor β″-(BEDT-TTF)2SF5CHFCF2SO3. J. Mater. Chem. 2001, 11, 2008–2013. [Google Scholar]
- Kaiser, S.; Dressel, M.; Sun, Y.; Greco, A.; Schlueter, J.A.; Gard, G.L.; Drichko, N. Bandwidth tuning triggers interplay of charge order and superconductivity in two-dimensional organic materials. Phys. Rev. Lett. 2010, 105, 206402:1–206402:4. [Google Scholar]
- Yamamoto, T.; Onishi, K.; Nakazawa, Y. Private communication. Osaka University: Toyonaka, Japan, 2012. [Google Scholar]
- Tanaka, M.; Yamamoto, K.; Uruichi, M.; Yamamoto, T.; Yakushi, K.; Kimura, S.; Mori, H. Infrared and Raman study of the charge-ordered state in the vicinity of the superconducting state in the organic conductor β-(meso-DMBEDT-TTF)2PF6. J. Phys. Soc. Jpn. 2008, 77, 024714:1–024714:8. [Google Scholar]
- Kimura, S.; Suzuki, H.; Maejima, T.; Mori, H.; Yamaura, J.; Kakiuchi, T.; Sawa, H.; Moriyama, H. Checkerboard-type charge-ordered state of a pressure-induced superconductor, β-(meso-DMBEDT-TTF)2PF6. J. Am. Chem. Soc. 2006, 128, 1456–1457. [Google Scholar]
- Kimura, S.; Maejima, T.; Suzuki, H.; Chiba, R.; Mori, H.; Kawamoto, T.; Mori, T.; Moriyama, H.; Nishio, Y.; Kajita, K. A new organic superconductor β-(meso-DMBEDT-TTF)2PF6. Chem. Commun. 2004, 2004, 2454–2455. [Google Scholar]
- Maxsimuk, M.; Yakishi, K.; Taniguchi, H.; Kanoda, K.; Kawamoto, A. The C=C stretching vibrations of κ-(BEDT–TTF)2Cu[N(CN)2]Br and its isotope analogues. J. Phys. Soc. Jpn. 2001, 70, 3728–3738. [Google Scholar] [CrossRef]
- Nishikawa, H.; Morimoto, T.; Kodama, T.; Ikemoto, I.; Kikuchi, K.; Yamada, J.; Yoshino, H.; Murata, K. New organic superconductors consisting of an unprecedented π-electron donor. J. Am. Chem. Soc. 2002, 124, 730–731. [Google Scholar]
- Mori, T. Estimaion of off-site coulomb integrals and phase diagrams of charge ordered states in the θ-phase organic conductor. Bull. Chem. Soc. Jpn. 2000, 73, 2243–2253. [Google Scholar] [CrossRef]
- Mori, T. Non-stripe charge order in the θ-phase organic conductors. J. Phys. Soc. Jpn. 2003, 72, 1469–1475. [Google Scholar] [CrossRef]
- Seo, H. Charge ordering in organic ET compounds. J. Phys. Soc. Jpn. 2000, 69, 805–820. [Google Scholar] [CrossRef]
- Clay, R.T.; Mazumdar, S.; Campbell, D.K. Charge ordering in θ-(BEDT-TTF)2X materials. J. Phys. Soc. Jpn. 2002, 71, 1816–1819. [Google Scholar] [CrossRef]
- Nishikawa, H.; Sato, Y.; Kikuchi, K.; Kodama, T.; Ikemoto, I.; Yamada, J.; Oshio, H.; Kondo, R.; Kagoshima, S. Charge ordering and pressure-induced superconductivity in β″-(DODHT)2PF6. Phys. Rev. B 2005, 72, 052510:1–052510:4. [Google Scholar]
- Dayal, S.; Clay, R.T.; Li, H.; Mazumdar, S. Paired electron crystal: Order from frustration in the quarter-filled band. Phys. Rev. B 2011, 83, 245106:1–245106:12. [Google Scholar]
© 2012 by the authors; licensee MDPI, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Yamamoto, T. Vibrational Spectra of β″-Type BEDT-TTF Salts: Relationship between Conducting Property, Time-Averaged Site Charge and Inter-Molecular Distance. Crystals 2012, 2, 893-934. https://doi.org/10.3390/cryst2030893
Yamamoto T. Vibrational Spectra of β″-Type BEDT-TTF Salts: Relationship between Conducting Property, Time-Averaged Site Charge and Inter-Molecular Distance. Crystals. 2012; 2(3):893-934. https://doi.org/10.3390/cryst2030893
Chicago/Turabian StyleYamamoto, Takashi. 2012. "Vibrational Spectra of β″-Type BEDT-TTF Salts: Relationship between Conducting Property, Time-Averaged Site Charge and Inter-Molecular Distance" Crystals 2, no. 3: 893-934. https://doi.org/10.3390/cryst2030893




