Achievements and Challenges in Molecular Conductors
Abstract
:1. Introduction
2. Metallic Molecular Solids of Charge Transfer Type
2.1. TTF-TCNQ
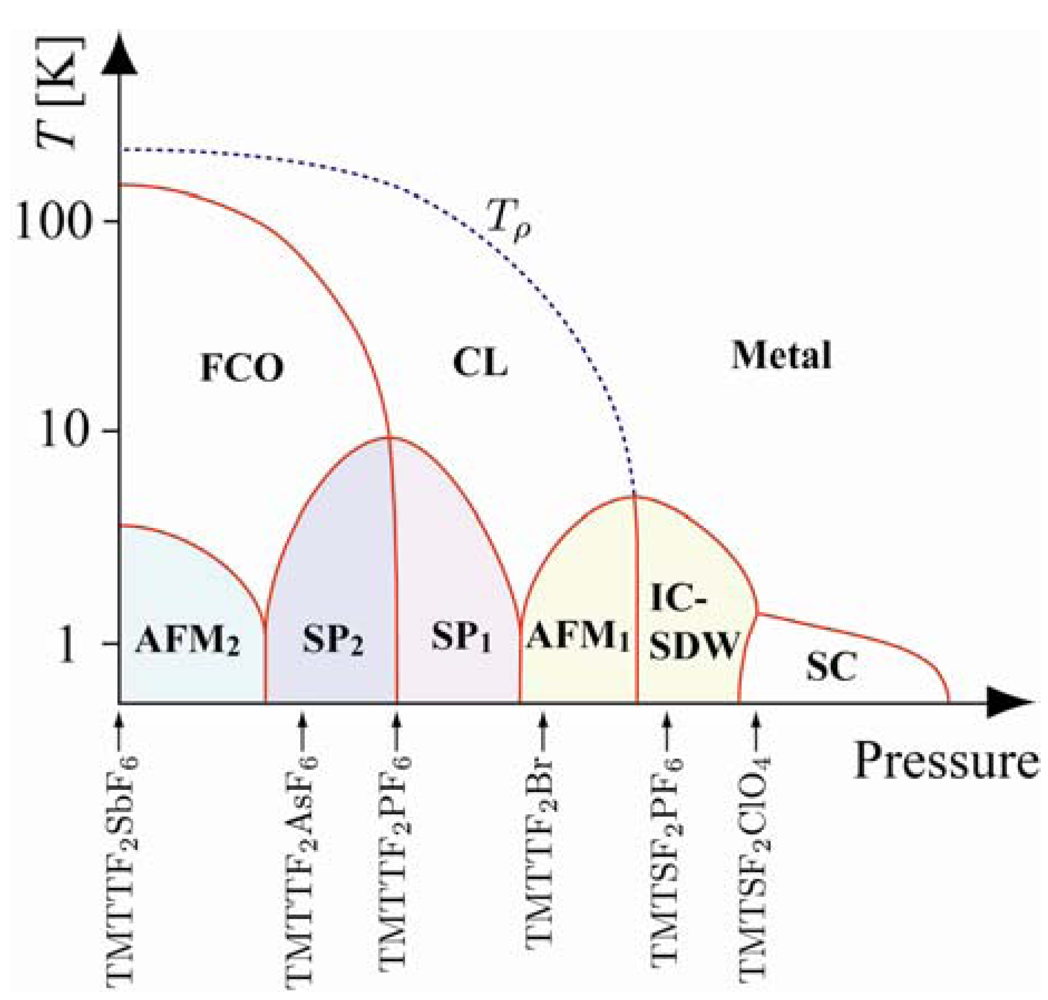
2.2. (TMTCF)2X

2.3. (ET)2X
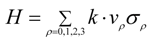
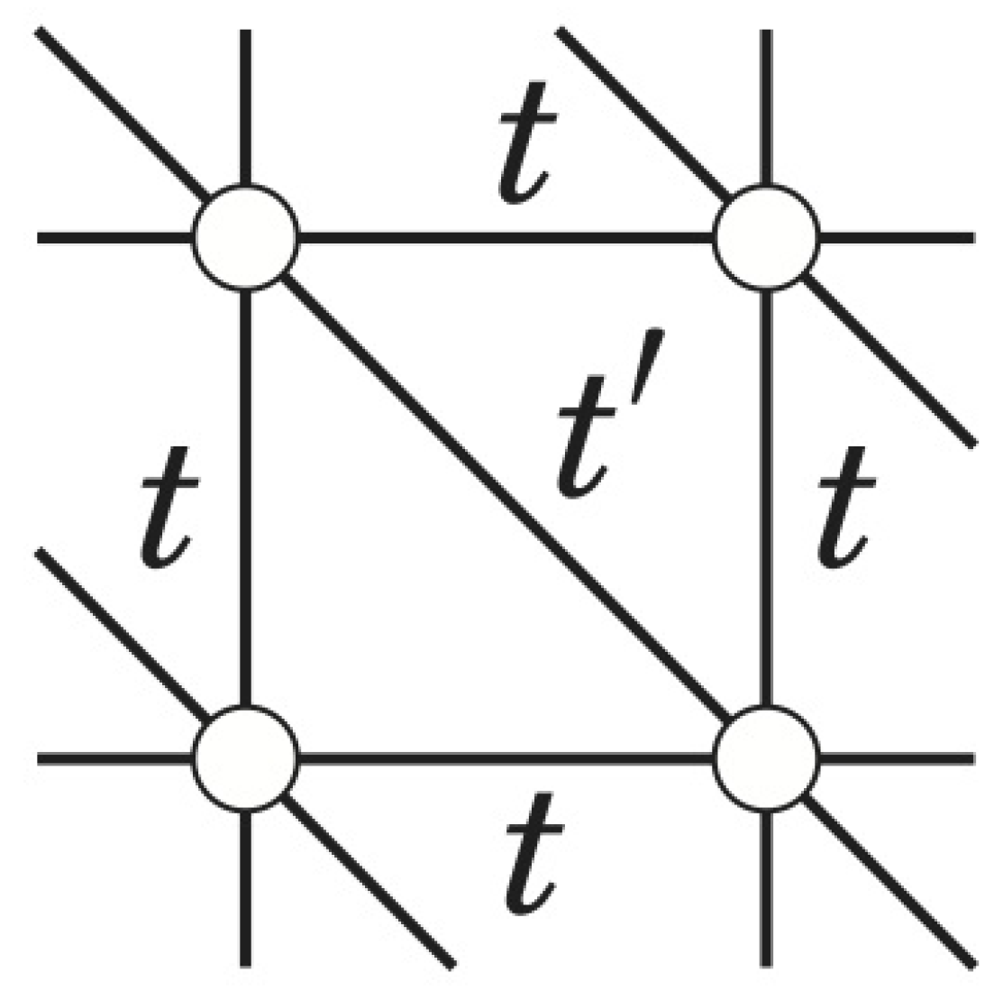
2.3.1. Spin Liquid State in κ-(ET)2 Cu2(CN)3

2.3.2. Charge Glass State in θ-polytype
2.3.3. Massless Dirac Electrons in α-(ET)2I3
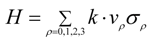
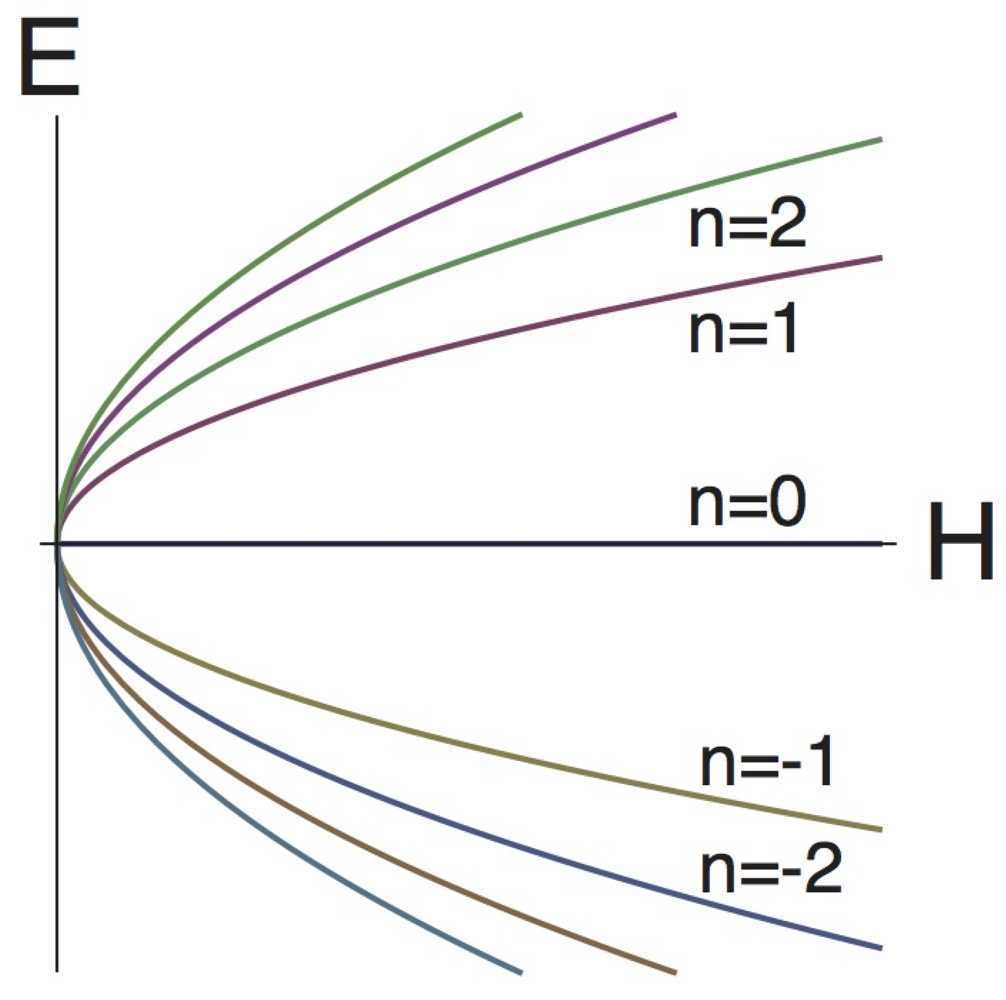
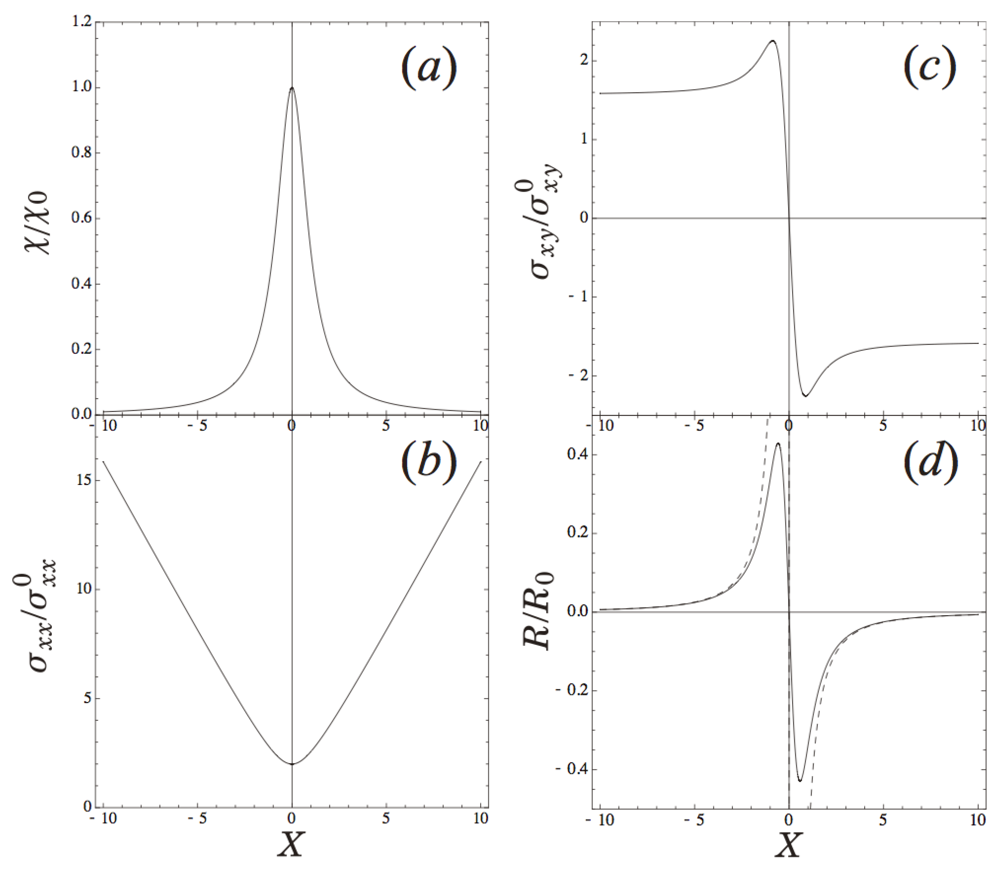
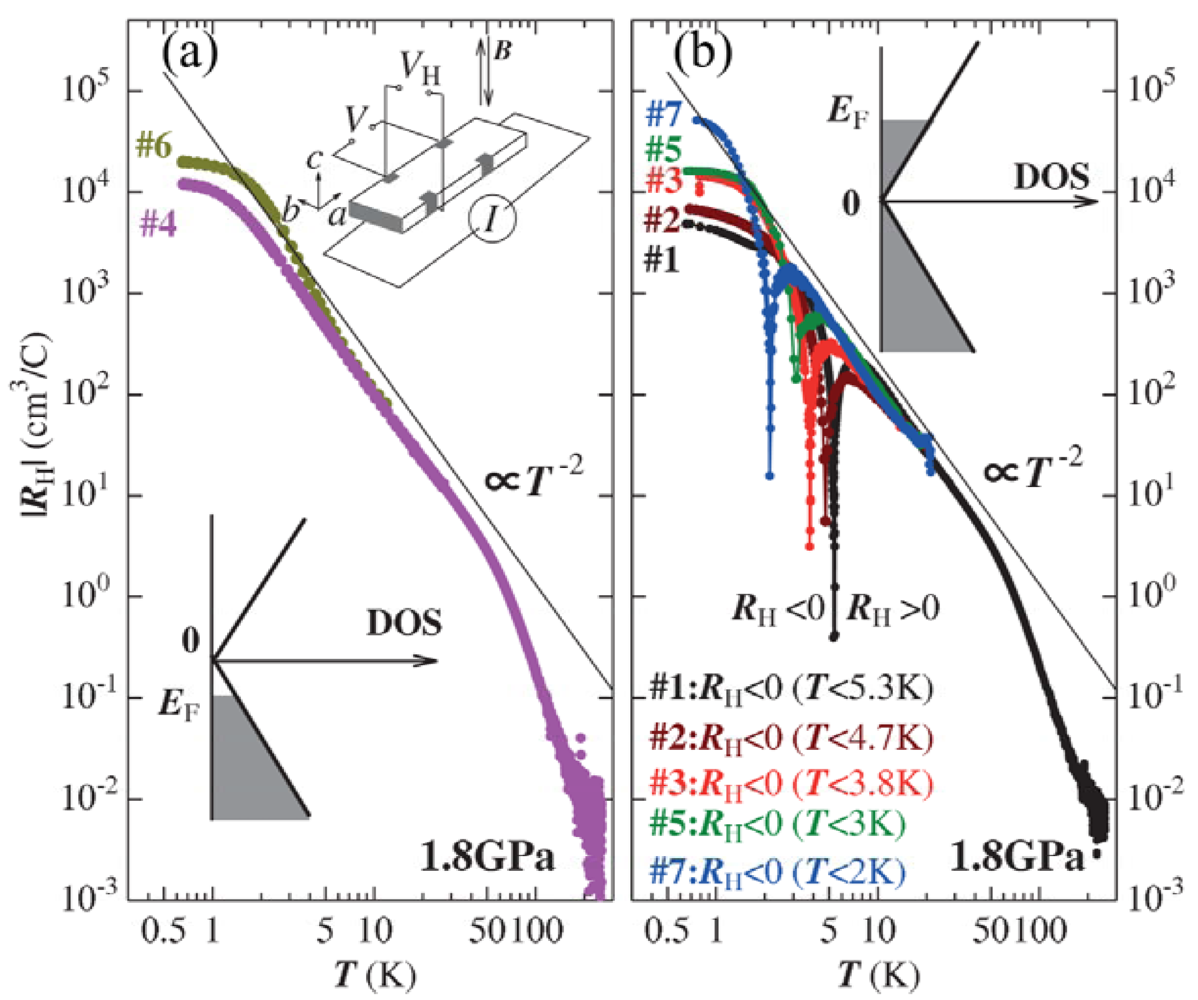
3. Charge Transfer Complexes with d Electrons
4. Single Component Molecular Metals

5. Challenges: Electronic States in Bio-material
6. Conclusion
Acknowledgments
References
- Anderson, P.W. More is different. Science 1972, 177, 393–396. [Google Scholar]
- Kobayashi, A.; Okano, Y.; Kobayashi, H. Molecular design and physical properties of single-component molecular metals. J. Phys. Soc. Jpn. 2006, 75, 051002:1–051002:12. [Google Scholar]
- Akamatsu, H.; Inokuchi, H.; Matsunaga, Y. Electrical conductivity of the perylene–bromine complex. Nature 1954, 173, 168–169. [Google Scholar] [CrossRef]
- Chiang, C.K.; Fincher, C.R., Jr.; Park, Y.W.; Heeger, A.J.; Shirakawa, H.; Louis, E.J.; Gau, S.C.; MacDiarmid, A.G. Electrical conductivity in doped polyacetylene. Phys. Rev. Lett. 1977, 39, 1098–1101. [Google Scholar]
- Bredas, J.L.; Beljonne, D.; Coropceanu, V.; Cornil, J. Charge-transfer and energy-transfer processes in π-conjugated oligomers and polymers: A molecular picture. Chem. Rev. 2004, 104, 4971–5004. [Google Scholar] [CrossRef]
- Yamamoto, T.; Takimiya, K. Facile synthesis of highly π-extended heteroarenes, dinaphtho[2,3-b:2',3'-f]chalcogenopheno[3,2-b]chalcogenophenes, and their application to field-effect transistors. J. Am. Chem. Soc. 2007, 129, 2224–2225. [Google Scholar] [CrossRef]
- Takimiya, K.; Ebata, H.; Sakamoto, K.; Izawa, T.; Otsubo, T.; Kunugi, Y. 2,7-Diphenyl[1]benzothieno[3,2-b]benzothiophene, a new organic semiconductor for air-stable organic field-effect transistors with mobilities up to 2.0 cm2 V−1 s−1. J. Am. Chem. Soc. 2006, 128, 12604–12605. [Google Scholar]
- Kawasugi, Y.; Yamamoto, H.M.; Tajima, N.; Fukunaga, T.; Tsukagoshi, K.; Kato, R. Field-induced carrier delocalization in the strain-induced Mott insulating state of an organic superconductor. Phys. Rev. Lett. 2009, 103, 116801:1–116801:4. [Google Scholar]
- Nagaoka, Y. Theory of Anderson localization—A historical survey. Prog. Theor. Phys. Suppl. 1985, 84, 1–15. [Google Scholar] [CrossRef]
- Coleman, L.B.; Cohen, M.J.; Sandman, D.J.; Yamagishi, F.G.; Garito, A.F.; Heeger, A.J. Superconducting fluctuations and the peierls instability in an organic solid. Solid State Commun. 1973, 12, 1125–1132. [Google Scholar] [CrossRef]
- Devreese, J.T.; Evrard, R.P.; van Doren, V.E. Highly Conducting One-Dimensional Solids; Plenum Press: New York, NY, USA, 1979. [Google Scholar]
- Jerome, D. Organic conductors: From charge density wave TTF−TCNQ to superconducting (TMTSF)2PF6. Chem. Rev. 2004, 104, 5565–5592. [Google Scholar] [CrossRef]
- Solyom, J. The Fermi gas model of one-dimensional conductors. Adv. Phys. 1979, 28, 201–303. [Google Scholar]
- Brown, S.E.; Chaikin, P.M.; Naughton, M.J. La Tour des Sels de Bechgaard. In The Physics of Organic Superconductors and Conductors; Lebed, A., Ed.; Spring Springer Series in Materials: Berlin/Heidelberg, Geramny, 2008; pp. 357–512. [Google Scholar]
- Jerome, D.; Mazaud, A.; Ribault, M.; Bechgaard, K. Superconductivity in a synthetic organic conductor (TMTSF)2PF6. J. Phys. Lett. (Paris) 1980, 41, L95–L98. [Google Scholar]
- Jerome, D. The physics of organic superconductors. Science 1991, 252, 1509–1514. [Google Scholar]
- Mori, H. Materials viewpoint of organic superconductors. J. Phys. Soc. Jpn. 2006, 75, 051003:1–051003:15. [Google Scholar]
- Yu, W.; Zhang, F.; Zamborsky, F.; Alavi, B.; Baur, A.; Merlic, C.A.; Brown, S.E. Electron-lattice coupling and broken symmetries of molecular salt (TMTTF)2SbF6. Phys. Rev. B 2004, 70, 121101:1–121101:4. [Google Scholar]
- Yoshimi, K.; Seo, H.; Ishibashi, S.; Brown, S.E. Tuning the magnetic dimensionality by charge ordering in the molecular TMTTF salts. Phys. Rev. Lett. 2012, 108, 096402:1–096402:5. [Google Scholar]
- Seo, H.; Merino, J.; Yoshioka, H.; Ogata, M. Theoretical aspects of charge ordering in molecular conductors. J. Phys. Soc. Jpn. 2006, 75, 051009:1–051009:20. [Google Scholar]
- Fukui, K.; Yonezawa, T.; Shingu, H. A molecular orbital theory of reactivity in aromatic hydrocarbons. J. Chem. Phys. 1952, 20, 722–725. [Google Scholar]
- Hoffman, R. An extended Hückel theory. I. Hydrocarbons. J. Chem. Phys. 1963, 39, 1397–1412. [Google Scholar] [CrossRef]
- Mori, T.; Kobayashi, A.; Sasaki, Y.; Kobayashi, H.; Saito, G.; Inokuchi, H. The intermolecular interaction of tetrathiafulvalene and bis(ethylenedithio)tetrathiafulvalene in organic metals. Calculation of orbital overlaps and models of energy-band structures. Bull. Chem. Soc. Jpn. 1984, 57, 627–633. [Google Scholar] [CrossRef]
- Chaikin, P. Field induced spin density waves. J. Phys. I Fr. 1996, 6, 1875–1898. [Google Scholar] [CrossRef]
- Osada, T.; Ohmichi, E. Magnetotransport and magnetic-field-induced density waves in low-dimensional layered conductors. J. Phys. Soc. Jpn. 2006, 75, 051006:1–051006:7. [Google Scholar]
- Ovchinnikov, A.A. On the possibility of a metal-dielectric transition in one-dimensional systems with noninteger numbers of electrons per unit. Sov. Phys. JETP 1973, 37, 176–177. [Google Scholar]
- Giamarchi, T. Theoretical framework for quasi-one dimensional systems. Chem. Rev. 2004, 104, 5037–5056. [Google Scholar] [CrossRef]
- Degiorgi, L.; Jerome, D. Transport and optics in quasi-one-dimensional organic conductors. J. Phys. Soc. Jpn. 2006, 75, 051004:1–051004:10. [Google Scholar]
- Seo, H.; Fukuyama, H. Antiferromagnetic phases of one-dimensional quarter-filled organic conductors. J. Phys. Soc. Jpn. 1997, 66, 1249–1252. [Google Scholar] [CrossRef]
- Hiraki, K.; Kanoda, K. Wigner crystal type of charge ordering in an organic conductor with a quarter-filled band: (DI-DCNQI)2Ag. Phys. Rev. Lett. 1998, 80, 4737–4740. [Google Scholar] [CrossRef]
- Kakiuchi, T.; Wakabayashi, Y.; Sawa, H.; Itou, T.; Kanoda, K. Wigner crystallization in (DI-DCNQI)2Ag detected by synchrotron radiation x-ray diffraction. Phys. Rev. Lett. 2007, 98, 066402:1–066402:4. [Google Scholar]
- Seo, H.; Motome, Y. Spiral charge frustration in the molecular conductor (DI-DCNQI)2Ag. Phys. Rev. Lett. 2009, 102, 196403:1–196403:4. [Google Scholar]
- Chow, D.S.; Zamborszky, F.; Alavi, B.; Tantillo, D.J.; Baur, A.; Merlic, C.A.; Brown, S.E. Charge ordering in the TMTTF family of molecular conductors. Phys. Rev. Lett. 2000, 85, 1698–1701. [Google Scholar]
- Nad, F.; Monceau, P.; Carcel, C.; Fabre, J.M. Dielectric response of the charge-induced correlated state in the quasi-one-dimensional conductor (TMTTF)2PF6. Phys. Rev. B 2000, 62, 1753–1756. [Google Scholar]
- Monceau, P.; Nad, F.; Brazovskii, S. Ferroelectric Mott-Hubbard phase of organic (TMTTF)2X conductors. Phys. Rev. Lett. 2001, 86, 4080–4083. [Google Scholar] [CrossRef]
- Nad, F.; Monceau, P. Dielectric response of the charge ordered state in quasi-one-dimensional organic conductors. J. Phys. Soc. Jpn. 2006, 75, 051005:1–051005:12. [Google Scholar]
- Coulon, C.; Parkin, S.S.S.; Laversanne, R. Structureless transition and strong localization effects in bis-tetramethyltetrathiafulvalenium salts [(TMTTF)2X]. Phys. Rev. B 1985, 31, 3583–3587. [Google Scholar]
- For CO in molecular conductors in general including studies in early stage by Verwey, Hubbard and others, see reference 20.
- Clay, R.T.; Mazumdar, S.; Campbell, D.K. Bond-order and charge–density waves in the isotropic interacting two-dimensional quarter-filled band and insulating state proximate to organic superconductivity. Phys. Rev. B 2003, 67, 115121:1–115121:9. [Google Scholar]
- Nakamura, T. Possible charge ordering patterns of the paramagnetic insulating states in (TMTTF)2X. J. Phys. Soc. Jpn. 2003, 72, 213–216. [Google Scholar] [CrossRef]
- Inagaki, S.; Fukuyama, H. Spin-peierls state vs. Neel state. II. Interchain exchange interaction. J. Phys. Soc. Jpn. 1983, 52, 3620–3629. [Google Scholar] [CrossRef]
- Zamborszky, F.; Yu, W.; Raas, W.; Brown, S.E.; Alavi, B.; Merlic, C.A.; Baur, A. Competition and coexistence of bond and charge orders in (TMTTF)2AsF6. Phys. Rev. B 2002, 66, 081103:1–081103:4. [Google Scholar]
- Nakamura, T.; Furukawa, K.; Hara, T. Redistribution of charge in the proximity of spin-peierls transition: 13C NMR investigation of (TMTTF)2PF6. J. Phys. Soc. Jpn. 2007, 76, 064715:1–064715:5. [Google Scholar]
- Itoi, M.; Hedo, M.; Uwatoko, Y.; Nakamura, T. Anomalously wide superconducting phase of one-dimensional organic conductor (TMTTF)2SbF6. J. Phys. Soc. Jpn. 2008, 77, 023701:1–023701:4. [Google Scholar]
- Iwase, F.; Sugiura, K.; Furukawa, K.; Nakamura, T. 13C NMR study of the magnetic properties of the quasi-one-dimensional conductor (TMTTF)2SbF6. Phys. Rev. B 2011, 84, 115140:1–115140:7. [Google Scholar]
- Kino, H.; Fukuyama, H. Phase diagram of two-dimensional organic conductors: (BEDT-TTF)2X. J. Phys. Soc. Jpn. 1996, 65, 2158–2169. [Google Scholar] [CrossRef]
- Seo, H. Charge ordering in organic ET compounds. J. Phys. Soc. Jpn. 2000, 69, 805–820. [Google Scholar] [CrossRef]
- Seo, H.; Hotta, C.; Fukuyama, H. Toward systematic understanding of diversity of electronic properties in low-dimensional molecular solids. Chem. Rev. 2004, 104, 5005–5036. [Google Scholar] [CrossRef]
- Kanoda, K. Recent progress in NMR studies on organic conductors. Hyperfine Interactions 1997, 104, 235–249. [Google Scholar] [CrossRef]
- Kanoda, K. Metal–insulator transition in κ-(ET)2X and (DCNQI)2M: Two contrasting manifestation of electron correlation. J. Phys. Soc. Jpn. 2006, 75, 051007:1–051007:15. [Google Scholar]
- Kino, H.; Fukuyama, H. Electronic states of conducting organic κ-(BEDT-TTF)2X. J. Phys. Soc. Jpn. 1995, 64, 2726–2729. [Google Scholar] [CrossRef]
- Shimizu, Y.; Miyagawa, K.; Kanoda, K.; Maesato, M.; Saito, G. Spin liquid state in an organic Mott insulator with a triangular lattice. Phys. Rev. Lett. 2003, 91, 107001:1–107001:4. [Google Scholar]
- Anderson, P.W. Resonating valence bonds: A new kind of insulator? Mater. Res. Bull. 1973, 8, 153–160. [Google Scholar] [CrossRef]
- Itou, T.; Oyamada, A.; Maegawa, S.; Tamura, M.; Kato, R. Quantum spin liquid in the spin-1/2 triangular antiferromagnet EtMe3Sb[Pd(dmit)2]2. Phys. Rev. B 2008, 77, 104413:1–104413:5. [Google Scholar]
- Kato, R.; Itou, T. Molecular Quasi-triangular Lattice Antiferromagnets. In Understanding Quantum Phase Transitions; Lincoln, D.C., Ed.; CRC Press: Boca Raton, FL, USA, 2010; pp. 419–443. [Google Scholar]
- Kanoda, K.; Kato, R. Mott physics in organic conductors with triangular lattices. Annu. Rev. Condens. Matter Phys. 2011, 2, 167–188. [Google Scholar] [CrossRef]
- Balants, L. Spin liquids in frustrated magnets. Nature 2010, 464, 199–208. [Google Scholar] [CrossRef]
- Abdel-Jawad, M.; Terasaki, I.; Sasaki, T.; Yoneyama, N.; Kobayashi, N.; Uesu, Y.; Hotta, C. Anomalous dielectric response in the dimer Mott insulator κ-(BEDT-TTF)2Cu2(CN)3. Phys. Rev. B 2010, 82, 125119:1–125119:5. [Google Scholar]
- Li, H.; Clay, R.T.; Mazumdar, S. The paired-electron crystal in the two-dimensional frustrated quarter-filled band. J. Phys. Condens. Matter 2010, 22, 272201:1–272201:7. [Google Scholar]
- Naka, M.; Ishihara, S. Electronic ferroelectricity in a dimer Mott insulator. J. Phys. Soc. Jpn. 2010, 79, 063707:1–063707:4. [Google Scholar]
- Gomi, H.; Imai, T.; Takahashi, A.; Aihara, M. Purely electronic terahertz polarization in dimer Mott insulators. Phys. Rev. 2010, B82, 035101:1–035101:4. [Google Scholar]
- Hotta, C. Quantum electric dipoles in spin-liquid dimer Mott insulator κ-ET2Cu2(CN)3. Phys. Rev. B 2010, 82, 241104:1–241104:4. [Google Scholar]
- Kishida, H. Possible interrelationship between dielectric responses and magnetic states has been elucidated by optical measurements. Nagoya University, Nagoya, Japan. Private communications, 2011.
- Ejima, S.; Gebhard, F.; Nishimoto, S.; Ohta, Y. Phase diagram of t-U-V1-V2 model at quarter filling. Phys. Rev. B 2005, 72, 033101:1–033101:4. [Google Scholar]
- Takahashi, T.; Nogami, Y.; Yakushi, K. Charge ordering in organic conductors. J. Phys. Soc. Jpn. 2006, 75, 051008:1–051008:17. [Google Scholar]
- Tajima, N.; Sugawara, S.; Tamura, M.; Nishio, Y.; Kajita, K. Electronic phases in an organic conductor α-(BEDT-TTF)2I3: Ultra narrow gap semiconductor, superconductor, metal, and charge-ordered insulator. J. Phys. Soc. Jpn. 2006, 75, 051010:1–051010:10. [Google Scholar]
- Kino, H.; Fukuyama, H. On the phase transition of α-(ET)2I3. J. Phys. Soc. Jpn. 1995, 64, 1877–1880. [Google Scholar] [CrossRef]
- Katayama, S.; Kobayashi, A.; Suzumura, Y. Pressure-induced zero-gap semiconducting state in organic conductor α-(BEDT-TTF)2I3 salt. J. Phys. Soc. Jpn. 2006, 75, 054705:1–054705:6. [Google Scholar]
- Kobayashi, A.; Katayama, S.; Noguchi, K.; Suzumura, Y. Superconductivity in charge ordered organic conductor α-(ET)2I3 salt. J. Phys. Soc. Jpn. 2004, 73, 3135–3148. [Google Scholar] [CrossRef]
- Ishibashi, S.; Tamura, M.; Kohyama, M.; Terakura, K. Ab Initio Electronic-Structure Calculations for α-(BEDT-TTF)2I3. J. Phys. Soc. Jpn. 2006, 75, 015005:1–015005:2. [Google Scholar]
- Kino, H.; Miyazaki, T. First-principles study of electronic structure in α-(BEDT-TTF)2I3 at ambient pressure and with uniaxial strain. J. Phys. Soc. Jpn. 2006, 75, 034704:1–034704:8. [Google Scholar]
- Kobayashi, A.; Katayama, S.; Suzumura, Y.; Fukuyama, H. Massless fermions in organic conductor. J. Phys. Soc. Jpn. 2007, 76, 034711:1–034711:6. [Google Scholar]
- McClure, J.W. Diamagnetism of graphite. Phys. Rev. 1956, 104, 666–671. [Google Scholar] [CrossRef]
- Shon, N.H.; Ando, T. Quantum transport in two-dimensional graphite system. J. Phys. Soc. Jpn. 1998, 67, 2421–2429. [Google Scholar] [CrossRef]
- Novoselov, K.S.; Geim, A.K.; Morozov, S.V.; Jiang, D.; Katsnelson, M.I.; Grigorieva, I.V.; Dubonosand, S.V.; Firsov, A.A. Two-dimensional gas of massless Dirac fermions in graphene. Nature 2005, 438, 197–200. [Google Scholar]
- Kubo, R.; Fukuyama, H. Interband Effects in Orbital Magnetism and Halll conductivity. In Proceedings of the 10th International Conference on Physics of Semiconductors, Cambridge, MA, USA, 17−21 August 1970; United States Atomic Energy Commission: Germantown, MD, USA, 1970; pp. 551–560. [Google Scholar]
- Osada, T. Negative interlayer magnetoresistance and zero-mode Landau level in multilayer Dirac electron systems. J. Phys. Soc. Jpn. 2008, 77, 084711:1–084711:5. [Google Scholar]
- McClure, J.W. Theory of diamagnetism of graphite. Phys. Rev. 1960, 199, 606–613. [Google Scholar] [CrossRef]
- Fukuyama, H. Anomalous orbital magnetism and Hall effect of massless fermions in two dimension. J. Phys. Soc. Jpn. 2007, 76, 043711:1–043711:3. [Google Scholar]
- Kobayashi, A.; Suzumura, Y.; Fukuyama, H. Hall effect and orbital diamagnetism in zerogap state of molecular conductor α-(BEDT-TTF)2I3. J. Phys. Soc. Jpn. 2008, 77, 064718:1–064718:9. [Google Scholar]
- Ando, T. Charged impurity scattering in graphenes: Effects of environmental screening, band gap, and AA stacking. J. Phys. Conf. Ser. 2011, 302, 012015:1–012015:8. [Google Scholar]
- Tajima, N.; Kato, R.; Sugawara, S.; Nishio, Y.; Kajita, K. Interband effects of magnetic field on Hall conductivity in the multilayered massless Dirac fermion system α-(BEDT-TTF)2I3. Phys. Rev. B 2012, 85, 033401:1–033401:4. [Google Scholar]
- Kanoda, K. NMR Knight shift has indicated the reduction of effective density of states compared with the result of the band-structure calculations near the crossing points, while it is enhanced at higher energies. Tokyo University, Tokyo, Japan. Private communications, 2011.
- Kotov, V.N.; Uchoa, B.; Pereira, V.M.; Guinea, F.; Castro, N.A.H. Electron-electron interactions in graphene: Current status and perspectives. Rev. Mod. Phys. 2012, in press.. [Google Scholar]
- Kobayashi, H.; Cui, H.; Kobayashi, A. Organic metals and superconductors based on BETS (BETS = Bis(ethylenedithio)tetraselenafulvalene). Chem. Rev. 2004, 104, 5265–5288. [Google Scholar] [CrossRef]
- Uji, S.; Brooks, J.S. Magnetic-field-induced superconductivity in organic conductors. J. Phys. Soc. Jpn. 2006, 75, 051014:1–051014:10. [Google Scholar]
- Inabe, T.; Tajima, H. Phthalocyanines versatile components of molecular conductors. Chem. Rev. 2004, 104, 5503–5534. [Google Scholar] [CrossRef]
- Manriquez, J.M.; Gordon, T.Y.; McLean, R.S.; Epstein, A.J.; Miller, J.S. A room-temperature molecular/organic-based magnet. Science 1991, 252, 1415–1417. [Google Scholar]
- Miller, J.S. Oliver Kahn lecture: Composition and structure of the V[TCNE]x (TCNE = tetracyanoethylene) room-temperature, organic-based magnet—A personal perspective. Polyhedron 2009, 28, 1596–1605. [Google Scholar] [CrossRef]
- Matuura, H.; Miyake, K.; Fukuyama, H. Theory of room temperature ferromagnet V(TCNE)x (1.5 < x < 2): Role of hidden flat bands. J. Phys. Soc. Jpn. 2010, 79, 034712:1–034712:10. [Google Scholar]
- Kato, R.; Kobayashi, H.; Kobayashi, A. Crystal and electronic structures of conductive anion-radical salts, (2,5-R1R2-DCNQI)2Cu (DCNQI = N,N'-dicyanoquinonediimine; R1, R2 = CH3, CH3O, Cl, Br. J. Am. Chem. Soc. 1989, 111, 5224–5232. [Google Scholar]
- Kato, R. Conductive copper salts of 2,5-Disubstituted N,N’-Dicyanobenzoquinonediimines (DCNQIs): Structural and physical properties. Bull. Chem. Soc. Jpn. 2000, 73, 515–534. [Google Scholar] [CrossRef]
- Tanaka, H.; Okano, Y.; Kobayashi, H.; Suzuki, W.; Kobayashi, A. A three-dimensional synthetic metallic crystal composed of single-component molecules. Science 2001, 291, 285–287. [Google Scholar] [CrossRef]
- Kobayashi, H.; Fujiwara, E.; Kobayashi, H. Single-component molecular metals with extended-TTF dithiolate ligands. Chem. Rev. 2004, 104, 5243–5264. [Google Scholar] [CrossRef]
- Tanaka, H.; Tokumoto, M.; Ishibashi, S.; Graf, D.; Choi, E.S.; Brooks, J.S.; Yasuzuka, S.; Okano, Y.; Kobayashi, H.; Kobayashi, A. Observation of three-dimensional Fermi surfaces in a single-component molecular metal, [Ni(tmdt)2]. J. Am. Chem. Soc. 2004, 126, 10518–10519. [Google Scholar]
- Rovira, C.; Novoa, J.J.; Mozos, J.L.; Ordejón, P.; Canadell, E. First-principles study of the neutral molecular metal Ni(tmdt)2. Phys. Rev. B 2002, 65, 081104:1–081104:4. [Google Scholar]
- Ishibashi, S.; Tanaka, H.; Kohyama, M.; Tokumoto, M.; Kobayashi, A.; Kobayashi, H.; Terakura, K. Ab Initio electronic structure calculation for single-component molecular conductor Au(tmdt)2 (tmdt = Trimethylenetetrathiafulvalenedithiolate). J. Phys. Soc. Jpn. 2005, 74, 843–846. [Google Scholar] [CrossRef]
- Ishibashi, S.; Terakura, K.; Kobayashi, A. Electronic structures of single component molecular metals based on ab initio calculation. J. Phys. Soc. Jpn. 2008, 77, 024702:1–024702:7. [Google Scholar]
- Yasuzuka, S.; Tanaka, H.; Tokumoto, M.; Graf, D.; Choi, E.S.; Brooks, J.S.; Kobayashi, H.; Kobayashi, A. Highly isotropic magnetoresistance in a single-component molecular metal [Ni(tmdt)2]. J. Phys. Soc. Jpn. 2008, 77, 034709:1–034709:5. [Google Scholar]
- Suzuki, W.; Fujiwara, E.; Kobayashi, A.; Fujishiro, Y.; Nishibori, E.; Takata, M.; Sakata, M.; Fujiwara, H.; Kobayashi, H. Highly conducting crystals based on single-component gold complexes with extended-TTF dithiolate ligands. J. Am. Chem. Soc. 2003, 125, 1486–1487. [Google Scholar]
- Zhou, B.; Shimamura, M.; Fujiwara, E.; Kobayashi, A.; Higashi, T.; Nishibori, E.; Sakata, M.; Cui, H.B.; Takahashi, K.; Kobayashi, H. Magnetic transitions of single-component molecular metal [Au(tmdt)2] and its alloy systems. J. Am. Chem. Soc. 2006, 128, 3872–3873. [Google Scholar]
- Hara, Y.; Miyagawa, K.; Kanoda, K.; Shimamura, M.; Zhou, B.; Kobayashi, A.; Kobayashi, H. NMR evidence for antiferromagnetic transition in the single-component molecular conductor, [Au(tmdt)2] at 110 K. J. Phys. Soc. Jpn. 2008, 77, 053706:1–053706:4. [Google Scholar]
- Seo, H.; Ishibashi, S.; Okano, Y.; Kobayashi, H.; Kobayashi, A.; Fukuyama, H.; Terakura, K. Single-component molecular metals as multiband π–d systems. J. Phys. Soc. Jpn 2008, 77, 023714:1–023714:4. [Google Scholar]
- Zhou, B.; Yajima, H.; Kobayashi, A.; Okano, Y.; Tanaka, H.; Kumashiro, T.; Nishibori, E.; Sawa, H.; Kobayashi, H. Single-component molecular conductor [Cu(tmdt)2] containing an antiferromagnetic Heisenberg chain. Inorg. Chem. 2010, 49, 6740–6747. [Google Scholar]
- Tsuneyuki, S.; Kobori, T.; Akagi, K.; Sodeyama, K.; Terakura, K.; Fukuyama, H. Molecular orbital calculation of biomolecules with fragment molecular orbitals. Chem. Phys. Lett. 2009, 476, 104–108. [Google Scholar] [CrossRef]
- Nishioka, H.; Ando, K. Electronic coupling calculation and pathway analysis of electron transfer reaction using ab initio fragment-based method. I. FMO–LCMO approach. J. Chem. Phys. 2011, 134, 204109:1–204109:12. [Google Scholar]
- Harada, Y.; Taguchi, M.; Miyajima, Y.; Tokushima, T.; Horikawa, Y.; Chainani, A.; Shiro, Y.; Senba, Y.; Ohashi, H.; Fukuyama, H.; et al. Ligand energy controls the Heme-Fe valence in aqueous myoglobins. J. Phys. Soc. Jpn. 2009, 78, 044802:1–044802:5. [Google Scholar]
- Day, P.; Smith, D.W.; Williams, R.J.P. Crystal spectra of a Heme and some Heme-protein complexes. Biochemistry 1967, 6, 1563–1566. [Google Scholar] [CrossRef]
- Day, P.; Smith, D.W.; Williams, R.J.P. Crystal spectra of some ferric hemoproteins. Biochemistry 1967, 6, 3747–3750. [Google Scholar] [CrossRef]
- Fukuyama, H. Physics of molecular conductors. J. Phys. Soc. Jpn. 2006, 75, 051001:1–051001:7. [Google Scholar]
- Fukuyama, H. Trends of Condensed Matter Science: A Personal View. In Frontiers in Materials Research; Fujikawa, Y., Nakajima, K., Sakurai, T., Eds.; Springer: Berlin/Heidelberg, Geramny, 2008; pp. 11–28. [Google Scholar]
© 2012 by the authors; licensee MDPI, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Fukuyama, H. Achievements and Challenges in Molecular Conductors. Crystals 2012, 2, 875-892. https://doi.org/10.3390/cryst2030875
Fukuyama H. Achievements and Challenges in Molecular Conductors. Crystals. 2012; 2(3):875-892. https://doi.org/10.3390/cryst2030875
Chicago/Turabian StyleFukuyama, Hidetoshi. 2012. "Achievements and Challenges in Molecular Conductors" Crystals 2, no. 3: 875-892. https://doi.org/10.3390/cryst2030875
APA StyleFukuyama, H. (2012). Achievements and Challenges in Molecular Conductors. Crystals, 2(3), 875-892. https://doi.org/10.3390/cryst2030875



