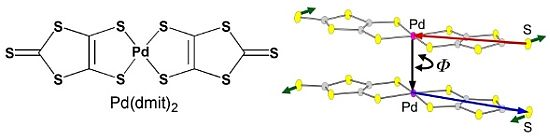
Cation Dependence of Crystal Structure and Band Parameters in a Series of Molecular Conductors, β'-(Cation)[Pd(dmit)2]2 (dmit = 1,3-dithiole-2-thione-4,5-dithiolate)
Abstract
:1. Introduction

2. Results and Discussion
2.1. Lattice Constants
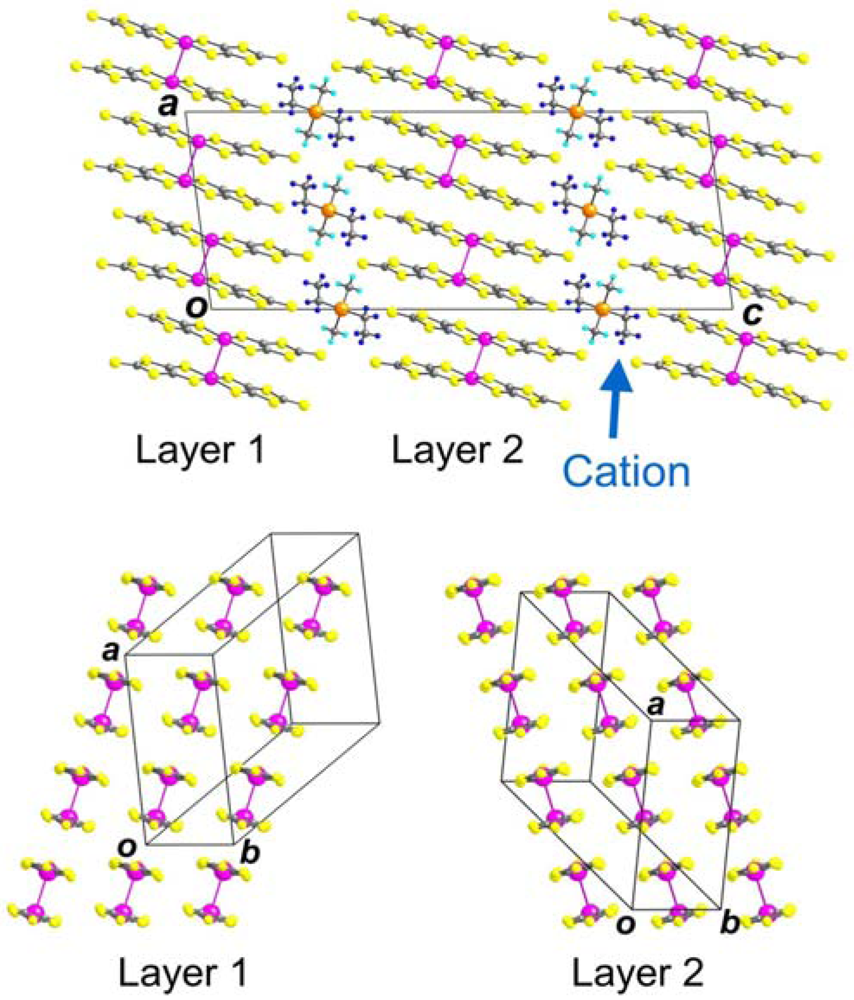
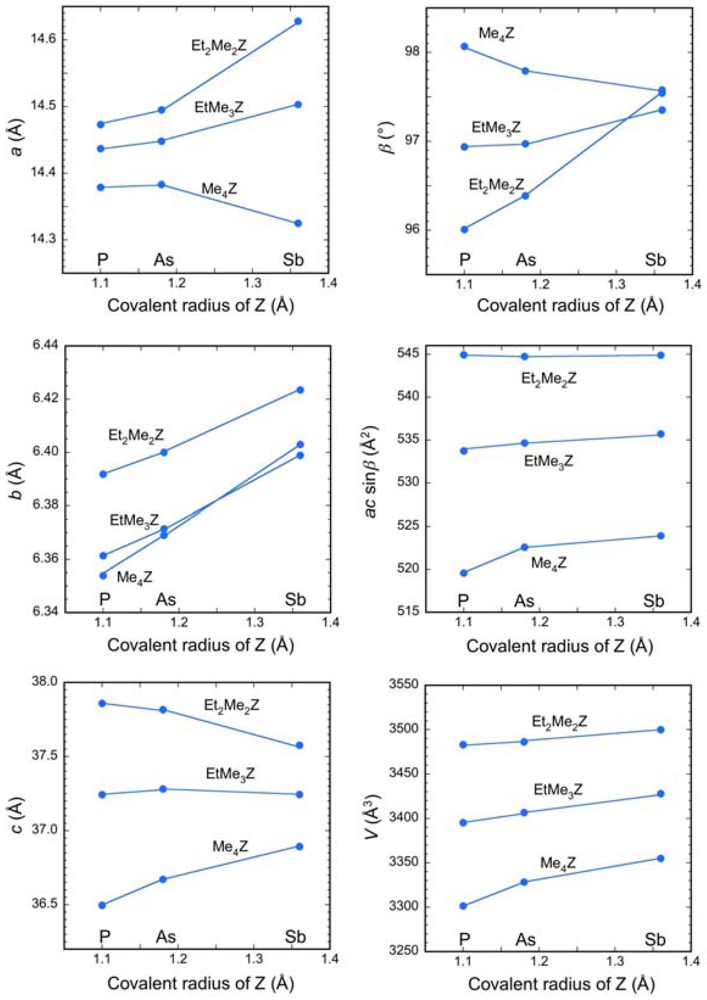
| Cation | a (Å) | b (Å) | c (Å) | β (°) | V (Å3) |
|---|---|---|---|---|---|
| Me4P | 14.379(3) | 6.3539(12) | 36.496(7) | 98.070(2) | 3301.5(11) |
| Me4As | 14.383(4) | 6.3691(15) | 36.672(9) | 97.793(3) | 3328.4(14) |
| EtMe3P | 14.437(4) | 6.3614(15) | 37.243(9) | 96.938(3) | 3395.3(14) |
| EtMe3As | 14.448(4) | 6.3715(18) | 37.282(11) | 96.973(3) | 3406.7(18) |
| Et2Me2P | 14.473(3) | 6.3918(13) | 37.859(8) | 96.009(3) | 3483.1(13) |
| Et2Me2As | 14.495(4) | 6.4000(15) | 37.816(10) | 96.388(3) | 3486.3(15) |
| Me4Sb | 14.325(7) | 6.403(3) | 36.893(19) | 97.543(5) | 3355(3) |
| EtMe3Sb | 14.503(3) | 6.3989(12) | 37.244(7) | 97.352(2) | 3427.9(12) |
| Et2Me2Sb | 14.628(4) | 6.4235(15) | 37.577(9) | 97.577(2) | 3500.0(15) |
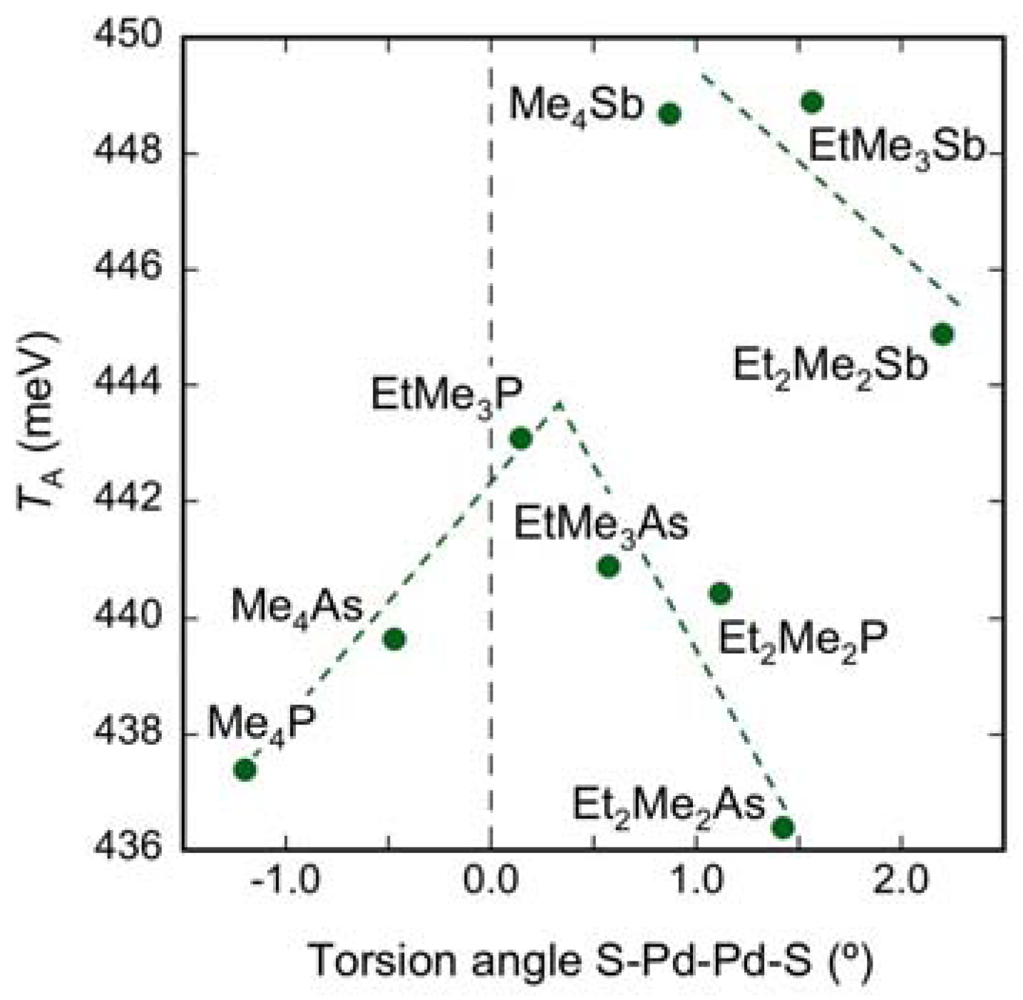
2.2. Interdimer Transfer Integrals
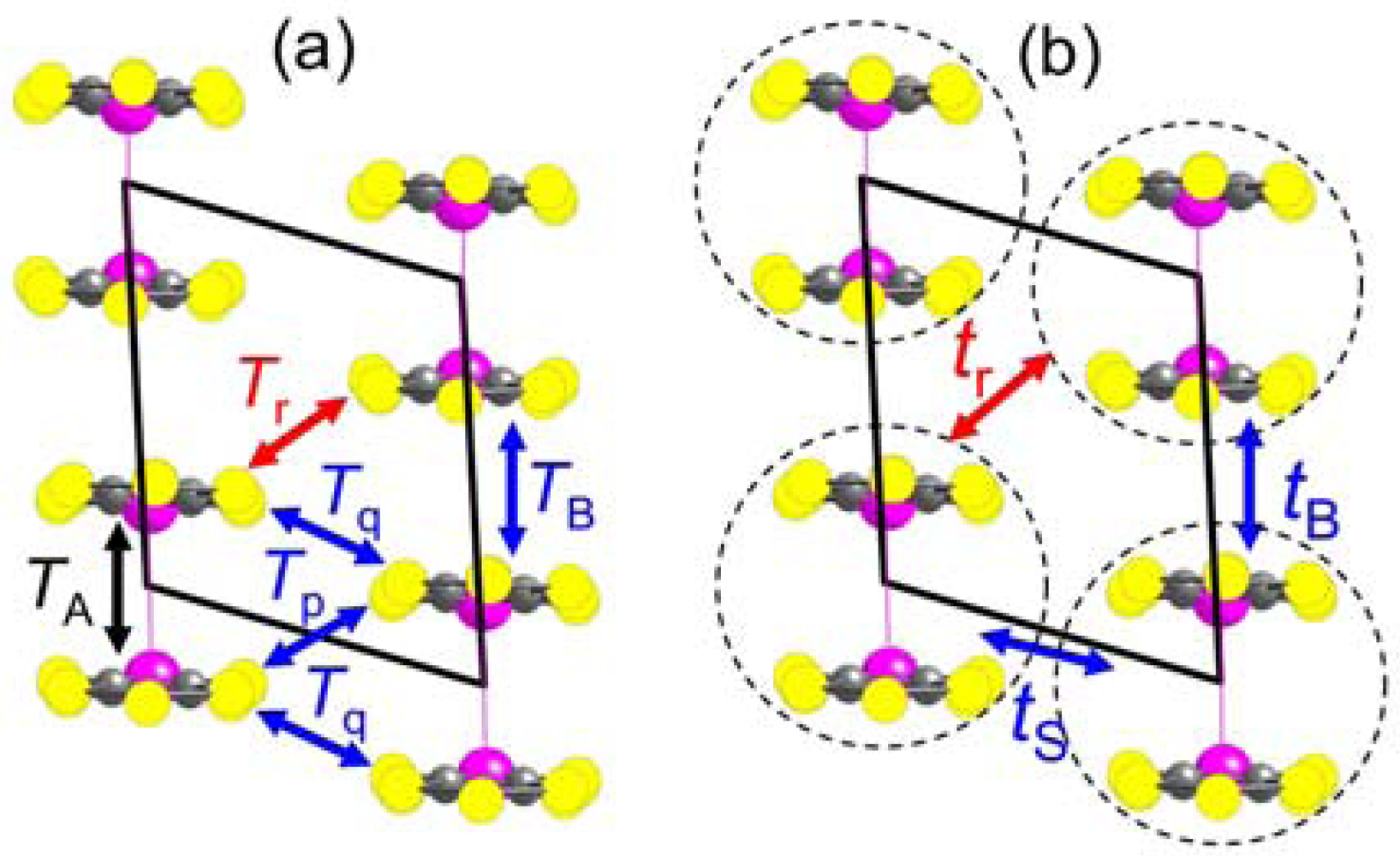
| Cation | TA (meV) | TB (meV) | Tp (meV) | Tq (meV) | Tr (meV) |
|---|---|---|---|---|---|
| Me4P | 437 | 68.2 | 29.5 | 18.2 | 41.6 |
| Me4As | 440 | 65.2 | 27.2 | 18.0 | 44.7 |
| EtMe3P | 443 | 64.7 | 25.3 | 18.6 | 45.1 |
| EtMe3As | 441 | 64.6 | 24.1 | 18.3 | 46.3 |
| Et2Me2P | 440 | 56.0 | 22. 0 | 17.3 | 47.2 |
| Et2Me2As | 436 | 53.7 | 21.1 | 17.1 | 47.5 |
| Me4Sb | 449 | 57.7 | 22.7 | 16.3 | 48.5 |
| EtMe3Sb | 449 | 56.4 | 20.4 | 16.8 | 50.1 |
| Et2Me2Sb | 445 | 52.5 | 18.3 | 15.9 | 51.6 |
| Cation | tB (meV) | tS (meV) | t (meV) | tr (meV) | tr/t | W (meV) |
|---|---|---|---|---|---|---|
| Me4P | 34.1 | 32.9 | 33.5 | 20.8 | 0.620 | 271 |
| Me4As | 32.6 | 31.6 | 32.1 | 22.3 | 0.696 | 264 |
| EtMe3P | 32.3 | 31.3 | 31.8 | 22.5 | 0.709 | 262 |
| EtMe3As | 30.5 | 30.3 | 30.4 | 23.2 | 0.761 | 254 |
| Et2Me2P | 28.0 | 28.3 | 28.1 | 23.6 | 0.839 | 240 |
| Et2Me2As | 26.9 | 27.6 | 27.2 | 23.8 | 0.873 | 235 |
| Me4Sb | 28.8 | 27.7 | 28.3 | 24.2 | 0.858 | 243 |
| EtMe3Sb | 28.2 | 27.0 | 27.6 | 25.0 | 0.907 | 241 |
| Et2Me2Sb | 26.3 | 25.1 | 25. 7 | 25.8 | 1.005 | 231 |
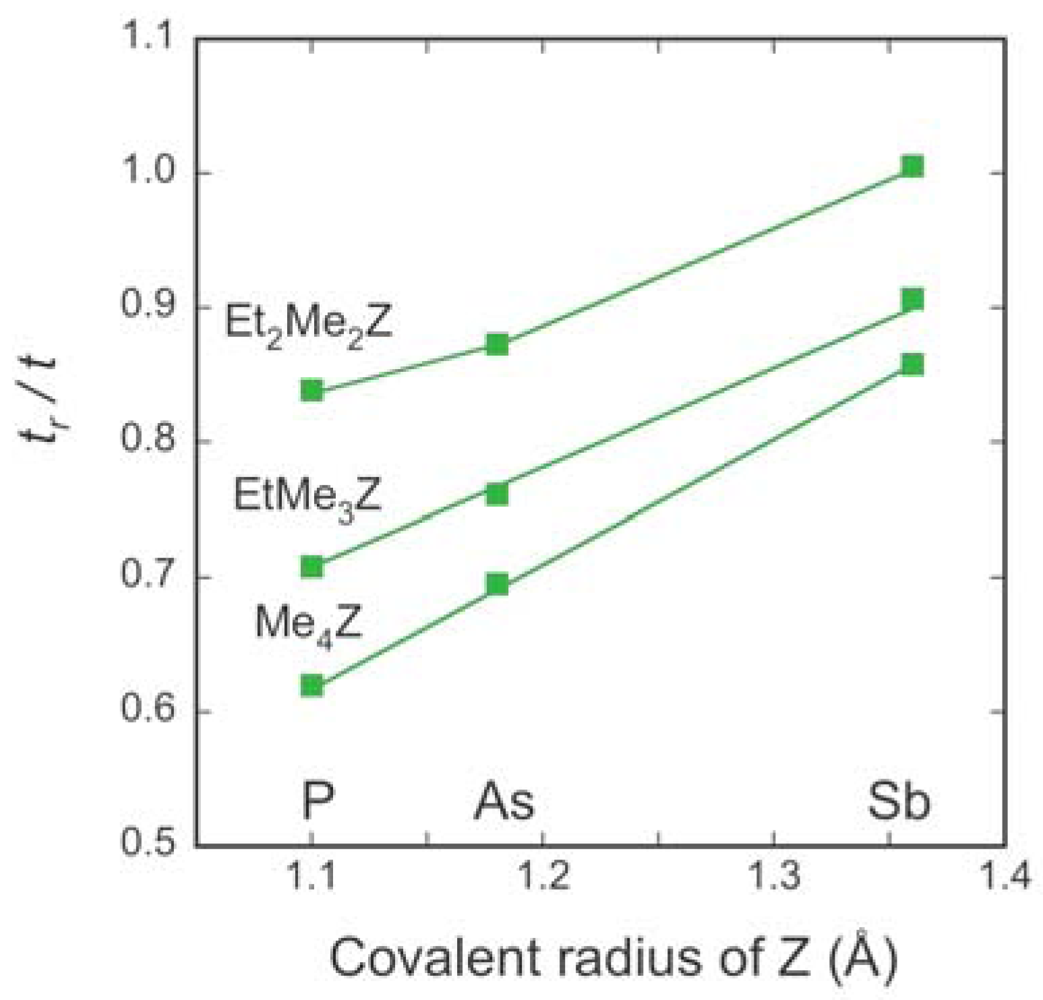

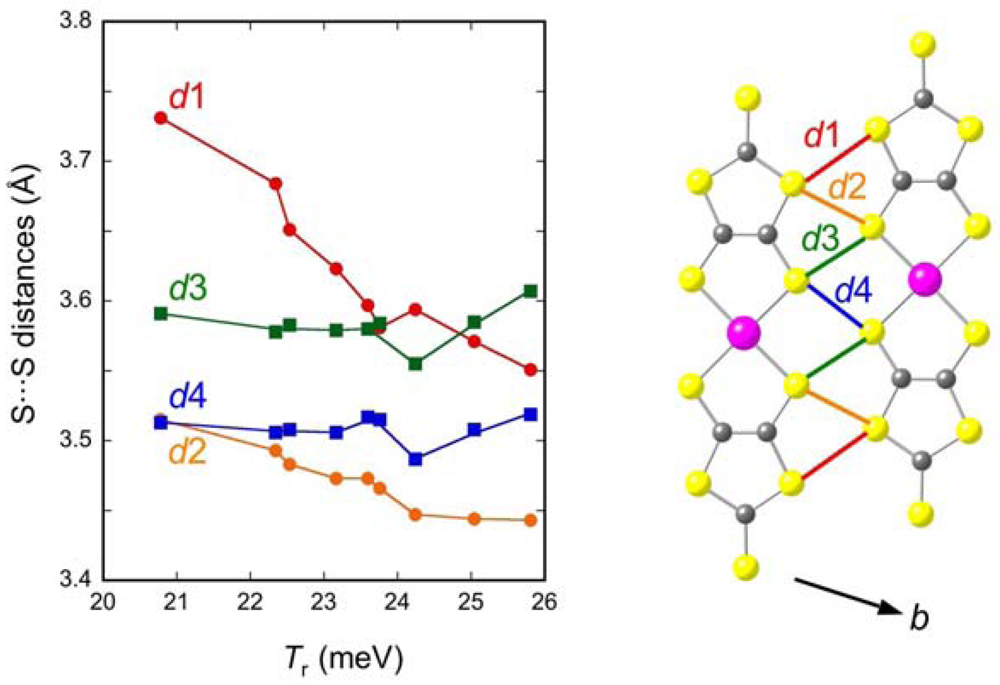


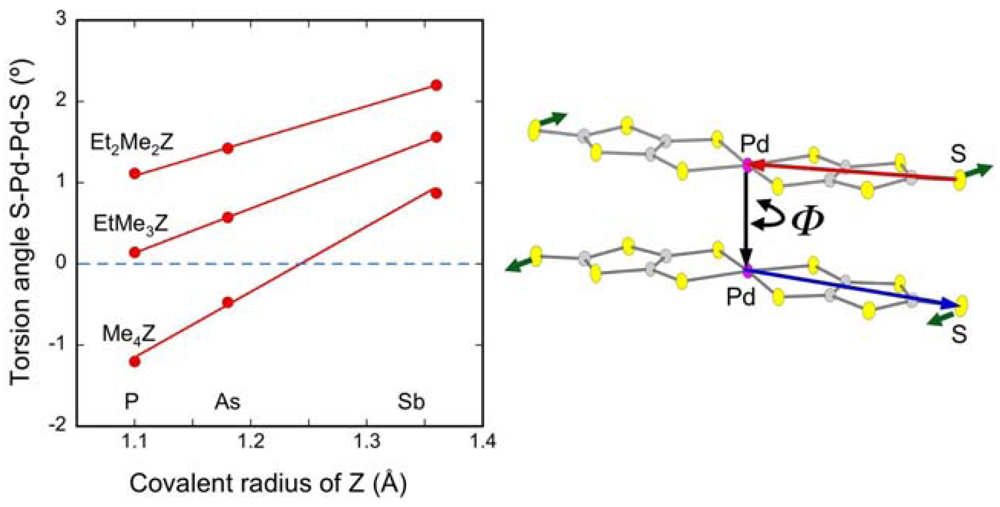
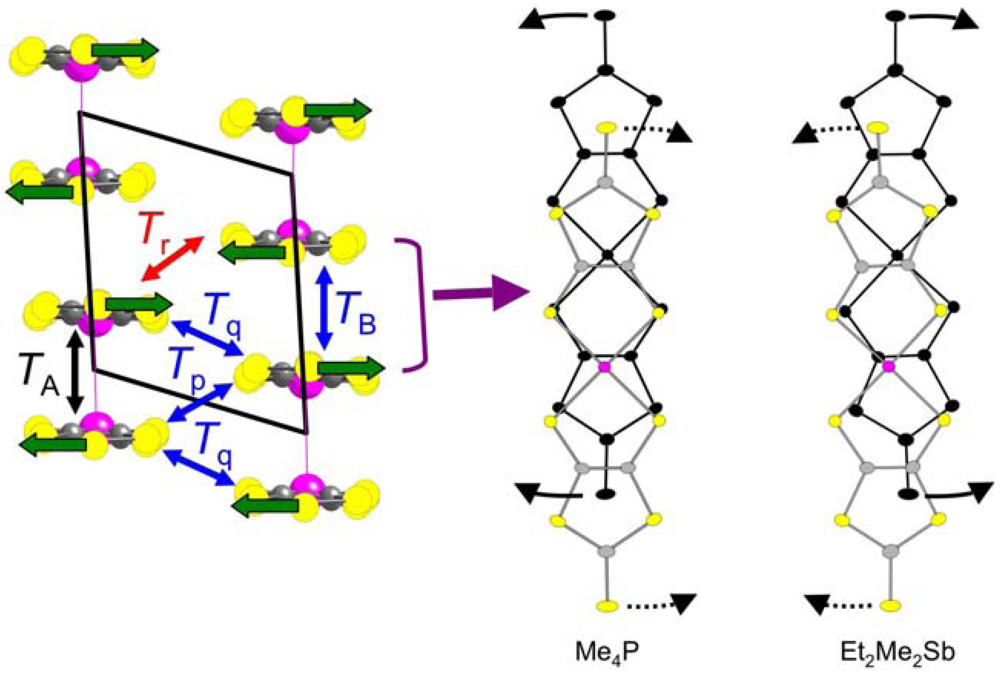

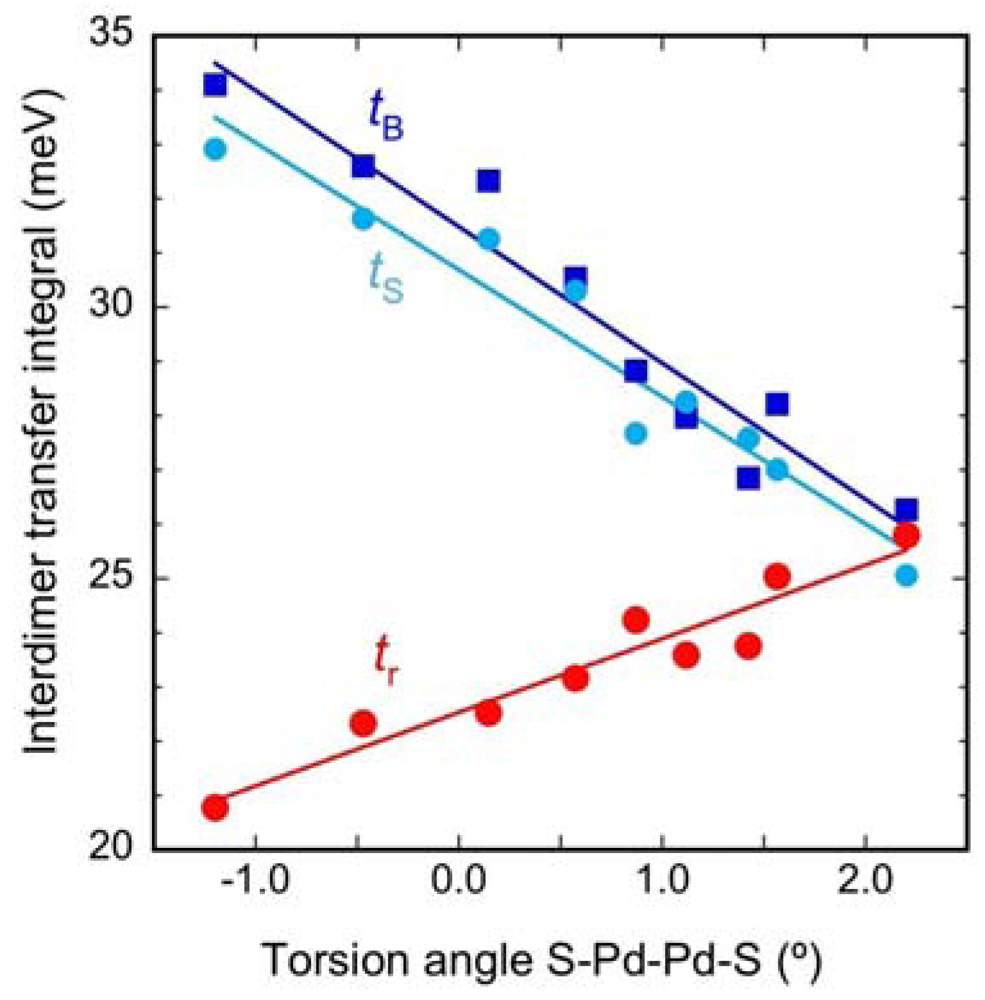
2.3. Intradimer Transfer Integrals
3. Experimental Section


| atom | orbital | Ip (Ryd) | ζ1 | ζ2 |
|---|---|---|---|---|
| C | 2s | 1.573 | 1.625 | |
| 2p | 0.838 | 1.625 | ||
| S | 3s | 1.620 | 2.122 | |
| 3p | 0.770 | 1.827 | ||
| Pd | 5s | 0.676 | 2.19 | |
| 5p | 0.390 | 2.15 | ||
| 4d | 0.949 | 5.98 | 2.613 | |
| (0.5264) * | (0.6372) * |
4. Conclusions
Acknowledgments
Conflict of Interest
References and Notes
- Mori, T.; Kobayashi, A.; Sasaki, Y.; Kobayashi, H.; Saito, G.; Inokuchi, H. The intermolecular interaction of tetrathiafulvalene and bis(ethylenedithio)tetrathiafulvalene in organic metals. Calculation of orbital overlaps and models of energy-band structures. Bull. Chem. Soc. Jpn. 1984, 57, 627–633. [Google Scholar]
- Kato, R. Conducting metal dithiolene complexes: Structural and electronic properties. Chem. Rev. 2004, 104, 5319–5346. [Google Scholar] [CrossRef]
- Tamura, M.; Kato, R. Variety of valence bond states formed of frustrated spins on triangular lattices based on a two-level System Pd(dmit)2. Sci. Technol. Adv. Mater. 2009, 10, 024304:1–024304:12. [Google Scholar]
- Tamura, M.; Kato, R. Spin-1/2 Heisenberg antiferromagnets on anisotropic triangular lattice, [Pd(dmit)2] salts—How do they release frustration? Polyhedron 2005, 24, 2817–2820. [Google Scholar] [CrossRef]
- Kanoda, K.; Kato, R. Mott physics in organic conductors with triangular lattices. Annu. Rev. Condens. Matter Phys. 2011, 2, 167–188. [Google Scholar] [CrossRef]
- Tamura, M.; Kato, R. Magnetic susceptibility of β'-[Pd(dmit)2] salts (dmit = 1,3-dithiol-2-thione-4,5-dithiolate, C3S5): Evidence for frustration in spin-1/2 Heisenberg antiferromagnets on a triangular lattice. J. Phys. Condens. Matter. 2002, 14, L729–L734. [Google Scholar] [CrossRef]
- Itou, T.; Oyamada, A.; Maegawa, S.; Tamura, M.; Kato, R. Quantum spin liquid in the spin-1/2 triangular antiferromagnet EtMe3Sb[Pd(dmit)2]2. Phys. Rev. B 2008, 77, 104413:1–104413:5. [Google Scholar]
- Itou, T.; Oyamada, A.; Maegawa, S.; Kato, R. Instability of a quantum spin liquid in an organic triangular-lattice antiferromagnet. Nat. Physics 2010, 6, 673–676. [Google Scholar] [CrossRef]
- Yamashita, M.; Nakata, N.; Senshu, Y.; Nagata, M.; Yamamoto, H.M.; Kato, R.; Shibauchi, T.; Matsuda, Y. Highly mobile gapless excitations in a two-dimensional candidate quantum spin liquid. Science 2010, 328, 1246–1248. [Google Scholar]
- Kato, R.; Itou, T. Molecular quasi-triangular lattice antiferromagnets. In Understanding Quantum Phase Transitions; Lincoln, D.C., Ed.; CRC Press: Boca Raton, FL, USA, 2010; pp. 419–443. [Google Scholar]
- Yamashita, S.; Yamamoto, T.; Nakazawa, Y.; Tamura, M.; Kato, R. Gapless spin liquid of an organic triangular compound evidenced by thermodynamic measurements. Nature Commun. 2011, 2, 275:1–275:6. [Google Scholar]
- Tamura, M.; Kato, R. Valence instability in a dimer of two-orbital system: Possible charge separation due to “Negative U” effect. Chem. Phys. Lett. 2004, 387, 448–452. [Google Scholar] [CrossRef]
- Nakao, A.; Kato, R. Structural study of low temperature charge-separated phases of Pd(dmit)2-based molecular conductors. J. Phys. Soc. Jpn. 2005, 74, 2754–2763. [Google Scholar] [CrossRef]
- Tamura, M.; Takenaka, K.; Takagi, H.; Sugai, S.; Tajima, A.; Kato, R. Spectroscopic evidence for the low-temperature charge-separated state of [Pd(dmit)2] salts. Chem. Phys. Lett. 2005, 411, 133–137. [Google Scholar] [CrossRef]
- Tamura, M.; Kato, R. Effective on-site repulsion in molecular conductors with dimeric structure: Is the transfer integral a good measure of correlation? J. Phys. Soc. Jpn. 2004, 73, 3108–3110. [Google Scholar] [CrossRef]
- Canadell, E.; Ravy, S.; Pouget, J.P.; Brossard, L. Concerning the band structure of D[M(dmit)2]2 (D=TTF,Cs,NMe4; M=Ni,Pd) molecular conductors and superconductors: Role of the M(dmit)2 HOMO and LUMO. Solid State Commun. 1990, 75, 633–638. [Google Scholar] [CrossRef]
- Tamura, M.; Nakao, A.; Kato, R. Frustration-induced valence-bond ordering in a new quantum triangular antiferromagnet based on [Pd(dmit)2]. J. Phys. Soc. Jpn. 2006, 75, 093701:1–093701:4. [Google Scholar]
- Kato, R.; Tajima, A.; Nakao, A.; Tamura, M. Two pressure-induced superconducting anion radical salts exhibiting different spin states at ambient pressure. J. Am. Chem. Soc. 2006, 128, 10016–10017. [Google Scholar]
- Ishii, Y.; Tamura, M.; Kato, R. Magnetic study of pressure-induced superconductivity in the [Pd(dmit)2] salt with spin-gapped ground state. J. Phys. Soc. Jpn. 2007, 76, 033704:1–033704:4. [Google Scholar]
- Shimizu, Y.; Akimoto, H.; Tsujii, H.; Tajima, A.; Kato, R. Mott transition in a valence-bond solid insulator with a triangular lattice. Phys. Rev. Lett. 2007, 99, 256403:1–256403:4. [Google Scholar]
- Itou, T.; Oyamada, A.; Maegawa, S.; Kubo, K.; Yamamoto, H.M.; Kato, R. Superconductivity on the border of a spin-gapped Mott insulator: NMR studies of the quasi-two-dimensional organic system EtMe3P[Pd(dmit)2]2. Phys. Rev. B 2009, 79, 174517:1–174517:6. [Google Scholar]
- Yamamoto, T.; Nakazawa, Y.; Tamura, M.; Nakao, A.; Ikemoto, Y.; Moriwaki, T.; Fukaya, A.; Kato, R.; Yakushi, K. Intradimer charge disproportionation in triclinic-EtMe3P[Pd(dmit)2]2 (dmit: 1,3-dithiole-2-thione-4,5-dithiolate). J. Phys. Soc. Jpn. 2011, 80, 123709:1–123709:4. [Google Scholar]
- Altomare, A.; Cascarano, G.; Giacovazzo, C.; Gualiardi, A.; Burla, M.C.; Polidori, G.; Camalli, M. SIR92—a program for automatic solution of crystal structures by direct methods. J. Appl. Cryst. 1994, 27, 435–435. [Google Scholar]
- Sheldrick, G.M. A short history of SHELX. Acta Crystallogr. Sect. A 2008, 64, 112–122. [Google Scholar] [CrossRef]
- Tsumuraya, T.; Seo, H.; Miyazaki, T.; Kato, R. Frustrated Mott system on the quasi-triangular lattice, Pd(dmit)2 salts; A first-principles study. J. Phys. Soc. Jpn. 2012. to be submitted for publication.. [Google Scholar]
© 2012 by the authors; licensee MDPI, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Kato, R.; Hengbo, C. Cation Dependence of Crystal Structure and Band Parameters in a Series of Molecular Conductors, β'-(Cation)[Pd(dmit)2]2 (dmit = 1,3-dithiole-2-thione-4,5-dithiolate). Crystals 2012, 2, 861-874. https://doi.org/10.3390/cryst2030861
Kato R, Hengbo C. Cation Dependence of Crystal Structure and Band Parameters in a Series of Molecular Conductors, β'-(Cation)[Pd(dmit)2]2 (dmit = 1,3-dithiole-2-thione-4,5-dithiolate). Crystals. 2012; 2(3):861-874. https://doi.org/10.3390/cryst2030861
Chicago/Turabian StyleKato, Reizo, and Cui Hengbo. 2012. "Cation Dependence of Crystal Structure and Band Parameters in a Series of Molecular Conductors, β'-(Cation)[Pd(dmit)2]2 (dmit = 1,3-dithiole-2-thione-4,5-dithiolate)" Crystals 2, no. 3: 861-874. https://doi.org/10.3390/cryst2030861