Next Article in Journal / Special Issue
Neutral Metal 1,2-Dithiolenes: Preparations, Properties and Possible Applications of Unsymmetrical in Comparison to the Symmetrical
Previous Article in Journal / Special Issue
Gate-Induced Thermally Stimulated Current on the Ferroelectric-like Dielectric Properties of (BEDT-TTF)(TCNQ) Crystalline Field Effect Transistor
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Crystals
Volume 2
Issue 3
10.3390/cryst2030741
crystals-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Review

Thermodynamic Properties of κ-(BEDT-TTF)2X Salts: Electron Correlations and Superconductivity

by
Yasuhiro Nakazawa
1,* and
Satoshi Yamashita
2
1
Department of Chemistry, Graduate School of Science, Osaka University, Machikaneyama 1-1, Toyonaka, Osaka 560-0043, Japan
2
Condensed Molecular Materials Lab., RIKEN, Hirosawa 2-1, Wako, Saitama 351-0198, Japan
*
Author to whom correspondence should be addressed.
Crystals 2012, 2(3), 741-761; https://doi.org/10.3390/cryst2030741
Submission received: 11 April 2012 / Revised: 16 June 2012 / Accepted: 18 June 2012 / Published: 29 June 2012
(This article belongs to the Special Issue Molecular Conductors)
Browse Figures
Versions Notes

Abstract

:
Heat capacity measurements of κ-(BEDT-TTF)2X (BEDT-TTF: Bis(ethylendithio)tetrathiafulvalene, X: counteranions) which are classified as two-dimensional (2D) dimer-Mott system are reported. At first, we explain structural and electronic features originated from rigid dimerization in donor arrangement in 2D layers. The antiferromagnetic Mott insulating phase located at low-pressure region in the phase diagram shows vanishing γ electronic heat capacity coefficient in the heat capacity, which claims opening of a charge-gap in this insulating state. Then, a systematic change of the γ around the Mott boundary region is reported in relation to the glass freezing of ethylene dynamics. The thermodynamic parameters determined by ∆Cp/γTc of 10 K class superconductors, κ-(BEDT-TTF)2Cu(NCS)2 and κ-(BEDT-TTF)2Cu[N(CN)2]Br demonstrate that a rather large gap with a strong coupling character appears around the Fermi-surface. On the other hand, the low temperature heat capacity clearly shows a picture of nodal-gap structure due to an anisotropic pairing. The comparison with lower Tc compounds in the κ-type structure is also performed so as to discuss overall features of the κ-type superconductors. The heat capacity measurements of hole-doped systems containing mercury in the counteranions show an anomalous enhancement of γ, which is consistent with the T1−1 of NMR experiments etc. The results of heat capacity measurements under high pressures are also reported.

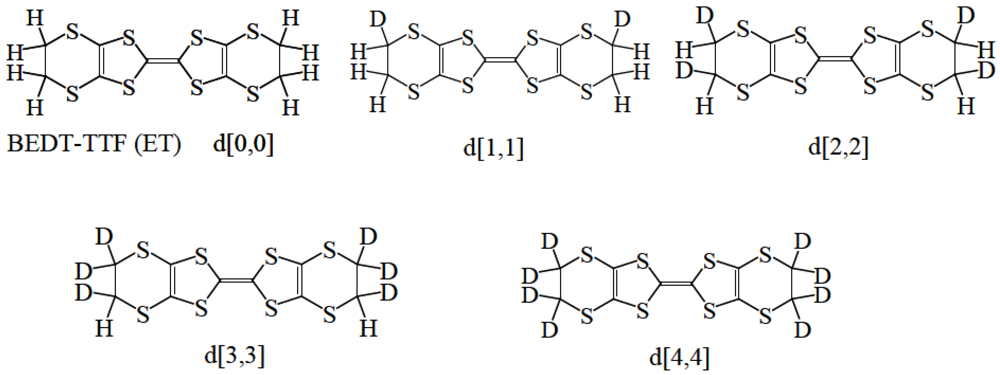
1. Introduction

Organic charge transfer salts consisting of donor/acceptor molecules with their counter ions provide us with interesting research stages to study various electronic properties peculiar for molecular systems. In these salts, the constitutive donor/acceptor molecules stack in segregated sheet/column structures from those of counter ions. Therefore, they are recognized as good candidate materials for studying electron systems with 1D or 2D structures. The relatively strong electron correlation and electron-phonon interaction coupled with these low-dimensional characters produce various electronic phases at low temperatures. The spin density wave (SDW), charge density wave (CDW), antiferromagnetic insulating (AFI) phase, and charge ordered (CO) phase, and superconductive (SC) phase etc. are known to exist around the metallic phase and they are closely related to each other. Numerous salts with simple compositions of 2:1 (D2X or A2Y) and 1:1 (DX or AY) where D, A denote donor and acceptor molecules and X, Y denote counter anions and cations were synthesized and their physical properties have been studied extensively up to now as is reviewed in literatures [1,2,3]. Among these organic charge transfer salts, 2:1 salts consisting of BEDT-TTF donor molecules and polymeric/linear/tetrahedral/octahedral anions show various molecular packing patterns in 2D donor sheets due to a rather large diagonal transfers originating from the overlap of surfer orbitals in neighboring BEDT-TTF molecules (S–S contacts), as well as face-to-face transfers between neighboring molecules in the stacking direction.
In discussing electronic properties of 2:1 salts consisting of BEDT-TTF, degree of dimerization is a good clue for classifying electronic structures. In the case of non-dimerized salts, for example α-, θ-, and β''-type structure, the band-filling is 3/4 and metallic nature tends to be stabilized even at low temperatures. When dimerization is strong, as is typically the case of κ-, λ-, β-, β'-type salts, electron correlations are disclosed. The appearance of superconductivity with relatively high transition temperatures, antiferromagnetism with localized spin characters, and a kind of spin liquid states are extensively studied in dimerized salts of κ-(BEDT-TTF)2X [4,5].
Heat capacity measurement is an important tool to explore fundamental researches of organic conductors especially to study electronic states in the low-energy region. One can detect various types of phase transformations by measuring heat capacity as a function of temperature and under magnetic fields. The determination of transition entropy and enthalpy can give direct information on degrees of ordering of microscopic freedoms existing in molecules and conduction electrons [6]. In this paper, we review thermodynamic investigations on organic charge transfer salts of BEDT-TTF focusing on κ-(BEDT-TTF)2X systems. The electron correlations and superconductivity studied by thermodynamic measurements are discussed.

2. Electronic Structure and Phase Diagram of κ-(BEDT-TTF)2X System

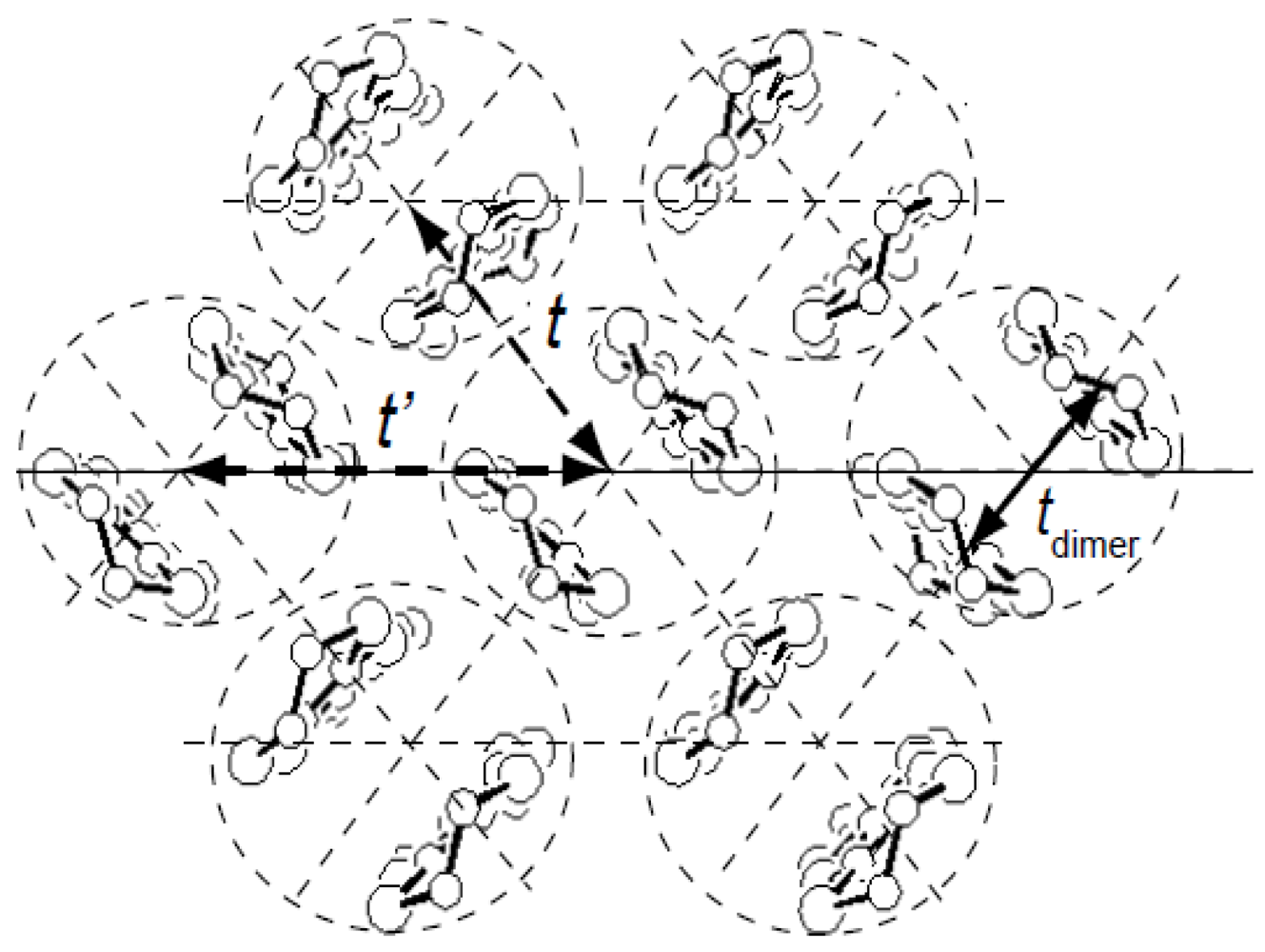
The κ-type structure of (BEDT-TTF)2X has a rigidly dimerized structure. BEDT-TTF dimers with face-to-face contact are arranged orthogonally as is shown in Figure 1. The intra-dimer transfer energy, tdimer, is usually larger than other transfers, t, t', and therefore each dimer is considered as a basic structural unit to form a 2D lattice.
Crystals 02 00741 g001 1024
Figure 1. Molecular arrangement of κ-type structure of (BEDT-TTF)2X system. BEDT-TTF molecules form a dimerized structure. The transfers between neighboring dimer units are denoted by t and t', which are relatively smaller than intra-dimer transfer tdimer.
Figure 1. Molecular arrangement of κ-type structure of (BEDT-TTF)2X system. BEDT-TTF molecules form a dimerized structure. The transfers between neighboring dimer units are denoted by t and t', which are relatively smaller than intra-dimer transfer tdimer.
Crystals 02 00741 g001
The originally 3/4 filled HOMO (highest occupied molecular orbital) band determined by 2:1 concentration splits into two bands due to opening of the dimerization gap. Therefore, the electronic state is interpreted as effectively half filling of the upper HOMO band and so-called Mott-Hubbard physics dominated by a competition of on-site (on-dimer) U and band width W appears. When U is larger than W (U > W), the system becomes a Mott insulating state with an antiferromagnetic ground state. On the other hand, in the region of U < W, the ground state would be metallic with a strong electron correlation and the superconductivity appears in this region. In the intermediate region of U ≈ W, a first-order phase boundary, known as a Mott boundary, appears. 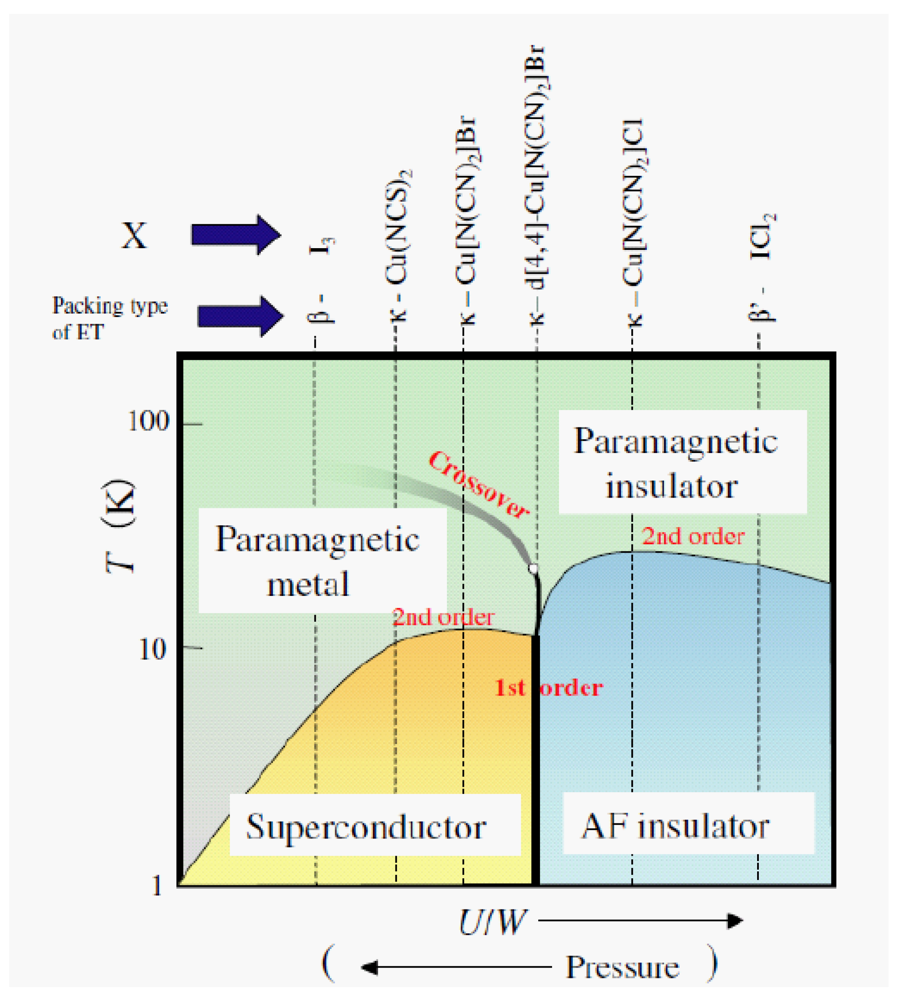The conceptual pressure versus temperature phase diagram in which the antiferromagnetic phase is adjacent to the superconducting phase was established by Kanoda et al. [4,7,8], which was confirmed precisely by Kagawa et al. by gas-pressure controlled experiments [9]. According to the phase diagram, the insulating and metallic/superconducting states are tunable by external or chemical pressures. 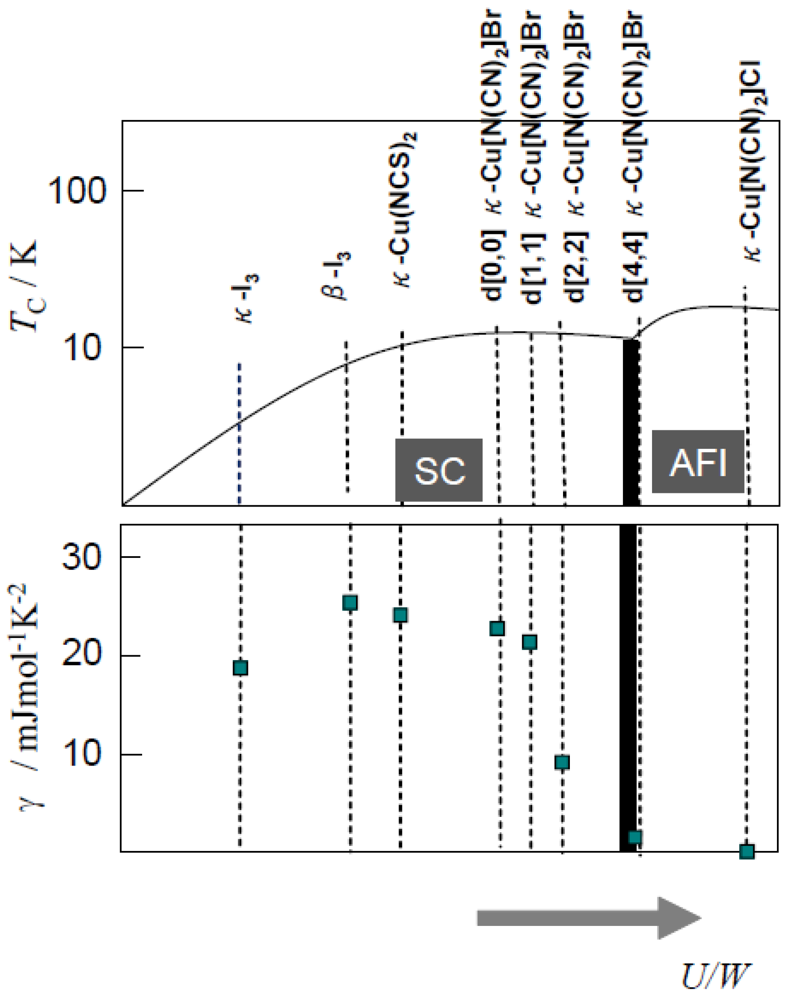As is also shown in Figure 2, the transition temperatures of the κ-type superconductors reach about 10 K in the salts located near the boundary region. The well known high-Tc superconductors among organic systems are κ-(BEDT-TTF)2Cu(NCS)2 (Tc = 10.4 K) and κ-(BEDT-TTF)2Cu[N(CN)2]Br (Tc = 11.6 K). On the other hand, deuterated κ-(BEDT-TTF)2Cu[N(CN)2]Br (eight hydrogen atoms in ethylene group of BEDT-TTF molecule were deuterated) and κ-(BEDT-TTF)2Cu[N(CN)2]Cl located in the low pressure region show insulating behaviors. Thermodynamic measurements on these salts have been performed by several groups with the purpose of characterizing the 10 K class superconductivity and electronic structure in the phase diagram surrounding it. For unveiling the origin and character of high-Tc superconductivity in organics, thermodynamic information is inevitable.
Crystals 02 00741 g002 1024
Figure 2. Conceptual electronic phase diagram of the dimer-Mott system based on κ-type and β-type salts consisting of BEDT-TTF molecules. The salts with κ-type structure with different counteranions and other dimerized structure salts are indicated in the phase diagram [4].
Figure 2. Conceptual electronic phase diagram of the dimer-Mott system based on κ-type and β-type salts consisting of BEDT-TTF molecules. The salts with κ-type structure with different counteranions and other dimerized structure salts are indicated in the phase diagram [4].
Crystals 02 00741 g002
In the κ-type structure, the ratio of the two transfer energies, t, t', shown in Figure 1, is also related to a subject of frustration in the 2D system. Usually, t is larger than t' (t > t') and the κ-type arrangement is considered as a square lattice or a rectangular lattice of the dimer unit in this case. If the transverse transfer between dimers denoted as t' is comparable with face-to-face transfer, t (t ≈ t'), the dimer lattice is considered as a triangular system, which is discussed from the viewpoint of frustration physics. The spin-liquid state has been recently observed in κ-(BEDT-TTF)2Cu2(CN)3 that has an ideal triangular lattice structure [10]. The antiferromagnetic insulating salts and superconductive salts in Figure 2 are considered as a rectangular lattice system.
In the following sections, we discuss low temperature heat capacity results of insulating, and metallic compounds with κ-type salts focusing on the electronic states and the phase diagram.

3. Antiferromagnetic Mott Insulator Region

To characterize the electronic properties and to establish an overall picture of the electronic structure of 2D dimerized systems from a standpoint of electron correlations, Kanoda and his co-workers performed systematic transport, NMR, magnetic susceptibility, and heat capacity measurements of κ-(BEDT-TTF)2X salts. Thermodynamic characterization of the insulating phase by measuring low temperature heat capacity was performed in order to confirm the nature of the Mott insulator [11,12]. 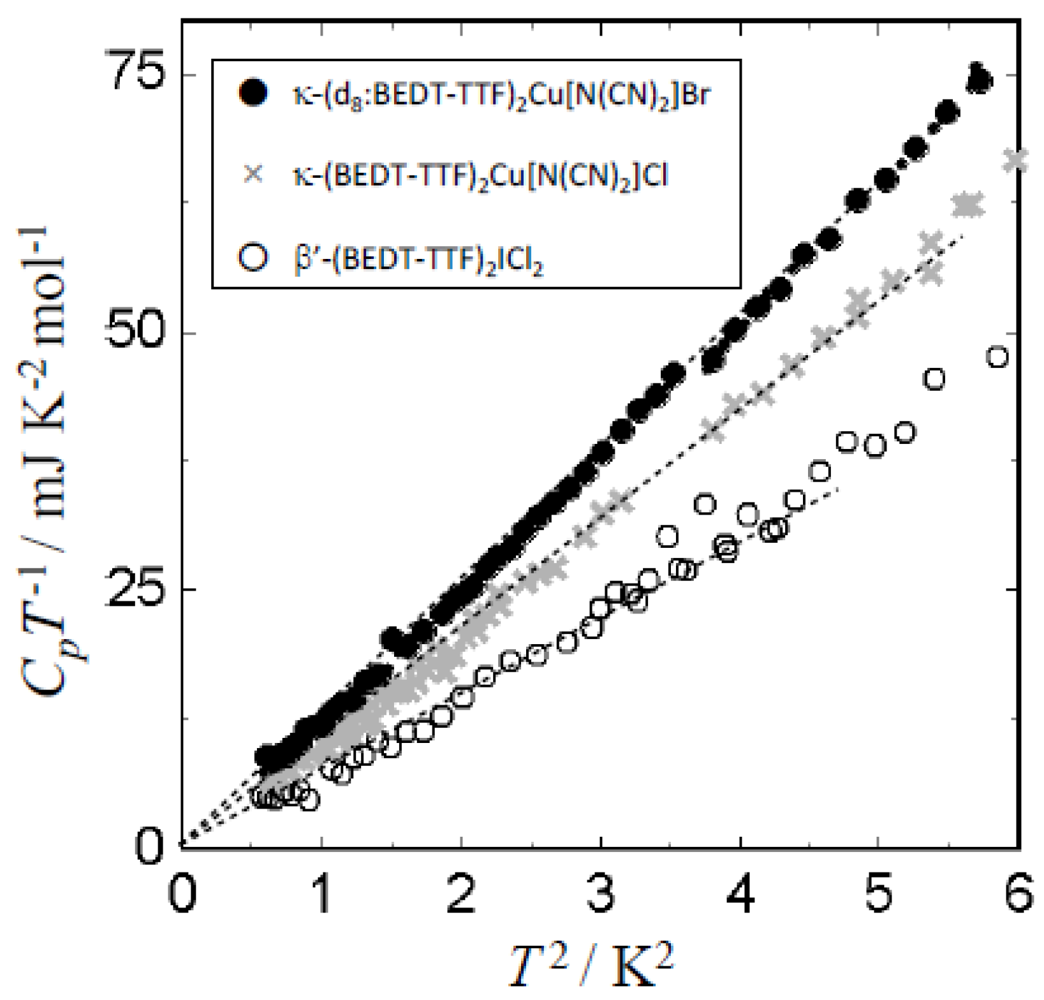The low temperature heat capacity data of two typical antiferromagnetic insulator salts of κ-(BEDT-TTF)2X are shown in Figure 3. Although strong antiferromagnetic fluctuations and antiferromagnetic ordering with localized spin moments were observed in the κ-(BEDT-TTF)2Cu[N(CN)2]Cl and deuterated κ-(BEDT-TTF)2Cu[N(CN)]2]Br by 13C-NMR, thermodynamic features, especially at low temperatures, show typical behavior of a charge-gapped insulating system. As is shown in Figure 3, heat capacity clearly shows vanishing γ values determined by a linear extrapolation of in CpT−1 vs. T2 plot down to T = 0.
Crystals 02 00741 g003 1024
Figure 3. CpT−1 vs. T2 plot of low temperature heat capacity of typical Mott insulating salts. The extrapolation of the data down to T = 0 gives a distinct evidence of opening of the charge gap. The crosses and closed circles denote the data of κ-(BEDT-TTF)2 Cu[N(CN)2]Cl and deuterated κ-(BEDT-TTF)2Cu[N(CN)]2]Br. The open circles are data for β'-(BEDT-TTF)2ICl2.
Figure 3. CpT−1 vs. T2 plot of low temperature heat capacity of typical Mott insulating salts. The extrapolation of the data down to T = 0 gives a distinct evidence of opening of the charge gap. The crosses and closed circles denote the data of κ-(BEDT-TTF)2 Cu[N(CN)2]Cl and deuterated κ-(BEDT-TTF)2Cu[N(CN)]2]Br. The open circles are data for β'-(BEDT-TTF)2ICl2.
Crystals 02 00741 g003
The β value defined as a coefficient of the T3 term of κ-(BEDT-TTF)2Cu[N(CN)2]Cl and deuterated κ-(BEDT-TTF)2Cu[N(CN)]2]Br was 10.8 mJ K−4 mol−1, 11.3 mJ K−4 mol−1, respectively. The magnetic fields up to 8 T do not affect the heat capacity in either salt. This is in fine contrast with the pristine salt of κ-(BEDT-TTF)2Cu[N(CN)2]Br which shows superconductivity with Tc = 11.4 K. The absence of electron density of states at Fermi energy even though the system is effectively in a half filling state supports the picture of the Mott insulating ground state with a charge gap. These data also exclude the possibility of electron localization produced by impurities or disorders in crystals. The fully charge-gapped nature due to the Mott-Hubbard mechanism was observed in β'-(BEDT-TTF)2ICl2 as is shown by open circles in Figure 3, which is also known as a rigidly dimerized system. According to the result of single crystal calorimetry, this compound does not show any γ and relatively smaller lattice heat capacity expressed by smaller β = 7.46 mJ K−4 mol−1. This compound was known to convert to 14.6 K superconductor under strong pressure of about 80 GPa observed by Taniguchi et al. [13].
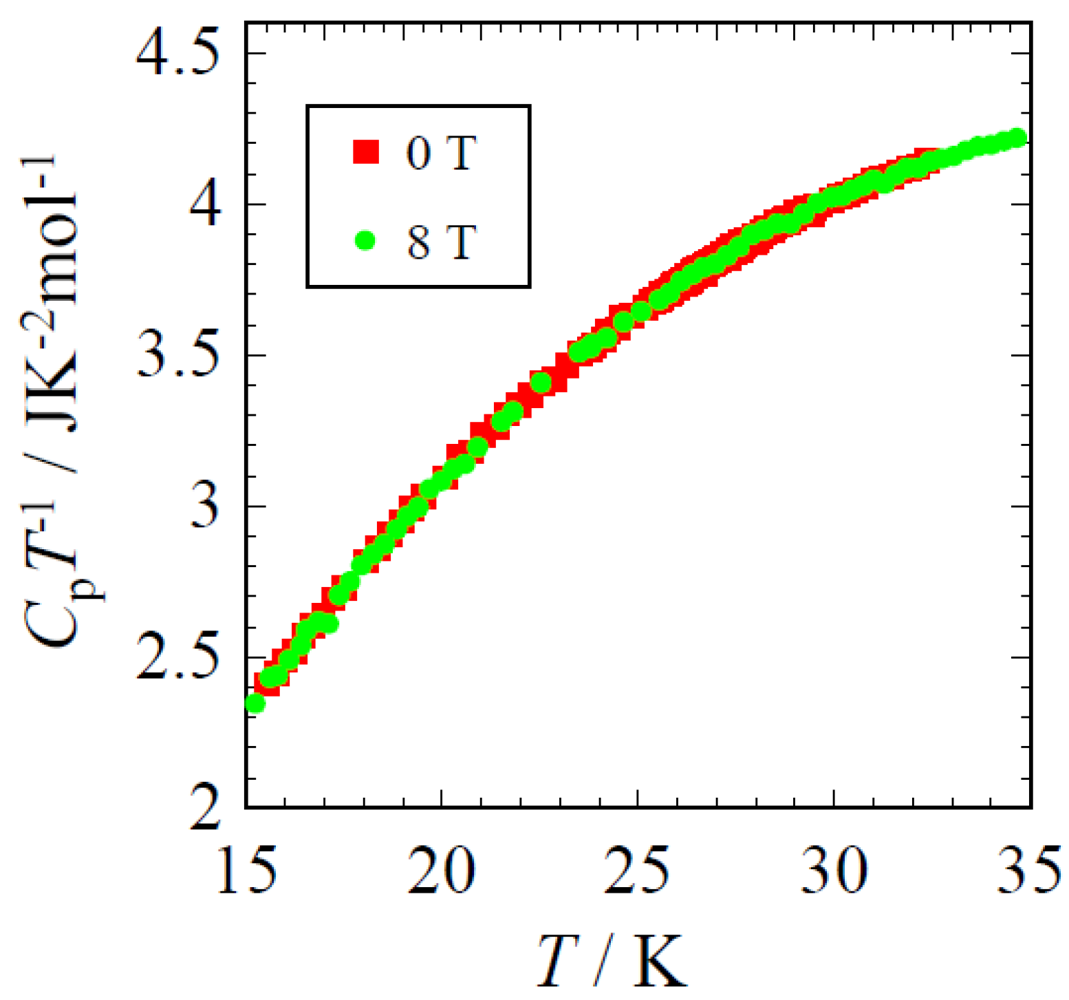
In dimer-Mott insulating system of (BEDT-TTF)2X, electron spins localize on each dimer interact with each other through intra-layer magnetic interactions. Antiferromagnetic long-range orderings due to the weak intra-layer magnetic interaction were observed by the splitting of line shapes of 13C-NMR and the existence of an interanl field by μSR measurements. An important point for discussing the electronic properties of the insulating salts by the thermodynamic measurements is whether the peak associated with the long-range ordering exists or not. Heat capacity measurements by adiabatic technique for κ-(BEDT-TTF)2Cu[N(CN)2]Cl and deuterated κ-(BEDT-TTF)2Cu[N(CN)2]Br did not show any thermal anomaly. The absence of a thermal anomaly around the Néel temperatures in the Mott Hubbard system has more precisely been investigated by Yamashita et al. [14] using the thermal relaxation method for κ-(BEDT-TTF)2Cu[N(CN)2]Cl as is shown in Figure 4.
Crystals 02 00741 g004 1024
Figure 4. CpT−1 vs. T plot of κ-(BEDT-TTF)2Cu[N(CN)2]Cl around the magnetic transition temperature obtained under 0 T and 8 T.
Figure 4. CpT−1 vs. T plot of κ-(BEDT-TTF)2Cu[N(CN)2]Cl around the magnetic transition temperature obtained under 0 T and 8 T.
Crystals 02 00741 g004
A similar situation occurs in 2:1 salt of β'-(BEDT-TTF)2ICl2 [15] and a donor-acceptor salt of β'-(BEDT-TTF)(TCNQ) of which the charge transfer rate is nearly 0.5 and effectively half-filled states are realized [14]. In these dimerized salts, magnetic interactions between dimers are given by the formula of J = 2t2/Udimer, where t is a transfer energy between dimers. The J/kB value is evaluated as 200–250 K in the typical κ-(BEDT-TTF)2X system, which is one order of magnitude larger than the Néel temperatures where the 3D orderings take place. Therefore, the magnetic entropy related to the 3D ordering should be much smaller than R ln2 due to the short range fluctuations that exist at higher temperatures. In addition to these low-dimensional characters, strong quantum fluctuations also work to obscure the long-range nature of magnetic ordering and broaden the thermal peaks. This is considered as a common feature in Mott insulating systems with 2D-layered structures with strong intra-layer magnetic interactions [16].

4. Boundary Region of Antiferromagnetic Phase and Superconductive Phase

It is well known that κ-(BEDT-TTF)2Cu[N(CN)2]Br changes its conducting and magnetic properties drastically by changing the cooling rate around the liquid N2 temperature region. Although deuterated κ-(BEDT-TTF)2Cu[N(CN)2]Br is located in the insulating region just close to the boundary, it shows superconductivity with Tc = 10 K in the case of slow cooling with a rate smaller than 0.1 K min−1. The difference originates from a slight difference in volume of the unit cell produced by order/disorder arrangements in molecular packing. In the case of a hydrogenated sample which is a bulk superconductor, the superconductive nature and volume fraction is affected by changing the cooling rate.
The origin of this cooling rate dependence is attributed to a glass freezing of the ethylene groups located at both edges of BEDT-TTF molecules as was detected by thermodynamic measurements. According to the result of high-resolution ac heat capacity measurements of κ-(BEDT-TTF)2Cu[N(CN)2]Br by Akutsu et al. [17], a broad hump structure in heat capacity was observed around 90 K with a modulation frequency of 0.24 Hz. The hump structure broadens gradually and shifts to higher temperatures with increasing frequency. The hump temperature was reported as 105 K at 1 Hz and 110 K at 4 Hz. They concluded that the ethylene groups at the edge of BEDT-TTF molecules have two stable conformations and freezing of this molecular motion occurs during the cooling process. The temperature of the glass formation was evaluated as Tg = 77 K in the static limit and this is consistent with the temperatures where resistivity and thermal expansion show anomalies. The dilatometry work by Müller et al. [18] also claims the existence of glass transition around this temperature. Shown in Figure 5 is the ac heat capacity data of the κ-(BEDT-TTF)2Cu[N(CN)2]Br salt obtained by our group for a tiny single crystal sample less than 1 μg by the usage of a microchip calorimeter.
Crystals 02 00741 g005 1024
Figure 5. Temperature dependences of ac heat capacity of κ-(BEDT-TTF)2Cu[N(CN)2]Br which detect hump-like anomalies in association with freezing of ethylene dynamics in BEDT-TTF molecules in different frequencies.
Figure 5. Temperature dependences of ac heat capacity of κ-(BEDT-TTF)2Cu[N(CN)2]Br which detect hump-like anomalies in association with freezing of ethylene dynamics in BEDT-TTF molecules in different frequencies.
Crystals 02 00741 g005
The frequency dependences of the thermodynamic hump in Figure 5 reproduce well the results of Akutsu et al. [17]. This glass transition works as a kind of volume effect in the low temperature electronic states and low temperature transport and magnetic properties near the boundary is influenced by the volume of the glassy parts. Similar behavior was also observed in κ-(BEDT-TTF)2Cu[N(CN)2]Cl. The freezing of molecular dynamics during the cooling process is expected for other charge transfer salts consisting of asymmetric donor molecules of DMET (Dimethyl(ethylendithio)diselenadithiafulvalene) and DIMET (Dimethyl(ethylendithio) tetrathiafulvalene), which was also studied by ac calorimetry [19]. The glass transition was also observed in (DMET)2BF4, (DMET)2ClO4 and (DIMET)2BF4, although the behavior of the frequency dependence was different from the BEDT-TTF system.
In order to investigate the thermodynamic nature around the boundary region of the superconductive phase and insulating phase, low-temperature thermodynamic measurements were performed for a deuterated sample with different cooling rates of 0.07 K min−1 and 1.7 K min−1 [20]. The γ value is 0.65 ± 0.36 mJ K−2 mol−1 for the 0.07 K min−1 case and 0.73 ± 0.47 mJ K−2 mol−1 for the 1.7 K min−1 case, and β in both cooling rates show almost the same value of 11.3 mJ K−4 mol−1, meaning that a slight change of electronic heat capacity occurs in the thermodynamic sense. The sample experienced an annealing process around the liquid nitrogen temperature shows an increase up to about γ = 1.0 mJ K−2 mol−1, which means that the conducting domains in deuterated κ-(BEDT-TTF)2Cu[N(CN)2]Br forms domain structures of superconductive and insulating regions. In the BEDT-TTF-based system, a partial deuteration technique is effective for fine tuning of chemical pressures. Synthesizing partial deuterated molecules of the ethylene groups gives an effective method to see the variation of electronic structure in the metallic region near the boundary region. The κ-(BEDT-TTF)2Cu[N(CN)2]Br sample with different partial deuteration (Figure 6) ratios was synthesized and thermodynamic parameters were investigated for the superconductive samples [21,22]. From the results of heat capacity obtained under magnetic fields up to 10 T, we observed that the γ term increases systematically with the decrease of deuteron numbers. The d4 sample denoted as d[2,2], that means two hydrogens in each ethylene group on both sides of BEDT-TTF have been deuterated, shows 9–10 mJ K−2 mol−1. The d2 sample denoted as d[1,1] has nearly 20 mJ K−2 mol−1 [21]. Systematic changes of the γ value in the superconductive phase of κ-(BEDT-TTF)2X is shown in Figure 7, together with the data of different compounds in the conceptual phase diagram. In the bulk superconductive region far from the boundary, the so called Brinkmann-Rice enhancement that predicts the increase of γ with the increase of U/W appears.
It is emphasized that the decrease of normal state γ just close to the boundary region detected by the partial deuteration is related to the decrease of the superconductive volume fraction due to the intrinsic inhomogeneity around the first order phase boundary. The transition temperatures of the partial deuterated samples keep the similar values around 10 K, even though the γ changes drastically. This decrease of γ by approaching from the superconductive region to the antiferromagnetic insulating region in the phase diagram was studied by Tayor et al. [23] by controlling the cooling rate across the glass temperatures in the non-deuterated sample. They controlled the cooling rate between 80 K and 65 K, and measured heat capacity at low temperatures.
Crystals 02 00741 g006 1024
Figure 6. Molecular structures of BEDT-TTF of which ethylene groups in both edges are partially deuterated. The labeling d[n,m] denotes the number of deuterons in each side.
Figure 6. Molecular structures of BEDT-TTF of which ethylene groups in both edges are partially deuterated. The labeling d[n,m] denotes the number of deuterons in each side.
Crystals 02 00741 g006
Crystals 02 00741 g007 1024
Figure 7. The normal states electronic heat capacity coefficient γ obtained by heat capacity data above Hc2 is plotted according to U/W ratio as a parameter.
Figure 7. The normal states electronic heat capacity coefficient γ obtained by heat capacity data above Hc2 is plotted according to U/W ratio as a parameter.
Crystals 02 00741 g007
According to their report, the cooling slower than 20 K min−1 for non-deuterated sample shows bulk superconductivity but the γ value obtained under magnetic fields decreases in the case of a higher cooling rate. At 53 K min−1, they observed that the normal state γ is suppressed down to about 1/2 of the original value, although the decrease of Tc itself is only 0.4 K. The data of this rapid cooling case correspond to those of d[2,2] samples, and this behavior can be interpreted as a kind of partial phase separation of a superconductive region and an antiferromagnetic insulator region as is mentioned above.

5. 10 K Class Superconductors: κ-(BEDT-TTF)2Cu(NCS)2 and κ-(BEDT-TTF)2Cu[N(CN)2]Br

Calorimetry techniques with high accuracy and precision are required to understand the nature of the superconducting transition, since the separation of the electronic part and the lattice part from the total heat capacity is necessary. In the case of 10 K class superconductors, the lattice heat capacity exceeds 2 J K−1 mol−1 at 5 K and 10 J K−1 mol−1 at 10 K, even though the electronic heat capacity jump ∆Cp due to superconductive transition is in the order of 102–3 mJ K−1 mol−1. With the increase of transition temperatures, the difficulty in detecting the thermal anomaly also increases in organic systems. The heat capacity measurements around Tc of κ-type organic superconductors were performed mainly by thermal relaxation calorimetry and also by high-resolution ac calorimetry techniques. Up to now, several groups have reported the heat capacity measurements around Tc for κ-(BEDT-TTF)2Cu(NCS)2 and κ-(BEDT-TTF)2Cu[N(CN)2]Br [24,25,26,27,28,29], but the temperature region is limited due to the difficulty of getting high-resolution data in the wide temperature range. For the former salt, the normal state electronic heat capacity coefficient γ obtained by applying magnetic fields of 12.5 T gives (25 ± 3) mJ K−2 mol−1 and a heat capacity jump ∆CpT−1 was evaluated as >50 mJ K−2 mol−1 by Andraka et al. [24]. These data claim that the superconductivity is in a strong coupling region, with ∆Cp/γTc larger than 2. It reaches about 2.8, if the mean field peak is considered by keeping the entropy balance between the normal and the superconductive states. Shown in Figure 8 is the peak shape of the electronic heat capacity of κ-(BEDT-TTF)2Cu(NCS)2 observed by Yamashita et al., which gives rather large ∆CpT−1 with 60 mJ K−2 mol−1 [25]. The data are consistent with those reported in [24].
Crystals 02 00741 g008 1024
Figure 8. Temperature dependence of electronic heat capacity around the superconductive transition for κ-(BEDT-TTF)2Cu(NCS)2.
Figure 8. Temperature dependence of electronic heat capacity around the superconductive transition for κ-(BEDT-TTF)2Cu(NCS)2.
Crystals 02 00741 g008
Graebner et al. [26] developed a new ac technique, called the modulation bath technique, which is available for tiny single crystal measurements with higher resolution. They reported similar magnitude of heat capacity jump as that of Andraka et al. [24] and claimed a strong coupling nature in superconductors. The data under magnetic fields obtained by them give −dHc2/dT = 16 T/K in the H//2D layer direction and −dHc2/dT = 0.75 T/K in the H┴ 2D layer direction, and a two-dimensional nature of the organic superconductor was also suggested by thermodynamic measurements. For κ-(BEDT-TTF)2Cu[N(CN)2]Br, γ was evaluated as (22 ± 3) mJ K−2 mol−1 by the extrapolation of low temperature heat capacities under 14 T and the heat capacity jump was evaluated as ∆Cp/γTc = 2 ± 0.5 from these data [27]. Temperature dependence of the electronic heat capacity was more precisely studied by Elsinger et al. [28] between 1.7 K and 21 K for κ-(BEDT-TTF)2Cu[N(CN)2]Br and Müller et al. [29] for κ-(BEDT-TTF)2Cu(NCS)2 between 2 K and 30 K under 0 T and magnetic fields larger than Hc2. The overall peak shape was analyzed by comparing the α-model of strong coupling superconductors with appropriate parameters of α = 2.7 and α = 2.8, respectively [28,29].
For discussing the pairing states and structures of the superconductive gap, it is required to study temperature dependence of the heat capacity at the low temperature region which should reflect the quasi-particle excitations over the gap. In the case of BCS type superconductors, a fully-gapped structure around the Fermi surface leads to an activation-type temperature dependence in heat capacity which should give a very small contribution below about 1 K. In order to discuss this point, we performed heat capacity measurements of κ-(BEDT-TTF)2Cu[N(CN)2]Br in the dilution temperature region. The details are described in [30,31]. Figure 9 shows the data obtained for five different single crystals in the dilution temperature region. Through the analysis of low temperature data, we indicate that the CpT−1 vs. T2 plot does not give a simple linear relation in this region, but fits well by including a quadratic term of temperature. Using the data of the deuterated κ-(BEDT-TTF)2Cu[N(CN)2]Br as reference for evaluating the lattice part, it is possible to derive electronic heat capacity as a function of temperature. After the correction of the difference of molecular weight produced by isotope substitution in the deuterated salt, we observed that the electronic heat capacity below about 3 K has a T2 term with a coefficient of 2.2 mJ K−3 mol−1 as is discussed in [30]. The temperature dependence of electronic heat capacity especially at low temperatures below 1 K deviates from the BCS curve calculated by assuming a full-gap structure with 2∆/kBTc = 3.52, and the T2 dependence demonstrates that the line-node structure exists in the superconductive gap. The data shown in Figure 9 also claims that the residual T-linear term of which coefficients are γres = 1.2–3.0 mJ K−2 mol−1 exist even in the superconductive state. The residual γres with these values correspond to 5%–13% of electrons remaining as normal in the superconductive state. According to the discussion in [30], the recovery of γ in the vortex state obeys the formula of γ = kγn(H/Hc2)1/2 where k is a coefficient of order of unity. These results demonstrate that the superconductivity is d-wave, with line nodes in the cylindrical Fermi surface. A similar tendency was observed in κ-(BEDT-TTF)2Cu(NCS)2 [31]. The heat capacity results at extremely low temperature regions were consistent with the temperature dependence of T1−1 probed by 13C-NMR experiments, demonstrating the d-wave paring from the observation of the T3 term in the superconductive state [32,33,34]. The thermal conductivity result reported in ref. [35] implies dxy symmetry from the analysis of angle-dependences in the T-linear term obtained under magnetic fields applied parallel to the 2D layer. The temperature dependences of the penetration depth reported in the early stage give contradictory results showing both s-wave [36] and d-wave [37] -like temperature dependence. The pairing symmetry is still an open subject for such layered superconductors.
Crystals 02 00741 g009 1024
Figure 9. Low temperature heat capacity of five different single crystals plotted in CpT−1 vs. T2. The data show a deviation from linearity due to the existence of the T2 term and the residual T-linear in Cp term remains even in the superconductive state.
Figure 9. Low temperature heat capacity of five different single crystals plotted in CpT−1 vs. T2. The data show a deviation from linearity due to the existence of the T2 term and the residual T-linear in Cp term remains even in the superconductive state.
Crystals 02 00741 g009
The rather large heat capacity jump at Tc due to the strong coupling nature seems to be contradictory with the low-temperature heat capacity claiming a nodal nature of the gap. The consistent explanation of these pictures was confirmed by Tayor et al. [33]. They measured heat capacity of the two salts with a high resolution technique at 0 T and 14 T and analyzed the peak by α-model which takes account of the coupling strength. They analyzed electronic heat capacity data using s-wave and d-wave models and compared the result. Their data at the low temperature region clearly indicated that the low temperature behaviors below 4 K can be well fitted by the d-wave model with strong coupling region of α = 1.73, γn = 26.6 mJ K−2 mol−1 for κ-(BEDT-TTF)2Cu[N(CN)2]Br and α = 1.45, γn = 33.3 mJ K−2 mol−1 for κ-(BEDT-TTF)2Cu(NCS)2. The quadratic temperature dependence existing at low temperatures are consistent with the results in [30], although the deviation from T 2 above 3 K is probably attributable to underestimating the lattice term using the data of the deuterated sample. Malone et al. [38] studied in-plane magnetic field dependence in heat capacity at extremely low temperatures below 1 K for κ-(BEDT-TTF)2Cu[N(CN)2]Br and κ-(BEDT-TTF)2Cu(NCS)2. They observed a fourfold symmetric oscillation in γ, which arises from the node structures in the superconductive gap. Their results are suggestive of the dxy order parameter of the superconductivity in these materials.
The Fulde-Ferrell-Larkin-Ovchinnikov (FFLO) state in κ-(BEDT-TTF)2Cu(NCS)2 under extremely high magnetic fields applied parallel to the 2D layer was found by thermodynamic measurement up to 28 T by Lortz et al. [39]. They observed that the heat capacity peak changes from a second order to a first order around 21.5 T and the curvature of H–T phase diagram shows upward deviation of Hc2 at low temperature and in the high magnetic fields region. Bergk et al. [40] reported more detailed information by combining magneto-torque measurement and heat capacity under magnetic fields up to 32 T and determined H–T phase diagram.

6. κ-(BEDT-TTF)2Ag(CN)2H2O and κ-(MDT-TTF)2AuI2

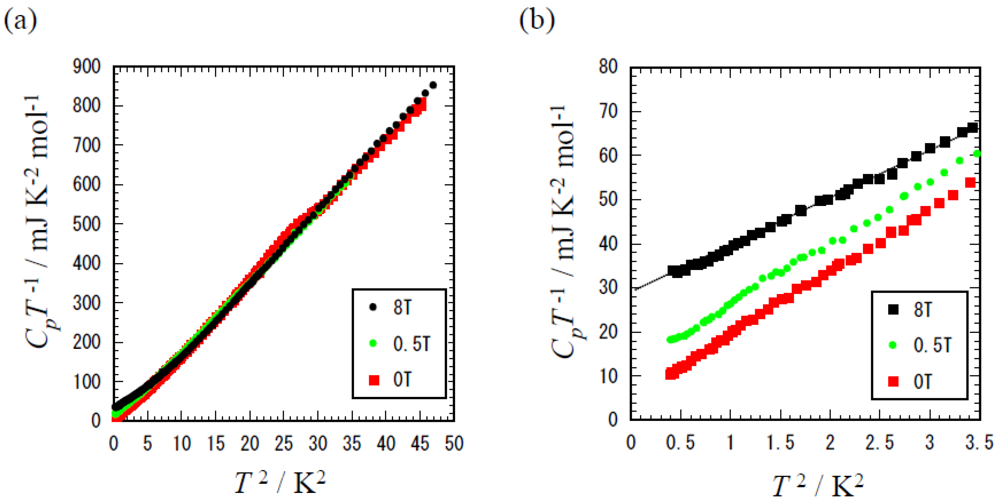
Heat capacity data of other κ-type superconductors which have middle class transition temperature (3–5 K) as organics are also important for the comparative discussion with 10 K class superconductors, since they are necessary to construct an overall picture of the superconductive phase. The superconductivity of κ-(BEDT-TTF)2Ag(CN)2H2O was reported by Mori et al. of which transition temperature is about 5 K [41]. The temperature dependence of heat capacity of this compound obtained under 0 T and 0.5 T and 8 T are shown in Figure 10a,b. Existence of the thermal anomaly in heat capacity was observed clearly around 5 K. Subtraction of normal state data obtained under 8 T from 0 T data gives a temperature dependence of electronic heat capacity and the heat capacity jump was evaluate as ∆Cp/Tc = 30 mJ K−2 mol−1. The data below 1.8 K under magnetic fields up to 8 T in Figure 10b claim that the normal state γ is evaluated as 28–30 mJ K−2 mol−1 [39]. Therefore, ∆Cp/γTc of this compound is evaluated as 1.0–1.1. The data in Figure 10 shows that a relatively large residual γres of about 5.1 mJ K−2 mol−1, corresponding to 18% of the normal state γ, remains in the superconductive state, even though the sample is a shiny single crustal which shows sharp diamagnetic signals.
Crystals 02 00741 g010 1024
Figure 10. (a)Temperature dependence of heat capacity of κ-(BEDT-TTF)2Ag(CN)2H2O. The inset shows temperature dependence of electronic heat capacity obtained by subtracting the data obtained under magnetic fields above Hc2; (b) The extended plot of CpT−1 vs. T 2 at low temperature region.
Figure 10. (a)Temperature dependence of heat capacity of κ-(BEDT-TTF)2Ag(CN)2H2O. The inset shows temperature dependence of electronic heat capacity obtained by subtracting the data obtained under magnetic fields above Hc2; (b) The extended plot of CpT−1 vs. T 2 at low temperature region.
Crystals 02 00741 g010
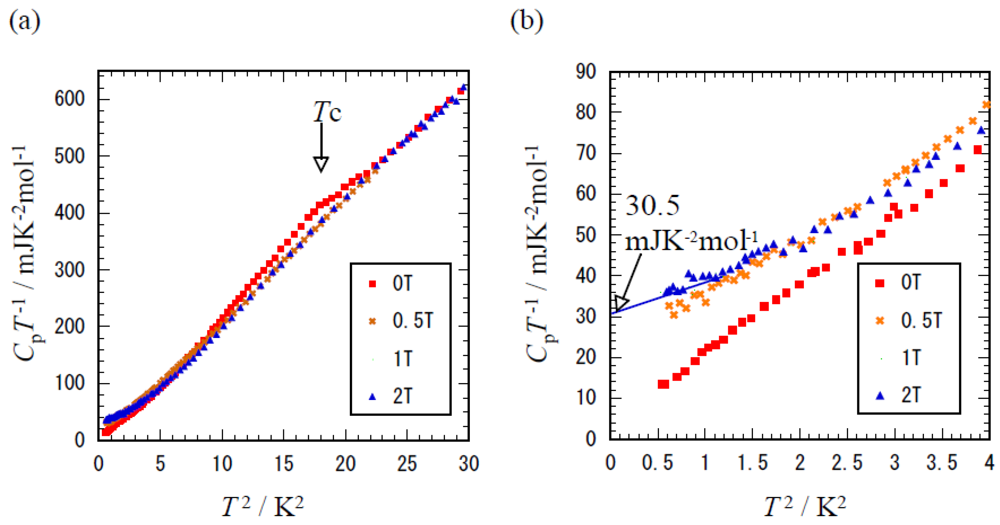
Crystals 02 00741 g011 1024
Figure 11. (a)Temperature dependence of heat capacity of κ-(MDT-TTF)2AuI2 obtained under 0 T, 0.5 T, 1 T and 2 T. (b) The extended plot of CpT−1 vs. T2 in the low temperature region.
Figure 11. (a)Temperature dependence of heat capacity of κ-(MDT-TTF)2AuI2 obtained under 0 T, 0.5 T, 1 T and 2 T. (b) The extended plot of CpT−1 vs. T2 in the low temperature region.
Crystals 02 00741 g011
A similar tendency is observed in the κ-(MDT-TTF)2AuI2 (MDT-TTF: Methylendithiotetrathiafulvalene) system of which the superconductive transition temperature is 4.5 K [43]. This compound consists of an asymmetric donor molecule composed of a half fragment of BMDT-TTF (Bis(methlenedithio)tetrathiafulvalene) and TTF. The similarly-layered structure with κ-type donor arrangement is known, as in BEDT-TTF molecules. The heat capacity under 0 T, 0.5 T, 1 T and 2 T are shown in Figure 11 with CpT−1 vs. T2 plot. The superconductive transition has been detected at Tc which also gives superconductive jump expressed as ∆Cp/Tc = 30 mJ K−2 mol−1. The data of low temperature region is shown in Figure 11b which show γ = 30.5 mJ K−2 mol−1 and γres = 5.9 mJ K−2 mol−1. Although the donor molecule and counteranions are different, the two middle Tc compounds have a similar aspect. The magnitude of the heat capacity jump observed in CpT−1 vs. T2 is reduced as compared with 10 K class superconductors. The ∆Cp/γTc is 1.0–1.1 for κ-(BEDT-TTF)2Ag(CN)2H2O and 1.0 for κ-(BEDT-TTF)2Ag(CN)2H2O. Thermodynamic data on κ-(BEDT-TTF)2I3 with transition temperature of 3.4 K was reported by Wosnitza et al. [44] using a high resolution heat pulse technique between 0.25 K and 20 K with magnetic fields up to 6 T. They determined that the γ = 18.9 mJ K–2 mol–1 and the analysis of ∆Cp/γTc in κ-(BEDT-TTF)2I3 gives 1.6.
The smaller ∆Cp/γT values obtained in these compounds suggest that the paring state of these middle-class superconductors turn out to be weaker coupling that those of 10 K class superconductors. It is suggested that the pairing state gradually changes from strong coupling to a weaker coupling one, with the decrease of Tc and by shifting from the Mott boundary to a normal metallic region. The change of coupling nature of superconductivity may demonstrate the importance of electron correlations for superconductivity.

7. Hole Doped System: κ-(BEDT-TTF)4Hg2.89Br8 and κ-(BEDT-TTF)4Hg2.78Cl8

Since the κ-(BEDT-TTF)2X is a typical example of a strongly-correlated electron system with a 2D structure, an interesting subject for them is to control the number of electrons or holes from the effectively half-filled state and trace the change occurring in the electronic structures. This scenario is related to the occurrence of high-Tc superconductivity in cuprates. The κ-type salts containing mercury and halogens in the counteranions were developed by Lubovskaya et al. in 1987 [45]. In this system, heavy mercury ions form a chain structure of their own periodicity in the anion layers. The periodicity is incommensurate with that of the donor and halogen arrangement. The non-stoichiometric concentration of divalent mercury produced by this incommensurate structure gives a hole-doped electronic state from the effectively half-filled band. The κ-(BEDT-TTF)4Hg2.89Br8 (abbreviated as HgBr) is considered as a 10% hole-doped system, while κ-(BEDT-TTF)4Hg2.78Cl8 (abbreviated as HgCl) is 18% doped, which is a quite unique situation in organic conducting salts. The temperature dependence of the heat capacity obtained by the thermal relaxation technique is shown in the CpT−1 vs. T2 plot in Figure 12 [46,47].
Here we show the heat capacity values normalized for two BEDT-TTF molecules in a formula unit, so as to compare the thermodynamic parameters with κ-(BEDT-TTF)2Cu(NCS)2. The HgBr gives an anomalous lattice contribution even below 2 K, due to a 1D arrangement of heavy mercury ions. The lattice heat capacity reflecting peculiar temperature dependences was successfully fitted by a model given by Tarasov, where the 1D phonons (with θ1D = 200 K) varies to 3D phonons (θ3D = 6.5 K) with a decrease in temperature as has been discussed already in [43]. The crossover observed in lattice heat capacity due to low energy phonon structures give such an anomalous heat capacity, even at low temperatures. In the case of HgCl salt, the decrease of mercury number tends to suppress the 1D characters and the crossover temperature from a 1D to a 3D phonon shift to higher temperatures. Consequently, the heat capacity does not show an anomalous phonon structure. It is emphasized that the magnitude of the γ values are enhanced up to 55 mJ K−2 mol−1 for HgBr and 52 mJ K−2 mol−1 for HgCl. Kurosaki et al. [48] observed by 13C-NMR that antiferromagnetic fluctuations are much enhanced from the usual κ-(BEDT-TTF)2X system anomalously down to the dilution temperature region. The enhancement of static parameters observed by heat capacity and magnetic susceptibility and T1−1 means that the effective mass is enhanced due to the electron correlations, just as in the case of itinerant magnetic systems in intermetallic compounds based on 3d transition metal and 4f, 5f heavy ferimion electron systems.
Crystals 02 00741 g012 1024
Figure 12. CpT−1 vs. T2 plot of heat capacity of κ-(BEDT-TTF)4Hg2.89Br8 (black) and κ-(BEDT-TTF)4Hg2.78Cl8 (green and blue colors denote the data for different samples). To compare with the thermodynamic parameters with other κ-type salts, the data are plotted using a composition of two BEDT-TTF molecules in a formula unit. The data of κ-(BEDT-TTF)2Cu(NCS)2 (red) are also plotted.
Figure 12. CpT−1 vs. T2 plot of heat capacity of κ-(BEDT-TTF)4Hg2.89Br8 (black) and κ-(BEDT-TTF)4Hg2.78Cl8 (green and blue colors denote the data for different samples). To compare with the thermodynamic parameters with other κ-type salts, the data are plotted using a composition of two BEDT-TTF molecules in a formula unit. The data of κ-(BEDT-TTF)2Cu(NCS)2 (red) are also plotted.
Crystals 02 00741 g012
The superconductive transition of the HgBr salt was also studied by Naito et al. [46] and Yamashita et al. [49] and a very broad peak with ∆CpT−1= 15–20 mJ K−2 mol−1 was reported. Yamashita et al. reported that the cooling rate from room temperature to liquid helium temperature affects the volume fraction estimated from the heat capacity jump around Tc [49]. The reason for this cooling rate dependence is not attributed to the dynamic nature of the ethylene groups sometimes observed in BEDT-TTF salts, but the disorders produced by mercury chain may be responsible for this phenomenon.

8. Heat Capacities under Pressures for κ-(BEDT-TTF)2X Superconductors

To investigate the variation of superconductive characters in the phase diagram of κ-type salts, chemical pressure effects produced by changing counter anions is effective in the κ-(BEDT-TTF)2X system. However, the ambiguities due to disorders in molecular stacking in the donor layers are serious problems. The comparison of thermodynamic behaviors produced by chemical pressure effects with those obtained under hydrostatic pressures are required. In order to get thermodynamic data under pressure, the ac calorimetric system for single crystal samples of organic salts were developed by Kubota et al. [50] and Tokoro et al. [50,51]. Two small ruthenium oxide sensor chips with 100 Ω and 1 kΩ were used as a thermometer and a heater respectively, and small temperature modulation was detected by a four probe technique with a high resolution ac bridge system. Single crystals with 1–3 mg are sandwiched by these two chips and coated by a small amount of epoxy (Stycast 1266 or 2850FT) and sealed in the Teflon cell with the pressure medium of Daphne 7373. The pressure was applied by Cu–Be and a Cu–Be + NiCrAl piston cylinder, details of which are shown schematically in Figure 13.
Crystals 02 00741 g013 1024
Figure 13. Schematic view of high pressure ac calorimeter for single crystal samples with 1–3 mg. The small ruthenium oxide chip type resistances utilized as a heater and a thermometer are attached on single crystal sample.
Figure 13. Schematic view of high pressure ac calorimeter for single crystal samples with 1–3 mg. The small ruthenium oxide chip type resistances utilized as a heater and a thermometer are attached on single crystal sample.
Crystals 02 00741 g013
Using the apparatus shown here, Tokoro et al. measured the ac heat capacity of κ-(BEDT-TTF)2Ag(CN)2H2O and observed that a thermal anomaly around 5 K suppressed by applying pressure of 0.5 GPa. The data displayed in Figure 14 is the heat capacity obtained for the x = 0.10 composition of the alloying system of κ-(BEDT-TTF1−xBEDSe-TTFx)2Cu[N(CN)2]Br under pressure. Partial substitution of the BEDT-TTF site by BEDSe-TTF molecules with a concentration smaller than 20% produce positive chemical pressure effects and decrease the transition temperature continuously. The thermal anomaly existing around 10 K at ambient pressure is reduced to 7 K at 0.3 GPa and 6.4 K at 0.45 GPa. The observation of thermodynamic peak under pressures means that the shift of the transition temperature by external pressures occurs as a bulk form. Although it is possible to detect the existence or absence of thermal anomalies associated with superconductive transition, the background value is still so large as to prohibit the quantitative discussion and entropy evaluation of the peak.
Crystals 02 00741 g014 1024
Figure 14. Temperature dependence of heat capacity around the superconductive transition of κ-[(BEDT-TTF)0.90(BEDSe-TTF)0.10]2Cu[N(CN)2]Br.
Figure 14. Temperature dependence of heat capacity around the superconductive transition of κ-[(BEDT-TTF)0.90(BEDSe-TTF)0.10]2Cu[N(CN)2]Br.
Crystals 02 00741 g014

9. Summary

Thermodynamic investigations by low temperature heat capacity measurements in κ-(BEDT-TTF)2X are reported, where X = Cu(NCS)2, Cu[N(CN)2]Br including partially and fully deuterated compounds, Cu[N(CN)2]Cl, Ag(CN)2H2O and κ-(BEDT-TTF)4Hg2.89Br8, κ-(BEDT-TTF)4Hg2.78Cl8 and κ-(MDT-TTF)2AuI2 which are known as 2D strongly correlated electron systems. We explain the structural and electronic features originating from dimerization in the 2D layer. The Mott insulating salts of κ-(BEDT-TTF)2Cu[N(CN)2]Cl and deuterated κ-(BEDT-TTF)2Cu[N(CN)2]Br shows vanishing γ, which is insensitive to magnetic fields in heat capacity, which claims the opening of the charge-gap in the Mott insulating state. The γ around the Mott boundary region is drastically affected by the influence of glass freezing of ethylene groups. Through the studies of cooling rate dependences and measurements combined with fine tuning of the chemical pressure by partial deuteration technique, we observed systematic changes of thermodynamic parameters. The strong coupling nature in superconductivity in κ-(BEDT-TTF)2Cu(NCS)2 and κ-(BEDT-TTF)2Cu[N(CN)2]Br is intrinsic for the 10 K class superconductors, which have a nodal-gap picture in the low temperature heat capacities. Through the comparison with lower Tc compounds in the κ-type structure, the coupling strength tends to be suppressed with the decrease of U/W ratio in the superconductive phase. The heat capacity measurements of hole-doped systems containing mercury in the counteranions show an anomalous enhancement of electronic heat capacity coefficient, which is consistent with the NMR experiments. We also reported the systematic shift of superconductive transitions and changes of thermodynamic anomalies in heat capacity with the increase of external pressures by ac calorimetry in a clamp-type pressure cell.

Acknowledgments

This work is partly supported by Grant-in-Aid for Scientific Research Nos. 22014007, 23654122 from JSPS and No.23110717 from the Ministry of Education, Science, Sports and Culture of Japan.

Conflict of Interest

The authors declare no conflict of interests.

References and Notes

  1. Ishiguro, T.; Yamaji, K.; Saito, G. Organic Superconductors; Springer-Verlag: Heidelberg, Germany, 1998. [Google Scholar]
  2. Williams, J.M.; Ferraro, J.R.; Thorn, R.J.; Carlson, K.D.; Geiser, U.; Wang, H.-H.; Kini, A.M.; Whangbo, M.-H. Organic Superconductors; Prentice-Hall, Inc.: Upper Saddle River, NJ, USA, 1992; pp. 65–179. [Google Scholar]
  3. Bidan, G.; Bernier, P.; Lefrant, S. Advances in Synthetic Metals; Elsevier: Lausanne, Switzerland, 1999; pp. 262–348. [Google Scholar]
  4. Kanoda, K. Metal-insulator transitions in κ-(ET)2X and (DCNQI)2M: Two contrasting manifestation of electron correlation. J. Phys. Soc. Jpn. 2006, 75, 051007:1–051007:16. [Google Scholar]
  5. Miyagawa, K.; Kanoda, K.; Kawamoto, A. NMR Studies in Two-Dimensional Molecular Conductors and Superconductors: Mott Transition in κ-(BEDT-TTF)2X. Chem. Rev. 2004, 104, 5635–5653. [Google Scholar] [CrossRef]
  6. Gopal, E.S.R. Specific Heats at Low Temperatures; Plenum Press: New York, NY, USA, 1966. [Google Scholar]
  7. Kanoda, K. Recent progress in NMR studies on organic conductors. Hyperfine Interactions 1997, 104, 235–249. [Google Scholar] [CrossRef]
  8. Kanoda, K. Electron correlation, metal-insulator and superconductivity in quasi-2D organic system, (ET)2X. Physica C 1997, 287, 299–302. [Google Scholar] [CrossRef]
  9. Kagawa, F.; Miyagawa, K.; Kanoda, K. Unconventional critical behaviour in a quasi-two-dimensional organic conductor. Nature 2005, 436, 534–537. [Google Scholar] [CrossRef]
  10. Shimizu, Y.; Miyagawa, K.; Kanoda, K.; Maesato, M.; Saito, G. Spin Liquid State in an Organic Mott Insulator with a Triangular Lattice. Phys. Rev. Lett. 2003, 91, 107001:1–107001:4. [Google Scholar]
  11. Nakazawa, Y.; Kanoda, K. Electronic structure of insulating salts of the κ-(BEDT-TTF)2X family studied by low-temperature specific-heat measurements. Phys. Rev. B 1996, 53, R8875–R8878. [Google Scholar] [CrossRef]
  12. Nakazawa, Y.; Kanoda, K. Thermodynamics of BEDT-TTF based Dimeric Salts. Synth. Met. 1999, 103, 1903–1904. [Google Scholar] [CrossRef]
  13. Taniguchi, H.; Miyashita, M.; Uchiyama, K.; Satoh, K.; Mori, N.; Okamoto, K.; Miyagawa, K.; Kanoda, K.; Hedo, M.; Uwatoko, Y. Superconductivity at 14.2 K in layered organics under extreme pressure. J. Phys. Soc. Jpn. 2003, 72, 468–471. [Google Scholar] [CrossRef]
  14. Yamashita, S.; Nakazawa, Y. Heat Capacities of Antiferromagnetic Dimer-Mott Insulators in Organic Charge-Transfer Complexes. J. Therm. Anal. Calorim. 2009, 99, 153–157. [Google Scholar] [CrossRef]
  15. Nakazawa, Y.; Taniguchi, H.; Kawamoto, A.; Miyagawa, K.; Hiraki, K.; Kanoda, K. Thermodynamic studies of electron correlation effects on organic salts based on BEDT-TTF and DCNQI molecules. J. Phys. Chem. Solids 2001, 62, 385–388. [Google Scholar] [CrossRef]
  16. Sun, K.; Cho, J.H.; Chou, F.C.; Lee, W.C.; Miller, L.L.; Johnston, D.C.; Hidaka, Y.; Murakami, T. Heat capacity of single-crystal La2CuO4 and polycrystalline La2 − xSrxCuO4 (0 ≤ x ≤ 0.20) from 110 to 600 K. Phys. Rev. B 1991, 43, 239–246. [Google Scholar]
  17. Akutsu, H.; Saito, K.; Sorai, M. Phase behavior of the organic superconductors κ-(BEDT-TTF)2Cu[N(CN)2]X (X = Br and Cl) studied by ac calorimetry. Phys. Rev. B 2000, 61, 4346–4352. [Google Scholar] [CrossRef]
  18. Müller, J.; Lang, M.; Steglich, F.; Schlueter, J.A.; Kini, A.M.; Sasaki, T. Evidence for structural and electronic instabilities at intermediate temperatures in κ-(BEDT-TTF)2X for X = Cu[N(CN)2]Cl, Cu[N(CN)2]Br and Cu(NCS)2: implications for the phase diagram of these quasi-two-dimensional organic superconducors. Phys. Rev. B 2002, 65, 144521:1–144521:14. [Google Scholar]
  19. Akutsu, H.; Saito, K.; Yamamura, Y.; Kikuchi, K.; Nishikawa, H.; Ikemoto, I.; Sorai, M. Metal-Insulator, SDW, and Glass Transitions in the Organic Conductors, (DMET)2BF4 and (DMET)2ClO4, Studied by ac Calorimetry. J. Phys. Soc. Jpn. 1999, 68, 1968–1974. [Google Scholar] [CrossRef]
  20. Nakazawa, Y.; Kanoda, K. Thermodynamic investigation of the electronic states of deuterated κ-(BEDT-TTF)2Cu[N(CN)2]Br. Phys. Rev. B 1999, 60, 4263–4267. [Google Scholar] [CrossRef]
  21. Nakazawa, Y.; Taniguchi, H.; Kawamoto, A.; Kanoda, K. Electronic specific heat at the boundary region of the metal-insulator transition in the two-dimensional electronic system of κ-(BEDT-TTF)2Cu[N(CN)2]Br. Phys. Rev. B 2000, 61, R16295–R16298. [Google Scholar]
  22. Nakazawa, Y.; Taniguchi, H.; Kawamoto, A.; Kanoda, K. Electronic specific heat of BEDT-TTF based organic conductors. Physica B 2000, 281–282, 899–900. [Google Scholar] [CrossRef]
  23. Taylor, O.J.; Carrington, A.; Schlueter, J.A. Superconductor-insulator phase separation induced by rapid cooling of κ-(BEDT-TTF)2Cu[N(CN)2]Br. Phys. Rev. B 2008, 77, 060503:1–060503:4. [Google Scholar]
  24. Andraka, B.; Kim, J.S.; Stewart, G.R.; Stewart, G.R.; Wang, H.H.; Williams, J.M. Specific heat in high magnetic field of κ-di[bis(ethylenedithio)tetrathiafulvalene]-di(thiocyano)cuprate [κ-(ET)2Cu(NCS)2]: Evidence for strong-coupling superconductivity. Phys. Rev. B 1989, 40, 11345–11347. [Google Scholar]
  25. Yamashita, S.; Ishikawa, T.; Fujisaki, T.; Naito, A.; Nakazawa, Y.; Oguni, M. Thermodynamic Behavior of the 10 K Class organic Superconductor κ-(BEDT-TTF)2Cu(NCS)2 Studied by Relaxation Calorimetry. Thermochim. Acta 2005, 431, 123–126. [Google Scholar] [CrossRef]
  26. Graebner, J.E.; Haddon, R.C.; Chichester, S.V.; Glarum, S.H. Specific heat of superconducting κ-(BEDT-TTF)2Cu(NCS)2 near Tc [where BEDT-TTF is bis(ethylenedithio)tetrathiafulvalene]. Phys. Rev. B 1990, 41, 4808–4810. [Google Scholar] [CrossRef]
  27. Andraka, B.; Jee, C.S.; Kim, J.S.; Stewart, G.R.; Calson, K.D.; Wang, H.H.; Crouch, A.V.S.; Kini, A.M.; Williams, J.M. Specific heat of the high Tc organic superconductor κ-(ET)2Cu[N(CN)2]Br. Solid State Commun. 1991, 79, 57–59. [Google Scholar] [CrossRef]
  28. Elsinger, H.; Wosnizta, J.; Wanka, S.; Hagel, J.; Schweitzer, D.; Strunz, W. κ-(BEDT-TTF)2Cu[N(CN)2]Br: A Fully Gapped Strong-Coupling Superconductor. Phys. Rev. Lett. 2000, 84, 6098–6101. [Google Scholar] [CrossRef]
  29. Müller, J.; Lang, M.; Helfrich, R.; Steglich, F.; Sasaki, T. High-resolution ac-calorimetry studies of the quasi-two-dimensional organic superconductor κ-(BEDT-TTF)2Cu(NCS)2. Phys. Rev. B 2002, 65, 140509:1–140509:4. [Google Scholar]
  30. Nakazawa, Y.; Kanoda, K. Low-temperature specific heat of κ-(BEDT-TTF)2Cu[N(CN)2]Br in the superconducting state. Phys. Rev. B 1997, 55, R8670–R8673. [Google Scholar] [CrossRef]
  31. Nakazawa, Y.; Kanoda, K. Thermodynamic property of organic superconductor κ-(BEDT-TTF)2X [C = Cu(NCS)2, Cu[N(CN)2]Br]. Physica C 1997, 282–287, 1897–1898. [Google Scholar] [CrossRef]
  32. Kanoda, K.; Miyagawa, K.; Kawamoto, A.; Nakazawa, Y. NMR relaxation rate in the superconducting state of the organic conductor κ-(BEDT-TTF)2Cu[N(CN)2]Br. Phys. Rev. B 1996, 54, 76–79. [Google Scholar]
  33. Mayaffre, H.; Wzietek, P.; Lenoir, C.; Jerome, D.; Batail, P. 13C-NMR Study of a Quasi-Two-Dimensional Organic Superconductor κ-(ET)2Cu[N(CN)2]Br. Europhys. Lett. 1994, 28, 205–210. [Google Scholar] [CrossRef]
  34. De Soto, S.M.; Slichter, C.P.; Kini, A.M.; Wang, H.H.; Geiser, U.; Williams, J.M. 13C-NMR studies of the normal and superconducting states of the organic superconductor κ-(ET)2Cu[N(CN)2]Br. Phys. Rev. B 1995, 52, 10364–10368. [Google Scholar]
  35. Izawa, K.; Yamaguchi, H.; Sasaki, T.; Matsuda, Y. Superconducting Gap Structure of κ-(BEDT-TTF)2Cu(NCS)2 Probed by Thermal Conductivity Tensor. Phys. Rev. Lett. 2002, 88, 027002:1–027002:4. [Google Scholar]
  36. Harshman, D.R.; Fiory, A.T.; Haddon, R.C.; Kaplan, M.L.; Pfiz, T.; Koster, E.; Shinkoda, I.; Williams, D.Ll. Magnetic Penetration Depth and Fluxon-Line Dynamics in the Organic Superconductor κ-[BEDT-TTF]2Cu[NCS]2. Phys. Rev. B 1994, 49, 12990–12997. [Google Scholar]
  37. Le, L.P.; Luke, G.M.; Sternlieb, B.J.; Wu, W.D.; Uemura, Y.J.; Brewer, J.H.; Riseman, T.M.; Stronach, C.E.; Saito, G.; Yamochi, H.; et al. Muon-Spin-Relaxation Measurements of Magnetic Penetration Depth in Organic Superconductors (BEDT-TTF)2-X:X=Cu(NCS)2 and Cu[N(CN)2]Br. Phys. Rev. Lett. 1992, 68, 1023–1926. [Google Scholar]
  38. Malone, L.; Taylor, O.J.; Schlueter, J.A.; Carrington, A. Location of gap nodes in the organic superconductors κ-(ET)2Cu(NCS)2 and κ-(ET)2Cu[N(CN)2]Br determined by magnetocalorimetry. Phys. Rev. B 2010, 82, 014522:1–014522:5. [Google Scholar]
  39. Lortz, R.; Wang, Y.; Demuer, A.; Bottger, P.H.M.; Bergk, B.; Zwicknagl, G.; Nakazawa, Y.; Wosnizta, J. Calorimetric Evidence for a Fulde-Ferrell-Larkin-Ovchinnikov Superconducting State in the Layered Organic Superconductor κ-(BEDT-TTF)2Cu(NCS)2. Phys. Rev. Lett. 2007, 99, 187002:1–187002:4. [Google Scholar]
  40. Berg, B.; Demuer, A.; Sheikin, I.; Wang, Y.; Wosnizta, J.; Nakazawa, Y.; Lortz, R. Location of gap nodes in the organic superconductors κ-(ET)2Cu(NCS)2 and κ-(ET)2Cu[N(CN)2]Br determined by magnetocalorimetry. Phys. Rev. B 2010, 82, 014522:1–014522:5. [Google Scholar]
  41. Mori, H.; Hirabayashi, I.; Tanaka, S.; Mori, T.; Inokuchi, H. A new ambient-pressure organic superonductor, κ-(BEDT-TTF)2Ag(CN)2H2O (TC = 5.0 K). Solid State Commun 1990, 76, 35–37. [Google Scholar] [CrossRef]
  42. Ishikawa, T.; Yamashita, S.; Nakazawa, Y.; Kawamoto, A.; Oguni, M. Calorimetric Study of Molecular Superconductor κ-(BEDT-TTF)2Ag(CN)22H2O which Contains Water in the Anion Layers. J. Therm. Anal. Calorim. 2008, 92, 435–438. [Google Scholar] [CrossRef]
  43. Ishikawa, T.; Nakazawa, Y.; Yamashita, S.; Oguni, M.; Saito, K.; Takimiya, K.; Otsubo, T. Thermodynamic Study of an Incommensurate Organic Superconductor (MDT-TSF)(AuI2)0.436. J. Phys. Soc. Jpn. 2006, 75, 074606:1–074606:4. [Google Scholar]
  44. Wosnitza, J.; Liu, X.; Schweitzer, D.; Keller, H.J. Specific heat of the organic superconductor κ-(BEDT-TTF)2I3. Phys. Rev. B 1994, 50, 12747–12751. [Google Scholar]
  45. Lyubovskaya, R.N.; Zhilyaeva, E.I.; Pesotskii, S.I.; Lyubovskii, R.B.; Atovmyan, L.O.; D’yachenko, O.A.; Takhirov, T.G. Superconductivity at the atmospheric pressure in the (ET)4H2.89Br8 at Tc = 4.3 K and anisotropy of critical fields. JETP Lett. 1987, 46, 188–191. [Google Scholar]
  46. Naito, A.; Nakazawa, Y.; Saito, K.; Taniguchi, H.; Kanoda, K.; Sorai, M. Anomalous enhancement of electronic heat capacity in the organic conductors κ-(BEDT-TTF)4Hg3−δX8 (X = Br,Cl). Phys. Rev. B 2005, 71, 054514:1–054514:4. [Google Scholar]
  47. Naito, A.; Nakazawa, Y.; Saito, K.; Taniguchi, H.; Kanoda, K.; Sorai, M. Low-temperature heat capacity measurements of κ-(BEDT-TTF)4Hg2.89Br8. Physica C 2003, 388, 595–596. [Google Scholar] [CrossRef]
  48. Kurosaki, Y.; Furuta, A.; Taniguchi, H.; Miyagawa, K.; Kanoda, K. Inhomogeneous spin state in the organic conductor κ-(BEDT-TTF)4Hg2.78Cl8. Physica B 2009, 404, 3138–3140. [Google Scholar]
  49. Yamashita, S.; Naito, A.; Nakazawa, Y.; Saito, K.; Taniguchi, H.; Kanoda, K.; Oguni, M. Drastic Cooling Rate Dependence of Thermal Anomaly Associated with the Superconducting Transition in κ-(BEDT-TTF)4Hg3−δBr8. J. Therm. Anal. Calorim. 2005, 81, 591–594. [Google Scholar] [CrossRef]
  50. Kubota, O.; Nakazawa, Y. Construction of a low-temperature thermodynamic measurement system for single crystal of molecular compounds under pressures. Rev. Sci. Instrum. 2008, 79, 053901:1–053901:6. [Google Scholar]
  51. Tokoro, N.; Kubota, O.; Yamashita, S.; Kawamoto, A.; Nakazawa, Y. Thermodynamic Study of κ-(BEDT-TTF)2Ag(CN)2H2O under Pressures and with Magnetic Fields. J. Phys. Conf. Series 2008, 132, 012010:1–012010:8. [Google Scholar]
  52. Tokoro, N.; Fukuoka, S.; Kubota, O.; Nakazawa, Y. Low-temperature heat capacity measurements of κ-type organic superconductors under pressure. PhysicaB 2010, 405, S273–S276. [Google Scholar]

Share and Cite

MDPI and ACS Style

Nakazawa, Y.; Yamashita, S. Thermodynamic Properties of κ-(BEDT-TTF)2X Salts: Electron Correlations and Superconductivity. Crystals 2012, 2, 741-761. https://doi.org/10.3390/cryst2030741

AMA Style

Nakazawa Y, Yamashita S. Thermodynamic Properties of κ-(BEDT-TTF)2X Salts: Electron Correlations and Superconductivity. Crystals. 2012; 2(3):741-761. https://doi.org/10.3390/cryst2030741

Chicago/Turabian Style

Nakazawa, Yasuhiro, and Satoshi Yamashita. 2012. "Thermodynamic Properties of κ-(BEDT-TTF)2X Salts: Electron Correlations and Superconductivity" Crystals 2, no. 3: 741-761. https://doi.org/10.3390/cryst2030741

Article Metrics

Back to TopTop