Structural Aspects of the Bechgaard and Fabre Salts: An Update
Abstract
:1. Introduction
- (i) Their pπ electron bandwidth is comparable to the electron–electron Coulomb repulsions which, being weakly screened, decrease slowly with the intermolecular separation.
- (ii) Their lattice is soft and quite compressible, which leads to rapid change of the electronic properties under pressure or uniaxial stress, while providing a sizeable coupling between the electronic and structural degrees of freedom.
- (iii) Their crystal array is quite perfect, which allows a fine control of the perturbation of physical properties by defects intentionally introduced in the structure.
2. Basic Aspects of the Crystallographic Structure in Relationship with Electronic Properties
2.1. Structural Arrangement
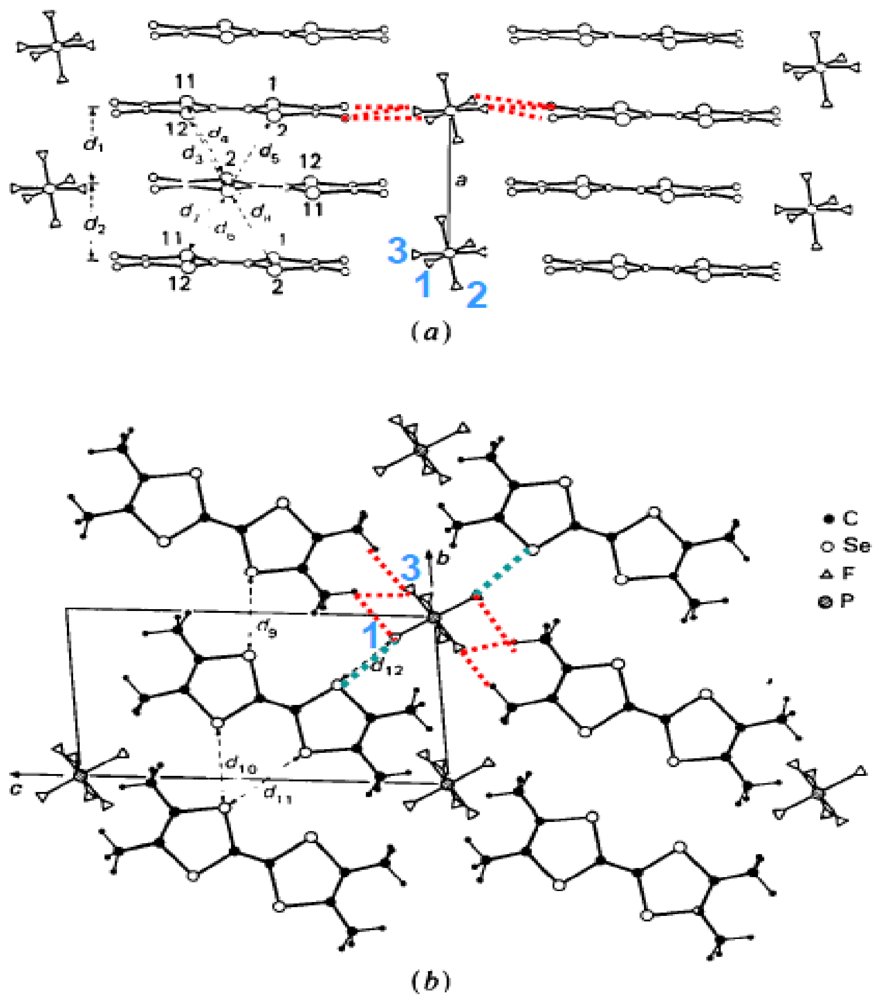
2.2. Dimerization of the Stack
2.3. Anion Cavities
2.4. Anion and Methyl Group Disorders
3. The Bond Order Wave Instability in the Bechgaard and Fabre Salts
3.1. The Interplay between 2kF BOW and SDW Instabilities in (TMTSF)2PF6
3.1.1. Quantitative Analysis of the 1D 2kF BOW Instability

3.1.2. Interchain Coupling between the 2kF Density Waves and the Vanishing of the Anion Disorder
- - The (2kF)−1 periodicity is achieved in stack direction by repeating periodically two neighboring maxima of hole concentration with two neighboring minima of hole concentration.
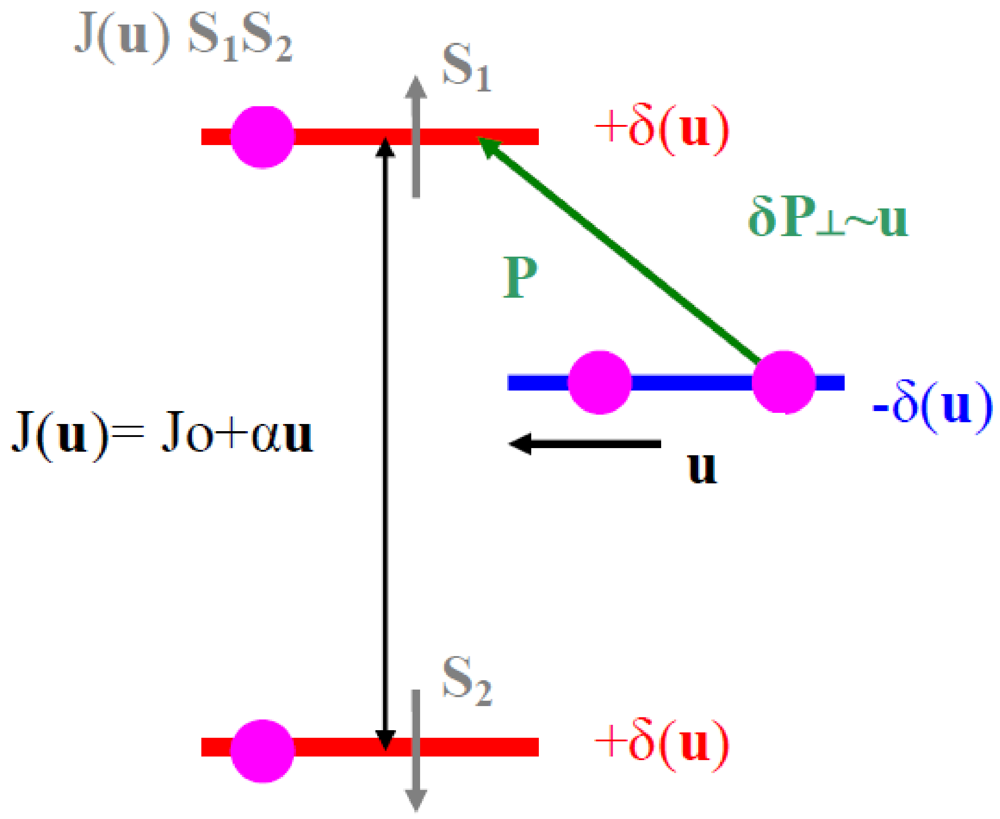
- - The anion shift allows to achieve a 3D coupling between neighboring 2kF CDW by locking a maxima of the 2kFπ hole CDW on the molecule towards which the anion approaches and concomitantly a minimum of π hole density on the molecule that the anion leaves.
- - By combining these two features, the 3D CDW pattern requires a synchronous staggered shift of near-neighbor anions along a, along the d1 = a − b + c direction (which achieves the coupling of anions with the closest Se atom of the donor) and along the d2 = a + b + c direction (which achieves the coupling of the anions with the methyl groups and the polarization of σ bonds of the donor).


3.2. Evolution of the 2kF BOW Instability along the TMTSF-TMTTF Series
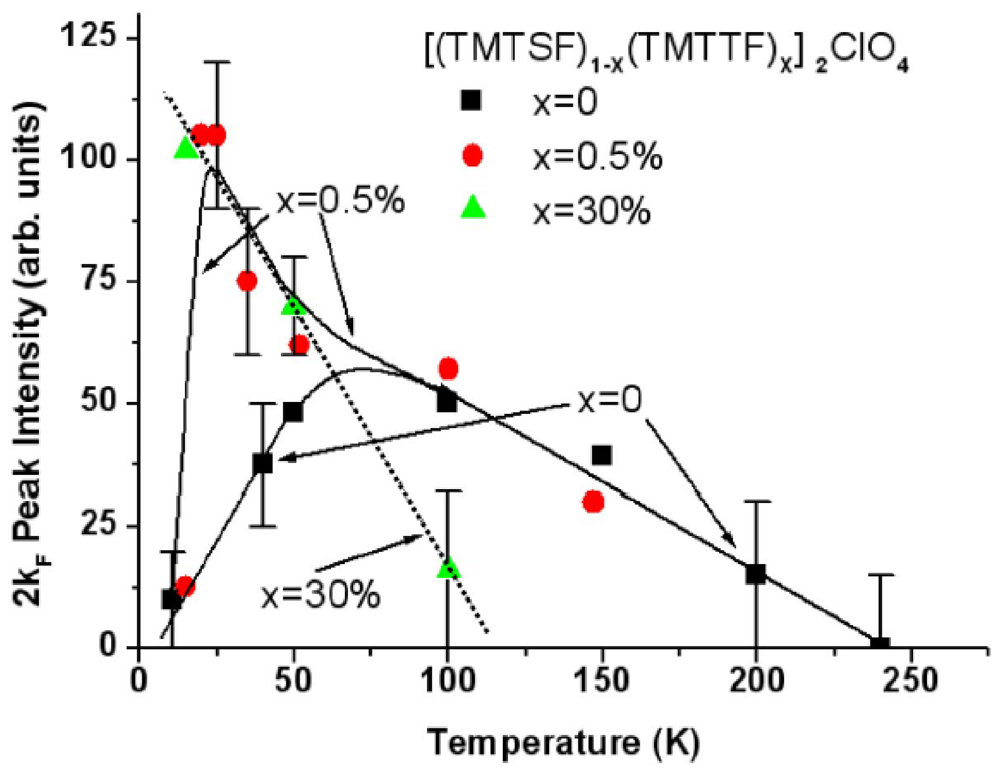
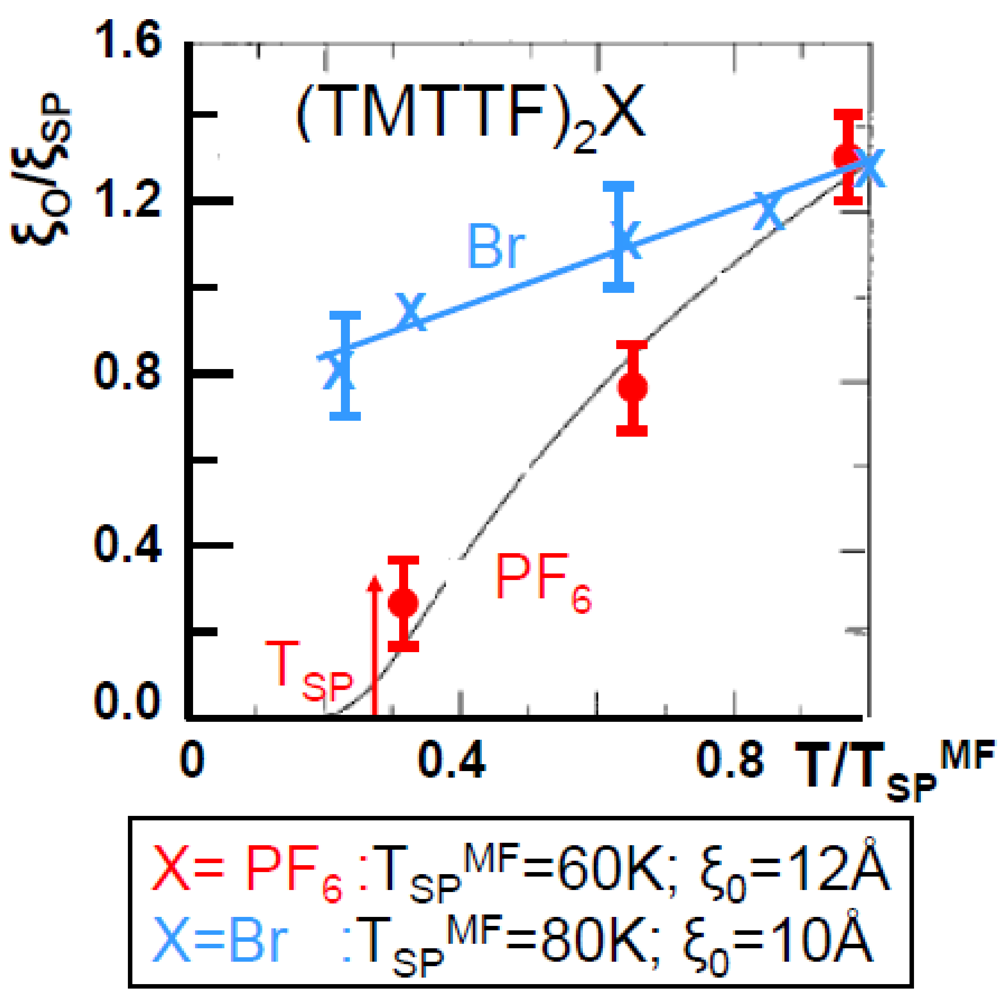
3.3. The Spin-Peierls Instability
4. The Magnetic Ground States of the Bechgaard and Fabre Salts
4.1. The AF Phase of (TMTTF)2Br and the Pre-Transitional Anomalies
- - The thermal dependence of the electrical conductivity exhibits, depending on the measurements, either a kink at T* or a slope anomaly at T*, or even a plateau below T* (to my knowledge the T* anomaly was first reported in Figure 1 of [78]).
- - A broadening of the NMR spectra, interpreted as being due to non-homogeneities in the electronic states, is observed below T* [80].
4.2. The SDW Phase of (TMTSF)2PF6
- - a1, associated to the 2kF SDW order parameter, changes of sign near TSDW, which means that the 2kF SDW susceptibility, a1−1, should diverge. Such a divergence is detected by NMR [46].
- - a2, associated to the 2kF CDW order parameter, should be very small, which means that the system should present incipient 2kF CDW instability. This is the case above ~30K for the 2kF BOW previously discussed in Section 3.1.
5. The Charge Ordering Transition in the Fabre Salts
5.1. Basic Features: The Historical Scenario
5.2. Structural Ingredients of the CO Transition
- - an internal deformation of the TMTTF molecules following their charge occupancy,
- - a deformation of the methyl group cavities associated to the loss of inversion symmetry,
- - a shift of the anions from the inversion centers.
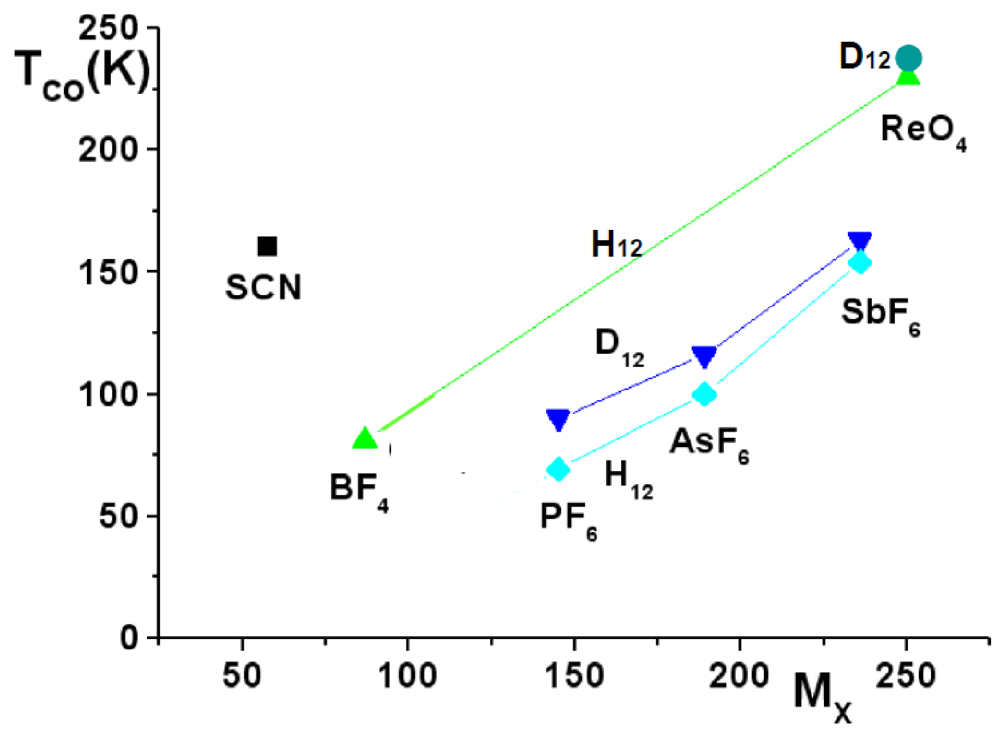
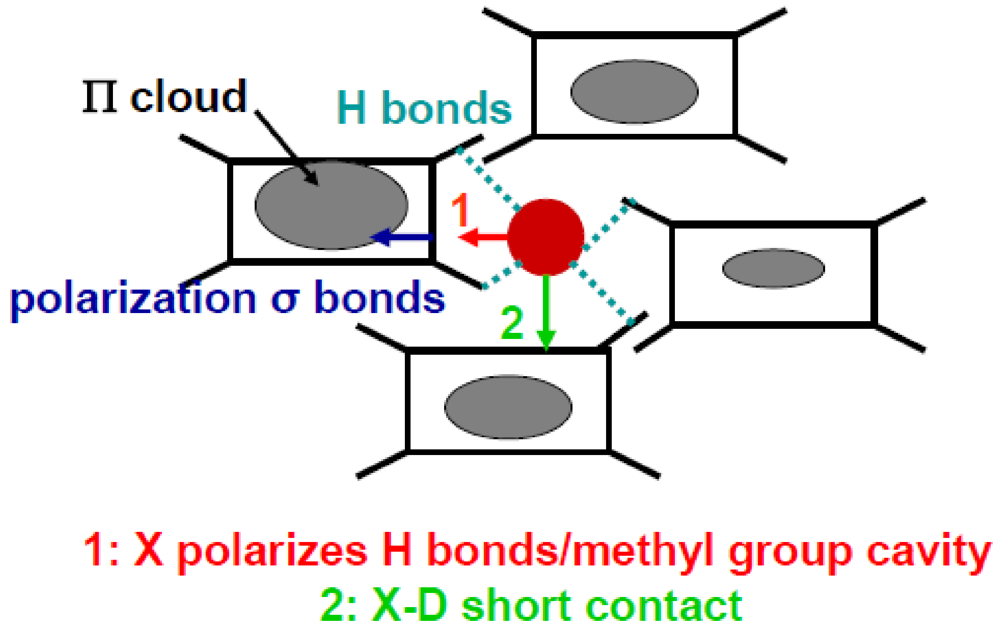
- - TCO increases when, with the larger size (and polarizability) of octahedral and tetrahedral anions, the contact between the anion and the periphery of the cavity delimited by the methyl groups is strengthened,
- - Far infrared measurements show there is a modification of the coupling between the methyl groups and the anions at the CO transition [109].
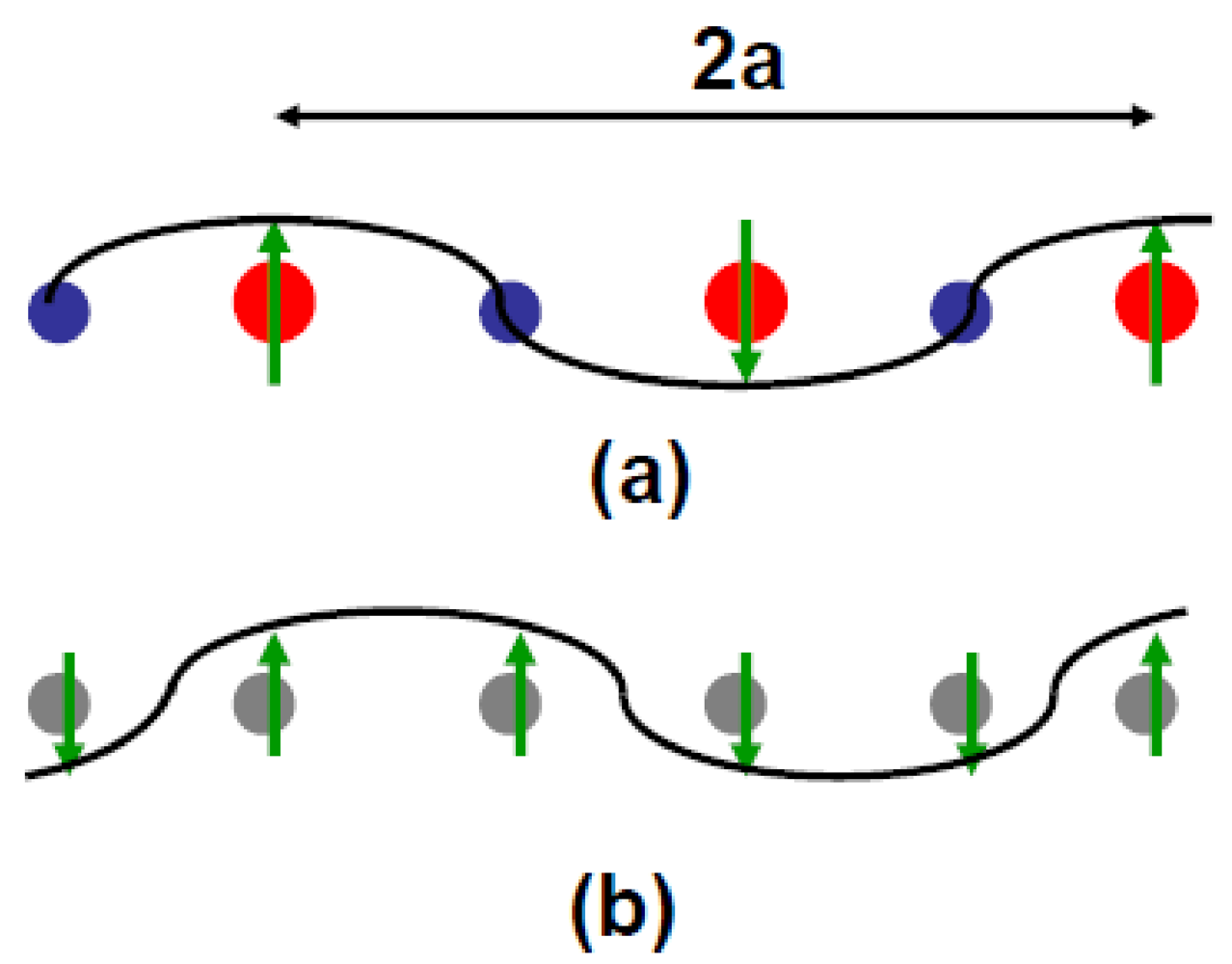
5.3. The Underlying CO Instability
- - charge localization on the bonds, stabilizes a 4kF BOW or Dimer Mott (DM) ground state,
- - charge localization on the sites, stabilizes a 4kF CDW or CO ground state.
6. The Spin-Peierls Transition in the Fabre Salts
6.1. Basic Features
6.2. Competition with the Charge Ordering

- - SP transition does not occur in (TMTTF)2SbF6 and SCN because the spin-phonon coupling is smaller than the zero-point lattice fluctuations (this condition corresponds to TSPMF < Ω/4 ~ 15 K, or TSP < 5 K because in the PF6 and AsF6 salts TSP ~ TSPMF/3). These salts are thus located in the spin-liquid phase outlined in Figure 11phase the inter-chain exchange coupling stabilizes a low temperature (TN ~ 7K) AF ground state.
- - SP transitions of (BCPTTF)2PF6 and AsF6 occur in the adiabatic limit.
- - SP transitions of (TMTTF)2PF6 and AsF6 are located between the adiabatic limit and the spin-liquid phase, close to the crossover line between the adiabatic and anti-adiabatic regimes.
6.3. The Vanishing of the SP Phase under Pressure
7. The Anion Ordering Transitions
7.1. Basic Features
7.2. The (1/2, 1/2, 1/2) AO Transition of Tetrahedral Anions
- - TMTSF salts where the AO transition coincides with a MI transition.
- - TMTTF salts where 4kF charge localization takes place above the AO transition.
- - Salts with dipolar anions which incorporate additional degrees of freedom.
7.2.1. TMTSF Salts
7.2.2. TMTTF Salts
- - a sizeable 2kF CDW with an amplitude of 0.25 electrons estimated from the bond lengths of the two inequivalent TMTTF of the dimer, and which must add to a CO amplitude of 0.17 electrons estimated by NMR between TCO and TAO [154],
- - a sizeable 2kF BOW achieving a quite large dimerization of the stack of dimers with substantially different inter-dimer distances of 3.9 Å and 3.75 Å; the intra-dimer distance being of 3.7 Å.
7.2.3. Salts with Dipolar Tetrahedral Anions
7.3. The (0, 1/2, 0) AO Transition of (TMTSF)2ClO4
7.3.1. Basic Aspects of the AO Superstructure and of Its Electronic Structure
7.3.2. Texture of the AO Phase
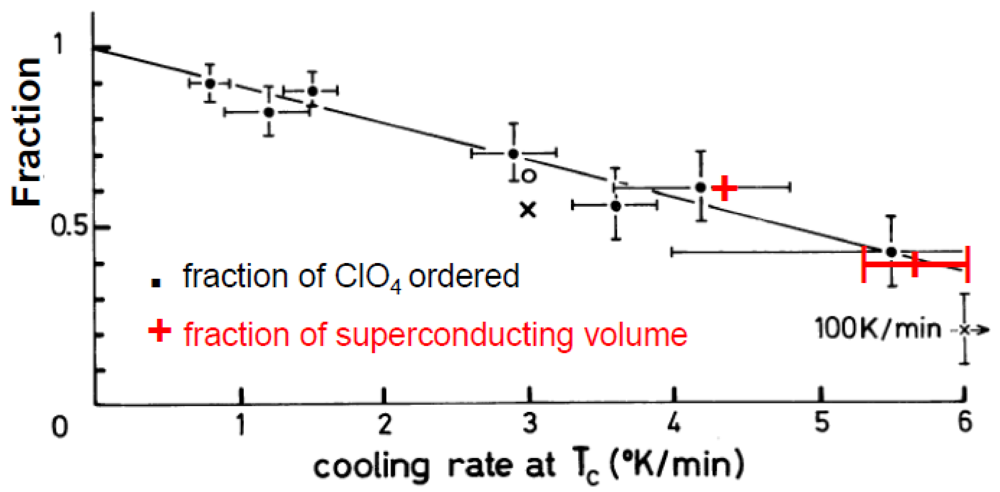

7.4. The AO/CO Transitions of the SCN Salts
7.5. The (1/2, 0, 0) AO Transition of the NO3 Salts
8. Conclusions
Conflict of Interest
Acknowledgments
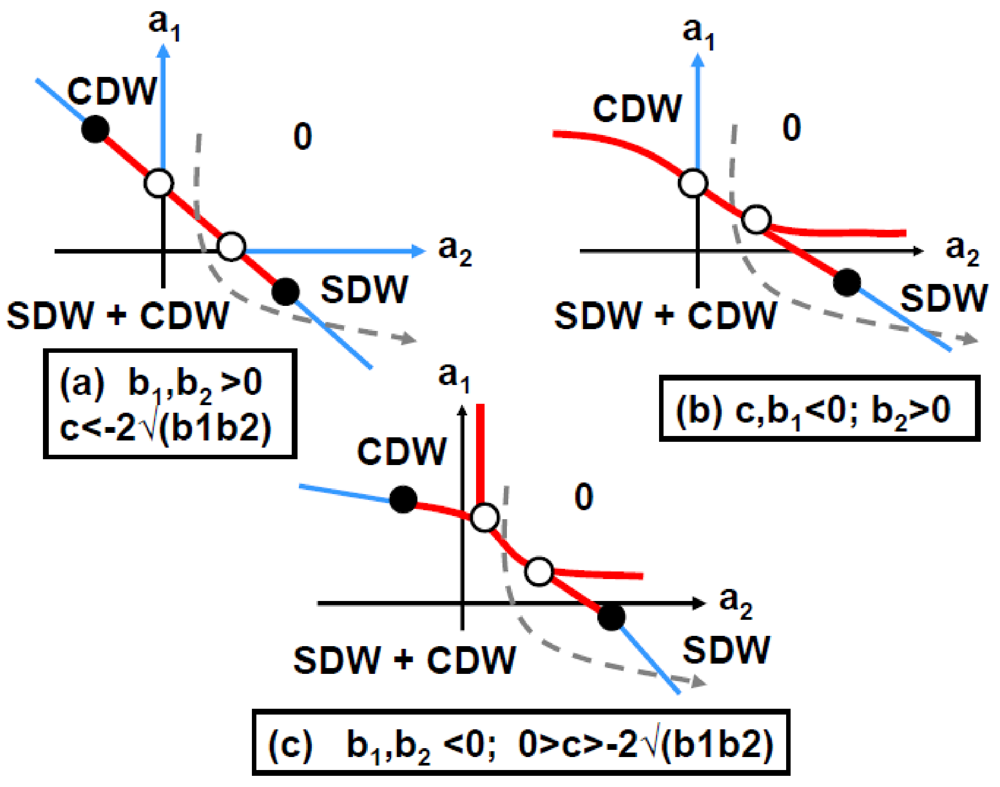
Appendix: Landau Theory with Coupled Order Parameters Applied at the Phase Diagram of the Bechgaard and Fabre Salts
A.1. The AF Phase of (TMTTF)2Br



A.2. The Density Wave Phases of (TMTSF)2PF6

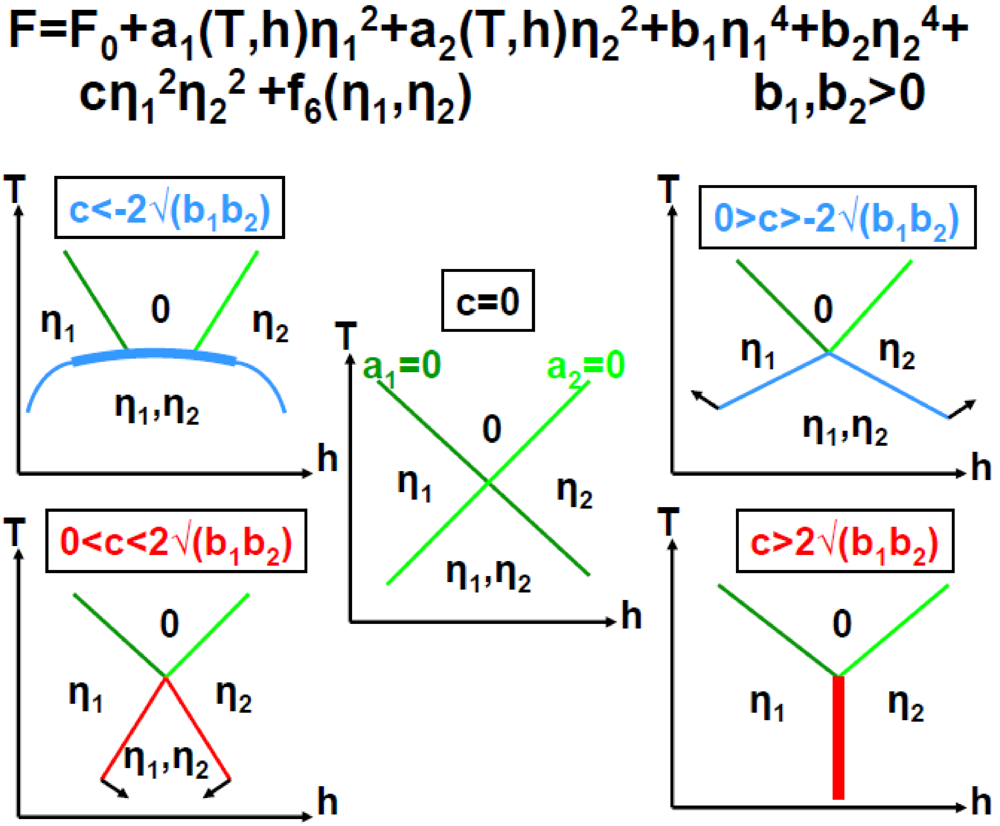
A.3. Competition between CO and SP Transitions


References and Notes
- Jérome, D.; Schulz, H.J. Organic conductors and superconductors. Adv. Phys. 1982, 31, 299–490. [Google Scholar] [CrossRef]
- Ishiguro, T.; Yamaji, K.; Saito, G. Organic Super-Conductors, 2nd ed; Springer-Verlag: Berlin/Heidelberg, Germany, 1998; Volume 88. [Google Scholar]
- Toyota, N.; Lang, M.; Műller, J. Low-Dimensional Molecular Metals; Springer-Verlag: Berlin/Heidelberg, Germany, 2007; Volume 154. [Google Scholar]
- Henriques, R.T.; Alcácer, L.; Pouget, J.P.; Jérome, D. Electrical conductivity and x-ray diffuse scattering study of organic conductors (perylene)2M(mnt)2, (M=Pt, Pd, Au). J. Phys. C: Solid State Phys. 1984, 17, 5197–5208. [Google Scholar] [CrossRef]
- Rovira, C.; Veciana, J.; Ribera, E.; Tarrès, J.; Canadell, E.; Rousseau, R.; Mas, M.; Molins, E.; Almeida, M.; Henriques, R.T.; et al. An organic spin-ladder molecular material. Angew. Chem. Int. Ed. 1997, 36, 2324–2326. [Google Scholar] [CrossRef]
- Canadell, E.; Rachidi, I. E.-I.; Ravy, S.; Pouget, J.-P.; Brossard, L.; Legros, J.P. On the band electronic structure of X[M(dmit)2]2 (X = TTF, (CH3)4N; M = Ni, Pd) molecular conductors and superconductors. J. Phys. France 1989, 50, 2967–2981. [Google Scholar] [CrossRef]
- Pouget, J.-P.; Ravy, S. Structural aspects of the bechgaard salts and related compounds. J. Phys. I France 1996, 6, 1501–1525. [Google Scholar] [CrossRef]
- Pouget, J.-P. Structural features of the Bechgaard salts and related compounds. J. Phys. IV France 2000, 10, Pr3-43–Pr3-56. [Google Scholar] [CrossRef]
- Thorup, N.; Rindorf, G.; Soling, H.; Bechgaard, K. The structure of Di(2,3,6,7-tetramethyl-1,4,5,8-tetraselenafulvalenium) Hexafluorophosphate, (TMTSF)2PF6, the First Superconducting Organic Solid. Acta Cryst. B 1981, 37, 1236–1240. [Google Scholar] [CrossRef]
- Pashkin, A.; Dressel, M.; Ebbinghaus, S.G.; Hanfland, M.; Kuntscher, C.A. Pressure-induced structural phase transition in the Bechgaard-Fabre salts. Synth. Met. 2009, 159, 2097–2100. [Google Scholar] [CrossRef]
- Gallois, B.; Gaultier, J.; Hauw, C.; Lamcharfi, T.; Filhol, A. Neutron Low-Temperature (4 and 20K) and X-ray High-Pressure (6.5 × 102 and 9.8 × 102 MPa) Structures of the Organic Superconductor Di(2,3,6,7-tetramethyl-1,4,5,8-tetraselenafulvalenium) Hexafluorophosphate, (TMTSF)2PF6. Acta Cryst. B 1986, 42, 564–575. [Google Scholar] [CrossRef]
- Emery, V.J.; Bruinsma, R.; Barisic, S. Electron-electron umklapp scattering in organic superconductors. Phys. Rev. Lett. 1982, 48, 1039–1043. [Google Scholar] [CrossRef]
- Ishibashi, S.; Manuel, A.A.; Kohyama, M. Ab initio pseudopotential calculation for (TMTSF)2ClO4. J. Phys. Cond. Matt. 1999, 11, 2279–2283. [Google Scholar] [CrossRef]
- Liautard, B.; Peytavin, S.; Brun, G.; Maurin, M. Corrélations structurales dans la série (TMTTF)2X. J. Phys. (Paris) 1982, 43, 1453–1459. [Google Scholar] [CrossRef]
- Liautard, B.; Peytavin, S.; Brun, G.; Maurin, M. Structural studies and physical properties in the organic conductors series (TMTTF)2X and (TMTSF)2X. J. Phys. (Paris) 1983, 44, C3-951–C3-956. [Google Scholar] [CrossRef]
- Kistenmacher, T.J. Cavity size versus anion size in (TMTSF)2X salts: Possible implications for the uniqueness of (TMTSF)2ClO4. Solid State Commun. 1984, 50, 729–733. [Google Scholar] [CrossRef]
- This assertion is incorrect for TMTSF and TMTSF salts because the anion modifies mainly the c parameter [14,15] while pressure leads to a relative decrease of the parameter a twice larger than for parameters b and c [10,11].
- Kistenmacher, T.J. Anion-donor coupling in (TMTSF)2X salts: Symmetry considerations. Solid State Commun. 1984, 51, 931–934. [Google Scholar] [CrossRef]
- Beno, M.A.; Blackman, G.S.; Leung, P.C.W.; Williams, J.M. Hydrogen bond formation and anion ordering in superconducting (TMTSF)2ClO4 and (TMTSF)2AsF6. Solid State Commun. 1983, 48, 99–103. [Google Scholar] [CrossRef]
- Granier, T.; Gallois, B.; Fritsch, A.; Ducasse, L.; Coulon, C. 135K Crystallographic and Electronic Structure of (TMTTF)2SbF6. In Lower-Dimensional Systems and Molecular Electronics; Metzger, R.M., Day, P., Papavassiliou, G.C., Eds.; Plenum Press: New York, NY, USA, 1990; Volume 248, pp. 163–168. [Google Scholar]
- Pouget, J.-P.; Foury-Leylekian, P.; Alemany, P.; Canadell, E. Charge ordering in low dimensional organic conductors: structural aspects. Phys. Status Solidi B 2012, 249, 937–942. [Google Scholar] [CrossRef]
- Jacobsen, C.S.; Tanner, D.B.; Bechgaard, K. Optical and infrared properties of tetramethyltetraselenafulvalene [(TMTSF)2X] and tetramethyltetrathiafulvalene [(TMTTF)2X] compounds. Phys. Rev. B 1983, 28, 7019–7032. [Google Scholar] [CrossRef]
- de Souza, M.; Hofmann, D.; Foury-Leylekian, P.; Moradpour, A.; Pouget, J.-P.; Lang, M. Exploring the charge-ordering transition in (TMTTF)2X via thermal expansion measurements. Phys. B 2010, 405, S92–S94. [Google Scholar] [CrossRef]
- de Souza, M.; Foury-Leylekian, P.; Moradpour, A.; Pouget, J.-P.; Lang, M. Evidence for lattice effects at the charge-ordering transition in (TMTTF)2X. Phys. Rev. Lett. 2008, 101, 216403. [Google Scholar] [CrossRef] [PubMed]
- Lang, M.; Műller, J.; Steglich, F.; Brűhl, A.; Wolf, B.; Dressel, M. Anomalous thermal expansion behaviour in (TMTTF)2PF6 and (TMTSF)2PF6 around 100K: evidence for a strong spin-phonon interaction? J. Phys. IV France 2004, 114, 111–112. [Google Scholar] [CrossRef]
- Bechgaard, K.; Jacobsen, C.S.; Mortensen, K.; Pedersen, H.J.; Thorup, N. The properties of five highly conducting salts: (TMTSF)2X, X=PF6−, AsF6−, SbF6−, BF4− and NO3− derived from tetramethyltetraselenafulvalene (TMTSF). Solid State Commun. 1980, 33, 1119–1125. [Google Scholar] [CrossRef]
- Yu, W.; Zhang, F.; Zamborszky, F.; Alavi, B.; Baur, A.; Merlic, C.A.; Brown, S.E. Electron-lattice coupling and broken symmetries of the molecular salt (TMTTF)2SbF6. Phys. Rev. B 2004, 70, 121101 (R). [Google Scholar]
- Furukawa, K.; Hara, T.; Nakamura, T. Deuteration effect and possible origin of the charge-ordering transition of (TMTTF)2X. J. Phys. Soc. Jpn. 2005, 74, 3288–3294. [Google Scholar] [CrossRef]
- Williams, J.M.; Beno, M.A.; Sullivan, J.C.; Banovetz, L.M.; Braam, J.M.; Blackman, G.S.; Carlson, C.D.; Greer, D.L.; Loesing, D.M.; Carneiro, K. The design of organic metals based on TMTSF and TMTTF: novel structural implications and predictions. J. Phys. (Paris) 1983, 44, C3-941–C3-949. [Google Scholar] [CrossRef]
- Scott, J.C.; Pedersen, H.J.; Bechgaard, K. Proton NMR in the organic conductor tetramethyltetraselenafulvalenium hexafluorophosphate. Phys. Rev. B 1981, 24, 475–477. [Google Scholar] [CrossRef]
- McBrierty, V.J.; Douglass, D.C.; Wudl, F.; Aharon-Shalom, E. Nuclear resonance and relaxation in ditetramethyltetraselenafulvalenium salts. Phys. Rev. B 1982, 26, 4805–4809. [Google Scholar] [CrossRef]
- Scott, J.C.; Engler, E.M.; Clark, W.G.; Murayama, C.; Bechgaard, K.; Pedersen, H.J. NMR studies of (TMTSF)2PF6. Mol. Cryst. Liq. Cryst. 1982, 79, 61–65. [Google Scholar]
- Stein, P.C.; Moradpour, A.; Jérome, D. Nuclear relaxation in tetramethyltetraselenafulvalene salts (TMTSF)2X, (X=PF6, ClO4). J. Phys. Lett. (Paris) 1985, 46, L241–L247. [Google Scholar] [CrossRef]
- Foury-Leylekian, P.; Petit, S.; André, G.; de Souza, M.; Lang, M.; Ressouche, E.; Moradpour, A.; Pouget, J.-P*. Low temperature structural ordering in the (TMTSF)2PF6 and AsF6 Bechgaard salts. In preparation, 2012.*; Laboratoire de Physique des Solides, Université Paris-sud: 91405 Orsay, France.
- Aoyagi, B.; Kato, K.; Ota, A.; Yamochi, A.; Saito, G.; Suematsu, H.; Sakata, M.; Takata, M. Direct Observation of Bonding and Charge Ordering in (EDO-TTF)2PF6. Angew. Chem. Int. Ed. 2004, 43, 3670–3676. [Google Scholar] [CrossRef]
- Pouget, J.-P. Structural Instabilities. In Highly Conducting Quasi One Dimensional Organic Crystals; Conwell, E.M., Ed.; Academic Press: New York, NY, USA, 1988; Semiconductors and Semimetals; Volume 27, pp. 87–215. [Google Scholar]
- Shirane, G.; Shapiro, S.M.; Comès, R.; Garito, A.F.; Heeger, A.J. Phonon dispersion and Kohn anomaly in tetrathiafulvalene-tetracyanoquinodimethane (TTF-TCNQ). Phys. Rev. B 1976, 14, 2325–2334. [Google Scholar] [CrossRef]
- Pouget, J.P. Structural Instabilities of One-Dimensional Conductors. In Low-Dimensional Conductors and Superconductors; Jérome, D., Caron, L.G., Eds.; Plenum Press: New York, NY, USA, 1987; Volume 155, pp. 17–45. [Google Scholar]
- Ribault, M.; Pouget, J.-P.; Jérome, D.; Bechgaard, K. Superconductivity and Absence of a Kohn Anomaly in the Quasi One Dimensional Organic Conductor: (TMTSF)2AsF6. J. Phys. Lett. (Paris) 1980, 41, L607–L610. [Google Scholar] [CrossRef]
- Pouget, J.-P.; Moret, R.; Comès, R.; Bechgaard, K.; Fabre, J.M.; Giral, L. X-Ray Diffuse Scattering Study of Some (TMTSF)2X and (TMTTF)2X Salts. Mol. Cryst. Liq. Cryst. 1982, 79, 129–143. [Google Scholar]
- Slater, J.C. Magnetic Effect and the Hartree-Fock Equation. Phys. Rev. 1951, 82, 538–541. [Google Scholar] [CrossRef]
- Pouget, J.-P. X-ray diffuse scattering as precursor of incommensurate Peierls transitions in one-dimensional organic charge transfer conductors. Z. Kristallogr. 2004, 219, 711–718. [Google Scholar] [CrossRef]
- Cao, N.; Timusk, T.; Bechgaard, K. Unconventional Electrodynamic Response of the Quasi-One-Dimensional Organic Conductor (TMTSF)2ClO4. J. Phys. I France 1996, 6, 1719–1726. [Google Scholar] [CrossRef]
- Dressel, M.; Schwartz, A.; Grüner, G.; Degiorgi, L. Deviations from Drude Response in Low-Dimensional Metals: Electrodynamics of the Metallic State of (TMTSF)2PF6. Phys. Rev. Lett. 1996, 77, 398–401. [Google Scholar] [CrossRef] [PubMed]
- Schwartz, A.; Dressel, M.; Grüner, G.; Vescoli, V.; Degiorgi, L.; Giamarchi, T. On-chain electrodynamics of metallic (TMTSF)2X salts: observation of Tomonaga-Luttinger liquid response. Phys. Rev. B 1998, 58, 1261–1271. [Google Scholar] [CrossRef]
- Wzietek, P.; Creuzet, F.; Bourbonnais, C.; Jérome, D.; Bechgaard, K.; Batail, P. Nuclear-relaxation and electronic correlations in quasi-one-dimensional organic conductors. 2. Experiments. J. Phys. I France 1993, 3, 171–201. [Google Scholar] [CrossRef]
- Chaikin, P.M.; Tiedje, T.; Bloch, A.N. Sound velocity measurements in (TMTSF)2PF6. Solid State Commun. 1982, 41, 739–742. [Google Scholar] [CrossRef]
- Shi, X.D.; Chiang, L.; Upasani, R.; Chaikin, P.M. Sound velocity studies of Bechgaard salts (TMTSF)2PF6 and(TMTSF)2ClO4. In Advanced Organic Solid State Materials; Chiang, L.Y., Chaikin, P.M., Cowan, D.O., Eds.; Materials Research Society: Pittsburgh, PA, USA, 1990; pp. 239–244. [Google Scholar]
- Fertey, P.; Poirier, M.; Batail, P. Microwave transport approach to the coherence of interchain hopping in (TMTSF)2PF6. Eur. Phys. J. B 1999, 10, 305–309. [Google Scholar] [CrossRef]
- Fertey, P.; Poirier, M.; Batail, P. H-T behaviors of the transverse microwave conductivity of (TMTSF)2X crystals. Synth. Met. 1999, 103, 2076–2077. [Google Scholar] [CrossRef]
- Bourbonnais, C. Organic Superconductors: Reduced Dimensionality and Correlation Effects. Synth. Met. 1997, 84, 19–24. [Google Scholar] [CrossRef]
- Bourbonnais, C.; Jérome, D. Electronic confinement in organic metals. Science 1998, 281, 1155–1156. [Google Scholar] [CrossRef]
- Giamarchi, T. Theoretical Framework for Quasi-One Dimensional Systems. Chem. Rev. 2004, 104, 5037–5055. [Google Scholar] [CrossRef]
- Delrieu, J.M.; Roger, M.; Toffano, Z.; Moradpour, A.; Bechgaard, K. NMR proton lineshape in (TMTSF)2X- incommensurability of nesting wave vector and order parameter. J. Phys. (Paris) 1986, 47, 839–861. [Google Scholar] [CrossRef]
- Takahashi, T.; Maniva, Y.; Kawamura, H.; Saito, G. Determination of SDW characteristics in (TMTSF)2PF6 by 1H NMR analysis. J. Phys. Soc. Jpn. 1986, 55, 1364–1373. [Google Scholar] [CrossRef]
- Ducasse, L.; Abderrabba, M.; Gallois, B. Temperature dependence of the Fermi surface topography in the (TMTSF)2X and (TMTTF)2X families. J. Phys. C: Solid State Phys. 1985, 18, L947–L951. [Google Scholar] [CrossRef]
- Vaca, P.; Coulon, C. Magnetic phase-transition in Bechgaard salts and related-compounds - electronic localization and competing interchain couplings. Phase Transitions 1991, 30, 49–62. [Google Scholar] [CrossRef]
- Moret, R.; Pouget, J.P.; Comès, R.; Bechgaard, K. X-ray Scattering evidence for anion ordering and structural distortions in the low-temperature phase of Di (Tetramethyltetraselenafulvalenium) perrhenate [(TMTSF)2ReO4]. Phys. Rev. Lett. 1982, 49, 1008–1012. [Google Scholar] [CrossRef]
- Rindorf, G.; Soling, H.; Thorup, N. Di(4,4',5,5'-tetramethyl-2,2'-bi-&,3-diselenolyliden)ium Perrhenate, C20H24Se+8.ReO4, (TMTSF)2ReO4. Detailed superstructure at 120 K. Acta Cryst. C 1984, 40, 1137–1139. [Google Scholar] [CrossRef]
- By the same argument one obtains a 3D 4kF CDW or CO if the alternation of charge rich and charge poor molecules along a given stack is fixed by uniform shifts of anions separated by a and di = a ± b – c (± corresponding to the two coupling process considered in the text and in Figure 9). qa = qdi = 0 (mod. 2π) leads to qa=0 and qa ± qb + qc = 0 (mod. 1). These relationships leads to ±qb + qc =0 (mod.1) which has two solutions: qb=qc=0 and qb = qc = 1/2. They corresponds respectively to the ferroelectric qF = (0, 0, 0) and antiferroelectric qAF = (0, 1/2, 1/2) CO patterns.
- Pouget, J.-P.; Shirane, G.; Bechgaard, K.; Fabre, J.M. X-ray evidence of a structural phase transition in di-tetramethyltetraselenafulvalenium perchlorate [(TMTSF)2ClO4], pristine and slightly doped. Phys. Rev. B 1983, 27, 5203–5206. [Google Scholar] [CrossRef]
- Pouget, J.-P.; Moret, R.; Comès, R.; Shirane, G.; Bechgaard, K.; Fabre, J.M. X-ray evidence of competing orderings in (TMTSF)2ClO4 and related alloys. J. Phys. (Paris) 1983, 44, C3-969–C3-975. [Google Scholar] [CrossRef]
- Liu, Q.; Ravy, S.; Pouget, J.P.; Johannsen, I. X-ray investigation of the tetramethyldithiadiselenafulvalene (TMDTDSF)2X series of organic conductors. II. Influence of the orientational disorder on the structural instabilities. J. Phys. I France 1993, 3, 821–837. [Google Scholar] [CrossRef]
- Liu, Q.; Ravy, S.; Pouget, J.P.; Johannsen, I.; Bechgaard, K. X-ray investigation of the tetramethyldithiadiselenafulvalene (TMDTDSF)2X series of organic conductors. I. Study of the orientational disorder of the TMDTDST molecule. J. Phys. I France 1993, 3, 803–819. [Google Scholar] [CrossRef]
- Pouget, J.-P.; Ravy, S. X-Ray evidence of charge density wave modulations in the magnetic phases of (TMTSF)2PF6 and (TMTTF)2Br. Synth. Met. 1997, 85, 1523–1528. [Google Scholar] [CrossRef]
- Coulon, C.; Delhaes, P.; Flandrois, S.; Lagnier, R.; Bonjour, E.; Fabre, J.M. A new survey of the physical properties of the (TMTTF)2X series. Role of the counterion ordering. J. Phys. (Paris) 1982, 43, 1059–1067. [Google Scholar] [CrossRef]
- Coulon, C.; Delhaes, P.; Amiell, J.; Manceau, J.P.; Fabre, J.M.; Giral, L. Effet of doping (TMTSF)2ClO4 with TMTTF I. Ambient pressure result: A competition between the different possible ground states. J. Phys. (Paris) 1982, 43, 1721–1729. [Google Scholar] [CrossRef]
- Foury-Leylekian, P.; Le Bolloc’h, D.; Hennion, B.; Ravy, S.; Moradpour, A.; Pouget, J.-P. Neutron-scattering evidence for a spin-Peierls ground state in (TMTTF)2PF6. Phys. Rev. B 2004, 70, 180405 (R). [Google Scholar]
- Dumoulin, L.; Bourbonnais, C. Theory of lattice and electronic fluctuations in weakly localized spin-peierls systems. J. Phys. I France 1996, 6, 1727–1744. [Google Scholar] [CrossRef]
- Liu, Q.; Ravy, S.; Pouget, J.-P.; Coulon, C.; Bourbonnais, C. Structural fluctuations and spin-Peierls transitions revisited. Synth. Met. 1993, 56, 1840–1845. [Google Scholar] [CrossRef]
- Dumm, M.; Loidl, A.; Alavi, B.; Starkey, K.P.; Montgomery, L.K.; Dressel, M. Comprehensive ESR studies of the antiferromagnetic ground states in the one dimensional spin systems (TMTSF)2PF6, (TMTSF)2AsF6 and (TMTTF)2Br. Phys. Rev. B 2000, 62, 6512–6520, and references there in.. [Google Scholar] [CrossRef]
- Pouget, J.-P. Microscopic interactions in CuGeO3 and organic Spin-Peierls systems deduced from their pretransitional fluctuations. Eur. Phys. J. B 2001, 20, 321–333, (Erratum Eur. Phys. J. B 2001, 24, 415).. [Google Scholar] [CrossRef]
- Pouget, J.-P. Bond and charge ordering in low-dimensional organic conductors. Phys. B 2012, 407, 1762–1770. [Google Scholar] [CrossRef]
- Creuzet, F.; Bourbonnais, C.; Caron, L.G.; Jérome, D.; Bechgaard, K. A 13C NMR study of the interplay between the spin-Peierls and antiferromagnetic ground states in (TMTTF)2PF6 under pressure. Synth. Met. 1987, 19, 289–294. [Google Scholar] [CrossRef]
- Nakamura, T.; Nobutoki, T.; Kobayashi, Y.; Takahashi, T.; Saito, G. 1H-NMR investigation of the SDW wave-number in (TMTTF)2Br. Synth. Met. 1995, 70, 1293–1294. [Google Scholar] [CrossRef]
- Seo, H.; Merino, J.; Yoshioka, H.; Ogata, M. Theoretical aspects of charge ordering in molecular conductors. J. Phys. Soc. Jpn. 2006, 75, 051009. [Google Scholar] [CrossRef]
- Zorina, L.; Simonov, S.; Mézière, C.; Canadell, E.; Suh, S.; Brown, S.E.; Foury-Leylekian, P.; Fertey, P.; Pouget, J.P.; Batail, P. Charge ordering, symmetry and electronic structures issues and Wigner crystal structure of the quarter-filled band Mott insulators and high pressure metalsδ-(EDT-TTF-CONMe2)2X, X=Br and AsF6. J. Mat. Chem. 2009, 19, 6980–6994. [Google Scholar] [CrossRef] [Green Version]
- Tomic, S.; Biskup, N.; Babic, S.D.; Maki, K. Commensurate spin-density–wave state in (TMTTF)2Br- single particle and collective charge dynamics. Europhys. Lett. 1994, 26, 295–301. [Google Scholar] [CrossRef]
- Ashikawa, A.; Matsunaga, N.; Nomura, K.; Nakamura, T.; Takahashi, T.; Saito, G. Pressure and Magnetic Field Dependence of SDW transition in (TMTTF)2Br. Phys. Stat. Sol. B 2001, 223, 539–543. [Google Scholar] [CrossRef]
- Fujiyama, S.; Nakamura, T. NMR studies of the localized states of (TMTTF)2Br. J. Phys. Chem. Solids 2002, 63, 1259–1261. [Google Scholar] [CrossRef]
- Javadi, H.H.S.; Laversanne, R.; Epstein, A.J. Microwave conductivity and dielectric constant of tetramethyltetrathiafulvalene salts [(TMTTF)2X, X=SCN, ReO4, SbF6. Phys. Rev. B 1988, 37, 4280–4283. [Google Scholar] [CrossRef]
- Nad, F.; Monceau, P.; Fabre, J.M. Low frequency dielectric permittivity of quasi-one-dimensional conductor (TMTTF)2Br. Eur. Phys. J. B 1998, 3, 301–306. [Google Scholar] [CrossRef]
- Clark, W.G.; Hanson, M.E.; Wong, W.H.; Alavi, B. Evidence that the SDW transition in (TMTSF)2PF6 is first order. Phys. B 1994, 194–196, 285–286. [Google Scholar]
- Kagoshima, S.; Saso, Y.; Maesato, M.; Kondo, R.; Hasegawa, T. Low temperature diffuse X-ray studies of charge-density waves coexisting with spin-density waves in the organic conductors (TMTSF)2PF6 and (TMTSF)2AsF6. Solid State Commun. 1999, 110, 479–483. [Google Scholar] [CrossRef]
- Gufan; Yu, M.; Larin, E.S. Theory of phase transitions described by two order parameters. Sov. Phys. Solid State 1980, 22, 270–275. [Google Scholar]
- Takahashi, T.; Maniwa, Y.; Kawamura, H.; Saito, G. Determination of SDW characteristics in (TMTSF)2PF6 by 1H-NMR analysis. Phys. B 1986, 143, 417–421. [Google Scholar]
- Takahashi, T.; Maniwa, Y.; Kawamura, H.; Murata, K.; Saito, G. NMR analysis of electronic properties in organic superconductors (TMTSF)2PF6 and β-(BEDT-TTF)2I3. Synth. Met. 1987, 19, 225–230. [Google Scholar] [CrossRef]
- Nickel, J.C.; Duprat, R.; Bourbonnais, C.; Dupuis, N. Triplet Superconductivity Pairing and Density Wave Instabilities in Organic Conductors. Phys. Rev. Lett. 2005, 95, 247001. [Google Scholar] [CrossRef] [PubMed]
- Nickel, J.C.; Duprat, R.; Bourbonnais, C.; Dupuis, N. Superconductivity pairing and density wave instabilities in quasi-one-dimensional conductors. Phys. Rev. B 2006, 73, 165126. [Google Scholar] [CrossRef]
- Kuroki, K. Pairing symmetry considerations in organic superconductors. J. Phys. Soc. Jpn. 2006, 75, 051013. [Google Scholar] [CrossRef]
- Ng, H.K.; Timusk, T.; Bechgaard, K. Far infra-red studies of bis (tetramethyltetraselenafulvalene) hexafluoroantimonate [(TMTSF)2SbF6]: Coexistence of metallic and semiconducting states. Phys. Rev. B 1984, 30, 5842–5846. [Google Scholar] [CrossRef]
- Grüner, G. The dynamics of spin-density waves. Rev. Mod. Phys. 1994, 66, 1–24. [Google Scholar] [CrossRef]
- Laversanne, R.; Coulon, C.; Gallois, B.; Pouget, J.P.; Moret, R. Structural and electrical properties of (TMTTF)2MF6 salts (M=P, As, Sb). Role of the anions. J. Phys. Lett.(Paris) 1984, 45, L393–L399. [Google Scholar] [CrossRef]
- Coulon, C.; Maaroufi, A.; Amiell, J.; Dupart, E.; Flandrois, S.; Delhaes, P.; Moret, R.; Pouget, J.P.; Morand, J.P. Antiferromagnetic and structural instabilities in tetramethyltetrathiafulvalene thiocyanate [(TMTTF)2SCN]. Phys. Rev. B 1982, 26, 6322–6325. [Google Scholar] [CrossRef]
- Coulon, C.; Parkin, S.S.P.; Laversanne, R. Structureless transition and strong localization effects in bis-tetramethyltetrathiafulvalenium salts [(TMTTF)2X]. Phys. Rev. B 1985, 31, 3583–3587. [Google Scholar] [CrossRef]
- Brown, S.E.; Javadi, H.H.S.; Laversanne, R. Sound Velocity Measurements in (TMTTF)2X Salts, X= ReO4, AsF6, SbF6. In Advanced Organic Solid State Materials; Chiang, L.Y., Chaikin, P.M., Cowan, D.O., Eds.; Materials Research Society: Pittsburgh, PA, USA, 1990; pp. 245–250. [Google Scholar]
- Chow, D.S.; Zamborsky, F.; Alavi, B.; Tantillo, D.J.; Baur, A.; Merlic, C.A.; Brown, S.E. Charge ordering in the TMTTF family of molecular conductors. Phys. Rev. Lett. 2000, 85, 1698–1701. [Google Scholar] [CrossRef] [PubMed]
- Dumm, M.; Salameh, B.; Abaker, M.; Montgomery, L.K.; Dressel, M. Magnetic and optical studies of spin and charge ordering in (TMTTF)2AsF6. J. Phys. IV (France) 2004, 114, 57–60. [Google Scholar] [CrossRef]
- Dumm, M.; Abaker, M.; Dressel, M.; Montgomery, L.K. Charge order in (TMTTF)2PF6 investigated by infrared spectroscopy. J. Low. Temp. Phys. 2006, 142, 609–612. [Google Scholar] [CrossRef]
- Monceau, P.; Nad, F.; Brazovski, S. Ferroelectric Mott-Hubbard phase of organic (TMTTF)2X conductors. Phys. Rev. Lett. 2001, 86, 4080–4083. [Google Scholar] [CrossRef] [PubMed]
- Foury-Leylekian, P.; Ravy, S.; Pouget, J.-P. Stuctural properties of strongly correlated quasi-1D organic systems. Phys. B 2002, 312–313, 574–577. [Google Scholar] [CrossRef]
- Ravy, S.; Foury-Leylekian, P.; Le Bolloc’h, D.; Pouget, J.-P.; Fabre, J.M.; Prado, R.J.; Lagarde, P. Structural instability and electronic localization in the 2/1 salts: The case of the Fabre and the (DMtTTF)2ClO4 salts. J. Phys. (Paris) IV 2004, 114, 81–85. [Google Scholar]
- Nogami, Y.; Nakamura, T. X-ray observation of 2kF and 4kF charge orderings in (TMTTF)2ReO4 and (TMTTF)2SCN associated with anion orderings. J. Phys. (Paris) IV 2002, 12, Pr9-145–Pr9-148. [Google Scholar]
- Coulon, C.; Lalet, G.; Pouget, J.-P.; Foury-Leylekian, P.; Moradpour, A.; Fabre, J.M. Anisotropic conductivity and charge ordering in (TMTTF)2X salts probed by ESR. Phys. Rev. B 2007, 76, 085126. [Google Scholar] [CrossRef]
- Foury-Leylekian, P.; Petit, S.; Andre, G.; Moradpour, A.; Pouget, J.P. Neutron scattering evidence for a lattice displacement at the charge ordering transition of (TMTTF)2PF6. Phys. B 2010, 405, S95–S97. [Google Scholar] [CrossRef]
- Granier, T.; Gallois, B.; Ducasse, L.; Fritsch, A.; Filhol, A. 4K crystallographic and electronic structures of (TMTTF)2X salts (X−: PF6−; AsF6−). Synth. Met. 1988, 24, 343–356. [Google Scholar] [CrossRef]
- Sawa, H. Direct Observation of Electronic State of (TMTTF)2PF6 Using Synchrotron Radiation X-ray Analysis. In Proceedings of International Research School and Workshop on Electronic Crystals; ECRYS, Cargèse, France, 15–27 August 2011.
- In this respect the analysis performed in [105] and which considers only the shift of the anion sublattice is incomplete. As the neutron scattering length is similar for all the nucleus of (TMTTF)2PF6, the 3 contributions given in the text have to be treated on equal footing in the structural refinement. Note that in deuterated samples the neutron scattering could be particularly sensitive to the deformation of the methyl group cavity at TCO
- Dressel, M.; Dumm, M.; Knoblauch, T.; Masimo, M. Comprehensive optical investigation of Charge Order in Organic chain compounds (TMTTF)2X. Crystals 2012, in press.. [Google Scholar]
- Rose, E.; Dressel, M. Coupling between molecular chains and anions in (TMTTF)2X salts. Phys. B 2012, 407, 1787–1892. [Google Scholar] [CrossRef]
- Riera, J.; Poilblanc, D. Influence of the anion potential on the charge ordering in quasi-one-dimensional charge-transfer salts. Phys. Rev. B 2001, 63, 241102(R). [Google Scholar]
- Pouget, J.-P.; Foury-Leylekian, P.; Le Bolloc’h, D.; Hennion, B.; Ravy, S.; Coulon, C.; Cardoso, V.; Moradpour, A. Neutron-Scattering Evidence for a Spin-Peierls ground State in (TMTTF)2PF6. J. Low. Temp. Phys. 2006, 142, 147–152. [Google Scholar] [CrossRef]
- Kőhler, B.; Rose, E.; Dumm, M.; Untereiner, G.; Dressel, M. Comprehensive transport study of anisotropy and ordering phenomena in quasi-one-dimensional (TMTTF)2X salts (X=PF6, AsF6, SbF6, BF4, ClO4, ReO4. Phys. Rev. B 2011, 84, 035124. [Google Scholar] [CrossRef]
- Nad, F.; Monceau, P.; Nakamura, T.; Furukawa, K. The effect of deuteration on the transition into a charge ordered state of (TMTTF)2X salts. J. Phys.: Condens. Matter 2005, 35, L399–L406. [Google Scholar]
- Moret, R.; Pouget, J.P.; Comès, R.; Bechgaard, K. X-ray study of the anion ordering transition in di(tetramethyltetraselenafulvalen)-ium perchlorate (TMTSF)2ClO4: quenching and irradiation effects. J. Phys. (Paris) 1985, 46, 1521–1732. [Google Scholar] [CrossRef]
- Zamborszky, F.; Yu, W.; Raas, W.; Brown, S.E.; Alavi, B.; Merlic, C.A.; Baur, A. Competition and coexistence of bond and charge orders in (TMTTF)2AsF6. Phys. Rev. B 2002, 66, 081103(R). [Google Scholar]
- Nad, F.; Monceau, P. Dielectric Response of the Charge Ordered State in Quasi-One Dimensional Organic Conductors. J. Phys. Soc. Jpn. 2006, 75, 051005. [Google Scholar] [CrossRef]
- Coulon, C.; Foury-Leylekian, P.; Fabre, J.M.; Pouget, J.-P. Electronic instabilities and irradiation effects in the (TMTTF)2X series. Centre de Recherche Paul Pascal, Université Bordeaux I, France, 2012; Unpublished work. [Google Scholar]
- Brazovskii, S. Ferroelectricity and Charge Ordering in Quasi-1D Organics Conductors. In The Physics of Organic Superconductors and Conductors; Lebed, A., Ed.; Springer-Verlag: Berlin, Germany, 2008; pp. 313–355. [Google Scholar]
- Kirova, N.; Brazovskii, S. Ferroelectricity: From organic conductors to electronic polymers. Phys. B 2009, 404, 382–384. [Google Scholar] [CrossRef]
- Yamamoto, K.; Iwai, S.; Boyko, S.; Kashiwazaki, A.; Hiramatsu, F.; Okabe, C.; Nishi, N.; Yakushi, K. Strong optical nonlinearity and its ultrafast response associated with electron ferroelectricity in an organic conductor. J. Phys. Soc. Jpn. 2008, 77, 074709. [Google Scholar] [CrossRef]
- Alemany, P.; Pouget, J.-P.; Canadell, E. Essential role of anions in the charge ordering transition of α-(BEDT-TTF)2I3. Phys. Rev. B 2012, 85, 195118. [Google Scholar] [CrossRef]
- Pouget, J.-P.; Khanna, S.K.; Denoyer, F.; Comès, R.; Garito, A.F.; Heeger, A.J. X-ray Observation of 2kF and 4kF Scatterings in Tetrathiafulvalene-Tetracyanoquinodimethane (TTF-TCNQ). Phys. Rev. Lett. 1976, 37, 437–440. [Google Scholar] [CrossRef]
- Nogami, Y.; Moret, R.; Pouget, J.-P.; Yamamoto, Y.; Oshima, K.; Hiraki, K.; Kanoda, K. X-ray structural study of 4kF Superlattice in (DMDCNQI)2Ag. Synth. Met. 1999, 102, 1778. [Google Scholar] [CrossRef]
- Foury-Leylekian, P.; Auban-Senzier, P.; Coulon, C.; Jeannin, O.; Fourmigué, M.; Pasquier, C.; Pouget, J.-P. Phase diagram of the correlated quarter-filled-band organic salt series (o-DMTTF)2X (X=Cl, Br, I) . Phys. Rev. B 1994, 50, 7131–7139. [Google Scholar]
- Zamborszky, F.; Yu, W.; Raas, W.; Brown, S.E.; Alavi, B.; Merlic, C.A.; Baur, A.; Lefebvre, S.; Wzieteck, P. Influence of charge order on the ground state of TMTTF conductors. J. Phys. (Paris) IV 2002, 12, Pr9-139–Pr9-144. [Google Scholar]
- In contrast 75As NMR T1−1 does not exhibit a divergence at TCO but only a change of slope. This result could be understood if AsF6 plays a weaker role in the CO transition (through process 1) than in the SP transition (through process 2).
- de Souza, M.; Brűhl, A.; Műller, J.; Foury-Leylekian, P.; Moradpour, A.; Pouget, J.-P.; Lang, M. Thermodynamic studies at the charge ordering and spin-Peierls transitions in (TMTTF)2X. Phys. B 2009, 404, 494–498. [Google Scholar] [CrossRef]
- Dumm, M.; Loidl, A.; Fravel, B.W.; Starkey, K.P.; Montgomery, L.K.; Dressel, M. Electron spin resonance studies on the organic linear chain compounds (TMTTF)2X (C= S, Se; X= PF6, AsF6, ClO4, Br). Phys. Rev. B 2001, 61, 511–521. [Google Scholar]
- Salameh, B.; Yasin, S.; Dumm, M.; Untereiner, G.; Montgomery, L.; Dressel, M. Spin dynamics of the organic linear chain compounds (TMTTF)2X (X = SbF6, AsF6, BF4, ReO4, and SCN). Phys. Rev. B 2011, 83, 205126. [Google Scholar] [CrossRef]
- Foury-Leylekian, P.; Petit, S.; Coulon, C.; Hennion, B.; Moradpour, A.; Pouget, J.-P. Inelastic neutron scattering investigation of the magnetic excitations in the spin-Peierls ground state of (TMTTF)2PF6. Phys. B 2009, 404, 537–540. [Google Scholar] [CrossRef]
- Langlois, A.; Poirier, M.; Bourbonnais, C.; Foury-Leylekian, P.; Moradpour, A.; Pouget, J.-P. Microwave dielectric study of spin-Peierls and charge ordering transitions in (TMTTF)2PF6 salts. Phys. Rev. B 2010, 81, 125101. [Google Scholar] [CrossRef]
- Brown, S.E.; Clark, W.G.; Zamborszky, F.; Klemme, B.J.; Kriza, G.; Alavi, B.; Merlic, C.; Kuhns, P.; Moulton, W. 13C NMR measurements of the high-magnetic-field, low-temperature phases of (TMTTF)2PF6. Phys. Rev. Lett. 1998, 80, 5429–5432. [Google Scholar] [CrossRef]
- Brown, S.E.; Clark, W.G.; Alavi, B.; Hall, D.; Naughton, M.J.; Tantillo, D.J.; Merlic, C.A. High–field magnetization of the spin-Peierls compound (TMTTF)2PF6. Phys. Rev. B 1999, 60, 6270–6272. [Google Scholar] [CrossRef]
- Hirsch, J.E.; Scalapino, D.J. 2pF and 4pF instabilities in the one-quarter-filled-band Hubbard model. Phys. Rev. B 1983, 27, 7169–7185. [Google Scholar] [CrossRef]
- Hirsch, J.E.; Scalapino, D.J. 2pF and 4pF instabilities in the one dimensional Hubbard model. Phys. Rev. B 1984, 29, 5554–5561. [Google Scholar] [CrossRef]
- Ilakovac, V.; Ravy, S.; Pouget, J.P.; Lenoir, C.; Boubekeur, K.; Batail, P.; Dolanski Babic, S.; Biskup, N.; Korin-Hamzic, B.; Tomic, S.; Bourbonnais, C. Enhanced charge localization in the organic alloys [(TMTSF)1-x(TMTTF)x]2ReO4. Phys. Rev. B 2011, 84, 195134. [Google Scholar] [CrossRef]
- The assertion done in [137] that the inversion symmetry is broken on the anion sites at RT above the AO transition is incorrect. Only inversion centers located on the organic stacks between the donors are removed by the chemical CO.
- Chow, D.S.; Wzietek, P.; Fogliatti, D.; Alavi, B.; Tantilo, D.J.; Merlic, C.A; Brown, S.E. Singular behavior in the pressure-tuned competition between spin-Peierls and antiferromagnetic ground states of (TMTTF)2PF6. Phys. Rev. Lett. 1998, 81, 3984–3987. [Google Scholar] [CrossRef]
- Rose, E.; Loose, C.; Kortus, J.; Pashkin, A.; Kuntscher, C.A.; Ebbinghaus, S.G.; Hanfland, M.; Lissner, F.; Schleid, Th.; Dressel, M. Pressure dependence of Crystal Structure and Electronic Band Structure of (TMTTF)2PF6. J. Phys.: Condens. Matter 2012, in press.. [Google Scholar]
- Le Pévelen, D.; Gaultier, J.; Barrens, Y.; Chasseau, D.; Castet, F.; Ducasse, L. Temperature and pressure dependencies of the crystal structure of the organic superconductor (TMTSF)2ClO4. Eur. Phys. J. B 2001, 19, 363–373. [Google Scholar] [CrossRef]
- Jacobsen, C.S.; Pedersen, H.J.; Mortensen, K.; Rindorf, G.; Thorup, N.; Torrance, J.B.; Bechgaard, K. An unusual metal-insulator transition: bis(tetramethyltetraselenafulvalenium)-perrhenate (TMTSF)2ReO4. J. Phys. C: Solid State Phys. 1982, 15, 2651–2663. [Google Scholar] [CrossRef]
- Pouget, J.-P.; Moret, R.; Comès, R.; Bechgaard, K. X-ray diffuse scattering study of superstructure formation in tetramethyltetraselenafulvalenium perrhenate (TMTSF)2ReO4 and nitrate (TMTSF)2NO3. J. Phys. Lett. (Paris) 1981, 42, L543–L546. [Google Scholar] [CrossRef]
- Grant, P.M. Broken-Symmetry Band Structure of Ditetramethyltetradelenafulvalene-X [(TMTSF)2X]. Phys. Rev. Lett. 1983, 50, 1005–1008. [Google Scholar] [CrossRef]
- Grant, P.M. Electronic structure of the 2:1 charge transfer salts of TMTCF. J. Phys. (Paris) 1983, 44, C3-847–C3-857. [Google Scholar] [CrossRef]
- Emery, V.J. Some basic questions in organic superconductivity. J. Phys. (Paris) 1983, 44, C3-977–C3-982. [Google Scholar] [CrossRef]
- Brazovslii, S.; Yakovenko, V. On the theory of phase transitions in organic superconductors. J. Phys. Lett.(Paris) 1985, 46, L111–L116. [Google Scholar] [CrossRef]
- Bruinsma, R.; Emery, V.J. Theory of anion ordering in TMTSF compounds. J. Phys. (Paris) 1983, 44, C3-1115–C3-1120. [Google Scholar] [CrossRef]
- Emge, T.J.; Wang, M.H.; Beno, M.A.; Williams, J.M.; Whangbo, M.H.; Evain, M. Effect of anion ordering on the H-anion interaction and band electronic structure of (TMTSF)2BF4 at 20K. J. Am. Chem. Soc. 1986, 108, 8215–8223. [Google Scholar] [CrossRef]
- Ducasse, L.; Abderrabba, M.; Gallois, B.; Chasseau, D. Influence of temperature on the band structures of (TMTSF)2X and (TMTTF)2X (X−= tetrahedral anion). Synth. Met. 1987, 19, 327–332. [Google Scholar] [CrossRef]
- Tomic, S.; Jérome, D.; Bechgaard, K. Influence of the cooling rate on the ground state of the organic conductor (TMTSF)2ReO4. J. Phys. C: Solid State Phys. 1984, L11–L16. [Google Scholar]
- Moret, R.; Ravy, S.; Pouget, J.P.; Comès, R.; Bechgaard, K. Anion-Ordering Phase Diagram of di(tetramethyltetraselenafulvalenium)-Perrhenate, (TMTSF)2ReO4. Phys. Rev. Lett. 1986, 57, 1915–1918. [Google Scholar] [CrossRef] [PubMed]
- Jo, Y.J.; Kang, H.; Kang, W. Review of the P-T phase diagram of the organic superconductor (TMTSF)2ReO4. Synth. Met. 2001, 120, 1043–1044. [Google Scholar] [CrossRef]
- Nakamura, T.; Furukawa, K.; Hara, T. 13C NMR Analyses of Successive Charge Ordering in (TMTTF)2ReO4. J. Phys. Soc. Jpn. 2006, 75, 013707. [Google Scholar] [CrossRef]
- Nogami, Y.; Ito, T.; Yamamoto, K.; Irie, N.; Horita, S.; Kambe, T.; Nagao, N.; Oshima, K.; Ikeda, N.; Nakamura, T. X-ray structural study of charge and anion orderings of TMTTF salts. J. Phys. (Paris) IV 2005, 131, 39–42. [Google Scholar]
- Ravy, S.; Pouget, J.-P.; Moret, R.; Wudl, F. Successive phase transitions in the organic conductor (TMTSF)2PF2O2. J. Phys. I France 1991, 1, 703–720. [Google Scholar] [CrossRef]
- Moret, R.; Pouget, J.-P.; Comès, R.; Bechgaard, K. Structural phase transitions in the (TMTSF)2X and (TMTTF)2X series: A survey with some new results. J. Phys. (Paris) 1983, 44, C3-957–C3-962. [Google Scholar] [CrossRef]
- Yamaura, J.; Jo, Y.J.; Kang, H.; Chung, O.H.; Kang, W. X-ray study at low temperature and under pressure in (TMTSF)2FSO3. 2005. Unpublished work.. [Google Scholar]
- Lacoe, R.C.; Wolf, S.A.; Chaikin, P.M.; Wudl, F.; Aharon-Shalom, E. Metal-insulator transitions and superconductivity in ditetramethyltetraselenafulvalenium fluorosulfonate [(TMTSF)2FSO3]. Phys. Rev. B 1983, 27, 1947–1950. [Google Scholar] [CrossRef]
- Jo, Y.J.; Choi, E.S.; Kang, H.; Kang, W.; Seo, I.S.; Chung, O.H. Refinement of the pressure-temperature phase diagram of the organic superconductor with asymmetric anion (TMTSF)2FSO3. Phys. Rev. B 2003, 67, 014516. [Google Scholar] [CrossRef]
- Takahashi, T. Charge fluctuation, charge ordering, and zero-gap state in organic conductors. Phys. B 2012, 407, 1757–1761. [Google Scholar] [CrossRef]
- Alemany, P.; Canadell, E.; Pouget, J.-P. Ab-initio electronic structure of (TMTSF)2ClO4. Institut de Ciència de Materials de Barcelona: Bellaterra, Spain, 2012; Unpublished work. [Google Scholar]
- Nagai, Y.; Nakamura, H.; Machida, M. Superconducting gap function in the organic superconductor (TMTSF)2ClO4 with anion ordering; First-principles calculations and quasiclassical analysis for angle-resolved heat capacity. Phys. Rev. B 2011, 83, 104523. [Google Scholar] [CrossRef]
- Pouget, J.-P.; Kagoshima, S.; Tamegai, T.; Nogami, Y.; Kubo, K.; Nakajima, T.; Bechgaard, K. High resolution x-ray scattering study of the anion ordering phase transition of (TMTSF)2ClO4. J. Phys. Soc. Jpn. 1990, 59, 2036–2053. [Google Scholar] [CrossRef]
- Barrens, Y.; Gaultier, J.; Brachetti, S.; Guionneau, P.; Chasseau, D.; Fabre, J.M. Low temperature structural properties of the (TMTSF)2NO3 salt. Synth. Met. 1999, 103, 2042–2043. [Google Scholar] [CrossRef]
- Matsunaga, N.; Ishikawa, A.; Hoshikawa, A.; Nomura, K.; Takasaki, S.; Yamada, J.; Nakatsuji, S.; Anzai, H. Anion disorder and two-dimensionality in the superconducting and SDW states of (TMTSF)2ClO4. J. Low Temp. Phys. 1999, 117, 1735–1739. [Google Scholar] [CrossRef]
- In the case of a random distribution of domain sizes, the probability that two sites separated by x belong to the same domain is given by exp-μx, where μ is the constant probability to cross a domain wall per unit length. The 3D Fourier transform of this probability function, assuming μ isotropic, is a Lorentzian squared function, whose HWHM Δq is linearly related to μ by Δq ≈ 0.64 μ. μ is connected to the linear density of domain walls along the direction of measurement of Δq. μ should also depend upon the geometry the domain pattern.
- The average domain size L in a given direction is inversely proportional to the HWHM Δq of the reflection (expressed in Å-1), measured in this direction. In a general manner the profile of the reflection is the Fourier transform of the average shape of the ordered domain. L is given by the relationship L≈C(d)/Δq, where the constant C(d) depends upon the dimension, d, of independent directions involved in the Fourier transform. For a segment of length L (or along one edge of a parallelepiped): C(1)≈2.79; for a disc of diameter L: C(2) ≈ 3.2, and for a sphere of diameter L: C(3)≈3.72. L depends weakly of the shape of the domain. In [164], L is obtained using C(1).
- Haddad, S.; Charfi-Kaddour, S.; Pouget, J.-P. Inhomogeneous superconductivity in organic conductors: the role of disorder and magnetic field. J. Phys.: Condens. Matter 2011, 23, 464205. [Google Scholar] [CrossRef]
- Ilakovac, V.; Ravy, S.; Boubekeur, K.; Lenoir, C.; Batail, P.; Pouget, J.-P. Substitutional disorder and anion ordering transition in the (TMTSF)2(ReO4)1-x(ClO4)x solid solution. Phys. Rev. B 1997, 56, 13878–13887. [Google Scholar] [CrossRef]
- μ−1, which is quasi-isotropic, amounts to 400 Å in relaxed samples and decreases rapidly to 25Å / 20 Å for x = 5% / 7% of ReO4. Interestingly for these last two concentrations, μ-1 amounts to the average distance between ReO4 substituent (24 Å and 21 Å respectively).
- In this respect one observes at low temperature for x = 7% of ReO4 a coexistence of (0, 1/2, 0) AO and (1/2, 1/2, 1/2) AO domains in close contact and whose diffraction pattern is a superimposition of LS shaped superlattice reflections [170]. As there is a random distribution of the two species of anion, (1/2, 1/2, 1/2) AO domains are nucleated in regions of excess of ReO4 (with respect to the average concentration) while (0, 1/2, 0) AO domains are nucleated in regions deficient in ReO4.
- Joo, N.; Auban-Senzier, P.; Pasquier, C.R.; Monod, P.; Jérome, D.; Bechgaard, K. Supression of superconductivity by non-magnetic disorder in the organic superconductor (TMTSF)2(ClO4)1-x(ReO4)x. Eur. Phys. J. B 2004, 40, 43–48. [Google Scholar] [CrossRef]
- Joo, N.; Auban-Senzier, P.; Pasquier, C.R.; Jérome, D.; Bechgaard, K. Impurity-controlled superconductivity/spin density wave interplay in the organic superconductor (TMTSF)2ClO4. Europhys. Lett. 2005, 72, 645–651. [Google Scholar] [CrossRef]
- Fertey, P.; Sayetat, F.; Muller, J.; Pouget, J.-P.; Lenoir, C.; Batail, P. Thermal behaviour of (TMTSF)2ClO4 lattice parameters in the range 10K-300K. Physica C 1994, 235–240, 2459–2460. [Google Scholar]
- Fertey, P.; Canadell, E.; Pouget, J.-P.; Sayetat, F.; Lenoir, C.; Batail, P; Muller, J. Cooling rate dependence of the lattice parameters of (TMTSF)2ClO4. Synth. Met. 1995, 70, 761–762. [Google Scholar] [CrossRef]
- Nakamura, T.; Kinami, R.; Takahashi, T.; Saito, G. 1H NMR Study of the Magnetic Structure in (TMTTF)2SCN. Synth. Met. 1997, 86, 2053–2054. [Google Scholar] [CrossRef]
- Parkin, S.S.P.; Coulon, C.; Moret, R.; Pouget, J.-P. Incommensurate structural modulation and electronic localization in bis-tetramethyltetraselenafulvalene thiocyanate. Phys. Rev. B 1987, 36, 2246–2250. [Google Scholar] [CrossRef]
- Kang, W.; Chung, O.H. Quasi-one-dimensional Fermi surface of (TMTSF)2NO3. Phys. Rev. B 2009, 79, 045115. [Google Scholar] [CrossRef]
- Hiraki, K.; Nemoto, T.; Takahashi, T.; Kang, K.; Jo, Y.; Kang, W.; Cung, O.-H. NMR studies of the exotic members of the Bechgaard salts, NO3 and FSO3 salts. Synth. Met. 2003, 135–136, 691–692. [Google Scholar]
- Poirier, M.; Langlois, A.; Bourbonnais, C.; Foury-Leylekian, P.; Moradpour, A.; Pouget, J.-P. Magneto-elastic coupling in the spin-Peierls ground state of hydrogenated and deuterated (TMTTF)2PF6 salts. Departement de Physique, Université de Sherbrooke: Shergrooke, Canada, 2012; Unpublished work. [Google Scholar]
- Pasquier, C.R.; Kang, N.; Salameh, B.; Auban-Senzier, P.; Jérome, D.; Brazovskii, S. Evolution of the spin-density wave-superconductivity texture in the organic superconductor (TMTSF)2PF6 under pressure. Phys. B 2012, 407, 1806–1809, and references there in.. [Google Scholar] [CrossRef]
- Giovannetti, G.; Kumar, S.; Pouget, J.-P.; Cappone, M. Magnetic and charge orderings in predicting multiferroicity in TMTTF2-PF6 organic crystals. 2012. Unpublished work.. [Google Scholar] [CrossRef]
- Khomskii, D.I. Multiferroics: Different ways to combine magnetism and ferroelectricity. J. Magn. Magn. Mater. 2006, 306, 1–8. [Google Scholar] [CrossRef]
- van den Brink, J.; Khomskii, D.I. Multiferroicity due to charge ordering. J. Phys.: Condens. Matter 2008, 20, 434217. [Google Scholar] [CrossRef]
- Holakovský, J. A New Type of Ferroelectric Phase Transition. Phys. Stat. Sol. B 1973, 56, 615–619. [Google Scholar] [CrossRef]
- Imry, Y. On the statistical mechanics of coupled order parameters. J. Phys. C: Solid State Phys. 1975, 8, 567–577. [Google Scholar] [CrossRef]
© 2012 by the authors; licensee MDPI, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Pouget, J.-P. Structural Aspects of the Bechgaard and Fabre Salts: An Update. Crystals 2012, 2, 466-520. https://doi.org/10.3390/cryst2020466
Pouget J-P. Structural Aspects of the Bechgaard and Fabre Salts: An Update. Crystals. 2012; 2(2):466-520. https://doi.org/10.3390/cryst2020466
Chicago/Turabian StylePouget, Jean-Paul. 2012. "Structural Aspects of the Bechgaard and Fabre Salts: An Update" Crystals 2, no. 2: 466-520. https://doi.org/10.3390/cryst2020466



