Role of the Support Effects on the Catalytic Activity of Gold Clusters: A Density Functional Theory Study
Abstract
: It is demonstrated that the support effects play a crucial role in the gold nanocatalysis. Two types of support are considered—the “inert” support of hexagonal boron nitride (h-BN) with the N and B vacancy defects and the “active” support of rutile TiO2(110). It is demonstrated that Au and Au2 can be trapped effectively by the vacancy defects in h-BN. In that case, the strong adsorption on the surface defects is accompanied by the charge transfer to/from the adsorbate. The excess of the positive or negative charge on the supported gold clusters can considerably promote their catalytic activity. Therefore gold clusters supported on the defected h-BN surface can not be considered as pseudo-free clusters. We also demonstrate that the rutile TiO2(110) support energetically promotes H2 dissociation on gold clusters. We show that the formation of the OH group near the supported gold cluster is an important condition for H2 dissociation. We demonstrate that the active sites towards H2 dissociation on the supported Aun are located at corners and edges of the gold cluster in the vicinity of the low coordinated oxygen atoms on TiO2(110). Thus catalytic activity of a gold nanoparticle supported on the rutile TiO2(110) surface is proportional to the length of the perimeter interface between the nanoparticle and the support.1. Introduction
Since the pioneering work of Haruta on the oxidation of carbon monoxide on small gold nanoparticles supported by metal oxides [1], an extensive interest has been devoted to understanding the catalytic properties of gold. Such an interest is stipulated by the fact that gold nanoparticles are catalytically active even at room temperatures and demonstrate extraordinary selectivity. This feature makes gold clusters very attractive for a wide range of industrial, chemical and environmental applications [2–4].
Two types of catalytic reactions on gold nanoparticles—oxidation by O2 and hydrogenation by H2—are extremely important for applications. The most explored types of oxidation reaction include the oxidation of carbon monoxide at mild temperatures, alcohol oxidation, the direct synthesis of hydrogen peroxide and alkene epoxidation; see, e.g., References [1,5–11] and references therein. Heterogeneously catalyzed hydrogenation is another type of reactions where gold nanoparticles have shown their great potential as catalysts. It has been demonstrated experimentally that gold nanoparticles supported on metal oxides such as SiO2, Al2O3, TiO2, ZnO, ZrO2, and Fe2O3 are effective catalysts for selective hydrogenation of several classes of organic molecules, including α, β-unsaturated aldehydes, unsaturated ketones, and unsaturated hydrocarbons [12–21]. Moreover, supported gold nanoparticles are very selective for the direct formation of hydrogen peroxide from H2/O2 mixtures [9].
In spite of intensive theoretical and experimental studies the origin of catalytic activity of gold nanoparticles remains elusive and has yet to be fully understood. It is commonly accepted that several factors can influence the catalytic activity of gold nanoparticles. One of them is the size effect. It has been shown that the unique properties of gold in oxidation reactions emerge when the size of catalytic particles decreases down to 1–5 nm, while larger sized particles are catalytically inactive [5]. It has been shown that small gold clusters consisting of a few atoms can also possess extraordinarily high catalytic activity [22,23]. This is the regime where each atom counts, physical and chemical properties of clusters are extremely size sensitive and cannot be deduced from those known for larger sizes [4,24,25]. On the one hand, the size effects in nanocatalysis are determined by quantum effects, resulting from the spatial confinement of the valence electrons in the cluster [4]; on the other hand, in such clusters a dominant fraction of atoms are under-coordinated (in comparison with the bulk), hence they exhibit an enhanced chemical reactivity [4,26,27].
The charge state of the gold nanoparticles can considerably influence their reactivity [11,28]. For example, in the case of the negatively charged gold nanoparticles, an extra electron from the gold readily transfers to the anti-bonding 2π* orbital of the adsorbed O2, which weakens the O–O bond and activates oxygen molecule for further catalytic reaction; see, e.g., References [10,11,29–31] and references therein. Such mechanism of the charge-transfer-mediated activation of O2 by gold clusters has been intensively studied [32–35]. On the other hand, the positive charge accumulated on the gold can promote adsorption of some reactants, such as CO and hydrocarbons [36,37].
Interaction with the support material is another important factor that considerably influences the reactivity of gold nanoparticles [4,38]. Most of the experimental studies have been performed for gold nanoparticles supported on various metal oxides, such as MgO, ZnO, TiO2, ZrO2, Al2O3, Fe2O3, see, e.g., Reference [2] and references therein. It was demonstrated that the catalytic activity of gold nanoparticles strongly depends on the type of the support material [2,5,39]. Often, an electron transfer from the support to the gold cluster promotes its catalytic activity because it opens a route for an extra charge transfer to the adsorbed O2. Catalytic activity of the supported nanoparticles can also be promoted by defects in the support material. Defects can trap the metal nanoparticle and enhance charge transfer between the support and the nanoparticle. Thus, it was demonstrated that Au8 clusters supported on the MgO(100) surface rich of F-center defects show high catalytic activity, while Au8 deposited on the defect-poor MgO(100) surface are inert [40,41]. Defects are not the only factor responsible for charging of the supported metal nanoparticles. Recently, it was demonstrated that the charge accumulated on the supported gold nanoparticle can be tuned by varying the thickness of the metal oxide layer deposited on the metal support [42–46]. Thus, the support effects can play even larger role in gold nanocatalysis than the particle size.
In the present work we demonstrate that the charge transfer from the support to the deposited gold clusters is not the only mechanism responsible for the promotion of the cluster's catalytic activity. Two types of support will be considered—the hexagonal boron nitride (h-BN) with N and B vacancy defects and the rutile TiO2(110). Using these two examples we show that the support effects on the catalytic activity of gold clusters can be rather diverse and can have different origins.
It is commonly accepted that “inert” supports, such as, h-BN do not affect the electronic and geometric structure of the supported clusters, and hence such clusters can be considered as pseudo-free. This suggestion is widely used to study intrinsic properties of metal clusters that are free from the support effects [6]. Indeed, h-BN is an electrical insulator with a wide band gap (∼5.8 eV) and high thermal and chemical stability [47,48]. It is unlikely that such a support can promote an electron transfer to or from the deposited gold nanoparticle and influence their physical and chemical properties.
Recently, it has been demonstrated experimentally that small gold clusters deposited on h-BN support are efficient and robust catalysts [6]. However, very little attention has been paid to theoretical investigations concerning the role of the h-BN support on the catalytic properties of gold. Whether the origin of catalytic activity of gold clusters supported on h-BN surface derives from the cluster itself, or h-BN support can modify or tune catalytic properties of gold?
Contrary to the case of the “inert” h-BN support, the rutile TiO2(110) surface is considered as an active surface that can even possess catalytic properties itself. It has been found experimentally that catalytic activity of gold nanoparticles supported on the rutile TiO2(110) surface towards H2 dissociation depends on the number of gold atoms located at the perimeter nanoparticle-support interface, irrespective of the cluster size [38]. It has been also shown that the active sites for the H2 + O2 reaction over a Au/TiO2 nanoparticle catalyst are located at dual perimeter sites at the interface between Au and TiO2 [49]. To the best of our knowledge there are only few theoretical studies concerning the role of the support on the processes of adsorption and dissociation of molecular hydrogen on the supported gold nanoparticles [50–52]. In Reference [50] the authors performed an elegant theoretical study on elucidation of active sites for H2 adsorption and activation on Au13 cluster supported on the anatase TiO2(001) surface. It has been shown that Au atoms that are active for H2 dissociation must have a net charge close to zero, be located at corner or edge low coordinated positions, and not be directly bonded to the support [50]. An important role of the low coordinated oxygen atoms at the nanoparticle/TiO2 interface has been discussed [52]. In Reference [51] it was shown that small two-dimensional Au nanoparticles supported on TiC(001) can dissociate H2 in a more efficient way than when supported on oxides. The active sites for H2 dissociation on Au/TiC(001) are located at the particle edge and in direct contact with the underlying substrate [51]. In the present work we clarify how hydrogen molecule adsorbs and dissociates on the supported gold nanoparticles.
We demonstrate that the support effects are very important in the gold nanocatalysis. Even the “inert” h-BN support, if it contains point defects, can promote or quench the catalytic properties of gold in oxidation reaction by O2. Therefore gold clusters supported on the defected h-BN surface can not be considered as pseudo-free clusters. We demonstrate that rutile TiO2(110) support energetically promotes H2 dissociation on gold clusters. We show that the formation of the OH group near the supported gold cluster is an important condition for H2 dissociation and the conventional charge transfer mechanism does not play an important role for H2 dissociation. The considered phenomena can be particularly important for understanding the mechanisms of the catalytic activity of the supported gold clusters in oxidation reactions by O2 and hydrogenation reactions by H2.
2. Computational Details
The calculations are carried out using density-functional theory (DFT) with the gradient-corrected exchange-correlation functionals of Wu and Cohen (WC) [53] and Perdew, Burke and Ernzerhof (PBE) [54] for O2Aun/h-BN and H2Aun/TiO2(110) systems, respectively. The choice of DFT functionals is stipulated by the fact that WC gives significant improvements for lattice constants, crystal structures, and surface energies over the most popular PBE functional, while PBE remains superior for the energetics of covalent and noncovalent bonds [55]. In particular, the PBE functional demonstrates very poor performance for the layered-systems like graphite or h-BN, whose distances between the layers are determined by rather weak interactions [55]. Thus, in the case of h-BN lattice the PBE functional demonstrate only marginal binding of the hexagonal layers along “c”, while WC provides very accurate results that are close to experiment [55]. On the other hand PBE can reproduce well the tetragonal rutile TiO2 structure, and therefore it has been selected to treat H2Aun/TiO2(110) system.
The atom-centered, strictly confined, numerical basis functions [56,57] are used to treat the valence electrons of H (1s1), B (2s22p1), N (2s22p3), O (2s22p4), Ti (4s23d2) and Au (6s15d10). Double-ζ plus polarization function (DZP) basis sets are used for B, N, O, Ti, Au and triple-ζ plus polarization function (TZP) for H. Basis set for hydrogen was optimized with the use of the Nelder–Mead simplex method [58] according to the procedure described in Reference [57]. The core electrons are represented by the Troullier–Martins norm-conserving pseudopotentials [59] in the Kleinman-Bylander factorised form [60]. Relativistic effects are taken into account for Au.
In the present work, the h-BN lattice has been optimized using the Monkhorst-Pack [61] 10 × 10 × 4 k-point mesh for Brillouin zone sampling. The calculated lattice parameters a = b = 2.504 Å and c = 6.656 Åare in excellent agreement with the experimental values of a = b = 2.524 ± 0.020 Å and c = 6.684 ± 0.020 Å, reported in Reference [62]. The h-BN surface is represented by the two-layer slab containing 7 × 7 unit cells (98 units of BN per slab) with the surface area of 3.07 nm2. The bottom layer in the h-BN slab is fixed while the top layer is fully relaxed. The rutile lattice was optimized using the 6 × 6 × 9 k-point mesh. The calculated lattice parameters a = 4.594 Å and c = 2.959 Å are in agreement with the experimental values of a = b = 4.587 Å, c = 2.954 Å at 15 K [63,64]. The optimized lattice of the bulk rutile was used to construct slabs for the TiO2(110) surface. The six-layer slab containing four units of TiO2 represents the element of the (110) rutile face with the surface area of . For rutile surface the bottom two layers in the slab are fixed, and all other atoms are fully relaxed. In the present work we study adsorption of Aun clusters containing n = 1, 2, 8 and 20 atoms on the rutile (110) surface. In the case of Au and Au2 the TiO2(110) surface is modeled by the p (2 × 5) slab (40 units of TiO2 per slab), while for Au8 and Au20 we use p (3 × 6)(72 units of TiO2) and p (4 × 9)(144 units of TiO2) slabs, respectively. The periodically replicated slabs for h-BN and TiO2(110) surfaces are separated by the vacuum region of 25 Å. Only the Γ point is used for sampling the Brillouin zone of the slabs due to the large size of the supercell.
The cluster geometries have been determined with the use of the cluster fusion algorithm [65] which belongs to the class of genetic global optimization methods. This method has been successfully used in order to find the optimized geometries of various types of metal clusters [66–68]. Additionally, the global reaction route mapping (GRRM) technique within the scaled hypersphere search (SHS) method has been used in order to find equilibrium structures [69–71]. The optimized structures of the gold clusters are in a good agreement with those reported in previous theoretical studies; see, e.g., References [30,72–75]. The most stable isomers of gold clusters have been further optimized on the support starting from the several (up to 15) initial orientations and positions of the cluster on the surface.
All calculations have been carried out with the use of the SIESTA package [76–78]. Within the SIESTA approach, the basis functions and the electron density are projected onto a uniform real-space grid. The mesh size of the grid is controlled by an energy cutoff, which defines the wavelength of the shortest plane wave that can be represented on the grid. In the present work the energy cutoff of 200 Ry is chosen to guarantee convergence of the total energies and forces. The self-consistency of the density matrix is achieved with a tolerance of 10−4. For geometry optimization the conjugate-gradient approach was used with a threshold of 0.02 eV Å−1. The atoms in molecules method of Bader (AIM) has been used for charge analysis [79,80]. The electron density has been plotted using XCRYSDEN visualisation program [81].
To validate our approach we have calculated the dissociation energies and interatomic distances for several diatomic molecules. Our calculations demonstrate that the dissociation energy, De, and bond length in H2 (4.55 eV, 0.75 Å), O2 (5.88 eV, 1.24 Å), Au2 (2.28 eV, 2.55 Å) are in a good agreement with experimental data H2 (4.74 eV, 0.74 Å), O2 (5.23 eV, 1.21 Å), Au2 (2.29 eV, 2.47 Å)[82]. We also tested the gold–hydrogen interaction by optimizing AuH dimer. The calculated dissociation energy and bond length in AuH (3.09 eV, 1.547 Å) are in a good agreement with experimental data (3.36 eV, 1.524 Å)[82].
3. Theoretical Results
3.1. Adsorption and Activation of O2 on Au/h-BN and Au2/h-BN. Role of the Defected h-BN Support
We start our study with investigation of the catalytic activity of small gold clusters supported on the defected hexagonal BN surface. The h-BN lattice has a layered structure which is very similar to graphite. The planar networks of B3N3 hexagons are regularly stacks on top of each other [83]. Due to the partially ionic character of the B–N bonding, the B atoms in one layer are located on top of the N atoms of the neighboring layer and vice versa, as it is shown in Figure 1(a). Both graphite and h-BN materials are strongly bonded within the layers, while interaction between the layers is weak. In spite of similar structures, physical and chemical properties of graphite and h-BN are different. Thus, graphite is an electrical conductor, while h-BN is a dielectric with a wide band gap of 5–6 eV.
In the present work we study adsorption of gold clusters on the h-BN surface with boron (VB) and nitrogen (VN) vacancy defects, which are schematically shown in Figure 1(b). The point VB and VN defects are the simplest and relatively stable types of defects in h-BN. It was suggested that single boron and nitrogen vacancy defects can exist in h-BN and VN is more stable than VB [84,85]. The stability of divacancies in graphitic boron nitride (g-BN) sheets has been studied in Reference [86]. It was shown that the divacancies are more frequently formed in graphene than in the g-BN [86]; however, it was demonstrated that in BN single-wall nanotubes the most stable type of point defect is the BN divacancy [87]. Formation of the triangle defects in h-BN monolayer has been also investigated; see, e.g., References [88,89] and references therein. It has been demonstrated that N(B) triangle defect states of h-BN atomic layer with N(B) edge atoms have acceptor (donor) levels [89]. A cohesive energy calculation indicates that the h-BN atomic layer with N triangle defects is more or less stable, respectively, than that with B triangle defects when it is negatively or positively charged [89]. The relative stability of particular type of defects in h-BN often depends on the experimental conditions. Therefore, in the present work we study only the simplest types of single point defects, such as VB and VN.
Recently, it was demonstrated that h-BN monolayer binds to surfaces of many 3d, 4d, and 5d transition metals, forming the so-called nanomesh structure [90]. The interaction between the h-BN monolayer and transition metal support is mainly driven by mixing of N-pz and B-pz orbitals of h-BN monolayer with the dz2 transition metal orbitals [91]. Similar effect is responsible for bonding of gold clusters to the h-BN surface. In the case of defect-free h-BN surface, both Au and Au2 adsorb on top of the N atom. Our calculations confirm that Au and Au2 interact weakly with the pristine h-BN surface. Thus, the calculated binding energies of Au and Au2 on h-BN are Eb(Au/h-BN) = 0.25 eV and Eb(Au2/h-BN) = 0.77 eV, respectively. Here, the binding energy of Au and Au2 to the h-BN surface is defined as
However, the interaction of Au and Au2 with the support becomes stronger when the h-BN surface contains VB or VN point defects. The strong adsorption on vacancy defects is accompanied by the large charge transfer to/from the gold particles. The calculated binding energies of Au and Au2 to h-BN, VB@h-BN and VN@h-BN as well as Bader charges localized on the adsorbed gold are summarized in Table 1.
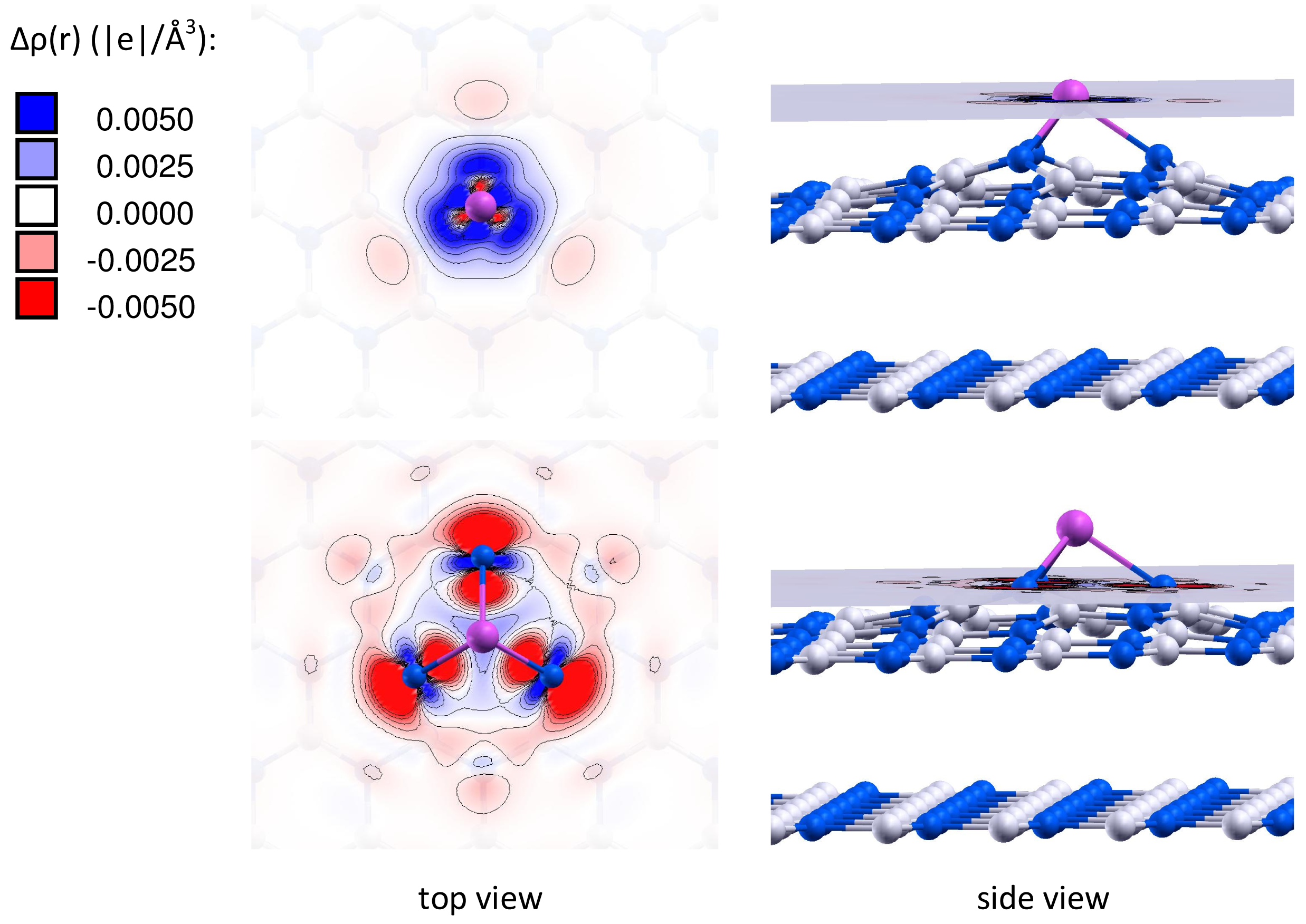
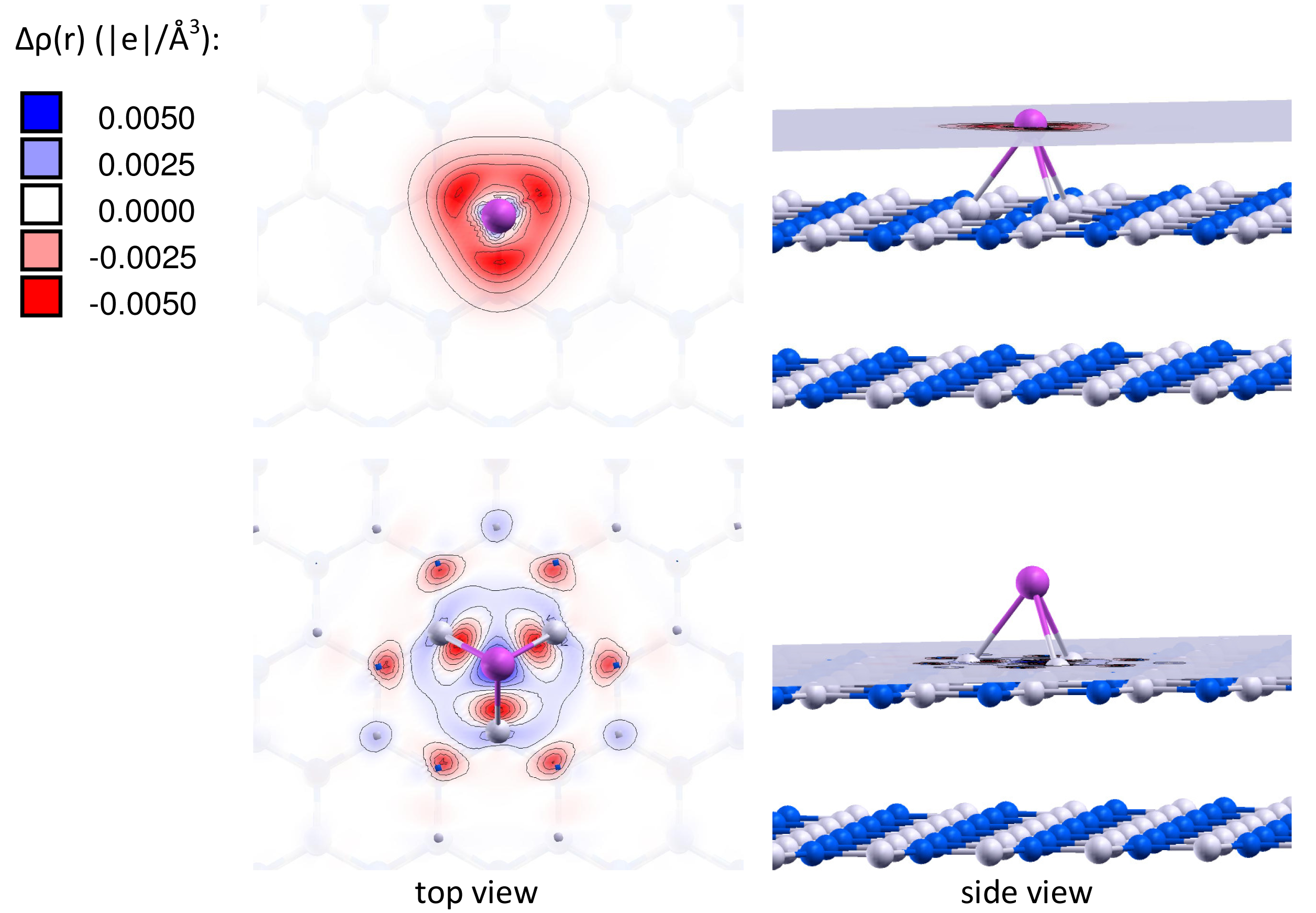
It is important to note that the charge of the adsorbed gold particles strongly depends on the type of vacancy defects, and can possess either negative or positive values. Figures 2 and 3 present the electron density differences Δρ(r) in Au/VB@h-BN and Au/VN @h-BN, respectively. Upper rows in Figures 2 and 3 present the electron density differences Δρ(r) projected on the plane passing through the adsorbed Au atom; while lower rows demonstrate Δρ(r) projected on the plane passing through three atoms N (B) atoms in the vicinity the VB (VN) vacancy defect on the h-BN surface. Blue and violet regions are electron poor, whereas red and pink are electron rich. It is seen from Figures 2 and 3 that VN donates electrons to the adsorbed Au and Au2; while VB acts as an electron acceptor. Hence, it is possible to modify considerably the cluster's electron donor-acceptor capacity and its catalytic properties via the support design. To demonstrate this effect and to study the specific role played by the defected h-BN support in formation of the catalytic properties of gold we perform systematic investigation of adsorption and activation of O2 on Au/h-BN and Au2/h-BN systems.
Adsorption of molecular oxygen on free gold clusters has been intensively investigated; see, e.g., References [10,29–31] and references therein. It was found that O2 readily adsorbs and becomes catalytically activated on small neutral gold clusters with an odd number of atoms as well as on gold cluster anions. Such an ability of small gold clusters to bind and activate molecular oxygen has been explained by the transfer of unpaired valence electron from the cluster to the oxygen anti-bonding 2π* orbital, see, e.g., References [10,29–31] and references therein. Our calculations demonstrate that O2 adsorbs on the free Au and Au2 with the binding energy of 0.49 eV and 0.48 eV, respectively. The O–O bond length enlarges from 1.24 Å (free O2) to 1.27 Å and 1.26 Å, upon O2 adsorption on gold monomer and dimer, respectively. Slight increase in the O–O bond length of the adsorbed O2 demonstrates its catalytic activation.
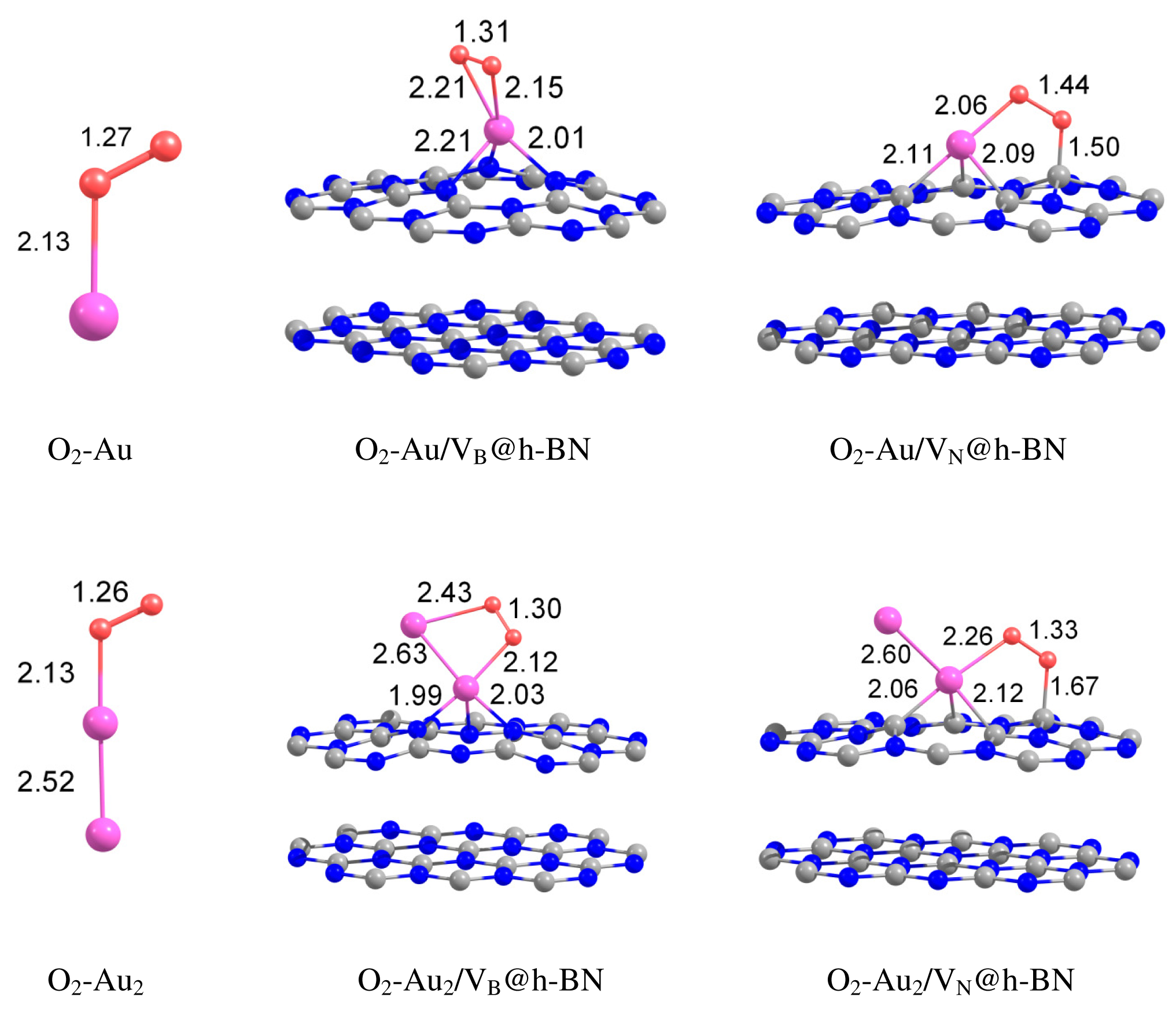
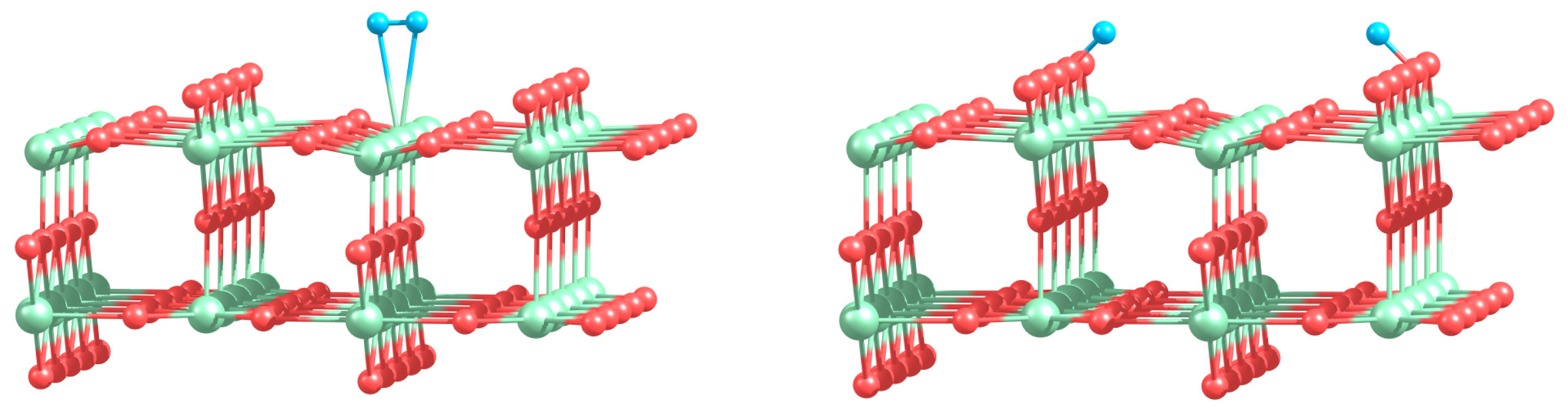
Can the defected h-BN support modify the catalytic properties of gold? Our calculations demonstrate that O2 readily adsorbs on Au and Au2 trapped by the defected h-BN surface. Figure 4 presents optimized geometries of O2 adsorbed on the free and supported Au and Au2. It is seen from Figure 4 that oxygen molecule adsorbs on top of the Au atom trapped by the VB@h-BN defect and bridges Au and B atoms in the case of adsorption on Au/VN @h-BN. In the case of the supported gold dimer, O2 bridges two gold atoms on Au2/VB@h-BN; while for the Au2/VN @h-BN system, O2 bridges nearest to the surface Au atom, which is located on top of VN and B atom on the surface. Therefore an interface between the supported gold cluster and the h-BN surface might play an important role in oxidation reactions on the supported gold clusters.
Interaction of Au and Au2 with the support results in additional activation of the adsorbed O2 and weakening of the O–O bond. This effect is especially strong for VN vacancy defect, which acts as an electron donor for the supported Au and Au2. Figure 4 demonstrates that the O–O bond length in adsorbed O2 is enlarged similar to superoxide and peroxide states (the O–O bond distances in O2− and are 1.33 Å and 1.49 Å [92], respectively). The results of our calculations demonstrate that interaction of Au and Au2 with the defected h-BN surface can lead to a dramatic change in the catalytic activity of gold.
Table 2 presents the binding energies of O2, Eb(O2), to the free and h-BN supported Au and Au2. Interaction of Au and Au2 with the h-BN support results in the considerable change in oxygen binding. Thus, O2 adsorbs on Au/VB@h-BN and Au/VN @h-BN with binding energies of 0.90 eV and 1.10 eV, respectively. This is twice larger than the binding energy of O2 to the free Au. The strong change in binding of O2 to Au/VB@h-BN and Au/VN @h-BN can be explained by the large charge transfer between the corresponding point defects and the trapped Au atom. It is interesting that binding of O2 to Au2/VB@h-BN center is weaker if compared with free Au2. However, adsorption of O2 on Au2/VN @h-BN is highly promoted. In the latter case O2 bridges one of the gold atoms and the nearest boron atom on the surface, with binding energy of 1.30 eV. Thus, the oxygen binding to the supported gold particles considerably depends on the number of gold atoms and the type of the support. Activation and reactivity of the adsorbed O2 are strongly affected by the charge transfer from the gold hybridized 5d6s orbitals to the anti-bonding 2π* orbital of O2. In the case of O2 adsorption on free Au, the Bader charge localized on O2 is −0.19 e. The charge transfer from Au to O2 is responsible for the catalytic activation of the adsorbed O2 and weakening of the O−O bond. Interaction of Au with the defected h-BN support results in the drastic increase in charge transfer to the adsorbed O2. That means that the interaction of Au and Au2 with the defected h-BN support considerably promotes the charge transfer from the gold to O2. Such an effect becomes very clear for O2 adsorbed on the Au/VB@h-BN center. As we have discussed above, the B vacancy acts as an electron acceptor. Thus, Au trapped by the VB@h-BN defect possesses a positive charge. It is well known that free gold cluster cations are inert toward molecular oxygen. However, our calculations demonstrate that O2 readily adsorbs and becomes highly activated on the positively charged Au/VB@h-BN center. Interaction with the VB@h-BN support promotes additional charge transfer (in comparison with O2 adsorbed on free Au) from the gold to the adsorbed O2, even if the adsorbed Au has a positive charge. This effect is rather similar to that of promotion of oxygen activation by the small gold clusters with coadsorbed hydrogen [27] or ethylene [11] molecules. In the case of O2 adsorption on the Au/VN @h-BN center, gold atom trapped by the N vacancy has a negative charge. That promotes charge transfer to the adsorbed O2. However, in contrast to the case of the Au/VB@h-BN adsorption center, the additional charge transfer to the oxygen adsorbed on Au/VN @h-BN occurs mainly due to the charge transfer from the support.
It is seen from Table 2 that adsorption of O2 on Au2/VB@h-BN is accompanied by the additional charge transfer from Au2, while the total charge transfer from the VB@h-BN support to the Au2 and O2–Au2 adsorbates remains unchanged. Hence, interaction of Au2 with the VB@h-BN defect promotes charge transfer from the gold to the oxygen. However, in the case of O2 adsorption on Au2/VN @h-BN center an additional charge transfer to O2 occurs mainly due to the charge transfer from the VN @h-BN center, but not from the gold dimer. In both cases charge transfer to O2 is accompanied by its strong activation.
Thus, we found that strong adsorption of Au and Au2 on the surface defects is accompanied by the charge transfer to/from the adsorbate. The value and the sign of the charge accumulated on the adsorbate depend on the adsorption sites. Thus, VN donates electrons to the adsorbed Au and Au2; while VB acts as an electron acceptor. The excess of the positive or negative charge on the supported gold clusters can considerably promote their catalytic properties and enhance activation of the adsorbed O2.
3.2. Adsorption and Dissociation of H2 on Aun/TiO2(110). Interface Effects
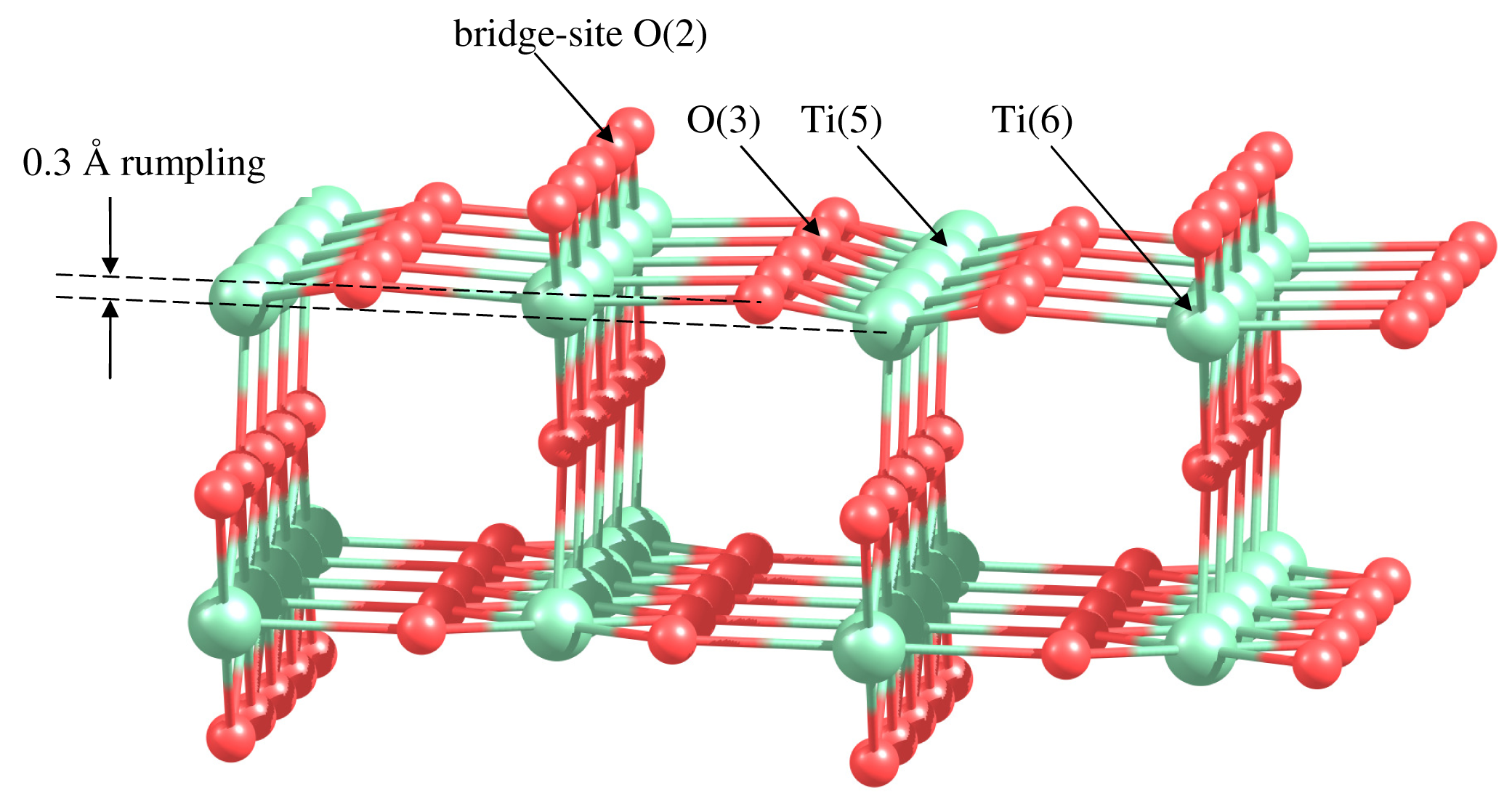
Let us consider catalytic activity of gold clusters supported on the active surface of rutile TiO2(110). The TiO2(110) surface contains oxygen and titanium atoms with different coordination. The fivefold coordinated Ti atoms are undercoordinated relatively to the bulk sixfold coordinated Ti, as it is shown in Figure 5. The O atoms raised above the plane of Ti atoms are twofold coordinated. These atoms are called bridge-site O. The oxygen atoms lying in the plane of Ti atoms are threefold coordinated. Relaxation of the TiO2(110) surface results in a surface rumpling, as it is shown in Figure 5. The undercoordinated Ti and O atoms are moving inward by 0.10 Å, decreasing the distance with subsurface atoms. The sixfold coordinated Ti atoms and threefold coordinated O atoms are moving outward by 0.1 Å and 0.2 Å, respectively. The similar puckered structure of the rutile (110) surface has been reported in References [93,94].
Our calculations demonstrate that H2 can be adsorbed on the pure, defect-free TiO2(110) surface, even in the absence of the gold particle. The most stable geometries calculated for the molecular and dissociative adsorption of H2 on the pure rutile TiO2(110) surface are presented in Figure 6. It is seen that H2 preferably adsorbs on top of the Ti(5) atom with the binding energy of 0.14 eV. The H–H bond length of 0.78 Å is slightly increased in comparison with the free H2. The dissociative state of H2 on TiO2(110) corresponds to the situation when both H atoms form the OH group with the low coordinated O(2) bridge atoms on the rutile surface. The binding energy of the dissociated configuration of H2 is 1.50 eV; however, the distance between two rows of O(2) atoms on TiO2(110) is 6.50 Å, which is too large to promote dissociation of the H2 adsorbed on top of Ti(5) atom. In this case H2 would dissociate in the vicinity of the adsorption center as a first step, followed by adsorption of H atoms on O(2). This process requires to overcome a dissociation barrier of ∼4.3 eV which is much higher than the energy of the molecular adsorption. In this situation H2 would desorb from the surface and fly away rather than dissociate. Therefore, to promote H2 dissociation on TiO2(110), it is necessary to have adsorption centers on the rutile surface in the vicinity of low coordinated O(2) atoms. Supported gold clusters can serve as a source of such centers.
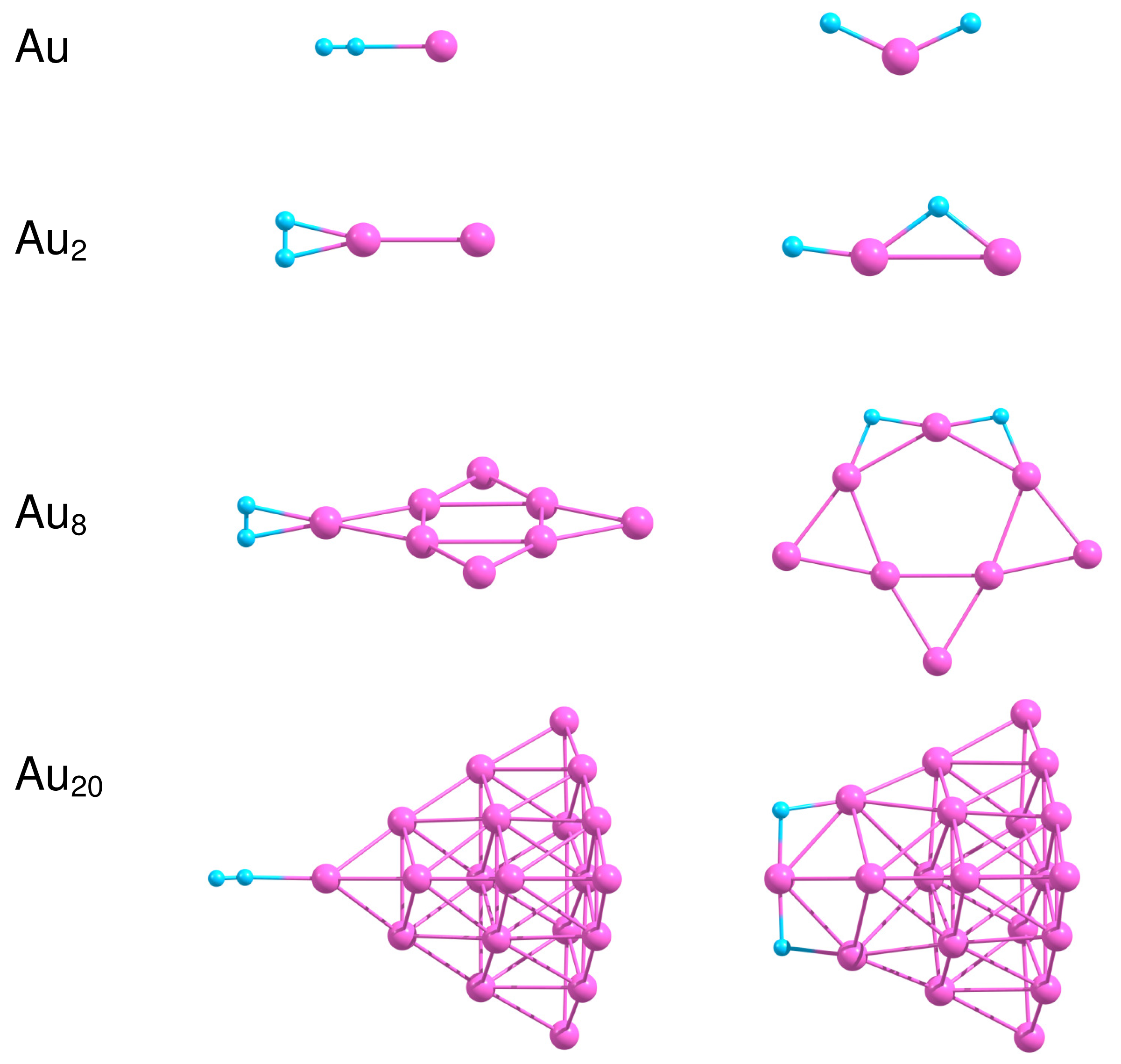
In the present work we consider adsorption of H2 on the most stable isomers of free and supported gold clusters Aun consisting of n = 1, 2, 8 and 20 atoms. Figure 7 presents the optimized geometries of H2−Aun systems in the case of molecular and dissociative adsorption of H2 on free Aun clusters. In order to obtain the most stable configuration of H2 adsorbed on Aun, we have created a large number of starting geometries by adding H2 molecule in different positions (up to 30) on the surface of the considered clusters. The starting structures have been optimized further without any geometric constraints. We have successfully used a similar approach to find the optimized geometries of O2 and C2H4 molecules adsorbed on small neutral, anionic and cationic gold clusters [10,11,37,95]. The binding energies for molecular, , and dissociative, , adsorption of H2 on free Aun as well as the H–H bond length in H2 adsorbed molecularly are summarized in Table 3.
Results of our calculations demonstrate that H2 binds weakly to Au as a molecule, with . Dissociation of H2 on Au is not favorable energetically. The H–H bond length in H2 adsorbed on Au is slightly enlarged in comparison with the free H2. Adsorption of H2 on Au2 is relatively strong, with the binding energy equal to 0.59 eV both for the molecular and the dissociative adsorption. Table 3 demonstrates that the H–H bond length increases to 0.845 Å in H2–Au2, indicating that H2 is highly activated. With the further increase in cluster size the binding energy calculated for molecular adsorption of H2 decreases to 0.26 eV for Au8 and 0.09 eV both for Au20. On the other hand, the dissociative adsorption of H2 becomes energetically favorable both for Au8 and Au20.
One of the factors that influence H2 dissociation is coordination of Au atoms interacting with hydrogen and flexibility of cluster structure, as was discussed in [96]. It is seen from Figure 7 that H2 dissociates at the low coordinated corner Au atom with formation of the slightly bent H–Au–H bond. Note, that the Au–Au bond length in Au2 does not change noticeably upon molecular adsorption of H2; but increases up to 2.753 Å for dissociative adsorption. In the case of Au8 and Au20 dissociation of H2 on the cluster surface is accompanied by the structural (at least local) transformations, although Au20 demonstrates rather strong structural stability, due to the “magic” nature of this cluster.
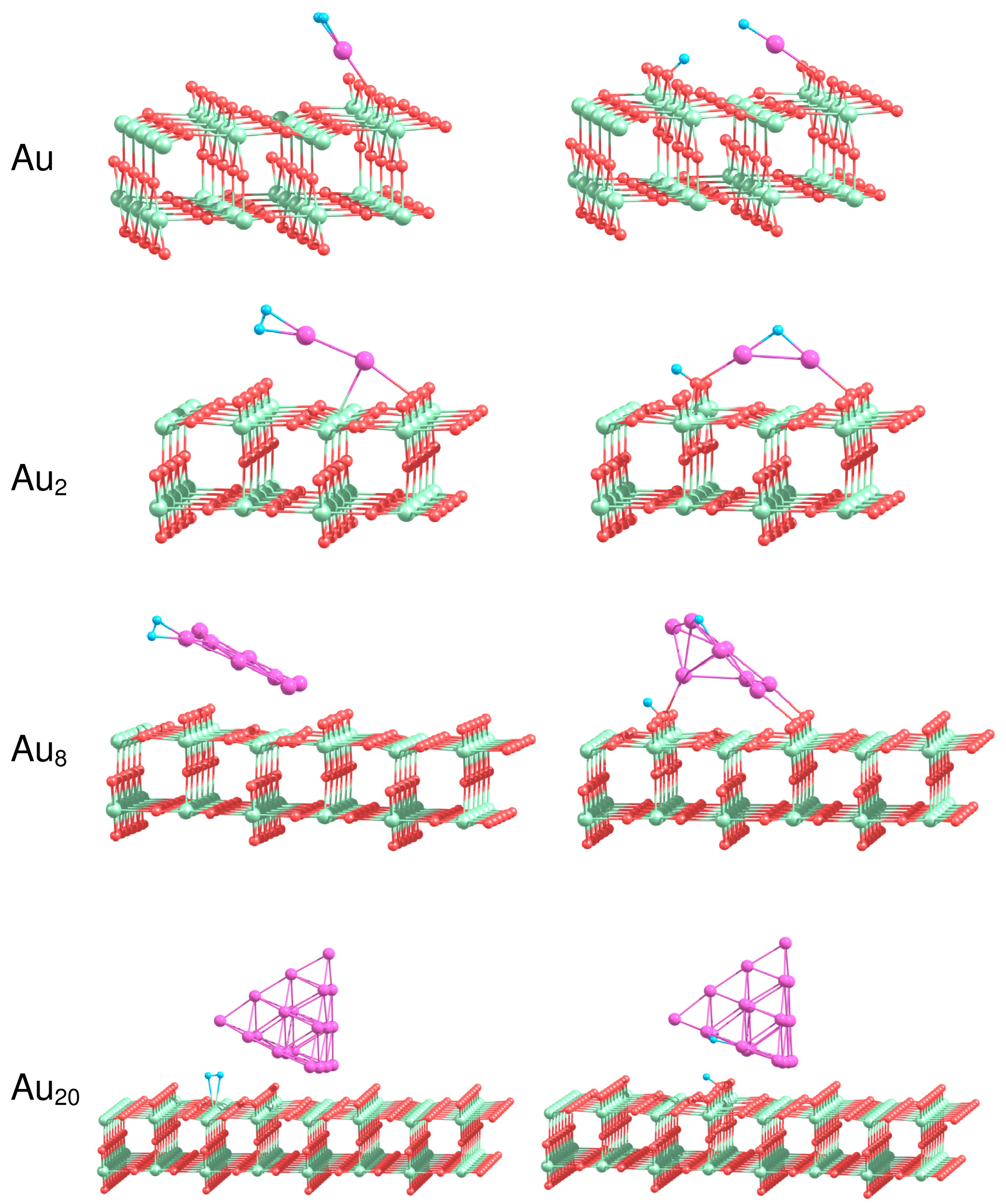
How does the interaction with the support influence the reactivity of gold clusters? In the present work we perform a systematic theoretical study of the structure and energetics of H2 adsorbed on Au1, Au2, Au8 Au20 clusters supported on the rutile TiO2(110) surface. The analysis of the energetics of H2 adsorption on the supported gold clusters provides deep insights into the nature of bonding and dissociation of the H2 molecule and reveals the details of the reaction mechanism. Figure 8 shows the most stable geometries of H2 adsorbed on the supported gold clusters. The binding energies calculated for molecular, , and dissociative, , adsorption of H2 on Aun/TiO2, and the H–H bond length, , in the case of molecular adsorption of H2 are summarized in Table 4.
It is seen from Table 4 that H2 adsorbs molecularly on Au/TiO2 with a binding energy of 1.15 eV, which is considerably larger than the corresponding energy calculated for H2 adsorbed on free Au atom. The adsorbed H2 is highly activated, with the H–H bond length . As a result of H2 adsorption, the supported Au atom shifts slightly towards the row of the low coordinated O(2) bridge atoms. In the previous section we demonstrated that H2 dissociation is not favorable on the free Au atom. However, in the case of the supported Au atom, dissociation of H2 can occur with formation of the OH group with the O(2) atom located either in the nearest to Au row of O(2) or in the next row of O(2), as is shown in Figure 8. In the latter case the calculated binding energy is higher, not only if compared with the binding energy for molecular adsorption of H2 on Au/TiO2(110), but also if compared with the binding energy of the dissociated state of H2 on the pure TiO2(110) surface. Thus, we can conclude, from the energetic point of view, that the TiO2(110) support considerably promotes H2 dissociation on Au atom.
We found that molecular H2 binds to the supported Au2 in a similar way as for the free Au2. However, the binding energy calculated for the molecular adsorption of H2 on Au2/TiO2 is lower than the corresponding energy obtained for free Au2. The dissociated hydrogen atom can migrate to the row of O(3) atoms, or to the row of O(2) bridge atoms on the rutile surface, forming OH bonds. The interaction of Au2 with the support results in the energetic promotion of H2 dissociation on the supported Au2.
The optimized geometries of H2 in the case of its molecular adsorption on the supported Au8 cluster similar to those obtained for the corresponding free Au8. However, the dissociative adsorption of H2 on Au8 results in the considerable rearrangement of the cluster structure. The dissociative configuration of H2 on the supported Au8 is promoted energetically. Migration of H on the low coordinated O(2) atom results in formation of the OH bond and considerable increase in binding energies calculated for H2 adsorbed dissociatively.
The Au20 clusters supported on TiO2(110) are the largest systems studied in the present work. It was shown above that the hydrogen molecule binds weakly to the free Au20 clusters. We have found that, in the case of the supported Au20, the hydrogen molecule adsorbs on top of the Ti(5) atoms on the rutile surface in the vicinity of Au20, rather than directly on the Au20 clusters. After H2 dissociation in the vicinity of Au20/TiO2 one of the H atoms binds to the edge of Au20 that are oriented perpendicularly to the rows of O(2) surface atoms, while another H forms the OH bond with the O(2) atom on the rutile surface. However, this configuration is not stable in comparison with the situation when both of H atoms form OH surface group. Therefore, H atom on the edge of the supported Au20 cluster will further migrate towards the low coordinated O(2) atoms on the rutile surface.
Our calculations demonstrate that combination (interplay) of several factors such as geometric structure, presence of the low coordinated oxygen atoms in the vicinity of the cluster-surface interface, etc., are important for H2 dissociation. What is the role of the charge transfer from the gold cluster to hydrogen in H2 dissociation? As it was discussed in previous section, the charge transfer from the gold to the antibonding orbital of O2 is responsible for the catalytic activation of O2. However, in the case of H2 dissociation the analysis of the Bader charges [79,80] demonstrate that there is no considerable charge transfer between the adsorbed hydrogen and the gold clusters (free or supported). Thus, the largest charge transfer occurs for H2 adsorbed molecularly on Au/TiO2. In this case the calculated Bader charge localized on H2 is +0.11 e, where e is the elementary charge. Although such a charge transfer is relatively small, it might be responsible for the strong enlargement of the H–H bond length in H2–Au/TiO2 up to 0.906 Å. In most cases of molecular adsorption of hydrogen, the adsorbed molecule possesses some small positive charge. However, after dissociation, the hydrogen atoms can get an excess of negative charge. Depending on the geometric configuration, either both of the hydrogen atoms possess some small negative charge, or one H is charged negatively, while another H is charged positively. Thus, for example the H–H bond cleavage on the unsupported Au2 can be considered as heterolytic—one H possesses negative charge of −0.11 e, while another H possesses very small positive charge of +0.01 e. In this case the gold dimer becomes positively charged upon H2 dissociation with the net charge of +0.1 e. On the other hand, formation of the OH group with the bridge O(2) atom on the rutile surface is accompanied by the large charge transfer from H atom to O(2), resulting in a Bader net charge of H in OH equal to +0.75 e. Another H on Au cluster remains negatively charged. Note that formation of the hydrogen anions on the gold surface can influence probability of further hydrogenation reactions catalyzed by the supported gold clusters.
We can conclude that the catalytic activity of gold nanoparticles for O2 dissociation would depend on the electronic structure and the size of the nanoparticles; however in the case of H2 dissociation it will be proportional to the number of gold atoms located in the vicinity of the low coordinated O(2) atoms at the nanoparticle-surface interface.
4. Conclusions
The present theoretical study demonstrates the support effects are very important in the gold nanocatalysis. Even “inert” h-BN support, if it contains vacancy defects, can promote the catalytic properties of gold clusters in oxidation reaction by O2. It is demonstrated that Au and Au2 interact weakly with the regular defect-free h-BN surface; however they can be trapped effectively by N or B vacancy defects in h-BN. Strong adsorption on the surface defects is accompanied by the charge transfer to/from the adsorbate. The value and the sign of the charge accumulated on the adsorbate depend on the adsorption sites. Thus, VN donates electrons to the adsorbed Au and Au2, while VB acts as an electron acceptor. The excess of the positive or negative charge on the supported gold clusters can considerably promote their catalytic properties and enhance activation of the adsorbed O2. Our finding leads to a very important conclusion that gold clusters supported on the defected h-BN surface can not be considered as pseudo-free clusters. The support effects have to be taken into account.
We also demonstrate that the “active” rutile TiO2(110) support energetically promotes H2 dissociation on gold clusters. For this reaction the conventional charge transfer mechanism does not play an important role. However, adsorption of H2 on Aun and Aun/TiO2(110) (n = 1, 2, 8, 20) strongly depends on cluster size, geometric structure, flexibility and interaction with the support material. We demonstrate that the formation of the OH group near the supported gold cluster is an important condition for H2 dissociation. We have shown that the active sites towards H2 dissociation on the supported Aun are located at corners and edges of the gold cluster in the vicinity of the low coordinated oxygen atoms on TiO2(110). Therefore catalytic activity of a gold nanoparticle supported on the rutile TiO2(110) surface is proportional to the length of the perimeter interface between the nanoparticle and the support, in accordance with the recent experimental findings [38].

| Surface | Eb(Au) (eV) | QAu(|e|) | Eb(Au2) (eV) | QAu2 (|e|) |
|---|---|---|---|---|
| h-BN | 0.25 | −0.08 | 0.77 | −0.14 |
| VB@h-BN | 3.72 | 0.70 | 3.24 | 0.57 |
| VN @h-BN | 3.48 | −0.39 | 3.07 | −0.59 |
| Surface | Eb(O2)(eV) | dO−O (Å) | QAu1,2 (|e|) | QO2 (|e|) | QO2–Au1,2 (|e|) |
|---|---|---|---|---|---|
| Au | 0.49 | 1.27 | 0.19 | −0.19 | 0.00 |
| Au/VB@h-BN | 0.90 | 1.31 | 0.98 | −0.33 | 0.66 |
| Au/VN@h-BN | 1.10 | 1.44 | −0.10 | −1.31 | −1.41 |
| Au2 | 0.48 | 1.26 | 0.15 | −0.15 | 0.00 |
| Cluster | |||
|---|---|---|---|
| Au | 0.780 | 0.13 | 0.04 |
| Au2 | 0.845 | 0.59 | 0.59 |
| Au8 | 0.806 | 0.26 | 0.68 |
| Au20 | 0.768 | 0.09 | 0.14 |
| Cluster | |||
|---|---|---|---|
| Au/TiO2 | 0.906 | 1.15 | 2.06 |
| Au2/TiO2 | 0.821 | 0.37 | 1.55 |
| Au8/TiO2 | 0.792 | 0.24 | 1.55 |
| Au20/TiO2 | 0.795 | 0.17 | 0.83 |
Acknowledgments
This work was supported by the Global COE Program (Project No. B01: Catalysis as the Basis for Innovation in Materials Science) from the Ministry of Education, Culture, Sports, Science and Technology, Japan; the Grant-in-Aid for the Project on Strategic Utilization of Elements; the JSPS Grant-in-Aid for Scientific Research C; and the Collaborative Research Program 2011, Information Initiative Center, Hokkaido University, Sapporo, Japan. The computations were partly performed using the Research Center for Computational Science, Okazaki, Japan.
References
- Haruta, M.; Kobayashi, T.; Sano, H.; Yamada, N. Novel gold catalysts for the oxidation of carbon monoxide at a temperature far below 0 °C. Chem. Lett. 1987, 16, 405–408. [Google Scholar]
- Haruta, M. When gold is not noble: Catalysis by nanoparticles. Chem. Rec. 2003, 3, 75–87. [Google Scholar]
- Thompson, D.T. Using gold nanoparticles for catalysis. Nanotoday 2007, 2, 40–43. [Google Scholar]
- Nanocatalysis; Heiz, U., Landman, U., Eds.; Springer: Berlin, Heidelberg, Germany, 2007.
- Haruta, M. Size- and support-dependency in the catalysis of gold. Catal. Today 1997, 36, 153–166. [Google Scholar]
- Turner, M.; Golovko, V.B.; Vaughan, O.P.H.; Abdulkin, P.; Berenguer-Murcia, A.; Tikhov, M.S.; Johnson, B.F.G.; Lambert, R.M. Selective oxidation with dioxygen by gold nanoparticle catalysts derived from 55-atom clusters. Nature 2008, 454, 981–984. [Google Scholar]
- Hughes, M.D.; Xu, Y.J.; Jenkins, P.; McMorn, P.; Landon, P.; Enache, D.I.; Carley, A.F.; Attard, G.A.; Hutchings, G.J.; King, F.; Stitt, E.H.; Johnston, P.; Griffin, K.; Kiely, C.J. Tunable gold catalysts for selective hydrocarbon oxidation under mild conditions. Nature 2005, 437, 1132–1135. [Google Scholar]
- Tsunoyama, H.; Sakurai, H.; Negishi, Y.; Tsukuda, T. Size-specific catalytic activity of polymer-stabilized gold nanoclusters for aerobic alcohol oxidation in water. J. Am. Chem. Soc. 2005, 127, 9374–9375. [Google Scholar]
- Landon, P.; Collier, P.J.; Papworth, A.J.; Kiely, C.J.; Hutchings, G. Direct formation of hydrogen peroxide from H2/O2 using a gold catalyst. Chem. Commun. 2002, 2058–2059. [Google Scholar] [CrossRef]
- Lyalin, A.; Taketsugu, T. Cooperative adsorption of O2 and C2H4 on small gold clusters. J. Phys. Chem. C 2009, 113, 12930–12934. [Google Scholar]
- Lyalin, A.; Taketsugu, T. Reactant-promoted oxygen dissociation on gold clusters. J. Phys. Chem. Lett. 2010, 1, 1752–1757. [Google Scholar]
- Jia, J.; Haraki, K.; Kondo, J.N.; Domen, K.; Tamaru, K. Selective hydrogenation of acetylene over Au/Al2O3 catalyst. J. Phys. Chem. B 2000, 104, 11153–11156. [Google Scholar]
- Choudhary, T.V.; Sivadinarayana, C.; Datye, A.K.; Kumar, D.; Goodman, D.W. Acetylene hydrogenation on Au-based catalysts. Catal. Lett. 2003, 86, 1–8. [Google Scholar]
- Bailie, J.E.; Hutchings, G.J. Promotion by sulfur of gold catalysts for crotyl alcohol formation from crotonaldehyde hydrogenation. Chem. Commun. 1999, 2151–2152. [Google Scholar] [CrossRef]
- Schimpf, S.; Martin Lucas, M.; Mohra, C.; Rodemerck, U.; Brückner, A.; Radnik, J.; Hofmeister, H.; Claus, P. Supported gold nanoparticles: In-depth catalyst characterization and application in hydrogenation and oxidation reactions. Catal. Today 2002, 72, 63–78. [Google Scholar]
- Okumura, M.; Akita, T.; Haruta, M. Hydrogenation of 1,3-butadiene and of crotonaldehyde over highly dispersed au catalysts. Catal. Today 2002, 74, 265–269. [Google Scholar]
- Mohr, C.; Hofmeister, H.; Radnik, J.; Claus, P. Identification of active sites in gold-catalyzed hydrogenation of acrolein. J. Am. Chem. Soc. 2003, 125, 1905–1911. [Google Scholar]
- Zanella, R.; Louis, C.; Giorgio, S.; Touroude, R. Crotonaldehyde hydrogenation by gold supported on TiO2: Structure sensitivity and mechanism. J. Catal. 2004, 223, 328–339. [Google Scholar]
- Claus, P. Heterogeneously catalysed hydrogenation using gold catalysts. Appl. Catal. A Gen. 2005, 291, 222–229. [Google Scholar]
- Zhu, Y.; Qian, H.; Drake, B.A.; Jin, R. Atomically precise Au25(SR)18 nanoparticles as catalysts for the selective hydrogenation of α,β-unsaturated ketones and aldehydes. Angew. Chem. Int. Ed. 2010, 49, 1295–1298. [Google Scholar]
- Zhu, Y.; Wu, Z.; Gayathri, C.; Qian, H.; Gil, R.R.; Jin, R. Exploring stereoselectivity of Au25 nanoparticle catalyst for hydrogenation of cyclic ketone. J. Catal. 2010, 271, 155–160. [Google Scholar]
- Herzing, A.A.; Kiely, C.J.; Carley, A.F.; Landon, P.; Hutchings, G.J. Identification of active gold nanoclusters on iron oxide supports for CO oxidation. Science 2008, 321, 1331–1335. [Google Scholar]
- Rodrílguez-Vázquez, M.J.; Blanco, M.C.; Lourido, R.; Vázquez-Vázquez, C.; Pastor, E.; Planes, G.A.; Rivas, J.; López-Quintela, M.A. Synthesis of atomic gold clusters with strong electrocatalytic activities. Langmuir 2008, 24, 12690–12694. [Google Scholar]
- Heiz, U.; Sanchez, A.; Abbet, S.; Schneider, W.D. Catalytic oxidation of carbon monoxide on monodispersed platinum clusters: Each atom counts. J. Am. Chem. Soc. 1999, 121, 3214–3217. [Google Scholar]
- Bonačić-Koutecký, V.; Mitrić, R.; Bürgel, C.; Bchäfer-Bung, B. Cluster properties in the regime in which each atom counts. Comput. Mater. Sci. 2006, 35, 151–157. [Google Scholar]
- Hvolbæk, B.; Janssens, T.V.W.; Clausen, B.S.; Falsig, H.; Christensen, C.H.; Nørskov, J.K. Catalytic activity of Au nanoparticles. Nanotoday 2007, 2, 14–18. [Google Scholar]
- Lang, S.M.; Bernhardt, T.M.; Barnett, R.N.; Yoon, B.; Landman, U. Hydrogen-promoted oxygen activation by free gold cluster cations. J. Am. Chem. Soc. 2009, 131, 8939–8951. [Google Scholar]
- Bürgel, C.; Reilly, N.M.; Johnson, G.E.; Mitrić, R.; Kimble, M.L.; Castleman, A.W., Jr.; Bonačić-Koutecký, V. Influence of charge state on the mechanism of CO oxidation on gold clusters. J. Am. Chem. Soc. 2008, 130, 1694–1698. [Google Scholar]
- Coquet, R.; Howard, K.L.; Willock, D.J. Theory and simulation in heterogeneous gold catalysis. Chem. Soc. Rev. 2008, 37, 2046–2076. [Google Scholar]
- Ding, X.; Li, Z.; Yang, J.; Hou, J.G.; Zhu, Q. Adsorption energies of molecular oxygen on Au clusters. J. Chem. Phys. 2004, 120, 9594–9600. [Google Scholar]
- Fernández, E.; Ordejón, P.; Balbás, L.C. Theoretical study of O2 and CO adsorption on Aun clusters (n = 5–10). Chem. Phys. Lett. 2005, 408, 252–257. [Google Scholar]
- Häkkinen, H.; Landman, U. Gas-phase catalytic oxidation of CO by Au2−. J. Am. Chem. Soc. 2001, 123, 9704–9705. [Google Scholar]
- Yoon, B.; Häkkinen, H.; Landman, U. Interaction of O2 with gold clusters: Molecular and dissociative adsorption. J. Phys. Chem. A 2003, 107, 4066–4071. [Google Scholar]
- Socaciu, L.D.; Hagen, J.; Bernhardt, T.M.; Wöste, L.; Heiz, U.; Häkkinen, H.; Landman, U. Catalytic CO oxidation by free Au2−: Experiment and theory. J. Am. Chem. Soc. 2003, 125, 10437–10445. [Google Scholar]
- Häkkinen, H.; Abbet, S.; Sanchez, A.; Heiz, U.; Landman, U. Structural, electronic, and impurity-doping effects in nanoscale chemistry: Supported gold nanoclusters. Angew. Chem. Int. Ed. 2003, 42, 1297–1300. [Google Scholar]
- Hutchings, G.J.; Hall, M.S.; Carley, A.F.; Landon, P.; Solsona, B.E.; Kiely, C.J.; Herzing, A.; Makkee, M.; Moulijn, J.A.; Overweg, A.; Fierro-Gonzalez, J.C.; Guzman, J.; Gates, B.C. Role of gold cations in the oxidation of carbon monoxide catalyzed by iron oxide-supported gold. J. Catal. 2006, 242, 71–81. [Google Scholar]
- Lyalin, A.; Taketsugu, T. Adsorption of ethylene on neutral, anionic, and cationic gold clusters. J. Phys. Chem. C 2010, 114, 2484–2493. [Google Scholar]
- Fujitani, T.; Nakamura, I.; Akita, T.; Okumura, M.; Haruta, M. Hydrogen dissociation by gold clusters. Angew. Chem. Int. Ed. 2009, 48, 9515–9518. [Google Scholar]
- Okumura, M.; Tsubota, S.; Haruta, M. Preparation of supported gold catalysts by gas-phase grafting of gold acethylacetonate for low-temperature oxidation of CO and of H2. J. Mol. Catal. A Chem. 2003, 199, 73–84. [Google Scholar]
- Sanchez, A.; Abbet, S.; Heiz, U.; Schneider, W.D.; Hakkinen, H.; Barnett, R.N.; Landman, U. When gold is not noble: Nanoscale gold catalysts. J. Phys. Chem. A 1999, 103, 9573–9578. [Google Scholar]
- Yoon, B.; Häkkinen, H.; Landman, U.; Wörz, A.S.; Antonietti, J.M.; Abbet, S.; Judai, K.; Heiz, U. Charging effects on bonding and catalyzed oxidation of CO on Au8 clusters on MgO. Science 2005, 307, 403–407. [Google Scholar]
- Zhang, C.; Yoon, B.; Landman, U. Predicted oxidation of CO catalyzed by Au nanoclusters on a thin defect-free MgO film supported on a Mo(100) surface. J. Am. Chem. Soc. 2007, 129, 2228–2229. [Google Scholar]
- Sterrer, M.; Risse, T.; Pozzoni, U.; Giordano, L.; Heyde, M.; Rust, H.; Pacchioni, G.; Freund, H. Control of the charge state of metal atoms on thin MgO films. Phys. Rev. Lett. 2007, 98, 096107:1–096107:4. [Google Scholar]
- Frondelius, P.; Häkkinen, H.; Honkala, K. Adsorption of gold clusters on metal-supported MgO: Correlation to electron affinity of gold. Phys. Rev. B 2007, 76, 073406:1–073406:4. [Google Scholar]
- Honkala, K.; Häkkinen, H. Au adsorption on regular and defected thin MgO(100) films supported by Mo. J. Phys. Chem. C 2007, 111, 4319–4327. [Google Scholar]
- Harding, C.; Habibpour, V.; Kunz, S.; Farnbacher, A.N.S.; Heiz, U.; Yoon, B.; Landman, U. Control and manipulation of gold nanocatalysis: Effects of metal oxide support thickness and composition. J. Am. Chem. Soc. 2009, 131, 538–548. [Google Scholar]
- Arenal, R.; Stéphan, O.; Kociak, M.; Taverna, D.; Loiseau, A.; Colliex, C. Electron energy loss spectroscopy measurement of the optical gaps on individual boron nitride single-walled and multiwalled nanotubes. Phys. Rev. Lett. 2005, 95, 127601:1–127601:4. [Google Scholar]
- Golberg, D.; Bando, Y.; Huang, Y.; Terao, T.; Mitome, M.; Tang, C.; Zhi, C. Boron nitride nanotubes and nanosheets. ACS Nano 2010, 4, 2979–2993. [Google Scholar]
- Green, I.X.; Tang, W.; Neurock, M.; Yates, J.T. Low-temperature catalytic H2 oxidation over Au nanoparticle/TiO2 dual perimeter sites. Angew. Chem. Int. Ed. 2011, 50, 10186–10189. [Google Scholar]
- Boronat, M.; Illas, F.; Corma, A. Active sites for H2 adsorption and activation in Au/TiO2 and the role of the support. J. Phys. Chem. A 2009, 113, 3750–3757. [Google Scholar]
- Florez, E.; Gomez, T.; Liu, P.; Rodríguez, J.A.; Illas, F. Hydrogenation reactions on Au/TiC(001): Effects od Au-C interactions on the dissociation of H2. ChemCatChem 2010, 2, 1219–1222. [Google Scholar]
- Lyalin, A.; Taketsugu, T. A computational investigation of H2 adsorption and dissociation on Au nanoparticles supported on TiO2 surface. Faraday Discuss. 2011, 152, 185–201. [Google Scholar]
- Wu, Z.; Cohen, R.E. More accurate generalized gradient approximation for solids. Phys. Rev. B 2006, 73, 235116:1–235116:6. [Google Scholar]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar]
- Tran, F.; Laskowski, R.; Blaha, P.; Schwarz, K. Performance on molecules, surfaces, and solids of the Wu-Cohen GGA exchange-correlation energy functional. Phys. Rev. B 2007, 75, 115131:1–115131:14. [Google Scholar]
- Artacho, E.; Sánchez-Portal, D.; Ordejón, P.; García, A.; Soler, J.M. Linear-scaling ab-initio calculations for large and complex systems. Phys. Status Solidi B 1999, 215, 809–817. [Google Scholar]
- Junquera, J.; Paz, O.; Sánchez-Portal, D.; Artacho, E. Numerical atomic orbitals for linear-scaling calculations. Phys. Rev. B 2001, 64, 235111:1–235111:9. [Google Scholar]
- Nelder, J.A.; Mead, R. A simplex method for function minimization. Comput. J. 1965, 7, 308–313. [Google Scholar]
- Troullier, N.; Martins, J.L. Efficient pseudopotentials for plane-wave calculations. Phys. Rev. B 1991, 43, 1993–2006. [Google Scholar]
- Kleinman, L.; Bylander, D.M. Efficacious form for model pseudopotentials. Phys. Rev. Lett. 1982, 48, 1425–1428. [Google Scholar]
- Monkhorst, H.J.; Pack, J.D. Special points for Brillouin-zone integrations. Phys. Rev. B 1976, 13, 5188–5192. [Google Scholar]
- Yoo, C.S.; Akella, J.; Cynn, H.; Nicol, M. Direct elementary reactions of boron and nitrogen at high pressures and temperatures. Phys. Rev. B 1997, 56, 140–146. [Google Scholar]
- Burdett, J.K.; Hughbanks, T.; Miller, G.J.; Richardson, J.W., Jr.; Smith, J.V. Structural-electronic relationships in inorganic solids: Powder neutron diffraction studies of the rutile and anatase polymorphs of titanium dioxide at 15 and 295 K. J. Am. Chem. Soc. 1987, 109, 3639–3646. [Google Scholar]
- Muscat, J.; Swamy, V.; Harrison, N.M. First-principles calculations of the phase stability of TiO2. Phys. Rev. B 2002, 65, 224112:1–224112:15. [Google Scholar]
- Solov'yov, I.A.; Solov'yov, A.V.; Greiner, W.; Koshelev, A.; Shutovich, A. Cluster growing process and a sequence of magic numbers. Phys. Rev. Lett. 2003, 90, 053401:1–053401:4. [Google Scholar]
- Lyalin, A.; Solov'yov, I.A.; Solov'yov, A.V.; Greiner, W. Evolution of the electronic and ionic structure of Mg clusters with increase in cluster size. Phys. Rev. A 2003, 67, 063203:1–063203:13. [Google Scholar]
- Lyalin, A.; Solov'yov, A.V.; Greiner, W. Structure and magnetism of lanthanum clusters. Phys. Rev. A 2006, 74, 043201:1–043201:10. [Google Scholar]
- Lyalin, A.; Solov'yov, I.A.; Greiner, W. Interplay of electronic and geometry shell effects in properties of neutral and charged Sr clusters. Phys. Rev. A 2007, 75, 053201:1–053201:13. [Google Scholar]
- Ohno, K.; Maeda, S. A scaled hypersphere search method for the topography of reaction pathways on the potential energy surface. Chem. Phys. Lett. 2004, 384, 277–282. [Google Scholar]
- Maeda, S.; Ohno, K. Global mapping of equilibrium and transition structures on potential energy surfaces by the scaled hypersphere search method: Applications to ab initio surfaces of formaldehyde and propyne molecules. J. Phys. Chem. A 2005, 109, 5742–5753. [Google Scholar]
- Ohno, K.; Maeda, S. Global reaction route mapping on potential energy surfaces of formaldehyde, formic acid, and their metal-substituted analogues. J. Phys. Chem. A 2006, 110, 8933–8941. [Google Scholar]
- Fernández, E.; Soler, J.M.; Garzón, I.L.; Balbás, L.C. Trends in the structure and bonding of noble metal clusters. Phys. Rev. B 2004, 70, 165403:1–165403:14. [Google Scholar]
- Walker, A.W. Structure and energetics of small gold nanoclusters and their positive ions. J. Chem. Phys. 2005, 122, 094310:1–094310:12. [Google Scholar]
- Xiao, L.; Tollberg, B.; Hu, X.; Wang, L. Structural study of gold clusters. J. Chem. Phys. 2006, 124, 094310:1–094310:10. [Google Scholar]
- Häkkinen, H. Atomic and electronic structure of gold clusters: Understanding flakes, cages and superatoms from simple concept. Chem. Soc. Rev. 2008, 37, 1847–1859. [Google Scholar]
- Sánchez-Portal, D.; Ordejón, P.; Artacho, E.; Soler, J.M. Density-functional method for very large systems with LCAO basis sets. Int. J. Quantum Chem. 1997, 65, 453–461. [Google Scholar]
- Soler, J.M.; Artacho, E.; Gale, J.D.; García, A.; Junquera, J.; Ordejón, P.; Sánchez-Portal, D. The siesta method for ab initio order-N materials simulation. J. Phys. Condens. Matter 2002, 14, 2745–2779. [Google Scholar]
- Sánchez-Portal, D.; Ordejón, P.; Canadell, E. Computing the properties of materials from first principles with siesta. Struct. Bond. 2004, 113, 103–170. [Google Scholar]
- Bader, R. Atoms in Molecules: A Quantum Theory; Oxford University Press: New York, NY, USA, 1990. [Google Scholar]
- Henkelman, G.; Arnaldsson, A.; Jònsson, H. A fast and robust algorithm for Bader decomposition of charge density. Comput. Mater. Sci. 2006, 36, 354–360. [Google Scholar]
- Kokalj, A. Computer graphics and graphical user interfaces as tools in simulations of matter at the atomic scale. Comput. Mater. Sci. 2003, 28, 155–168. [Google Scholar]
- Huber, K.P.; Herzberg, G. Molecular Spectra and Molecular Structure Constants of Diatomic Molecules; Van Nostrand Reinhold: New York, NY, USA, 1979. [Google Scholar]
- Furthmüller, J.; Hafner, J.; Kresse, G. Ab initio calculation of the structural and electronic properties of carbon and boron nitride using ultrasoft pseudopotentials. Phys. Rev. B 1994, 50, 15606–15622. [Google Scholar]
- Orellana, W.; Chacham, H. Stability of native defects in hexagonal and cubic boron nitride. Phys. Rev. B 2001, 63, 125205:1–125205:7. [Google Scholar]
- Kuzubov, A.A.; Serzhantova, M.V.; Fedorov, A.S.; Tomilin, F.N.; Kozhevnikova, T.A. Theoretical study of vacancies and adatoms in white graphene. JETP Lett. 2011, 93, 335–338. [Google Scholar]
- Si, M.S.; Li, J.Y.; Shi, H.G.; Niu, X.N.; Xue, D.S. Divacancies in graphitic boron nitride sheets. Europhys. Lett. 2009, 86, 46002:1–46002:6. [Google Scholar]
- Zobelli, A.; Ewels, C.P.; Gloter, A.; Seifert, G.; Stephan, O.; Csillag, S.; Colliex, C. Defective structure of BN nanotubes: From single vacancies to dislocation lines. Nano Lett. 2006, 6, 1955–1960. [Google Scholar]
- Jin, C.; Lin, F.; Suenaga, K.; Iijima, S. Fabrication of a freestanding boron nitride single layer and its defect assignments. Phys. Rev. Lett. 2009, 102, 195505:1–195505:4. [Google Scholar]
- Yin, L.C.; Cheng, H.M.; Saito, R. Triangle defect states of hexagonal boron nitride atomic layer: Density functional theory calculations. Phys. Rev. B 2010, 81, 153407:1–153407:4. [Google Scholar]
- Corso, M.; Auwärter, W.; Muntwiler, M.; Tamai, A.; Greber, T.; Osterwalder, J. Boron nitride nanomesh. Science 2004, 303, 217–220. [Google Scholar]
- Laskowski, R.; Blaha, P.; Schwarz, K. Bonding of hexagonal BN to transition metal surfaces: An ab initio density-functional theory study. Phys. Rev. B 2008, 78, 045409:1–045409:10. [Google Scholar]
- Inorganic Chemistry; Wiberg, N., Holleman, A.F., Wiberg, E., Eds.; Academic Press: Waltham, MA, USA, 2001.
- Ramamoorthy, M.; Vanderbilt, D.; King-Smith, R.D. First-principles calculations of the energetics of stoichiometric TiO2 surfaces. Phys. Rev. B 1994, 49, 16721–16727. [Google Scholar]
- Perron, H.; Domain, C.; Roques, J.; Drot, R.; Simoni, E.; Catalette, H. Optimisation of accurate rutile TiO2(110), (100), (101) and (001) surface models from periodic DFT calculations. Theor. Chem. Acc. 2007, 117, 565–574. [Google Scholar]
- Lyalin, A.; Taketsugu, T. Catalitic activity of gold clusters. AIP Conf. Proc. 2009, 1197, 65–75. [Google Scholar]
- Barrio, L.; Liu, P.; Rodríguez, J.A.; Campos-Martín, J.M.; Fierro, J.L.G. A density functional theory study of the dissociation of H2 on gold clusters: Importance of fluxionality and ensemble effects. J. Chem. Phys. 2006, 125, 164715:1–164715:5. [Google Scholar]
© 2011 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Gao, M.; Lyalin, A.; Taketsugu, T. Role of the Support Effects on the Catalytic Activity of Gold Clusters: A Density Functional Theory Study. Catalysts 2011, 1, 18-39. https://doi.org/10.3390/catal1010018
Gao M, Lyalin A, Taketsugu T. Role of the Support Effects on the Catalytic Activity of Gold Clusters: A Density Functional Theory Study. Catalysts. 2011; 1(1):18-39. https://doi.org/10.3390/catal1010018
Chicago/Turabian StyleGao, Min, Andrey Lyalin, and Tetsuya Taketsugu. 2011. "Role of the Support Effects on the Catalytic Activity of Gold Clusters: A Density Functional Theory Study" Catalysts 1, no. 1: 18-39. https://doi.org/10.3390/catal1010018




