1. Introduction
Ken Binmore [
1] demarcates two modes of analysis in game theory. The eductive mode (comprised of deduction, induction, and adduction) analyzes social behavior according to the strict idealizations of rational choice theory. The evolutive mode analyzes social behavior according to dynamic models that relax said idealizations. I substitute the disciplines of epistemic and evolutionary game theory for Binmore’s modes of analysis. Epistemic game theory provides the epistemic foundations for rational justification of social behavior. Conversely, evolutionary game theory establishes social behavior that is evolutionarily fit and stable. It is descriptive and provides for the causal explanation of social behavior.
A recent discipline—I denote it ‘naturalistic game theory’—splits the difference between epistemic and evolutionary game theory. The disciplines of neuroeconomics and behavioral game theory [
2], the application of heuristics from an adaptive toolbox to real-world uncertainty [
3,
4], and the study of optimization under cognitive constraints [
5,
6] are three converging approaches to a more realistic basis for game theory. All foundational concepts are analyzed vis-à-vis real people with cognitive limits. Work has started on common knowledge, convention, and salience; I contribute to this discipline with my analysis of strategy and the rationality of belief-revision policies.
I argue that the very concept of strategy is best understood vis-à-vis real people’s cognitive limits. A strategy is traditionally defined as a complete plan of action, which evaluates every contingency in a game of strategy. However, only ideal agents can evaluate every contingency. Real people require policies to revise their beliefs and guide their choices when confronted with unforeseen contingencies. The very concept of strategy requires belief-revision policies. Yet, in epistemic game theory, belief-revision policies are part of those idealizations (the game’s structure, the agents’ rationality, and the game’s epistemic context) stipulated to formally prove conditional results about the game’s outcomes. The rationality of strategies or acts depends on belief-revision policies, but the rationality of belief-revision policies remains unanalyzed.
The rationality of belief-revision policies is the subject of Bayesian epistemology. The objects of belief-revision policies are doxastic or epistemic states (I, henceforth, use ‘epistemic’ to refer to both types of states). Hence, the objects of analysis of belief-revision policies are epistemic states, not strategies and acts. Whereas traditional epistemology studies three basic judgments (belief, disbelief, or suspension of belief), Bayesian epistemology studies degrees of belief as credences, which indicate the confidence that is appropriate to have in various propositions. I extend the epistemic foundations of game theory to issues in Bayesian epistemology. I construct an arbitrary belief-revision policy by establishing its components: agents’ credences are constrained by the probability axioms, by conditionalization, and by the principles of indifference and of regularity. I also consider non-evidential factors that affect credence distributions, despite those credences being rationally constrained.
I explain the general program of naturalistic game theory in
Section 2. The main claim is that foundational concepts are best understood vis-à-vis real people’s cognitive limits, which explains why analyzing said concepts in highly abstract and artificial circumstances is problematic. I then argue the same case for strategy and belief-revision policies in
Section 3. Indeed, the charge of incoherence to backward induction is best explained by naturalism. However, this leaves open the question of how we analyze the rationality of belief-revision policies. I suggest doing so through Bayesian epistemology in
Section 4 and
Section 5. I place the epistemic foundations of game theory into a more foundational epistemology.
3. Strategy for Ideal Agents and for Real People
The concept of strategy has the same fate as rationality and common knowledge: strategy is best conceived vis-à-vis real people’s cognitive limits. Indeed, I argue that the charge of incoherence to backward induction is an excellent example of the limits of the traditional concept of strategy.
The charge of incoherence is presented as either one of two problems. The first problem is that backward induction requires agents to evaluate all contingencies in a game to settle on the backward induction profile, but certain contingencies cannot be evaluated without violating backward induction [
17,
18,
19,
20,
21,
22,
23]. The second problem is that backward induction ‘seems logically inescapable, but at the same time it is intuitively implausible’ ([
24], p. 171).
A game theorist analyzes a game from an outside perspective to provide a game’s complete analysis, which is its theory [
18]. The game theorist specifies the game’s structure, the set of agents’ strategies, and their payoffs. He defines the agents’ rationality, and then specifies the game’s epistemic context, which is the agents’ epistemic states concerning their circumstances. The game theorist then proves conditional results about the game’s outcomes as profiles of agents’ strategies [
25,
26,
27,
28]. Backward induction applies to the formation of strategies.
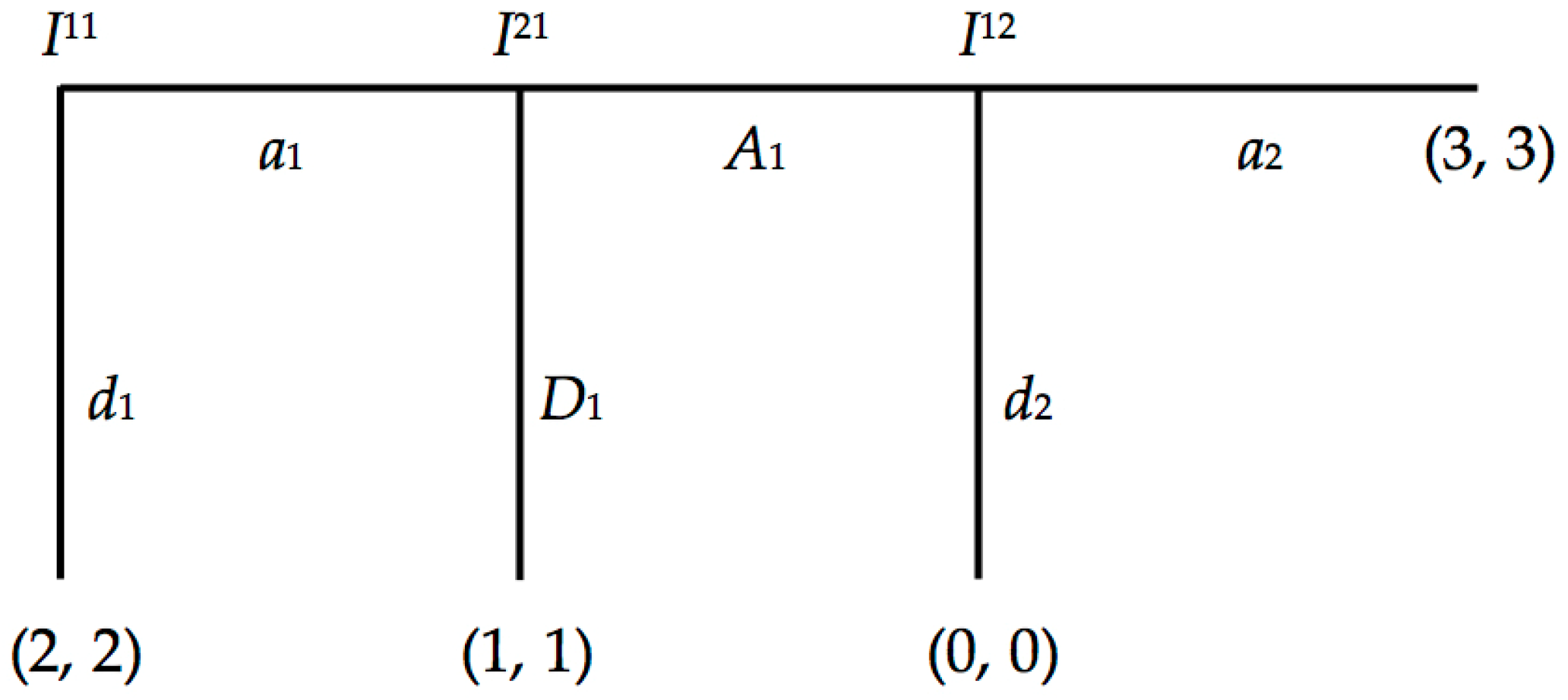
For any sequential game with perfect (and complete) information, a strategy is a function that assigns an action at every stage the agent can possibly reach, including those stages not reached during gameplay ([
29], p. 108). Consider Robert Stalnaker’s [
30,
31] sequential game in
Figure 1:
Suppose we differentially distribute the agents’ epistemic states across the game’s stages and consider each stage as an agent’s information state such that:
- (1)
The first agent is rational at I12.
- (2)
The second agent is rational at I21 and knows (1).
- (3)
The first agent is rational at I11 and knows (2).
The agents are rational insofar as they maximize their expected payoffs. Then the distributed epistemic states are all that are required to construct the agents’ strategies through backward induction. Beginning at the third stage and reasoning our way backwards to the first stage, backward induction settles the first agent’s strategy (a1, a2) as the best response to the second agent’s strategy (A1), and vice versa. The outcome (a1a2, A1) is the sub-game perfect equilibrium and the game’s solution entailed by (1), (2) and (3). Though it is not the case in this game, an important condition of the formal definition of strategy is that agents assign actions for those stages that will not be reached by the agent during gameplay.
Robert Aumann argues that common knowledge of rationality implies the backward induction profile in sequential games with perfect information [
32,
33,
34]. Backward induction requires that there are no stages where it is unclear whether a choice maximizes an agent’s expected payoff. Aumann introduces clarity by providing agents with the right sort of rationality throughout the game. An agent is substantively rational just in case every choice maximizes his expected payoffs at all stages the agent can possibly reach. Substantive rationality includes those stages that an agent will not actually reach during gameplay. This is the sort of rationality Aumann associates with backward induction. This is different from evaluating acts that have occurred. An agent is materially rational just in case every choice the agent actually acts on maximizes his expected payoffs. Notice the trivial case that if an agent never acts in a game, that agent is materially rational.
Consider the following case from Stalnaker [
31] with the profile (
d1a2,
D1). This profile is a deviation from the backward induction profile, and Stalnaker uses it to show the difference between substantive and material rationality. Suppose the first agent knows the second agent is following strategy
D1. The first agent’s act
d1 maximizes his expected payoff, given
D1. And the first agent’s act
a2 maximizes his expected payoff, given the game’s structure and payoffs. The first agent is substantively rational. Now suppose the second agent knows the first agent is following strategy
d1a2. Thus, the second agent knows that the first agent initially chooses
d1, and, if the first agent reaches the third stage, the first agent chooses
a2. Stalnaker explains that the second agent is materially rational, since the second agent never acts on his strategy. His material rationality is preserved through inaction. Is the second agent, nonetheless, substantively rational? Aumann argues that the second agent is not substantively rational, because his choice
D1 does not maximize his payoff at the second stage. However, Stalnaker argues that there is insufficient information about what the second agent knows about the first agent, to assess the second agent’s choice
D1 at the second stage.
Stalnaker explains that substantive rationality conflates two types of conditionals, given deviations from the backward induction profile. The first conditional is causal: if the second stage were reached, the second agent only evaluates subsequent stages and believes the first agent would choose a2, since the first agent is rational. The causal conditional expresses a belief about an opponent’s disposition to act in a contingency that will not arise. The second conditional is epistemic: suppose there is a deviation from the backward induction profile. The second agent revises his beliefs about his opponent, given that the second stage is reached. The epistemic conditional concerns the second agent’s belief-revision policy. The second agent is not required to maintain his current beliefs about his opponent upon learning there is a deviation from the backward induction profile. Therefore, if the formal definition of strategy requires agents to evaluate all contingencies in a game to settle on the backward induction profile, and if deviations cannot be evaluated without violating backward induction, then a belief-revision policy is required to evaluate deviations without violating backward induction. The epistemic conditional is the conditional relevant to evaluating deviations and circumventing the charge of incoherence to backward induction.
I argue, however, that the charge of incoherence to backward induction presumes a concept of strategy that requires an
explicit choice of action for every contingency, which further presumes an ideal agent. Dixit, et al. [
35] provide a simple test to determine whether a strategy is a complete plan of action. A strategy:
…should specify how you would play a game in such full detail—describing your action in every contingency—that, if you were to write it all down, hand it to someone else, and go on vacation, this other person acting as your representative could play the game just as you would have played it. He would know what to do on each occasion that could conceivably arise in the course of play, without ever needing to disturb your vacation for instructions on how to deal with some situation that you have not foreseen.
The test is whether your strategy is sufficient for your representative to play the game just as you would without requiring further instruction. If so, your strategy is a complete plan of action. The representative test requires an ideal agent. An ideal agent has no cognitive limits, can perform any deduction, knows all logical and mathematical truths, and has all information (traditionally in the form of common knowledge) required to choose rationally. Only an ideal agent can evaluate and then assign a choice of action for every contingency.
However, does an ideal agent have use for a belief-revision policy to account for deviations from the backward induction profile? I argue ‘no’. An ideal agent is provided with all the information about his opponent to properly strategize. The ideal agent knows his opponent. An ideal agent can consider counterfactual circumstances about his opponent (supposing he were mistaken about his opponent or circumstances). However, the ideal agent does not need to strategize based on possible mistakes, because those mistakes are not matter-of-fact. Indeed, an ideal agent maintains his current beliefs about his opponent. Hence, strategizing precludes any deviations from expected gameplay. If an ideal agent has little need for a belief-revision policy, then an ideal agent has little need for strategizing with epistemic conditionals. The ideal agent will take his circumstances and evaluate them as they are.
Stalnaker anticipates my objection.
Now it may be that if I am absolutely certain of something, and have never even imagined the possibility that it is false, then I will not have an explicit policy in mind for how to revise my beliefs upon discovering that I am wrong. But I think one should think of belief-revision policies as dispositions to respond, and not necessarily as consciously articulated policies. Suppose Bob is absolutely certain that his wife Alice is faithful to him—the possibility that she is not never entered his mind. And suppose he is right—she is faithful, and he really knows that she is. We can still ask how Bob would revise his beliefs if he walked in one day and found his wife is bed with another man. We need not assume that Bob’s absolute certainty implies that he would continue to believe in his wife’s faithfulness in these circumstances, and we need not believe that these circumstances are logically impossible. We can make sense of them, as a logical possibility, even if they never occur to Bob. And even if Bob never thought of this possibility, it might be true that he would react to the situation in a certain way, revising his beliefs in one way rather than another.
However, what Bob knows about Alice is crucial to how he evaluates his choices in this case. What is relevant to Bob is how he will actually interact with Alice, and how he will actually interact with Alice depends on what he knows about her. Bob can consider a hypothetical case of his wife’s infidelity and still know Alice is faithful—they are not logically incompatible. However, Bob will choose how he interacts with his wife based on his knowledge of her faithfulness, not on a hypothetical case of infidelity. Bob can even devise the most sophisticated belief-revision policy to acount for myriad hypothetical cases of Alice’s infidelity. But that policy is based on nothing more than fictions: epistemic conditionals with false antecedents. Bob does not include his belief-revision policy in his decision-making when interacting with his wife, because of what he knows about her. Indeed, I can make sophisticated decisions about how I will interact in Harry Potter’s world. I can devise a belief-revision policy to account for myriad magical circumstances, a policy that considers that I am mistaken about not existing in Harry Potter’s world, but it is a fictional world and it does not affect how I will act in this world.
Choices track efficacy, not auspiciousness ([
8],
Section 1). Evidential conditionals have false antecedents. Hence, an ideal agent will not consider deviations, because they are not efficacious, regardless of their auspiciousness. The information provided to an ideal agent is information that tracks efficacy. Hence, an ideal agent evaluates his choices’ causal influence on an outcome. An ideal agent’s belief-revision policy just accounts for a fictional world.
Therefore, ideal agents do not require belief-revision policies. If strategy does require belief-revision policies, it is for real people with cognitive limits. Real people can only foresee some contingencies and require a strategy with a belief-revision policy to address unforeseen contingencies. Their plan of action is provisional and open-ended. Real people do not know their choice’s efficacy. Moreover, the representative test is not intelligible to real people. It is not simply a listing of instructions of the form: ‘If contingency C occurs, choose action A’. A strategy includes the complete reasoning behind the forming of instructions, and that reasoning includes what is known about every contingency. A complete plan of action is incomprehensible and too complex for real people. It takes an ideal agent to make sense of the representative test.
I propose a more realistic understanding of the representative test. A realistic strategy can pass the test without the need of providing a complete plan of action. A representative might play the game in your favor by following a simple strategy in the form of an algorithm that can still evaluate any unforeseen contingency. The strategy Tit-For-Tat passes the representative test. The instructions might be written as:
Step 1: Cooperate at the first stage of the game.
Step 2: If the opponent cooperates at stage n − 1 (for n > 2), cooperate at stage n. Otherwise, defect at stage n.
The strategy is simple, yet provides sufficient information for a representative to play the game exactly as you specify, knowing what to do in any contingency without needing to contact you for further instructions given an unforeseen situation. Notice the strategy does not assign specific actions for every contingency in a sequential game. There is no need for such specification. This simple strategy ably passes the representative test, because it has an implicit belief-revision policy.
The implicit belief-revision policy (without formally stating it for the moment) includes epistemic dependence between an opponent’s prior acts and an agent’s future choice of action. I shall address this more in the next section. Belief-revision polices are crucial to the evaluation of real people’s strategies and acts, but only if belief-revision policies themselves are rational. How do we assess a policy’s rationality?
4. The Fitness of Belief-Revision Policies
I shall briefly discuss the potential role of evolutionary game theory for investigating the rationality of belief-revision policies. It can evaluate belief-revision policies by testing which polices are ‘better’ than others through evolutionary fitness. Robert Axelrod’s tournaments [
36] are well-known for directly testing strategies for evolutionary fitness. These same tournaments can indirectly test belief-revision policies for fitness, because strategies in said tournaments have corresponding belief-revision policies.
The strategy Tit-For-Tat has the following implicit policy:
Tit-For-Tat Policy: Cooperate at the first stage of the game. If the opponent cooperates at stage n − 1 (for n > 2), treat the opponent as a cooperator in future stages and choose cooperation at stage n. Otherwise, treat the opponent as a defector in future stages and choose defection at stage n.
The strategy calls for an agent to initially cooperate, and then consider his opponent’s previous act, and then revise his belief about his opponent’s subsequent act. It is a policy that has epistemic dependence between an opponent’s prior acts and the agent’s future choice of action.
There is nothing preventing us from devising strategies and corresponding policies with as much or as little detail as we desire. We simply include Robert Stalnaker’s condition of epistemic dependence between prior acts and future choice of action. Any belief-revision policy can be represented as follows:
Generic Belief-Revision Policy: If an opponent does action aj at stage n − 1 (for n > 2), treat the opponent with disposition D and respond with action Aj at stage n. Otherwise, continue with current set of beliefs and choice of action at stage n.
The response simply depends on the agent’s belief-revision policy, which attributes a disposition to the opponent (for example, the opponent’s hand trembled, is irrational, is a cooperator, etc.).
This program is fruitful and necessary: it explains the fitness of belief-revision policies. However, it is limited. It provides only as much information about which policy is fittest, as it does about which strategy is fittest. Kristian Lindgren and Mats Nordahl [
37] have studied numerous strategies in Axelrod tournaments and found that there is no ‘optimal’, ‘best’, or outright ‘winning’ strategy. A strategy such as Tit-For-Tat performs better than other strategies for a period of time, before another strategy replaces it. The same might be said about corresponding belief-revision policies.
5. Constructing Belief-Revision Policies
An ideal agent with no cognitive limits can settle on a strategy for every contingency in a game. He has no need for a belief-revision policy as Robert Stalnaker envisions. However, real people with cognitive limits can only consider some contingencies. They do require a belief-revision policy for contingencies they have not considered. Thus, if a strategy requires a belief-revision policy, the concept is best understood vis-à-vis real people’s cognitive limits. I shall focus on this realism in this section.
Epistemic game theory has developed Bayesian analyses of agents revising their beliefs during gameplay. However, the discipline has not fully considered some foundational issues in Bayesian epistemology. The most significant issue is that virtually any rational credence distribution can be assigned to a set of propositions (without changing the evidential circumstances). The aim is to compute a unique credence distribution for a set of propositions, given the evidential circumstances. I provide insight into the rationality of belief-revision policies by introducing their components through an example. The aim is for a unique credence distribution that is actionable. belief-revision policies have evidential and non-evidential components. The evidential components are Bayesian principles that guide how agents ought to revise their beliefs during gameplay. The non-evidential component that I consider is agents’ temperaments. I show that evidential components can pare down an agent’s credences into a unique distribution, but temperaments change credence distributions between agents—a concern that might have to be accepted about belief-revision policies.
Traditional epistemology treats three sorts of judgments: Belief, disbelief, and suspension of belief [
38]. Bayesian epistemology instead treats credences, which indicate the differences in an agent’s confidence in a set of propositions. Bayesian epistemology provides rational constraints on credences. The two fundamental rational constraints are synchronic and diachronic [
39]. The synchronic thesis states that an agent’s credences are rational at a given moment just in case those credences comply with Andrey Kolmogorov’s [
40] probability axioms. The diachronic thesis states that an agent’s credences are rational across time just in case those credences update through conditionalization in response to evidence. Both the synchronic and diachronic theses are typically justified by Dutch Book arguments.
The credence function Cr maps a set of propositions to real numbers. Conditionalization applies Bayes’s theorem to a conditional credence Cr(H|E) = (Cr(E|H)Cr(H))/Cr(E), given that Cr(E) > 0. Cr(H) is the unconditional credence in the hypothesis. Cr(E|H) is the likelihood of the hypothesis on the total evidence. An unconditional credence distribution is computed for a set of propositions from the conditional credence distribution for those propositions, given the total evidence. Conditionalization provides rational closure. If an unconditional credence distribution is constrained by the probability axioms and updates by conditionalization, the resulting credence distribution is constrained by the probability axioms, too.
An arbitrary belief-revision policy is thus far composed of credences constrained by the probability axioms and by conditionalization. In general, I apply credences to finitely repeated and sequential (two-agent) games with perfect (but incomplete) information. Propositions are about agents’ strategies. Agents have cognitive limits, but they know certain features of a game. They have perfect information: they know all acts that occur during gameplay. This might not be a fair specification for real people (real people have imperfect memories), but it tracks conditionalization. Agents also know the structure of the game, its payoffs, and the set of available strategies. However, they do not know each other’s chosen strategy or immediate acts. Indeed, I specify that agents do not settle on a complete plan of action before gameplay. They instead settle on an immediate choice of action. An agent applies conditionalization on his opponent’s acts during gameplay. Furthermore, they do not know each other’s rationality. I specify that each agent is rational insofar as they each maximize their expected payoffs, but they do not know about each other’s rationality. Each agent has some initial credence that his opponent is irrational, given that some of his opponent’s available strategies might not maximize expected payoffs.
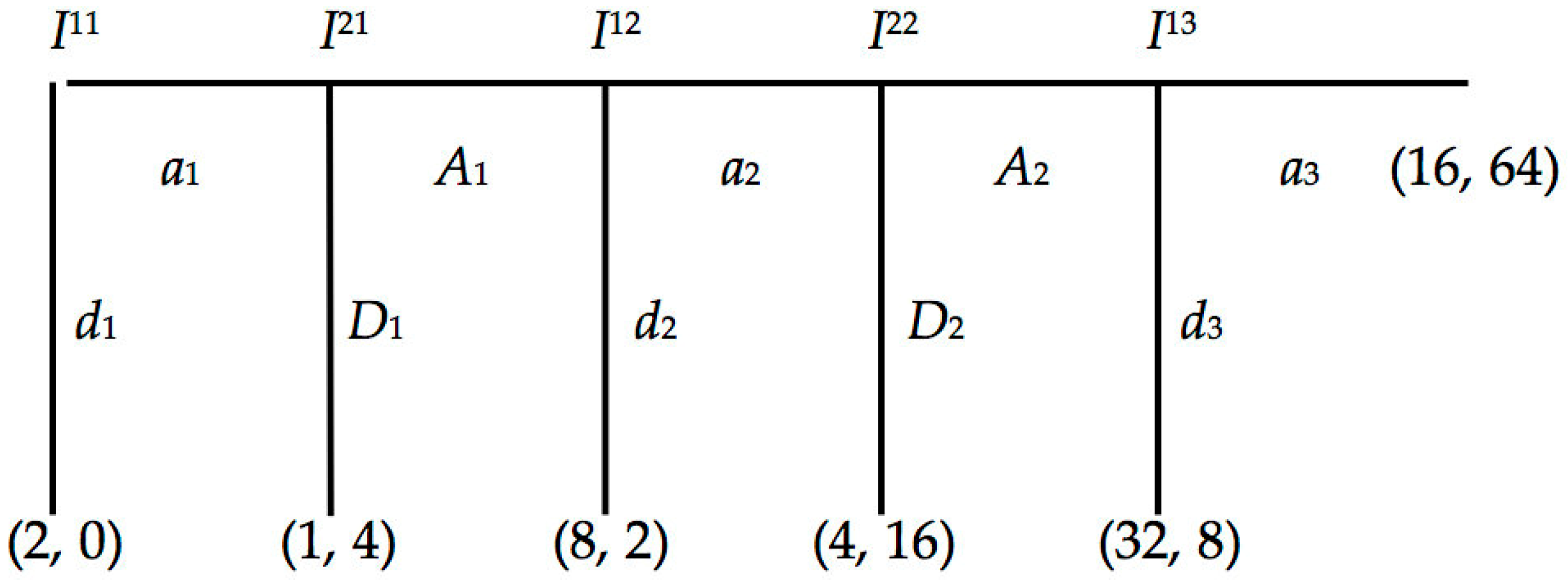
I use the Centipede Game in
Figure 2 as an example. Agents are not endowed with any evidence about each other’s strategies before gameplay. The first agent has 2
3 available strategies: (
a1a2a3), (
a1a2d3), (
a1d2a3), (
a1d2d3), (
d1a2a3), (
d1a2d3), (
d1d2a3), and (
d1d2d3). The second agent has 2
2 available strategies: (
A1A2), (
A1D2), (
D1A2), and (
D1D2).
Agents are thus far not precluded from assigning
Cr = 1 or
Cr = 0 to contingent propositions. Agents might have certainty or complete unbelief about contingent propositions. But it is more plausible that real people with cognitive limits are uncertain about opponents’ strategies. Any evidence about opponents’ strategies accumulated during gameplay will provide some credence about those strategies. Thus, a credence distribution assigns each strategy some credence. I thus include the principle of regularity into any belief-revision policy. It states that a contingent proposition in a rational credence distribution receives 1 >
Cr > 0 [
41]. The principle of regularity is an additional rational constraint to the probability axioms and conditionalization. It pares down credence distributions that can be assigned to a set of contingent propositions.
However, it does not, together with the probability axioms and conditionalization, compute a unique credence distribution. Suppose each agent begins the game with a
Cr = 1/
n for a number
n of an opponent’s available strategies. The second agent is assigned
Cr = 1/8, while the first agent is assigned
Cr = 1/4 for each of his opponent’s available strategies. Suppose the first agent chooses and acts on
a1 at
I11, and the second agent must decide whether to choose
D1 or
A1 at
I21, which depends on whether the first agent will choose
d2 or
a2 at
I12. The second agent’s choice is between his opponent’s four remaining available strategies: (
a1a2a3), (
a1a2d3), (
a1d2a3), (
a1d2d3). It is important to recognize that the act
a1 at
I11 is evidence that alone does not favor any particular strategy over another in the remaining set of available strategies. The second agent, thus, applies conditionalization on said evidence and evenly assigns credences to those strategies (the evidence does not favor one strategy over another). This is a reasonable application of the principle of indifference. It states that an agent updates his credences proportionally to the evidence, and no more [
42]. The second agent applies conditionalization upon the current evidence of
a1 at
I11, and has
Cr = 1/4 in strategies (
a1a2a3), (
a1a2d3), (
a1d2a3), (
a1d2d3). Removing acts that have occurred, he has
Cr = 1/4 in (
a2a3), (
a2d3), (
d2a3), (
d2d3). The principle of indifference guides the second agent’s judgment of his opponent’s future choice of action. It is an additional rational constraint to regularity, to the probability axioms, and to conditionalization.
How does the second agent choose an action, given his current credence distribution? The second agent has a simplified decision problem at I21. He has two choices between D1 for the immediate payoff of 4, or A1 for the chance of a payoff of 16 at I22. This depends on the likelihood of the first agent choosing a2 at I12. We can compute a credence threshold for the second agent. His expected payoff for A1 at I21 is Cr(a2 at I12)(16) + (1 − Cr(a2 at I12))(2), which is set equal to 4. Apply some algebra and the second agent has a threshold Cr(a2 at I12) = 1/7. If the second agent’s credence at I21 surpasses his threshold, he maximizes his expected payoff by choosing A1 at I22. The second agent’s credence in my example is 1/2 that a2 at I12.
Now, suppose the first agent chooses a2 at I12, and the second agent must decide whether to choose D2 or A2 at I22. This depends on whether the first agent will choose d3 or a3 at I13. Again, the act a2 at I12 is evidence that does not alone favor any particular strategy over another in the remaining set of available strategies. The second agent thus updates his credences proportionally to the evidence, and no more. The second agent applies conditionalization upon the current evidence of a2 at I12, and has Cr = 1/2 in strategies (a1a2a3), (a1a2d3). Removing acts that have occurred, he has Cr = 1/2 in a3 and d3. The second agent’s credence threshold that a3 at I13 is 1/7, as computed above. He maximizes his expected payoff by choosing A2 at I22. The reader might find this result surprising, because it is stipulated that each agent is rational—the first agent will choose d3 at I13. However, remember that agents only know about their own rationality, not about each other’s.
The principle of indifference is an additional rational constraint to regularity, to the probability axioms, and to conditionalization. It pares down credence distributions that can be assigned to a set of contingent propositions. However, there are objections to the principle that it recommends different credences for the same evidence, depending on how we partition a set of propositions. Here is a standard example. I explain that my ugly sweater is some color. You consider whether my ugly sweater is red, and partition the choices to red and not-red. The principle of indifference recommends that Cr(R) = 1/2, and that Cr(~R) = 1/2. However, you then consider whether my ugly sweater is one of the primary colors. Then the principle recommends that Cr(R) = 1/3, and that Cr(~R) = 2/3. The principle recommends different credences depending on how you partition the choice of colors, given the same evidence.
I argue, however, that the problem is not with the principle of indifference. Evidence is both subject to evidential and non-evidential components, and this objection to the principle of indifference is an example of the influence of non-evidential components. Consider that epistemology has two comprehensive goals. One goal is to minimize the amount of falsehoods an agent obtains. The other goal is to maximize the amount of truth an agent obtains. No goal is guaranteed, and realistically an agent balances between both in evaluating evidence. Thus, some agents have a skeptical temperament. They cautiously accept evidence, which is reflected by low credences in particular propositions. Some agents have a credulous temperament. They too willingly accept evidence, which is reflected by high credences in particular propositions. Temperaments affect how agents partition a set of propositions, or agents’ confidence in the evidence they evaluate. This non-evidential component combines with evidential components to establish credence distributions. Non-evidential components make the difference between two agents applying conditionalization with the same evidence, resulting in different credence distributions, despite their rational constraint.
How is epistemic game theory to account for non-evidential components? Epistemic game theory is traditionally concerned with the use of epistemic states to rationally justify a game’s outcome as a profile of agents’ strategies—the solution to the game. A Bayesian approach to belief-revision policies (for agents with cognitive limits, where temperaments affect their credences) might have to concede that there is no rational prescription for games as an outcome with a unique profile of strategies—no ultimate solution. It might prescribe a set of profiles where many of a game’s outcomes will satisfy that set of profiles. But this is simply saying that a game can have many outcomes real people might rationally settle on. This is not to say their beliefs and corresponding actions are not rational. If there is a lesson to learn from Bayesianism, agents’ beliefs and their corresponding acts can be rational while simultaneously not settling on an optimal outcome.
As a side note, naturalistic game theory does investigate non-evidential components. The study of heuristics [
3,
4] is a study of temperaments, or, more specifically, cognitive biases. The term ‘cognitive bias’ has a negative connotation, but biases can provide better outcomes in specific circumstances than more sophisticated tools, especially in uncertainty. The study of biases as heuristics is a study of the environment in which the biases evolved; and there is ongoing investigation into how agents’ temperaments (non-evidential components) are environmentally constrained.