Abstract
This paper analyzes a reward system that uses a club good to promote recycling. In particular, we examine a context of incomplete information in which the administrator is unable to observe the resident’s attitude towards recycling. The results suggest that despite the lack of information, the administrator is able to induce all types of residents to recycle when the reward is sufficiently high. Furthermore, we show that education programs, technologies that help to reduce the residential recycling cost and penalties for garbage dumping are complementary tools that could also promote recycling.
JEL classification:
D82; Q53; Q58
1. Introduction
Greenhouse gas (GHG) emissions have become one of the major issues in today’s economy. The Stern Review [1] calls for an immediate decisive action to stabilize GHG emissions because the benefits of strong, early action on climate change outweigh the costs. Specifically, it concludes that, without action, the overall costs would be equivalent to losing at least 5 percent of global gross domestic product each year. The number of studies examining this problem has substantially increased during the last decade. In particular, those papers mainly focus on policies that ameliorate firms’ pollution such as markets for emission permits, quotas, and pollution taxes [2,3,4,5]. From an environmental perspective, regulation is essential for reducing gas emissions. However, it is difficult to design and implement due mainly to political opposition [6]. In addition, some researchers argue that policies that help to slow down emissions might decrease total factor productivity [7].
This paper analyzes a residential recycling promotion model, which complements those studies focused on environmental policies targeting producers. The U.S. Environmental Protection Agency [8] reports that 11 percent of global GHG emissions are generated from commercial and residential buildings. Although residential pollution is lower than its industrial counterpart, the reported percentage suggests that promoting recycling would certainly help to reduce emissions. For example, U.S. consumers use about 70 million tons of paper per year, since recycling one ton of paper saves 4100 kilowatt hours of electricity. This amount of energy is enough to power the average American home for five months [9].1
We develop a Recycling Reward System (RRS) that provides incentives to residents by rewarding a club good when they commit to recycling.2 For instance, if the resident commits, she has access to free Wi-Fi in her town or access to eBooks from the public library. However, if the resident does not commit, she does not receive access to the club good. We examine under which conditions an administrator who does not observe the resident’s recycling preferences decides to establish the system.3 Specifically, the model considers two types of residents: a resident who favors the protection of the environment (friendly resident), and another who is not concerned about the environment (neutral resident). We assume that a resident’s payoff depends on the environmental benefit, the cost of recycling, and the reward. The structure of the game is the following, in the first stage, a resident decides whether or not to commit to the RRS and, in the second stage, the administrator, after observing the resident’s action, responds with choosing whether to establish the system. If the RRS is established, residents who committed benefit from a club good independent of their type.4
We find a Separating Perfect Bayesian Equilibrium in which only the environmentally friendly type commits to the RRS, and the administrator establishes the recycling system after observing commitment. In addition, we find two Pooling Perfect Bayesian Equilibria. In the first pooling equilibrium, both types of residents commit to the RRS and the administrator responds by establishing the recycling system. In the second equilibrium, in contrast, neither type of resident commits and the administrator does not establish the system. The results suggest that a cooperative outcome (in which both types of residents recycle) can be achieved, despite the administrator’s lack of information about the resident’s environmental concerns. In this case, the amount of the reward is crucial for the establishment of the RRS. In particular, the administrator must evaluate the appropriate amount of reward that induces recycling considering his monetary resources. On the one hand, a resident is more likely to commit to recycling as the reward increases. On the other hand, the administrator cannot provide an amount beyond his budget constraint.
We also provide a social welfare analysis and find that both the separating and the pooling equilibrium are socially desirable compared to the case in which the RRS is not implemented. When the environmental benefit rises, it increases the environmentally friendly resident’s incentives to recycle and, hence, promotes the emergence of the separating equilibrium. In addition, both types of residents are more likely to recycle when the amount of club good becomes larger. Furthermore, we observe that the pooling equilibrium is socially preferred if the net benefit from recycling by a neutral resident is positive. However, if the environmental damage generated by a neutral type is sufficiently large and the aggregate benefit does not exceed her cost from recycling, the social welfare under the separating equilibrium is unambiguously larger than that under the pooling equilibrium. We also develop a numerical simulation to evaluate the welfare improvements of each equilibrium relative to the status quo (no recycling program). From a policy perspective, our results indicate that, in order to promote recycling, the administrator should develop educational programs that highlight its benefits, thus rising environmental concerns among residents.5 These educational programs would help to reduce the gap between the two types of residents, thus favoring the emergence of the cooperative result in which everybody recycles.
Some studies have examined the effect of certain factors such as monetary incentives, opportunity cost and social norms, among others, on resident recycling behavior finding, for example, that monetary incentives and proximity of recycling facilities are important when people decide whether or not to recycle [14,15,16]. Halvorsen [17] concludes that the opportunity cost of time has a negative effect on recycling, while warm glow, social norms and moral norms have a positive effect. Moreover, Viscusi et al. [18] empirically show that social norms that encourage pro-environmental actions, personal valuations of the environment and economic incentives are the most important factors influencing individuals’ recycling decision.
One policy to increase recycling is charging for every unit of waste of garbage disposal (unit-pricing). Even though some studies show that unit-pricing has a positive effect on the recycling rate [19], Fullerton and Kinnaman [20] demonstrate that this policy is not always effective, since some residents stomp more garbage into each unit in order to decrease cost. An alternative policy is to charge tipping fees for waste disposal at landfills. Some studies find that increasing tipping fees raises the likelihood of a community adopting a curbside recycling program [21]. Both policies mentioned above are based on imposing penalties to non-recycling behavior. While these policies can increase residential recycling to some extent, charging a mandatory fee hurts residents’ welfare when they are not willing to pay for it.
Other policies provide residents easy recycling access. In some regions, local recycling organizations charge residents a fixed monthly fee to establish curbside recycling programs.6 Aadland and Caplan [23,24] and Koford et al. [25] estimate the willingness to pay (WTP) for curbside recycling based on contingent valuation surveys from different regions in the United States. They both show that residents’ WTP is positive. However, under the unrewarded curbside recycling system, not only paying for the programs can decrease residents’ benefit, but they may also not recycle all the qualified items, since residents are not sufficiently motivated by the benefits associated with recycling.
As a substitute to reducing the opportunity cost of recycling, some states have established deposit-refund systems that provide financial incentives [26].7 A few studies have shown that such a policy is effective on increasing the recycling rate of water bottles [18,27]. Nonetheless, the current financial reward system only works for some recyclable items, including water bottles and batteries. Other items such as paper, hardboards and carpets are not included. Our paper contributes to the existing literature by examining a context in which the resident’s predisposition to recycle is unknown by administrators and considers a reward in the form of a club good.
2. Theoretical Model
In this section, we analyze agents’ strategic behavior under the RRS. Specifically, in our model, a representative resident chooses whether to commit to the recycling system and an uninformed administrator responds by choosing whether to establish the RRS.8 We next discuss the strategic behavior of the resident and afterwards a similar analysis is provided for the administrator.
Resident’s Payoffs from Recycling. Consider two types of representative residents differentiated by their attitude towards the environment: an environmental-friendly , who cares about the positive environmental effects from recycling, and an environmental-neutral type , who does not. If an F-type resident recycles, she obtains an environmental benefit .9 In contrast, if an N-type recycles, her environmental benefit is zero. In addition, if an i-type resident recycles, where , she bears a cost of from committing to the system i.e., the opportunity cost of registering in the system. A registered resident is eligible to receive a reward in the form of a club good, G.10 The cost for residential garbage disposal and for recycling are and , respectively, where .11 Note that, in each household, there is a share of waste that is non-recyclable despite the efforts of an individual. However, recyclable materials allow a resident to decide between disposing of or recycling under the reward system. Our analysis focuses on this share of waste and normalizes the quantity to one. Hence, under the RRS, an i-type resident decides to recycle if
Intuitively, the left-hand side of represents the resident’s benefit from recycling under the RRS while the right-hand side is the cost of committing to the program, i.e., its direct cost, , and the increase in the garbage cost, . Importantly, independent of the resident’s type, if she participates in the RRS, she bears a cost from recycling and committing to the RRS. Hence, the resident commits to the system as long as the benefits from recycling outweigh the cost from recycling, α.
Administrator’s Payoffs. The administrator must consider not only the positive environmental effects from recycling but also the financial burden of establishing the RRS. Before it is established, the recyclable material deposited in the landfill causes a damage on the environment. The collection and processing of the garbage have a cost . Therefore, the total cost is under the current system.12 If the RRS is established and the resident recycles, the total environmental damage is reduced to and , i.e., the environmental damage generated by a friendly type resident is smaller than that by a neutral type.13 In addition, the administrator can get a revenue I by selling the recycled materials to a wholesaler who processes recyclable items. As an incentive, the administrator provides a club good to the local resident for recycling. The cost of processing the recycled items is . Finally, there is a strictly positive fixed cost to establish the system.14 Therefore, the administrator prefers to establish the RRS if
Inequality can also be expressed as follows,
The left-hand side represents the administrator’s benefit if the i-type recycles under the RRS. Specifically, the first element in parenthesis represents the difference between the administrator’s net revenue from selling the recycled material, this term can be positive (zero) if the revenue is partially (totally) transferred to the residents as a club good; the second term represents the marginal environmental benefit from the participation of an i-type resident. The first term on the right-hand side represents the processing cost difference between recycling and garbage disposing. Finally, is the fixed cost from establishing the RRS. Intuitively, inequality states that the administrator has incentive to establish the RRS as long as the total net benefits from the recycling system outweigh costs.
3. Signaling Game
We next examine a context in which the administrator is uninformed about the resident’s environmental concern. As aforementioned, there are two types of residents, F (Friendly) and N (Neutral). Nature decides the realization of the resident’s type, with probability , she is a friendly type, and she is an environmental-neutral type. The resident sends a costly message to the administrator by either committing or not committing to the system. Hence, if the administrator observes that the resident commits, C, to the system, he forms beliefs about the resident’s type. Let denote the administrator’s posterior belief that the resident’s type is friendly. Given these beliefs, the administrator decides whether or not to establish the RRS. After observing no commitment, the administrator’s beliefs are , where denotes no commitment.
3.1. Equilibrium
In this section, we first examine the separating equilibrium, and we next analyze the pooling equilibria.
3.1.1. Separating Equilibrium
There are two candidate combinations of the resident’s strategy for the separating equilibrium (SE). The first strategy profile considers that the resident only commits when she is environmentally friendly, and the second strategy describes the case in which the resident only commits if she is a neutral type. Let us next analyze the first case. The administrator’s belief about the resident’s type is
that is, if the administrator observes commitment, he assigns full probability to such announcement originating from a friendly type. In the case of observing no commitment, the administrator believes that the resident’s type is neutral. Proposition 1 describes under which conditions a separating equilibrium exists.
Proposition 1.
In the recycling game, the following separating strategy profile can be supported as the unique pure-strategy Perfect Bayesian Equilibrium (PBE):
- The friendly resident commits and the resident does not commit if .
- The administrator responds by establishing the RRS when he observes commitment, given that his posterior beliefs are and , and , where . However, he does not establish the RRS upon observing no commitment for all parameter values.
The SE exists if , this condition guarantees that the administrator provides a club good for which the neutral resident has not incentives to deviate (commit). Moreover, condition also needs to be satisfied. In this case, the administrator provides a club good, G, that only induces the friendly resident to commit. Hence, a friendly type always commits, independent of the reward, if the environmental benefit outweighs the cost of recycling, i.e., . However, if the resident’s cost of recycling increases, or if the cost of garbage dumping or the environmental benefit decreases, the former condition becomes more restrictive. In addition, a neutral type resident does not commit since the reward does not compensate the additional cost of recycling.
In order to ensure that the administrator establishes the system, the investment in the club good needs to be sufficiently low, . Note that cutoff β decreases in , and but increases with d, I and . That is, an increase in the administrator’s processing cost of recycling, fixed cost of establishing the system or the environmental damage after recycling makes less likely the establishment of the RRS. However, an increase in the marginal benefit of recycling, the administrator’s revenue of recycling, or the resident’s cost of garbage processing makes the condition less restrictive, thus making the establishment of the RRS more likely. Interestingly, the administrator faces a trade off when considering the establishment of the recycling system. Specifically, a decrease in G relaxes the administrator’s participation constraint, which makes the administrator more likely to establish the system. However, it provides the friendly resident with lower incentives to commit.
We next briefly discuss why the SE in which the neutral type resident commits, but the friendly type does not cannot be supported.
Proposition 2.
The separating strategy profile in which only the environmental neutral resident commits cannot be supported as a pure-strategy PBE of the recycling game.
Intuitively, an environmentally friendly resident always gets a higher payoff than an N-type resident from recycling. Therefore, if an environmentally neutral resident decides to commit to the RRS, then under the same parameter values, an F-type resident would also commit.
The following corollary compares the social welfare resulted from Proposition 1 to that under complete information in which the administrator observes the resident’s type. Social welfare is defined as the aggregate payoffs of the administrator and the resident.
Corollary 1.
The social welfare under the SE coincides with that under complete information.
Social welfare under the SE and under complete information are the same since the resident’s action is type-dependent in the separating strategy. Thus, the administrator is able to identify the resident’s type even under incomplete information, thus yielding an identical outcome as under perfect information.
3.1.2. SE Versus Status Quo
Under the SE the aggregate benefits from recycling are higher than the total cost for the administrator and resident since . Therefore, the establishment of the RRS leads to a positive net benefit. Thus, there is a welfare improvement when the SE is promoted relative to the case in which the system is not implemented (status quo). Since an SE emerges when , the administrator can guarantee the existence of the equilibrium by increasing the amount of the club good, G, or raising the environmental valuation of friendly resident, . For example, education is found to have significant effects on public’s environmental concern and recycling behavior [28]. Moreover, many studies conclude that warm glow plays an important role in individuals’ contribution to public goods [29,30]. In particular, these articles conclude that subjects obtain warm glow from donating. In the recycling game, the warm glow could be understood as the benefit from recycling being enlarged by the positive feedback that a resident experiences from contributing to her neighborhood or reducing pollution in her community. Therefore, warm glow can be achieved through dissemination of information on the benefits of recycling.15 In addition, encouragement and promotion of recycling behavior in a community can also enhance the level of warm glow a resident obtains from recycling. For instance, Community Facility Grants by the United States Department of Agriculture [31] and Recycling and Litter Prevention Grants by the Ohio Environmental Protection Agency [32] are good examples of policies that could help to promote recycling.
3.1.3. Pooling Equilibrium
There are two candidate combinations of a resident’s strategy for a pooling equilibrium (PE). The first strategy profile considers that the resident commits independent of her type. The second strategy represents the case in which the resident does not commit regardless of her type. Let us first analyze the administrator’s beliefs about the resident’s type if she commits, , that is, if the administrator observes commitment, he assigns a probability p to such announcement originating from a friendly type. In the case of observing no commitment, the administrator’s off-the-equilibrium beliefs can be arbitrarily specified, i.e., . Proposition 3 describes the first pooling equilibrium, PE1, in which both residents commit and, in addition, it survives the Cho and Kreps’ [33] Intuitive Criterion.
Proposition 3.
In the recycling game, the following pooling strategy profile can be supported as a pure-strategy PBE:
- (1)
- The resident commits regardless of her type if .
- (2)
- The administrator responds by establishing the RRS when he observes commitment, given that his posterior beliefs are , and , where . However, he does not establish the RRS upon observing no commitment for all parameter values.
Condition (1) in Proposition 3 becomes more restrictive if the resident’s cost of recycling and the cost of committing increases or the cost of garbage dumping decreases. That is, more efficient recycling technology that reduces the residential recycling cost and stringent penalization on garbage dumping are tools that could induce the emergence of the PE. In addition, the administrator establishes the RRS if the investment in the club good is sufficiently low, . Specifically, cutoff decreases in , , and the difference but increases with d, I and . That is, a decrease in the recycling processing cost, the fixed cost of establishing the system, or the remaining environmental damage makes the administrator more likely to establish the RRS. Similarly, an increase in the initial environmental damage, the revenue of recycling or the garbage processing cost makes the RRS more desirable. Finally, a decrease in the value of the club good, G, makes the administrator more likely to establish the system, but it provides both types of residents with lower incentives to commit.
Now let us focus on the case in which both types of resident do not commit. We first analyze the administrator’s beliefs about the resident’s type. In the case of observing no commitment, . Hence the administrator, upon observing no commitment, assigns probability p to such announcement coming from a friendly type. In the case of observing commitment, the administrator’s off-the-equilibrium beliefs can be arbitrarily specified, i.e., . Proposition 4 discusses the second pooling equilibrium, PE2, that survives the Intuitive Criterion.
Proposition 4.
In the recycling game, the following pooling strategy profile can be supported as a pure-strategy PBE:
- Both types of residents do not commit if .
- The administrator does not establish the RRS if he observes no commitment, given that his posterior belief is , and establishes it otherwise if .
Under these conditions, the club good reward does not outweigh either type of resident’s net cost of recycling. Therefore, the resident does not recycle regardless of her type, and the outcome in this equilibrium is the same as in the status quo.
4. Discussion
We next discuss the conditions under which each equilibrium is supported, followed by a comparison in terms of social welfare, and a simulation.
4.1. Comparison of Equilibrium Conditions
Figure 1A describes parameter values that support each equilibrium. The slashed area represents the SE, the dotted area depicts the PE1 in which both types of resident commit, and the blocked area depicts the PE2 in which the friendly and the neutral type do not commit. We can observe that PE1 is supported under more restrictive condition than the SE and than the PE2 since it requires a narrow range of G. When β and become smaller, i.e., the participation constraint for the administrator becomes more restrictive and the ranges of equilibria shrink accordingly (see Figure 1B). In this case, the cooperative pooling equilibrium, PE1, is not supported. This is due to the fact that the administrator has to set the club good at a lower level than β and under the separating and pooling equilibria, respectively.

Figure 1.
Equilibria when β > α.
As shown in Figure 1A, if only a friendly resident has the incentive to recycle () and the administrator’s constraint is satisfied (), then the SE is supported. In this case, the administrator would establish the system, but only a friendly resident commits. Similarly, when the amount of club good is relatively low but the environmental valuation is sufficiently high, the SE is supported (point A in Figure 1A). However, when the amount of club good is sufficiently high, i.e., , both types of residents recycle and the administrator implements the system, that is, the PE1 is supported. Finally, if the club good is provided at a level in which even a friendly resident does not have the incentive to recycle (), the PE2 is supported. In this case, neither type of resident recycles, independent of the establishment of the system. If a neutral resident does not have incentive to commit (), then whether the SE or the PE2 is supported depends on the environmental benefit, . Specifically, when is large enough, the friendly resident is more likely to recycle and, thus, the SE is more likely to be supported.
4.2. Comparison between SE and PE
In this section, we aim to compare the social welfare in the SE and the PE. Under the PE1, both types commit to the RRS. Hence, the social welfare by an F-type resident is the same under the PE1 and SE, but they do not coincide when the resident is an N-type, since she only commits under the PE1. Therefore, we focus our comparison on the case of a neutral resident. Specifically, we find that if benefits outweigh costs of recycling for an N-type, then the PE1 dominates the SE in terms of social welfare. The following lemma discusses this condition.
Lemma 2
When the resident’s type is , the social welfare is larger under the PE1 than under the SE if and only if the resident’s net benefit from recycling is greater than zero, i.e., . In addition, the difference increases with the probability of a resident being environmentally neutral, .
Therefore, the administrator is not able to unambiguously determine which equilibrium dominates in terms of social welfare (SW). Let be the expected welfare difference between the pooling and separating equilibria, and denote the pooling and separating equilibrium for the neutral type, respectively. As shown in Figure 2, the PE1 dominates the SE if the environmental damage generated by an N-type resident when she recycles, , is smaller than δ. However, if is sufficiently large, that is, the aggregate net benefit does not exceed the net cost for a neutral resident to recycle, i.e., , the social welfare is higher under the SE. In addition, as p increases, i.e., the curve rotates counter clockwise in Figure 2, describing that the magnitude of the difference between both equilibria decreases. Intuitively, since an F-type resident recycles in both equilibria, if the probability of facing a friendly type is larger, then the social welfare under these two equilibria converge. For example, if the resident is environmentally friendly, the SE yields the same social welfare as PE1 since . However, if a resident is certainly an environmentally neutral type, the social welfare difference between these two equilibria can be expressed as .
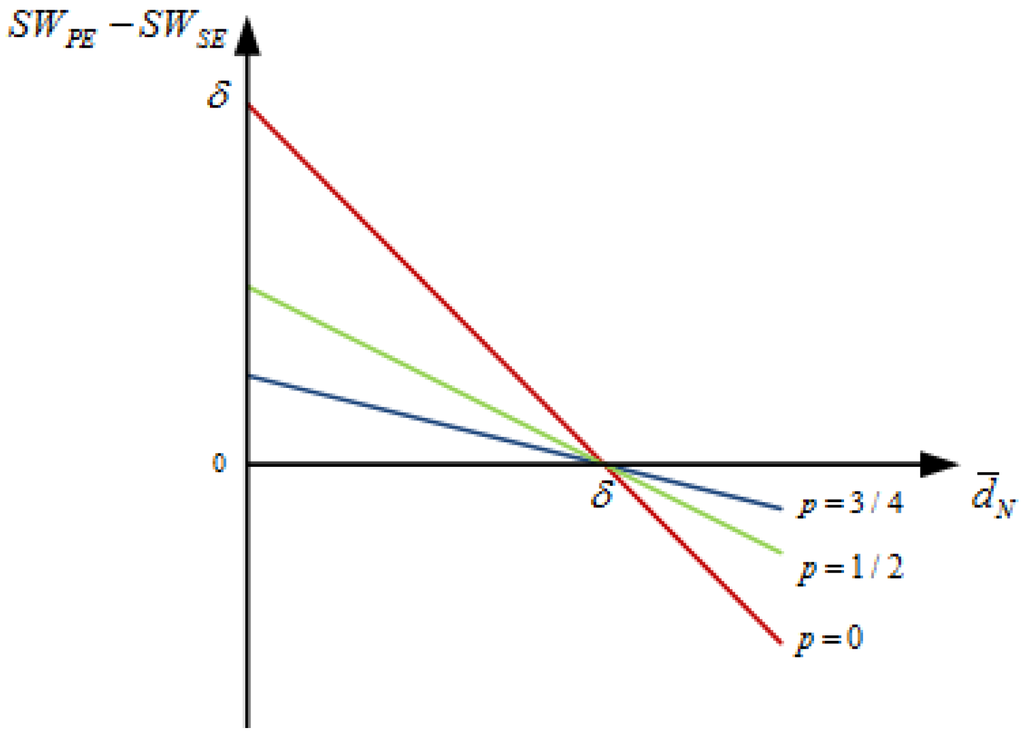
Figure 2.
Social welfare difference.
4.3. Simulation
We next present a numerical simulation of the change in social welfare (SWC) under the SE and PE1.16 The SWC is the difference between the welfare under the equilibrium result (either SE or PE1) and that in the status quo (the case in which the RRS is not implemented). We first assign values to all parameters and scale them between 0 and 1 (see Table 1).17

Table 1.
Initial values.
The settings of these values are based on the assumptions discussed in Section 2. Figure 3 presents a simulation considering the value of the social welfare change on the vertical axes, and parameters ( and in Figure 3a, and in Figure 3b, and in Figure 3c, in Figure 3d, I in Figure 3e, d and in Figure 3f, d and in Figure 3g and p in Figure 3h) on the horizontal axes.18 The solid lines represent the SWC in the SE, and the dashed lines depict the SWC in the PE1.

Figure 3.
Social welfare difference.
As shown in Figure 3a, social welfare change under both the SE and PE1 increases with the aggregate cost of garbage disposing. However, the slope of the PE1 is steeper than that of the SE, indicating that when the aggregate cost of garbage disposing is sufficiently high, the promotion of the RRS in which both types of resident recycle is socially desirable. Figure 3b shows that social welfare decreases with the aggregate cost of recycling. The change in social welfare with respect to the costs is, however, more sensitive in the PE1 than the SE since the SE is only affected by the F-type resident. Figure 3c shows that when the fixed cost of establishing the system increases, the social welfare in both equilibria decreases, decreasing faster in the PE1 than in the SE. This suggests that if the cost of implementing the RRS is relatively high, , the SE is more desirable than the PE1. However, if this cost is higher than , neither the PE1 or the SE results in higher welfare compared to the status quo since the total benefit of recycling does not outweigh its cost. Figure 3d indicates that when the environmental valuation increases, both SE and PE1 increase at the same rate, however, the SWC in the PE1 is slightly higher than that in the SE. Figure 3e shows that as the revenue collected by the administrator from recycling increases, both SWCs increase, but at a higher rate under the PE1 given that a neutral resident also recycles. Therefore, the administrator has more incentives to promote the PE1 when his revenue from recycling is high. In Figure 3f, we observe that higher environmental damage reduction by an F-type resident, when she recycles, results in higher social welfare in both equilibria. In addition, as shown in Figure 3g, the social welfare in the PE1 increases if such a reduction in damage by an N-type resident increases as well. However, the social welfare in the SE is not affected by it. Therefore, when is relatively low, i.e., , the social welfare is lower in the PE1 than in the SE, even though the conditions to support the former are more restrictive than the latter. Finally, Figure 3h depicts how the social welfare change in each equilibrium is affected by the probability of a resident being an F-type. As the probability rises, social welfare increases under both equilibria. However, the change occurs more rapidly under the SE, and the difference converges when this probability approaches one.
5. Conclusions
This paper proposes an alternative Recycling Reward System (RRS) to promote residential recycling rate. As a complementary tool to existing recycling systems, the RRS provides economic incentives to residents by rewarding them with a club good when they commit to recycling. We analyze an incomplete information game in which a resident decides whether or not to commit to the RRS, and then the administrator chooses whether to establish the system. The results suggest that, despite of facing incomplete information on the resident’s environmental preferences, an administrator can induce both types of residents to recycle. Moreover, we conduct a social welfare analysis and find that both the separating equilibrium and the pooling equilibrium in which both types of residents commit are socially desirable compared to the status quo.
Interestingly, our analyses show that, although the pooling equilibrium is supported under more restrictive conditions, it does not always result in higher social welfare than the separating equilibrium. The pooling dominates the separating equilibrium if the net benefit from recycling for a neutral type is greater than zero. However, when a neutral resident recycles, the environmental damage can remain large so that the aggregate benefit does not necessarily compensate the cost. In this case, the separating equilibrium is socially preferable. A simulation is conducted to illustrate the welfare difference between these two equilibria. We find that both the probability of a resident favoring environmental improvement and the magnitude of a resident’s environmental valuation significantly influence the welfare outcomes of the RRS. Therefore, from a policy perspective, promoting information and education about the benefits of recycling would increase the likelihood of the pooling equilibrium in which both types of resident recycle. However, if the neutral type is very damaging to the environment since her attitude towards recycling is poor, i.e., she is apathetic towards recycling and more inclined to adopt a consumerist approach, then the policy maker would achieve a higher social welfare by only targeting the friendly resident (separating equilibrium).
Our paper can be extended by modifying our modeling assumption. For instance, if the administrator faces uncertainty about the cost of implementing the RRS, rather than the resident’s environmental concerns, the conditions that support our equilibrium results as well as the social welfare comparisons could change. In addition, the consideration of a setting similar to the one empirically analyzed by Germani et al. [34], in which there is illegal garbage disposal and trafficking, could modify our results. Furthermore, the model could be enriched by considering that residents have different preferences over the club good, and this setting introduces an additional layer of uncertainty to the administrator. Finally, one could allow an extensive form game in which the administrator is able to monitor the recycled amount at the end of each period, which can also change a resident’s recycling behavior.
Acknowledgments
We would like to especially thank Michael Finus, Paola Labrecciosa, Miaoru Liu, Ron Mittelhammer, Félix Muñoz-García, Tohru Naito, two anonymous referees, and participants at the 88th WEAI annual conference and the 5th workshop on Game Theory in Energy, Resources and Environment for their insightful comments and suggestions.
Author Contributions
All authors contributed equally to the conception of the research idea. T.L. and A.EA. contributed to the game theoretic analysis and wrote the paper, J.M. provided input on the applications of the model.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
Appendix A.1. Proof of Proposition 1
If the resident commits to recycling, and the administrator responds establishing the RRS, her payoff is if she is a friendly type and if her type is neutral. However, if the administrator does not establish the system, the resident’s payoff is , when she commits to recycling, and when she does not commit, both of them being the independent type.
In addition, if the administrator establishes the RRS after observing commitment, his payoff is ; however, if the administrator does not establish the RRS when a resident commits, his payoff is . Moreover, if the administrator establishes the system after observing no commitment, his payoff is , but if he does not establish it, his payoff is .
The administrator establishes the RRS if he observes commitment when the following inequality holds:
Rearranging and solving for G, we obtain
Upon observing that the resident does not commit and given the administrator’s beliefs, he does not establish the RRS since his payoff of establishing is always lower than if not establishing the system, i.e., , for all values of .
Let us now focus on the resident’s strategic behavior.
Friendly type: the friendly resident is able to anticipate that her announcement (commit) will be responded with establishment of the RRS. Hence, she does not have incentive to deviate if
Neutral type: this type of resident is also able to anticipate the administrator’s behavior when she decides not to commit. Therefore, a neutral resident does not have incentive to deviate if
Thus, there exists a Separating Nash Equilibrium when inequalities (A1)–(A3) hold simultaneously.
Appendix A.2. Proof of Proposition 2
The administrator establishes the RRS if he observes commitment when , that is,
Upon observing that the resident does not commit and given the administrator’s beliefs, he does not establish the RRS since holds for all values of .
Now, we focus on the resident’s strategic behavior.
Friendly type: the friendly resident is able to anticipate that her announcement (not commit) will be responded with the non-establishment of the RRS. Hence, she does not deviate if
Neutral type: this type of resident is also able to anticipate the administrator’s behavior when she chooses . Therefore, a neutral resident does not deviate if
Note that inequalities (A5) and (A6) are not compatible since , so . Therefore, the strategy in which only the environmental neutral resident commits cannot be sustained as an SE.
Appendix A.3. Corollary 1
In the case of complete information, if the administration observes that resident i’s commits, he responds implementing the RRS if
and he responds by not implementing the RRS upon observing that resident i’s does not commit, that is,
The type-i resident commits to the RRS if
These conditions coincide with those identified in proposition 1. Hence, in a context of complete information, the administrator responds implementing the RRS if the friendly type commits. Otherwise, he does not establish the system. As a consequence, social welfare (measured as the administrator’s and the resident’s payoff) coincides in the SE and the complete information context.
Appendix A.4. Proof of Proposition 3
The administrator establishes the RRS if he observes commitment when the following inequality holds:
Let us next analyze the off-equilibrium. Upon observing that the resident does not commit and given the administrator’s beliefs, he does not establish the RRS since holds for all values of .
Now, we focus on the resident’s optimal message under two scenarios. (1) inequality (A7) holds; (2) inequality (A7) does not hold.
- If (A7) holds, the administrator’s optimal strategy is to establish the RRS when the resident commits. Under this circumstance, the resident does not have the incentive to deviate if and only ifNote that this condition is less restrictive for the friendly resident since her payoff under establishment of the RRS is strictly higher than the neutral type resident. For this reason, no resident deviates if . Therefore, the condition in which both types of residents commit, and the administrator establishes the RRS, can be sustained as a pooling equilibrium if inequality (A7) holds and .Rearranging the inequality,
- If inequality (A7) does not hold, the administrator’s optimal strategy is to not establish the RRS when the resident commits. Therefore, the resident has no incentive to commit since . This contradicts with the strategy in which both types of residents commit. Therefore, if (A7) does not hold, the PE in which both types of residents commit cannot be supported.
Now let us analyze if the pooling equilibrium in which both types of residents commit, and the administrator establishes the RRS violates the Cho and Kreps’ (1987) Intuitive Criterion (IC). First, we eliminate the off-the-equilibrium messages that are equilibrium dominated. We know that under the PE in which both types of resident commit, inequality (A8) holds. Thus, and . Intuitively, the first inequality states that the F-type resident does not have incentive to deviate. However, if , the N-type resident could deviate to not commit. As a consequence, the administrator’s beliefs when observing no commitment are . Second, we use the restriction on beliefs to study if the N-type resident would deviate. When the administrator observes no commitment, he believes the message is sent from an N-type resident, and responds with no establishment since . Note , i.e., the payoff to the N-type resident is lower than if she deviates from the equilibrium. As a result, the resident prefers not to deviate, regardless of her type. Therefore, this pooling equilibrium does not violate the IC.
Appendix A.5. Proof of Proposition 4
Upon receiving no commitment, the administrator establishes the RRS only under the condition . This condition never holds since is always true for all . Therefore, the administrator never establishes the RRS upon observing no commitment.
Let us now check the off-equilibrium path. Upon observing a commitment announcement, the administrator establishes the RRS if
Rearranging and solving for (A7), we obtain
Now, we focus on the resident’s optimal message.
- If inequality (A9) holds, the administrator establishes the RRS upon observing that the resident commits. Therefore, the resident deviates from no commitment if her payoff, given the administrator establishes the RRS, is larger than the payoff under the current system. Note that the deviation incentive is more likely for the friendly type resident. Hence, the resident does not deviate if
If (A10) holds, neither type of resident has incentives to recycle. Therefore, there exists a pooling equilibrium in which both types of residents do not commit, and the administrator does not establish the RRS if he observes no commitment, and establishes otherwise.
- 2.
- If (A9) does not hold, the administrator’s participation constraint is not achieved whether the resident commits or not, and he does not establish the RRS. Under this condition, the resident does not have incentive to deviate because . Therefore, the case in which both types do not commit and the administrator does not establish the system can be sustained as a PE.
Now, let us analyze if the pooling equilibrium under which both types of residents do not commit, and the administrator does not establish the RRS violates the IC. First, we know that under this PE, inequality (A10) holds. Thus, the equality holds if . In addition, for all . Intuitively, the inequalities state that the F-type resident has incentive to deviate if and only if while the N-type resident always does not deviate. As a consequence, the administrator’s beliefs when observing commitment are . Second, we use the restriction on beliefs to study if the F-type resident would deviate. When the administrator observes commitment, he assigns full probability of the message coming from an F-type resident, and responds with establishment. However, note that if , then , i.e., the F-type resident’s payoff is not higher when she deviates from the equilibrium. As a result, the resident prefers not to deviate, regardless of her type. Therefore, this pooling equilibrium does not violate the IC.
Appendix A.6. Proof of Lemma 2
Let be the social welfare by the N-type resident under the PE1 compared to the SE:
which is strictly positive if , or equivalently, . Moreover, since the probability of a resident being environmentally neutral is , the expected social welfare difference between the SE and PE1 is , which is positively correlated with and, therefore, negatively correlated with p when .■
- 1.Furthermore, producing a soda can from recycling saves 95 percent energy more than it does to create one from virgin materials. Specifically, the Department of Environmental Conservation [10] reports that recycling one aluminum can could save 0.4 kWh electricity. Despite the fact U.S. consumers use over 80 billion aluminum soda cans every year, only about half of them are recycled.
- 2.Club goods are considered a subtype of public goods. They are excludable but non-rivalrous in consumption. Alternatively, the reward system could also allow for private goods.
- 3.The assessment of residents’ recycling preferences is difficult and often costly for the administrator. Guy and Rogers [11] found that individuals’ attachment to the community affects their attitudes toward recycling. Blaine et al. [12] argue that older individuals who live in rural settings are more likely to recycle.
- 4.The time structure represents the case in which an uninformed local government develops an initiative to infer the median voter’s preference on recycling. Residents decide whether or not to commit to the initiative, and after it is approved or defeated, the local government decides whether to implement the recycling system. Several states in the U.S. follow this time structure, for instance, the Arizona Establishing Waste Reduction, Recycling and Management Plan, Proposition 202 (1990), the Maine Recycling and Solid Waste Landfill Clean Up and Closures, Question 6 (1991), or the Massachusetts Recyclable Packaging Initiative, Question 3 (1992).
- 5.Folz [13] empirically shows that communities that encouraged participation in recycling through education and dissemination of public information were successful in increasing the number of participants in recycling.
- 6.Several cities in the U.S. offer this service. For example, Austin, Texas provides a weekly curbside recyclables pick-up service, and Seattle, Washington provides the same service monthly. Processing procedure and fees vary by local governments [22].
- 7.For example, until 2011, five states (California, Connecticut, Hawaii, Maine and Oregon) had enacted bottle deposit laws for plastic water bottles.
- 8.In the sequential move game, the resident acts as a leader while the administrator acts as a follower. This setting allows the administration to infer some information from the resident’s decision.
- 9.This valuation can be rationalized by individual’s warm glow of recycling, social norms, or belief of benefits from recycling, as suggested by Viscusi et al. [18].
- 10.The Philadelphia Recycling Rewards program promotes recycling by providing rewards points to residents who correctly recycle. In this program, members use the rewards points to get local deals.
- 11.The per-unit cost of recycling for residents is larger or equal to the per-unit cost of garbage disposing because recycling requires extra handling of the waste such as sorting into different categories, as shown by Halvorson [17].
- 12.In a different setting, the administrator could recycle a certain percentage of the garbage under the current system. However, the existence of equilibria is robust to that context, and the qualitative results remain unaffected.
- 13.Since a friendly resident cares more about the environmental damage, under the same conditions, her behavior is more beneficial to the environment.
- 14.For instance, the establishment of the RRS requires an investment in recycling containers and pick-up vehicles.
- 15.For example, the EPA in 2013 developed a study about the benefits of recycling. The study argues that: recycling helps create jobs, reduces the need for new landfills, saves energy, supplies valuable raw materials to industry, and adds significantly to the U.S. economy.”
- 16.Note that neither type of resident recycles under PE2. Thus, it does not yield different social welfare.
- 17.The simulation results are robust under different parameter values and can be provided by the authors upon request.
- 18.Because , we only present Figure 3f,g under the parameter values that satisfy this condition.
References
- Stern, N. Climate. Stern Review: The Economics of Climate Change. N. Engl. J. Public Policy 2007, 21, 23–50. [Google Scholar]
- Palmer, K.; Walls, M. Optimal Policies for Solid Waste Disposal: Taxes, Subsidies, and Standards. J. Public Econ. 1997, 65, 193–205. [Google Scholar] [CrossRef]
- McKibbin, W.J.; Wilcoxen, P. The Role of Economics in Climate Change Policy. J. Econ. Perspect. 2002, 16, 107–129. [Google Scholar] [CrossRef]
- Gillingham, K.; Newell, R.; Pizer, W. Modeling Endogenous Technological Change for Climate Policy Analysis. Energy Econ. 2008, 30, 2734–2753. [Google Scholar] [CrossRef]
- Fischer, C.; Newell, R. Environmental and Technology Policies for Climate Mitigation. J. Environ. Econ. Manag. 2008, 55, 142–162. [Google Scholar] [CrossRef]
- Cremer, H.; Donder, P.D.; Gahvari, F. Political Competition within and between Parties: An Application to Environmental Policy. J. Public Econ. 2008, 92, 532–547. [Google Scholar] [CrossRef]
- Klein, N. Capitalism vs. the Climate. 9 November 2011. Available online: https://www.thenation.com/article/capitalism-vs-climate/ (accessed on 15 August 2016).
- Environmental Protection Agency (EPA). Reducing Greenhouse Gas Emission through Recycling and Composting; EPA 910-R-11-003; Environmental Protection Agency: Washington, DC, USA, 2011.
- Environmental Protection Agency (EPA). Communicating the Benefits of Recycling. 2013. Available online: http://www.epa.gov/osw/conserve/tools/localgov/benefits/ (accessed on 15 August 2016). [Google Scholar]
- Department of Environmental Conservation. 2013. Available online: http://www.dec.ny.gov/chemical/44787.html (accessed on 15 August 2016).
- Guy, S.M.; Rogers, D.L. Community surveys: Measuring citizens’ attitudes toward sustainability. J. Ext. 1999, 37, 3. [Google Scholar]
- Blaine, T.W.; Mascarella, K.D.; Davis, D.N. An Examination of Rural Recycling Drop-Off Participation. J. Ext. 2001, 39, 5. [Google Scholar]
- Folz, D.H. Recycling Program Design, Management, and Participation: A National Survey of Municipal Experience. Public Adm. Rev. 1991, 51, 222–231. [Google Scholar] [CrossRef]
- Hong, S.; Adams, R.M.; Love, H.A. An Economic Analysis of Resident Recycling of Solid Waste: The Case of Portland, Oregon. J. Environ. Econ. Manag. 1993, 25, 136–146. [Google Scholar] [CrossRef]
- Tiller, K.H.; Jakus, P.M.; Park, W.M. Resident Willingness to Pay for Dropoff Recycling. J. Agric. Resour. Econ. 1997, 22, 310–320. [Google Scholar]
- Bruvoll, A. Factors Influencing Solid Waste Generation and Management. J. Solid Waste Technol. Manag. 2001, 27, 156–162. [Google Scholar]
- Halvorsen, B. Effects of Norms and Opportunity Costs of Time on Resident Recycling. Land Econ. 2008, 84, 501–516. [Google Scholar] [CrossRef]
- Viscusi, W.K.; Huber, J.; Bell, J. Alternative Policies to Increase Recycling of Plastic Water Bottles in the United States. Rev. Environ. Econ. Policy 2012, 6, 190–211. [Google Scholar] [CrossRef]
- Ferrara, I.; Missios, P. Recycling and Waste Diversion Effectiveness: Evidence from Canada. Environmental and Resource Economics. Eur. Assoc. Environ. Resour. Econ. 2005, 30, 221–238. [Google Scholar] [CrossRef]
- Fullerton, D.; Kinnaman, T.C. Resident Responses to Pricing Garbage by the Bag. Am. Econ. Rev. 1996, 86, 971–984. [Google Scholar]
- Kinnaman, T.C.; Fullerton, D. Garbage and Recycling with Endogenous Local Policy. J. Urban Econ. 2000, 48, 419–442. [Google Scholar] [CrossRef]
- Environmental Protection Agency (EPA). Waste Prevention, Recycling, and Composting Options: Lessons from 30 US Communities. 2013. Available online: http://www.epa.gov/waste/conserve/downloads/recy-com/index.html (accessed on 15 August 2016). [Google Scholar]
- Aadland, D.; Caplan, A.J. Willingness to Pay for Curbside Recycling with Detection and Mitigation of Hypothetical Bias. Am. J. Agric. Econ. 2003, 85, 492–502. [Google Scholar] [CrossRef]
- Aadland, D.; Caplan, A.J. Curbside Recycling: Waste Resource or Waste of Resources? J. Policy Anal. Manag. 2006, 25, 855–874. [Google Scholar] [CrossRef]
- Koford, B.C.; Blomquist, G.C.; Hardesty, D.M.; Troske, K.R. Estimating Consumer Willingness to Supply and Willingness to Pay for Curbside Recycling. Land Econ. 2012, 88, 745–763. [Google Scholar] [CrossRef]
- Ashenmiller, B. Cash Recycling, Waste Disposal Costs, and the Incomes of the Working Poor: Evidence from California. Land Econ. 2009, 85, 539–551. [Google Scholar] [CrossRef]
- Viscusi, W.K.; Huber, J.; Bell, J. Promoting Recycling: Private Values, Social Norms, and Economic Incentives. Am. Econ. Rev. Pap. Proc. 2011, 101, 65–70. [Google Scholar] [CrossRef]
- Simmons, D.; Widmar, R. Motivations and Barriers to Recycling: Toward A Strategy for Public Education. J. Environ. Educ. 1990, 27, 13–18. [Google Scholar] [CrossRef]
- Andreoni, J. Giving with Impure Altruism: Applications to Charity and Ricardian Equivalence. J. Political Economy 1989, 97, 1447–1458. [Google Scholar] [CrossRef]
- Palfrey, T.R.; Prisbrey, J.E. Anomalous Behavior in Public Goods Experiments: How Much and Why? Am. Econ. Rev. 1997, 87, 829–846. [Google Scholar]
- United States Department of Agriculture (USDA). Community Facility Grants. United States Department of Agriculture, 2013. Available online: http://www.rurdev.usda.gov/HAD-CF_Grants.html (accessed on 15 August 2016). [Google Scholar]
- Ohio Environmental Protection Agency (Ohio EPA). Ohio EPA Awards 18 Community Recycling Grants. Ohio Environmental Protection Agency, 2013. Available online: http://www.epa.state.oh.us/ news/onlinenewsroom/newsbycategory/tabid/5980/vw/1/itemid/314/ohio-epa-awards-18-community-recycling-grants.aspx (accessed on 15 August 2016).
- Cho, I.; Kreps, D. Signaling Games and Stable Equilibrium. Q. J. Econ. 1987, 102, 179–222. [Google Scholar] [CrossRef]
- Germani, A.; Pergolizzi, A.; Reganati, F. Law Enforcement and Illegal Trafficking of waste: Evidence from Italy. Econ. Bull. 2015, 35, 1–13. [Google Scholar]
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).