Evolutionary Exploration of the Finitely Repeated Prisoners’ Dilemma—The Effect of Out-of-Equilibrium Play
Abstract
:1. Introduction
2. Evolutionary Dynamics
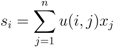

 , the replicator-mutation dynamics can be written,
, the replicator-mutation dynamics can be written,
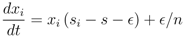
 (which can be derived by subtraction and division by S and R − S, respectively, in the replicator-mutation dynamics equation, Equation (3)).
(which can be derived by subtraction and division by S and R − S, respectively, in the replicator-mutation dynamics equation, Equation (3)). 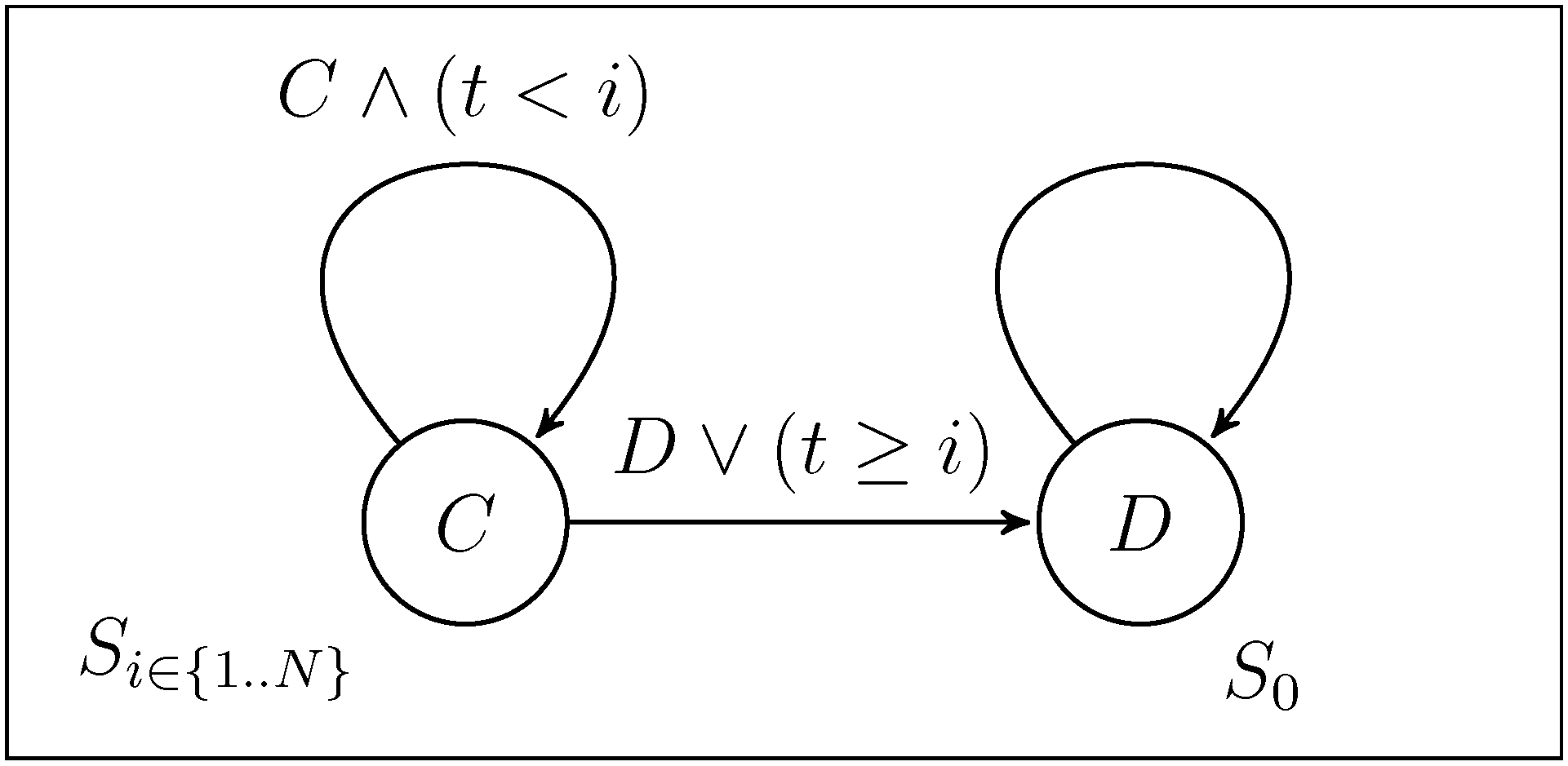
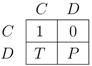
2.1. Selecting the Strategy Set

3. Dynamic Behaviour and Stability Analysis
 and N, respectively. We are mainly interested in which influence the presence of Convincers and Followers has on the stability of fixed points and its impact on the dynamics. This will be illustrated in three different ways as follows. First, we present and examine a few specific examples of the evolutionary dynamics and discuss the qualitative difference between the strategy sets. For the simple strategy set, we show analytically that the fixed point associated with the Nash equilibrium remains stable for a sufficiently small mutation rate. A numerical investigation is then performed for the extended strategy set, characterising the fixed point stability. Finally, for different lengths of the game, we study realisations of the evolutionary dynamics from an initial condition of full cooperation (xN = 1 and xi = 0 for i ≠ N, with xk denoting the fraction of strategy Sk in the population) to examine to which degree cooperation survives and whether the dynamics is attracted to a fixed point or characterized by oscillations. By studying variation of the dynamics over the different regions in the parameter space and changing the payoff parameters T and P (by adhering to the inequalities between T, P, R, S as described in Section 2), it is studied how the population evolves in various games over time.
and N, respectively. We are mainly interested in which influence the presence of Convincers and Followers has on the stability of fixed points and its impact on the dynamics. This will be illustrated in three different ways as follows. First, we present and examine a few specific examples of the evolutionary dynamics and discuss the qualitative difference between the strategy sets. For the simple strategy set, we show analytically that the fixed point associated with the Nash equilibrium remains stable for a sufficiently small mutation rate. A numerical investigation is then performed for the extended strategy set, characterising the fixed point stability. Finally, for different lengths of the game, we study realisations of the evolutionary dynamics from an initial condition of full cooperation (xN = 1 and xi = 0 for i ≠ N, with xk denoting the fraction of strategy Sk in the population) to examine to which degree cooperation survives and whether the dynamics is attracted to a fixed point or characterized by oscillations. By studying variation of the dynamics over the different regions in the parameter space and changing the payoff parameters T and P (by adhering to the inequalities between T, P, R, S as described in Section 2), it is studied how the population evolves in various games over time. 3.1. Dynamics with the Simple and the Extended Strategy Set
 is varied to illustrate how it affects the dynamics.
is varied to illustrate how it affects the dynamics.  , the extended strategy set exhibits meta-stability with recurring cooperation, while for the simple strategy set cooperation disappears.
, the extended strategy set exhibits meta-stability with recurring cooperation, while for the simple strategy set cooperation disappears.
 , the extended strategy set exhibits meta-stability with recurring cooperation, while for the simple strategy set cooperation disappears.
, the extended strategy set exhibits meta-stability with recurring cooperation, while for the simple strategy set cooperation disappears. 
 may offset the situation. For the higher mutation rate, cooperative strategies re-emerge after a period of influx from other strategies. The mutations gradually introduce cooperative behaviour to a critical point where some degree of cooperation has a selective advantage over full defection, and we see a shift in the level of cooperation. After a while, cooperative behaviour is again overtaken by full defection and a cyclic behaviour becomes apparent. Comparing with the next realisation of the simple strategies we see that this can happen only when the mutation rate is high enough. As mutation rate becomes smaller, here illustrated with
may offset the situation. For the higher mutation rate, cooperative strategies re-emerge after a period of influx from other strategies. The mutations gradually introduce cooperative behaviour to a critical point where some degree of cooperation has a selective advantage over full defection, and we see a shift in the level of cooperation. After a while, cooperative behaviour is again overtaken by full defection and a cyclic behaviour becomes apparent. Comparing with the next realisation of the simple strategies we see that this can happen only when the mutation rate is high enough. As mutation rate becomes smaller, here illustrated with  = 2−12, there is no re-appearance of cooperation. When the mutation rate gets too low, strategies other than defection are kept on a level that is too low to promote further cooperation. This demonstrates that the mutation rate can affect whether cooperation re-appears or not.
= 2−12, there is no re-appearance of cooperation. When the mutation rate gets too low, strategies other than defection are kept on a level that is too low to promote further cooperation. This demonstrates that the mutation rate can affect whether cooperation re-appears or not. 3.2. Existence of Stable Fixed Points
 turns more evolutionary dynamics into having stable fixed points. Runs for N = 5, 6, 7 indicate a convergence, as the mutation rate is decreased, towards a fraction of games being without stable fixed points, as seen in the lower left of the parameter space for the different game lengths. To the bottom right the boundary is shown for a particular T = 1.1.
turns more evolutionary dynamics into having stable fixed points. Runs for N = 5, 6, 7 indicate a convergence, as the mutation rate is decreased, towards a fraction of games being without stable fixed points, as seen in the lower left of the parameter space for the different game lengths. To the bottom right the boundary is shown for a particular T = 1.1.
 turns more evolutionary dynamics into having stable fixed points. Runs for N = 5, 6, 7 indicate a convergence, as the mutation rate is decreased, towards a fraction of games being without stable fixed points, as seen in the lower left of the parameter space for the different game lengths. To the bottom right the boundary is shown for a particular T = 1.1.
turns more evolutionary dynamics into having stable fixed points. Runs for N = 5, 6, 7 indicate a convergence, as the mutation rate is decreased, towards a fraction of games being without stable fixed points, as seen in the lower left of the parameter space for the different game lengths. To the bottom right the boundary is shown for a particular T = 1.1. 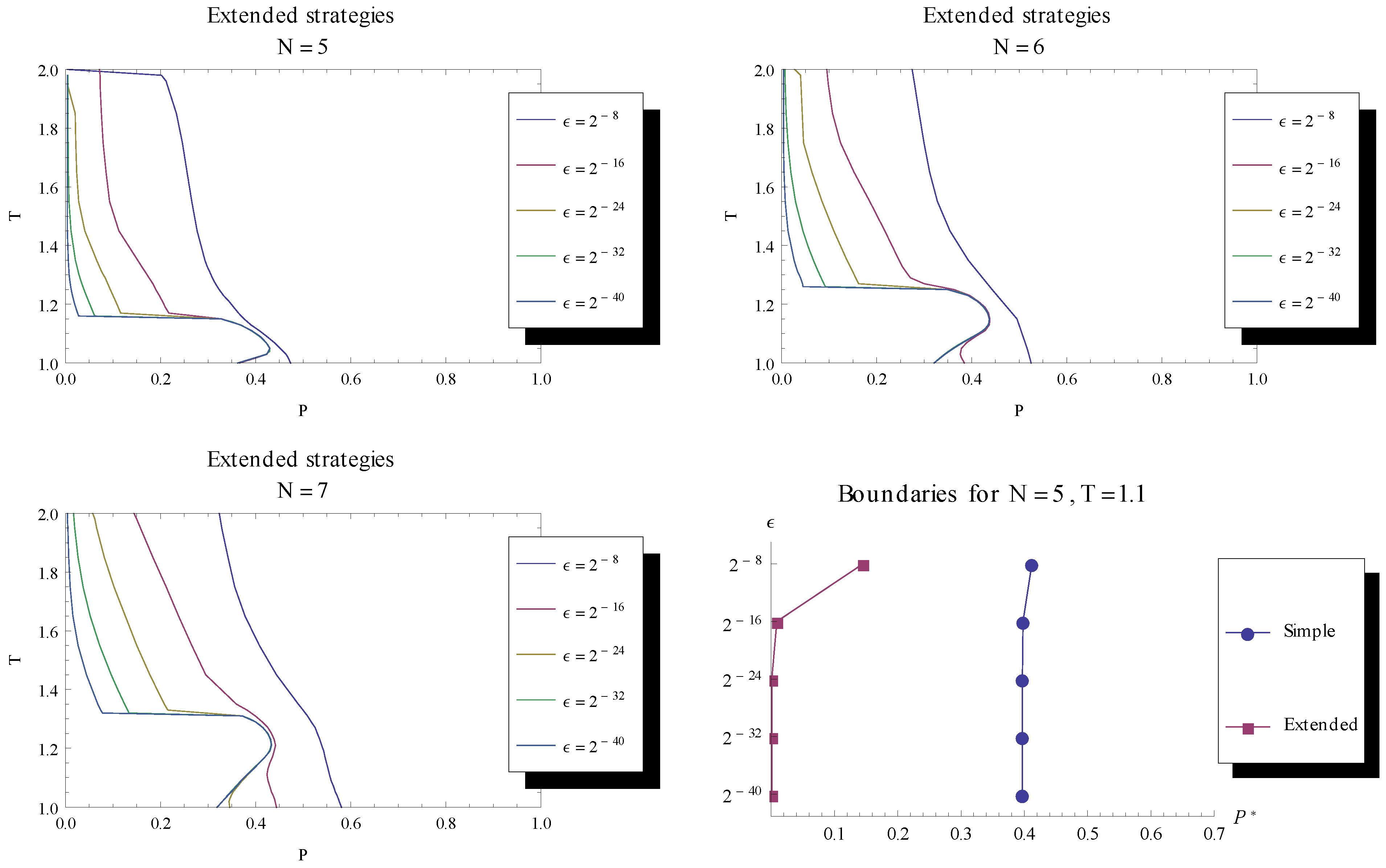
 the dynamics is characterised by stable fixed points. We are especially interested in the case of lowering
the dynamics is characterised by stable fixed points. We are especially interested in the case of lowering  towards 0 to examine whether fixed points become stable when mutation rate is sufficiently small, like in the case of the simple strategy set.
towards 0 to examine whether fixed points become stable when mutation rate is sufficiently small, like in the case of the simple strategy set.  , while to the left of the line no stable fixed points were found. When decreasing the mutation rate
, while to the left of the line no stable fixed points were found. When decreasing the mutation rate  towards 0, we see that an increasing fraction of parameter space is characterised by a stable fixed point. Unlike the case for the simple strategy set, the numerical investigation shows a convergence of the delimiting line between stable and unstable fixed points, indicating that there is a remaining region in parameter space (with low P and low T ) for which fixed points are unstable in the limit of zero mutation rate.
towards 0, we see that an increasing fraction of parameter space is characterised by a stable fixed point. Unlike the case for the simple strategy set, the numerical investigation shows a convergence of the delimiting line between stable and unstable fixed points, indicating that there is a remaining region in parameter space (with low P and low T ) for which fixed points are unstable in the limit of zero mutation rate. 3.3. Recurring Phases of Cooperation
 << 1, and, in particular, numerical analyses were made with a series of decreasing mutation rates. The population is initialized as before, described in Section 3.1.
<< 1, and, in particular, numerical analyses were made with a series of decreasing mutation rates. The population is initialized as before, described in Section 3.1. 3.4. Co-existence between Fixed Point Existence and Recurring Cooperation
 . Combining the different findings by considering their boundaries in the parameter space, this suggests an additional property of the evolutionary dynamics. By considering the joint results of our findings (in Figure 4 and Figure 5), one can note that there is a part of parameter space for which there is co-existence between a stable fixed point of defect strategies and a stable cycle with recurring cooperation.
. Combining the different findings by considering their boundaries in the parameter space, this suggests an additional property of the evolutionary dynamics. By considering the joint results of our findings (in Figure 4 and Figure 5), one can note that there is a part of parameter space for which there is co-existence between a stable fixed point of defect strategies and a stable cycle with recurring cooperation.  steadily reduces the part of parameter space dominated by recurrent cooperation. In the bottom row, the delimiting line is shown for a variety of game lengths and for two levels of mutation (left and right), illustrating the fact that the longer the game the larger the parameter region supporting cooperative phases in the evolutionary dynamics.
steadily reduces the part of parameter space dominated by recurrent cooperation. In the bottom row, the delimiting line is shown for a variety of game lengths and for two levels of mutation (left and right), illustrating the fact that the longer the game the larger the parameter region supporting cooperative phases in the evolutionary dynamics.
 steadily reduces the part of parameter space dominated by recurrent cooperation. In the bottom row, the delimiting line is shown for a variety of game lengths and for two levels of mutation (left and right), illustrating the fact that the longer the game the larger the parameter region supporting cooperative phases in the evolutionary dynamics.
steadily reduces the part of parameter space dominated by recurrent cooperation. In the bottom row, the delimiting line is shown for a variety of game lengths and for two levels of mutation (left and right), illustrating the fact that the longer the game the larger the parameter region supporting cooperative phases in the evolutionary dynamics. 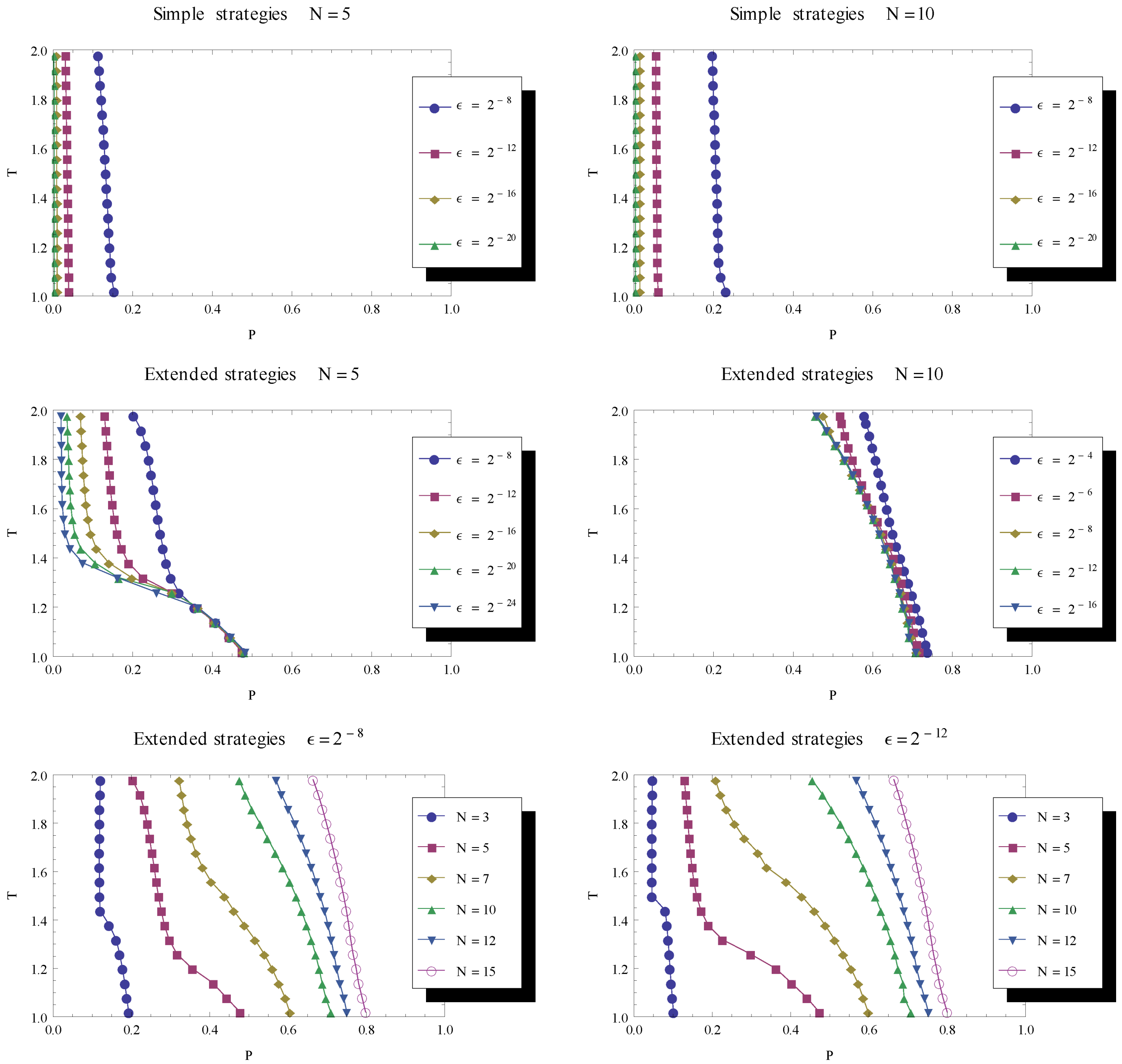
4. Discussion and Conclusion
 .
. Acknowledgements
Appendix A. Stability of fixed point in the simple strategy set for small mutation rates
 = 0, continuously translates into a stable fixed point as the mutation rate becomes positive,
= 0, continuously translates into a stable fixed point as the mutation rate becomes positive,  > 0, we investigate the fixed point more thoroughly. First, we note that the stability of the fixed point without mutations (
> 0, we investigate the fixed point more thoroughly. First, we note that the stability of the fixed point without mutations (  = 0), characterised by x1 = 1 (strategy S0 dominating), can be determined by the largest eigenvalue of the Jacobian matrix (∂ẋi/∂xj) derived from the dynamics, Equation (3), where we use the notation ẋi = dxi/dt. One finds that the largest eigenvalue is given by λmax = −P < 0, which shows that the fixed point is stable. This is also known from the stability analysis of the finitely iterated game by Cressman [19].
= 0), characterised by x1 = 1 (strategy S0 dominating), can be determined by the largest eigenvalue of the Jacobian matrix (∂ẋi/∂xj) derived from the dynamics, Equation (3), where we use the notation ẋi = dxi/dt. One finds that the largest eigenvalue is given by λmax = −P < 0, which shows that the fixed point is stable. This is also known from the stability analysis of the finitely iterated game by Cressman [19].  > 0, which is a set of n polynomial equations given by ẋi = 0 (with i = 1, ..., n), into an equation of only one variable x1. Based on this we show that the Nash equilibrium fixed point for zero mutation rate
> 0, which is a set of n polynomial equations given by ẋi = 0 (with i = 1, ..., n), into an equation of only one variable x1. Based on this we show that the Nash equilibrium fixed point for zero mutation rate  = 0, characterised by x1 = 1, continuously moves into the interval x1 ∈ [0, 1], with retained stability.
= 0, characterised by x1 = 1, continuously moves into the interval x1 ∈ [0, 1], with retained stability. 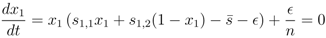
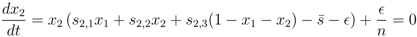
 > 0, all strategies are present, xi > 0, and we can divide these equations by x1 and x2, respectively. Then, taking the difference between the equations gives us an equation for the relation between x1 and x2,
> 0, all strategies are present, xi > 0, and we can divide these equations by x1 and x2, respectively. Then, taking the difference between the equations gives us an equation for the relation between x1 and x2,
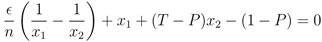
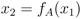
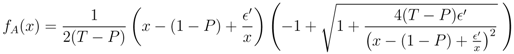
 ′ =
′ =  /n. In the same way, for xk−1 and xk (for k = 3, ..., N − 1), the fixed point implies that
/n. In the same way, for xk−1 and xk (for k = 3, ..., N − 1), the fixed point implies that
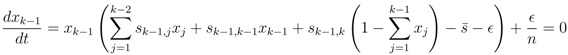
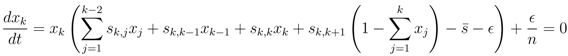
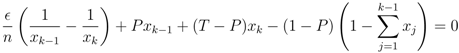
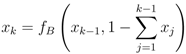

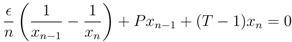
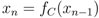
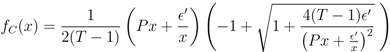
 .
.
 .
. 
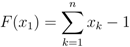
 = 0, since all functions fA, fB and fC are identical to zero in that case and we simply get F(x1) = x1 − 1, capturing the Nash equilibrium fixed point x1 = 1. (Note, though, that in this extension none of the other fixed points at
= 0, since all functions fA, fB and fC are identical to zero in that case and we simply get F(x1) = x1 − 1, capturing the Nash equilibrium fixed point x1 = 1. (Note, though, that in this extension none of the other fixed points at  =0 are captured; any xk =1 defines a fixed point for zero mutation rate, but all except the first one are of no interest for us.)
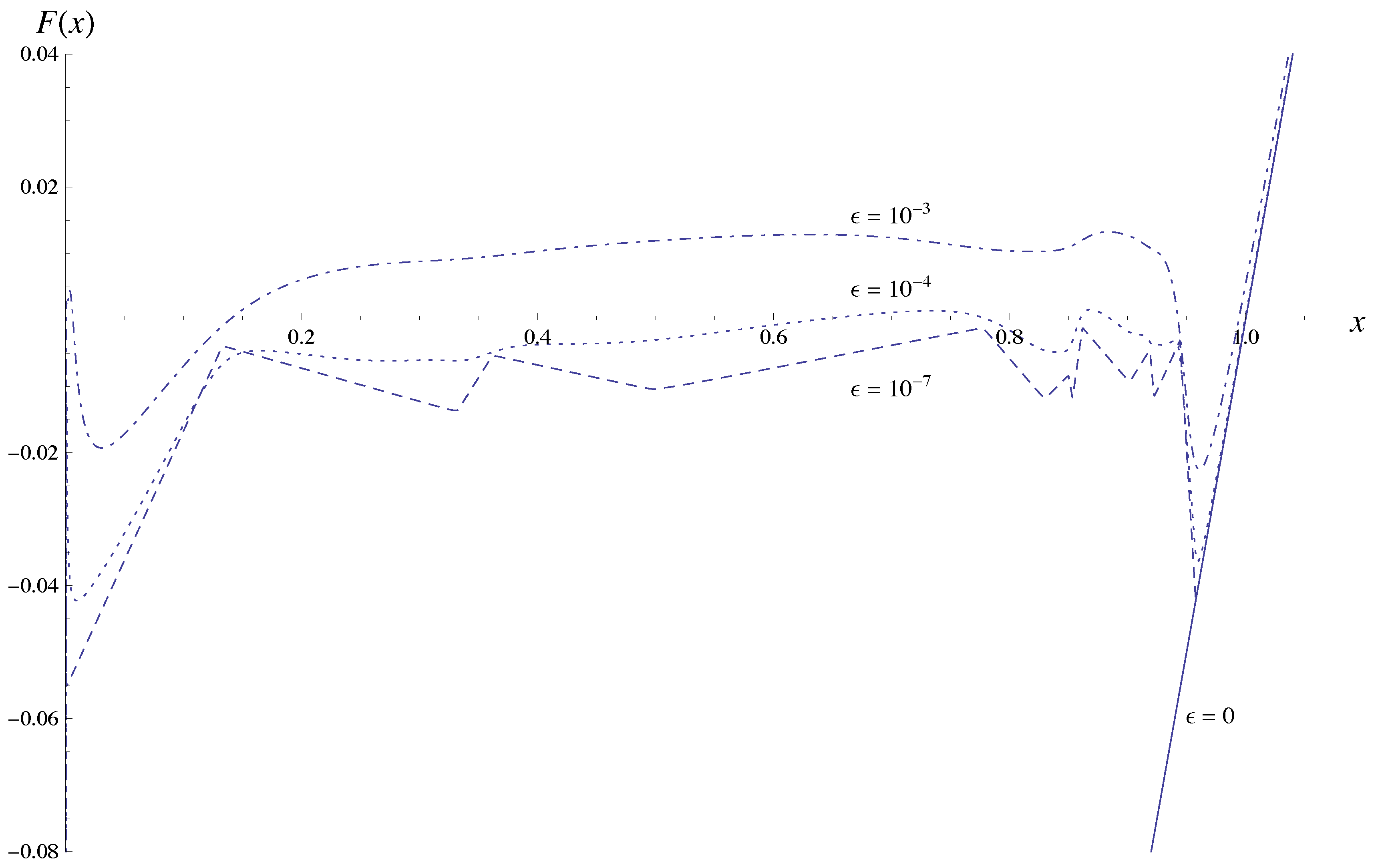
=0 are captured; any xk =1 defines a fixed point for zero mutation rate, but all except the first one are of no interest for us.)  is. We also see that g(y) → 0 as |y| → ∞. Thus, F(x) being composed of these functions is continuous in the interval [0, 1].
is. We also see that g(y) → 0 as |y| → ∞. Thus, F(x) being composed of these functions is continuous in the interval [0, 1].  . The graph shows that as the mutation rate increases the fixed point at x1 = 1 moves to the left and also that new fixed points may emerge. Most importantly, though, the graph indicates a discontinuous change of the function for x below about 0.95, when going from
. The graph shows that as the mutation rate increases the fixed point at x1 = 1 moves to the left and also that new fixed points may emerge. Most importantly, though, the graph indicates a discontinuous change of the function for x below about 0.95, when going from  = 0 to
= 0 to  > 0. In order to show that the fixed point always moves continuously from x1 = 1, we need to be sure that any such a discontinuity is bounded away from x1 = 1.
> 0. In order to show that the fixed point always moves continuously from x1 = 1, we need to be sure that any such a discontinuity is bounded away from x1 = 1.  = 0 there is a zero in x = (1, 0, ..., 0). We want to show that as
= 0 there is a zero in x = (1, 0, ..., 0). We want to show that as  increases, this fixed point, characterised by F(x1) = 0 for x1 = 1, continuously moves into the unit interval, 0 < x1 < 1. We accomplish this by performing a series expansion of F(x) around x = 1 and
increases, this fixed point, characterised by F(x1) = 0 for x1 = 1, continuously moves into the unit interval, 0 < x1 < 1. We accomplish this by performing a series expansion of F(x) around x = 1 and  = 0, by showing that F′(x1) = 1 for x1 = 1, that F is increasing with
= 0, by showing that F′(x1) = 1 for x1 = 1, that F is increasing with  in the neighbourhood of x1 = 1, and that the coordinates xk (k > 1) of the fixed point move continuously with x1 when sufficiently close to 1.
in the neighbourhood of x1 = 1, and that the coordinates xk (k > 1) of the fixed point move continuously with x1 when sufficiently close to 1.  = 0, we have already noted that F(x1) = x1 − 1, and thus the derivative F′(x1) = 1.
= 0, we have already noted that F(x1) = x1 − 1, and thus the derivative F′(x1) = 1.  , F increases with
, F increases with  . We do this term by term in the sum of F . First assume that the point x1 is close to fixed point value 1 at zero mutation rate, i.e., x1 = 1 − δ, and that
. We do this term by term in the sum of F . First assume that the point x1 is close to fixed point value 1 at zero mutation rate, i.e., x1 = 1 − δ, and that  is small, so that
is small, so that  << P and δ << P . The first term in F is x1 and does not depend on
<< P and δ << P . The first term in F is x1 and does not depend on  . The second term, x1, is given by fA,
. The second term, x1, is given by fA,

 ′. For the next term x3, using Equation (13), we find that to first order in
′. For the next term x3, using Equation (13), we find that to first order in  ′ and δ,
′ and δ,
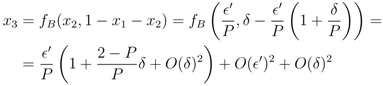

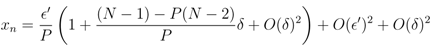
 ′ is given by the n − 1 terms x2, ..., xn, or dF(x1)/d
′ is given by the n − 1 terms x2, ..., xn, or dF(x1)/d  ′ ∼ (n − 1)/P > 0. Adding the fixed point constraint, F(x1) = 0, to the linearisation determines x1 and thus δ in terms of
′ ∼ (n − 1)/P > 0. Adding the fixed point constraint, F(x1) = 0, to the linearisation determines x1 and thus δ in terms of  ′. To first order in
′. To first order in  the fixed point is given by
the fixed point is given by
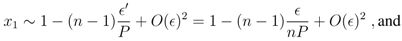

 . This analysis shows that as f increases from 0, the fixed point gradually moves into the unit interval.
. This analysis shows that as f increases from 0, the fixed point gradually moves into the unit interval.  = 0, the eigenvalues of the Jacobian also change continuously. The fixed point at
= 0, the eigenvalues of the Jacobian also change continuously. The fixed point at  = 0 is stable, with the largest eigenvalue being λmax = −P < 0, and we can conclude that for sufficiently small
= 0 is stable, with the largest eigenvalue being λmax = −P < 0, and we can conclude that for sufficiently small  > 0, the real part of the largest eigenvalue remains negative. From this we can conclude that the fixed point associated with the Nash equilibrium in the finitely repeated Prisoner’s Dilemma remains stable in the simple strategy set if the mutation rate is sufficiently small. This concludes the proof of Proposition 1.
> 0, the real part of the largest eigenvalue remains negative. From this we can conclude that the fixed point associated with the Nash equilibrium in the finitely repeated Prisoner’s Dilemma remains stable in the simple strategy set if the mutation rate is sufficiently small. This concludes the proof of Proposition 1. - 1. An instance of the dynamics was counted as oscillating when the average payoff A repeatedly returns to at least 5% above full defection, i.e. A > 1.05N P . Frequently, it was the case that the oscillations had phases of cooperation well above the 5% threshold.
References
- Handbook of Computational Economics, 1st; Tesfatsion, L.S.; Judd, K.L. (Eds.) Elsevier: Amsterdam, The Netherlands, 2006; Vol. 2.
- Arthur, W.B.; Holland, J.H.; Lebaron, B.; Palmer, R.; Tayler, P. Asset pricing under endogenous expectations in an artificial stock market model. In The Economy as an Evolving Complex System II; Arthur, W.B., Durlauf, S.N., Lane, D.A., Eds.; Addison-Wesley: Boston, MA, USA, 1997; pp. 15–44. [Google Scholar]
- Samanidou, E.; Zschischang, E.; Stauffer, D.; Lux, T. Agent-based models of financial markets. Rep. Prog. Phys. 2007, 70, 409–450. [Google Scholar] [CrossRef]
- Bosetti, V.; Carraro, C.; Galeotti, M.; Massetti, E.; Tavoni, M. A world induced technical change hybrid model. The Energy Journal 2006, 0, 13–38. [Google Scholar]
- Parker, D.C.; Manson, S.M.; Janssen, M.A.; Hoffmann, M.J.; Deadman, P. Multi-agent systems for the simulation of land-use and land-cover change: A review. Ann. Assoc. Am. Geogr. 2003, 93, 314–337. [Google Scholar] [CrossRef]
- Simon, H.A. A Behavioral Model of Rational Choice. Models of Man, Social and Rational: Mathematical Essays on Rational Human Behavior in a Social Setting; Wiley: New York, NY, USA, 1957; pp. 99–118. [Google Scholar]
- Camerer, C. Behavioral Game Theory: Experiments in Strategic Interaction; The Roundtable series in behavioral economics; Russell Sage Foundation: New York, NY, USA, 2003. [Google Scholar]
- Aumann, R.J. Rule-Rationality versus Act-Rationality. In Discussion paper series; Center for Rationality and Interactive Decision Theory, Hebrew University: Jerusalem, Israel, 2008. [Google Scholar]
- Binmore, K. Modeling rational players: Part I. Economics and Philosophy 1987, 3, 179–214. [Google Scholar] [CrossRef]
- Binmore, K. Modeling rational players: Part II. Economics and Philosophy 1988, 4, 9–55. [Google Scholar] [CrossRef]
- Nash, J.F. Equilibrium points in n-person games. In Proceedings of the National Academy of Sciences of the United States of America; 1950; 36, pp. 48–49. [Google Scholar]
- Pettit, P.; Sugden, R. The backward induction paradox. J. Phil. 1989, 86, 169–182. [Google Scholar]
- Bosch-Domnech, A.; Montalvo, J.G.; Nagel, R.; Satorra, A. One, two, (three), infinity, ... : Newspaper and lab beauty-contest experiments. Am. Econ. Rev. 2002, 92, 1687–1701. [Google Scholar]
- Basu, K. The traveler’s dilemma: Paradoxes of rationality in game theory. Am. Econ. Rev. 1994, 84, 391–395. [Google Scholar]
- Selten, R.; Stoecker, R. End behavior in sequences of finite Prisoner’s Dilemma supergames A learning theory approach. J. Econ. Behav. Organ. 1986, 7, 47–70. [Google Scholar] [CrossRef]
- Schuster, P.; Sigmund, K. Replicator dynamics. J. Theor. Biol. 1983, 100, 533–538. [Google Scholar] [CrossRef]
- Hofbauer, J. The selection mutation equation. J. Math. Biol. 1985, 23, 41–53. [Google Scholar] [CrossRef]
- Nachbar, J.H. Evolution in the finitely repeated prisoner’s dilemma. J. Econ. Behav. Organ. 1992, 19, 307–326. [Google Scholar] [CrossRef]
- Cressman, R. Evolutionary stability in the finitely repeated Prisoner’s Dilemma game. J. Econ. Theory 1996, 68, 234–248. [Google Scholar] [CrossRef]
- Cressman, R. Evolutionary Dynamics and Extensive Form Games; MIT Press Series on Economic Learning and Social Evolution; MIT Press: Cambridge, MA, USA, 2003. [Google Scholar]
- Noldeke, G.; Samuelson, L. An evolutionary analysis of backward and forward induction. Games Econ. Behav. 1993, 5, 425–454. [Google Scholar] [CrossRef]
- Cressman, R.; Schlag, K. The dynamic (in)stability of backwards induction. J. Econ. Theory 1998, 83, 260–285. [Google Scholar] [CrossRef]
- Binmore, K.; Samuelson, L. Evolutionary drift and equilibrium selection. Rev. Econ. Stud. 1999, 66, 363–393. [Google Scholar]
- Hart, S. Evolutionary dynamics and backward induction. Games Econ. Behav. 2002, 41, 227–264. [Google Scholar]
- Hofbauer, J.; Sandholm, W.H. Survival of dominated strategies under evolutionary dynamics. Theor. Econ. 2011, 6, 341–377. [Google Scholar] [CrossRef]
- Gintis, H.; Cressman, R.; Ruijgrok. Subgame perfection in evolutionary dynamics with recurrent perturbations. In Handbook of Research on Complexity; Barkley Rosser, J., Ed.; Edward Elgar Publishing: Northampton, MA, USA, 2009; pp. 353–368. [Google Scholar]
- Ponti, G. Cycles of learning in the centipede game. Games Econ. Behav. 2000, 30, 115–141. [Google Scholar] [CrossRef]
- Rosenthal, R. Games of perfect information, predatory pricing and the chain-store paradox. J. Econ. Theory 1981, 25, 92–100. [Google Scholar] [CrossRef]
- Aumann, R.J. Backward induction and common knowledge of rationality. Games Econ. Behav. 1995, 8, 6–19. [Google Scholar] [CrossRef]
- Aumann, R.J. Reply to Binmore. Games Econ. Behav. 1996, 17, 138–146. [Google Scholar] [CrossRef]
- Binmore, K. Rationality and backward induction. J. Econ. Methodol. 1997, 4, 23–41. [Google Scholar] [CrossRef]
- Gintis, H. Towards a renaissance of economic theory. J. Econ. Behav. Organ. 2010, 73, 34–40. [Google Scholar] [CrossRef]
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Lindgren, K.; Verendel, V. Evolutionary Exploration of the Finitely Repeated Prisoners’ Dilemma—The Effect of Out-of-Equilibrium Play. Games 2013, 4, 1-20. https://doi.org/10.3390/g4010001
Lindgren K, Verendel V. Evolutionary Exploration of the Finitely Repeated Prisoners’ Dilemma—The Effect of Out-of-Equilibrium Play. Games. 2013; 4(1):1-20. https://doi.org/10.3390/g4010001
Chicago/Turabian StyleLindgren, Kristian, and Vilhelm Verendel. 2013. "Evolutionary Exploration of the Finitely Repeated Prisoners’ Dilemma—The Effect of Out-of-Equilibrium Play" Games 4, no. 1: 1-20. https://doi.org/10.3390/g4010001




