Voluntary versus Enforced Team Effort
Abstract
: We present a model where each of two players chooses between remuneration based on either private or team effort. Although at least one of the players has the equilibrium strategy to choose private remuneration, we frequently observe both players to choose team remuneration in a series of laboratory experiments. This allows for high cooperation payoffs but also provides individual free-riding incentives. Due to significant cooperation, we observe that, in team remuneration, participants make higher profits than in private remuneration. We also observe that, when participants are not given the option of private remuneration, they cooperate significantly less.1. Introduction
This paper presents a theoretical model of voluntary participation in a team effort and compares voluntary and enforced team effort in the experimental economics laboratory. To foster team effort, many firms use team incentive schemes that account for a small portion of employee income [1]. Following Lazear [2], there are good reasons to suppose that team incentive schemes are more effective than individual incentive schemes in inducing high employee effort, in particular when the measurement of individual contributions is impossible or very costly. On the other hand, team incentive schemes are likely to induce free-riding behavior [3,4].
Team incentive schemes are typically based on profit sharing: employees are paid annual bonuses that vary with profitability defined at the overall corporate level or at the level of an individual division. Several empirical studies find evidence that profit sharing is associated with higher productivity (for an overview, see [5]) and better financial performance of firms (e.g., [6] for the US, [7] for China, [8] for the UK, and [9] for Germany). An extreme form of profit sharing is when employees own all of the company as, for example, in partnerships that are typical in law, medicine, management consulting or architecture, or in production cooperatives. There is a huge body of literature on worker-owned firms, both theoretical and empirical. The latter suggests that producer cooperatives tend to enjoy higher levels of productivity than conventional firms [10].
Putterman and Skillman [11] present a theoretical model of effort choice in a cooperative firm in which they examine the role of exit costs in order to reconcile the seemingly contradictory lines of reasoning by MacLeod [12] and Lin [13]: MacLeod argues that repetition of the production relationship in a cooperative allows for the use of trigger strategies to punish deviations from efficient output. He points out that worker mobility might hamper threats of future punishment and thus calls for exit costs as an important criterion for a successful cooperative. Lin, on the other hand, suggests that effective cooperation depends on the freedom to exit. She argues “that high-effort outcomes were achieved in Chinese farm cooperatives prior to 1958 because members enjoyed the right to return to private farming at will, and could thus credibly use the threat of exit to deter shirking by fellow team members. When, by Lin's account, individual rights of withdrawal were removed in 1958, productivity dropped sharply” ([11], p. 598).
Supporting Lin's argument, Orbell and Dawes [14] show in the experimental economics laboratory that participants' choice between playing a prisoner's dilemma game or an outside option depend on their own propensity to cooperate. This propensity is in turn closely tied to their beliefs about others' likelihood of cooperation. Since only the more cooperative participants choose to play the prisoner's dilemma game, it turns out to be worthwhile to play and cooperate.
Another aspect, implicit in Lin's argument, is that prior to 1958 participation was voluntary, while later on it was enforced. Enforcement could also have been one of the reasons for the failure of the labor-managed firm created in former Yugoslavia, which attracted of lot of attention in the 1960s and 1970s. In this paper, we examine the behavioral difference in voluntary versus enforced collaboration in a series of experiments on team effort under profit sharing. The team-effort situation allows for many more than the binary choices in the prisoner's dilemma game. Our experiments are furthermore novel in that they (1) consider a situation that involves an interior optimum; and (2) distinguish between a symmetric and an asymmetric parameterization. In the voluntary collaboration experiments we allow, in keeping with Lin's line of reasoning, the choice to renounce team effort. We address several questions. Our major interest is whether teaming should be voluntary or enforced by management. Thus, we compare an environment where employees can choose between private and team remuneration to one where they have no choice but to work under team remuneration. Suppose a small work group in a research organization. Should management ask the group members to all work on one single project or allow them to work on individual projects? A follow-up question, which is beyond the scope of our study, would relate to the choice of team partners as, for example, in Ehrhart and Keser [15].
In our experiments, pairs of participants have to provide costly effort over 30 periods. In each period, each participant individually chooses an effort as an integer number between 0 and 100. Effort costs are represented by a quadratic function. In an environment where teaming is enforced, a participant's remuneration is based on the average of the participant's own effort and the effort of the participant he or she is paired with. In an environment where teaming is voluntary, each participant chooses between private or team remuneration before deciding on the effort in each period. While private remuneration is based on the participant's individual effort only, team remuneration is based on the average of the participant's own effort and the effort of his or her team member.
In the case of team remuneration, each of the two participants faces an individual incentive to take a free ride on the other's effort. The effort of each participant may be considered as a voluntary contribution to the public good team effort. We have modeled the situation such that through cooperation the team can realize higher profits than the maximum sum of profits that the two players can realize under private remuneration. This is based on the assumption of a higher payment per effort unit under team remuneration than under private remuneration, possibly reflecting that, in the case of team remuneration, the firm has a cost advantage relative to the case of private remuneration due to reduced monitoring costs. Another justification for this asymmetry in payment could be due to scale effect in team production (see also [13] for further discussion). In real life, effort is difficult to measure, so incentive payment has to be based on a surrogate, typically an output variable. In a work team it is often very hard if not impossible to measure an individual's contribution to the team output. While there is a large theoretical literature on team incentives when individual effort is not observable [4,16–19], only few empirical studies have examined the impact of teams on output [20,21]. Even though data at the firm level may be available, they might not allow for the comparison of outcomes with and without team incentives, or of voluntary and enforced teaming. Comparisons across firms are likely to suffer from issues of worker self-selection and distorting factors due to additional differences in human resource and production processes. Thus, controlled laboratory experiments are a valuable method of collecting data.
Nalbantian and Schotter [22] for example, present an experimental analysis of the functionality of various team-incentive schemes. Their revenue-sharing scheme is very similar to our team-remuneration scheme with profit sharing, except for a stochastic element in their experiment. More concretely, their participants face a moral hazard problem, while in our experiment effort is observable and verifiable. Both experiments, however, involve a free-riding incentive. Nalbantian and Schotter observe declining effort over time, i.e., an increase in free-riding behavior. They impose the incentive scheme on their participants. Recently, Mellizo, Carpenter and Matthews [23] observe in a real-effort experiment that groups of workers that voted to determine their compensation scheme provided significantly more effort than groups that had no say in how much they would be compensated.
In the experimental economics literature, we find a large number of studies on prisoner's dilemmas [24] and on voluntary contributions to finance a public good to which our experiment relates [25–27]. These studies provide a good picture of the kind of environments that are needed to facilitate cooperation and of the behavioral dynamics. The prisoner's dilemma game only allows for binary choices (cooperate, defect), while public goods games and our game permit an enlarged strategy space. The most important finding in public goods experiments is that people do make voluntary contributions above those that are in their egoistic individual interest and that their contribution decisions tend to be based on conditional cooperation [28–32].
In the majority of experiments, including those by Nalbantian and Schotter, participants are told that they are members of a team or a group. They cannot choose whether to be in a group or select the group or individual group members. Exceptions are the studies by Ehrhart and Keser [15], Hauk and Nagel [33], Hauk [34], Coricelli, Fehr and Fellner [35], Page, Putterman and Unel [36], Charness and Yang [37] that do allow for group choice. Our experiment allows for the choice of teaming with an exogenously determined other participant that remains the same other person during the entire experiment. Less closely related to our experiment, Gächter and Thöni [38], Ones and Putterman [39] and Gunnthorsdottir, Houser and McCabe [40] use controlled group formation mechanisms that depend on previous contributions.
It is an important point of our investigation whether participants, when they have the choice of either private or team remuneration, will choose team remuneration at all. We have parameterized our experimental games such that in the subgame perfect equilibrium participants choose private remuneration although social efficiency would require them to choose team remuneration. Beyond the actual choice of team remuneration, we want to investigate the level of cooperative efforts and the dynamics in the decision making, which could not only affect effort but also remuneration choices.
To evaluate the robustness of our observations with respect to the choice of the remuneration mode and effort, we examine both a symmetric and an asymmetric parameterization of our game. Most public-goods experiments examine symmetric parameterizations. Asymmetry in the players' effort costs makes the definition and thus the realization of a cooperative goal more difficult [41]. It reflects heterogeneity of the team members, an important aspect in real life that is often neglected in experimental investigations that tend to focus on symmetric situations. Different effort costs can reflect diverse abilities or skills among team members. They can also reflect diverse organizational cultures coming together after a merger. The understanding of divergent behavior in symmetric and asymmetric team situations is an important human capital management issue. Abramson et al. [42], for example, argue that increased attention to differences and how individuals from different backgrounds work together is necessary to create workplaces in which employees work together in a cooperative, productive manner. It is sometimes argued that worker heterogeneity in teams leads to better team outcomes due to mutual learning and complementarities [21,43]. Our experimental design, however, does not allow for such effects.
We point out that our experiments are based on games that have a social optimum in the interior of the strategy space. This is different from the typical experiment on public-goods provision where the efficient solution lies at the upper end of the strategy space. It has been largely neglected in the literature that this design issue renders the observation of an aggregate outcome close to the efficient solution almost impossible. Thus, the specific non-linear design of our experiment is an important aspect. Despite the computational difficulties, it renders the game more realistic.
In Section 2, we present the model and its theoretical solutions. Section 3 develops behavioral predictions. Section 4 describes the experimental design. In Section 5, we present the experimental results. Section 6 concludes the article.
2. The Model
Our experiments with voluntary choice of the remuneration mode are based on the effort game presented in Section 2.1. This game has a unique subgame perfect equilibrium (Section 2.2) that is different from the joint profit-maximizing solution (Section 2.3).
2.1. The Effort Game
Consider a game with two players i = 1, 2 and two decision stages. Let us start by describing the second decision stage in which each of the two players chooses an effort level, before we consider the first stage in which the players decide on their remuneration mode.
In the second decision stage, each player i knows the remuneration mode and independently chooses an effort level, ei, where ei ∈ [0,100]. Effort is costly. Player i's cost function Ci depends on his individual effort ei and a constant ki, and is quadratic:
In the first decision stage, each player i independently chooses between private remuneration or team remuneration. If both players choose team remuneration, team remuneration is applied: each player i is paid, at the end of the second decision stage, based on both players' average effort multiplied by a constant, t. The team remuneration Ti for each player i is
If at least one of the players chooses private remuneration, private remuneration is applied: each player i is paid at the end of the second decision stage, based on his private effort multiplied by a constant, p. The private remuneration Pi for each player i is
Note that we assume t > p. This reflects that in the case of team remuneration the firm has a cost advantage relative to the case of private remuneration due to reduced monitoring costs.
The effort game ends at the end of the second decision stage. Player i's profit ∏i is determined by his remuneration minus his individual cost of effort:
2.2. The Subgame Perfect Equilibrium
The subgame perfect equilibrium of the effort game can be found by backward induction. We start by considering the second decision stage in which each player chooses a profit-maximizing effort level. We have to distinguish whether private or team remuneration applies, which depends on the players' choices in the first stage.
In the case of private remuneration, each player i solves an individual profit-maximization problem that is independent of the other player's effort choice:
The resulting optimal effort
In the case of team remuneration, each of the two players, i = 1, 2, independently chooses his effort to maximize his individual profit, taking the other player's effort into account:
The solution is independent of the other player's effort and, thus, implies the following dominant strategy for each player i:
The resulting equilibrium profit for player i is:
Consider, now, the first stage of the effort game taking the above solutions into account. If ΠI ** > ΠI *, then player i chooses team remuneration; if Πi ** < ΠI *, then player i chooses private remuneration. If player i is indifferent between team and private remuneration, we assume that player i chooses private remuneration. Only when both players choose team remuneration does the subgame perfect equilibrium predict team remuneration; in all other cases, it predicts private remuneration.
2.3. Joint Profit Maximization
In the case of team remuneration, the two players find themselves in a kind of prisoner's dilemma situation: their efforts represent voluntary contributions to the public good team effort. To some extent, each player has an incentive to take a free ride on the effort of the other player. The effort levels predicted by the equilibrium in dominant strategies are not optimal for the team. We find Pareto-optimal team-effort levels by solving the joint profit-maximization problem:
We equally weigh both players' profits. By using different weights we would find other Pareto optimal solutions.
For each player i, the optimal effort is given by:
As t > p, it follows that ei′ > ei* and Πi′ > Πi*. Thus, we have a Pareto-optimal solution for the effort game in which both players choose team remuneration and the effort ei′.
3. Predictions
We develop a number of theoretical and behavioral predictions to be tested in the experiments. Predictions 1 and 2 are theoretical while predictions 3 to 6 are behavioral and apply only if Prediction 1 is rejected.
Prediction 1: Participants choose private remuneration when it is in their (egoistic) self-interest to do so.
This follows directly from the subgame perfect equilibrium prediction derived above.
Prediction 2: Under private remuneration, participants choose the optimal effort level.
Under private remuneration, participants make an individual decision without strategic interactions. Their profit-maximizing effort can be directly read from a table in the instructions, which provides the respective cost and profit for each effort level (see Appendix).
Prediction 3: Under voluntary team remuneration, participants choose an effort above the equilibrium prediction.
Under team remuneration, participants are in a decision situation that is strategically equivalent to making a voluntary contribution to the provision of a public good. Over-provision relative to the dominant strategy prediction is a stylized fact [44].
Prediction 4: Participants choose higher team effort under voluntary teaming than under enforced teaming where participants do not have the choice of private remuneration.
One could argue that a participant who chooses team remuneration signals interest in cooperation. Theoretically, this kind of signaling relates to a forward induction argument [45–47] rather than the backward induction on which the subgame perfect equilibrium is built. Assume that the population of participants consists of a constant proportion of “free riders”—participants who prefer to play the equilibrium strategy under team remuneration—and “cooperators”—participants who prefer to cooperate under team remuneration. If the signaling argument holds, it implies a self-selected group of cooperators in voluntary teaming, while the participants in enforced teaming are represented by the entire population, including the constant proportion of free riders. It may, thus, simply be said that the pairs who are playing under team remuneration in any given period are a self-selected group as opposed to all pairs, in the other treatment. Since those who have been more successful in cooperating are more likely to select into the team-remuneration group, their average level of cooperation can be expected to be higher. This argument still holds if we consider the opportunity for self-interested participants to mimic cooperative behavior.
Gächter and Thöni [38], Ones and Putterman [39], and Gunnthorsdottir, Houser and McCabe [40] provide evidence that cooperation is easier to maintain among like-minded cooperators than in a random group. Thus, we expect a higher level of cooperation in voluntary teaming than in enforced teaming.
Prediction 5: A participant chooses his team effort in reaction to the other player's previous team effort.
Many public-goods experiments provide evidence in favor of conditional cooperation, which implies a kind of tit-for-tat strategy [48]: “if somebody is nice to you or others, you are inclined to be nice to him; if somebody is mean to you or others, you are inclined to be mean to him” [49].
Prediction 6: A participant's choice of remuneration depends on his partner's previous team effort.
We hypothesize that a participant chooses team remuneration if he expects to earn a higher payoff than under private remuneration. This depends on the effort level by the other participant. If team remuneration has been previously experienced, the higher the observed effort level, the more likely the team remuneration mode will be maintained. It could also be possible that noncooperative team effort by the other player may lead to a choice of private remuneration as a kind of opting out to enforce future cooperation. Hauk [34], for example, examines a game that provides the opportunity to opt out of a finitely repeated prisoner's dilemma game and finds that defection in early periods is punished by opting out.
4. Experimental Design
To test the above predictions we design several experimental treatments that are specified in Section 4.1. Section 4.2 describes the organization of the experiments.
4.1. Treatments
In a 2 × 2 treatment design, we examine the four combinations resulting from two different parameterizations and two structural variants of the effort game. The two parameterizations are symmetric (SYM), where the two players have the same parameters, and asymmetric (ASYM), where the two players have different effort costs.
The two structural variants are voluntary teaming (VOLUNTARY), which is exactly the effort game described above, and enforced teaming (ENFORCED), where the players play only the second stage of the game in enforced team remuneration. This allows us to investigate Prediction 4, which says that participants choose higher team effort under voluntary teaming than under enforced teaming.
Table 1 presents the parameters used in the SYM and ASYM treatments and the theoretical predictions for the second stage of the game in each of the two parameterizations. Note that, in the case of team remuneration, the second stage has the nature of a voluntary-contribution-to-a-public-good game where both the dominant strategy solution and the optimum (joint profit-maximizing solution) lie in the interior of the strategy space.
In the SYM parameterization, each player's maximal profit in the case of private remuneration is larger than his equilibrium profit in the case of team remuneration. It follows that in the subgame perfect equilibrium solution of the symmetric effort game both players choose private remuneration and an effort of 45. This yields a profit of 202.5 to each player. However, if both players choose team remuneration and an effort of 50 they can make a profit as high as 250 each. This solution maximizes the sum of profits of both players in the group.
In the ASYM parameterization, the player with the lower effort cost, player 1, makes a maximum profit in the case of private remuneration that is larger than his equilibrium profit in the case of team remuneration, while the opposite is true for the player with the higher effort cost, player 2. Thus, in the subgame perfect equilibrium solution, private remuneration will be realized. The low-cost player chooses an effort of 35 and makes a profit of 122.5, while the high-cost player chooses an effort of 28 and makes a profit of 98. Each of the two players can do better by choosing team remuneration and an effort of 40 by the low-cost player and 32 by the high-cost player. In this joint-profit-maximizing solution, the low-cost player's profit is 128 while the high-cost player's profit is 160, which implies that the high-cost player makes a higher profit than the low-cost player. Since each of the two players has an incentive to individually deviate, this solution does not describe an equilibrium of the second-stage subgame.
The last two columns of Table 1 present the minimum profit that a player can earn under team remuneration if he chooses the joint-profit maximizing effort, while the other chooses his individually profit-maximizing effort, and the maximum profit that he can earn under team remuneration if he chooses the individually profit-maximizing effort, while the other chooses the joint- profit-maximizing effort.
4.2. Organization
In the experiments, participants played 30 repetitions, called periods, of the effort game in two-player groups that remained unchanged during the entire experiment (“partners” design). Based again on the backward induction principle, the subgame perfect equilibrium prediction of the finitely repeated effort game prescribes in each period the subgame perfect equilibrium prediction presented above. Behaviorally, however, the repetition opens up room for reciprocal behavior or conditional cooperation.
In the beginning of the second decision stage, in the VOLUNTARY treatments, each participant was informed of the actual remuneration mode, depending on both players' decisions in the first stage. At the end of each period, each participant was informed about his or her individual profit. In the case of team remuneration the average effort level (and, thus, implicitly the effort level chosen by the other player) was also communicated to each participant. A participant's sum of profits in all 30 periods determined his or her individual earnings in the experiment.
The computerized experiments were run at the experimental economics laboratory at CIRANO (Centre Interuniversitaire de Recherche en Analyse des Organisations) in Montréal. Participants were students from various disciplines at the University of Montreal, who had been recruited by posters into a subject pool. For each session, we invited randomly chosen participants out of this pool. None of the participants had previous experience in economic experiments.
For each of the four treatments we have eight independent observations, based on eight pairs of two participants each. This implies that we have a total of 64 participants. We conducted sessions with eight participants, each having two sessions per treatment. In the beginning of a session, the participants were randomly and anonymously assigned into four two-player groups, and, in the ASYM treatments, they were also randomly allocated the role of either a low-cost or a high-cost player for the entire experiment.
Participants received written instructions (an English translation can be found in the Supplementary Files Repository, the French version is available upon request), which were also read aloud to them. Before the experiment could start, each participant had to provide correct answers to a number of questions regarding the understanding of the instructions. Participants were not allowed to communicate with each other during the entire experiment. They did not know with whom they interacted among the other participants. After the experiment, each participant was paid in private based on his or her individual earnings in the experiment plus a show-up fee. The individual earnings were converted into Canadian dollars with a factor announced in the experiment instructions. On average, participants earned 30 Canadian dollars, including the show-up fee, for a session that lasted about 90 minutes.
5. Experimental Results
In this section we evaluate, based both on non-parametric data analysis and regressions, the six predictions made in Section 3 above. Each pair of participants forming a two-player group represents an independent observation in the non-parametric analysis. Unless otherwise mentioned, all non-parametric tests are two-sided. If no significance level is given, we require significance at the 10-percent level. We denote the Wilcoxon signed ranks test as Wilcoxon test and the Mann-Whitney u-test as u-test. Table 2 provides the most important summary statistics.
Prediction 1: Participants do not choose the team remuneration mode when it is in their egoistic self-interest to choose private remuneration.
In the VOLUNTARY SYM treatment, team remuneration is chosen by both players and thus realized in 45 percent of all periods. In 34 percent of all periods both players choose private remuneration, while in 21 percent of all periods, private remuneration is realized due to one player choosing team remuneration but the other player choosing private remuneration. This is in sharp contrast to the subgame perfect equilibrium of the game with its specific parameterization. Comparing the first set of 15 periods to the final set of 15 periods, the relative frequency of team remuneration exhibits no tendency to increase or decrease over time (Wilcoxon test).
In the VOLUNTARY ASYM treatment, team remuneration is chosen by both players and thus realized in 72 percent of all periods. Again, this is in sharp contrast to the subgame perfect equilibrium of the game with its specific parameterization. The relative frequency of team remuneration in this treatment exhibits a tendency to increase over time: when we compare the first set of 15 periods to the last set of 15 periods, we observe an increase that is statistically significant (Wilcoxon test, 5-percent significance).
In the subgame perfect equilibrium of the VOLUNTARY ASYM treatment the high-cost player has an interest in choosing team remuneration. Thus, we hypothesize that high-cost players tend to choose team remuneration more often than low-cost players. We find support for this hypothesis in that the high-cost players chose team remuneration in 89 percent of all periods while the low-cost players chose team remuneration in 78 percent of all periods. The difference just fails significance: in six of the eight independent groups the high-cost player chooses team remuneration more often than the low-cost player. Note that this result replicates the empirical finding of Hamilton, Nickerson and Owan [21]. The individual interest of the high-cost player in choosing team remuneration also explains the much higher number of observed team remuneration in the VOLUNTARY ASYM than in the SYM treatment.
Conclusion 1: A large number of participants do choose team remuneration, in contrast to the subgame perfect equilibrium solution of the game.
Prediction 2: Participants choose the optimal effort level under private remuneration.
In the VOLUNTARY SYM treatment, the average effort over all periods with private remuneration is 45.27 (standard deviation of 16.81) and is not significantly different from 45, the optimal effort in the case of private remuneration (binomial test). This might be interpreted as evidence in favor of the participants' rationality. However, only about one half (52 percent) of all individual decisions under private remuneration are exactly 45. Participants tend to learn the optimal effort, though: the percentage of optimal private-effort choices increases from 47 in the first set of 15 periods to 63 in the last set of 15 periods. This increase is statistically significant (Wilcoxon test, 10-percent significance).
In the VOLUNTARY ASYM treatment, the average private effort of the low-cost players is 34.87 (standard deviation of 9.88), which is not significantly different from the optimal level of 35 (binomial test), and the average private effort of the high-cost players is 27.22 (standard deviation of 15.58), which is not significantly different from the optimal level of 28 (binomial test). However, only 51 percent of the effort choices by the low-cost players and 46 of those by the high-cost players are optimal. Pooling low-cost and high-cost players due to only four independent observations in each category, we observe that participants learn the optimal private effort: from the first set of 15 periods to the last set of 15 periods, the percentage of optimal choices significantly increases (Wilcoxon test, 10-percent significance).
Conclusion 2: On the aggregate, participants choose the optimal private effort. However, only about 50 percent of the individual choices are optimal. The percentage of optimal choices shows a significant tendency to increase over time.
Prediction 3: Under voluntary team remuneration, participants choose an effort above the equilibrium prediction.
In the VOLUNTARY SYM treatment, the average effort over all periods with team remuneration is 50.10 (standard deviation of 17.34) and significantly above 25, the dominant strategy in the case of team remuneration (binomial test, 5-percent significance). Thus, in the case of team remuneration, our experimental evidence is similar to the results in public-goods experiments: effort is higher than predicted by the game-theoretical solution. Note that from the first set of 15 periods to the last set of 15 periods, we observe no significant increase or decrease in the team effort, but a decrease in its standard deviation from 20.54 to 11.91 (Wilcoxon test, 5-percent significance) signaling a larger cooperative consensus over time.
Interestingly, the observed effort is not significantly different from the Pareto optimum of 50 (Wilcoxon test). In our experimental game, in contrast to most public-goods experiments, the optimum lies in the interior of the strategy space. This allows for the phenomenon that effort levels above the optimum have been chosen to the same extent as those below. If the Pareto optimum lies at the upper limit of the strategy space, participants can never err around it: deviations from the Pareto optimum are always below. This raises the concern whether it is due to this design issue that in most public-goods experiments contributions, although higher than in equilibrium, are still far below the Pareto optimum (see the related discussion on corner equilibria in [27,44,50–52]). Our experimental results give support to this concern as they show that, on the aggregate, participants make efforts right at the Pareto-optimal level.
Over all periods, the resulting average profit in team remuneration is 220.08 and significantly higher than in private remuneration, where it is 174.35 (Wilcoxon test, 10-percent significance). We observe no significant increase or decrease of profit from the first set of 15 periods to the last set of 15 periods, neither in team nor in private remuneration. The standard deviation, however, decreases from 165.34 to 81.31 in team remuneration (Wilcoxon test, 10-percent significance) and from 51.89 to 22.25 in private remuneration (Wilcoxon test, 5-percent significance).
The average profit in team remuneration is significantly below the optimal profit of 250 (Wilcoxon test, 1-percent significance). While the efforts are not significantly different from the Pareto optimum of 50, the rather large dispersion around the mean explains why the average profit is significantly below the optimum. Due to one outlier, the average profit is not significantly different from the equilibrium profit of 187.5.
In the VOLUNTARY ASYM treatment, the average team effort of the low-cost players is 34.51 (standard deviation of 11.09), while the average team effort of the high-cost players is 30.14 (standard deviation of 8.01). Both effort levels are significantly above the respective dominant strategy of 20 or 16 (binomial test, 1-percent significance). Neither effort level is significantly different from the respective Pareto optimum of 40 or 32 (Wilcoxon test). Furthermore, neither the low-cost players' average effort nor its standard deviation is significantly different from the respective value of the high-cost players (Wilcoxon test). Note that, comparing the average team effort in the first set of 15 periods to that in the final set of 15 periods, we observe a decrease both for the low-cost and the high-cost players. Neither is statistically significant (Wilcoxon test) although the decrease of the low-cost players' effort just fails significance.
The resulting average profit of the low-cost players (127.26, standard deviation of 74.05) is not significantly different from the one of the high-cost players (137.1, standard deviation of 59.85) in team remuneration (Wilcoxon test). While the high-cost players' average profit is significantly above their equilibrium profit (Wilcoxon test, 5-percent significance), the low-cost players' average profit is not significantly different from their equilibrium profit (Wilcoxon test). At the same time, neither low-cost nor high-cost players' profits are significantly different from their respective joint profit-maximizing solution (Wilcoxon test): the low-cost players realize 99 percent and the high-cost players realize 86 percent of it. Note that the profit of the low-cost players tends to increase from the first set of 15 periods to the last set of 15 periods under team remuneration (Wilcoxon test, 5-percent significance). The profit of the high-cost players shows no tendency to increase or decrease under team remuneration (Wilcoxon test).
The high-cost players' average profit is significantly higher in team remuneration than in private remuneration, where it is 68.06 (Wilcoxon test, 2-percent significance). In six of the eight groups, the low-cost players' average profit is higher in team remuneration than in private remuneration. However, this difference is statistically not significant (Wilcoxon test). The low-cost players' profit under private remuneration is 112.89 on average.
Conclusion 3: Under voluntary team remuneration, participants do choose an effort level that is above the equilibrium prediction. Low- and high-cost players realize profits that are not significantly different from their respective joint profit-maximizing solutions.
Prediction 4: Participants choose higher team effort under voluntary teaming than under enforced teaming.
Comparing average effort in the ENFORCED SYM to that in the VOLUNTARY SYM treatment, we observe that under enforced teaming effort is 35.68 (standard deviation of 19.45) and, thus, significantly lower than under voluntary teaming where it is 50.10 (u-test, 5-percent significance). Initially, however there is no statistically significant difference: enforced team effort in the first period is 41.88; whereas, voluntary team effort in the first period that team remuneration is realized is 45.00 (u-test). Similar to the voluntary team effort, enforced team effort shows neither a statistically significant decrease nor a statistically significant increase from the first set of set of 15 periods to the second set of set of 15 periods, nor does its standard deviation (Wilcoxon tests).
Enforced team effort is significantly above the equilibrium effort of 25 (Wilcoxon test, 5-percent significance) and significantly below the joint profit-maximizing effort of 50 (Wilcoxon test, 2-percent significance). Recall that, in contrast to this latter result, voluntary team effort is not significantly different from 50.
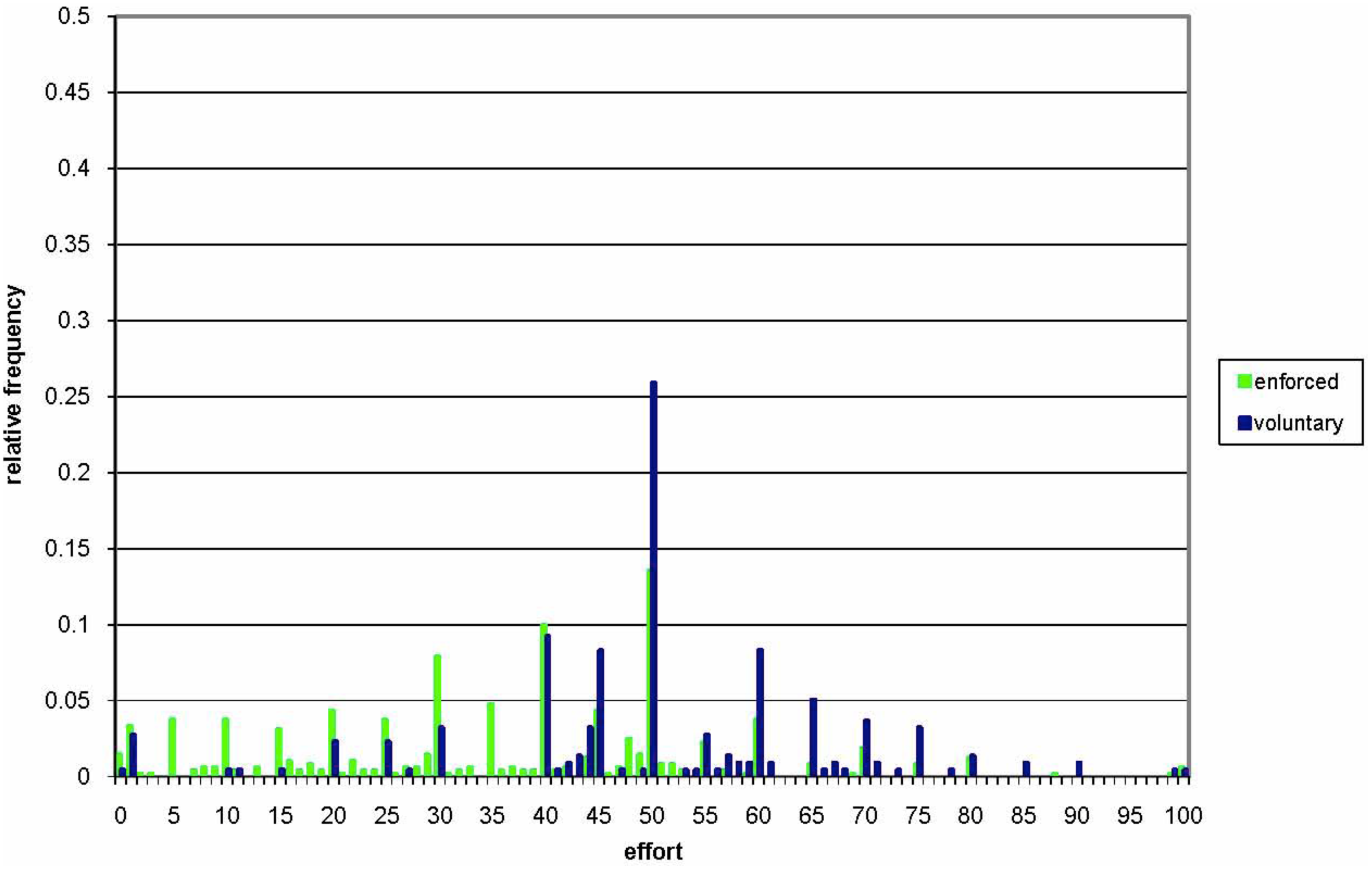
Figure 1 compares the density of effort under voluntary and enforced teaming. While we rarely observe enforced effort above the joint profit-maximizing level of 50 (15 percent of all observations above 50, 72 percent below), voluntary effort seems to be allocated at and around 50 (37 percent of all observations above, 38 below). Effort levels above 50 might be used as a signal for one's willingness to cooperate with the other, in particular if one expects the other to make an effort below 50 in the current period. The payoff function is relatively flat around the optimum so that the cost of going slightly above it is not very high. But, effort levels above 50 could also simply be due to random decision making and/or misunderstanding of the payoff function. The latter is unlikely to account for the majority of the observations above 50 in the voluntary teaming treatment as we observe only relatively few effort choices above 50 in the enforced teaming treatment. It could be seen as an unfortunate drawback of our experimental design that the middle of the strategy space coincides with the joint profit-maximizing effort, as in some cases participants might have just gone toward the middle of the strategy space. However, as will be seen below, this middle point was not chosen very often in the asymmetric cases, except by the low-cost players in the ENFORCED ASYM treatment. Note that when the Pareto optimum lies at the border of the strategy space so that participants have no opportunity to go above, either intentionally or erroneously, this might cause the observed cooperation level to lie much further below the Pareto optimum than it otherwise would.
The average profit under enforced teaming is 191.73 (standard deviation of 120.56). It is significantly higher than the team equilibrium profit of 187.5 (Wilcoxon test, 5-percent significance), but lower than the joint profit-maximizing profit of 250 (Wilcoxon test, 2-percent significance). It is also lower than the average profit of 220.08 under voluntary teaming; but this difference is statistically not significant (u-test). The standard deviations of effort and profit, such as the absolute difference between the two players' effort levels are not significantly different between the two treatments.
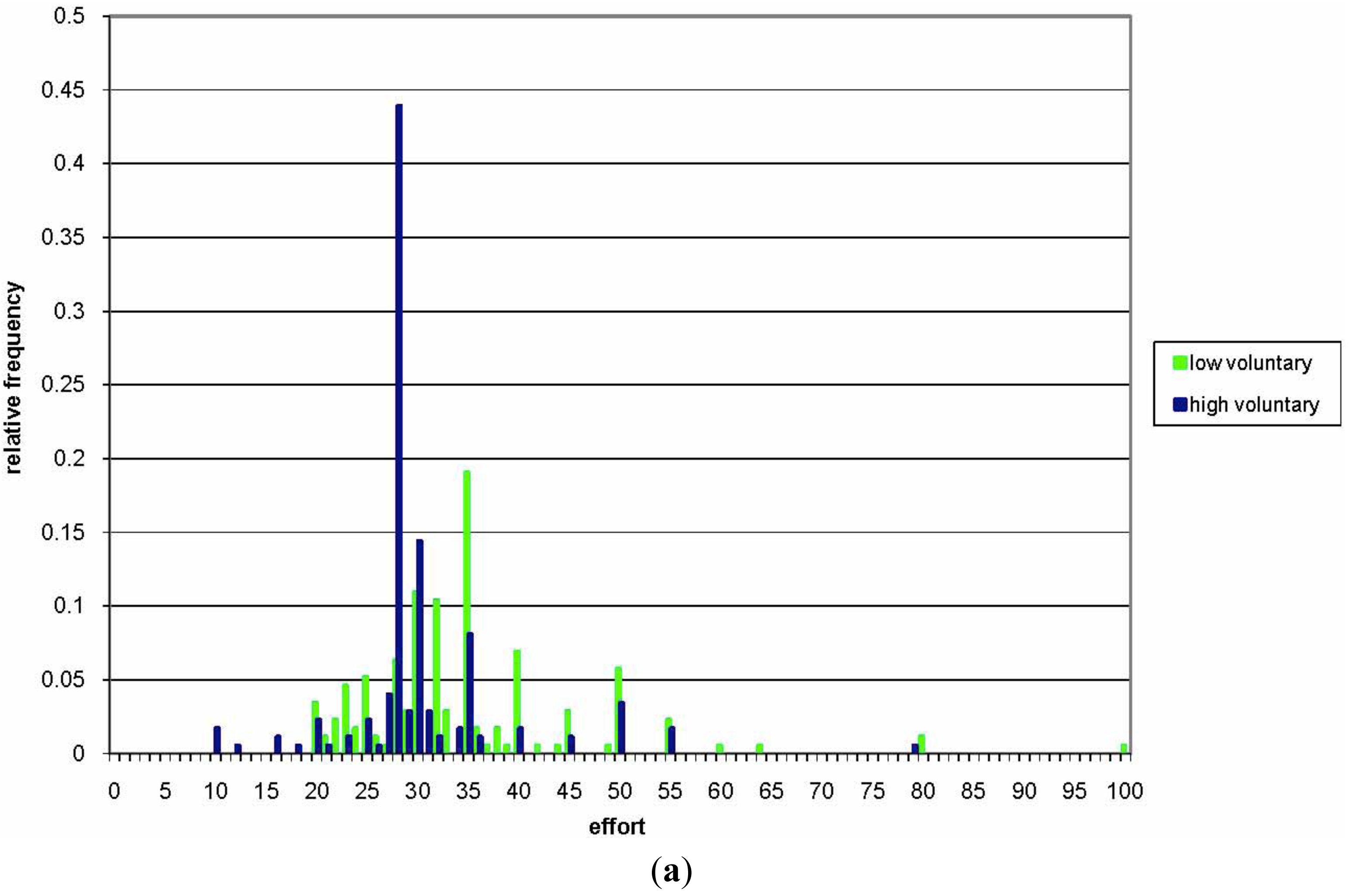
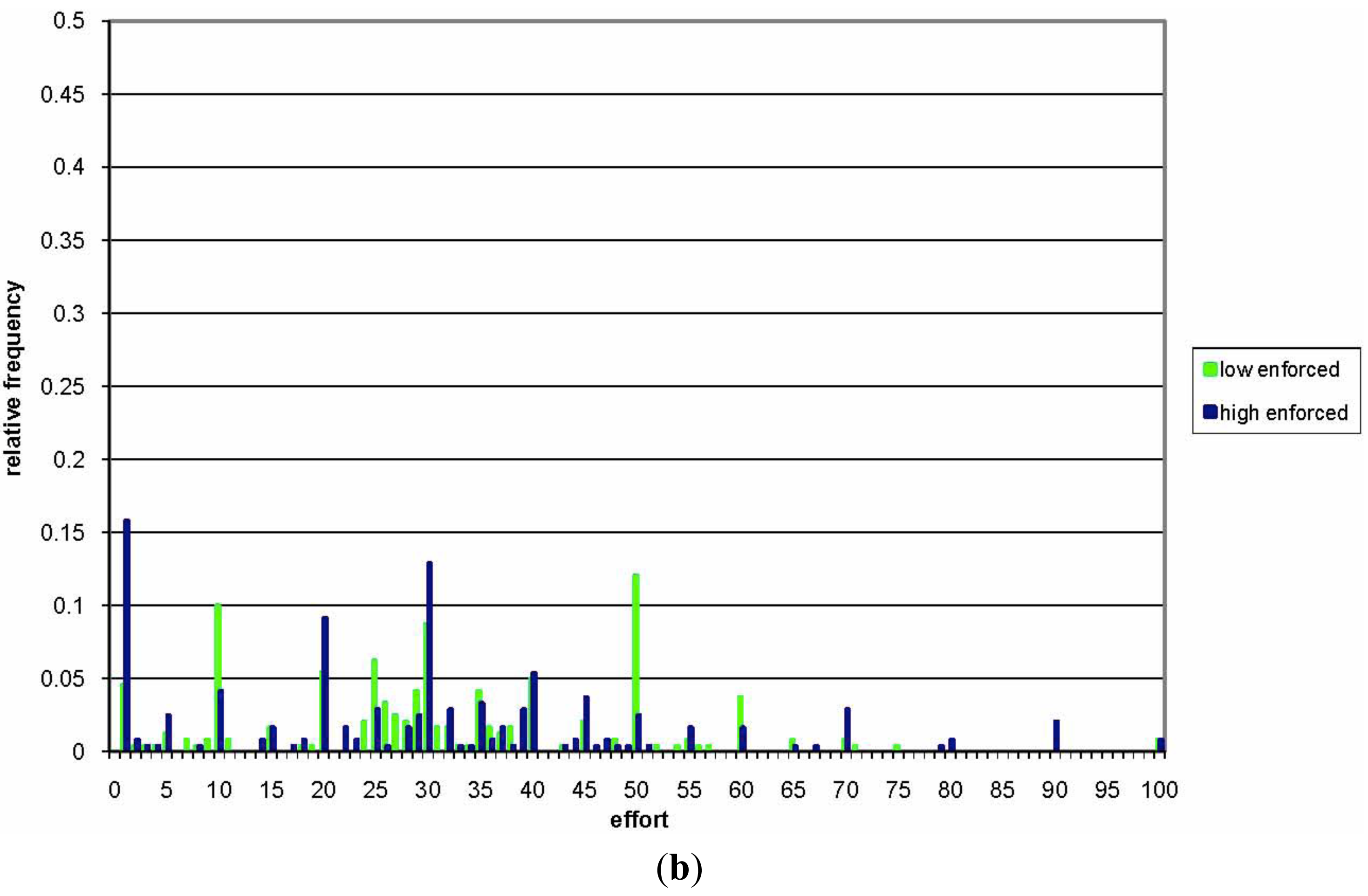
Comparing average effort levels in the ENFORCED ASYM treatment to those in the VOLUNTARY ASYM treatment, we observe that under enforced teaming the low-cost players' effort is 31.14 (standard deviation of 17.78) and not significantly different from the effort of 34.51 under voluntary teaming. The standard deviation is not significantly different either. The high-cost players' effort under enforced teaming is 29.32 (standard deviation of 21.67). While the effort is not significantly different from the effort of 30.14 under voluntary teaming, the standard deviation is significantly higher than under voluntary teaming (u-test, 10-percent significance). This could be due to (1) the observation below that under voluntary teaming players often use their respective optimal private effort as a reference point; and (2) a peak at an effort level of one in Figure 2(b) for the high-cost players in the ENFORCED ASYM treatment. This peak at the lower bound of the strategy space is coherent with the high frequency of free-riding behavior observed in public-goods-game experiments.
The difference of the low-cost minus the high-cost players' effort is not significantly different from the respective value in the VOLUNTARY ASYM treatment (u-test). Effort of the low-cost players is not significantly different from effort of the high-cost players (Wilcoxon test).
The low-cost players' effort is significantly above their equilibrium effort and significantly below their joint profit-maximizing effort (Wilcoxon tests, 5-percent significance). Recalling that in voluntary teaming the low-cost players' effort is not significantly different from their joint profit-maximizing effort, we have thus got indirect evidence for higher effort by the low-cost players in voluntary teaming compared to enforced teaming. The high-cost players' effort is significantly above their equilibrium effort but not significantly different from their joint profit-maximizing effort. This is similar to what we observe under voluntary teaming. When we compare the first set of 15 periods to the last set of 15 periods, for neither player type, neither effort nor profit shows a significant tendency to decrease or increase over time (Wilcoxon tests). The decrease in the low-cost players' effort, however, just fails significance. This is similar to the results under voluntary teaming.
Figures 2(a) and 2(b) show the density of team effort of the low- and the high-cost players, respectively, under enforced and voluntary teaming. We see that under voluntary teaming the observed effort levels are much less spread out than under enforced teaming. Furthermore, it appears as if under voluntary teaming both player types use their respective optimal private effort as a reference point: Figure 2(a) exhibits peaks at 35 for the low-cost and 28 for the high-cost player.
The low-cost players' profit is 113.38 (standard deviation of 98.53) and not significantly different from the profit of 127.26 under voluntary teaming. The profit of 75.98 (standard deviation of 151.41) of the high-cost player in the ENFORCED ASYM treatment is significantly lower than 137.1 in the VOLUNTARY ASYM treatment (u-test, 2-percent significance). The standard deviations are not significantly different, neither for the low- nor for the high-cost players. Profit of the low-cost players is not significantly different from the one of the high-cost players (Wilcoxon tests).
The low-cost players' profit is significantly different neither from their equilibrium profit nor from their joint profit-maximizing payoff, while the high-cost players' payoff is not significantly different from their equilibrium payoff but significantly below their joint profit-maximizing payoff (Wilcoxon test, 2-percent significance). In contrast to this, under voluntary teaming the high-cost players' payoff is not significantly different from their joint profit-maximizing payoff.
Conclusion 4: In the SYM treatment, we observe voluntary team effort that is higher than enforced team effort. In the ASYM treatment, we observe less standard deviation of the team effort choices by the high-cost players if teaming is voluntary rather than enforced. It is only the high-cost players in the ASYM treatment who gain a higher profit under voluntary teaming than under enforced teaming.
Prediction 5: A participant chooses his team effort in reaction to the other player's previous team effort.
Let us interpret participants' voluntary contributions to the public good team effort in terms of conditional cooperation, following Keser and van Winden [28]: when a player changes his effort from one period to the next, he increases the effort if he had contributed a lower effort in the previous period than the other player but decreases it if he had contributed a higher effort in the previous period than the other player. Our definition of conditional cooperation in the case of asymmetric effort costs is specific. However, due to a large number of potential reference points and rules for conditional cooperation, any other definition would be arbitrary.
In the VOLUNTARY SYM treatment, considering all the observations where the realization of team remuneration followed team remuneration and where the two players' efforts were different in the previous period, we identify seven groups that obeyed this conditional cooperation rule in the majority of cases; only one group did not follow it in the majority of cases. Similarly, in the ENFORCED SYM treatment, we identify seven of the eight groups that follow the conditional cooperation rule in the majority of cases. Thus, participants show in both SYM treatments a significant tendency to follow this specific rule of conditional cooperation (binomial tests, 10-percent significance).
In the VOLUNTARY ASYM treatment, considering all cases where team remuneration followed team remuneration and where the two players' efforts were different in the previous period, we observe that the low-cost players significantly tend to obey the conditional cooperation rule (binomial test, 5-percent significance). The high-cost players do not show a significant tendency to behave according to that rule. In the ENFORCED ASYM treatment, we find that neither the low nor the high-cost players show a significant tendency for conditional cooperation. Thus, only when teaming is voluntary, do we observe conditional cooperation in the low-cost players' effort choices.
We also use regression analysis on the change in effort to investigate conditional cooperation. We use least-squares regressions with clustering. This method takes into account that the decisions made by a participant over time may not be independent; it leads to the same coefficients as the ordinary least-squares estimates but the standard errors may be impacted by the clustering. In the regressions we investigate conditional cooperation based on the difference between the two players' effort levels in the last period they played under team remuneration. The obvious clustering variable here is simply the identification of the participant. We construct two dummy variables: the variable “Less” equals “1” when the player's effort has been more than three units smaller than the other player's effort, and it equals “0” otherwise. The variable “More” equals “1” when the player's effort has been more than three units larger than the other player's effort, and it equals “0” otherwise. The choice of more than three units of difference is arbitrary. However, analyses with other numbers around three have not changed the results. The conditional-cooperation argument suggests a positive sign of the coefficient for “Less” and a negative sign of the coefficient for “More”.
Explanatory variables also include a dummy variable “Last 5 periods”, which equals “1” if the participants played in the remuneration mode in the last five periods of the game and “0” otherwise. We expect a negative sign of this variable to account for an end-game effect [53].
The regression results are reported in Table 3 for VOLUNTARY teaming and in Table 4 for ENFORCED teaming. In the VOLUNTARY teaming treatments, we observe for the low-cost player conditional cooperation in both directions: as expected, we find a significantly positive coefficient for “Less” and a significantly negative coefficient for “More”. The effect is particularly strong when the player's effort has been less than the other player's effort in the last period they played in the team-remuneration mode. For the high-cost player, conditional cooperation arises only when his effort has been less than the other player's effort in the last period they played in the team-remuneration mode. In the SYM case, the “Less” variable barely misses the 5-percent significance level. An end-game effect (i.e., a significantly negative coefficient of “Last 5 periods”) is observed in the SYM case.
The results in the ENFORCED SYM treatment show that the reciprocity variables “Less” and “More” have a significant effect on the change in effort of the participants. Lower effort by a player relative to the other player's effort in the previous period under team remuneration prompts the player to increase his effort. He is even more strongly inclined to reduce his effort if he contributed a higher effort than the other player. Low- and high-cost players in the ENFORCED ASYM treatment react with a decrease in effort if they have contributed a higher effort than their respective partner in the previous period under team remuneration.
These results complement the non-parametric tests of conditional cooperation, which concern the direction rather than the intensity of the reaction of the parametric estimations. Overall and particularly in the SYM treatments, the regression results show that the intensity of conditional cooperation is more important when the team-remuneration mode is enforced rather than chosen by the participants.
Conclusion 5: In both SYM treatments, we observe conditional cooperation according to the qualitative definition following Keser and van Winden [28]. Regression results indicate conditional cooperation also in the ASYM treatments.
Prediction 6: A participant's choice of remuneration depends on his partner's previous team effort.
We analyze participants' choice of the remuneration mode with a linear probability model with clustering. Although the results are not qualitatively different with a random-effect probit model or a probit model with clustering, the linear probability model is retained for its robustness. The dependent variable “Voluntary teaming” equals “1” if the player chooses team remuneration and “0” otherwise. To account for an end-game effect, we consider the explanatory variable “Last 5 periods”, which is equal to “1” for the last five periods and “0” otherwise. We expect a negative coefficient for this variable.
We also construct the explanatory variables “Partner's effort below a strategic level” and “Partner's effort above a strategic level” based on the following hypothesis. A participant chooses team remuneration (opts in) if he expects to earn a higher payoff than under private remuneration. Assume that he chooses his dominant strategy in team remuneration and, thus, to achieve higher or equal payoff than in private remuneration, he needs a minimum effort from his team partner. In the symmetric cost situation, the partner's minimum required effort is 28. (The participant's dominant strategy in the case of team remuneration is 25. We solve the following equation to determine the partner's effort X that makes the participant indifferent to team and private remuneration: 203 = 10(25 + X)/2 − (252/10), where 203 is the (rounded) maximum profit in private remuneration.) In the asymmetric cost situation, the low-cost player requires from his partner a minimum effort of 20, while the high-cost player requires a minimum effort of 17. (The following equations are solved for X, respectively: (1) 123 = 8(20 + X)/2 − (202/10), where 123 is the low-cost player's (rounded) maximum profit in private remuneration and 20 his dominant strategy in team remuneration; (2) 98 = 8(16 + X)/2 − (162/8), where 98 is the high-cost player's maximum profit in private remuneration and 16 his dominant strategy in team remuneration.) The high-cost player's requirement is likely to be satisfied since the low-cost player's dominant strategy in team remuneration is 20 and thus above the required minimum.
We do not expect participants to be able to compute exactly those numbers and therefore create the following two binary variables. “Partner's effort above a strategic level” takes a value of “1” if the last time that team remuneration was realized the partner chose an effort larger or equal to six units above the required effort as determined above, or “0” otherwise. “Partner's effort below a strategic level” takes a value of “1” if the last time that team remuneration was realized the partner chose an effort smaller or equal to six units below the required effort as determined above, or “0” otherwise. The choice of six units around the required minimum is arbitrary. However, analyses with other numbers around six have not changed the results. Based on the above opt-in hypothesis, we expect a positive coefficient for “Partner's effort above a strategic level”. Inversely, accounting for opting out, we expect a negative coefficient for “Partner's effort below a strategic level”.
The results of the linear probability models with clustering are presented in Table 5. The results differ according to the type of participants. In the VOLUNTARY SYM treatment, the only statistically significant coefficient is the negative end-game effect: in the final periods of the game, participants are more likely than before to choose private remuneration. In the other treatments, we observe no end game effect.
In the VOLUNTARY ASYM treatment and for both cost types, we observe that, in accordance with our opt-in hypothesis, “Partner's effort above a strategic level” significantly increases the probability of choosing team remuneration. The low-cost players participate in team remuneration because the high-cost players do provide high enough effort. However, as for the SYM treatment, the coefficient of “Partner's effort below a strategic level,” is not statistically significant for the low-cost player, which implies that participants do not use an opt-out strategy. Note that the low-cost players have indeed very little incentive to participate in team remuneration, giving up 122.5 under private remuneration in order to gain 128 in the optimal solution under team remuneration.
For the high-cost player this coefficient is statistically significant but positive. This is not surprising since the high-cost players have, according to the game-theoretical solution, an interest in team remuneration that is independent of the other player's effort. This is also reflected in the relatively high and statistically significant constant for the high-cost players.
Conclusion 6: The probability to choose team remuneration increases when the partner's team effort was above a strategic level in the asymmetric case. The opting-out hypothesis of leaving when the partner's team effort was below a strategic level is not supported by the data.
6. Conclusions
Our experiments provide evidence in favor of Lin's [13] argument that effort under voluntary teaming is higher than effort under enforced teaming. We observe many instances of team remuneration: both players chose team remuneration in 45 percent of the periods in the symmetric specification of the game, where the two players have the subgame perfect equilibrium strategy to choose private remuneration, and in 72 percent of the periods in the asymmetric specification, where the player with the lower effort costs has the subgame perfect equilibrium strategy to choose private remuneration. We also observe that, under team remuneration, the average effort is significantly higher than predicted by the subgame perfect equilibrium. Thus, participants make higher profits in team remuneration than in private.
In a symmetric cost situation, we observe that voluntary teaming implies significantly higher effort levels than enforced teaming. However, this does not come alongside a significantly higher efficiency, if we define efficiency as the realized percentage of the maximal team profit. The reason for this is that, when teaming is voluntary, participants choose effort levels above the efficient level significantly more often than when teaming is enforced. In both the voluntary and the enforced teaming environment, team effort is driven by conditional cooperation: if a player intends to change his team effort from one period to the next, he increases (decreases) it if his own effort was lower (higher) than the other player's effort.
In an asymmetric cost situation, we do not observe statistically significant differences in the effort levels of the voluntary and the enforced teaming environment. We do, however, observe higher efficiency, due to larger payoffs for the high-cost players, in the voluntary teaming environment. The principle of conditional cooperation defined above plays a minor role (only for the low-cost players when teaming is voluntary). It is not obvious for the two players in the asymmetric situation where to cooperate.
We observe that in contrast to the theoretical prediction people do build teams. They make higher efforts in teams than under private remuneration. The degree of team cooperation, however, depends on whether teaming is enforced or voluntary. We observe more cooperation in voluntary teaming than in enforced teaming. This effect is most obvious in the symmetric cost situation where it is relatively obvious to the team members, who cannot communicate other than through their decision making, where to cooperate.
The higher cooperation in voluntary teaming is in keeping with the results by Fehr and Gächter [54]. They provide experimental evidence that, compared to complete labor contracts, incomplete contracts have an advantage in that they leave room for cooperation between the employer and the employee.
In our experiment there is room to “overdo” one's effort by going beyond the individual effort level that would be joint profit maximizing. We observe that participants often overdo effort in the voluntary symmetric treatment but not in the enforced symmetric treatment. Thus, simple error making cannot be the sole explanation for choosing effort levels above the joint profit-maximizing level. Another explanation could be that participants are signaling that they are interested in cooperation. A participant who expects the other to make a very low effort and who wants to send a very strong signal could have an interest in making an effort above the joint profit-maximizing level. In the bulk of experiments on voluntary contributions to finance a public good, this is excluded by design.
In the asymmetric experiments, where it is not so clear where cooperation should take place, the effort increase by voluntary teaming is not very significant. A more striking difference between voluntary and enforced teaming shows in the dispersion of the effort levels. The voluntary team efforts are much more contained around and between the subgame perfect equilibrium and the joint profit-maximizing solution than in the case of enforced teaming, where effort levels are spread out over the entire strategy space. Obviously, voluntary teaming helps participants to better coordinate than enforced teaming. Once they have agreed on team remuneration, participants have already made some investment by giving up on their higher private remuneration rate. Similar evidence has been found by Cachon and Camerer [55], who observe that a fixed entry fee for subjects participating in a coordination game improves coordination significantly.
In our experiments, considering the game-theoretical solution, it is in particular the low-cost players who signal a commitment to attempt cooperation by their choice of team remuneration. Having made that choice, they are willing to make a somewhat higher effort than in enforced teaming. Neither in the symmetric nor in the asymmetric case do we observe a tendency that players opt out of team remuneration due to a too low effort by the other player.
Our results bear relevant implications for workforce management. Teams with a strong heterogeneity of abilities are likely to show a relatively large dispersion of efforts. Our experimental observations suggest that this dispersion can be reduced by allowing for voluntary teaming. In general, voluntary team effort will be higher than enforced team effort. The effect is likely to be the stronger the less heterogeneity there is.
| Treatment | ki | ei* | ei** | ei′ | Πi* | Πi** | Πi′ | ΠiMin | ΠiMax |
|---|---|---|---|---|---|---|---|---|---|
| SYM | |||||||||
| i = 1, 2 | 1/10 | 45 | 25 | 50 | 202.5 | 187.5 | 250 | 125 | 312.5 |
| p = 9, t = 10 | |||||||||
| ASYM | |||||||||
| i = 1 (low cost) | 1/10 | 35 | 20 | 40 | 122.5 | 104 | 128 | 64 | 168 |
| i = 2 (high cost) | 1/8 | 28 | 16 | 32 | 98 | 112 | 160 | 80 | 192 |
| p = 7, t = 8 | |||||||||
ei* player i's optimal effort under private remuneration; ei** player i's equilibrium effort (dominant strategy) under team remuneration; ei′ player i's joint profit-maximizing effort under team remuneration; Πi* player i's maximum profit under private remuneration; Πi** player i's equilibrium profit under team remuneration; Πi′ player i's profit in the joint profit-maximizing solution under team remuneration; ΠiMin player i's minimum profit under team remuneration; ΠiMax player i's maximum profit under team remuneration; p factor of private remuneration; t factor of team remuneration; ki individual cost factor.
| VOLUNTARY | ENFORCED | ||||||
|---|---|---|---|---|---|---|---|
| Private | Team | Team | |||||
| # Periods | Effort | Profit | Effort | Profit | Effort | Profit | |
| SYM | 16.5 | 45.27 (16.81) | 174.35 (62.24) | 50.10 (17.34) | 220.08 (118.51) | 35.68 (19.45) | 191.73 (120.56) |
| ASYM-low cost | 8.375 | 34.87 (9.88) | 112.89 (15.86) | 34.51 (11.09) | 127.26 (74.05) | 31.14 (17.78) | 113.38 (98.53) |
| ASYM-high cost | 8.375 | 27.22 (15.58) | 68.06 (90.73) | 30.14 (8.01) | 137.10 (59.85) | 29.32 (21.67) | 75.98 (151.41) |
| (Least squares with clustering) | |||
|---|---|---|---|
| SYM | ASYM | ||
| Low cost | High cost | ||
| Constant | 0.1086 (1.42) | −0.2724 (0.305) | −0.7404 (0.837) |
| Last 5 Periods | −7.144 ** (3.15) | 0.6909 (0.567) | −0.1753 (0.718) |
| Less | 5.142 (2.71) | 2.453 * (0.627) | 3.582 * (1.411) |
| More | −3.871 (3.67) | −1.996 ** (0.678) | −3.600 (2.62) |
| adjR2 | 0.061 | 0.023 | 0.086 |
| Nobs | 202 | 165 | 165 |
*Significant at 5%;**Significant at 1%; ( ) Standard error.
| (Least squares with clustering) | |||
|---|---|---|---|
| SYM | ASYM | ||
| Low cost | High cost | ||
| Constant | 0.6847 (0.924) | 0.3266 (0.337) | 2.558 (1.41) |
| Last 5 periods | −4.631 (5.59) | −0.5420 (1.25) | −1.516 (0.990) |
| Less | 4.970 ** (1.57) | 2.487 (1.425) | −1.100 (2.040) |
| More | −8.180 ** (1.49) | −7.596 ** (2.30) | −5.806 * (2.36) |
| adjR2 | 0.091 | 0.098 | 0.025 |
| Nobs | 464 | 232 | 232 |
*Significant at 5%;**Significant at 1%; ( ) Standard error.
| (Linear probability model with clustering) | |||
|---|---|---|---|
| SYM | ASYM | ||
| Low cost | High cost | ||
| Constant | 0.5261 (0.215) | 0.3809 (0.179) | 0.5094** (0.145) |
| Last 5 periods | −0.1745 ** (0.068) | −0.0373) (0.069) | 0.0575 (0.030) |
| Partner's effort below a strategic level | −0.0974 (0.241) | 0.1454 (0.278) | 0.4906 ** (0.145) |
| Partner's effort above a strategic level | 0.3220 (0.220) | 0.5571 ** (0.197) | 0.4558 ** (0.156) |
| adjR2 | 0.157 | 0,339 | 0.338 |
| Nobs | 464 | 464 | 464 |
*Significant at 5%;**Significant at 1%; () Standard error.
References
- Milgrom, P.; Roberts, J. Economics, Organization and Management; Prentice Hall: Englewood Cliffs, NJ, USA, 1992. [Google Scholar]
- Lazear, E.P. Personnel Economics; MIT Press: Cambridge, MA, USA, 1992. [Google Scholar]
- Alchian, A.A.; Demsetz, H. Production, information costs, and economic organization. Am. Econ. Rev. 1972, 62, 777–795. [Google Scholar]
- Holmstrom, B. Moral hazard in teams. Bell J. Econ. 1982, 13, 324–340. [Google Scholar]
- OECD. Profit Sharing in OECD Countries. In Employment Outlook; OECD: Paris, France, 1995; pp. 139–169. [Google Scholar]
- Mitchell, D.; Lewin, D.; Lawler, E. Alternative pay systems, firm performance and productivity. In Paying for Productivity: A Look at the Evidence; Blinder, A.S., Ed.; The Brookings Institution: Washington, DC, USA, 1990; pp. 15–94. [Google Scholar]
- Zhuang, J.; Xu, C. Profit-sharing and financial performance in the Chinese state enterprises: Evidence from panel data. Econ. Plan. 1996, 29, 205–222. [Google Scholar]
- Bhargava, S. Profit sharing and the financial performance of companies: Evidence from UK panel data. Econ. J. 1994, 104, 1044–1056. [Google Scholar]
- Kraft, K.; Ugarkovic, M. Profit sharing and the financial performance of firms: Evidence from Germany. Econ. Lett. 2006, 92, 333–338. [Google Scholar]
- Bonin, J.P.; Jones, D.C.; Putterman, L. Theoretical and empirical studies of producer cooperatives: Will ever the twain meet? J. Econ. Lit. 1993, 31, 1290–1320. [Google Scholar]
- Putterman, L.; Skillman, G.L. The role of exit costs in the theory of cooperative teams. J. Comp. Econ. 1992, 16, 596–618. [Google Scholar]
- MacLeod, B. Equity, efficiency, and incentives in cooperative teams. In Advances in the Economic Analysis of Participatory and Labor-Managed Firms; Jones, D.C., Svejnar, J., Eds.; JAI Press: Greenwich, CT, USA, 1988; Volume 3, pp. 5–23. [Google Scholar]
- Lin, J.Y. Collectivization and China's agricultural crisis in 1959–1961. J. Polit. Econ. 1990, 98, 1228–1252. [Google Scholar]
- Orbell, J.M.; Dawes, R.M. Social welfare, cooperators' advantage, and the option of not playing the game. Am. Sociol. Rev. 1993, 58, 787–800. [Google Scholar]
- Ehrhart, K.M.; Keser, C. Mobility and Cooperation: On the Run; CIRANO: Montréal, Canada, 1999. [Google Scholar]
- Rasmusen, E. Moral hazard in risk-averse teams. Rand J. Econ. 1987, 18, 428–435. [Google Scholar]
- Itoh, H. Incentives to help in multi-agent situations. Econometrica 1991, 59, 611–636. [Google Scholar]
- Itoh, H. Cooperation in hierarchical organizations: An incentive perspective. J. Law Econ. Organ. 1992, 8, 321–345. [Google Scholar]
- McAffee, R.P.; McMillan, J. Optimal contracts for teams. Int. Econ. Rev. 1991, 32, 561–577. [Google Scholar]
- Weitzman, M.L.; Kruse, D.L. Profit sharing and productivity. In Paying for Productivity: A Look at the Evidence; Blinder, A.S., Ed.; The Brookings Institution: Washington, DC, USA, 1990; pp. 95–140. [Google Scholar]
- Hamilton, B.H.; Nickerson, J.A.; Owan, H. Team incentives and worker heterogeneity: An empirical analysis of the impact of teams on productivity and participation. J. Polit. Econ. 2003, 111, 465–497. [Google Scholar]
- Nalbantian, H.R.; Schotter, A. Productivity under group incentives: An experimental study. Am. Econ. Rev. 1997, 87, 314–341. [Google Scholar]
- Mellizo, P.; Carpenter, J.P.; Matthews, P.H. Workplace Democracy in the Lab; IZA DiscussionPaper No. 5460; IZA: Bonn, Germany; January; 2011. [Google Scholar]
- Axelrod, R. The Evolution of Cooperation; Basic Books: New York, NY, USA, 1984. [Google Scholar]
- Isaac, R.M.; Walker, J.M.; Williams, A.W. Group size and the voluntary provision of public goods. J. Public Econ. 1994, 54, 1–36. [Google Scholar]
- Andreoni, J. Why free ride? Strategies and learning in public goods experiments. J. Public Econ. 1988, 37, 291–304. [Google Scholar]
- Andreoni, J. Cooperation in public goods experiments: Kindness or confusion. Am. Econ. Rev 1995, 85, 891–904. [Google Scholar]
- Keser, C.; van Winden, F. Conditional cooperation and voluntary contributions to public goods. Scand. J. Econ. 2000, 102, 23–39. [Google Scholar]
- Keser, C. Strategically Planned Behavior in Public Goods Experiments; CIRANO Scientific Series 2000s-35; CIRANO: Brussels, Belgium, 2000. [Google Scholar]
- Keser, C. Cooperation in public goods experiments. In Surveys in Experimental Economics: Bargaining, Cooperation and Election Stock Markets; Bolle, F., Lehmann-Waffenschmidt, M., Eds.; Physica-Verlag: Heidelberg, Germany, 2002; pp. 71–90. [Google Scholar]
- Fehr, E.; Gächter, S. Cooperation and punishment in public goods experiments. Am. Econ. Rev. 2000, 90, 980–994. [Google Scholar]
- Fischbacher, U.; Gächter, S.; Fehr, E. Are people conditionally cooperative? Evidence from a public goods experiment. Econ. Lett. 2001, 71, 397–404. [Google Scholar]
- Hauk, E.; Nagel, R. Choice of partners in multiple two-person prisoner's dilemma games. J. Confl. Resolut. 2001, 45, 770–793. [Google Scholar]
- Hauk, E. Multiple prisoner's dilemma games with (out) an outside option: An experimental study. Theor. Decis. 2003, 54, 207–229. [Google Scholar]
- Coricelli, G.; Fehr, D.; Fellner, G. Partner selection in public goods experiments. J. Confl. Resolut. 2004, 48, 356–378. [Google Scholar]
- Page, T.; Putterman, L; Unel, B. Voluntary association in public goods experiments: Reciprocity, mimicry and efficiency. Econ. J. 2005, 115, 1032–1053. [Google Scholar]
- Charness, G.; Yang, C.-L. Endogenous group formation and public goods provision: Exclusion, exit, mergers, and redemption; Departmental Working Papers, Department of Economics, UCSB, UC Santa Barbara: Santa Barbara, CA, USA, 2008. [Google Scholar]
- Gächter, S.; Thöni, C. Social learning and voluntary cooperation among like-minded people. J. Eur. Econ. Assoc. 2005, 3, 303–314. [Google Scholar]
- Ones, U.; Putterman, L. The ecology of collective action: A public goods and sanctions experiment with controlled group formation. J. Econ. Behav. Organ. 2006, 62, 495–521. [Google Scholar]
- Gunnthorsdottir, A.; Houser, D.; McCabe, K. Disposition, history and contributions in public goods experiments. J. Econ. Behav. Organ. 2007, 62, 304–315. [Google Scholar]
- Selten, R.; Mitzkewitz, M.; Uhlich, G. Duopoly strategies programmed by experienced players. Econometrica 1997, 65, 517–555. [Google Scholar]
- Abramson, M.A.; Demesme, R.B.; Gardner, N.W. The chained gang-human capital management: The human capital challenge. J. Public Inq. 2002, 43–48. [Google Scholar]
- Surowiecki, J. The Wisdom of Crowds; Anchor Books: New York, NY, USA, 2005. [Google Scholar]
- Ledyard, J. Public Goods: A survey of experimental research. In Handbook of Experimental Economics; Roth, A.E., Kagel, J., Eds.; Princeton University Press: Princeton, NJ, USA, 1995; pp. 111–194. [Google Scholar]
- Kohlberg, E.; Mertens, J.-F. On the strategic stability of Equilibria. Econometrica 1986, 54, 1003–1038. [Google Scholar]
- Cho, I.-K.; Kreps, D. Signaling games and stable equilibria. Q. J. Econ. 1987, 102, 179–221. [Google Scholar]
- Van Damme, E. Stable equilibria and forward induction. J. Econ. Theor. 1989, 48, 476–496. [Google Scholar]
- Axelrod, R. The emergence of cooperation among egoists. Am. Polit. Sci. Rev. 1981, 75, 306–318. [Google Scholar]
- Rabin, M. Incorporating fairness into game theory and economics. Am. Econ. Rev. 1993, 83, 1281–1302. [Google Scholar]
- Keser, C. Voluntary contributions to a public good when partial contribution is a dominant strategy. Econ. Lett. 1996, 50, 359–366. [Google Scholar]
- Sefton, M.; Steinberg, R. Reward structures in public good experiments. J. Public Econ. 1996, 61, 263–287. [Google Scholar]
- Isaac, R.M.; Walker, J.M. Nash as an organizing principle in the voluntary provision of public goods: experimental evidence. Exp. Econ. 1998, 1, 191–206. [Google Scholar]
- Selten, R.; Stoecker, R. End behaviour in sequences of finitely repeated prisoner's dilemma supergames. J. Econ. Behav. Organ. 1986, 7, 47–70. [Google Scholar]
- Fehr, E.; Gächter, S. Fairness and retaliation: The economics of reciprocity. J. Econ. Perspect. 2000, 14, 159–181. [Google Scholar]
- Cachon, G.P.; Camerer, C.F. Loss avoidance and forward induction in experimental coordination games. Q. J. Econ. 1996, 111, 165–194. [Google Scholar]
- JEL classification: C72; C90; H41; J33
© 2011 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Keser, C.; Montmarquette, C. Voluntary versus Enforced Team Effort. Games 2011, 2, 277-301. https://doi.org/10.3390/g2030277
Keser C, Montmarquette C. Voluntary versus Enforced Team Effort. Games. 2011; 2(3):277-301. https://doi.org/10.3390/g2030277
Chicago/Turabian StyleKeser, Claudia, and Claude Montmarquette. 2011. "Voluntary versus Enforced Team Effort" Games 2, no. 3: 277-301. https://doi.org/10.3390/g2030277
APA StyleKeser, C., & Montmarquette, C. (2011). Voluntary versus Enforced Team Effort. Games, 2(3), 277-301. https://doi.org/10.3390/g2030277




