The Existence of Perfect Equilibrium in Discontinuous Games
Abstract
: We prove the existence of a trembling-hand perfect equilibrium within a class of compact, metric, and possibly discontinuous games. Our conditions for existence are easily verified in a variety of economic games.1. Introduction
A Nash equilibrium is trembling-hand perfect if it is robust to the players’ choice of unintended strategies through slight trembles. That is, in a world where agents make slight mistakes, trembling-hand perfection requires that there exist at least one perturbed model of low-probability errors with an equilibrium that is close to the original equilibrium, which is then thought of as an approximate description of “slightly constrained” rational behavior, or what could be observed if the players were to interact within the perturbed game. In this regard, a Nash equilibrium that is not trembling-hand perfect cannot be a good prediction of equilibrium behavior under any “conceivable” theory of (improbable, but not impossible) imperfect choice.
Ever since it was coined by Selten [1], trembling-hand perfection has been a popular solution concept. However, the fact that Selten's treatment is valid only for finite games poses a problem, since many strategic settings are most naturally modeled as games with a continuum of actions (e.g., models of price and spatial competition (Bertrand [2], Hotelling [3]), auctions (Milgrom and Weber [4]), and patent races (Fudenberg et al. [5])).
There have been attempts to use the notion of trembling-hand perfection in infinite economic games to rule out undesirable equilibria (examples include provision of public goods (Bagnoli and Lipman [6]), credit markets with adverse selection (Broecker [7]), budget-constrained sequential auctions (Pitchik and Schotter [8]), and principal-agent problems (Allen [9])).1 However, absent a theory of trembling-hand perfection for infinite games (and given that a well-accepted formulation for finite games has long been available), there has been a general tendency to study limits of sequences of trembling-hand perfect equilibria in discretized, successively larger versions of the original (infinite) game at hand (e.g., Bagnoli and Lipman [6], Broecker [7]).2 While this is a legitimate approach to trembling-hand perfection in infinite games, Simon and Stinchcombe [10] have shown that similar limit-of-finite approaches have limitations as general solution concepts even in continuous games. Moreover, since there are alternative formulations of trembling-hand perfection for infinite games, confining attention to a limit-of-finite approach, without any comparison with other concepts, seems unsatisfactory.
For continuous games, Simon and Sinchcombe [10] offer several notions of trembling-hand perfection and compare their properties. However, infinite economic games often exhibit discontinuities in their payoffs, and a treatment for this kind of games is not available. For instance, most of the above references feature discontinuous games. In the presence of discontinuities, existence of trembling-hand perfect equilibria is not guaranteed by standard arguments. By adapting arguments from Carbonell-Nicolau [11], this paper addresses the issue of existence for an infinite-game extension of Selten's [1] original notion of trembling-hand perfection. This extension corresponds to Simon and Stinchcombe's [10] strong approach when the universe of games is restricted by continuity of the players’ payoffs. Building on the existence results obtained here, a companion paper, Carbonell-Nicolau [12], compares the properties of various notions of trembling-hand perfection within families of discontinuous games, and states the analogue of the standard characterization of trembling-hand perfection for finite games (e.g., van Damme [13], p. 28), in terms of the strong approach and other formulations. This characterization is restated in Section 2.
We first illustrate that the existence of trembling-hand perfect equilibria depends crucially on the existence of Nash equilibria in Selten perturbations. Selten perturbations are perturbed games in which the players choose any strategy in their action space with positive probability. The strategy spaces in Selten perturbations of infinite, discontinuous games exhibit peculiarities that prevent a straightforward application of the results available in the literature on the existence of Nash equilibria. In fact, in Section 2 we show that Selten perturbations need not inherit Reny's [14] better-reply security from the original game. Even the available strengthenings of better-reply security—payoff security or uniform payoff security, along with upper semicontinuity of the sum of payoffs—do not generally give better-reply security (or some of its generalizations) in Selten perturbations. Thus, one must either rely on an appropriate generalization of the main existence theorem of Reny [14] or impose a suitable strengthening of better-reply security. We seek conditions on the payoffs of a game that prove useful in applications and imply better-reply security—and hence the existence of Nash equilibria—in Selten perturbations. Ideally, to avoid dealing with expected payoffs (defined on mixed strategies) and the weak convergence of measures, one would like to have conditions that can be verified using the payoffs of the original game, rather than its mixed extension.
Carbonell-Nicolau [11] introduces a condition—termed Condition (A)—that is used to prove the existence of a pure-strategy trembling-hand perfect equilibrium. This condition is used here to establish the existence of a mixed-strategy trembling-hand perfect equilibrium. While the current paper adapts arguments from [11], the results obtained here are not implied by those of [11]. We shall provide a detailed comparison with the results in [11] in Section 2.
Roughly speaking, Condition (A) is satisfied when there exists, for each player i, a measurable map f : Xi → Xi, where Xi represents player i's action space, with the following two properties: (1) for each pure strategy xi of player i, there is an alternative pure strategy f(xi) such that given any pure action profile y−i of the other players, the action f(xi) almost guarantees the payoff player i receives at (xi, y−i), even if the other players slightly deviate from y−i; and (2) given any pure action profile y−i of the other players, there is a subset of generic elements of Xi (which may depend upon y−i) such that given any generic pure strategy xi of player i, the action profile (xi, z−i), where z−i is a slight deviation from y−i, almost guarantees the payoff player i receives at (f(xi), z−i).
We show that this condition gives payoff security of certain Selten perturbations (Lemma 2). We then combine this finding with known results to establish the existence of a trembling-hand perfect equilibrium in discontinuous games (Theorem 2). In addition, we derive (as in Carbonell-Nicolau [11]) corollaries of these results in terms of two independent conditions—generic entire payoff security and generic local equi-upper semicontinuity—that imply the existence of a map f with the above properties. In applications, verifying the two independent conditions can prove easier than checking Condition (A), for Condition (A) typically requires constructing a measurable map and verifying two conditions that depend on one another (via the said measurable map)3 The alternative hypothesis does not explicitly require the measurability of the map f, and proves easy to verify in applications.
The hypotheses of the main existence theorems are satisfied in many economic games and are often rather simple to verify. This is exemplified in Section 3.
2. Perturbed Games and Perfect Equilibria
A metric game is a collection , where N is a finite number of players, each Xi is a nonempty metric space, and each ui : X → ℝ is bounded and Borel measurable with domain . If in addition each Xi is compact, G is called a compact metric game.
In the sequel, by X−i we mean the set ×j≠iXj, and, given, i, xi ∈ Xi, and
The mixed extension of G is the game
Henceforth, the set ×j≠iMj is denoted as M−i, and given i, μi ∈ Mi, and
Given xi ∈ Xi, let δxi be the Dirac measure on Xi with support {xi}. We sometimes write, by a slight abuse of notation, xi in place of δxi. For δ ∈ [0, 1] and
A number of definitions of trembling-hand perfection for infinite normal-form games have been proposed (cf. Simon and Stinchcombe [10], Al-Najjar [15]). For continuous games, the refinement specification considered here is equivalent to the strong approach in [10] and to the formulation in [15]. In this paper, we focus on the issue of existence. In passing, we also illustrate certain limitations of what appears to be a natural approach to the question of existence of trembling-hand perfect equilibria in discontinuous games. This is done more transparently if we frame our discussion in terms of just one notion of trembling-hand perfection. A companion paper, Carbonell-Nicolau [12], compares the various notions of trembling-hand perfection and studies their properties, and contains the analogue of the standard three-way characterization of trembling-hand perfection for finite games (e.g., van Damme [13], p. 28), which will be stated here after several definitions.
Before presenting the formal definition of trembling-hand perfection, we need some terminology.
A Borel probability measure μi on Xi is said to be strictly positive if μi(O) > 0 for every nonempty open set O in Xi.
For each i, let stand for the set of all strictly positive members of Mi. Set . For νi ∈ and δ = (δ1,…, δN) ∈ [0, 1]N, define
When referring to these objects, we simply write with δ = δ1 = … = δN.
Definition 1
A strategy profile x = (x1,…, xN) ∈ X is a Nash equilibrium of G if for each i, ui(x) ≥ ui(yi, x−i) for every yi ∈ Xi.
Given a game , a Nash equilibrium of the mixed extension G̅ is called a mixed-strategy Nash equilibrium of G. By a slight abuse of terminology, we sometimes refer to a mixed-strategy Nash equilibrium of G simply as a Nash equilibrium of G.
Definition 2
A strategy profile μ ∈ M is a trembling-hand perfect (thp) equilibrium of G if there are sequences (δn), (νn), and (μn) with (0, 1)N ∋ δn → 0, and μn → μ, where each μn is a Nash equilibrium of the perturbed game .
In words, μ is a thp equilibrium of G if it is the limit of some sequence of exact equilibria of neighboring Selten perturbations of G. Intuitively, Selten perturbations of G may be interpreted as “models of mistakes”, i.e., formal descriptions of strategic interactions where any player may “tremble” and play any one of her actions. The requirement that μ be the limit of some sequence of equilibria of perturbations of G says that there exists at least one model of (low-probability) mistakes that has at least one equilibrium close to μ, so that μ is an approximate description of what the players would do (at the said equilibrium) were they to interact in the perturbed game.
Remark 1
Note that, in Definition 2, we do not require that μ be a Nash equilibrium of G. It is well-known that, for continuous games, the fact that a strategy profile μ is the limit of some sequence of equilibria of Selten perturbations of G guarantees that μ is a Nash equilibrium of G. While we do not impose continuity of payoff functions, we shall show that our conditions also ensure that the limit point is an equilibrium.4
For μ ∈ M, let Bri(μ) denote player i's set of best responses in Mi to the vector of strategies μ:
Consider the following distance function between members of Mi:
Definition 3
(Simon and Stinchcombe [10]). Given ∊ > 0, a strong ∊-perfect equilibrium of G is a vector such that for each i
The following result is taken from Carbonell-Nicolau [12] and establishes the relationship between trembling-hand perfection and strong perfection in the presence of payoff discontinuities. The equivalence of (1)-(3) is analogous to the standard characterization of trembling-hand perfect equilibria for finite games (e.g., van Damme [13], p. 28).
Theorem 1
For a metric game, the following three conditions are equivalent.
μ is a trembling-hand perfect equilibrium ofG.
μ is a strong perfect equilibrium of G.
μ is the limit of a sequence (μn) in with the property that for each i and every ∊ > 0
for any sufficient large n.
The following example illustrates that the set of thp equilibria of an infinite game may well be a strict refinement of the set of Nash equilibria.
Example 1
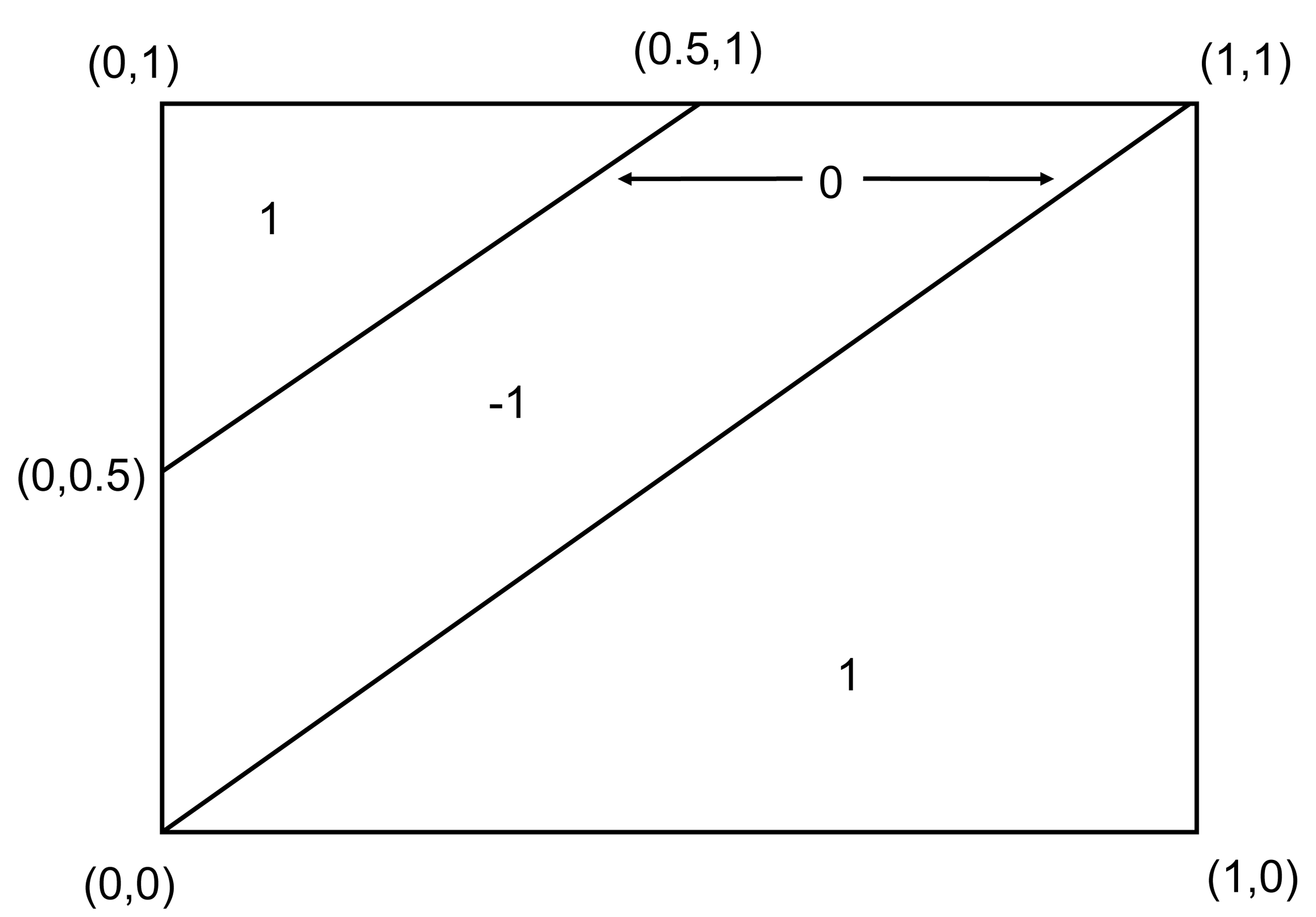
Consider the two-player game G = ([0, 1], [0, 1], u1,u2), where u1 and u2 are defined by u1(x1, x2):= x1(1 – 2x2) and .
It is easily seen that the strategy profile (0,1) is a Nash equilibrium of G. Note however that
The graph of G is the set
Given {A, B} ⊆ ℝ ∋ ε, we write
The following definition is taken from Reny [14].
Definition 4
The game G is better-reply secure if for every (x, α) ∈ Γ̅G such that x is not a Nash equilibrium of G, there exist i, yi ∈ Xi, a neighborhood Ox−i of x−i, and β ∈ ℝ such that ui(yi, Ox−i) ≥ β > αi.
The following proposition is analogous to Proposition 1 in Carbonell-Nicolau [11]5 It suggests that the existence of Nash equilibria surviving trembling-hand perfection depends crucially on the existence of Nash equilibria in Selten perturbations of G.
Proposition 1
Suppose that G is a compact, metric game. If G̅ is better-reply secure and there exists (α, μ) ∈ (0, 1) × such that G̅δμ has a Nash equilibrium for every δ ∈(0, α], then G possesses a trembling-hand perfect equilibrium, and all trembling-hand perfect equilibria of G are Nash.
Proof. Let (α, μ) be as in the statement of the proposition. Then, for large n, each G̅n−1μ possesses a Nash equilibrium ϱn. Because ϱn ∈ M and M is sequentially compact, we may write (passing to a subsequence if necessary) ϱn → ϱ for some ϱ ∈ M. Therefore, ϱ is a thp equilibrium of G.
To see that all thp equilibria of G are Nash, suppose that ϱ is a thp equilibrium of G, and let ϱn be the corresponding sequence of equilibria in Selten perturbations, i.e., each ϱn is a Nash equilibrium of Ḡδnμn, where δn → 0, , and ϱn → ϱ. We wish to show that ϱ is a (mixed-strategy) Nash equilibrium of G. To this end, we assume that ϱ is not an equilibrium and derive a contradiction.
Because ϱn → ϱ and each ui is bounded, we may write (passing to a subsequence if necessary)
We therefore have, in view of (1)
In light of Proposition 1, it is only natural to ask whether the machinery developed within the literature on the existence of Nash equilibria in discontinuous games can be employed to show that Selten perturbations of G possess Nash equilibria. Reny ([14], Theorem 3.1) proves that a compact, metric, quasiconcave, and better-reply secure game possesses a Nash equilibrium.6 If G is a compact, metric game, then, for , G̅δμ is a compact, metric game.7 In addition, Ḡδμ is easily seen to be quasiconcave. Consequently, a Selten perturbation Ḡδμ possesses a Nash equilibrium if it is better-reply secure. This observation, together with Proposition 1, gives the following lemma.
Lemma 1
If G is a compact, metric game and there exists such that G̅δμ is better-reply secure for every δ ∈ [0, α], then G possesses a trembling-hand perfect equilibrium, and all trembling-hand perfect equilibria of G are Nash.
In general, verifying the existence of such that G̅δμ is better-reply secure for every δ ∈ [0, α] is cumbersome, for it entails dealing with expected payoffs, defined on mixed strategies, and the weak* convergence of measures. Consequently, rather than imposing better-reply security directly on G̅δμ, one would like to have conditions on the payoffs of the original game G that (1) prove useful in applications and (2) imply better-reply security in perturbations of G.
Unfortunately, G̅δμ need not inherit better-reply security from G, and even standard strengthenings of better-reply security—payoff security or uniform payoff security (to be defined below), along with upper semicontinuity of —do not generally give the desired property in G̅δμ.
The following definition is taken from Reny [14].
Definition 5
The game G is payoff secure if for each ε > 0, x ∈ X, and i, there exists yi ∈ Xi such that ui(yi, Ox−i) > ui(x) − ε for some neighborhood Ox−i of x−i.
It is well-known (Reny [14], Proposition 3.2) that payoff security of G and upper semicontinuity of ensure better-reply security of G. However, payoff security of G and upper semicontinuity of need not give better-reply security of the mixed extension Ḡ. The following example illustrates this point.
Example 2
(Sion and Wolfe [17]). Consider the game G = ([0,1], [0, 1], u1, u2), where
This game is zero-sum (and so is constant) and payoff secure (Carmona [18], Proposition 4). Moreover, as shown by Sion and Wolfe [17], G has no mixed-strategy Nash equilibria. Hence, by Corollary 5.2 of Reny [14], G̅ fails better-reply security.
Now consider the following strengthening of payoff security (cf. Monteiro and Page [19]).
Definition 6.
Given Yi ⊆ Xi for each i, the game G is uniformly payoff secure over if for each i, ε > 0, and xi ∈ Yi, there exists yi ∈ Xi such that for every y−i ∈ X−i, there is a neighborhood Oy−i of y−i such that ui(yi, Oy−i) > ui(xi, y−i) − ε.
The game G is uniformly payoff secure if it is uniformly payoff secure over X.
Uniform payoff security of G yields payoff security of the mixed extension G̅ ([19], Theorem 1). By standard arguments, this means that uniform payoff security of G, together with upper semicontinuity of , implies better-reply security of G̅. Nonetheless, these two conditions need not lead to better-reply security of G̅δμ, as illustrated by the following example.8
Example 3
Let (αn) be a sequence in with αn ↗ 1. Let (fn) be a sequence of functions fn : [0, 1] → ℝ. with the following properties:
Consider the two-player game G = ([0, 1], [0, 1], u1, u2), where
It is easy to verify that is upper semicontinuous and G is uniformly payoff secure. However, G̅δμ fails payoff security whenever and δ ∈ (0, 1). To see this, fix and δ ∈ (0, 1). We need to show that there exist ε > 0, i, and ν ∈ M(δμ) such that for all σi ∈ Mi(δμi) there is a point σ−i ∈ Xj≠iMj(δμj) arbitrarily close to ν −i for which Ui(σi, σ−i) ≤ Ui(ν) − ε. Thus, it suffices to establish the following for ε > 0 sufficiently small: there is an n such that for each neighborhood O(1-δ)αn+δμ2 of (1 − δ)αn + δμ2 and every y1 ∈ [0, 1]
Choose ε > 0 with the property that for any large enough n
Therefore, because U1(y1, y2) ≤ 1 ≥ U1(y1, μ2) and
On the other hand, we have
The perturbation G̅δμ also fails better-reply security. To see this, choose and δ ∈ (0, 1), and observe that
In light of Example 3, any condition on the payoff functions of G leading to the hypothesis of Lemma 1 (when combined with upper semicontinuity of ) must be stronger than uniform payoff security.10
The following condition appears in Carbonell-Nicolau [11].
Condition (A)
There exists such that for each i and every ε > 0 there is a Borel measurable map f : Xi → Xi such that the following is satisfied:
For each xi ∈ Xi and every y−i ∈ X−i, there is a neighborhood Oy−i of y−i such that
For each y−i ∈ X−i, there is a subset Yi of Xi with μi(Yi) = 1 such that for every xi ∈ Yi, there is a neighborhood Vy−i of y−i such that ui(f(xi), z−i) < ui(xi, z−i) + ε for all z−i ∈ Vy−i.11
It is clear that (A) strengthens the concept of uniform payoff security.
Remark 2
The following implications are immediate:
| continuity ⇒ | (A) |
| ⇒ | uniform payoff security |
| ⇒ | payoff security |
We can establish payoff security of a Selten perturbation of G from Condition (A).
Lemma 2
Suppose that a compact, metric game G satisfies Condition (A). Then there exists such that G̅δμ is payoff secure for every δ ∈ [0, 1).
This result plays a central role in the proof of the main results of this paper.12 The proof of Lemma 2 can be found in Section 4.
Lemma 2 can be combined with known results to prove an existence theorem. In fact, under the hypothesis of Lemma 2, we obtain payoff security of G̅δμ for any δ ∈ [0, 1). If in addition is upper semicontinuous, since upper semicontinuity of gives upper semicontinuity of ΣiUi (Reny [14], Proposition 5.1), it follows that G̅δμ is better-reply secure for any δ ∈ [0, 1) (Reny [14], Proposition 3.2). Applying Lemma 1 gives a thp equilibrium in G.
The following statement summarizes this finding.
Theorem 2
Suppose that a compact, metric game G satisfies Condition (A). Suppose further that is upper semicontinuous. Then G has a trembling-hand perfect equilibrium, and all trembling-hand perfect equilibria of G are Nash.
Lemma 2 is similar to Lemma 1 in Carbonell-Nicolau [11]. Lemma 1 in [11] states that if a compact, metric game satisfies Condition (A), then there exists such that the game G(δ,μ) is payoff secure for every δ ∈ [0, 1), where G(δ,μ) is defined as
The statement of this lemma differs from that of Lemma 2 in that G(δ,μ) and G̅δμ are distinct objects. In fact, the latter can be shown to be homeomorphic to the mixed extension of the former. Consequently, since payoff security of a game does not generally imply payoff security of its mixed extension, Lemma 2 is not implied by Lemma 1 in [11]. On the other hand, it should be noted that Theorem 2 is not implied by Theorem 3 or Theorem 4 in [11]. In fact, both the hypothesis and the conclusion are weaker for Theorem 2.13
The remainder of this section derives a corollary of Theorem 2 in terms of two independent conditions introduced in [11]—generic entire payoff security and generic local equi-upper semicontinuity—that imply Condition (A). While stronger, these conditions prove useful in applications: they apply in a variety of economic games and do not explicitly require the measurability of the map f in Condition (A). Both Theorem 2 and its corollary (Corollary 1, in terms of generic entire payoff security and generic local equi-upper semicontinuity) are illustrated in Section 3.14
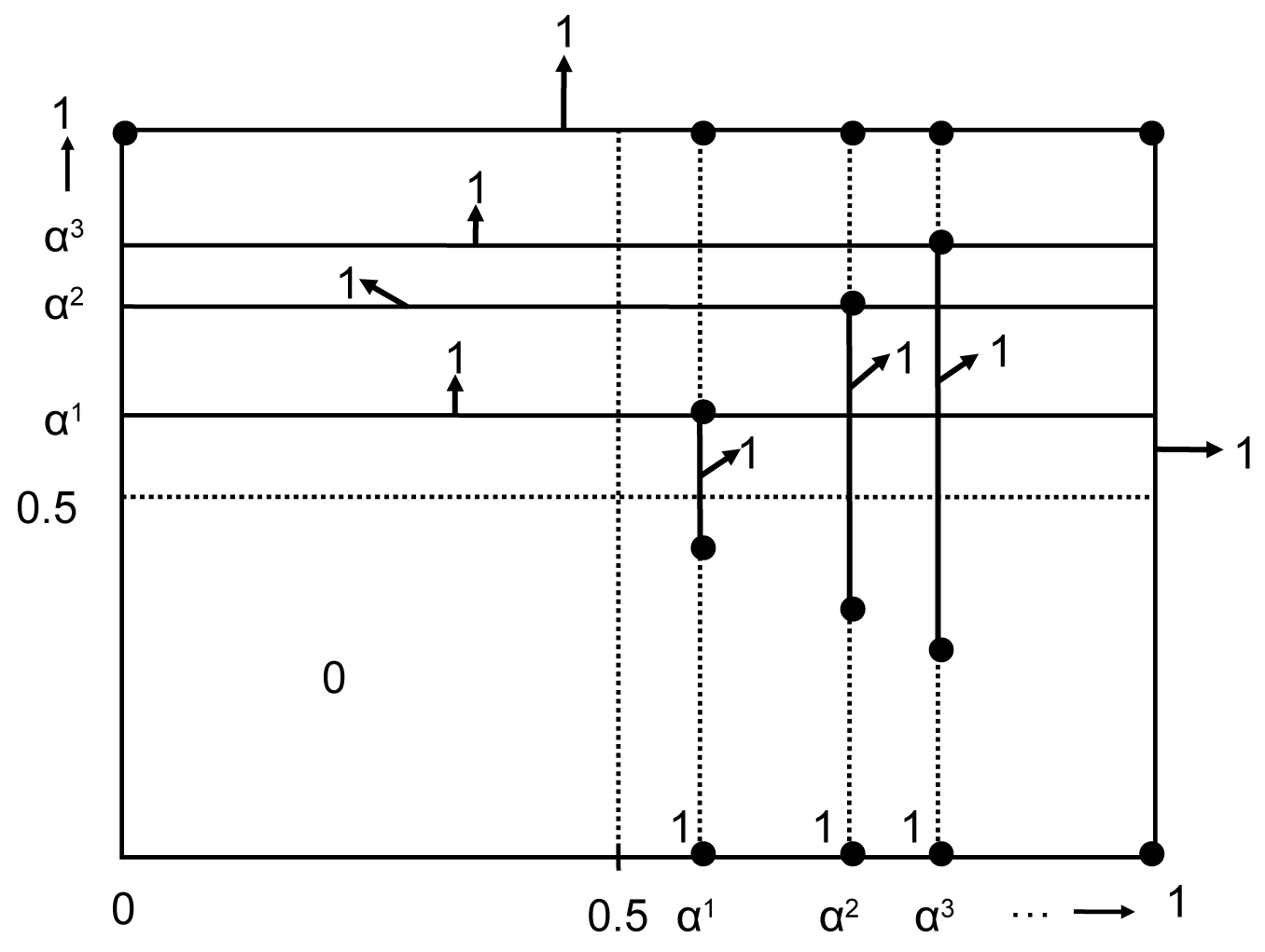
Let Ai be the set of all accumulation points of Xi (i.e., the set Ai of points xi ∈ Xi such that (V ∖ {xi}) ⋂ Ai ≠ ∅ for each neighborhood V of xi). Since Xi is compact and metric, it can be written as a disjoint union Ai ⋃ Ki, where Ai is closed and dense in itself (i.e., with no isolated points) and Ki is countable.
Let be the set of measures μi in Mi such that μi({xi}) = 0 and μi (Ne(xi)) > 0 for each xi ∈ Ai and every ∈ ≥ 0, and μi({xi}) > 0 for every xi ∈ Ki. Define .
Clearly, is a subset of . Moreover, is nonempty In fact, it is not difficult to show that is dense in Mi for each i.
Definition 7
Given Yi ⊆ Xi for each i, we say that G is entirely payoff secure over if for each i, ∈ > 0, and xi ∈ Yi, and for every neighborhood O of xi, there exist yi ∈ O and a neighborhood Oxi of xi such that for every y−i ∈ x−i, there is a neighborhood Oy−i of y−i for which ui(yi, Oy_i) > ui(Oxi, y−i) − ∈.
We say that G is entirely payoff secure if it is entirely payoff secure over X.
Definition 8
Given Yi ⊆ Xi for each i, we say that the game G is generically entirely payoff secure over if there is, for each i, a set Zi ⊆Yi with Yi∖Zi countable such that G is uniformly payoff secure over and entirely payoff secure over
A game G is generically entirely payoff secure if it is entirely payoff secure over and generically entirely payoff secure over (recall that Xi = Ai ⋃ Ki, where Ai is closed and dense in itself and Ki is countable).
Remark 3
The following implications are immediate:
| continuity ⇒ | entire payoff security |
| ⇒ | generic entire payoff security |
| ⇒ | uniform payoff security |
| ⇒ | payoff security |
Definition 9
The game G is locally equi-upper semicontinuous if for each i, x−i ∈ X−i, and xi ∈ Xi, and for each ε > 0, there exists a neighborhood Oxi of xi such that for every yi ∈ Oxi there exists a neighborhood Ox−i of x−i such that ui(yi, y−i) < ui(xi, y−i) + ε for all y−i ∈ Ox−i.
Definition 10
The game G is generically locally equi-upper semicontinuous if there exists such that for each i and x−i ∈ ×−i, there exists Yi ⊆ Xi with μi(Yi) = 1 such that for each xi ∈ Yi and ε > 0, there exists a neighborhood Oxi of xi such that for every yi ∈ Oxi there is a neighborhood Ox−i of x−i such that ui(yi, y−i) < ui(xi, y−i) + ∈ for all y−i ∈ Ox−i.
It turns out that generic entire payoff security and generic local equi-upper semicontinuity imply Condition (A).
Lemma 3
(Carbonell-Nicolau [11], Lemma 4). Suppose that G is generically entirely payoff secure and generically locally equi-upper semicontinuous. Then G satisfies Condition (A).
Lemma 3, combined with Theorem 2, gives the following result.
Corollary 1 (to Theorem 2)
Suppose that G is compact, metric, generically entirely payoff secure, and generically locally equi-upper semicontinuous. Suppose further that is upper semicontinuous. Then G has a trembling-hand perfect equilibrium, and all trembling-hand perfect equilibria of G are Nash.
3. Applications
The hypotheses of our main results are often satisfied in applications. This is illustrated by the following economic games.
Example 4 (Bertrand competition with discontinuous demand)
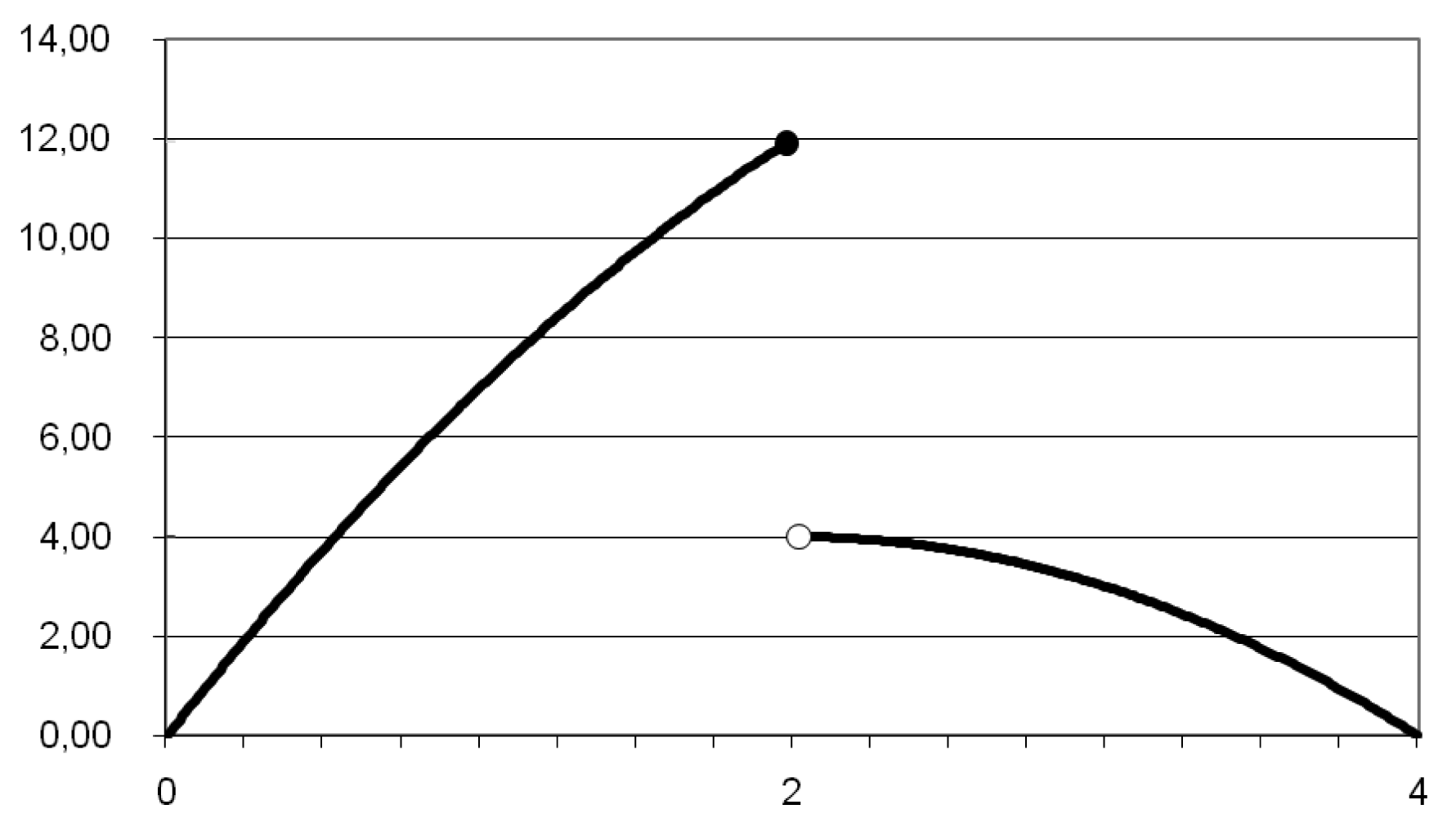
Consider a two-player Bertrand game G = ([0, 4], [0, 4], u1, u2), where
Similar duopoly games can be found in Baye and Morgan [22]. See also [22] for a discussion on economic phenomena that explain demand discontinuities.
It is readily seen that is upper semicontinuous. Moreover, G is entirely payoff secure. To see this, fix i, ∈ > 0, pi ∈ [0, 4], and a neighborhood O of pi. We wish to show that there exist ai ∈ O and a neighborhood Opi around pi such that for every p−i ∈ [0, 4], there is a neighborhood Op−i of p−i for which
If p−i > ai, then Op−i ⋂ {ai} = ∅.
If p−i ≤ ai, then Op−i ⋂ Opi = ∅.
Finally, G is generically locally equi-upper semicontinuous. In fact, take i, x−i ∈ [0, 1], xi ∈ [0, 1] ∖ {2, x−i}, and ε > 0. We only consider the case when xi < x−i and xi < 2, for the other cases can be dealt with similarly If xi < x−i and xi < 2, we have ui(yi, y−i) = yi(8 − yi) for all (yi, y−i) ∈ Vxi − Vx−i and for some neighborhoods Vxi and Vx−i of xi and x−i respectively, so it is clear that there exists a neighborhood Oxi of xi such that for every yi ∈ Oxi there is a neighborhood Ox−i of x−i such that ui(yi, y−i) < ui(xi, y−i) + ε for all y−i ∈ Ox−i.
Because G is generically locally equi-upper semicontinuous and entirely payoff secure, Corollary 1 can be invoked to establish the existence of a thp equilibrium.
Example 5 (all-pay auction)
There are N bidders competing for an object with a known value equal to 1. The highest bidder wins and every bidder pays his bid. Ties are broken via an equal probability rule. Given a profile of bids (b1, …, bN) ∈ [0, 1]N, the winning bid is maxi∈ {1,…,N} bi.
This situation can be modeled as an N-person normal-form game , where Xi = [0, 1] and
This game is generically locally equi-upper semicontinuous. To see this, fix i and b−i ∈ X−i, and choose any bi ∈ [0, 1]∖ {b̅−i} and any ∈ > 0, where b̅−i : = maxj∈ {1,…, N}∖{i}bj. We only consider the case when bi < b̅ −i, for the case when bi > b̅ −i can be handled analogously. Take a neighborhood (bi − δ,bi+ δ) of bi such that (bi − δ, bi + δ) ⋂ {b̅ −i} = ∅ and δ < ∈. For each ai ∈ (bi − δi, bi + δ) ⋂[0,1] and for every a−i ∈ X−i in a neighborhood Ob−i of b−i such that
We now show that G is generically entirely payoff secure.15 Fix a player i, and choose ∈ > 0, bi ∈ (0, 1), and a neighborhood O of bi (we omit the case when bi ∈ {0, 1}, which is easy to handle). We wish to show that there exist ai ∈ O and a neighborhood Obi such that for all b−i ∈ [0, 1]N−1, there is a neighborhood Ob−i of b−i for which
Choose ai ∈ O ∩ (bi, bi + ∈), and fix a neighborhood Obi of bi such that Obi ⊆ [0, 1], ai ∈ [0, 1] ∩ (bi, bi + ∈), and {ai} ∩ Obi = ∅. Pick any b−i ∈ [0, 1]N−1, and let Ob−i be a neighborhood of b−i with the following property: if maxj∈ {1, …, N} bj < bi, then Ob−i ∩ {ai}N−1 = ∅. It is easy to verify that the choices of ai, Obi, and Ob−i yield Equation (6).
Finally, it is routine to verify that the sum of the bidders’ payoffs is continuous. Hence, Corollary 1 gives a thp equilibrium.
Example 6 (catalog games)
Page and Monteiro [23] consider a common agency contracting game in which firms compete for the business of an agent of unknown type t ∈ T, where T is a Borel subset of a separable, complete, and metric space. The distribution of types is represented by a Borel probability measure μ defined on T. There are two firms competing simultaneously in prices and products. The set of products each firm can offer is represented by a compact metric space X, and it is assumed that X contains an element 0, which denotes “no contracting”. The universe of prices that a firm can charge is denoted by D:= [0, d̅], with d̅ > 0. The agent can only contract with one firm and can choose to abstain from contracting altogether. Given i ∈ {1,2} and a closed subset Xi of X, let Ki:= Xi × D be the feasible set of products and prices that a firm i can offer. Assume the existence of a fictitious firm i = 0 with feasible set K0 : = {(0, 0)}. The agent chooses to abstain from contracting by choosing to contract with firm i = 0.
Each firm i competes by offering the agent a nonempty, closed subset Ci ⊆ Ki, a catalog, of products and prices. Thus, each firm i's action space is P(Ki), the compact, metric space of catalogs, equipped with the Hausdorff distance. The utility of a type t agent who chooses (i, x, p) ∈ {0, 1, 2} × Ci is denoted as vt(i, x, p); we have vt(i, x, p) : = 0 if i = 0 and vt(i, x, p) : = ut(i, x) − p if i ∈ {1, 2}. It is assumed that utility is measurable in type t and continuous in contract choice (i, x, p). The agent's choice set given catalog profile (C1, C2) is given by
Example 7 (provision of public goods)
Bagnoli and Lipman [6] study the following contribution game. There are I finitely many agents. By a slight abuse of notation, the set of agents is denoted by I. Each agent i ∈ I is endowed with an amount of wealth wi > 0. A collective decision d ∈ {0, 1} must be made (say, d = 1 designates the decision to provide streetlight, d = 0 represents the decision not to provide it). An outcome is a social decision together with an allocation of the private good (wealth) among the agents. The set of feasible outcomes is
The agents simultaneously choose a contribution to the public project, each agent i's contribution being an element of Si : = [0, wi]. Let w denote the vector of endowments. Given a profile s = (si)i∈I of contributions, the public project is undertaken if Σi∈I si ≥ c, in which case the realized outcome is (1, w – s); otherwise (i.e.,Σi∈I si < c) the outcome (0, w) obtains.
Let S : = X i∈I Si. The associated normal-form game is G = (Si, ui)i∈I, where ui : S → ℝ. is defined by
Specifically, assuming vi(0, wi) = 0 for each i (a normalization that does not affect generality) and vi(1, 0) < 0 for each i (so that we do not need to consider cases when some agents would like to contribute more than their wealth), we can define ai implicitly by vi(1, wi − ai) = 0. Assume Σi∈I wi > c. Clearly, the elimination of the interior of the set of weakly dominated strategies in G removes all si ∈ Si such that si > ai. Consider the “subgame” g of G in which i's strategy space is restricted to [0, ai] and g is otherwise identical to G.
Bagnoli and Lipman replace each Si by finite counterparts of varying grid sizes, and consider sequences of finite games in which the grid size converges to zero. They define an undominated perfect equilibrium in G as the limit of some sequence of undominated perfect equilibria of approximating finite versions of G.
The authors’ main result is that the game form G fully implements the core of the associated economy in undominated perfect equilibrium (i.e., any undominated perfect equilibrium of G induces a core allocation and vice versa). In view of our results, one may ask the following: Can one apply the characterization exercise conducted in [6] directly on the infinite game g? Can one obtain a similar theorem on the full implementation of the core in terms of trembling-hand perfection? While answering these questions requires a thorough analysis, Theorem 2 can be used to establish the existence of a thp equilibrium in g.
It is easily seen that the restriction of ui to [0, ai] is upper semicontinuous, so the sum of payoffs for g is upper semicontinuous.
We now show that g is entirely payoff secure. Take i, ∈ > 0, si [0, ai], and a neighborhood O of si. We need to show that there exist bi ∈ O and a neighborhood Osi of si such that for every s-i ∈ Xj≠i[0, aj], there is a neighborhood Os−i for which
Finally, we show that g is generically locally equi-upper semicontinuous. For each i, let μi be the normalized Lebesgue measure over [0, ai]. Fix i and s-i ∈ ×j≠i[0, aj]. Consider the set of all si ∈ [0, ai] such that Σj sj ≠ c, a set that has full Lebesgue measure (i.e., it has μi-measure 1), and take any si in this set, and ∈ > 0. We only consider the case when Σj sj > c (the case when Σj sj < c can be dealt with analogously). Clearly, we may choose a neighborhood Osi of si in [0, ai] such that bi + Σj≠i sj > c and vi(1, wi − bi) < vi(1, wi − si) + ∈ for all bi ∈ Osi. Further, given bi ∈ Osi, we may choose a neighborhood Os−i of s−i in ×j≠i[0, aj] such that
In light of Theorem 2, therefore, we obtain the non-emptiness of the set of trembling-hand perfect equilibria in g.
4. Proof of Lemma 2
To begin, we state a number of intermediate results.
Given a metric space X and Y ⊆ X, ℙ(Y) denotes the set of Borel probability measures on Y, and ℙ*(Y) is the subset of finitely supported measures in ℙ(Y) that assign rational values to each Borel set.
Lemma 4 (Carbonell-Nicolau [11], Lemma 6)
Let X be a compact metric space. Suppose that f : X → ℝ is bounded and Borel measurable. For each μ ∈ ℙ(X) and every ∈ > 0, there exists v* ∈ ℙ* (X) ∩ Nɛ (μ) such that | ∫X fdμ− ∫X fdv*| < ɛ.
Lemma 5 (Carbonell-Nicolau [11], Lemma 7)
Suppose that G is compact, metric, and satisfies Condition (A). Then there exists such that for each i and every ε > 0 there is a map f : Xi → Xi such that the following is satisfied:
For each xi ∈ Xi and every σ−i ∈ M−i, there is a neighborhood Oσ−i of σ−i such that
For every σ−i ∈ M−i, there is a neighborhood Vσ−i of σ−i such that for all p−i ∈ Vσ−i, where is defined by
Lemma 2
Suppose that a compact, metric game G satisfies Condition (A). Then there exists μ ∈ Mˆ such that G̅δμ is payoff secure for every δ ∈ [0, 1).
Proof. Fix δ ∈ [0, 1), and let be the measure given by Condition (A). We fix ε > 0, σ = (σ1, …, σN) ∈ M(δμ), and i, and show that there exists νi ∈ Mi(δμi) such that Ui (νi, Oσ − i) > Ui(σ) – ε for some neighborhood Oσ − i of σ −i.
Lemma 5 gives a Borel measurable map f : Xi → Xi satisfying the following:
For every yi ∈ Xi, there is a neighborhood Oσ−i of σ−i such that
There is a neighborhood Vσ −i of σ −i such that for all p-i ∈ Vσ–i, where is defined by
Claim 1
There exists a neighborhood Oσ−i of σ−i such that
Proof. By (i), for every yi ∈ Xi there is a neighborhood Oσ−i of σ−i such that
Now observe that we have and Consequently, for any large enough n,
Because σ ∈ M(δμ), there exists, for each i, ϱi ∈ Mi such that σi = (1 − δ) ϱi + δμi. Define
By (ii), there exists a neighborhood Oσ−i of σ−i such that
Acknowledgments
I am indebted to Efe Ok for his insights and encouragement; Efe read previous drafts and provided detailed comments. I also thank Rich McLean and Joel Sobel for several conversations, several anonymous referees for very useful remarks, and seminar participants at Barcelona Jocs and Rutgers for their comments. Part of this research was conducted while the author was visiting Universitat Autonoma de Barcelona. The author is grateful to this institution for its hospitality.
References
- Selten, R. Reexamination of the perfectness concept for equilibrium points in extensive games. Int. J. Game Theory 1975, 4, 25–55. [Google Scholar]
- Bertrand, J. Théorie mathématique de la richesse sociale. J. Savants 1883, 499–508. [Google Scholar]
- Hotelling, H. The stability of competition. Econ. J. 1929, 39, 41–57. [Google Scholar]
- Milgrom, P.; Weber, R. A theory of auctions and competitive bidding. Econometrica 1982, 50, 1089–1122. [Google Scholar]
- Fudenberg, D.; Gilbert, R.; Stiglitz, J.; Tirole, J. Preemption, leapfrogging, and competition in patent races. Eur. Econ. Rev. 1983, 22, 3–31. [Google Scholar]
- Bagnoli, M.; Lipman, B.L. Provision of public goods: Fully implementing the core through private contributions. Rev. Econ. Stud. 1989, 56, 583–601. [Google Scholar]
- Broecker, T. Credit-worthiness tests and interbank competition. Econometrica 1990, 58, 429–452. [Google Scholar]
- Pitchik, C.; Schotter, A. Perfect equilibria in budget-constrained sequential auctions:An experimental study. Rand J. Econ. 1988, 19, 363–388. [Google Scholar]
- Allen, B. Using trembling-hand perfection to allieviate the interlinked principal-agent problem. Scand. J. Econ. 1988, 90, 373–382. [Google Scholar]
- Simon, L.K.; Stinchcombe, M.B. Equilibrium refinement for infinite normal-form games. Econometrica 1995, 63, 1421–1443. [Google Scholar]
- Carbonell-Nicolau, O. On the existence of pure-strategy perfect equilibrium in discontinuous games. Games Econ. Behav. 2011, 71, 23–48. [Google Scholar]
- Carbonell-Nicolau, O. Perfect and limit admissibe perfect equilibria in discontinuous games. J. Math. Econ. (forthcoming).
- Van Damme, E.E.C. Stability and Perfection of Nash Equilibria; Springer-Berlag: Berlin, Germany, 2002. [Google Scholar]
- Reny, P.J. On the existence of pure and mixed strategy Nash equilibria in discontinuous games. Econometrica 1999, 67, 1029–1056. [Google Scholar]
- Al-Najjar, N. Strategically stable equilibria in games with infinitely many pure strategies. Math. Soc. Sci. 1995, 29, 151–164. [Google Scholar]
- Dunford, N.; Schwartz, J.T. Linear Operators, Part I: General Theory; John Wiley and Sons: New York, NY, USA, 1957. [Google Scholar]
- Sion, M.; Wolfe, P. On a game without a value. In Contributions to the Theory of Games, Volume III; Dresher, M., Tucker, A.W., Wolfe, P., Eds.; Princeton University Press: Princeton, NJ, USA, 1957. [Google Scholar]
- Carmona, G. On the existence of equilibria in discontinuous games: Three counterexamples. Int. J. Game Theory 2005, 33, 181–187. [Google Scholar]
- Monteiro, P.K.; Page, F.H. Uniform payoff security and Nash equilibrium in compact games. J. Econ. Theory 2007, 134, 566–575. [Google Scholar]
- Barelli, P.; Soza, I. On the existence of Nash equilibria in discontinuous and qualitative games. 2008. (mimeo). [Google Scholar]
- Baye, M.R.; Tian, G.; Zhou, J. Characterizations of the existence of equilibria in games with discontinuous and non-quasiconcave payoffs. Rev. Econ. Stud. 1993, 60, 935–948. [Google Scholar]
- Baye, M.R.; Morgan, J. Winner-take-all price competition. Econ. Theory 2002, 19, 271–282. [Google Scholar]
- Page, F.H.; Monteiro, P.K. Three principles of competitive nonlinear pricing. J. Math. Econ. 2003, 39, 63–109. [Google Scholar]
- 1For instance, sometimes the Nash equilibrium concept is too weak to sustain a given result, and the notion of trembling-hand perfection constitutes a natural refinement of the set of Nash equilibria. Beyond its intuitive appeal, trembling-hand perfection is weaker than other refinements, and therefore permits more general theories.
- 2Allen [9] and Pitchik and Schotter [8] finitize their respective games at the outset, rather than approaching an infinite game by a series of successively larger finite games. However, their models are most conveniently analyzed in terms of continua of actions.
- 3Constructing a measurable map can sometimes be cumbersome, especially if pure strategies are, say, maps between metric spaces rather than points in Euclidean space.
- 4In Definition 2, each μn is an exact equilibrium of the perturbed game
. Should one insist upon requiring that these equilibria be exact? While letting each μn be an ∈n-equilibrium (with (∈n, δn) → 0) would still give a (weak) refinement of Nash equilibrium, any Nash equilibrium would survive this weakening of Definition 2. In fact, given a Nash equilibrium μ of G, take ν ∈ Mˆ and a sequence (0, 1) ∋ δn → 0, and observe that each
is an ∈n -equilibrium of for some ∈n → 0, and we have (1 − δn)μ + δnν → μ.
- 5The reader is referred to the discussion following the statement of Theorem 2 for a comparison between Proposition 1 and Proposition 1 in [11].
- 6A game G = is quasiconcave if each Xi is a convex subset of a vector space and for each i and every x−i ∈ X−i, ui (.,x−i) is quasiconcave of Xi.
- 7If Xi is compact and metric, the weak* topology on Mi coincides with the topology induced by the Prokhorov metric on Mi. Hence, if Xi is nonempty, compact, and metric, then Mi(δiμi) is nonempty and metric. In addition, if Xi is nonempty, compact, and metric, Mi(δμi) is a nonempty convex subset of the weakly* compact set Mi. It is easy to check that Mi(δμi) is strongly closed, and therefore (Dunford and Schwartz ([16], Theorem V.3.13, p. 422)) weakly* closed, so Mi(δμi) is weakly* compact.
- 8Even the generalized notion of better-reply security of Barelli and Soza [20] or the conditions for existence of Baye et al. [21] need not hold for the perturbation G̅δμ when G is uniformly payoff secure and is upper semicontinuous.
- 9While G is quasi-symmetric in the sense of Reny [14], and so an appropriate choice of μ renders quasi-symmetric, also violates diagonal better-reply security (as defined in [14]).
- 10This means that the machinery developed in the literature on the existence of Nash equilibria cannot be employed to establish the existence of a Nash equilibrium in under the assumption that G is uniformly payoff secure and is upper semicontinuous. We ignore if uniform payoff security of G and upper semicontinuity of implies the existence of a thp equilibrium in G. If this were true, its proof would require an appropriate generalization of the main theorem ofReny [14].
- 11The following generalization of Condition (A) leaves all of our results intact.Condition(A′).There exists
such that for each i and every ε > 0 there is a sequence (fk) of Borel measurable maps fk : Xi → Xi such that the following is satisfied:
For each k, xi ∈ Xi and y−i ∈ X−i there is a neighborhood Oy−iof y−i such that ui(fk(xi), Oy−i > ui(xi, y−i) – ε.
For each y−i ∈ X−i there is a subset Yi of Xi with μi (Yi) = 1 such that for each xi∈ Yi and every sufficiently large k, there is a neighborhood Vy−i of y−i such that ui(fk(xi), z−i)< ui(xi, z−i) + ε for all z−i ∈ Vy−i
- 12Lemma 2 is similar to Lemma 1 in Carbonell-Nicolau [11]. We provide a comparison between these two results after the statement of Theorem 2.
- 13The hypothesis is weaker because it does not assume concavity or quasiconcavity-like conditions, while the conclusion is weaker because trembling-hand perfect equilibria may be in mixed strategies.
- 14The relationship between Corollary 1 and Corollaries 1 and 3 in [11] is similar to that between Theorem 2 and Theorems 3 and 4 in [11]. In particular, Corollary 1 is not implied by the results in [11].
- 15This game fails entire payoff security.
- 16It is shown in [23] that v* is measurable in types and continuous in catalog profiles, while the correspondence Φ is jointly measurable in types and catalog profiles and upper hemicontinuous in catalog profiles.
© 2011 by the author; licensee MDPI, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Carbonell-Nicolau, O. The Existence of Perfect Equilibrium in Discontinuous Games. Games 2011, 2, 235-256. https://doi.org/10.3390/g2030235
Carbonell-Nicolau O. The Existence of Perfect Equilibrium in Discontinuous Games. Games. 2011; 2(3):235-256. https://doi.org/10.3390/g2030235
Chicago/Turabian StyleCarbonell-Nicolau, Oriol. 2011. "The Existence of Perfect Equilibrium in Discontinuous Games" Games 2, no. 3: 235-256. https://doi.org/10.3390/g2030235



