Intergroup Prisoner’s Dilemma with Intragroup Power Dynamics
Abstract
: The Intergroup Prisoner's Dilemma with Intragroup Power Dynamics (IPD^2) is a new game paradigm for studying human behavior in conflict situations. IPD^2 adds the concept of intragroup power to an intergroup version of the standard Repeated Prisoner's Dilemma game. We conducted a laboratory study in which individual human participants played the game against computer strategies of various complexities. The results show that participants tend to cooperate more when they have greater power status within their groups. IPD^2 yields increasing levels of mutual cooperation and decreasing levels of mutual defection, in contrast to a variant of Intergroup Prisoner's Dilemma without intragroup power dynamics where mutual cooperation and mutual defection are equally likely. We developed a cognitive model of human decision making in this game inspired by the Instance-Based Learning Theory (IBLT) and implemented within the ACT-R cognitive architecture. This model was run in place of a human participant using the same paradigm as the human study. The results from the model show a pattern of behavior similar to that of human data. We conclude with a discussion of the ways in which the IPD^2 paradigm can be applied to studying human behavior in conflict situations. In particular, we present the current study as a possible contribution to corroborating the conjecture that democracy reduces the risk of wars.1. Introduction
Erev and Roth have argued for the necessity of a Cognitive Game Theory that focuses on players' thought processes and develops simple general models that can be appropriately adapted to specific circumstances, as opposed to building or estimating specific models for each game of interest [1]. In line with this approach, Lebiere, Wallach, and West [2] developed a cognitive model of the Prisoner's Dilemma (PD) that generalized to other games from Rapoport et al.'s taxonomy of 2 × 2 games [3]. This model leverages basic cognitive abilities such as memory by making decisions based on records of previous rounds stored in long-term memory. A memory record includes only directly experienced information such as one's own move, the other player's move, and the payoff. The decision is accomplished by a set of rules that, given each possible action, retrieves the most likely outcome from memory and selects the move with the highest payoff. The model predictions originate from and are strongly constrained by learning mechanisms occurring at the sub-symbolic level of the ACT-R cognitive architecture [4]. The current work builds upon and extends this model. We use abstract representations of conflict as is common in the field of Game Theory [5], but we are interested in the actual (rather than normative) aspects of human behavior that explain how people make strategic decisions given their experiences and cognitive constraints [6].
In understanding human behavior in real world situations, it is also necessary to capture the complexities of their interactions. The dynamics of many intergroup conflicts can be usefully represented by a two-level game [7]. At the intragroup level, various factions (parties) pursue their interests by trying to influence the policies of the group. At the intergroup level, group leaders seek to maximize their gain as compared to other groups while also satisfying their constituents. For example, domestic and international politics are usually entangled: international pressure leads to domestic policy shifts and domestic politics impact the success of international negotiations [7]. A basic two-level conflict game extensively studied is the Intergroup Prisoner's Dilemma [8,9]. In this game, two levels of conflict (intragroup and intergroup) are considered simultaneously. The intragroup level consists of an n-person Prisoner's Dilemma (PD) game while the intergroup level is a regular PD game. A variant of this game, the Intergroup Prisoner's Dilemma—Maximizing Difference, was designed to study what motivates individual self-sacrificial behavior in intergroup conflicts [10]. This game disentangles altruistic motivations to benefit the in-group and aggressive motivations to hurt the out-group. As is often the case in these games, within-group communication dramatically influences players' decisions. This result suggests that intragroup interactions (such as communication, negotiation, or voting) might generally have a strong influence on individuals' decisions in conflict situations. In our view, games that incorporate abstracted forms of intragroup interactions more accurately represent real-world conflict situations. An open question that will be addressed here is whether groups with dynamic and flexible internal structures (e.g., democracies) are less likely to engage in conflicts (e.g., wars) than groups with static and inflexible internal structures (e.g., dictatorships).
A characteristic of social interactions that many two-level games currently do not represent is power. Although numerous definitions of power are in use both colloquially and in research literature, Emerson [11] was one of the first to highlight its relationship-specificity: “power resides implicitly in the other's dependency.” In this sense, a necessary and sufficient condition for power is the ability of one actor to exercise influence over another [11]. However, power can also affect relationships between groups, such that group members are confronted simultaneously with the goal of obtaining and maintaining power within the group, and with the goal of identifying with a group that is more powerful compared to other groups. Often, these two objectives pull individuals in opposite directions, leading unpredictably to allegiance with or defection from group norms. Researchers have focused on the contrast between groups of low power and those of high power in the extent to which they will attempt to retain or alter the status quo. Social dominance theories propose that in-group attachment will be more strongly associated with hierarchy-enhancing ideologies for members of powerful groups [12], especially when there is a perceived threat to their high status [13,14]. At the same time, system justification theory describes how members of less powerful groups might internalize their inferiority and thus legitimize power asymmetries [15], but this effect is moderated by the perceived injustice of low status [16]. Within dyads, the contrast between one's own power and the power of one's partner is especially salient in inducing emotion [17], suggesting that individual power is sought concurrently to group power.
Here we introduce intragroup power to an Intergroup Prisoner's Dilemma game as a determinant of each actor's ability to maximize long-term payoffs through between-group cooperation or competition. This game, the Intergroup Prisoner's Dilemma with Intragroup Power Dynamics (IPD^2), intends to reproduce the two-level interactions in which players are simultaneously engaged in an intragroup power struggle and an intergroup conflict. We introduce a power variable that represents both outcome power and social power. Outcome power (power to) is the ability of an actor to bring about outcomes, while social power (power over) is the ability of an actor to influence other actors [18]. The outcomes are reflected in payoff for the group. Oftentimes in the real world, power does not equate with payoff. Free riders get payoff without having power. Correspondingly, power does not guarantee profitable decision-making. However, a certain level of power can be a prerequisite for achieving significant amounts of payoff, and in return, payoff can cause power consolidation or shift. A leader who brings positive outcomes for the group can consolidate her position of power, whereas negative outcomes might shift power away from the responsible leader. We introduced these kinds of dynamics of payoff and power in the IPD^2.
As a consequence of the complex interplay between power and payoff, IPD^2 departs from the classical behavioral game theory paradigm in which a payoff matrix is either explicitly presented to the participants or easily learned through the experience of game playing. The introduction of the additional dimension of power and the interdependencies of a 2-group (4-player) game increases the complexity of interactions such that players might not be able to figure out the full range of game outcomes with limited experience. Instead of trying to find the optimal solution (compute equilibria), they might aim at satisficing as people do in many real-world situations [19].
This paper reports empirical and computational modeling work that is part of a larger effort to describe social and cognitive factors that influence conflict motivations and conflict resolution. Our main contribution is three-fold: (1) We present a new game paradigm, IPD^2, that can be used to represent complex decision making situations in which intragroup power dynamics interact with intergroup competition or cooperation; (2) We put forth a computational cognitive model that aims to explain and predict how humans make decisions and learn in this game; and (3) We describe a laboratory study aimed at exploring the range of behaviors that individual human participants exhibit when they play the game against computer strategies of various complexities.
The following sections will describe the IPD^2 game, the cognitive model, and the laboratory study, and end with discussions, conclusions, and plans for further research.
2. Description of the IPD^2 Game
IPD^2 is an extension of the well-known Repeated Prisoner's Dilemma paradigm [20]. This is a paradigm in Game Theory that demonstrates why two people might not cooperate even when cooperating would increase their long-run payoffs. In the Repeated Prisoner's Dilemma, two players, “Player1” and “Player2,” each decide between two actions that can be referred to as “cooperate” (C) and “defect” (D). The players choose their actions simultaneously and repeatedly. The two players receive their payoffs after each round, which are calculated according to a payoff matrix setting up a conflict between short-term and long-term payoffs (see example of the payoff matrix used in Table 1). If both players cooperate, they each get one point. If both defect, they each lose one point. If one defects while the other cooperates, the player who defects gets four points and the player who cooperates loses four points. Note that the Repeated Prisoner's Dilemma is a non-zero-sum game: one player's gain does not necessarily equal the other player's loss. While long-run payoffs are maximized when both players choose to cooperate, that is often not the resulting behavior. In a single round of the game, rational choice would lead each player to play D in an attempt to maximize his/her immediate payoff, resulting in a loss for both players. This can be seen as a conflict between short-term and long-term considerations. In the short-term (i.e., the current move), a player will maximize personal payoff by defecting regardless of the opponent's choice. In the long-term, however, that logic will lead to sustained defection, which is worse than mutual cooperation for both players. The challenge is therefore for players to establish trust in one another through cooperation, despite the threat of unilateral defection (and its lopsided payoffs) at any moment.
In IPD^2, two groups play a Repeated Prisoner's Dilemma game. Each group is composed of two players. Within a group, each player chooses individually whether to cooperate or defect, but only the choice of the player with the greatest power within the group counts as the group's choice. This is equivalent to saying that the two players simultaneously vote for the choice of the group and the vote of the player with more power bears a heavier weight. By analogy with the political arena, one player is the majority and the other is the minority. The majority imposes its decisions over the minority. In what follows, the player with the higher value of power in a group will be referred to as the majority and the player with the lower power in a group will be referred to as the minority.
A player's power is a quantity assigned at the start of the game and increased or decreased after each round of the game depending on the outcome of the interaction. The sum of power within a group remains constant throughout the game. Thus, the intragroup power game is a zero-sum game embedded in an intergroup non-zero-sum game. All players start the game with the same amount of power. A random value is added or subtracted from each player's power level at each round. This random noise serves the functions of breaking ties (only one player can be in power at any given time) and of adding a degree of uncertainty to the IPD^2 game. Arguably, uncertainty makes the game more ecologically valid, as uncertainty is a characteristic of many natural environments [21].
If the two members of a group made the same decision (both played C or both played D), their powers do not change after the round other than for random variation. If they made different decisions, their powers change in a way that depends on the outcome of the inter-group game, as follows:
For the player in majority i,
For the player in minority j,
Note that the values in the payoff matrix can be positive or negative (Table 1). Thus, if the group receives a positive payoff, the power of the majority player increases whereas the power of the minority player decreases. If the group receives a negative payoff, the power of the majority player decreases whereas the power of the minority player increases. The total power of a group is a constant equal to 1.0 in the IPD^2 game.
The total payoff to the group in each round is shared between the two group mates in direct proportion to their relative power levels as follows:
Power and payoff for individual players are expressed as cumulative values because we are interested in their dynamics (i.e., how they increase and decrease throughout the game). On a given round, individual power and payoff increases or decreases depending on the group payoff, the power status, and whether or not there is implicit consensus of choice between the two players on a group. The key feature is that in the absence of consensus, positive group payoffs will result in an increase in power for the majority while negative group payoffs will result in a decrease of power for the majority.
The players make simultaneous decisions and they receive feedback after each round. The feedback is presented in a tabular format as shown in Table 2. In this example, the human participant was randomly assigned to Group-2. The three computer strategies were given non-informative labels. The choice of the majority player (i.e., the choice that counts as the group choice) was colored in magenta (and shown in bold font and gray background in Figure 2). The cumulative payoff (payoff total) was shown in red when negative and in blue when positive (shown herein italics and underlined, respectively).
The participants choose between A and B. The labels A and B are randomly assigned to Cooperate and Defect for each participant at the beginning of the experimental session. In the example shown in Table 2, A was assigned to Defect and B to Cooperate. The labels keep their meaning throughout the session, across rounds and games. It is presumed that participants will discover the meaning of the two options from the experience of playing and the feedback provided in the table, given that the payoff matrix is not given explicitly.
3. A Cognitive Model of IPD^2
We developed a cognitive model of human behavior in IPD^2 to understand and explain the dynamics of power in two-level interactions. This model was inspired by the cognitive processes and representations proposed in the Instance-Based Learning Theory (IBLT) [22]. IBLT proposes a generic decision-making process that starts by recognizing and generating experiences through interaction with a changing environment, and closes with the reinforcement of experiences that led to good decision outcomes through feedback from the environment. The decision-making process is explained in detail by Gonzalez et al. [22] and it involves the following steps: The recognition of a situation from an environment (a task) and the creation of decision alternatives; the retrieval of similar experiences from the past to make decisions, or the use of decision heuristics in the absence of similar experiences; the selection of the best alternative; and the process of reinforcing good experiences through feedback.
IBLT also proposes a key form of cognitive information representation, an instance. An instance consists of three parts: a situation in a task (a set of attributes that define the decision context), a decision or action in a task, and an outcome or utility of the decision in a situation in the task. The different parts of an instance are built through a general decision process: creating a situation from attributes in the task, a decision and expected utility when making a judgment, and updating the utility in the feedback stage. In this model, however, the utility will be reflected implicitly rather than explicitly. The instances accumulated over time in memory are retrieved from memory and are used repeatedly. Their strength in memory, called “activation,” is reinforced according to statistical procedures reflecting their use and in turn determines their accessibility. These statistical procedures were originally developed by Anderson and Lebiere [4] as part of the ACT-R cognitive architecture. This is the cognitive architecture we used to build the current model for IPD^2.
3.1. The ACT-R Theory and Architecture of Cognition
ACT-R1 is a theory of human cognition and a cognitive architecture that is used to develop computational models of various cognitive tasks. ACT-R is composed of various modules. There are two memory modules that are of interest here: declarative memory and procedural memory. Declarative memory stores facts (know-what), and procedural memory stores rules about how to do things (know-how). The rules from procedural memory serve the purpose of coordinating the operations of the asynchronous modules. ACT-R is a hybrid cognitive architecture including both symbolic and sub-symbolic components. The symbolic structures are memory elements (chunks) and procedural rules. A set of sub-symbolic equations controls the operation of the symbolic structures. For instance, if several rules are applicable to a situation, a sub-symbolic utility equation estimates the relative cost and benefit associated with each rule and selects for execution the rule with the highest utility. Similarly, whether (or how fast) a fact can be retrieved from declarative memory depends upon sub-symbolic retrieval equations, which take into account the context and the history of usage of that fact. The learning processes in ACT-R control both the acquisition of symbolic structures and the adaptation of their sub-symbolic quantities to the statistics of the environment.
The base-level activation of memory elements (chunks) in ACT-R is governed by the following equation:
n: The number of presentations for chunk i. A presentation can be the chunk's initial entry into memory, its retrieval, or its re-creation (the chunk's presentations are also called the chunk's references).
tj: The time since the jth presentation.
d: The decay parameter
βi: A constant offset
In short, the activation of a memory element is a function of its frequency (how often it was used), recency (how recently it was used), and noise.
ACT-R has been used to develop cognitive models for tasks that vary from simple reaction time experiments to driving a car, learning algebra, and playing strategic games (e.g., [2]). The ACT-R modeling environment offers many validated tools and mechanisms to model a rather complex game such as IPD^2. Modeling IPD^2 in ACT-R can also be a challenge and thus an opportunity for further development of the architecture.
3.2. The Model
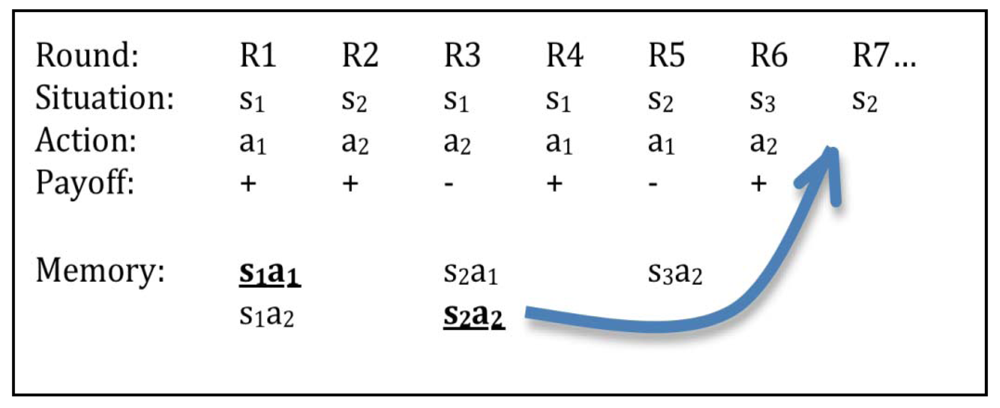
For each round of the game, the model checks whether it has previously encountered the same situation (attributes in the situation section of an instance), and if so, what action (decision) it took in that situation (see Figure 1, Rule 1). The situation is characterized by the choices of all the players and the group choices in the previous round. For example, let us assume that the current state of the game is the one represented in Table 2, where the human player is substituted by the model. We see that in the previous round the model played B, its group mate played A, and the two players on the opposite group played B (where A and B were randomly assigned to cooperate and defect, respectively). The group choice was B for both groups (because the model was in power). This information constitutes the situation components of the instance in which the model will make a decision for the next round. These attributes will act as the retrieval cues: the model will attempt to remember whether an identical situation has been previously encountered. The model's memory stores as an instance each situation that is encountered at each round of the game and the associated decision taken by the model in that situation.
Table 2 shows an example of an instance stored in the model's memory. Note that the situation part matches our presumed state of the game. The decision part of an instance specifies the action taken in that context. If such a memory element is retrieved, its decision part is used as the current decision of the model (see Figure 1, Rule 2). Thus, in the case of a repeated situation, the model decides to take the decision that is “recommended” by its memory. In our example, the model decides to play B.
The process might fail to retrieve an instance that matches2 the current situation either because the current situation has not been encountered before, or because the instance has been forgotten. In this case, the model repeats its previous decision (see Figure 1, Rule 3). This rule was supported by the observation of high inertia in the human data of this and other games (e.g., [21]). For the first round in the game, the model randomly chooses an action. For a given situation, the model can have up to two matching instances, one with A and the other one with B as the decision. If two instances match the current situation, the model will only retrieve the most active one. This model only uses the base-level activation and the activation noise from the ACT-R architecture (see Section 3.1).
Once a decision is made, the model receives positive or negative payoff. The real value of the payoff is not saved in memory as in other IBLT models. Instead, the valence of payoff (positive or negative) determines the course of action that is undertaken by the model3. When the payoff is positive, the activation of the memory element that was used to make the decision increases (a reference is added after its retrieval). This makes it more likely that the same instance will be retrieved when the same situation reoccurs. When the payoff is negative, activation of the retrieved instance increases, and the model additionally creates a new instance by saving the current situation together with the alternative decision. The new instance may be entirely new, or it may reinforce an instance that existed in memory but was not retrieved. Thus, after receiving negative payoff, the model has two instances with the same situation and opposite decisions in its memory. When the same situation occurs again, the model will have two decision alternatives to choose from. In time, the more lucrative decision will be activated and the less lucrative decision will decay. As mentioned above (section 3.2), retrieving and creating instances makes them more active and more available for retrieval when needed. A decay process causes the existing instances to be forgotten if they are not frequently and recently used. Thus, although instances are neutral with regard to payoff, the procedural process of retrieving and creating instances is guided by the perceived feedback (payoff); negative feedback causes the model to “consider” the alternative action, whereas positive feedback causes the model to persist in choosing the lucrative instance.
Figure 2 shows a possible situation in the game. In round 7, the model encounters situation s2, which was encountered before at rounds 2 and 5. Situation s2 is used as a retrieval cue. There are two actions associated with situation s2 in memory. Action a2 was chosen in round 2, which resulted in the creation of the s2a2 instance. Action a1 was recently followed by negative feedback at round 5, which caused s2a1 to be created and s2a2 to accumulate additional activation as the alternative of a failed action (see also Figure 1, Rule 4). Due to their history of use, the two instances end up with different cumulative activations: instance s2a2 is more active than instance s2a1. Notice that there is only one instance in memory containing situation s3 (s3a2). Whenever the model encounters situation s3, it will chose action a2, and it will continue to do so as long as the payoff remains positive. Only when action a2 causes negative payoff in situation s3, the alternative instance (s3a1) will be created.
This model meets our criteria for simplicity, in that it makes minimal assumptions and leaves the parameters of the ACT-R architecture at their defaults (see Section 5.4 for a discussion regarding parameter variation). The situation in an instance includes only the choices of all players and the resulting group choices in the previous round, all directly available information. This is the minimum amount of information that is necessary to usefully represent the behavior of individual players and the power standings in each group. However, one can imagine a more complex model that would store more information as part of the situation. For example, the real values of power and payoff can be stored in memory. This could help to model situations where players might behave differently when they have a strong power advantage than when they have a weak one. Another elaboration would be to store not only the decisions from the previous round, but also from several previous rounds (see, e.g., [23]). This would help the model learn more complex strategies, such as an alternation sequence of C and D actions. These elaborations will be considered for the next versions of the model.
4. Laboratory Study
A laboratory study was conducted to investigate the range of human decision making behaviors and outcomes in IPD^2 and to be able to understand how closely the predictions from the model described above corresponded to human behavior.
In this study, one human participant interacted with three computer strategies in a game: one as group mate and two as opponents. The reason for this design choice was twofold: (1) the game is new and there is no reference to what human behavior in this game looks like, so it makes sense to start with the most tractable condition that minimizes the complexities of human-human interactions; (2) the input to the cognitive model described in the previous section can be precisely controlled so as to perfectly match the input to the human participants.
Within this setup, we were particularly interested in the impact of intragroup power on intergroup cooperation and competition at both the individual level and the game level. The individual level refers to one player's decisions, and the game level refers to all players' decisions. For example, the amount of cooperation can be relatively high for one player but relatively low for the game in which the player participates. The following research questions guided our investigation: (1) Given the added complexity, are the human participants able to learn the game and play it successfully in terms of accumulated power and payoff? (2) What is the proportion of cooperative actions taken by human participants and how does it change throughout the game? (3) Does the proportion of cooperation differ depending on the participant's power status? (4) What are the relative proportions of the symmetric outcomes (CC and DD) and asymmetric outcomes (CD and DC), and how do they change throughout the game? Specifically, we expect that the intragroup power dynamics will increase the proportion of mutual cooperation and decrease the proportion of mutual defection. (5) How do the human participants and the cognitive model interact with computer strategies?
A far-reaching goal was to explore the contribution of the IPD^2 paradigm in understanding human motivations and behaviors in conflict situations.
4.1. Participants
Sixty-eight participants were recruited from the Carnegie Mellon University community with the aid of a web ad. They were undergraduate (51) and graduate students (16 Master's and 1 Ph.D. student). Their field of study had a wide range (see Annex 1 for a table with the number of participants from each field). The average age was 24 and 19 were females. They received monetary compensation unrelated to their performance in the IPD^2 game. Although it is common practice in behavioral game theory experiments to pay participants for their performance, we decided to not pay for performance in this game for the following reasons:
- -
Since this is the first major empirical study with IPD^2, we intended to start with a minimal level of motivation for the task: participants were instructed to try to increase their payoff. This was intended as a baseline for future studies that can add more complex incentive schemes.
- -
Traditional economic theory assumes that money can be used as a common currency for utility. IPD^2 challenges this assumption by introducing power (in addition to payoff) as another indicator of utility. By not paying for performance, we allowed motives that are not directly related to financial gain to be expressed.
4.2. Design
Five computer strategies of various complexities were developed. The intention was to have participants interact with a broad set of strategies representing the diverse spectrum of approaches that other humans might plausibly take in the game, yet preserve enough control over those strategies. As mentioned above, this is only the first step in our investigation of the IPD^2 game, and we acknowledge the need to follow up with a study of human-human interactions in IPD^2. The following are descriptions of the strategies that were used in this study:
Always-cooperate and Always-defect are maximally simple and predictable strategies, always selecting the C and D options, respectively. They are also extreme strategies and thus they broaden the range of actions to which the participants are exposed. For example, one would expect a player to adjust its level of cooperation or defection based on the way the other players in the game play. However, these two strategies are extremely cooperative and extremely non-cooperative, respectively.
Tit-for-tat repeats the last choice of the opposing group. This is a very effective strategy validated in several competitions and used in many laboratory studies in which human participants interact with computer strategies (e.g., [24]). Its first choice is D, unlike the standard Tit-for-tat that starts with C [25]. Starting with D eliminates the possibility that an increase in cooperation with repeated play would be caused by the initial bias toward cooperation of the standard Tit-for-tat.
Seek-power plays differently depending on its power status. When in the majority, it plays like Tit-for-tat. When in the minority, it plays C or D depending on the outcome of the intergroup Prisoner's Dilemma game in the previous round. The logic of this choice assumes that the minority player tries to gain power by sharing credit for positive outcomes and by avoiding blame for negative ones. In addition, this strategy makes assumptions with regard to the other players' most likely moves; it assumes that the majority players will repeat their moves from the previous round. If the previous outcome was symmetric (CC or DD), Seek-power plays C. Under the assumption of stability (i.e., previous move is repeated), C is the choice that is guaranteed to not decrease power (see description of how power is updated in section 2). If the previous outcome was asymmetric (CD or DC), Seek-power plays D. In this case, D is the move that is guaranteed to not lose power. Seek-power was designed as a “best response” strategy for a player that knows the rules of the game and assumes maximally predictable opponents. It was expected to play reasonably well and bring in sufficient challenge for the human players in terms of its predictability.
Exploit plays “Win-stay, lose-shift” when in the majority and plays Seek-power when in the minority. (“Win” and “lose” refer to positive and negative payoffs, respectively.) “Win-stay, lose-shift” (also known as Pavlov) is another very effective strategy that is frequently used against humans and other computer strategies in experiments. It has two important advantages over tit-for-tat: it recovers from occasional mistakes and it exploits unconditional cooperators [26]. By combining Pavlov in the majority with Seek-power in the minority, Exploit was intended to be a simple yet effective strategy for playing IPD^2.
Each human participant was matched with each computer strategy twice as group mates, along with different pairs of the other four strategies on the opposing group. Selection was balanced to ensure that each strategy appeared equally as often as partner or opponent. As a result, ten game types were constructed (Table 3). For example, the human participant is paired with Seek-power twice as group mates. One time, their opposing group is composed of Exploit and Always-cooperate (Game type 1), and the other time their opposing group is composed of Always-defect and Tit-for-tat (Game type 8). A Latin square design was used to counterbalance the order of game types. Thus, all participants played 10 games, with each participant being assigned to one of ten ordering conditions as determined by the Latin square design. Each game was played for 50 rounds, thus each participant played a total of 500 rounds.
4.3. Materials
The study was run in the Dynamic Decision Making Laboratory at Carnegie Mellon University. The task software4 was developed in-house using Allegro Common LISP and the last version of the ACT-R architecture [27]. The task software was used for both running human participants and the ACT-R model. ACT-R, however, is not necessarily needed for the implementation of the IPD^2 game involving human participants.
4.4. Procedure
Each participant gave signed and informed consent, and received detailed instructions on the structure of the IPD^2 game. The instructions explained the two groups, how the groups were composed of two players, what choices players have, how power and payoff are updated, and how many games would be played. No information was conveyed regarding the identity of the other players and no information was given regarding the strategies the other players used. Participants were asked to try to maximize their payoffs. After receiving the instructions, each human participant played a practice game followed by the ten game types. The practice game had Always-Defect as the group mate for the human and Always-Cooperate and Tit-For-Tat as the opposing group. The participants were not told the number of rounds per game in order to create a situation that approximates the theoretical infinitely repeated games in which participants cannot apply any backward reasoning.
5. Human and Model Results
We present the results at two levels: the player level and the game level. At the player level, we analyze the main variables that characterize the average player's behavior: payoff, power, and choice. At the game level, we analyze reciprocity, equilibria, and repetition propensities. In addition, we will discuss the variability of results across game types and participants.
We compare the human data to the data from model simulations. The model was run in the role of the human against the same set of opponents following the same design as in the laboratory study (see Table 3). The model was used to simulate 80 participants in order to obtain estimates within the same range of accuracy as in the human data (68 participants). Each simulated participant was run through the same set of ten games of 50 rounds each in the order determined by the Latin square design.
5.1. Player Level Analyses
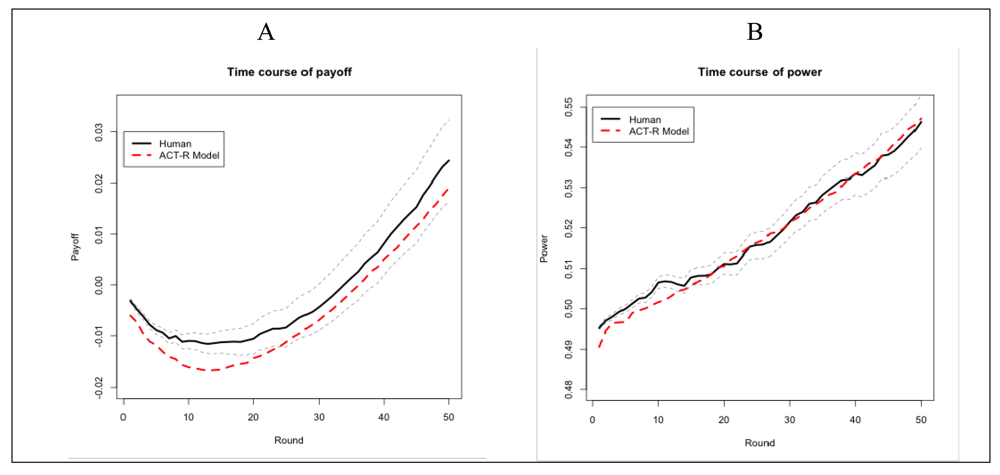
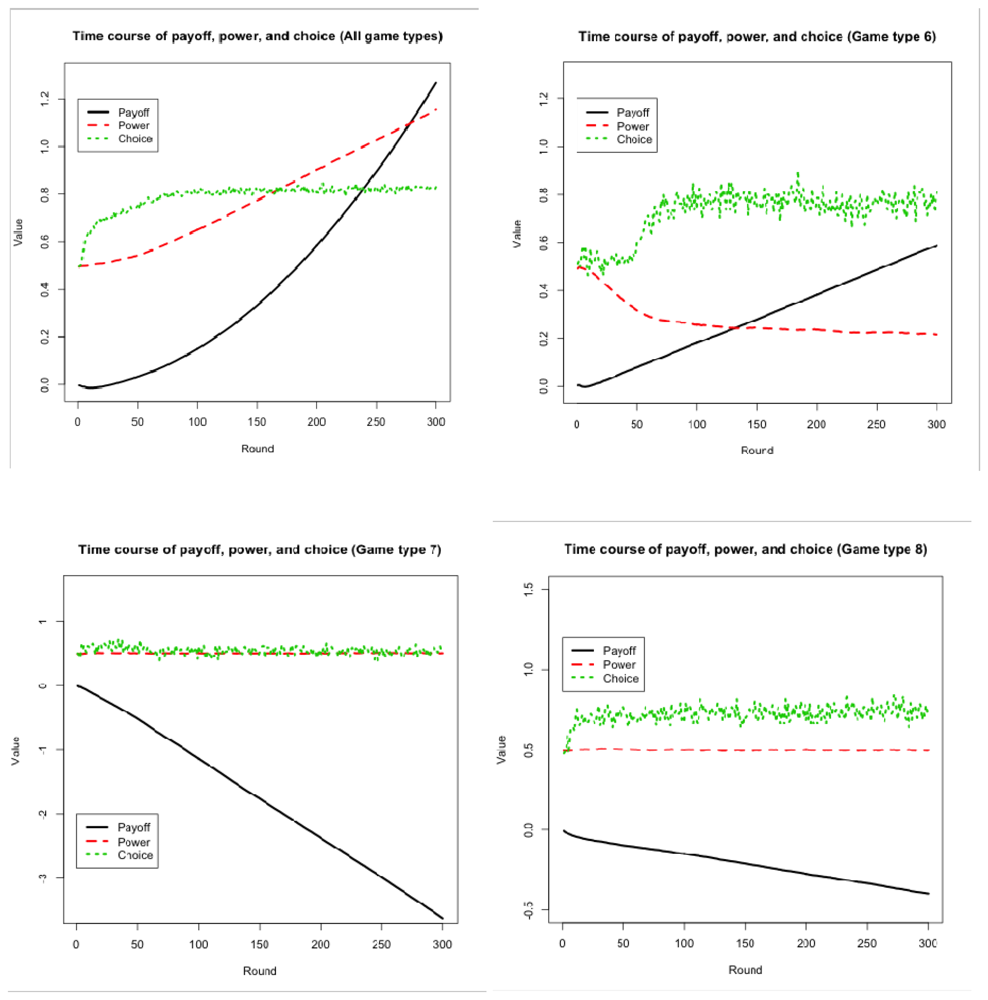
The human participants were able to learn the game and perform adaptively: on average they managed to achieve positive payoff by the end of the game (Figure 3A). Note that the learning curve is different than the typical learning curve where a steep increase in performance is followed by a plateau [1]. The learning curve found here starts with a decline and ends with a steep increase in the second half of the game. The learning curve of the model is a similar shape. At the beginning of the game, the model and presumably the human participants do not have enough instances in memory to identify and carry out a profitable course of action and thus engage in exploratory behavior. Similar behavior was observed in models of Paper-Rock-Scissors [23,28]. As the game progresses, more instances are accumulated, the effective ones become more active, and the ineffective ones are gradually forgotten. In addition, individual payoff depends on the synchronization of multiple players (achieving stable outcomes) in this task, which takes time. For instance, the stability of the mutual cooperation outcome depends on the two groups having cooperative leaders at the same time. In other words, the shape of the learning curve cannot be solely attributed to a slow-learning human or model, because individual performance depends also on the development of mutual cooperation at the intergroup level (see Annex 2 for model simulations with more than 50 trials).
Both human participants and the model exhibit a relatively linear increase of their power over the course of the game (Figure 3B). Participants were not explicitly told to increase their power. They were only told that being in power was needed to make their choice matter for their group. Similarly, the ACT-R model does not try to optimize power. The power status is only indirectly represented in an instance when the two players in a group make different decisions. In this case, the group choice indicates who is the majority player. With time, the model learns how to play so as to maximize payoff in both positions (minority and majority). Thus, the increase in power throughout the game that was observed in our study and simulation can be explained based on the impact that payoff has on power: good decisions lead to positive payoffs that lead to positive increments in power. This is not to say that power and payoff are confounded. Their correlation is significantly positive (r = 0.36, p < 0.05), reflecting the interdependence between power and payoff. However, the magnitude of this correlation is obviously not very high, reflecting the cases in which being in majority does not necessarily lead to gains in payoff (e.g., when faced with defecting partners) and also certain accumulation of payoff is possible when the player is in minority (e.g., when faced with cooperating partners).
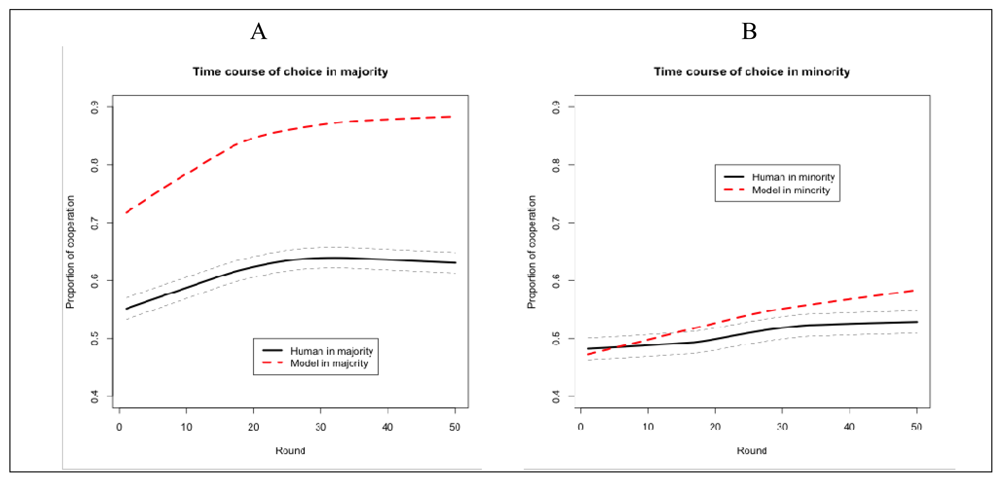
The human participants chose to cooperate more often than to defect: of all actions, 55% are cooperation and 45% are defection. In addition, the human participants tend to cooperate more when they are in majority (60%) than in minority (49%). The proportion of cooperation increased as they progress through the game, particularly in majority (Figure 4A). The model shows the same pattern of increasing cooperation when in majority, except that the amount of cooperation is much greater (Figure 4A). In minority (Figure 4B), both the human and the model show lower levels of cooperation than in majority. In addition, the model shows increasing cooperation as it progresses through the game.
Why does the model cooperate more when in majority than when in minority? We looked at the model simulation data and counted the number of times the model received positive versus negative feedback (payoff). As we explained in Section 3, when the model receives positive payoff, it reinforces the action that caused the positive payoff. When it receives negative payoff, it reinforces both the action that caused the negative payoff and its opposite action. For example, if the model cooperates in a particular situation and receives a negative payoff, it reinforces both cooperation and defection. When the model encounters the same situation later, either action is likely to be retrieved. Thus, the model has a chance to choose the action that will lead to positive payoff. If this chance materializes and the model does receive positive payoff, only the choice that caused positive payoff will be reinforced. In time, the choice that leads to negative payoff in a given situation tends to be forgotten. Figure 5A shows that the model receives positive feedback (payoff) more frequently when in majority and negative feedback more frequently when in minority. As a consequence, when in majority, the model will tend to reinforce a particular action (in this case cooperation), whereas when in minority the model will tend to create and reinforce alternatives for each action in a given situation. The human participants (Figure 5B) also receive positive feedback more frequently when in majority and negative feedback more frequently when in minority. When in majority, they would be able to engage in mutual cooperation “agreements” with the opposite group that generate positive payoffs. These positive payoffs will encourage them to continue cooperating. When in minority, they would not be able to enact inter-group mutual cooperation and will try out both options (cooperation and defection). Notice that the correspondence between model and humans is not perfect. Humans receive negative feedback in minority more frequently than the model, and the model receives positive feedback more frequently when in majority than the humans.
5.2. Game Level Analyses
The amount of mutual cooperation that was achieved in the IPD^2 game was higher than in other variants of the Repeated Prisoner's Dilemma game. Figure 6A shows the time course of the four possible outcomes of the Intergroup Prisoner's Dilemma game that is embedded in IPD^2 for human participants. After approximately 15 rounds, the amount of mutual cooperation (CC) starts to exceed the amount of mutual defection (DD). The asymmetric outcomes (CD and DC) tend to have lower and decreasing levels (they overlap in Figure 6A). The same trend has been reported in the classical Repeated Prisoner's Dilemma [3]. This trend can be described as convergence toward mutual cooperation (CC) and away from mutual defection (DD) and asymmetric outcomes. In Rapoport et al. [3], however, this convergence is much slower: the amount of mutual cooperation starts to exceed the amount of mutual defection only after approximately 100 rounds in the game.
As shown in Figure 6B, the time course of the four possible outcomes for the model simulation follows similar trends as in the human data. However, as shown at the player level (section 5.1), the model cooperates more than human participants. This additional cooperation is sometimes unreciprocated by the model's opponents (the CD outcome in Figure 6B), and other times it is reciprocated (CC). Although the model does not precisely fit the human data, the results of the simulation are informative. The model's sustained cooperation, even when unreciprocated by the model's opponents, is effective at raising the level of mutual cooperation in the game. This strategy of signaling willingness to cooperate even when cooperation is unreciprocated has been called “teaching by example” [3] and “strategic teaching” [6].
We claim that IPD^2 converges toward mutual cooperation and away from mutual defection due to the intragroup power dynamics. To test this claim we created a variant of IPD^2 in which the intragroup power game was replaced by a dictator game. In this variant, one of the players in each group is designated as the dictator and keeps this status throughout a game. A dictator gets all the power and consequently makes all the decisions for the group. Thus, this variant effectively suppresses the central feature of IPD^2 (i.e., the intragroup competition for power) while keeping everything else identical. It would correspond to a Prisoner's Dilemma game between two dictatorships. Although we do not have human data for this variant, we can use the cognitive model to simulate the outcomes of the game. As shown in Figure 6C, the level of mutual cooperation was much lower in the dictatorship variant than in the original IPD^2 game, proving that it was indeed the intragroup competition for power that determined convergence toward mutual cooperation and away from mutual defection in IPD^2.
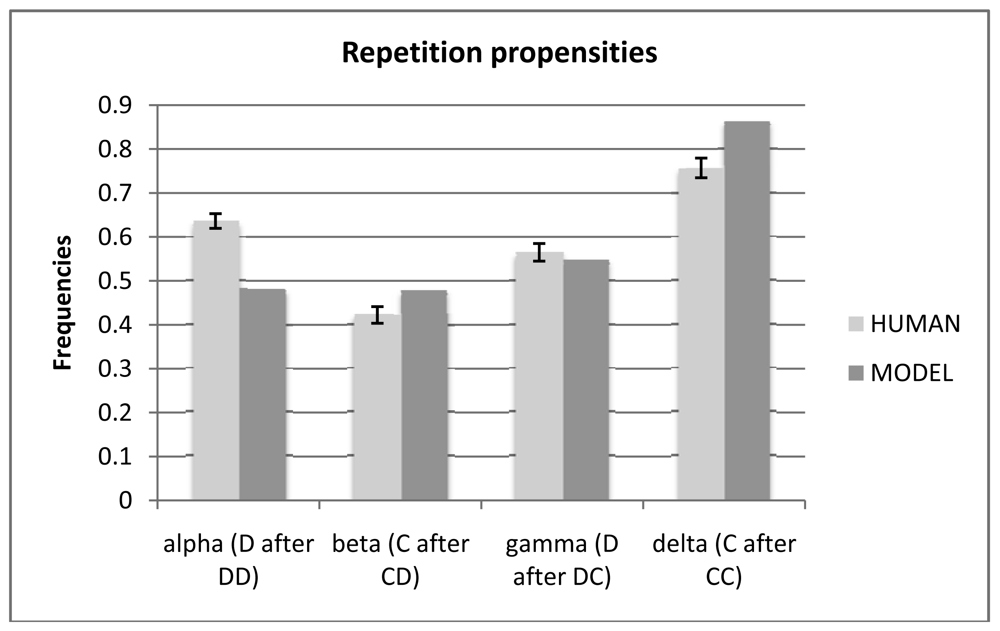
Rapoport et al. [3] defined a set of four repetition propensities in the Repeated Prisoner's Dilemma. They are referred to as alpha, beta, gamma, and delta, and are defined by Rapoport et al. [3] as follows:
Alpha refers to playing D after DD and denotes unwillingness to shift away from mutual defection because unilateral shifting reduces payoff.
Beta refers to playing C after CD, or repeating an unreciprocated call for cooperation, denotes forgiveness or teaching by example.
Gamma refers to playing D after DC, or repeating a lucrative defection, denotes a tendency to exploit the opponent.
Delta refers to playing C after CC, denotes resistance to the temptation to shift away in pursuit of the largest payoff.
Figure 7 shows the repetition propensities of humans as compared with the model. With regard to the human data, the relative differences between the four propensities are consistent with the literature [3]. Thus, the relatively higher frequencies of alpha and delta reflect the known tendency of the symmetrical outcomes (CC and DD) to be more stable than the asymmetrical ones (CD and DC). The difference between Beta and Gamma reflects the tendency of the human participants to punish the non-reciprocators (lower beta) and exploit the opponent (higher gamma). More interesting here are the differences between the model and the human participants. The model is much more apt than human participants to shift away from mutual defection (lower alpha) (t = 7.76, p = 0.000) and to persist in the mutually cooperating outcome (higher delta) (t = −3.99, p = 0.000). In addition, the model “teaches by example” (plays C after CD) more often than human participants (higher beta) (t = −2.63, p = 0.009). The difference in Gamma is non-significant.
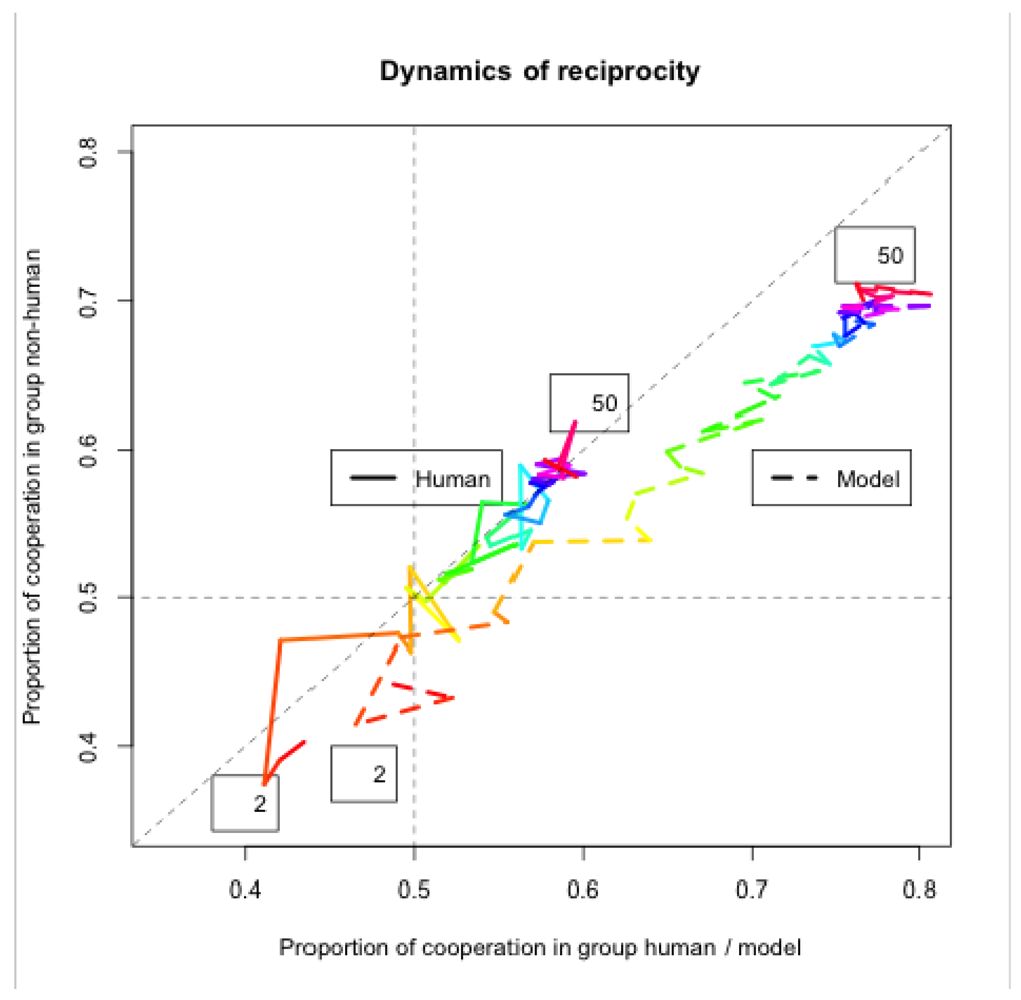
Figure 8 shows the dynamics of reciprocity between the two groups playing the IPD^2 game. The amount of cooperation in the group including the human participant (or the model) is represented on the X-axis. The amount of cooperation in the opposing group (comprised of two computer strategies; is represented on the Y-axis. The horizontal and vertical dashed lines mark an equal amount of cooperation and defection in each group (i.e., proportion of cooperation = 0.5). The diagonal dashed line is the reciprocity line where the two groups have equal proportions of cooperation. The color code marks the progression of a game. Red denotes the start (round 2, marked with number 2) and purple the end (round 50, marked with number 50) of the game, with the other colors following the rainbow order (the black-and-white printout shows nuances of gray instead of colors). The first round is dropped because it does not represent reciprocity (the first moves of the players are either random or set a priori by the experimenter). The group including a human participant achieves perfect reciprocity with the opposing group (on average), i.e. they do not exhibit a bias to “teach by example” by sustained (unreciprocated) cooperation, nor to “exploit the opponent” by repeated defection when the opposing group cooperates. In contrast, the model systematically departs from the reciprocity line (the diagonal in Figure 8) in the direction of “teaching by example.” This bias of the model brings about a higher level of cooperation in the opposing group as well (by about 10%). Notice that the changes in direction (switches from C to D and vice versa) are more radical at the beginning of the game (about 10 rounds) than toward the end of the game, when most of the games settle in mutual cooperation. The model tends to achieve mutual cooperation faster than humans, and it sustains it for a longer time.
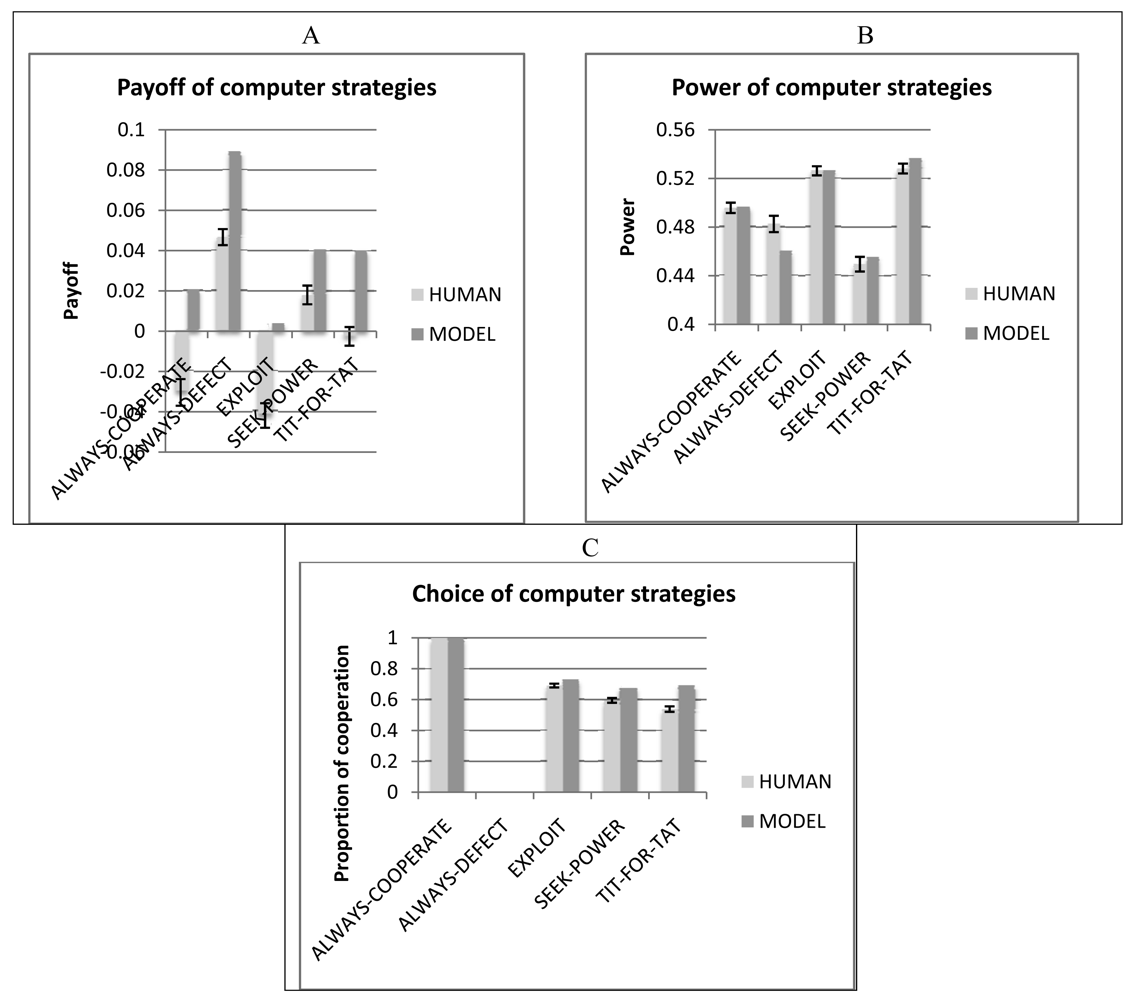
How do humans and the model impact the behavior of other players in the game (computer strategies)? Figure 9 shows the results of the five computer strategies when playing against human players as compared to when they play against the cognitive model. When playing against human participants, the computer strategies achieve lower levels of payoff (Figure 9A) and lower levels of cooperation (Figure 9C) than when they play against the cognitive model, likely due to the lower levels of mutual cooperation. With regard to power, there are small and inconclusive differences between the two cases. Although humans and the cognitive model achieve comparable levels of payoff (see Figure 3A), they have a differential impact on the other strategies: the human makes them weaker or the model makes them stronger, or both. This result suggests that there are important aspects of human behavior in IPD^2 that are not satisfactorily explained by the current version of our cognitive model.
5.3. Variability across Game Types and Individual Participants
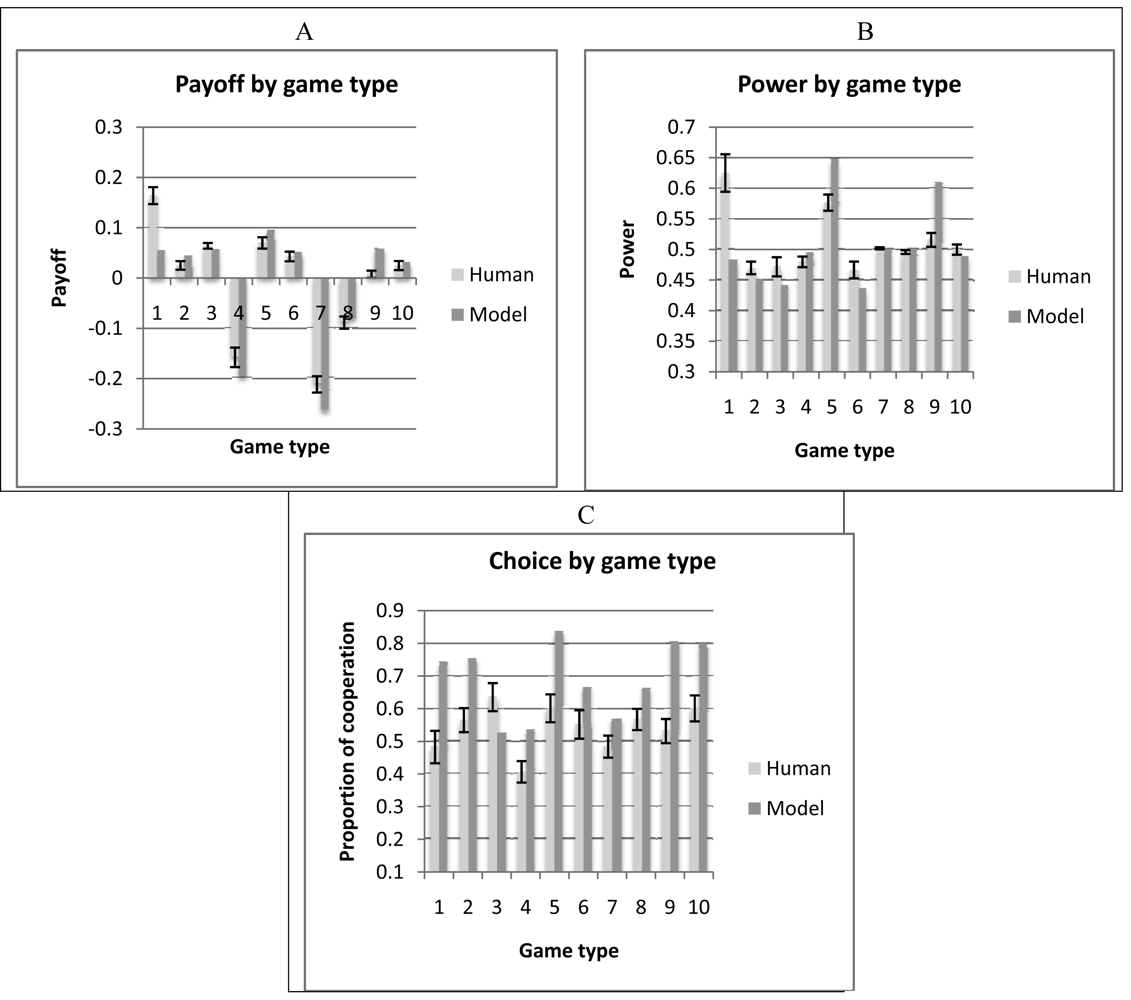
So far, we have presented the results aggregated across all game types. However, there is significant variability between game types with regard to human behavior and game outcomes. This variability reflects the differences between the computer strategies that are included in each game type. There is also variability across individual participants.
Figure 10 shows the values of payoff (10A), power (10B), and choice (10C) for each game type for the human participants and the corresponding model simulations. The numbers in the X-axis correspond to the types of game shown in Table 3. The standard errors of the mean are also plotted for the human data to suggest the range of variation across human participants. One can see that variability across game types greatly exceeds variability across human participants. This shows that an important determinant of human behavior in IPD^2 is the composition of the groups in terms of the players' strategies. The model seems to capture the relative differences between game types reasonably well, showing a level of adaptability to opponent strategies comparable to that of human participants. However, when looking at each game type in isolation, the model is less accurate in matching the human data. In addition, as for the aggregate data previously presented, the model matches the human data on payoff and power better than on choice, suggesting that there are aspects of human behavior in this game that are not captured by this simple model. We will discuss some limitations of the model in the following sections.
5.4. Discussion of Model Fit and Predictive Power
As mentioned in Section 3.2, our cognitive model of IPD^2 leaves the parameters of the ACT-R architecture at their default values. However, one could ask whether changes in the values of the key parameters would result in different predictions. We tested for this possibility and came to the conclusion that parameters have very little influence on the model outcomes/predictions. Table 4 shows a comparison between model predictions and human data with regard to payoff across game types (see also Figure 10A). A space of two parameters was considered, memory decay rate (d) and activation noise (s). Three values were considered for each parameter: one is the ACT-R default value, one is significantly lower, and another one is significantly higher than the default value. The cells show correlations and root mean squared deviations between the model predictions and the human data for each combination of the two parameters: these values do not significantly differ from one another. Two factors contributed to this low sensitivity of the model to parameter variation: (1) The IPD^2 task is different than other tasks that are used in decision making experiments and IBLT models. Since IPD^2 is a 4-player game, the number of unique situations and sequential dependencies is rather large. The length of a game (50 rounds) allows for very few repetitions of a given situation, thus leaving very little room for parameters controlling memory activation and decay to have an impact on performance. (2) The IPD^2 model learns from feedback (payoff) in an all-or-none fashion: it is not sensitive to the real value of payoff but only to its valence (see also the diagram of the model in Figure 1. We have attempted to build models that take the real value of payoff into account and, while these models achieve better performance in IPD^2, they are not as good at fitting the human data as the simple model described in this paper.
To assess the value of a particular model one needs to consider alternative models. Since IPD^2 is a new game, there are no alternative models proposed by independent researchers. We do expect such models to be available in the near future and in the meantime are exploring alternative models ourselves. A first version of a simple reinforcement learning (RL) model looks promising but it is not as good as the IBLT model described above. The RL model of IPD^2 (also implemented in ACT-R) chooses between two actions (C and D) implemented as production rules based on their expected utilities computed by the associated architectural mechanisms. Observed utilities (payoffs) are propagated back to the previous actions (with a temporal discount) and cause adjustments of the expected utilities. As shown in Figure 11, the RL model has a good fit to the payoff data and a poor fit to the power and choice data. Particularly, the model defects more often than the humans. This result could be explained by the fact that the RL model is only aware of its own choices and their associated rewards and it does not differentiate between various situations in the game such as who the majority player is in each group, and what decisions the other players take. We do acknowledge that more sophisticated RL models might be able to fit the data better than the current one, and we are currently exploring such models.
6. General Discussion and Conclusion
We have introduced IPD^2—a new game paradigm to study the impact of intragroup power on intergroup conflict and cooperation. We argue that IPD^2 offers a richer opportunity than the classical Repeated Prisoner's Dilemma for modeling real-world situations in which intra- and inter-group interactions are entangled [7]. IPD^2 complements other approaches that focus on the intra- and inter-group interactions [8-10] by the addition of an intragroup power variable. In the standard Repeated Prisoner's Dilemma, the outcome of mutual defection is self-reinforcing although it can be overcome if the game is played for long and indefinite periods. In IPD^2, mutual defection causes changes in the power structure of the two groups, thus creating the chance to break free from that pattern and possibly evolve toward mutual cooperation. Due to its intragroup power dynamics, IPD^2 predicts that indefinitely repeated interaction leads to a relatively high level of mutual cooperation while maintaining unilateral and mutual defection at relatively lower levels. This is analogous to the political sphere where there is competition for power. In such a setting, leaders who bring negative outcomes to their groups can only maintain their position of power for a limited time. IPD^2 has the potential to model various real-world scenarios. For example, Leopold II, a Belgian king in the late 19th century, behaved very differently toward his Belgian people than toward the Congolese people. He was an enlightened ruler in Belgium because his hold on power could be undermined by popular sentiment, whereas he behaved like a dictator in Congo because the locals had no way of affecting his power over them. To represent the case in which despots can eliminate their opposition, we have replaced the intragroup power game by a dictator game.
In our study, we find that human participants cooperate more and the level of n IPD^2 than in the classical Repeated Prisoner's Dilemma game. This is merely a preliminary trend and prediction for the human-human interactions for which we do not yet have data. This prediction is at odds with what is known in the literature as the “interindividual-intergroup discontinuity” effect (IID), which describes groups to be less cooperative than individuals [29]. In fact, we predict a reversal of this effect: two groups achieve more mutual cooperation in IPD^2 than do two individuals in the Repeated Prisoner's Dilemma. Wildschut et al. [29] predicted that a reverse IID effect was possible, although there was no study at that time to show it. We have suggestive evidence that the reverse IID effect in IPD^2 is caused by the addition of an intragroup power variable. The two groups cannot sustain mutual defection for long because mutual defection causes internal shifts in power. Individuals can maintain majority positions in their groups only when they consistently bring about positive outcomes for their groups. In other words, power instantiates an objective sense of payoff. Groups are able to sense gain or loss based on how these outcomes impact the group's power structure (gain consolidates and loss undermines power). As such, intragroup power dynamics could be seen as an institutional loss-aversion mechanism, because they prevent the groups from tolerating negative payoffs. This result contributes to the corroboration of the conjecture that democracy reduces the risk of wars. When we suppressed the intragroup power competition (i.e., created dictatorships) the groups were less likely to engage in mutual cooperation (i.e., build peace) and the probability of mutual defection (i.e., risk of war) remained high.
The pattern of cooperation in IPD^2 oscillates around the line of perfect reciprocity (Figure 8). This result corroborates what has been found in other studies regarding the human tendency to reciprocate. The human brain is specialized at detecting and discriminating against non-reciprocators. Negative emotions triggered by unreciprocated attempts at cooperation bias subsequent decision-making toward defection [30]. In our study, human participants tend to stay on the line of perfect reciprocity (on average); they do not “walk the extra mile” that would increase the overall mutual cooperation in the game. Most likely, they fear that their attempts at cooperation will not be reciprocated. In contrast, the ACT-R model does not capture this fear, which allows it to continue cooperating even when its cooperation is temporarily unreciprocated. As a consequence of this sustained cooperation, the model causes the level of mutual cooperation in the game to increase. This is also merely a prediction of our model, because we do not yet have humans at the other end of the interaction.
We have shown that simple cognitive mechanisms can explain a range of behavioral effects in IPD^2. These cognitive mechanisms were not designed specifically for this task. They are part of the ACT-R architecture and have been validated in many tasks that are unrelated to game playing. The default parameters of ACT-R that were used for the current model (and the model of Prisoner's dilemma that served as a starting point of the current model [2]) are used in most ACT-R models of various effects from the psychological literature. In addition, there is already a tradition of using ACT-R to model various game theoretic phenomena [2,23,28,31,32] including cases in which humans play against artificial opponents [23,24,28,33].
We used the model to try to understand what humans do, and we used the human data to test the assumptions of the model. For example, the model showed lower cooperation in minority, mimicking the same trend in human data. The model shows this effect because it increases the activation of the alternative option after receiving negative feedback (if C caused the negative feedback, then D is also activated, and vice versa). This could be an explanation for why participants cooperated less when in minority: they receive more negative feedback (see Figure 5B), and this might make them more tempted to explore alternative actions. In this case, the model informed the human data, because it generated a hypothesis about human behavior. An alternative hypothesis for this effect would be that minority players perceive their likelihood of winning as low and become less constructive [34]. In turn, the human data was used to test the model's assumptions. For example, the human data departed significantly from the predictions of the model regarding the amount of cooperation: the model predicted higher levels of cooperation than observed (Figures 4 and 6); in addition, the model shows lower alpha (D after DD) and higher beta (C after CD) repetition propensities than the human participants (Figure 7). These results are most likely caused by the fact that the model does not have emotional reactivity that would bias its decision making processes. We are currently exploring ways to improve the model's fit to the human data by adding an emotional component to the existing cognitive mechanisms of ACT-R. Some of the differences between the model simulations and the human data could be caused by social and cultural factors. This hypothesis can also be tested in future studies by varying such factors and observing the impact on power, payoff, and proportion of cooperation. If such biases exist, they could be added to our model.
Our cognitive modeling approach could complement the traditional equilibrium analyses in predicting the effect of game modifications. In repeated games, almost any outcome can be an equilibrium. Game simulations with validated cognitive models as players could be used to narrow down the set of possible equilibria to a limited number of cognitively plausible outcomes and, subsequently, generate specific predictions about human behavior in these games.
Based on its potential to represent many realistic aspects of social interaction, IPD^2 is an especially useful paradigm for studying human behavior in conflict situations. This paradigm complements the standard interindividual and intergroup Prisoner's Dilemma games by adding a new variable—intragroup power—that simultaneously represents both the ability of a player to bring about outcomes and the impact of those outcomes on the player's status. We have shown that cognitive modeling can be a useful tool for understanding the processes that underlie human behavior in IPD^2.
Evidently, more research within the IPD^2 paradigm is needed, particularly to test human behavior in interactions with other humans and to extend the model to include realistic emotional reactions to conflict. More research is also needed to extend IPD^2 to reflect a wider range of real-world conflict situations.





| Player2 | |||
|---|---|---|---|
| C | D | ||
| Player1 | C | 1,1 | −4,4 |
| D | 4,−4 | −1,−1 | |
| Group | Player | Choice | Power | Group payoff | Player payoff | Payoff total |
|---|---|---|---|---|---|---|
| Group-1 | P1-1 | B | 0.525 | 1 | 0.005 | −0.003 |
| P1-2 | B | 0.475 | 0.005 | −0.007 | ||
| Group-2 | P2-1 | A | 0.265 | 1 | 0.003 | 0.087 |
| Human | B | 0.735 | 0.007 | 0.143 |
| Situation | Own group | Choice own |
| Choice mate | ||
| Choice own group | ||
| Other group | Choice member1 of other group | |
| Choice member2 of other group | ||
| Choice other group | ||
| Decision | Next choice own | |
| Game type | Group-1 | Group-2 |
|---|---|---|
| 1 | Seek-Power HUMAN | Exploit Always-Cooperate |
| 2 | Tit-For-Tat Always-Cooperate | Exploit HUMAN |
| 3 | Always-Cooperate HUMAN | Seek-Power Tit-For-Tat |
| 4 | Exploit Always-Defect | HUMAN Always-Cooperate |
| 5 | Always-Cooperate Seek-Power | Always-Defect HUMAN |
| 6 | HUMAN Tit-For-Tat | Always-Cooperate Always-Defect |
| 7 | HUMAN Exploit | Always-Defect Seek-Power |
| 8 | Always-Defect Tit-For-Tat | HUMAN Seek-Power |
| 9 | HUMAN Always-Defect | Tit-For-Tat Exploit |
| 10 | Seek-Power Exploit | Tit-For-Tat HUMAN |
| d\s | 0.1 | 0.25 | 0.4 |
|---|---|---|---|
| 0.7 | 0.95 (0.037) | 0.95 (0.035) | 0.94 (0.04) |
| 0.5 | 0.93 (0.042) | 0.95 (0.035) | 0.94 (0.038) |
| 0.3 | 0.89 (0.05) | 0.94 (0.036) | 0.95 (0.035) |
| Field of study | Number of participants |
|---|---|
| Biology | 4 |
| Business | 1 |
| Chemical Engineering | 2 |
| Computer Science | 8 |
| Decision Science | 1 |
| Design | 5 |
| Economics | 2 |
| Education | 2 |
| English | 2 |
| Finance | 2 |
| History | 2 |
| Information systems | 4 |
| International Relations | 1 |
| Languages | 2 |
| Marketing | 1 |
| Mathematics | 1 |
| Mechanical Engineering | 7 |
| Neuroscience | 1 |
| Nursing | 1 |
| Occupational Therapy | 1 |
| Paralegal | 2 |
| Philosophy | 1 |
| Piano performance | 1 |
| Political science | 1 |
| Psychology | 1 |
| Public Policy & Management | 2 |
| Religious Studies | 1 |
| Sociology | 1 |
| Transportation Engineering | 1 |
| Non answer | 7 |
Acknowledgments
This research is supported by the Defense Threat Reduction Agency (DTRA) grant number: HDTRA1-09-1-0053 to Cleotilde Gonzalez and Christian Lebiere. The authors would like to thank Hau-yu Wong (Dynamic Decision Making Lab) for help with data collection and proofreading. We also thank the editor and two anonymous reviewers for helpful comments on a prior version of this paper.
References
- Erev, I.; Roth, A.E. Predicting how people play games: Reinforcement learning in experimental games with unique, mixed strategy equilibria. Am. Econ. Rev. 1998, 88, 848–881. [Google Scholar]
- Lebiere, C.; Wallach, D.; West, R.L. A Memory-Based Account of the Prisoner's Dilemma and Other 2 × 2 Games, Proceedings of the 3rd International Conference on Cognitive Modeling, Groningen, Netherlands, March 2000; pp. 185–193.
- Rapoport, A.; Guyer, M.J.; Gordon, D.G. The 2 × 2 Game; The University of Michigan Press: Ann Arbor, MI, USA, 1976. [Google Scholar]
- Anderson, J.R.; Lebiere, C. The Atomic Components of Thought; Erlbaum: Mahwah, NJ, USA, 1998. [Google Scholar]
- Rapoport, A. Game Theory as a Theory of Conflict Resolution; D. Reidel Publishing Company: Boston, MA, USA, 1974. [Google Scholar]
- Camerer, C.F. Behavioral Game Theory: Experiments in Strategic Interaction; Princeton University Press: Princeton, NJ, USA, 2003. [Google Scholar]
- Putnam, R.D. Diplomacy and domestic politics: The logic of two-level games. Int. Organ. 1988, 42, 427–460. [Google Scholar]
- Bornstein, G. The free rider problem in intergroup conflicts over step-level and continuous public goods. J. Pers. Soc. Psychol. 1992, 62, 597–606. [Google Scholar]
- Bornstein, G. Intergroup conflict: Individual, group and collective interests. Pers. Soc. Psychol. Rev. 2003, 7, 129–145. [Google Scholar]
- Halevy, N.; Bornstein, G.; Sagiv, L. “In-group love” and “out-group hate” as motives for individual participation in intergroup conflict. Psychol. Sci. 2008, 19, 405–411. [Google Scholar]
- Emerson, R.M. Power-dependence relations. Am. Sociol. Rev. 1962, 27, 31–41. [Google Scholar]
- Levin, S.; Sidanius, J.; Rabinowitz, J.L.; Federico, C. Ethnic Identity, Legitimizing ideologies, and social status: A matter of ideological asymmetry. Polit. Psychol. 1998, 19, 373–404. [Google Scholar]
- Morrison, K.R.; Fast, N.J.; Ybarra, O. Group status, perceptions of threat, and support for social inequality. J. Exp. Soi. Psychol. 2009, 45, 204–210. [Google Scholar]
- Morrison, K.R.; Ybarra, O. The effects of realistic threat and group identification on social dominance orientation. J. Exp. Soc. Psychol. 2008, 44, 156–163. [Google Scholar]
- Jost, J.T.; Banaji, M.R.; Nosek, B.A. A decade of system justification theory: Accumulated evidence of conscious and unconscious bolstering of the status quo. Polit. Psychol. 2004, 25, 881–919. [Google Scholar]
- Rabinowitz, J.L. Go with the flow or fight the power? The interactive effects of social dominance orientation and perceived injustice on support for the status quo. Polit. Psychol. 1999, 20, 1–24. [Google Scholar]
- Langner, C.A.; Keltner, D. Social power and emotional experience: Actor and partner effects within dyadic interactions. J. Exp. Soc. Psychol. 2008, 44, 848–856. [Google Scholar]
- Dowding, K. Power (Concepts in Social Thought); University of Minnesota Press: Minneapolis, MN, USA, 1996. [Google Scholar]
- Simon, H.A. Rational choice and the structure of the environment. Psychol. Rev. 1956, 63, 129–138. [Google Scholar]
- Rapoport, A.; Chammah, A.M. Prisoner's Dilemma; University of Michigan Press: Ann Arbor, MI, USA, 1965. [Google Scholar]
- Erev, I.; Ert, E.; Roth, A.E. A choice prediction competition for market entry games: An introduction. Games 2010, 1, 117–136. [Google Scholar]
- Gonzalez, C.; Lerch, J.F.; Lebiere, C. Instance-based learning in dynamic decision making. Cogn. Sci. 2003, 27, 591–635. [Google Scholar]
- West, R.L.; Lebiere, C. Simple games as dynamic, coupled systems: Randomness and other emergent properties. Cogn. Syst. Res. 2001, 1, 221–239. [Google Scholar]
- Baker, F.; Rachlin, H. Teaching and learning in a probabilistic Prisoner's Dilemma. Behav. Process. 2002, 57, 211–226. [Google Scholar]
- Alexrod, R. The Evolution of Cooperation; Basic Books: New York, NY, USA, 1984. [Google Scholar]
- Nowak, M.; Sigmund, K. A Strategy of Win-Stay, Lose-Shift that Outperforms Tit-for-Tat in the Prisoner's Dilemma Game. Nature 1993, 364, 56–58. [Google Scholar]
- Anderson, J.R. How Can the Human Mind Occur in the Physical Universe? Oxford University Press: New York, NY, USA, 2007. [Google Scholar]
- Lebiere, C.; West, R.L. A dynamic ACT-R model of simple games. Proceedings of the 21st Annual Meeting of the Cognitive Science Society, Vancouver, Canada, 1999; Available online at: http://act-r.psy.cmu.edu/papers/240/SDOC2298.pdf (accessed on 6 February 2011).
- Wildschut, T.; Pinter, B.; Vevea, J.L.; Insko, C.A.; Schopler, J. Beyond the group mind: A quantitative review of the interindividual-intergroup discontinuity effect. Psychol. Bull. 2003, 129, 698–722. [Google Scholar]
- Rilling, J.K.; Goldsmith, D.R.; Glenn, A.L.; Jairam, M.R.; Elfenbein, H.A.; Dagenais, J.E.; et al. The neural correlates of the affective response to unreciprocated cooperation. Neuropsychologia 2008, 46, 1256–1266. [Google Scholar]
- West, R.L.; Stewart, T.; Lebiere, C.; Chandrasekharan, S. Stochastic resonance in human cognition: ACT-R versus game theory, associative neural networks, recursive neural networks, q-learning, and humans. Proceedings of the 27th Annual Meeting of the Cognitive Science Society, Vancouver, Canada, July 2006; Available online: http://csjarchive.cogsci.rpi.edu/Proceedings/2005/docs/p2353.pdf (accessed on 6 February 2011).
- Lebiere, C.; Gray, R.; Salvucci, D.; West, R.L. Choice and learning under uncertainty: A case study in baseball batting. Proceedings of the 25th Annual Meeting of the Cognitive Science Society, Boston, USA, July 2003; Available online: http://csjarchive.cogsci.rpi.edu/Proceedings/2003/pdfs/142.pdf (accessed on 6 February 2011).
- West, R.L.; Lebiere, C.; Bothell, D.J. Cognitive architectures, game playing, and human evolution. In Cognitive Modeling and Multi-Agent Interactions; Sun, R., Ed.; Cambridge University Press: Cambridge, UK, 2006. [Google Scholar]
- Kamans, E.; Otten, S.; Gordijn, E.H.; Spears, R. How groups contest depends on group power and the likelihood that power determines victory and defeat. Group Process Intergroup Relat. 2010, 13, 715–724. [Google Scholar]
- 1Adaptive Control of Thought—Rational.
- 2Matching here refers to ACT-R's perfect matching. A model employing partial matching was not satisfactory in terms of performance and fit to the human data.
- 3Storing the real value of payoff in an instance would make the model sensitive to payoff magnitude and improve the performance of the model. However, this decreases the model's fit to the human data.
- 4The task software will be made available for download.
© 2011 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Juvina, I.; Lebiere, C.; Martin, J.M.; Gonzalez, C. Intergroup Prisoner’s Dilemma with Intragroup Power Dynamics. Games 2011, 2, 21-51. https://doi.org/10.3390/g2010021
Juvina I, Lebiere C, Martin JM, Gonzalez C. Intergroup Prisoner’s Dilemma with Intragroup Power Dynamics. Games. 2011; 2(1):21-51. https://doi.org/10.3390/g2010021
Chicago/Turabian StyleJuvina, Ion, Christian Lebiere, Jolie M. Martin, and Cleotilde Gonzalez. 2011. "Intergroup Prisoner’s Dilemma with Intragroup Power Dynamics" Games 2, no. 1: 21-51. https://doi.org/10.3390/g2010021





