Cycles of Conditional Cooperation in a Real-Time Voluntary Contribution Mechanism
Abstract
: This paper provides a new way to identify conditional cooperation in a real-time version of the standard voluntary contribution mechanism. We define contribution cycles as the number of contributors a player waits for before committing to a further contribution, and use a permutation test on contribution cycles to assign a measure of conditional cooperation to each group play. The validity of the measures is tested in an experiment. We find that roughly 20% of the plays exhibit dynamics of conditional cooperation. Moreover, notwithstanding a decline in contributions, conditional cooperation is found to be stable over time.1. Introduction
It is a well-established stylized fact that individuals contribute voluntarily to public goods even when material self-interest would make free-riding the individually best option. One of the most widely accepted explanations for this fact is the existence of “conditional cooperators”, i.e., individuals who have a taste for reciprocity and are therefore more willing to contribute when others also contribute or are expected to do so.1 Evidence of conditional cooperation has been found both in controlled laboratory experiments (see, e.g., [1,5–12]) and outside the laboratory (e.g., [2,13]).
Contributions to public goods are often made over long periods of time with information spill-overs.2 This structure allows for different manifestations of conditional cooperation than those captured by the existing experimental paradigms. To study conditional cooperation in this context, we consider a real-time version of the voluntary contribution mechanism (henceforth VCM), in which the players contribute incrementally to the public good and can respond dynamically to changes in the other players' contributions [14]. We introduce new measures of conditional cooperation, which allow us to study conditionally cooperative strategies in this dynamic setting. In the following, we first briefly describe the existing paradigms used to study conditional cooperation and then we introduce the new method.
Several papers have studied conditional cooperation by eliciting beliefs about others' contributions and then testing whether beliefs vary positively with one's own contributions [2,5,13,15]. A positive correlation between beliefs and choices is interpreted as conveying a willingness to contribute that increases with the others' expected contributions. However, this correlation does not necessarily arise from a causal relationship. For example, a simple alternative explanation is the (false) consensus effect [16,17]. In the presence of this effect, individuals are likely to use the knowledge of their own choice to predict the choices of others [18]. Hence a positive correlation between beliefs and choices is to be expected regardless of conditional cooperation.
Fischbacher et al. [1] introduced a further paradigm in which participants have to indicate how much they are willing to contribute for each possible value of the others' average contributions. Those who submit a ‘contribution schedule’ that is monotonically increasing with the others' average contribution are categorized as conditional cooperators. An approach similar to that of Fischbacher et al. was used by Kurzban and Houser [9], who allowed for repeated revisions of contributions, therefore coming closer to studying dynamic contributions. In each revision step, one participant could revise her contribution after having been informed about the group's current aggregate contribution. The number of revision steps was randomly determined and unknown to the participants. It is worth noting that, although it solves the problem of the correlational approach, Fischbacher et al.'s procedure and its iterated variant are somewhat susceptible to demand effects because the subject is explicitly asked to indicate how much he would contribute for each possible average contribution of the others.
The method we introduce in this paper allows subjects to implement conditional strategies in a dynamic and transparent way, using actual information about others' contributions. Conditional cooperation is then directly measured through the dynamics of actual play. We analyze the actions in the real-time version of the VCM by defining ‘cycles’ of contribution and applying a permutation test [19–21] to determine the likelihood of obtaining similar cycles without conditional cooperation. The remainder of the paper is organized as follows. Sections 2 and 3 describe the method and the new measures of conditional cooperation. Section 4 presents the design of an experiment aimed to test and validate our measures. Section 5 discusses the experimental results. Section 6 concludes.
2. The VCM with Real-Time Contributions
In order to be able to investigate the dynamics of conditional cooperation, we rely on a real-time version of the VCM.3 Specifically, let I = {1,…,4} stand for a group of 4 people. Each individual i ∈ I is endowed with income ei which can be either consumed privately or contributed to a public good. Contributions proceed in the following way. During a fixed time interval with duration T (the “round”), each player i can increase her contribution from 0 to anything up to ei in single-unit increments. The player's contribution at the end of the allotted time interval is taken to be her contribution for that round. Denoting the level of i's contribution at time t by ci,t (i ∈ I, 0 ≤ t ≤ T) the monetary payoff of i is given by
The current contribution status is observable by all players and updated in real time.4 Hence, player i's strategy determining the probability of making an increment to ci,t at any time t < T is
This procedure allows potential contributors to wait, observe what the others do, and then determine whether or not to “commit” to a further contribution. Conditionally cooperative individuals are expected to start contributing and then hold off their contribution until they see the others' response.6 More formally, if we construct H′t to be Ht with an additional contribution increment from player j ≠ i, a conditionally cooperative strategy σi,t would assign a higher probability of increasing ci,t to H′t than to Ht.
3. New Measures of Conditional Cooperation
Each round of the game described above results in a final history or contribution vector, in which the value of each coordinate indicates the identity of the player increasing her contribution by one unit.7 This contribution vector reflects the dynamics within the round. To assess conditional cooperation as manifested within the contribution vector, we examine contribution cycles. A contribution cycle is defined as the partial history between consecutive increments of a single player's contribution. Thus, the total number of cycles of player i is
However, we note that the MCL is sensitive to the group contribution levels and therefore to the unconditional probability to contribute. More specifically, the MCL may be higher in the VCM with real-time contributions simply because people tend to contribute more when they are observed, even if the observers' actions are not affected by this monitoring. Previous research has shown that the willingness to contribute increases with high accountability, as decisions are made public after the game [27]. Therefore increased accountability in the form of revealing the contribution process to the other players may, in itself, lead to higher tendency to contribute, and hence to higher MCL.
Furthermore, the MCL can be responsive to heterogeneity in contributions.To see this, consider the following hypothetical contribution vectors:
(1,2,1,2,1,2,1,2,1,2)
(1,1,1,1,1,2,2,2,2,2)
(1,1,2,2,3,1,4,3,1,1,4,4,4,3,3,3,2,2,4,2)
In vectors (a) and (b), players 1 and 2 contribute 5 units each and players 3 and 4 contribute 0, whereas in vector (c) all players contribute 5 units. The MCL is 2, 1, and 2 in vectors (a), (b), and (c), respectively. Vector (a) reflects perfect conditional cooperation between two players, whereas vector (b) reflects minimal conditional cooperation. This is indicated by the higher MCL of vector (a). In fact, 2 is the highest possible MCL given the group contributions in vectors (a) and (b). However, the MCL in vector (c), though identical to that in (a), falls shy of perfect conditional cooperation possible with the contribution profile in (c). Thus, the same mean cycle can reflect different level of conditional cooperation with different levels of heterogeneity in contributions.
To capture this difference as well as to account for the absolute levels of contribution, we develop a second measure of conditional cooperation, which takes into account the various levels of conditional cooperation that are attainable with the observed contribution profile. The new measure is defined as the level of significance derived from a random permutation test of the null hypothesis that the order of contribution increments within the round is random [20,28]. More specifically, we generate a null-hypothesis distribution of mean cycle lengths, based on random permutations of the observed contribution vector, and take the relative position of the observed MCL in this distribution as a measure of conditional cooperation. We refer to this measure as ‘normalized mean cycle length’ (henceforth NMCL).
The hypothesis used to generate the null-hypothesis distribution is that, at any point in time, all players who intend to increase their contributions are equally likely to do so. Thus, having observed contributions by others in the current cycle, or indeed at any time, does not affect the next contribution decision. Only the intended final contribution of the player determines the probability of her being the next to increase her contribution. Specifically, the sequence-generating procedure we use is the following: in each step of the procedure, one of the players in the group is randomly selected (with equal probabilities) to make the next contribution increment, as long as this player's (observed) full contribution is not already accounted for in the contribution sequence. This is repeated until all players have contributed their observed final amounts. Each contribution sequence obtained in such a way reflects one possible history leading to the observed final contribution levels and is in line with the null hypothesis of randomness.9 For each randomly generated contribution sequence we calculate the MCL. The proportion of resulting mean cycle lengths which are shorter than the observed MCL is taken as the measure of conditional cooperation. Thus, if behavior in the game is random, the NMCL should be uniformly distributed over the interval [0, 1]. Conversely, low and high values of the NMCL provide evidence for non-random behavior. Low values indicate that a contribution increment is more likely to come from a player who has made a recent increment than from other players. High values indicate the opposite, i.e., a player who made a recent increment is more likely to wait for others to contribute before making a further increment in her own contribution. Specifically, values greater than 0.95 point to significant conditional cooperation.
4. Experimental Design
In the following experiment we test the validity of our two new measures. We compare the performance of the MCL and the NMCL in two treatments that differ only in whether or not the others' actions are observable within the round. As conditional cooperation depends on the observability of the fellow members' contribution increments, our measures are validated if they indicate higher conditional cooperation under observability.
The basic game is the standard linear VCM with the real-time protocol of play described in Section 2. Groups of size 4 interact for 4 rounds in a partners design. The duration of each round T is set to 180 seconds, and the marginal per-capita return α in payoff function (1) equals 0.5. Individual endowments are asymmetric [29]: in each four-person group, two “rich” members are endowed with 15 ECU and two “poor” members with 5 ECU,10 i.e. e1 = e2 = 15 and e3 = e4 = 5.11 The type of each participant (either rich or poor) is randomly assigned at the beginning of the experiment and kept constant over an entire experimental session. The distribution of endowments is common knowledge, i.e., subjects know the others' individual endowment.
During each round, subjects receive on-screen information about the time (in seconds) elapsed in the round. The same screen informs each subject about her type, her initial endowment, her current level of contribution and her remaining endowment. In the instantaneous feedback treatment (henceforth IF treatment), participants can observe, in real time, the current contribution of the other group members, each of whom is identified by her type (rich vs. poor). In the standard feedback treatment (henceforth SF treatment), participants are informed about the individual contributions in their group only at the end of the round.
The computerized experiment was conducted at the laboratory of the Max Planck Institute in Jena. The experiment was programmed via z-Tree [30]. Participants were undergraduate students from different disciplines at the University of Jena. After being seated at a computer terminal, they received written instructions (see the online supplementary file for an English translation), which were also read aloud to establish public knowledge. Understanding of the payoff procedure was assured by a control questionnaire that subjects had to answer before the experiment started.
In total, we ran six sessions (three per treatment). Each session involved twenty-four participants. Because of the partner design, this yields 18 independent observations for each treatment. Sessions lasted, on average, an hour. Subjects received their accumulated round payoffs (plus a show up fee of €2.50) at the end of the experiment. Excluding the show-up payment, the average earnings per subject were €8.11.
5. Experimental Results
Table 1 presents descriptive statistics of the rich and the poor group members' final contributions as well as of the group's final contributions. Consistent with previous experimental results (e.g., [31]), mean group contributions begin high (overall, they start at 70% and 62% of the group total endowment in IF and SF, respectively) and decline with repetition (in the last round, the overall mean stands at 47% and 33% of the total endowment in IF and SF, respectively).12 The decline in contributions between the first and the last round is statistically significant for both treatments (p = 0.013 for the IF treatment, p < 0.001 for the SF treatment, two-sided Wilcoxon signed rank test with continuity correction).13
Comparing the two treatments, we find that, in line with the findings of Kurzban et al. [25], providing real-time information about the others' behavior significantly raises average contributions (p = 0.028, one-sided Wilcoxon rank sum test with continuity correction). Additionally, there is also more full free-riding (contributions of zero) in the SF treatment than in the IF treatment (14.93% versus 3.13% overall). Thus, the possibility of naturally implementing conditional strategies fosters contributions.
Having replicated previously established contribution patterns, we now turn to analyze the performance of our two measures in the current data. Since the cycle length of the four members of a group within a round are interdependent and constrained differently for the two player types (rich vs. poor),14 in the following analysis we differentiate between types.
Table 2 provides descriptive statistics on the observed cycle lengths. Cycle lengths in the IF treatment significantly exceed those in the SF treatment for both the rich and the poor group members (p < 0.001 for both comparisons; Wilcoxon rank sum test). Figure 1 presents histograms of the observed cycle lengths over all groups and rounds separately for each treatment and each player type. The distributions shift to the right in the IF treatment, confirming higher mean cycle lengths under observability of the others' contribution increments. Thus, our first measure of conditional cooperation, the MCL, gains construct validity.
Nonetheless, as observed in Section 3, this result may be due to the higher contribution levels in the IF treatment. Accordingly, we proceed to construct our second measure of conditional cooperation, the NMCL, which takes into account the observed contribution levels. We use the null hypothesis generation process described in Section 3 to compute the NMCL first at the treatment level (i.e., averaging over rounds and groups in each treatment), and then separately for every round and every group within a treatment.
To calculate the NMCL at the treatment level, we perform 30,000 permutations of our data set to generate, for each treatment, a distribution based on the null hypothesis that each contribution is equally likely to come from any of the players who have not yet contributed their observed final amounts. Thus, each permutation consists of 72 newly-generated random contribution sequences that correspond to the 72 actual, observed outcomes in each treatment (one outcome for each group and each round). Then, for each one of these 30,000 permutations we calculate the mean MCL in the treatment (averaging over groups and rounds, as the observed means presented in Table 2 were calculated) so as to obtain a distribution of 30,000 MCLs.15 The NMCL is determined by the relative position of the observed MCL within the distribution thus generated. A high relative position (or a high NMCL) not only means that the null hypothesis of randomness in the observed cycle lengths can be rejected, but also reflects conditional cooperation. On the other hand, a low relative position (or a low NMCL) indicates not only non-randomness but also separation of the contributions over the round, which we refer to as time separation.
The results are reported in Table 3. In the IF treatment, the observed MCL of the poor players is higher than all 30,000 randomly generated MCLs (the NMCL is higher than 0.999), and the observed MCL of the rich players is higher than all but 53 of the 30,000 randomly generated MCLs (the NMCL equals 0.996). These results provide strong evidence for conditional cooperation in the IF treatment. Conversely, in the SF treatment, the observed MCL of both player types is lower than all randomly generated MCLs, providing strong evidence for time separation due to differences in speed or patience across subjects. These findings offer construct validation for our second measure.
Next we use our measure to classify conditionally cooperative dynamics by groups and rounds, separately for the two poor members and the two rich members. We generate 10,000 additional random contribution sequences for each group and round, and compute for each sequence the MCL of the poor and rich group members.16 The relative position of the observed MCL within the corresponding randomly generated distribution (i.e., the NMCL at the group and round level) reflects a measure of conditional cooperation. These NMCLs are expressed as percentiles in Figure 2.
The difference between the top graphs in Figure 1 and Figure 2 is striking: in the IF treatment, the simulation analysis makes the evidence for conditional cooperation jump out of the raw cycle lengths data. Without conditional cooperation or time separation, the distribution of percentiles is expected to be uniform. On the contrary, the two distributions in the SF treatment reflect a tendency for time separation in around 25-30% of all rounds (see bottom graphs in Figure 2). The two distributions in the IF treatment reflect a tendency for both conditional cooperation and time separation (see top graphs in Figure 2). Specifically, 15 out of 72 rich member-observations and 19 out of 69 poor member-observations (20.8% and 27.5%, respectively) are in the top 5% of their corresponding randomly generated distribution; 12 rich member-observations and 13 poor member-observations (16.7% and 18.8%, respectively) are in the bottom 5% (see Table 4). For all of the top- and bottom-intervals mentioned above, the expected proportion of 5% is well outside the 95% confidence intervals depicted in Figure 2. A one-sample Kolmogorov-Smirnov test confirms that all four distributions differ significantly from the uniform distribution (p < 0.005 in all cases).
Finally, we look at the development of cycle lengths over time. A comparison of the MCLs in the first and last rounds shows a significant decrease only for the poor group members in the IF treatment (p = 0.022 according to a Wilcoxon signed rank test; p > 0.05 for the rich members in IF and for both types in SF). To investigate whether this decline indicates less conditional cooperation or is merely due to changes in the contribution levels, we turn again to the randomly generated distributions and perform a Wilcoxon signed rank test on the relative positions of the observed cycle lengths therein. Controlling for the effect of the different contribution levels in such a way causes the decline to disappear (p = 0.246). Specifically, 6 out of 18 groups are in the top 5% of their corresponding randomly generated distribution in both the first and the last round.17
6. Conclusion
In this paper we provided a new way of detecting conditional cooperation in a standard linear voluntary contribution mechanism. In order to allow subjects to endogenously implement conditional strategies, we relied on the real-time protocol of play. Within this context, we studied contribution strategies by introducing the concept of “cycle length”, which is derived from the sequence of contributions within a round. We complemented the measure of conditional cooperation based on the raw mean cycle length with an additional measure that takes into consideration the observed contribution profiles, thus allowing us to study the dynamics of conditional cooperation regardless of changes in the final contribution levels. To validate our measures, we compared behavior in a treatment where individual decisions were instantaneously transmitted to all partners (the so-called IF treatment) to behavior in a standard control treatment where conditional strategies within a round were ruled out.
In line with the results of Kurzban et al. [25], our experimental data indicate that allowing subjects to observe their partners' actual contributions before committing to a further contribution—namely, allowing for conditional cooperation—significantly increases average contributions. The sequences of contributions within a round enable us to determine how this occurs. We observe that compared to the control, the IF treatment engenders not only higher contribution levels, but also significantly higher cycle lengths. This suggests that, throughout the round, subjects tend to increase their contribution in small increments, waiting for others to contribute as well before making an additional contribution.
Although the IF treatment yields higher contributions than the control, contributions in both treatments significantly decline over as a few as four rounds, therefore resembling the typical pattern of standard public goods experiments. It would be tempting to conclude that, in the IF treatment, this is due to a breakdown in conditional cooperation. Yet, our analysis reveals that subjects continue to behave in a conditionally cooperative way within the bounds of the diminished contributions. This may be a result of some subjects attempting (mostly unsuccessfully) to reestablish conditional cooperation. Thus, our method corroborates the conclusion of Fischbacher and Gächter [12], without assuming stationary strategies.
Previous research mostly focused on individual preferences for conditional cooperation to conclude that approximately 50% of the studied population is conditionally cooperative (see, e.g., the survey by Gächter [11]). Looking at the group dynamics, we observe that over 20% of round plays result in a normalized measure larger than 0.95, therefore exhibiting conditional cooperation.
To sum up, by introducing the analysis of cycles in the sequence of contributions and using round-specific randomly generated counterfactual data, we were able to establish and validate two new measures for conditional cooperation. Our experiment illustrates how our normalized cycle length measure can be used to study issues of conditional cooperation in real-play dynamics independently of final contributions.
Supplementary Material
games-02-00001-s001.pdf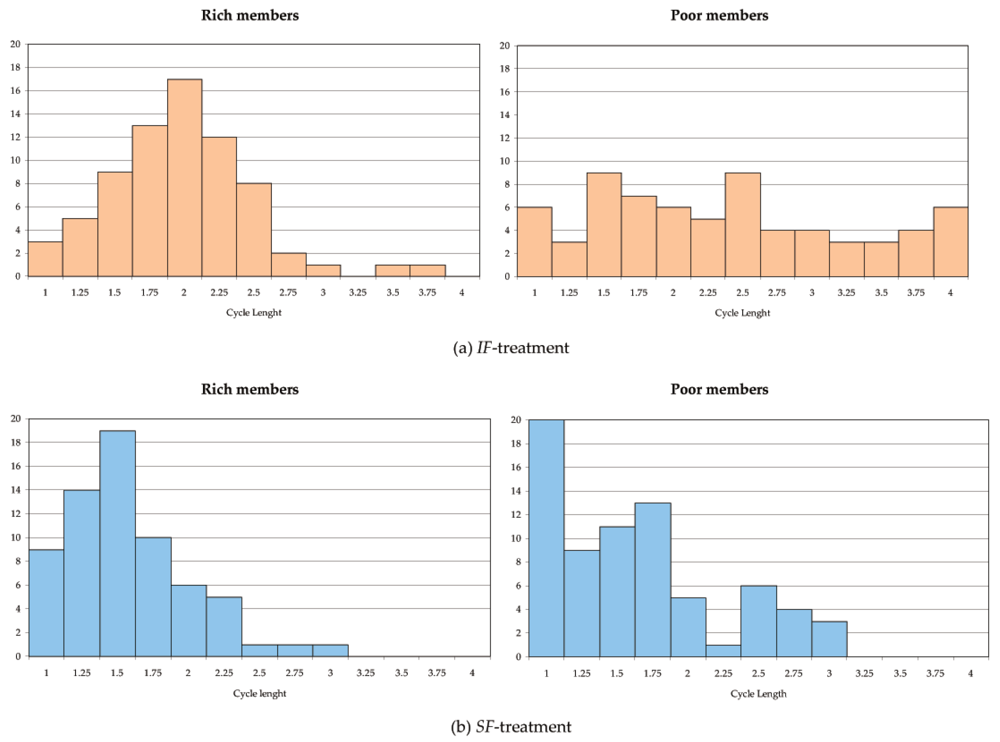

| Rich | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Round 1 | Round 2 | Round 3 | Round 4 | Overall | |||||||
| IF treatment | Median | 10.0 | 11.5 | 7.0 | 5.0 | 8.00 | |||||
| Mean | 10.0 | 9.8 | 8.6 | 6.1 | 8.60 | ||||||
| Std. dev. | 4.1 | 5.1 | 4.6 | 5.0 | 4.9 | ||||||
| % of ci = 0 | 0 | 2.8 | 0 | 2.8 | 1.4 | ||||||
| SF treatment | Median | 8.0 | 7.0 | 4.5 | 1.0 | 5.0 | |||||
| Mean | 8.1 | 8.1 | 4.9 | 3.6 | 6.2 | ||||||
| Std. dev. | 4.7 | 4.9 | 4.7 | 4.4 | 5.0 | ||||||
| % of ci = 0 | 5.6 | 5.6 | 25 | 36 | 18 | ||||||
| Poor | |||||||||||
| Round 1 | Round 2 | Round 3 | Round 4 | Overall | |||||||
| IF treatment | Median | 5.0 | 5.0 | 5.0 | 3.0 | 5.0 | |||||
| Mean | 4.0 | 4.1 | 4.0 | 3.4 | 3.87 | ||||||
| Std. dev. | 1.5 | 1.4 | 1.5 | 1.6 | 1.5 | ||||||
| % of ci = 0 | 2.8 | 5.6 | 5.6 | 5.6 | 4.9 | ||||||
| SF treatment | Median | 5.0 | 5.0 | 5.0 | 4.0 | 5.0 | |||||
| Mean | 4.3 | 4.1 | 3.5 | 3.0 | 3.7 | ||||||
| Std. dev. | 1.4 | 1.6 | 1.9 | 2.2 | 1.8 | ||||||
| % of ci = 0 | 5.6 | 8.3 | 11.1 | 22.2 | 11.9 | ||||||
| Group total | |||||||||||
| Round 1 | Round 2 | Round 3 | Round 4 | Overall | |||||||
| IF treatment | Median | 27.0 | 31.5 | 22.5 | 16.0 | 25.4 | |||||
| Mean | 27.9 | 27.8 | 25.1 | 18.9 | 25.5 | ||||||
| Std. dev. | 8.8 | 11.8 | 10.6 | 11.0 | 8.4 | ||||||
| % of ci = 0 | 1.4 | 4.2 | 2.8 | 4.2 | 3.1 | ||||||
| SF treatment | Median | 23.5 | 21.5 | 15.0 | 11.0 | 18.1 | |||||
| Mean | 24.7 | 24.3 | 16.8 | 13.3 | 19.8 | ||||||
| Std. dev. | 6.3 | 8.4 | 9.2 | 8.0 | 6.8 | ||||||
| % of ci = 0 | 5.6 | 6.9 | 18.1 | 29.2 | 14.9 | ||||||
| IF treatment | SF treatment | |||
|---|---|---|---|---|
| Rich | Poor | Rich | Poor | |
| Mean | 1.887 | 2.314 | 1.523 | 1.591 |
| Median | 1.903 | 2.146 | 1.466 | 1.530 |
| Std. dev. | 0.313 | 0.735 | 0.316 | 0.372 |
| IF treatment | SF treatment | |||
|---|---|---|---|---|
| Rich | Poor | Rich | Poor | |
| Mean | 1.800 | 2.081 | 1.729 | 1.923 |
| Std. dev. | 0.028 | 0.038 | 0.039 | 0.045 |
| Min | 1.696 | 1.944 | 1.553 | 1.763 |
| Max | 1.896 | 2.208 | 1.865 | 2.092 |
| Observed MCL | 1.887 | 2.314 | 1.523 | 1.591 |
| NMCL | 0.996 | 1.000 | 0.000 | 0.000 |
| IF treatment | SF treatment | |||
|---|---|---|---|---|
| Rich (N = 72) | Poor (N = 69) | Rich (N = 66) | Poor (N = 72) | |
| Top 10% (Cond. Cooperation) | 30.6% | 31.9% | 9.1% | 6.9% |
| Bottom 10% (Time Separation) | 22.2% | 23.9% | 40.1% | 36.1% |
| Top 5% (Cond. Cooperation) | 20.8% | 27.5% | 6.1% | 4.2% |
| Bottom 5% (Time Separation) | 16.7% | 18.8% | 28.8% | 25.0% |
Note: N denotes the number of observations.
Acknowledgments
The authors would like to thank Gil Ben-Zvi, Sven Fischer, Simon Gächter, Sebastian Kube, Andreas Stiehler, and two anonymous referees for helpful comments.
References
- Fischbacher, U.; Gächter, S.; Fehr, E. Are people conditionally cooperative? Evidence from a public goods experiment. Econ. Lett. 2001, 71, 397–404. [Google Scholar]
- Frey, B.S.; Meier, S. Social comparisons and pro-social behavior: Testing“ conditional cooperation” in a field experiment. Am. Econ. Rev. 2004, 94, 1717–1722. [Google Scholar]
- Sugden, R. Reciprocity: the supply of public goods through voluntary contributions. The Econ. J. 1984, 94, 772–787. [Google Scholar]
- Rabin, M. Incorporating Fairness into Game Theory and Economics. Am. Econ. Rev. 1993, 83, 1281–1302. [Google Scholar]
- Croson, R. Theories of commitment, altruism and reciprocity: Evidence from linear public goods games. Econ. Inq. 2007, 45, 199–216. [Google Scholar]
- Keser, C.; Van Winden, F. Conditional cooperation and voluntary contributions to public goods. Scand. J. Econ. 2000, 102, 23–39. [Google Scholar]
- Brandts, J.; Schram, A. Cooperation and noise in public goods experiments: Applying the contribution function approach. J. Public Econ. 2001, 79, 399–427. [Google Scholar]
- Levati, M.V.; Neugebauer, T. An application of the English clock market mechanism to public goods games. Exp. Econ. 2004, 7, 153–169. [Google Scholar]
- Kurzban, R.; Houser, D. Experiments investigating cooperative types in humans: A complement to evolutionary theory and simulations. P. Natl. Acad. Sci. USA 2005, 102, 1803–1807. [Google Scholar]
- Chaudhuri, A.; Paichayontvijit, T. Conditional cooperation and voluntary contributions to a public good. Econ. Bull. 2006, 3, 1–14. [Google Scholar]
- Gächter, S. Conditional cooperation: Behavioral regularities from the lab and the field and their policy implications. In Economics and Psychology. A Promising New Cross-Disciplinary Field; Frey, B.S., Stutzer, A., Eds.; MIT Press: Boston, MA, USA, 2007; pp. 19–50. [Google Scholar]
- Fischbacher, U.; Gachter, S. Social preferences, beliefs, and the dynamics of free riding in public goods experiments. Am. Econ. Rev. 2010, 100, 541–556. [Google Scholar]
- Heldt, T. Conditional cooperation in the field: Cross-country skiers' behavior in Sweden 2005. (Working paper).
- Dorsey, R.E. The voluntary contributions mechanism with real time revisions. Public Choice 1992, 73, 261–282. [Google Scholar]
- Neugebauer, T.; Perote, J.; Schmidt, U.; Loos, M. Selfish-biased conditional cooperation: On the decline of contributions in repeated public goods experiments. J. Econ. Psychol. 2009, 30, 52–60. [Google Scholar]
- Ross, L.; Greene, D.; House, P. The false consensus effect: An egocentric bias in social perception and attribution processes. J. Exp. Soc. Psychol. 1977, 13, 279–301. [Google Scholar]
- Dawes, R.M. The potential nonfalsity of the false consensus effect. In Insights in Decision Making: A Tribute to Hillel J. Einhorn; Hogarth, R.M., Ed.; University of Chicago Press: Chicago, IL, USA, 1990; pp. 179–199. [Google Scholar]
- Engelmann, D.; Strobel, M. The false consensus effect disappears if representative information and monetary incentives are given. Exp. Econ. 2000, 3, 241–260. [Google Scholar]
- Fisher, R.A. The Design of Experiments; Oliver and Boyd: Edinburgh, UK, 1935. [Google Scholar]
- Pitman, E.J.G. Significance tests which may be applied to samples from any populations. Biometrika 1937, 4, 119–130. [Google Scholar]
- Odén, A.; Wedel, H. Arguments for Fisher's permutation test. The Ann. Stat. 1975, 3, 518–520. [Google Scholar]
- Güth, W.; Levati, M.V.; Stiehler, A. Privately contributing to public goods over time-an experimental study. Jena Econ. Res. Pap. 2002, 2002-001. [Google Scholar]
- Goren, H.; Rapoport, A.; Kurzban, R. Revocable commitments to public goods provision under the real-time protocol of play. J. Behav. Decis. Making 2004, 17, 17–37. [Google Scholar]
- Goren, H.; Kurzban, R.; Rapoport, A. Social loafing vs. social enhancement: Public goods provisioning in real-time with irrevocable commitments. Organ. Behav. Hum. Dec. 2003, 90, 277–290. [Google Scholar]
- Kurzban, R.; McCabe, K.; Smith, V.L.; Wilson, B.J. Incremental commitment and reciprocity in a real-time public goods game. Pers. Soc. Psychol. B. 2001, 27, 1662–1673. [Google Scholar]
- Ostrom, E. Collective action and the evolution of social norms. J. Econ. Perspect. 2000, 14, 137–158. [Google Scholar]
- De Cremer, D.; Snyder, M.; Dewitte, S. The less I trust, the less I contribute (or not)? The effects of trust, accountability and self-monitoring in social dilemmas. Eur. J. Soc. Psychol. 2001, 31, 93–107. [Google Scholar]
- Good, P.; Wang, R. Permutation, Parametric and Bootstrap Tests of Hypotheses; Springer: New York, NY, USA, 2005. [Google Scholar]
- Buckley, E.; Croson, R. Income and wealth heterogeneity in the voluntary provision of linear public goods. J. Public Econ. 2006, 90, 935–955. [Google Scholar]
- Fischbacher, U. z-Tree: Zurich toolbox for ready-made economic experiments. Exp. Econ. 2007, 10, 171–178. [Google Scholar]
- Ledyard, J.O. Public goods: A survey of experimental research. In The Handbook of Experimental Economics; Kagel, J., Roth, A.E., Eds.; Princeton University Press: Princeton, NJ, USA, 1995; pp. 111–194. [Google Scholar]
- 1Fischbacher et al. [1] and Frey and Meier [2], among others, suggest that conditionally cooperative behavior can result from preferences for reciprocity (see, e.g., [3–5]).
- 2Think for instance of committees organized to raise funds for the (re)construction of a church (in Italy churches are built with private money). The campaign to raise funds usually lasts several weeks. Contributors are not forced to fix their contribution at the beginning, but can vary it till the last moment while observing (in an “ad hoc” list) if and how much others have contributed.
- 3The real-time protocol of play has been introduced by Dorsey [14] and subsequently employed by [22–25]. None of these studies, however, used the dynamics of contributions during the round to directly ascertain conditional cooperation.
- 4Although zero contribution is no longer a dominant strategy under the assumption of identical selfish players who maximize their own monetary payoff, zero contribution by everyone is the unique equilibrium of the game. Let S ⊆ T be the set of all t such that σi,t > 0 for some i ∈ I, and define t̄ = maxt∈S t. A contribution of player j at time t̄ strictly reduces j's payoff (∀j ∈ I). Therefore S must be empty in equilibrium.
- 5Ht may be also taken to include the timing of all previous increments.
- 6Ostrom [26] suggests that conditional cooperators are willing not only to cooperate if others do so, but to initiate cooperative actions when no cooperation norm has been set up.
- 7For example, the vector HT = (3,4,4,1,1,3) indicates that player 3 was the first to contribute one unit, then player 4 made two increments to her contribution, followed by player 1 with two increments. Finally, player 3 made a second increment. The final contributions are 2 for players 1, 3, and 4, and 0 for player 2.
- 8Intuitively, one may wish to look at the number of increments within a cycle rather at the number of players. However, player i's mean cycle length (our variable of interest) would then reduce to simply the number of contributions between i's first and last contributions plus one divided by NCi, and thus would not be sensitive to conditioning on other's contributions within this sequence.
- 9Other procedures, such as taking random permutations of the observed sequence, can also be used in this paradigm. We find our procedure to correspond better to the game structure.
- 10ECU is the experimental currency unit, which is converted to euro at the end of the experiment with a conversion rate of 1 ECU = 5 euro-cents.
- 11Asymmetric endowments provide the worst conditions for the emergence and evolution of conditional cooperation. If our measures detect conditional cooperation in this setting, they would perform at least equally well in a symmetric scenario.
- 12In a setting similar to our SF treatment, Levati and Neugebauer [8] found that average group contributions were about 65% (20%) of the group endowment in the first (last) period.
- 13The non-parametric tests reported in this section rely on independent group observations.
- 14For example, if the four group members contribute their whole endowment and always wait for each other before contributing a further ECU, the poor group members are expected to have four cycles of length 4 each, whereas the rich group members should have five cycles of length 4 and nine cycles of length 2 where the poor members do not appear.
- 15Since the analysis is done at the group and round levels and some players contributed less than 2 ECU within a round, there are some missing values in the cycle lengths. In particular, the MCL is not defined in 3 out of 72 cases for the poor members in IF and in 6 out of 72 cases for the rich members in SF.
- 16We re-run the simulations in order to avoid dependencies between the analyses.
- 17Of less interest is a significant increase for the poor group members in the SF treatment, which suggests diminished time separation. This may be due to the fact that in the first round some subjects take longer than others to decide on their contribution. More specifically, the relative position of 9 out of 18 groups in the first round is in the bottom 5% whereas no group lies in the lowest percentile in the last round. This interpretation is in line with the decline in average waiting time between two consecutive contributions observed in the SF treatment.
© 2011 by the authors; licensee MDPI, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Levati, M.V.; Zultan, R. Cycles of Conditional Cooperation in a Real-Time Voluntary Contribution Mechanism. Games 2011, 2, 1-15. https://doi.org/10.3390/g2010001
Levati MV, Zultan R. Cycles of Conditional Cooperation in a Real-Time Voluntary Contribution Mechanism. Games. 2011; 2(1):1-15. https://doi.org/10.3390/g2010001
Chicago/Turabian StyleLevati, M. Vittoria, and Ro’i Zultan. 2011. "Cycles of Conditional Cooperation in a Real-Time Voluntary Contribution Mechanism" Games 2, no. 1: 1-15. https://doi.org/10.3390/g2010001




