TaPT: Temperature-Aware Dynamic Cache Optimization for Embedded Systems
Abstract
:1. Introduction
2. Background and Related Work
2.1. Phase-Based Tuning and DTM
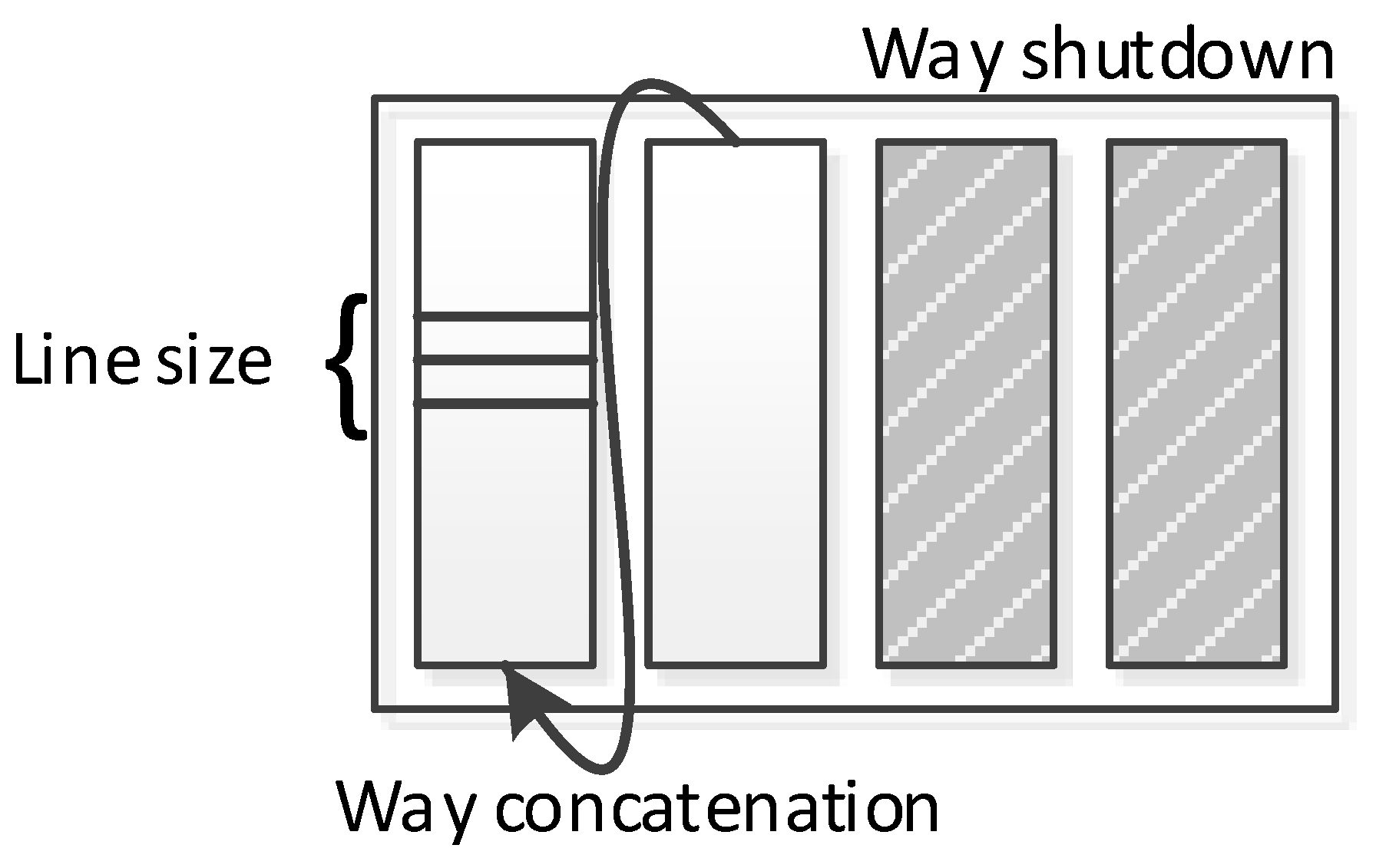
2.2. Configurable Hardware
2.3. SPEA2 Algorithm
3. Temperature-Aware Phase-based Tuning (TaPT)
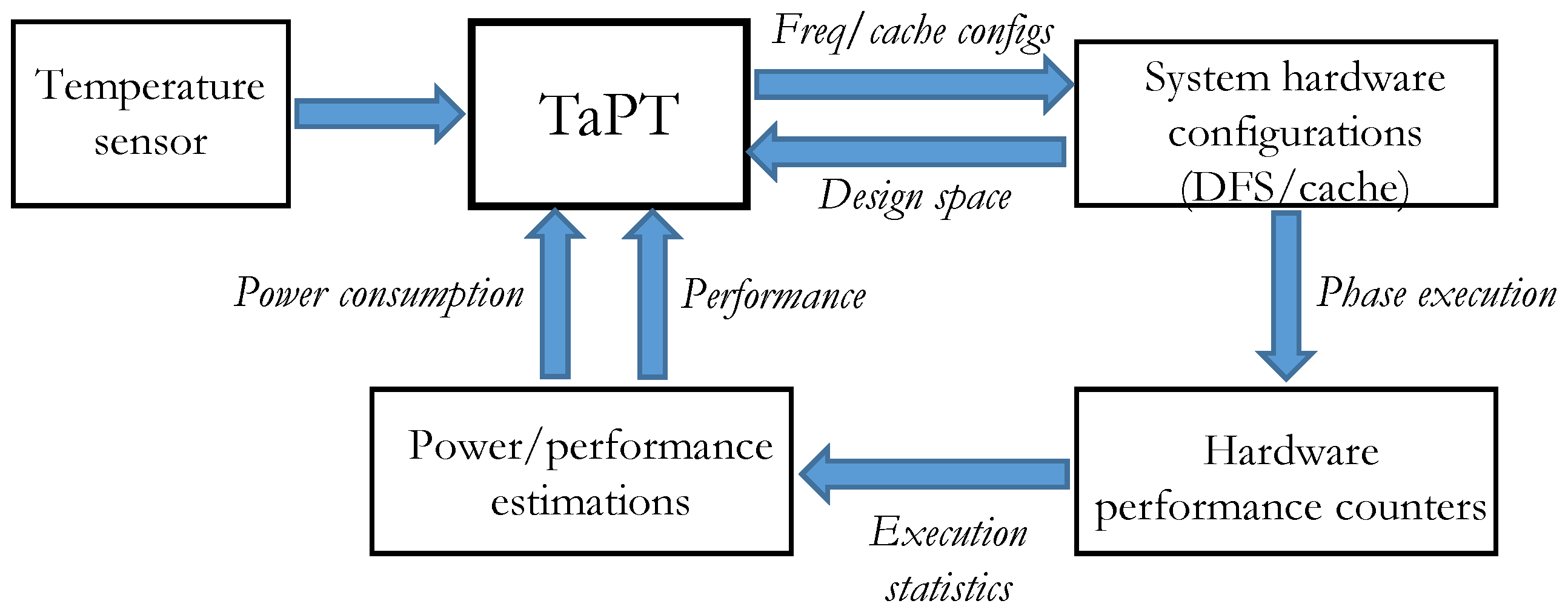
3.1. TaPT Overview
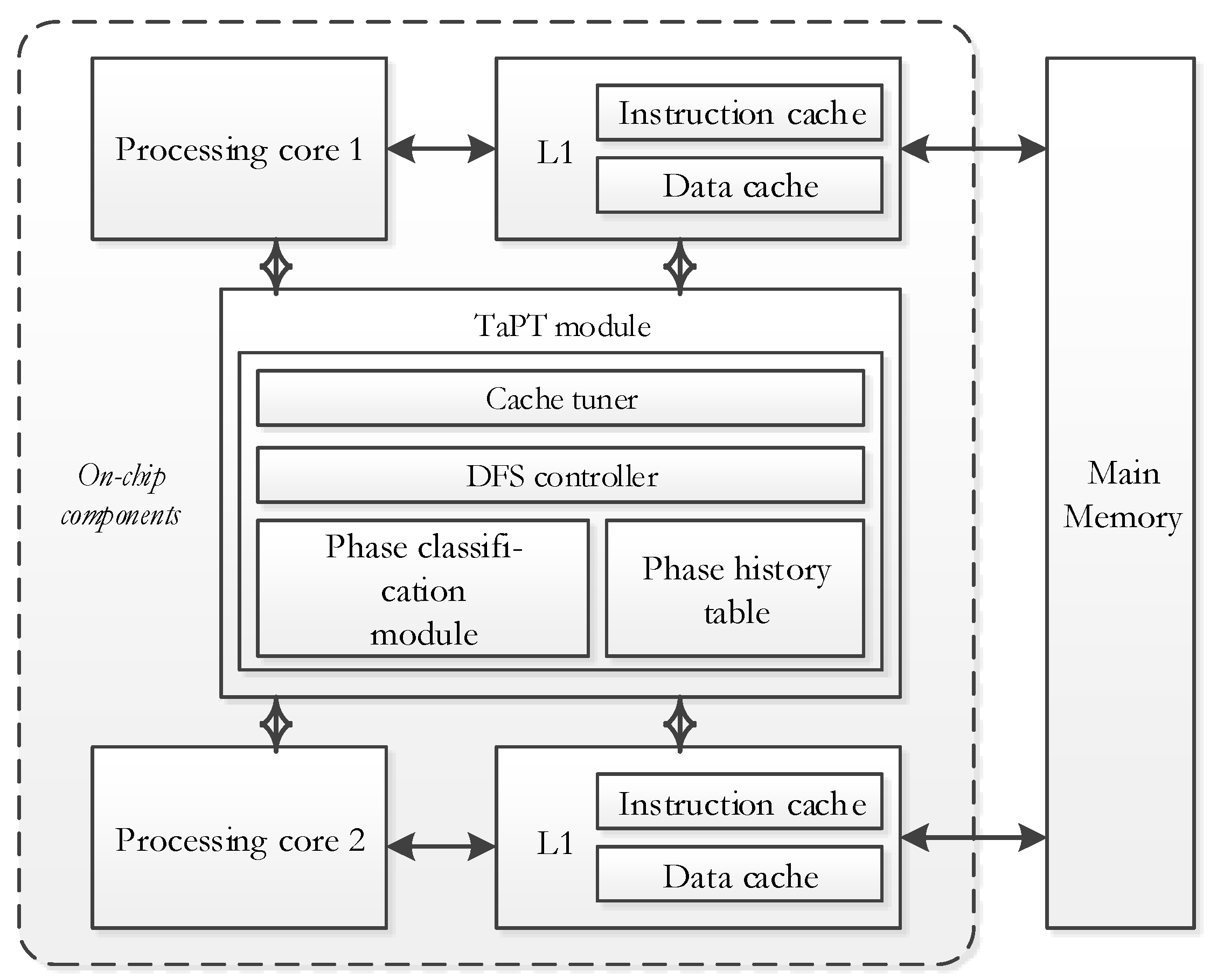
3.2. TaPT Architecture
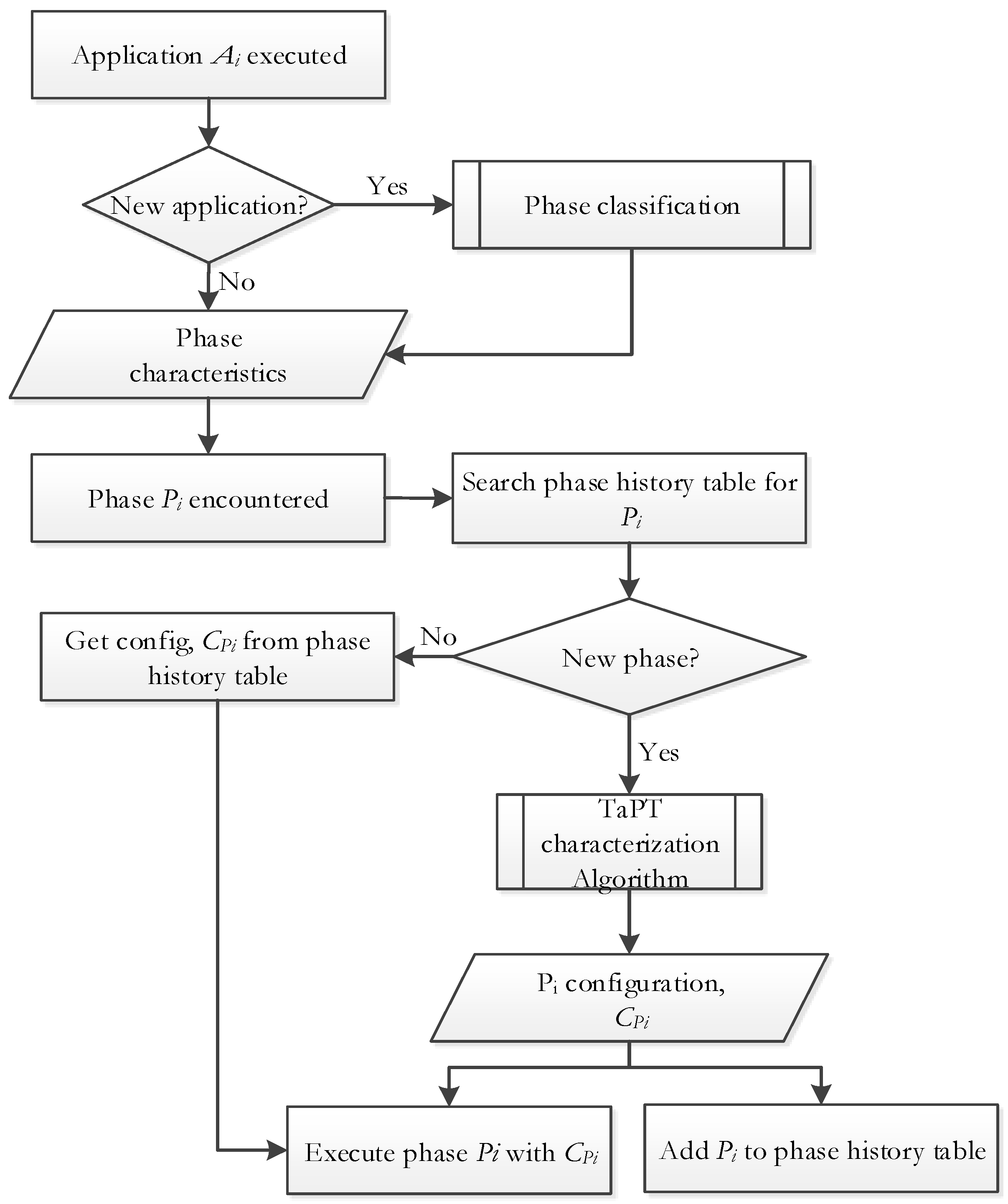
3.3. TaPT Characterization Algorithm
| Algorithm 1 TaPT Algorithm |
| Input: |
Output: ’s best configuration
|
3.4. Computational Complexity and Hardware Overhead
4. Experiments
4.1. Experimental Setup
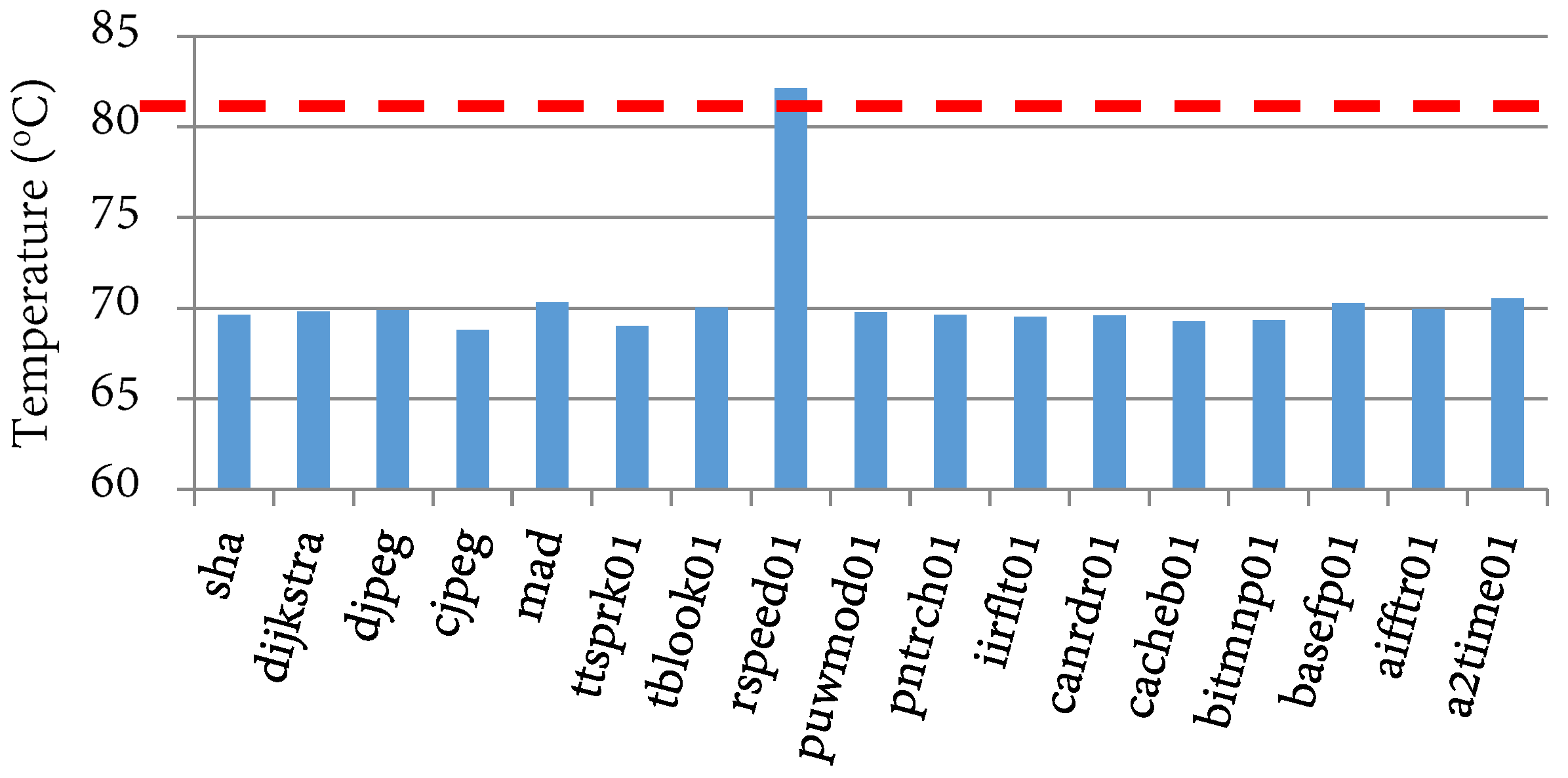
4.2. Temperature Impact of Cache Configurations
4.3. TaPT Parameters
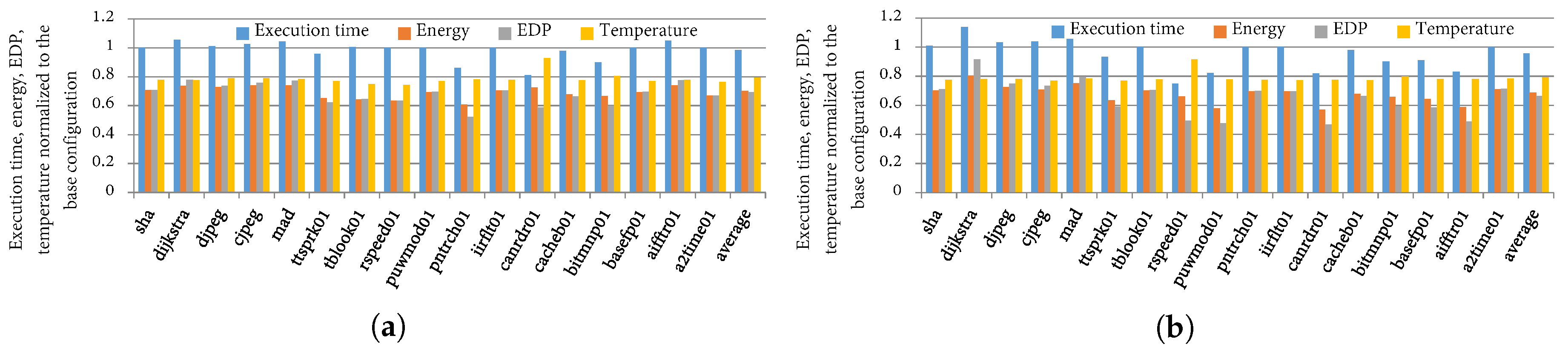
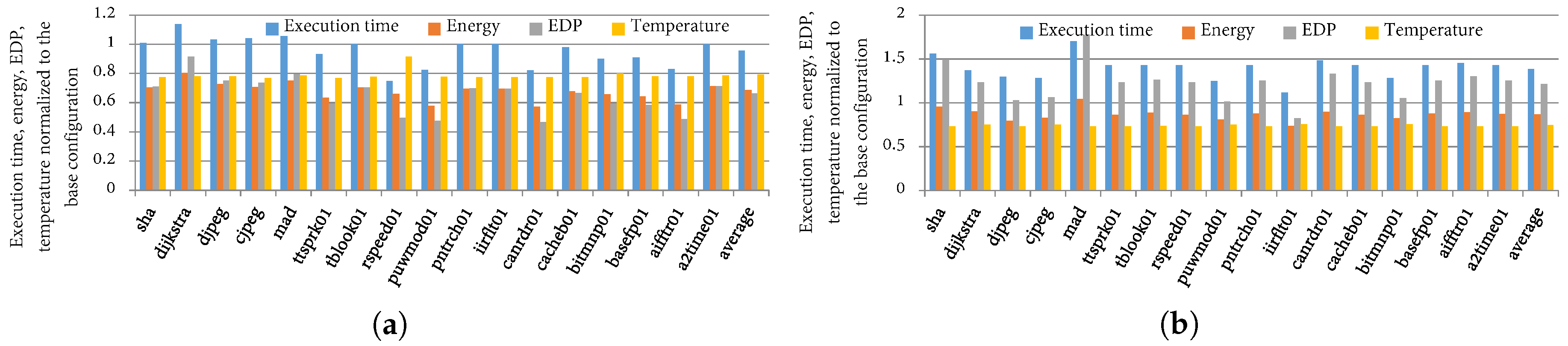
4.4. TaPT Optimization Results
4.5. Comparison to Prior Work
4.6. Tuning Overhead
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Brooks, D.; Martonosi, M. Dynamic thermal management for high-performance microprocessors. In Proceedings of the Seventh International Symposium on IEEE High-Performance Computer Architecture (HPCA), Monterrey, Nuevo Leon, Mexico, 19–24 January 2001; pp. 171–182. [Google Scholar]
- Skadron, K.; Stan, M.R.; Sankaranarayanan, K.; Huang, W.; Velusamy, S.; Tarjan, D. Temperature-aware microarchitecture: Modeling and implementation. ACM Trans. Archit. Code Optim. (TACO) 2004, 1, 94–125. [Google Scholar] [CrossRef]
- Heo, S.; Barr, K.; Asanović, K. Reducing power density through activity migration. In Proceedings of the 2003 International Symposium on Low Power Electronics and Design, Seoul, Korea, 25–27 August 2003; ACM: New York, NY, USA, 2003; pp. 217–222. [Google Scholar]
- ARM. Available online: http://www.arm.com (accessed on 21 December 2016).
- Pedram, M.; Nazarian, S. Thermal modeling, analysis, and management in VLSI circuits: Principles and methods. Proc. IEEE 2006, 94, 1487–1501. [Google Scholar] [CrossRef]
- Yeo, I.; Kim, E.J. Temperature-aware scheduler based on thermal behavior grouping in multicore systems. In Proceedings of the Conference on Design, Automation and Test in Europe, Nice, France, 20–24 April 2009; European Design and Automation Association: Leuven, Belgium, 2009; pp. 946–951. [Google Scholar]
- Jayaseelan, R.; Mitra, T. Temperature aware task sequencing and voltage scaling. In Proceedings of the 2008 IEEE/ACM International Conference on Computer-Aided Design, San Jose, CA, USA, 10–13 November 2008; IEEE Press: Piscataway, NJ, USA, 2008; pp. 618–623. [Google Scholar]
- Gordon-Ross, A.; Lau, J.; Calder, B. Phase-based cache reconfiguration for a highly-configurable two-level cache hierarchy. In Proceedings of the 18th ACM Great Lakes Symposium on VLSI, Orlando, FL, USA, 4–6 May 2008; ACM: New York, NY, USA, 2008; pp. 379–382. [Google Scholar]
- Gordon-Ross, A.; Vahid, F.; Dutt, N.D. Fast configurable-cache tuning with a unified second-level cache. IEEE Trans. Very Large Scale Integr. (VLSI) Syst. 2009, 17, 80–91. [Google Scholar] [CrossRef]
- Khaitan, S.K.; McCalley, J.D. Optimizing cache energy efficiency in multicore power system simulations. Energy Syst. 2014, 5, 163–177. [Google Scholar] [CrossRef]
- Zhang, C.; Vahid, F.; Najjar, W. A highly configurable cache architecture for embedded systems. In Proceedings of the IEEE 30th Annual International Symposium on Computer Architecture, San Diego, CA, USA, 9–11 June 2003; pp. 136–146. [Google Scholar]
- Homayoun, H.; Rahmatian, M.; Kontorinis, V.; Golshan, S.; Tullsen, D.M. Hot peripheral thermal management to mitigate cache temperature variation. In Proceedings of the IEEE Thirteenth International Symposium on Quality Electronic Design (ISQED), Santa Clara, CA, USA, 19–21 March 2012; pp. 755–763. [Google Scholar]
- Rohbani, N.; Ebrahimi, M.; Miremadi, S.G.; Tahoori, M.B. Bias Temperature Instability Mitigation via Adaptive Cache Size Management. IEEE Trans. Very Large Scale Integr. (VLSI) Syst. 2017, 25, 1012–1022. [Google Scholar] [CrossRef]
- Zitzler, E.; Laumanns, M.; Thiele, L. SPEA2: Improving the Strength Pareto Evolutionary Algorithm; Eurogen: Athens, Greece, 2001; Volume 3242, pp. 95–100. [Google Scholar]
- Adegbija, T.; Gordon-Ross, A.; Rawlins, M. Analysis of cache tuner architectural layouts for multicore embedded systems. In Proceedings of the IEEE International Performance Computing and Communications Conference (IPCCC), Austin, TX, USA, 5–7 December 2014; pp. 1–8. [Google Scholar]
- Hajimiri, H.; Mishra, P. Intra-task dynamic cache reconfiguration. In Proceedings of the IEEE 25th International Conference on VLSI Design (VLSID), Hyderabad, India, 7–11 January 2012; pp. 430–435. [Google Scholar]
- Salami, B.; Baharani, M.; Noori, H. Proactive task migration with a self-adjusting migration threshold for dynamic thermal management of multi-core processors. J. Supercomput. 2014, 68, 1068–1087. [Google Scholar] [CrossRef]
- Sherwood, T.; Calder, B. Time Varying Behavior of Programs; UCSD Technical Report CS99-630; UCSD: La Jolla, CA, USA, 1999. [Google Scholar]
- Balasubramonian, R.; Albonesi, D.; Buyuktosunoglu, A.; Dwarkadas, S. Memory hierarchy reconfiguration for energy and performance in general-purpose processor architectures. In Proceedings of the 33rd Annual ACM/IEEE International Symposium on Microarchitecture, Monterey, CA, USA, 10–13 December 2000; ACM: New York, NY, USA, 2000; pp. 245–257. [Google Scholar]
- Dhodapkar, A.S.; Smith, J.E. Comparing program phase detection techniques. In Proceedings of the 36th Annual IEEE/ACM International Symposium on Microarchitecture, San Diego, CA, USA, 3–5 December 2003; IEEE Computer Society: Washington, DC, USA, 2003; p. 217. [Google Scholar]
- Sembrant, A.; Eklov, D.; Hagersten, E. Efficient software-based online phase classification. In Proceedings of the 2011 IEEE International Symposium on Workload Characterization (IISWC), Austin, TX, USA, 6–8 November 2011; pp. 104–115. [Google Scholar]
- Huang, W.; Stan, M.R.; Skadron, K.; Sankaranarayanan, K.; Ghosh, S.; Velusam, S. Compact thermal modeling for temperature-aware design. In Proceedings of the 41st Annual Design Automation Conference, San Diego, CA, USA, 7–11 June 2004; ACM: New York, NY, USA, 2004; pp. 878–883. [Google Scholar]
- Liu, Z.; Xu, T.; Tan, S.X.D.; Wang, H. Dynamic thermal management for multi-core microprocessors considering transient thermal effects. In Proceedings of the IEEE 2013 18th Asia and South Pacific Design Automation Conference (ASP-DAC), Yokohama, Japan, 22–25 January 2013; pp. 473–478. [Google Scholar]
- Kong, J.; Chung, S.W.; Skadron, K. Recent thermal management techniques for microprocessors. ACM Comput. Surv. (CSUR) 2012, 44, 13. [Google Scholar] [CrossRef]
- Malik, A.; Moyer, B.; Cermak, D. A low power unified cache architecture providing power and performance flexibility. In Proceedings of the IEEE 2000 International Symposium on Low Power Electronics and Design (ISLPED), Rapallo, Italy, 26–27 July 2000; pp. 241–243. [Google Scholar]
- Singh, K.; Bhadauria, M.; McKee, S.A. Real time power estimation and thread scheduling via performance counters. ACM SIGARCH Comput. Archit. News 2009, 37, 46–55. [Google Scholar] [CrossRef]
- Kanungo, T.; Mount, D.M.; Netanyahu, N.S.; Piatko, C.D.; Silverman, R.; Wu, A.Y. An efficient k-means clustering algorithm: Analysis and implementation. IEEE Trans. Pattern Anal. Mach. Intell. 2002, 24, 881–892. [Google Scholar] [CrossRef]
- Herbert, S.; Marculescu, D. Variation-aware dynamic voltage/frequency scaling. In Proceedings of the IEEE 15th International Symposium on High Performance Computer Architecture (HPCA), Raleigh, NC, USA, 14–18 February 2009; pp. 301–312. [Google Scholar]
- Adegbija, T.; Gordon-Ross, A.; Munir, A. Phase distance mapping: A phase-based cache tuning methodology for embedded systems. Des. Autom. Embed. Syst. 2014, 18, 251–278. [Google Scholar] [CrossRef]
- Sherwood, T.; Sair, S.; Calder, B. Phase tracking and prediction. In ACM SIGARCH Computer Architecture News; ACM: New York, NY, USA, 2003; Volume 31, pp. 336–349. [Google Scholar]
- Design Compiler. Synopsys Inc. Available online: https://www.synopsys.com/ (accessed on 21 January 2017).
- MIPS32 M14K Processor Core Family. Available online: https://imagination-technologies-cloudfront-assets.s3.amazonaws.com/documentation/MD00668-2B-M14K-SUM-02.04.pdf (accessed on 21 April 2017).
- Binkert, N.; Beckmann, B.; Black, G.; Reinhardt, S.K.; Saidi, A.; Basu, A.; Hestness, J.; Hower, D.R.; Krishna, T.; Sardashti, S.; et al. The gem5 Simulator. Comput. Archit. News 2012, 40, 1–7. [Google Scholar] [CrossRef]
- Li, S.; Ahn, J.H.; Strong, R.D.; Brockman, J.B.; Tullsen, D.M.; Jouppi, N.P. The mcpat framework for multicore and manycore architectures: Simultaneously modeling power, area, and timing. ACM Trans. Archit. Code Optim. (TACO) 2013, 10, 5. [Google Scholar] [CrossRef]
- Sharifi, S.; Coskun, A.K.; Rosing, T.S. Hybrid dynamic energy and thermal management in heterogeneous embedded multiprocessor SoCs. In Proceedings of the 2010 Asia and South Pacific Design Automation Conference, Taipei, Taiwan, 18–21 January 2010; pp. 873–878. [Google Scholar]
- The Embedded Microprocessor Benchmark Consortium. Available online: http://www.eembc.org/ (accessed on 21 January 2017).
- Guthaus, M.R.; Ringenberg, J.S.; Ernst, D.; Austin, T.M.; Mudge, T.; Brown, R.B. MiBench: A free, commercially representative embedded benchmark suite. In Proceedings of the IEEE International Workshop on Workload Characterization (WWC), Austin, TX, USA, 2 December 2001; pp. 3–14. [Google Scholar]
- Gordon-Ross, A.; Vahid, F. A self-tuning configurable cache. In Proceedings of the 44th annual Design Automation Conference, San Diego, CA, USA, 4–8 June 2007; ACM: New York, NY, USA, 2007; pp. 234–237. [Google Scholar]
- Rawlins, M.; Gordon-Ross, A. An application classification guided cache tuning heuristic for multi-core architectures. In Proceedings of the IEEE 17th Asia and South Pacific Design Automation Conference (ASP-DAC), Sydney, NSW, Australia, 30 January–2 February 2012; pp. 23–28. [Google Scholar]
- Park, S.; Park, J.; Shin, D.; Wang, Y.; Xie, Q.; Pedram, M.; Chang, N. Accurate modeling of the delay and energy overhead of dynamic voltage and frequency scaling in modern microprocessors. IEEE Trans. Comput.-Aided Des. Integr. Circuits Syst. 2013, 32, 695–708. [Google Scholar] [CrossRef]




© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Adegbija, T.; Gordon-Ross, A. TaPT: Temperature-Aware Dynamic Cache Optimization for Embedded Systems. Computers 2018, 7, 3. https://doi.org/10.3390/computers7010003
Adegbija T, Gordon-Ross A. TaPT: Temperature-Aware Dynamic Cache Optimization for Embedded Systems. Computers. 2018; 7(1):3. https://doi.org/10.3390/computers7010003
Chicago/Turabian StyleAdegbija, Tosiron, and Ann Gordon-Ross. 2018. "TaPT: Temperature-Aware Dynamic Cache Optimization for Embedded Systems" Computers 7, no. 1: 3. https://doi.org/10.3390/computers7010003



