Construction of the Calibration Set through Multivariate Analysis in Visible and Near-Infrared Prediction Model for Estimating Soil Organic Matter
Abstract
:1. Introduction
2. Study Area and Materials
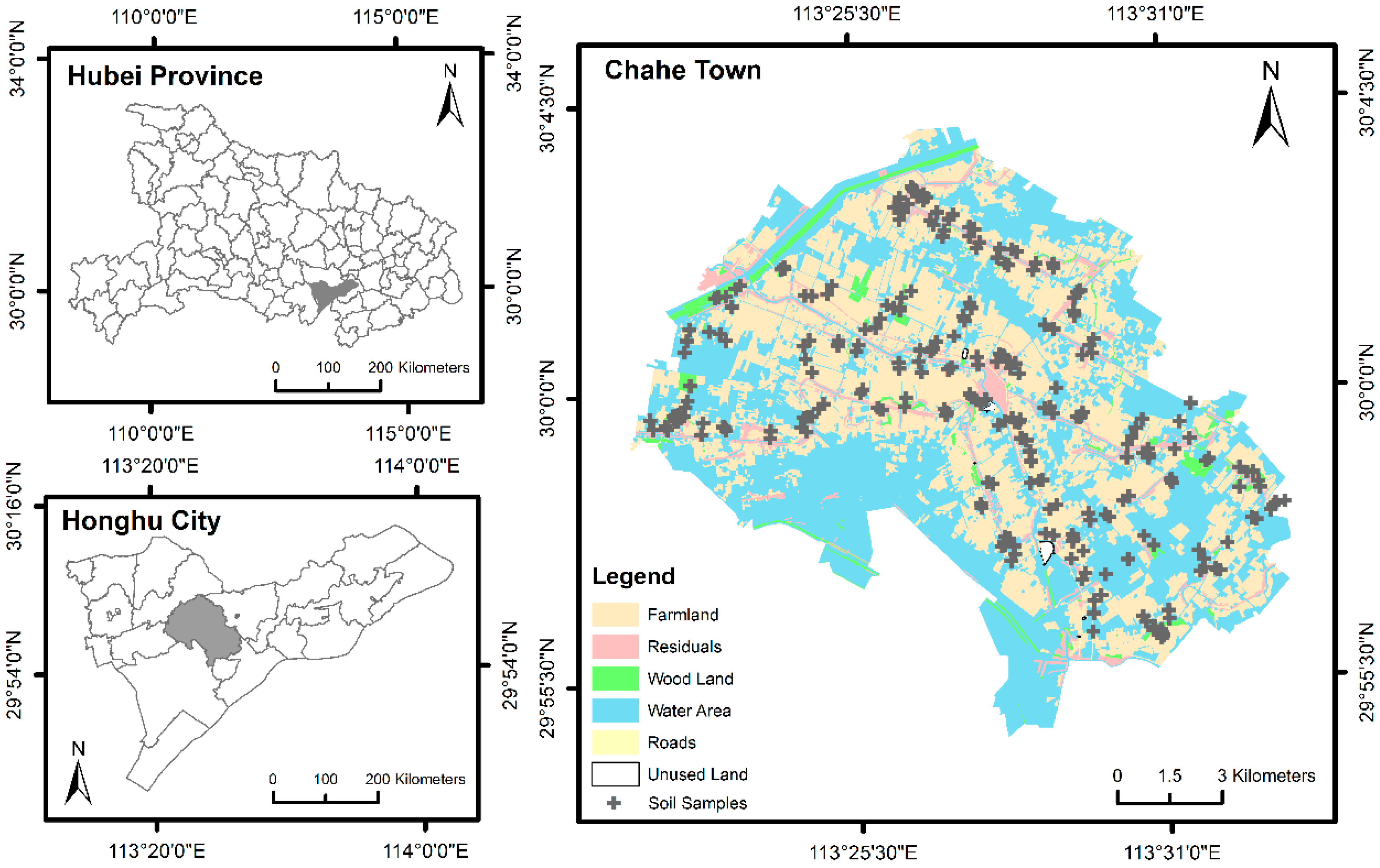
2.1. Study Area
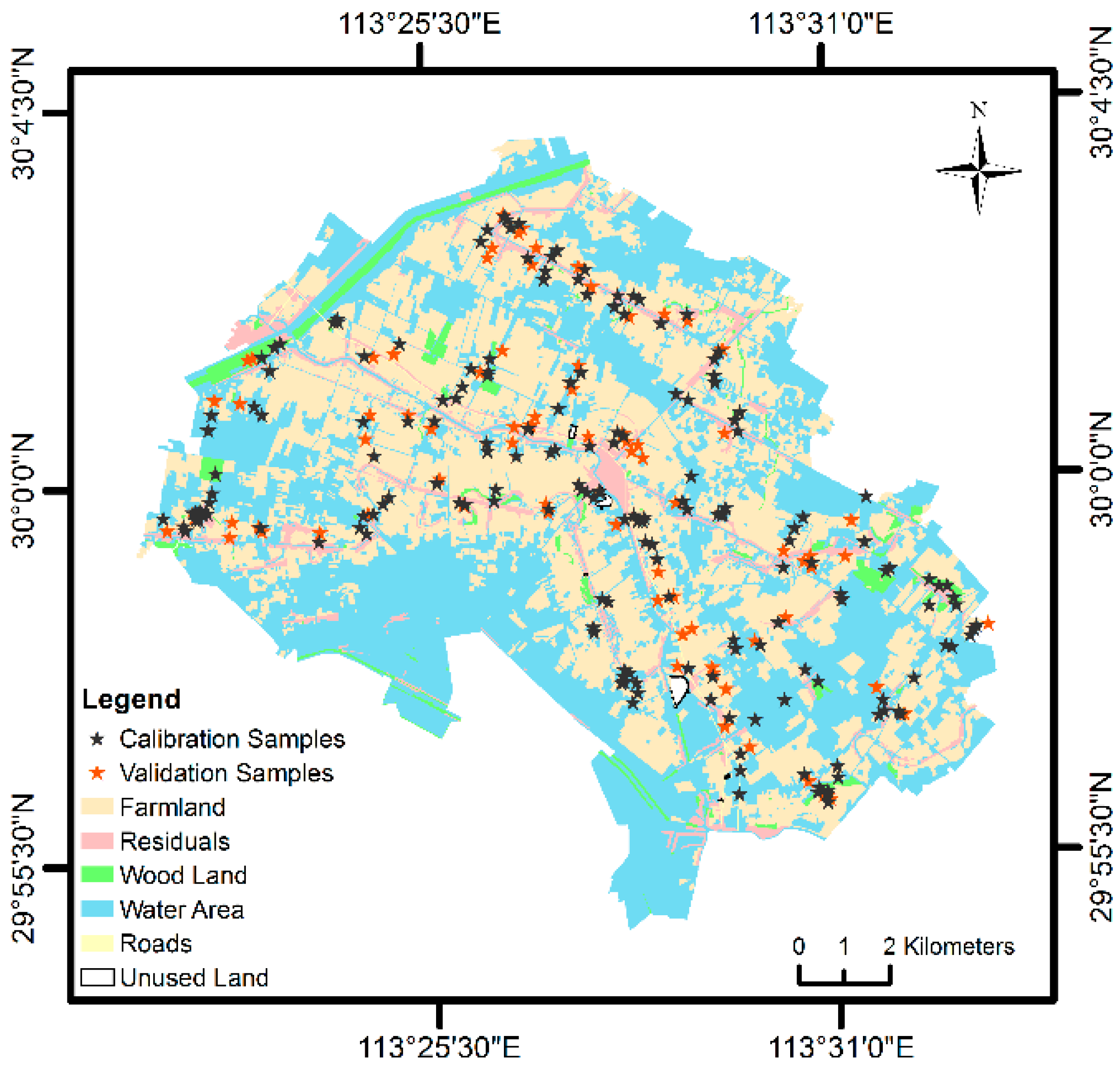
2.2. Sample Production and Spectral Measurement
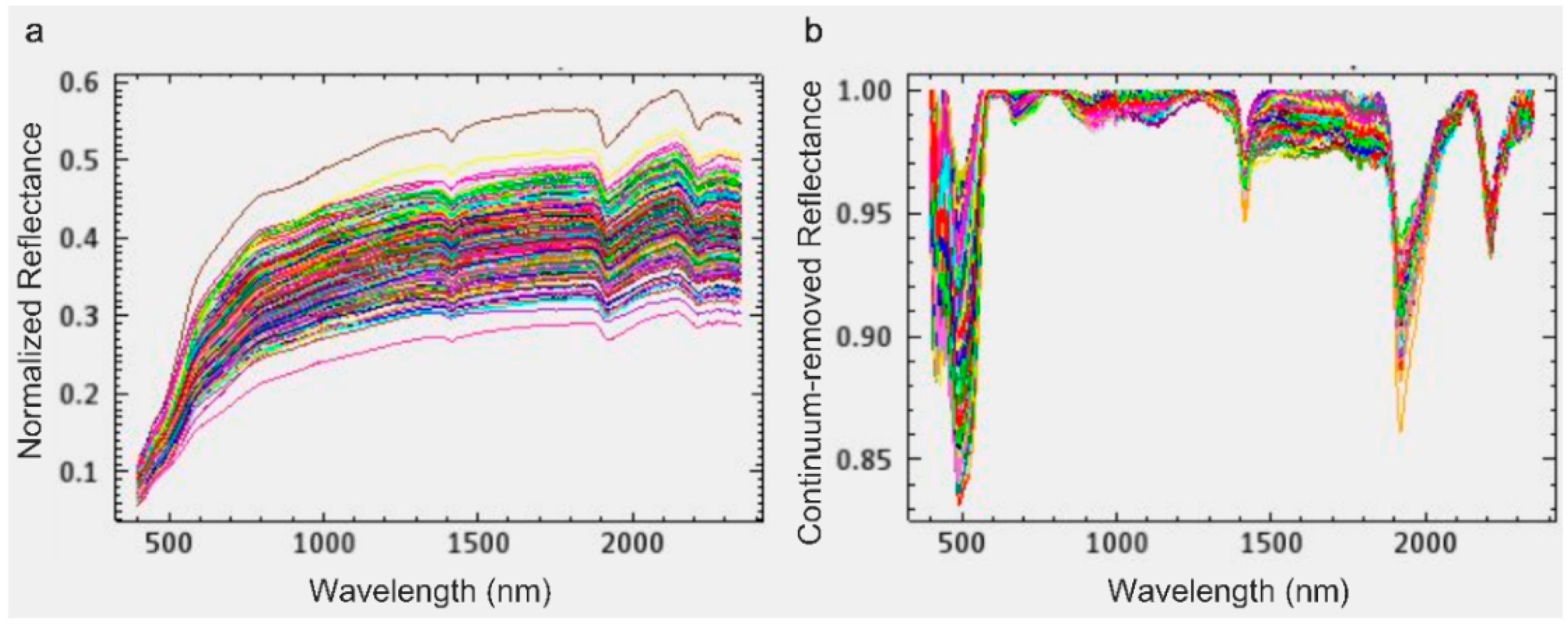
2.3. Spectral Preprocessing
2.4. Environmental Variables
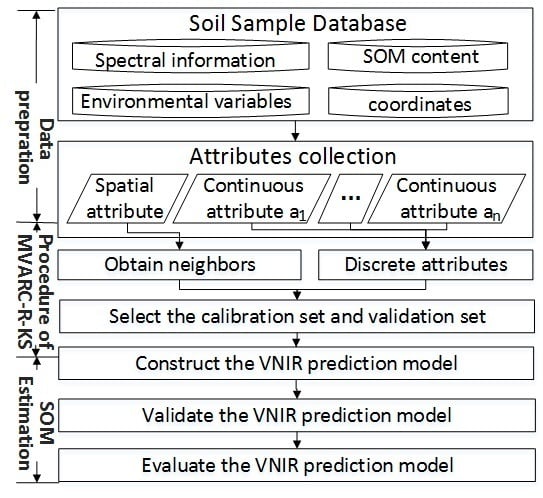
3. Methods
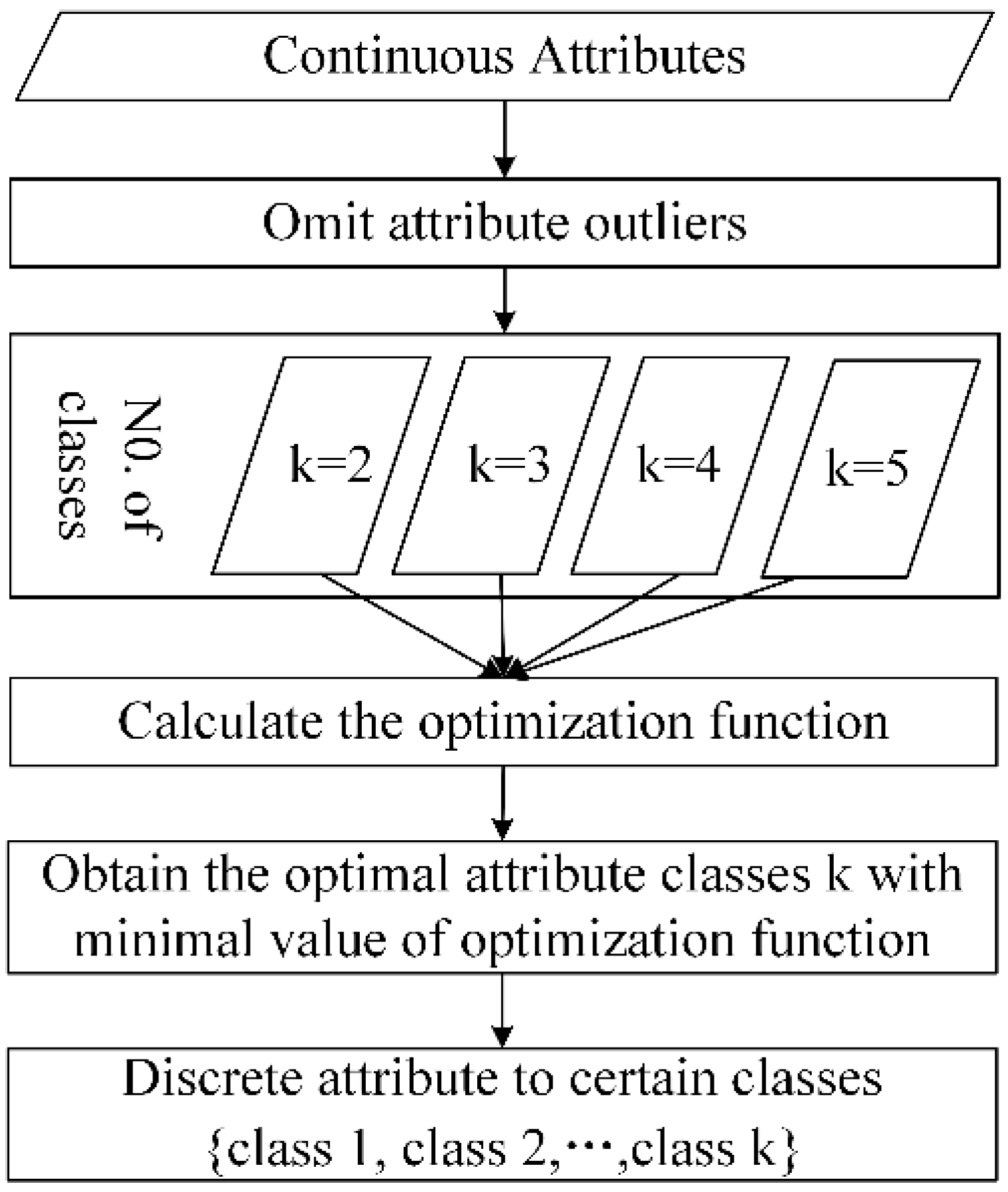
3.1. Calibration Set Selection Method
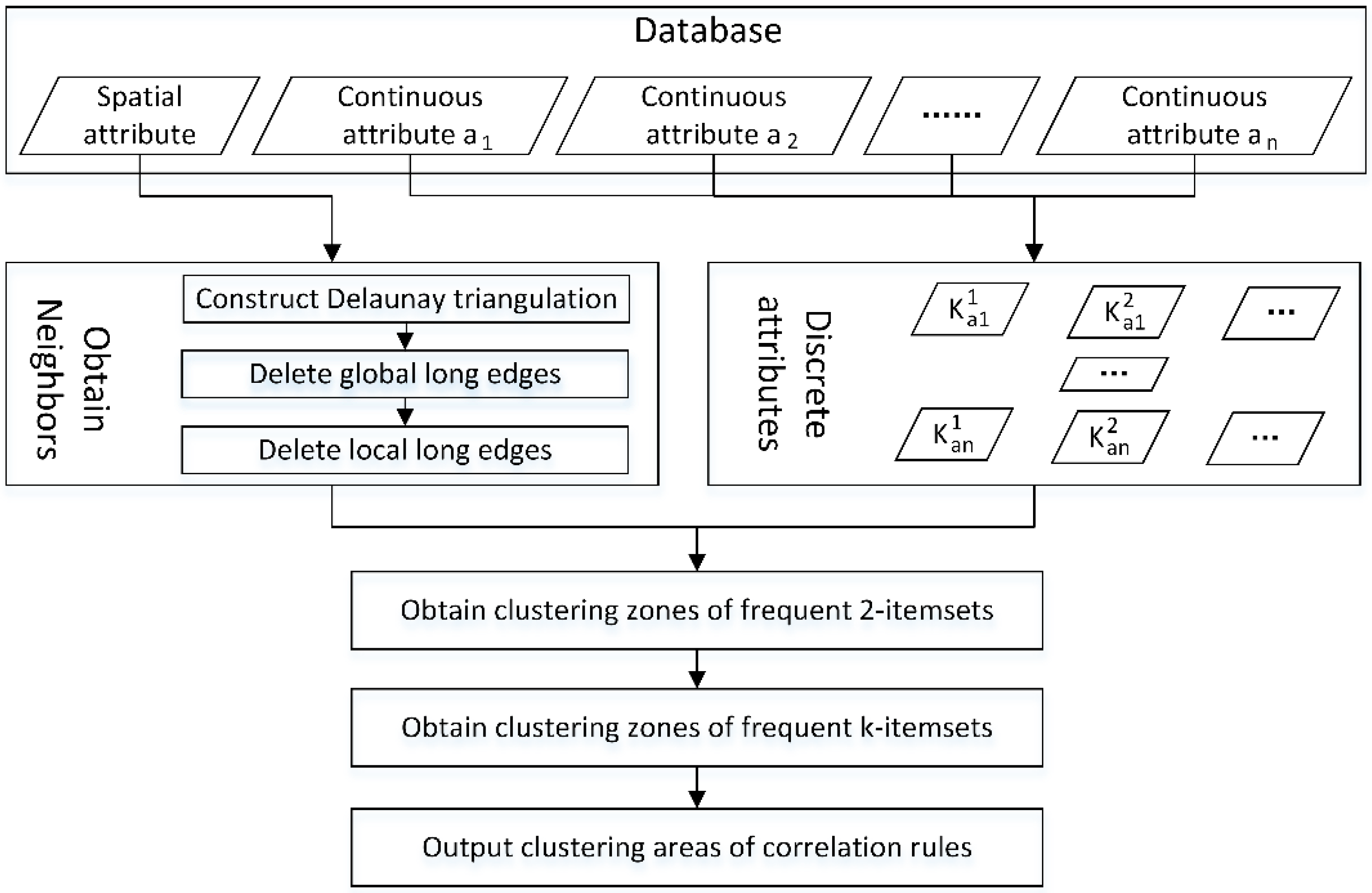
3.1.1. MVARC Method
- (1)
- Delete the noise with extreme values. The noise is detected and removed by the rule of three standard deviations.
- (2)
- Choose the optimal number of discretized classes. (Equation (3)) is used to select a suitable number (k) of discretized classes.
- (3)
- Discrete continuous attribute. The attribute is discretized to k classes by using the K-means algorithm, and the discretized classes are labeled as according to the attribute mean value of the discretized class, in ascending order.
- (1)
- Generate all possible item sets according to antecedents (e.g., SOM content) and consequents (e.g., environmental variables).
- (2)
- Select an unanalyzed two-item set and label it.
- (3)
- Calculate clustering cores. For object , if its attribute values equal the attribute values of the two-item set, is considered as a potential clustered object. For an potential clustered object its neighboring objects are defined as a neighboring area. In the neighboring area, if the 2 two-item sets are the frequent item sets (the support of the two-item sets is larger than MinS), then the object is defined as the clustering core.
- (4)
- Select an unlabeled clustering core and label.
- (5)
- Add the neighboring potential clustered objects of the clustering core and label them.
- (6)
- Judge the newly added objects. If the object is also a clustering core, iteratively return to (5).
- (7)
- A cluster of the frequent two-item sets is formed until no more objects can be added. The clustering area of the cluster is set as the minimum circumscribed convex polygon of objects in the cluster. In the present study, the minimum circumscribed convex polygon of the cluster is constructed using the edges of the Delaunay triangulation.
- (8)
- Implement operations (4) to (7), iteratively. When all the objects have been determined, the clustering zones of the analyzed two-item sets are all recognized.
- (9)
- Implement operations (2) to (8), iteratively. When all possible two-item sets have been determined, the detection of the clustering zones of all frequent two-item sets is finished.
3.1.2. Calibration Set Selection Based on the MVARC-R-KS Method
3.2. Construction and Fit Assessment of the VNIR Prediction Model
4. Results
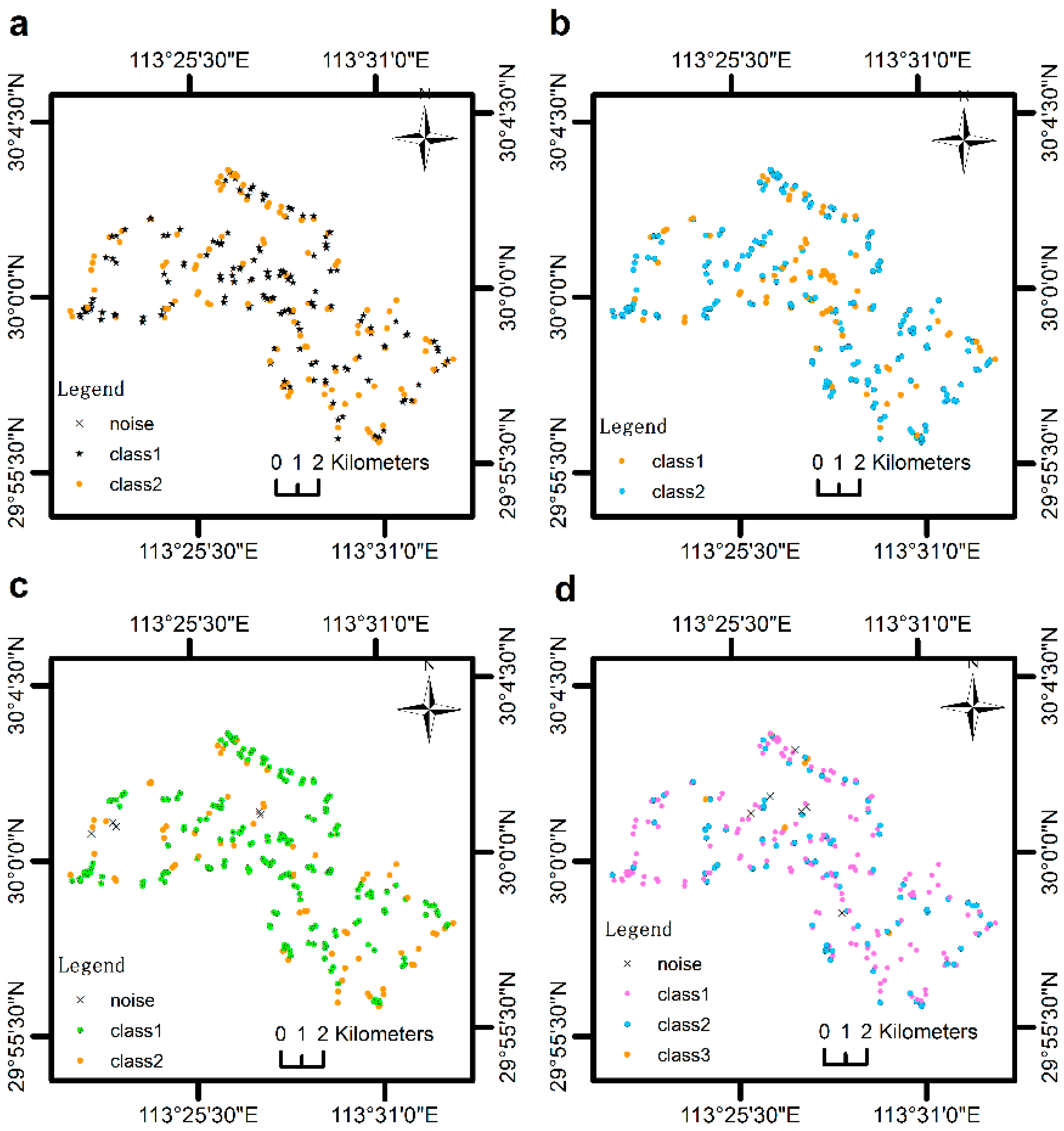
4.1. Validation of the MVARC Method on a Simulated Dataset
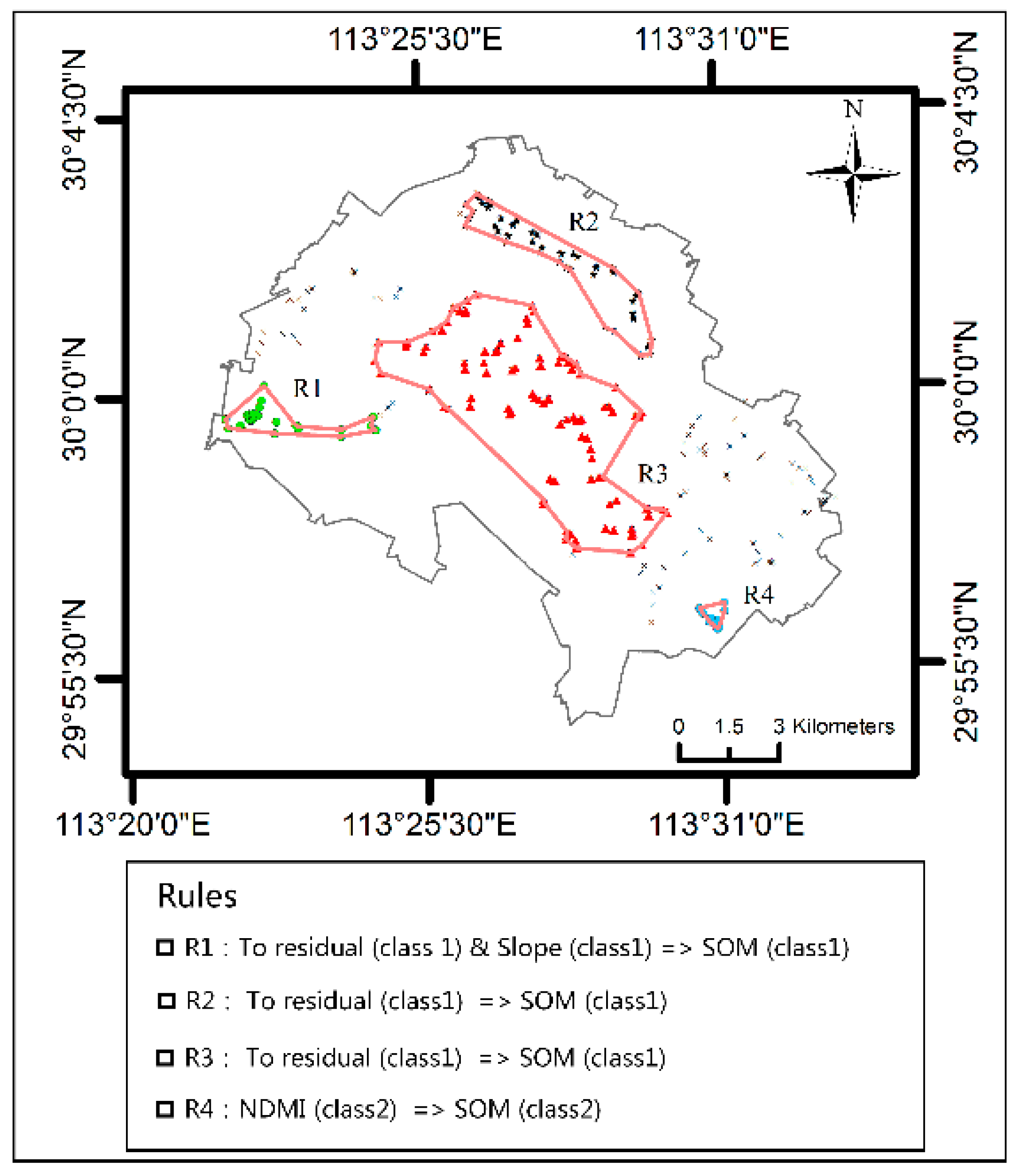
4.2. A Case Study of the MVARC-R-KS Method
4.2.1. VNIR Model Based on the Calibration Set Selected Using the MVARC-R-KS Method
4.2.2. Comparison of the MVARC-R-KS Method with Classical Methods for Selecting Calibration Sets
5. Discussion
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Batjes, N.H. Total carbon and nitrogen in the soils of the world. Eur. J. Soil Sci. 1996, 47, 151–163. [Google Scholar] [CrossRef]
- Mishra, U.; Torn, M.S.; Masanet, E.; Ogle, S.M. Improving regional soil carbon inventories: Combining the IPCC carbon inventory method with Regression Kriging. Geoderma 2012, 189–190, 288–295. [Google Scholar] [CrossRef]
- Simbahan, G.C.; Dobermann, A.; Goovaerts, P.; Ping, J.; Haddix, M.L. Fine-resolution mapping of soil organic carbon based on multivariate secondary data. Geoderma 2006, 132, 471–489. [Google Scholar] [CrossRef]
- Wu, C.F.; Wu, J.P.; Luo, Y.M.; Zhang, L.M.; Degloria, S.D. Spatial prediction of soil organic matter content using cokriging with remotely sensed data. Soil Sci. Soc. Am. J. 2009, 73, 1202–1208. [Google Scholar] [CrossRef]
- Gebbers, R.; Adamchuk, V.I. Precision agriculture and food security. Science 2010, 327, 828–831. [Google Scholar] [CrossRef] [PubMed]
- Song, H.; Qin, G.; Han, X.; Liu, H. Rapid prediction of soil organic matter by using visible infrared spectral technology. Trans. Chin. Soc. Agric. Mach. 2012, 43, 69–72. [Google Scholar]
- Daszykowski, M.; Walczak, B.; Massart, D.L. Representative subset selection. Anal. Chim. Acta 2002, 468, 91–103. [Google Scholar] [CrossRef]
- Qin, Y.; Xin, Z.; Yu, X.; Xiao, Y. Influence of vegetation restoration on topsoil organic carbon in a small catchment of the loess hilly region, china. PLoS ONE 2014, 9, e94489. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Guo, L.; Jiang, Q.; Zhang, H.; Chen, Y. Comparing geospatial techniques to predict soc stocks. Soil Tillage Res. 2015, 148, 46–58. [Google Scholar] [CrossRef]
- De Jong, E.; Schappert, H.J.V. Calculation of soil respiration and activity from CO2 profiles in the soil. Soil Sci. 1972, 113, 328–333. [Google Scholar] [CrossRef]
- Tang, J.; Baldocchi, D.D.; Qi, Y.; Xu, L. Assessing soil CO2 efflux using continuous measurements of CO2 profiles in soils with small solid-state sensors. Agric. For. Meteorol. 2003, 118, 207–220. [Google Scholar] [CrossRef]
- Guo, Y.; Shi, Z.; Li, H.Y.; Triantafilis, J. Application of digital soil mapping methods for identifying salinity management classes based on a study on Coastal Central China. Soil Use Manag. 2013, 29, 445–456. [Google Scholar] [CrossRef]
- Technometrics. Index to Contents, Volume 11, 1969. Available online: www.tandfonline.com/doi/abs/10.1080/00401706.1969.10490752 (accessed on 20 December 2016).
- Technometrics. Advances in Operations Research. Available online: http://amstat.tandfonline.com/doi/abs/10.1080/00401706.1977.10489604 (accessed on 20 December 2016).
- Wu, J. Research of NIR-Based Technology on Agriculture Products Detection; China Agricultural University: Beijing, China, 2006. (In Chinese) [Google Scholar]
- Liu, W.; Zhao, Z.; Yuan, H.; Song, C.; Li, X. An optimal selection method of samples of calibration set and validation set for spectral multivariate analysis. Spectrosc. Spectr. Anal. 2014, 34, 947–951. (In Chinese) [Google Scholar]
- Agrawal, R.; Srikant, R. Fast algorithmsfor mining association rules. In Proceedings of the 20th International Conference on Very Large Databases (VLDB), Santiago, Chile, 12–15 September 1994.
- Nosovskiy, G.V.; Liu, D.; Sourina, O. Automatic clustering and boundary detection algorithm based on adaptive influence function. Pattern Recognit. 2008, 41, 2757–2776. [Google Scholar] [CrossRef]
- Guerrero, C.; Wetterlind, J.; Bo, S.; Mouazen, A.M.; Gabarrón-Galeote, M.A.; Ruiz-Sinoga, J.D.; Zornoza, R.; Rossel, R.A.V. Do we really need large spectral libraries for local scale soc assessment with nir spectroscopy? Soil Tillage Res. 2015, 155, 501–509. [Google Scholar] [CrossRef]
- Liu, Y.; Song, Y.; Guo, L.; Chen, Y.; Lu, Y.; Liu, Y. Comparative analysis of soil organic carbon prediction model based on soil spectral reflectance. Trans. Chin. Soc. Agric. Eng. 2017, 33, 183–191. (In Chinese) [Google Scholar]
- Liu, Y.; Chen, Y. Feasibility of estimating cu contamination in floodplain soils using vnir spectroscopy—A case study in the le’an river floodplain, china. Soil Sediment Contam. Int. J. 2012, 21, 951–969. [Google Scholar] [CrossRef]
- Liu, Y.; Chen, Y. Estimation of total iron content in floodplain soils using vnir spectroscopy—A case study in the le’an river floodplain, China. Int. J. Remote Sens. 2012, 33, 5954–5972. [Google Scholar] [CrossRef]
- Liu, Y.; LU, Y.; Guo, L.; Xiao, F.; Chen, Y. Construction of calibration set based on the land use types in Visible and Near-Infrared (VIS-NIR) model for soil organic matter estimation. Acta Pedol. Sin. 2016, 53, 332–341. (In Chinese) [Google Scholar]
- Liu, Y.; Jiang, Q.; Fei, T.; Wang, J.; Shi, T.; Guo, K.; Li, X.; Chen, Y. Transferability of a visible and Near-Infrared Model for soil organic matter estimation in riparian landscapes. Remote Sens. 2014, 6, 4305–4322. [Google Scholar] [CrossRef]
- Li, W.; Zhang, C.; Wang, K. Comparison of geographically weighted regression and Regression Kriging for estimating the spatial distribution of soil organic matter. GISci. Remote Sens. 2012, 49, 915–932. [Google Scholar]
- Tan, R.; Liu, Y.; Liu, Y.; He, Q.; Ming, L.; Tang, S. Urban growth and its determinants across the Wuhan urban agglomeration, Central China. Habitat Int. 2014, 44, 268–281. [Google Scholar] [CrossRef]
- Koperski, K.; Han, J. Discovery of Spatial Association Rules in Geographic Information Databases; Springer: Berlin/Heidelberg, Germany, 2000; pp. 47–66. [Google Scholar]
- Celik, M.; Kang, J.M.; Shekhar, S. Zonal co-location pattern discovery with dynamic parameters. In Proceedings of the Seventh IEEE International Conference on Data Mining (ICDM 2007), Omaha, NE, USA, 28–31 October 2007; pp. 433–438.
- Ding, W.; Eick, C.F.; Yuan, X.; Wang, J.; Nicot, J.P. A framework for regional association rule mining and scoping in spatial datasets. Geoinformatica 2011, 15, 1–28. [Google Scholar] [CrossRef]
- Qian, F.; Chiew, K.; He, Q.; Huang, H. Mining regional co-location patterns with knng. J. Intell. Inf. Syst. 2013, 42, 485–505. (In Chinese) [Google Scholar] [CrossRef]
- Eick, C.F.; Parmar, R.; Ding, W.; Stepinski, T.F.; Nicot, J.P. Finding regional co-location patterns for sets of continuous variables in spatial datasets. In Proceedings of the ACM Sigspatial International Symposium on Advances in Geographic Information Systems, Irvine, CA, USA, 5–7 November 2008; pp. 20–193.
- Sha, Z. Algorithm of mining spatial association data under spatially heterogeneous environment. Geomat. Inf. Sci. Wuhan Univ. 2009, 34, 1480–1484. (In Chinese) [Google Scholar]
- Liu, Q.; Deng, M.; Shi, Y.; Wang, J. A density-based spatial clustering algorithm considering both spatial proximity and attribute similarity. Comput. Geosci. 2012, 46, 296–309. [Google Scholar] [CrossRef]
- Yaolin, L.; Xiaomi, W.; Dianfeng, L.; Leilei, L. An adaptive dual clustering algorithm based on hierarchical structure: A case study of settlements zoning. Trans. GIS 2016. [Google Scholar] [CrossRef]
- Rana, P.; Gautam, B.; Tokola, T. Optimizing the number of training areas for modeling above-ground biomass with als and multispectral remote sensing in subtropical Nepal. Int. J. Appl. Earth Obs. Geoinf. 2016, 49, 52–62. [Google Scholar] [CrossRef]
- Shi, T.; Cui, L.; Wang, J.; Fei, T.; Chen, Y.; Wu, G. Comparison of multivariate methods for estimating soil total nitrogen with Visible/Near-Infrared spectroscopy. Plant Soil 2012, 366, 363–375. [Google Scholar] [CrossRef]
- Viscarra Rossel, R.A.; McGlynn, R.N.; McBratney, A.B. Determining the composition of mineral-organic mixes using UV–VIS–NIR diffuse reflectance spectroscopy. Geoderma 2006, 137, 70–82. [Google Scholar] [CrossRef]
- Song, X.-D.; Brus, D.J.; Liu, F.; Li, D.-C.; Zhao, Y.-G.; Yang, J.-L.; Zhang, G.-L. Mapping soil organic carbon content by geographically weighted regression: A case study in the Heihe River Basin, China. Geoderma 2016, 261, 11–22. [Google Scholar] [CrossRef]
- Zeng, C.; Yang, L.; Zhu, A.X.; Rossiter, D.G.; Liu, J.; Liu, J.; Qin, C.; Wang, D. Mapping soil organic matter concentration at different scales using a mixed geographically weighted regression method. Geoderma 2016, 281, 69–82. [Google Scholar] [CrossRef]
- Kopačková, V.; Bendor, E. Normalizing reflectance from different spectrometers and protocols with an internal soil standard. Int. J. Remote Sens. 2016, 37, 1276–1290. [Google Scholar] [CrossRef]
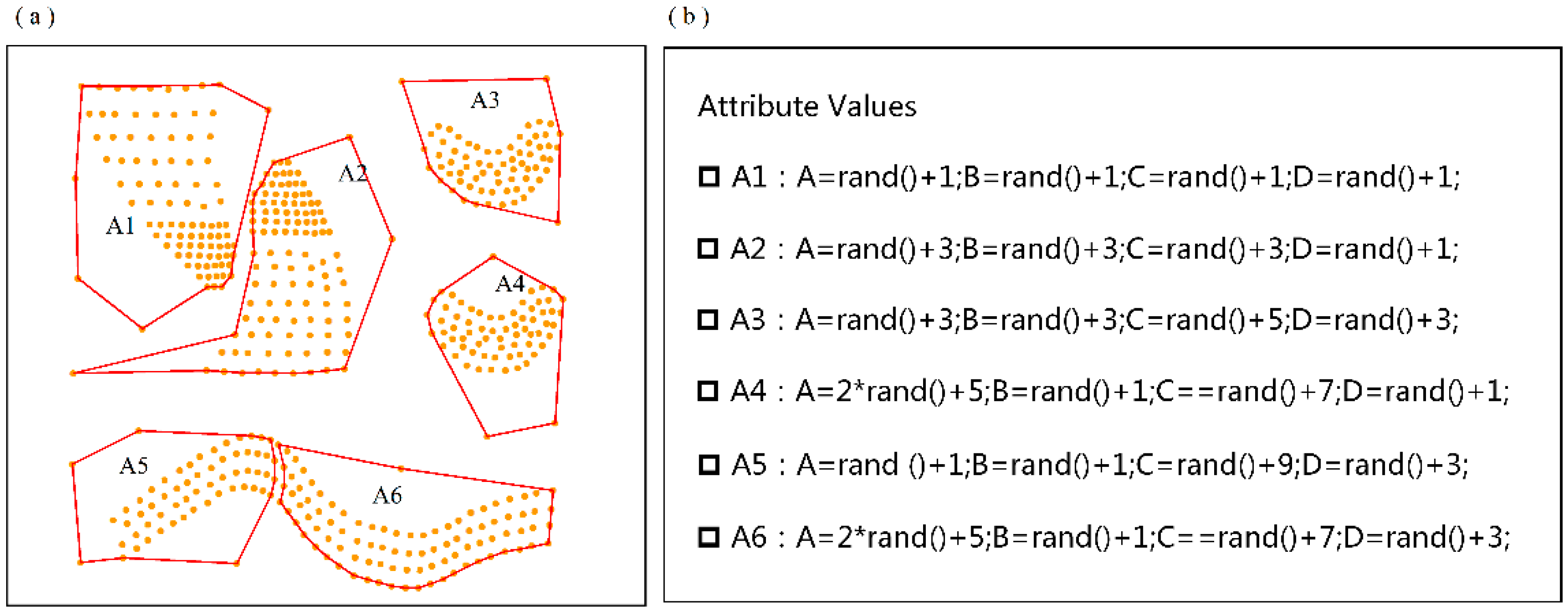
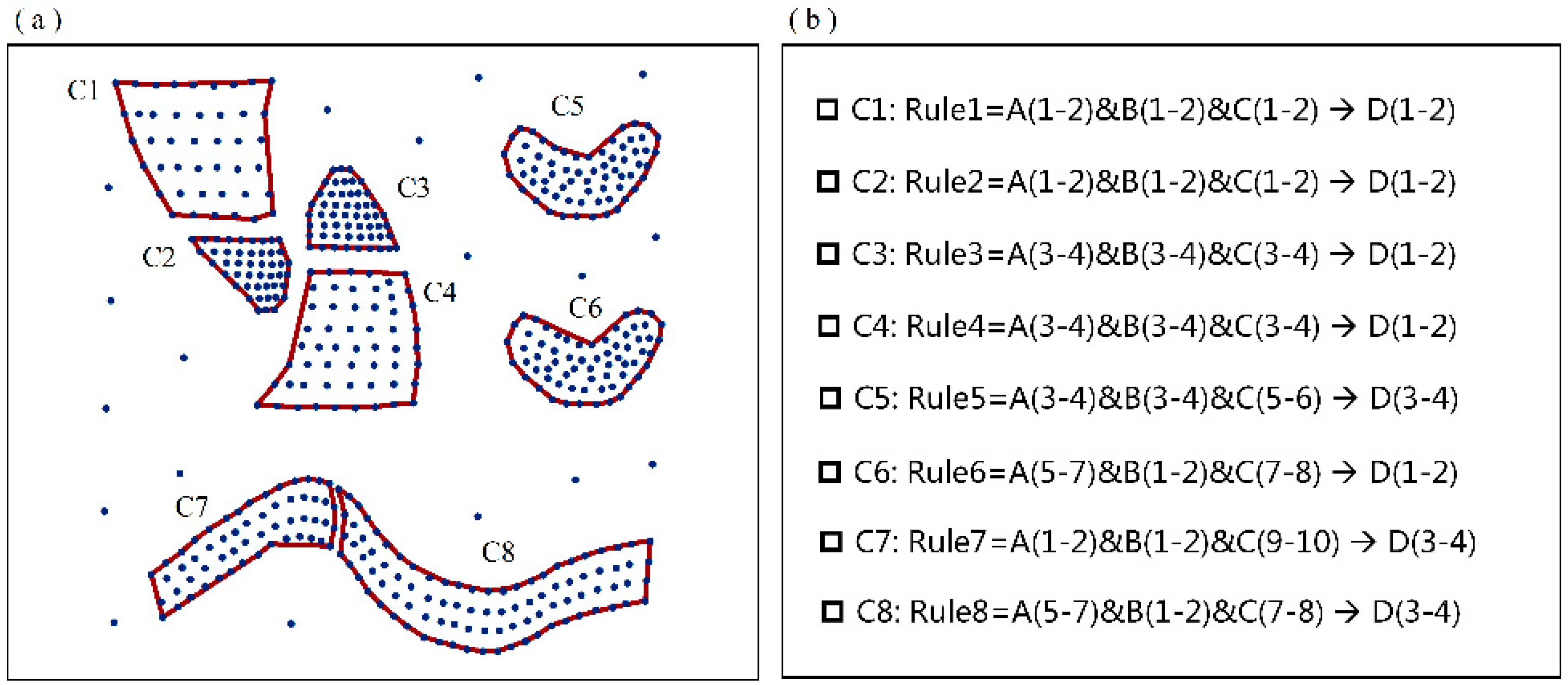
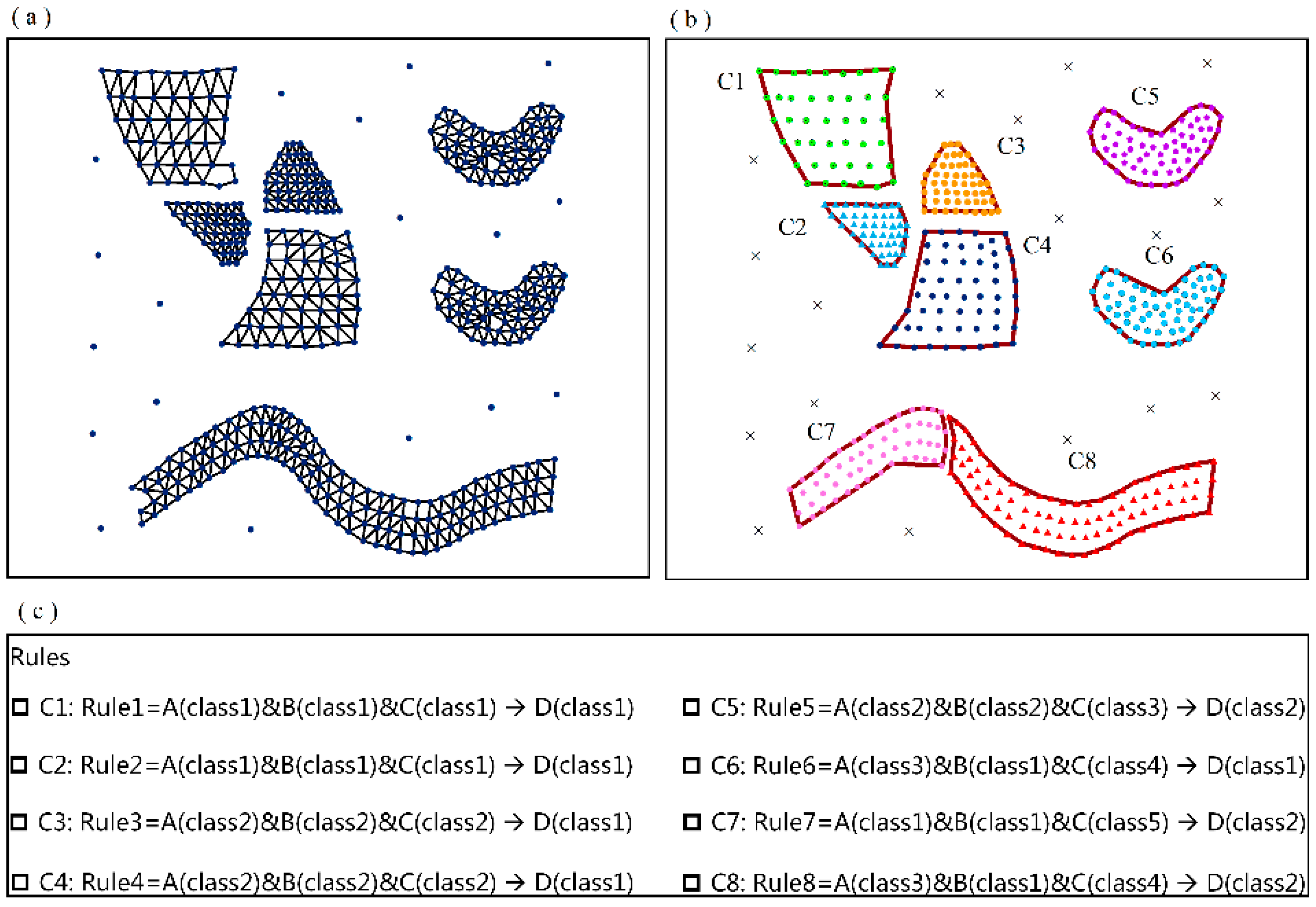
| Attributes | A | B | C | D | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Continuous attributes | 1–2 | 3–4 | 5–7 | 1–2 | 3–4 | 1–2 | 3–4 | 5–6 | 7–8 | 9–10 | 1–2 | 3–4 |
| Discretized attributes | class 1 | class 2 | class 3 | class 1 | class 2 | class 1 | class 2 | class 3 | class 4 | class 5 | class 1 | class 2 |
| Variables | Selection Method | RMSE | RPD | |||
|---|---|---|---|---|---|---|
| RMSEC (g·kg−1) | RMSEP (g·kg−1) | |||||
| Values of SOM | C | 0.73 | 0.53 | 6.39 | 8.21 | 1.48 |
| Spectral information | KS | 0.78 | 0.50 | 5.87 | 8.82 | 1.38 |
| SOM values, spectral information | Rank-KS | 0.71 | 0.56 | 6.51 | 8.48 | 1.51 |
| SOM values, spectral information, environmental variables | MVARC-R-KS | 0.79 | 0.70 | 5.83 | 6.98 | 1.81 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, X.; Chen, Y.; Guo, L.; Liu, L. Construction of the Calibration Set through Multivariate Analysis in Visible and Near-Infrared Prediction Model for Estimating Soil Organic Matter. Remote Sens. 2017, 9, 201. https://doi.org/10.3390/rs9030201
Wang X, Chen Y, Guo L, Liu L. Construction of the Calibration Set through Multivariate Analysis in Visible and Near-Infrared Prediction Model for Estimating Soil Organic Matter. Remote Sensing. 2017; 9(3):201. https://doi.org/10.3390/rs9030201
Chicago/Turabian StyleWang, Xiaomi, Yiyun Chen, Long Guo, and Leilei Liu. 2017. "Construction of the Calibration Set through Multivariate Analysis in Visible and Near-Infrared Prediction Model for Estimating Soil Organic Matter" Remote Sensing 9, no. 3: 201. https://doi.org/10.3390/rs9030201
APA StyleWang, X., Chen, Y., Guo, L., & Liu, L. (2017). Construction of the Calibration Set through Multivariate Analysis in Visible and Near-Infrared Prediction Model for Estimating Soil Organic Matter. Remote Sensing, 9(3), 201. https://doi.org/10.3390/rs9030201