Linear Multi-Task Learning for Predicting Soil Properties Using Field Spectroscopy
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Soil Field Spectroscopy Measurements
2.3. Soil Sampling and Physicochemical Lab Analysis
2.4. Spectral Preprocessing and Transformations
2.5. Learning Algorithms
2.6. Accuracy Comparison
3. Results
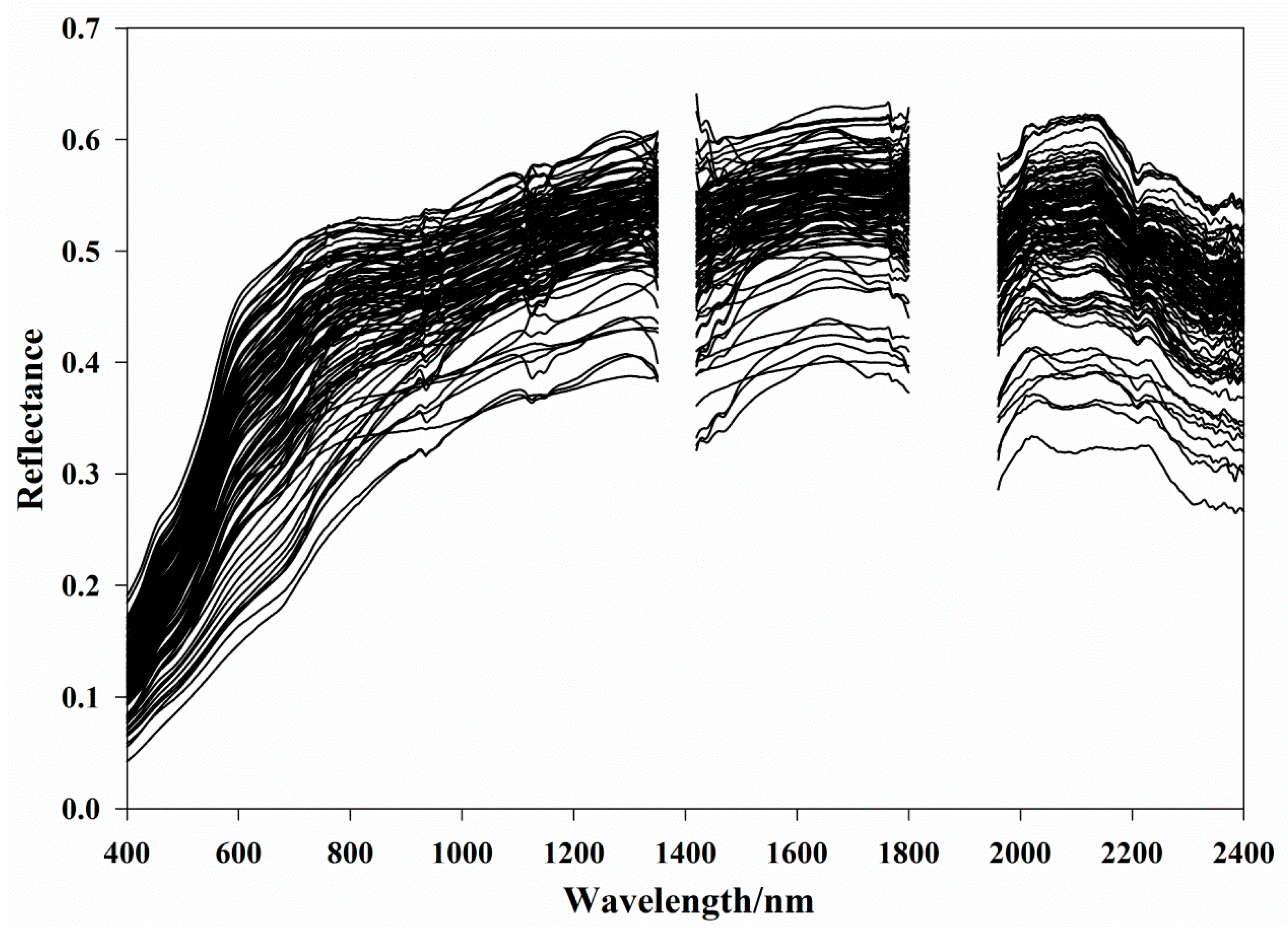
3.1. Soil Properties and Spectral Response
3.2. Model Performance of PLS-R
3.2.1. Prediction Results
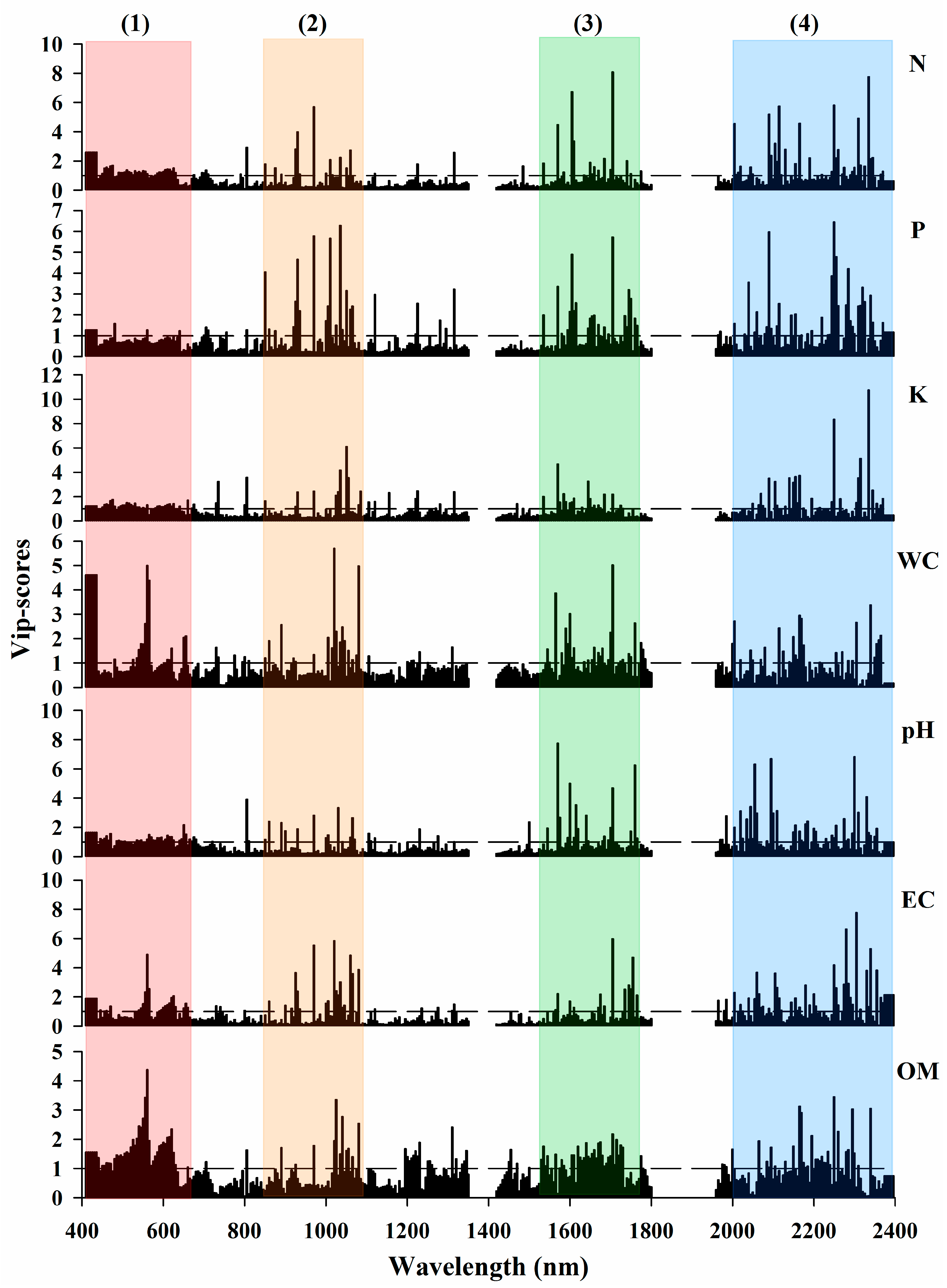
3.2.2. Feature Importance in PLS-R
3.3. Model Performance of LMTL
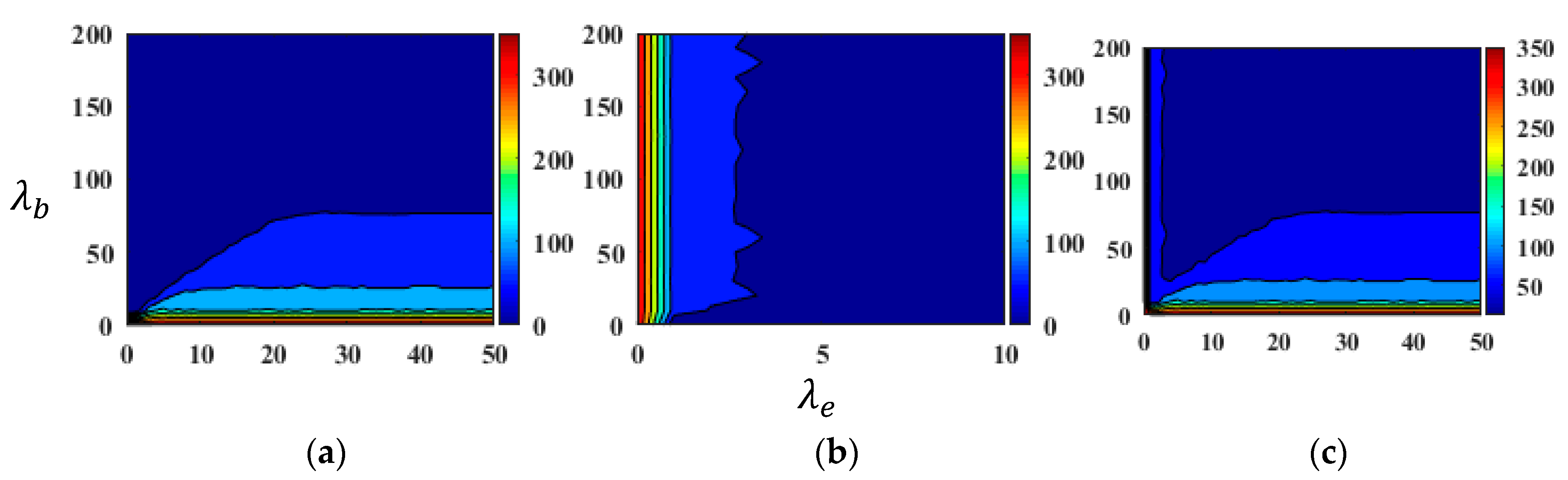
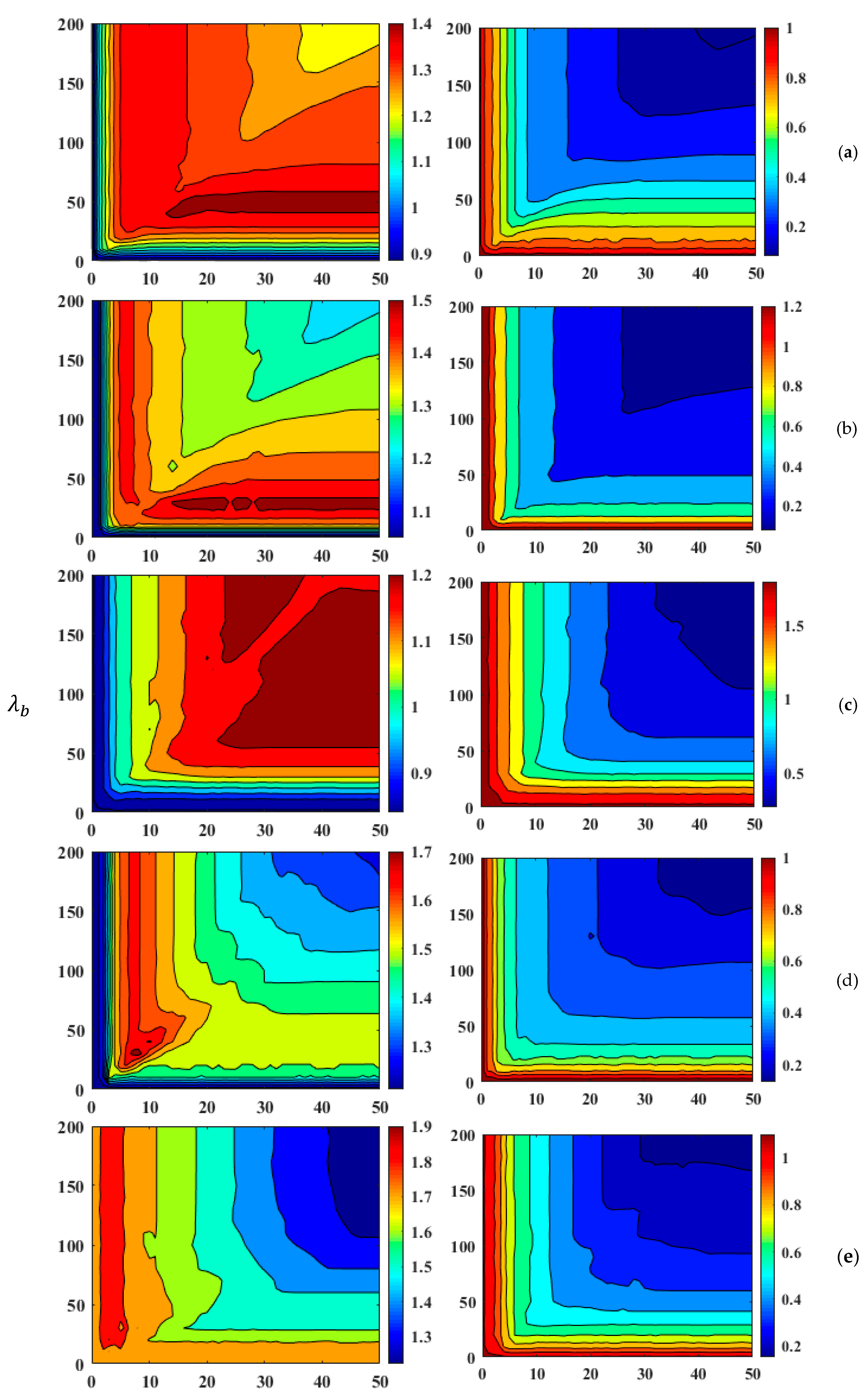
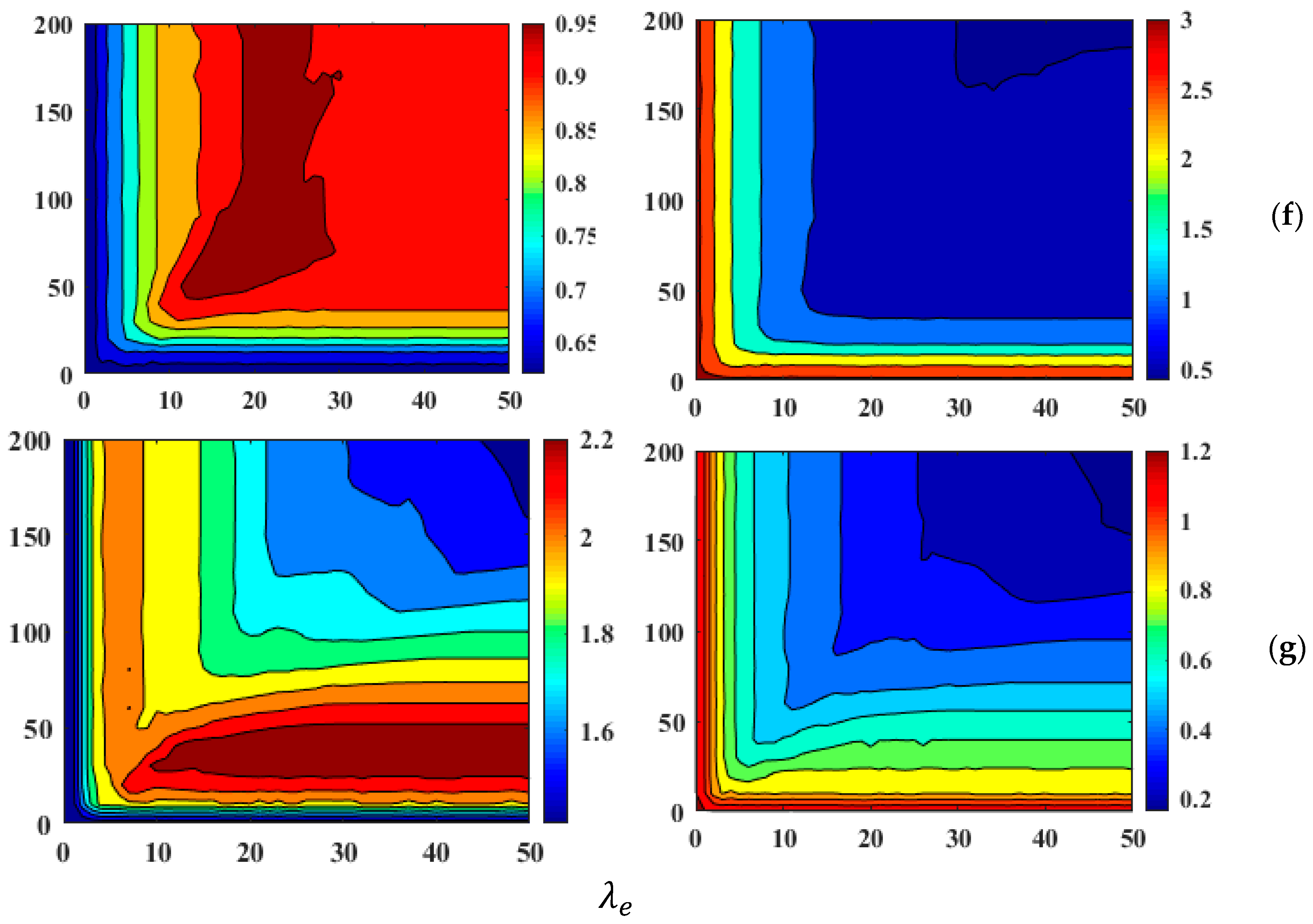
3.3.1. Effects of Regularization Parameters on Modeling
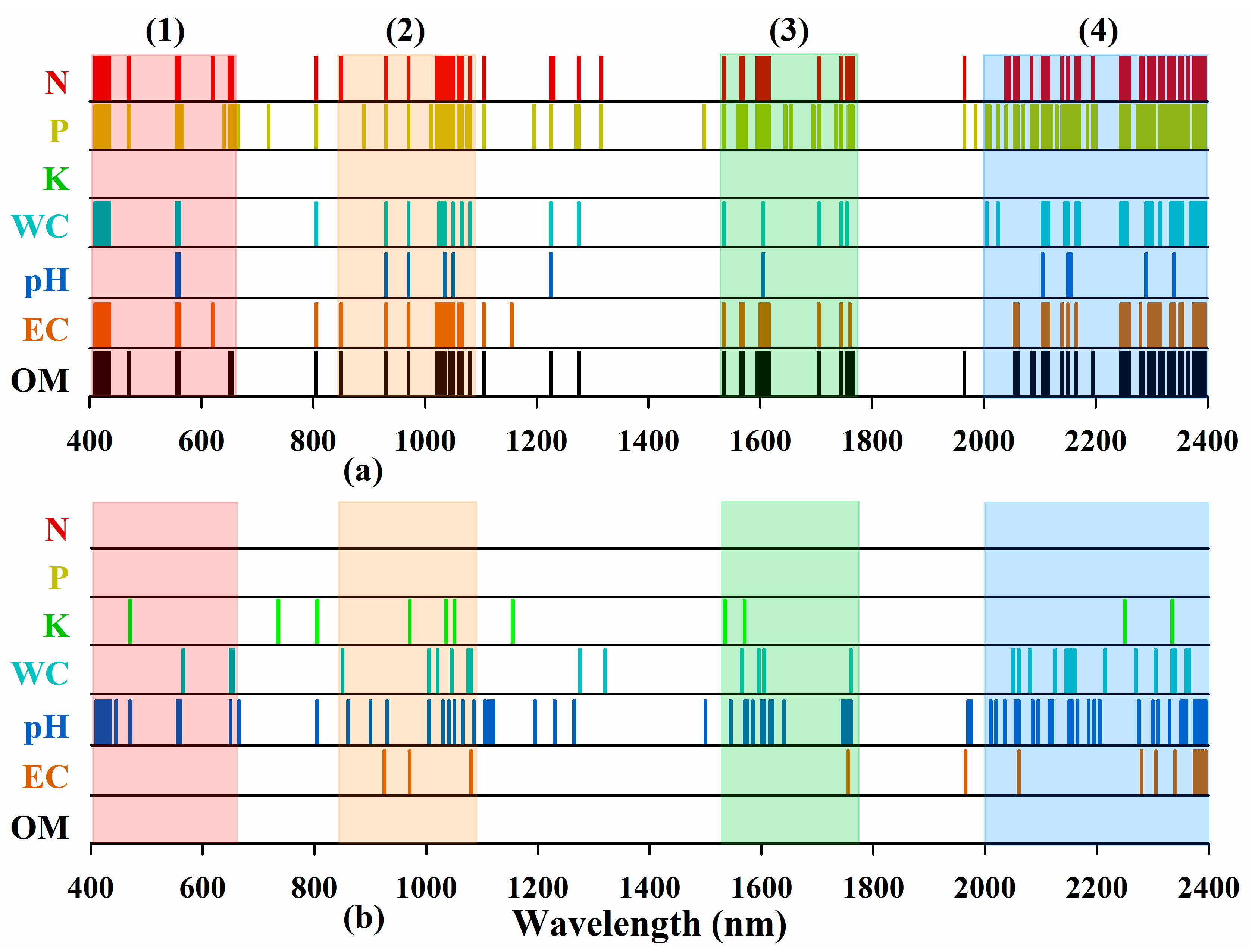
3.3.2. Prediction Results and Used Features
4. Discussion
4.1. Comparison of Two Algorithms
4.2. The Shared Features
4.3. Assessing the Performance of Field VNIR/SWIR Spectroscopy
4.4. Next Steps
5. Conclusions
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Ben-Dor, E.; Banin, A. Near-infared analysis as a rapid method to simultaneously evaluate several soil properties. Soil Sci. Soc. Am. J. 1995, 59, 364–372. [Google Scholar] [CrossRef]
- Rossel, R.A.V.; McBratney, A.B. Soil chemical analytical accuracy and costs: Implications from precision agriculture. Aust. J. Exp. Agric. 1998, 38, 765. [Google Scholar] [CrossRef]
- Stenberg, B.; Viscarra Rossel, R.A.; Mouazen, A.M.; Wetterlind, J. Chapter Five—Visible and Near Infrared Spectroscopy in Soil Science. Adv. Agron. 2010, 107, 163–215. [Google Scholar] [CrossRef]
- Jiang, Q.; Chen, Y.; Guo, L.; Fei, T.; Qi, K. Estimating Soil Organic Carbon of Cropland Soil at Different Levels of Soil Moisture Using VIS-NIR Spectroscopy. Remote Sens. 2016, 8, 755. [Google Scholar] [CrossRef]
- Selige, T.; Bohner, J.; Schmidhalter, U. High resolution topsoil mapping using hyperspectral image and field data in multivariate regression modeling procedures. Geoderma 2006, 136, 235–244. [Google Scholar] [CrossRef]
- Christy, C.D. Real-time measurement of soil attributes using on-the-go near infrared reflectance spectroscopy. Comput. Electron. Agric. 2008, 61, 10–19. [Google Scholar] [CrossRef]
- Mouazen, A.M.; Maleki, M.R.; De Baerdemaeker, J.; Ramon, H. On-line measurement of some selected soil properties using a VIS-NIR sensor. Soil Tillage Res. 2007, 93, 13–27. [Google Scholar] [CrossRef]
- Kodaira, M.; Shibusawa, S. Using a mobile real-time soil visible-near infrared sensor for high resolution soil property mapping. Geoderma 2013, 199, 64–79. [Google Scholar] [CrossRef]
- Viscarra Rossel, R.A.; Cattle, S.R.; Ortega, A.; Fouad, Y. In situ measurements of soil colour, mineral composition and clay content by vis-NIR spectroscopy. Geoderma 2009, 150, 253–266. [Google Scholar] [CrossRef]
- Kuang, B.; Mouazen, A.M. Effect of spiking strategy and ratio on calibration of on-line visible and near infrared soil sensor for measurement in European farms. Soil Tillage Res. 2013, 128, 125–136. [Google Scholar] [CrossRef]
- Maimaitiyiming, M.; Ghulam, A.; Bozzolo, A.; Wilkins, J.L.; Kwasniewski, M.T. Early Detection of Plant Physiological Responses to Different Levels of Water Stress Using Reflectance Spectroscopy. Remote Sens. 2017, 9, 745. [Google Scholar] [CrossRef]
- Sawut, M.; Ghulam, A.; Tiyip, T.; Zhang, Y.; Ding, J.; Zhang, F.; Maimaitiyiming, M. Estimating soil sand content using thermal infrared spectra in arid lands. Int. J. Appl. Earth Obs. Geoinf. 2014, 33, 203–210. [Google Scholar] [CrossRef]
- Qi, H.; Paz-Kagan, T.; Karnieli, A.; Jin, X.; Li, S. Evaluating calibration methods for predicting soil available nutrients using hyperspectral VNIR data. Soil Tillage Res. 2018, 175, 267–275. [Google Scholar] [CrossRef]
- Qi, H.; Jin, X.; Zhao, L.; Dedo, S.I.M.M.; Li, S. Predicting sandy soil moisture content with hyperspectral imaging. Int. J. Agric. Biol. Eng. 2017, 10. [Google Scholar] [CrossRef]
- Wold, S.; Ruhe, A.; Wold, H.; Dunn, W.J., III. The collinearity problem in linear regression. The partial least squares (PLS) approach to generalized inverses. SIAM J. Sci. Stat. Comput. 1984, 5, 735–743. [Google Scholar] [CrossRef]
- Ji, W.; Shi, Z.; Huang, J.; Li, S. In situ measurement of some soil properties in paddy soil using visible and near-infrared spectroscopy. PLoS ONE 2014, 9, e105708. [Google Scholar] [CrossRef] [PubMed]
- Daniel, K.W.; Tripathi, N.K.; Honda, K. Artificial neural network analysis of laboratory and in situ spectra for the estimation of macronutrients in soils of Lop Buri (Thailand). Aust. J. Soil Res. 2003, 41, 47–59. [Google Scholar] [CrossRef]
- Kuang, B.; Tekin, Y.; Mouazen, A.M. Comparison between artificial neural network and partial least squares for on-line visible and near infrared spectroscopy measurement of soil organic carbon, pH and clay content. Soil Tillage Res. 2015, 146, 243–252. [Google Scholar] [CrossRef]
- Bayer, A.; Bachmann, M.; Müller, A.; Kaufmann, H. A Comparison of feature-based MLR and PLS regression techniques for the prediction of three soil constituents in a degraded South African Ecosystem. Appl. Environ. Soil Sci. 2012, 2012, 1–20. [Google Scholar] [CrossRef]
- Nawar, S.; Mouazen, A.M. Predictive performance of mobile vis-near infrared spectroscopy for key soil properties at different geographical scales by using spiking and data mining techniques. CATENA 2017, 151, 118–129. [Google Scholar] [CrossRef]
- Wijewardane, N.K.; Ge, Y.; Morgan, C.L.S. Moisture insensitive prediction of soil properties from VNIR reflectance spectra based on external parameter orthogonalization. Geoderma 2016, 267, 92–101. [Google Scholar] [CrossRef]
- Dyar, M.D.; Carmosino, M.L.; Breves, E.A.; Ozanne, M.V.; Clegg, S.M.; Wiens, R.C. Comparison of partial least squares and lasso regression techniques as applied to laser-induced breakdown spectroscopy of geological samples. Spectrochim. Acta Part B At. Spectrosc. 2012, 70, 51–67. [Google Scholar] [CrossRef]
- Schirrmann, M.; Gebbers, R.; Kramer, E. Performance of Automated Near-Infrared Reflectance Spectrometry for Continuous in Situ Mapping of Soil Fertility at Field Scale. Vadose Zone J. 2013, 12, 1–14. [Google Scholar] [CrossRef]
- Melendez-Pastor, I.; Navarro-Pedreño, J.; Gómez, I.; Koch, M. Identifying optimal spectral bands to assess soil properties with VNIR radiometry in semi-arid soils. Geoderma 2008, 147, 126–132. [Google Scholar] [CrossRef]
- Rossel, R.A.V.; Behrens, T. Using data mining to model and interpret soil diffuse reflectance spectra. Geoderma 2010, 158, 46–54. [Google Scholar] [CrossRef]
- Gras, J.P.; Barthès, B.G.; Mahaut, B.; Trupin, S. Best practices for obtaining and processing field visible and near infrared (VNIR) spectra of topsoils. Geoderma 2014, 214–215, 126–134. [Google Scholar] [CrossRef]
- Ji, W.; Li, S.; Chen, S.; Shi, Z.; Viscarra Rossel, R.A.; Mouazen, A.M. Prediction of soil attributes using the Chinese soil spectral library and standardized spectra recorded at field conditions. Soil Tillage Res. 2016, 155, 492–500. [Google Scholar] [CrossRef]
- Soriano-Disla, J.M.; Janik, L.J.; Viscarra Rossel, R.A.; MacDonald, L.M.; McLaughlin, M.J. The Performance of Visible, Near-, and Mid-Infrared Reflectance Spectroscopy for Prediction of Soil Physical, Chemical, and Biological Properties. Appl. Spectrosc. Rev. 2014, 49, 139–186. [Google Scholar] [CrossRef]
- Evgeniou, T.; Pontil, M. Regularized Multi–Task Learning. In Proceedings of the Tenth ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Seattle, WA, USA, 22–25 August 2004; ACM: New York, NY, USA, 2004; pp. 109–117. [Google Scholar]
- Caruana, R. Multitask Learning. Mach. Learn. 1997, 28, 41–75. [Google Scholar] [CrossRef]
- Jalali, A.; Ravikumar, P.; Sanghavi, S.; Ruan, C. A Dirty Model for Multi-task Learning. In Proceedings of the Advances in Neural Information Processing Systems 23: 24th Annual Conference on Neural Information Processing Systems, Vancouver, BC, Canada, 6–9 December 2010; pp. 964–972. [Google Scholar]
- Liu, J.; Ji, S.; Ye, J. Multi-task feature learning via efficient l 2, 1-norm minimization. In Proceedings of the Twenty-Fifth Conference on Uncertainty in Artificial Intelligence, Montreal, QC, Canada, 18–21 June 2009. [Google Scholar]
- Zhang, M.L.; Zhou, Z.H. A Review On Multi-Label Learning Algorithms. IEEE Trans. Knowl. Data Eng. 2014, 26, 1819–1837. [Google Scholar] [CrossRef]
- Yair, A.; Danin, A. Spatial variations in vegetation as related to the soil moisture regime over an arid limestone hillside, northern Negev, Israel. Oecologia 1980, 47, 83–88. [Google Scholar] [CrossRef] [PubMed]
- Olsvig-Whittaker, L.; Shachak, M.; Yair, A. Vegetation patterns related to environmental factors in a Negev Desert watershed*. Plant Ecol. 1983, 54, 153–165. [Google Scholar] [CrossRef]
- Norman, R.; Stucki, J. The determination of nitrate and nitrite in soil extracts by ultraviolet spectrophotometry. Soil Sci. Soc. Am. 1981, 45, 347–353. [Google Scholar] [CrossRef]
- Olsen, S. Estimation of Available Phosphorus in Soils by Extraction with Sodium Bicarbonate; United States Department of Agriculture: Washington, DC, USA, 1954.
- Chen, S.; Peng, S.; Chen, B.; Chen, D.; Cheng, J. Effects of fire disturbance on the soil physical and chemical properties and vegetation of Pinus massoniana forest in south subtropical area. Acta Ecol. Sin. 2010, 30, 184–189. [Google Scholar] [CrossRef]
- McGill, R.; Tukey, J.W.; Larsen, W.A. Variations of Box Plots. Am. Stat. 1978, 32, 12. [Google Scholar] [CrossRef]
- Savitzky, A.; Golay, M.J.E. Smoothing and Differentiation of Data by Simplified Least Squares Procedures. Anal. Chem. 1964, 36, 1627–1639. [Google Scholar] [CrossRef]
- Helland, I.S.; Næs, T.; Isaksson, T. Related versions of the multiplicative scatter correction method for preprocessing spectroscopic data. Chemom. Intell. Lab. Syst. 1995, 29, 233–241. [Google Scholar] [CrossRef]
- Gholizadeh, A.; Boruvka, L.; Saberioon, M.M.; Kozák, J.; Vašát, R.; Nemecek, K. Comparing different data preprocessing methods for monitoring soil heavy metals based on soil spectral features. Soil Water Res. 2015, 10, 218–227. [Google Scholar] [CrossRef]
- Roberts, C.A.; Workman, J., Jr.; Reeves, J.B., III; Duckworth, J. Mathematical Data Preprocessing. In Near-Infrared Spectroscopy in Agriculture; American Society of Agronomy, Crop Science Society of America, Soil Science Society of America: Madison, WI, USA, 2004; pp. 115–132. [Google Scholar]
- Rinnan, Å.; van den Berg, F.; Engelsen, S.B. Review of the most common pre-processing techniques for near-infrared spectra. TrAC Trends Anal. Chem. 2009, 28, 1201–1222. [Google Scholar] [CrossRef]
- Wold, S.; Martens, H.; Wold, H. The multivariate calibration problem in chemistry solved by the PLS method. In Matrix Pencils. Lecture Notes in Mathematics; Kågström, B., Ruhe, A., Eds.; Springer: Berlin/Heidelberg, Germany, 1983; pp. 286–293. [Google Scholar]
- Wold, S.; Sjöström, M.; Eriksson, L. PLS-regression: A basic tool of chemometrics. Chemom. Intell. Lab. Syst. 2001, 58, 109–130. [Google Scholar] [CrossRef]
- Rossel, R.A.V.; Jeon, Y.S.; Odeh, I.O.A.; McBratney, A.B. Using a legacy soil sample to develop a mid-IR spectral library. Aust. J. Soil Res. 2008, 46, 1–16. [Google Scholar] [CrossRef]
- Paz-Kagan, T.; Shachak, M.; Zaady, E.; Karnieli, A. A spectral soil quality index (SSQI) for characterizing soil function in areas of changed land use. Geoderma 2014, 230–231, 171–184. [Google Scholar] [CrossRef]
- Hastie, T.; Tibshirani, R.; Friedman, J. The Elements of Statistical Learning; Data Mining, Inference and Prediction, 2nd ed.; Springer: New York, NY, USA, 2008; ISBN 9780387848570. [Google Scholar]
- Zhang, C.H.; Huang, J. The sparsity and bias of the lasso selection in high-dimensional linear regression. Ann. Stat. 2008, 36, 1567–1594. [Google Scholar] [CrossRef]
- Negahban, S.; Wainwright, M.J. Joint support recovery under high-dimensional scaling: Benefits and perils of 1,∞ -regularization. In Proceedings of the 21st International Conference on Neural Information Processing Systems, Vancouver, BC, Canada, 8–10 December 2008; pp. 1161–1168. [Google Scholar]
- Kennard, R.W.; Stone, L.A. Computer Aided Design of Experiments. Technometrics 1969, 11, 137–148. [Google Scholar] [CrossRef]
- Hsu, C.-W.; Chang, C.-C.; Lin, C.-J. A Practical Guide to Support Vector Classification. Available online: http://www.csie.ntu.edu.tw/~cjlin/papers/guide/guide.pdf (accessed on 12 October 2016).
- Chang, C.-W.; Laird, D.A.; Mausbach, M.J.; Hurburgh, C.R. Near-Infrared Reflectance Spectroscopy–Principal Components Regression Analyses of Soil Properties. Soil Sci. Soc. Am. J. 2001, 65, 480–490. [Google Scholar] [CrossRef]
- Weisberg, S. Applied Linear Regression, 3rd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2005; ISBN 9780471704096. [Google Scholar]
- Wen, W.; Hao, Z.; Yang, X. A heuristic weight-setting strategy and iteratively updating algorithm for weighted least-squares support vector regression. Neurocomputing 2008, 71, 3096–3103. [Google Scholar] [CrossRef]
- Peng, X. TSVR: An efficient Twin Support Vector Machine for regression. Neural Netw. 2010, 23, 365–372. [Google Scholar] [CrossRef] [PubMed]
- Shmueli, G. To explain or to predict? Stat. Sci. 2010, 25, 289–310. [Google Scholar] [CrossRef]
- Cope, M.; van der Zee, P.; Essenpreis, M.; Arridge, S.R.; Delpy, D.T. Data analysis methods for near-infrared spectroscopy of tissue: Problems in determining the relative cytochrome aa3 concentration. In Proceedings of the Time-Resolved Spectroscopy and Imaging of Tissues, Los Angeles, CA, USA, 23–24 January 1991; Volume 1431, pp. 251–262. [Google Scholar]
- Zhou, J.; Chen, J.; Ye, J. MALSAR: Multi-tAsk Learning via StructurAl Regularization. Arizona State University, 2012. Available online: http://www.yelab.net/software/MALSAR/ (accessed on 25 October 2016).
- Paz-Kagan, T.; Zaady, E.; Salbach, C.; Schmidt, A.; Lausch, A.; Zacharias, S.; Notesco, G.; Ben-Dor, E.; Karnieli, A. Mapping the spectral soil quality index (SSQI) using airborne imaging spectroscopy. Remote Sens. 2015, 7, 15748–15781. [Google Scholar] [CrossRef]
- Rollin, E.M.; Milton, E.J. Processing of high spectral resolution reflectance data for the retrieval of canopy water content information. Remote Sens. Environ. 1998, 65, 86–92. [Google Scholar] [CrossRef]
- Post, J.L.; Noble, P.N. The near-infrared combination band frequencies of dioctahedral smectites, micas, and illites. Clays Clay Miner. 1993, 41, 639–644. [Google Scholar] [CrossRef]
- Mouazen, A.M.; Kuang, B.; De Baerdemaeker, J.; Ramon, H. Comparison among principal component, partial least squares and back propagation neural network analyses for accuracy of measurement of selected soil properties with visible and near infrared spectroscopy. Geoderma 2010, 158, 23–31. [Google Scholar] [CrossRef]
- Wang, J.; He, T.; Lv, C.; Chen, Y.; Jian, W. Mapping soil organic matter based on land degradation spectral response units using Hyperion images. Int. J. Appl. Earth Obs. Geoinf. 2010, 12, S171–S180. [Google Scholar] [CrossRef]
- Rodriguez, J.M.; Ustin, S.L.; Riaño, D. Contributions of imaging spectroscopy to improve estimates of evapotranspiration. Hydrol. Process. 2011, 25, 4069–4081. [Google Scholar] [CrossRef]
- Dehaan, R.; Taylor, G.R. Image-derived spectral endmembers as indicators of salinisation. Int. J. Remote Sens. 2003, 24, 775–794. [Google Scholar] [CrossRef]
- Weidong, L.; Baret, F.; Xingfa, G.; Qingxi, T.; Lanfen, Z.; Bing, Z. Relating soil surface moisture to reflectance. Remote Sens. Environ. 2002, 81, 238–246. [Google Scholar] [CrossRef]
- Van Evert, F.K.; Van Der Schans, D.A.; Van Geel, W.C.A.; Malda, J.T.; Vona, V. From theory to practice: Using canopy reflectance to determine sidedress N rate in potatoes. In Precision Agriculture ’13; Stafford, J.V., Ed.; Wageningen Academic Publishers: Wageningen, The Netherlands, 2013; pp. 119–127. [Google Scholar]
- Parfitt, R.L.; Smart, R.S.C. The mechanism of sulfate adsorption on iron oxides. Soil Sci. Soc. Am. J. 1978, 42, 48–50. [Google Scholar] [CrossRef]
- Kusumo, B.H.; Hedley, C.B.; Hedley, M.J.; Hueni, A.; Tuohy, M.P.; Arnold, G.C. The use of diffuse reflectance spectroscopy for in situ carbon and nitrogen analysis of pastoral soils. Aust. J. Soil Res. 2008, 46, 623–635. [Google Scholar] [CrossRef]
- Summers, D.; Lewis, M.; Ostendorf, B.; Chittleborough, D. Visible near-infrared reflectance spectroscopy as a predictive indicator of soil properties. Ecol. Indic. 2011, 11, 123–131. [Google Scholar] [CrossRef]
- Baumgardner, M.; Silva, L.; Biehl, L.; Stoner, E. Reflectance properties of soils. Adv. Agron. 1986, 38, 1–44. [Google Scholar]
- Ji, W.; Viscarra Rossel, R.A.; Shi, Z. Accounting for the effects of water and the environment on proximally sensed vis-NIR soil spectra and their calibrations. Eur. J. Soil Sci. 2015, 66, 555–565. [Google Scholar] [CrossRef]
- Clark, R.N.; King, T.V.V.; Klejwa, M.; Swayze, G.; Vergo, N. High Spectral Resolution Reflectance Spectroscopy of Minerals. J. Geophys. Res. 1990, 12653–12680. [Google Scholar] [CrossRef]
- Stoner, E.R.; Baumgardner, M.F. Physicochemical, Site, and Bidirectional Reflectance Factor Characteristics of Uniformly Moist Soils; Laboratory for Applications of Remote Sensing, Purdue University: West Lafayette, IN, USA, 1980; Volume 1. [Google Scholar]
- Farifteh, J.; van der Meer, F.; van der Meijde, M.; Atzberger, C. Spectral characteristics of salt-affected soils: A laboratory experiment. Geoderma 2008, 145, 196–206. [Google Scholar] [CrossRef]
- Collobert, R.; Weston, J. A unified architecture for natural language processing: Deep neural networks with multitask learning. In Proceedings of the 25th International Conference on Machine Learning, Helsinki, Finland, 5–9 July 2008; ACM: New York, NY, USA, 2008; pp. 160–167. [Google Scholar]
- Seltzer, M.L.; Droppo, J. Multi-Task Learning in Deep Neural Networks for Improved Phoneme Recognition. In Proceedings of the 2013 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Vancouver, BC, Canada, 26–31 May 2013; pp. 6965–6969. [Google Scholar]
| Soil Properties | Units | Mean | STD | Min | Median | Max |
|---|---|---|---|---|---|---|
| N | mg/Kg | 27.42 | 15.57 | 5.73 | 22.66 | 72.56 |
| P | mg/Kg | 19.36 | 9.70 | 7.00 | 16.70 | 55.20 |
| K | mg/Kg | 25.44 | 13.49 | 7.30 | 23.45 | 64.80 |
| WC | % | 5.61 | 1.81 | 3.01 | 4.92 | 10.77 |
| pH | 7.20 | 0.21 | 6.78 | 7.14 | 7.87 | |
| EC | µS/cm | 0.50 | 0.22 | 0.18 | 0.46 | 1.77 |
| OM | % | 4.29 | 1.92 | 1.73 | 3.68 | 9.58 |
| Soil Properties | N | P | K | WC | pH | EC | OM |
|---|---|---|---|---|---|---|---|
| N | 1.00 | ||||||
| P | 0.69 | 1.00 | |||||
| K | 0.58 | 0.57 | 1.00 | ||||
| WC | 0.24 | 0.15 | 0.22 | 1.00 | |||
| pH | −0.25 | −0.27 | −0.24 | −0.30 | 1.00 | ||
| EC | 0.30 | 0.19 | 0.28 | 0.25 | −0.38 | 1.00 | |
| OM | 0.45 | 0.39 | 0.51 | 0.74 | −0.26 | 0.31 | 1.00 |
| Algorithm | Property | Parameter 1 | n 2 | Calibration | Validation | Accuracy Category | |||
|---|---|---|---|---|---|---|---|---|---|
| RPD | SSR/SST | RPD | SSR/SST | ||||||
| PLS-R | N | 5 | 355 | 2.15 | 0.78 | 1.27 | 0.66 | C | |
| P | 5 | 355 | 1.85 | 0.71 | 1.42 | 0.80 | B | ||
| K | 6 | 355 | 2.71 | 0.86 | 0.97 | - | C | ||
| WC | 4 | 355 | 1.99 | 0.75 | 1.53 | 0.72 | B | ||
| pH | 6 | 355 | 2.78 | 0.87 | 1.78 | 0.83 | B | ||
| EC | 6 | 355 | 2.33 | 0.81 | 0.64 | - | C | ||
| OM | 5 | 355 | 2.58 | 0.85 | 2.22 | 0.82 | A | ||
| LMTL | N | 40 | 20 | 81 | 1.94 | 0.53 | 1.40 | 0.58 | B |
| P | 20 | 21 | 114 | 2.18 | 0.54 | 1.49 | 0.64 | B | |
| K | 160 | 26 | 11 | 1.56 | 0.29 | 1.22 | 0.52 | C | |
| WC | 30 | 7 | 75 | 2.30 | 0.61 | 1.71 | 0.55 | B | |
| pH | 20 | 3 | 79 | 3.45 | 0.76 | 1.90 | 0.92 | B | |
| EC | 60 | 20 | 66 | 1.42 | 0.21 | 0.98 | - | C | |
| OM | 40 | 25 | 75 | 2.31 | 0.68 | 2.29 | 0.70 | A | |
| Property | Range (nm) | Measurement Method | Regression Algorithm | RPD | R2 | Accuracy Category | Literature |
|---|---|---|---|---|---|---|---|
| N | 500–1600 | Mobile | PLS-R | 1.60 | 0.69 | B | [8] |
| 350–2500 | Contact probe | LS-SVM | 1.91 | 0.76 | B | [16] | |
| P | 920–1718 | Mobile | PCR | - | 0.65 | B | [6] |
| 306.5–1710.9 | Mobile | PLS-R | 1.80 | 0.69 | B | [7] | |
| 500–1600 | Mobile | PLS-R | 1.80 | 0.72 | B | [8] | |
| 350–2500 | Contact probe | PLS | 1.33 | 0.43 | C | [16] | |
| 400–1050 | Non-contact | ANN | - | 0.87 | A | [17] | |
| 350–2500 | Contact probe | MPLS-R | 1.70 | 0.65 | B | [26] | |
| 1100–2300 | Mobile | PLS-R | 1.27 | 0.41 | C | [23] | |
| K | 920–1718 | Mobile | PCR | - | 0.26 | C | [6] |
| 350–2500 | Contact probe | LS-SVM | 0.91 | 0.14 | C | [16] | |
| 400–1050 | Non-contact | ANN | - | 0.85 | A | [17] | |
| 350–2500 | Contact probe | MPLS-R | 2.90 | 0.88 | A | [26] | |
| 1100–2300 | Mobile | PLS-R | 1.08 | 0.19 | C | [23] | |
| WC | 920–1718 | Mobile | PCR | - | 0.40 | C | [6] |
| 306.5–1710.9 | Mobile | PLS-R | 3.00 | 0.89 | A | [7] | |
| 500–1600 | Mobile | PLS-R | 3.60 | 0.93 | A | [8] | |
| 305–2200 | Mobile | PLS-R | 3.54 | - | A | [10] | |
| 305–2200 | Mobile | MARS | 3.25 | 0.72 | A | [20] | |
| pH | 920–1718 | Mobile | PCR | - | 0.43 | C | [6] |
| 306.5–1710.9 | Mobile | PLS-R | 2.14 | 0.71 | A | [7] | |
| 500–1600 | Mobile | PLS-R | 1.6 | 0.69 | B | [8] | |
| 350–2500 | Contact probe | LS-SVM | 2.23 | 0.80 | A | [16] | |
| 1100–2300 | Mobile | PLS-R | 1.88 | 0.71 | B | [23] | |
| EC | 500–1600 | Mobile | PLS-R | 1.30 | 0.60 | C | [8] |
| OM | 920–1718 | Mobile | PCR | - | 0.67 | B | [6] |
| 500–1600 | Mobile | PLS-R | 2.90 | 0.90 | A | [8] | |
| 350–2500 | Contact probe | LS-SVM | 2.18 | 0.81 | A | [16] | |
| 400–1050 | Non-contact | ANN | - | 0.84 | A | [17] | |
| 350–2500 | Contact probe | MPLS-R | 2.80 | 0.86 | A | [26] | |
| 350–2500 | Contact probe | PLS-R | 1.94 | 0.79 | B | [74] | |
| 1100–2300 | Mobile | PLS-R | 1.59 | 0.61 | B | [23] |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qi, H.; Paz-Kagan, T.; Karnieli, A.; Li, S. Linear Multi-Task Learning for Predicting Soil Properties Using Field Spectroscopy. Remote Sens. 2017, 9, 1099. https://doi.org/10.3390/rs9111099
Qi H, Paz-Kagan T, Karnieli A, Li S. Linear Multi-Task Learning for Predicting Soil Properties Using Field Spectroscopy. Remote Sensing. 2017; 9(11):1099. https://doi.org/10.3390/rs9111099
Chicago/Turabian StyleQi, Haijun, Tarin Paz-Kagan, Arnon Karnieli, and Shaowen Li. 2017. "Linear Multi-Task Learning for Predicting Soil Properties Using Field Spectroscopy" Remote Sensing 9, no. 11: 1099. https://doi.org/10.3390/rs9111099
APA StyleQi, H., Paz-Kagan, T., Karnieli, A., & Li, S. (2017). Linear Multi-Task Learning for Predicting Soil Properties Using Field Spectroscopy. Remote Sensing, 9(11), 1099. https://doi.org/10.3390/rs9111099





