Tree Species Classification in Temperate Forests Using Formosat-2 Satellite Image Time Series
Abstract
:1. Introduction
- Develop an optimal classification strategy for mapping tree species in natural forests and tree plantations at three class hierarchy levels using dense Formosat-2 SITS.
- Quantify the effect of removing noise (i.e., clouds and cloud shadows) in the time series on classification accuracy.
- Identify the best supervised learning classifier among parametric and nonparametric methods.
- Evaluate the sensitivity of the classification accuracy to the dimensionality of the data and to the feature space, by comparing the classification results based on different feature sets: spectral bands, NDVI index or spectral bands and NDVI.
2. Study Area and Data
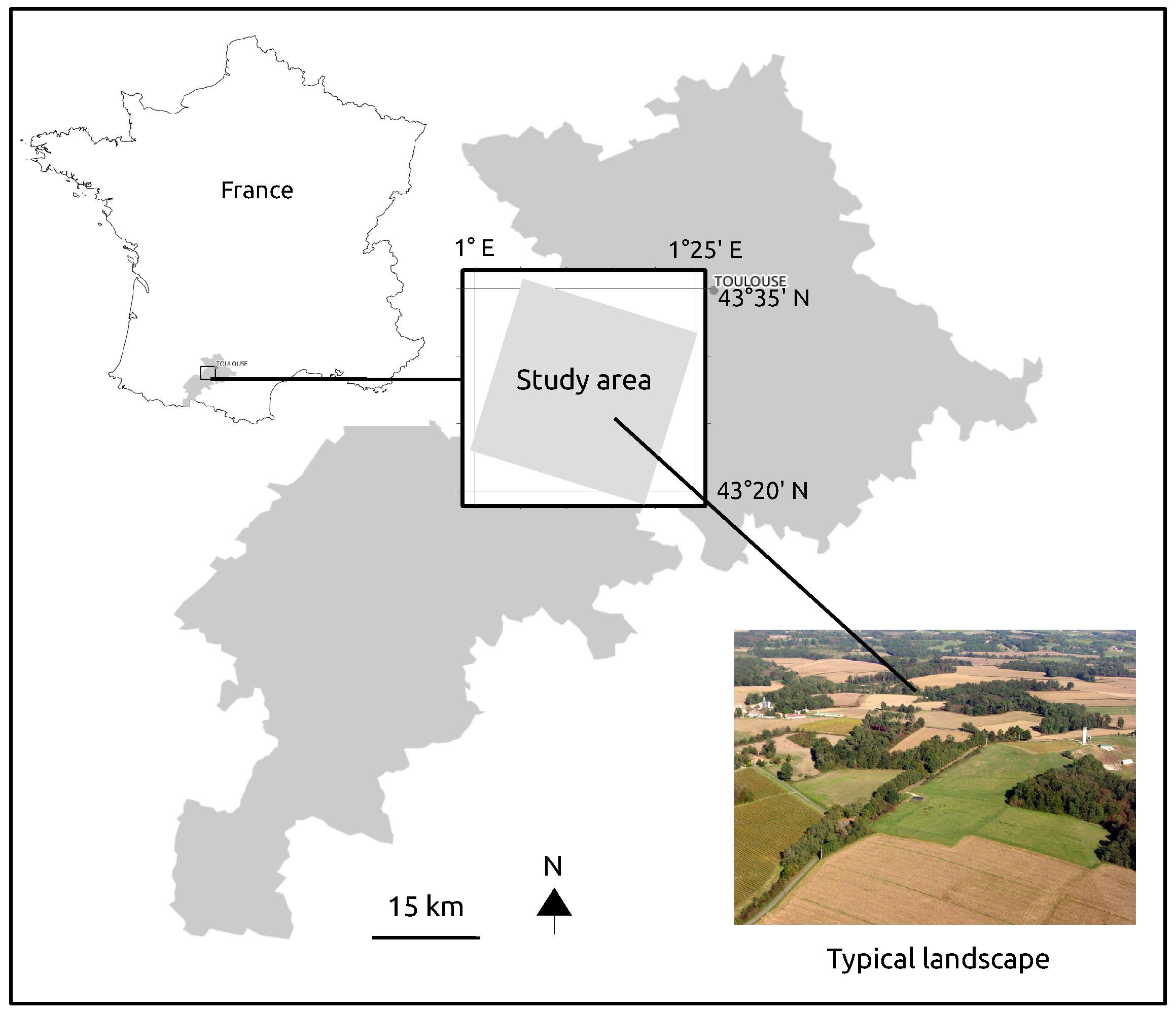
2.1. Study Site
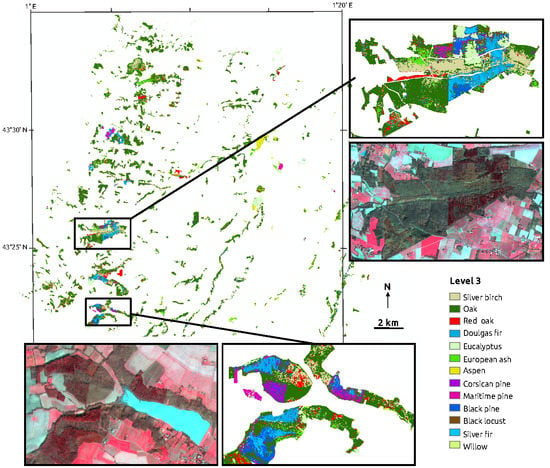
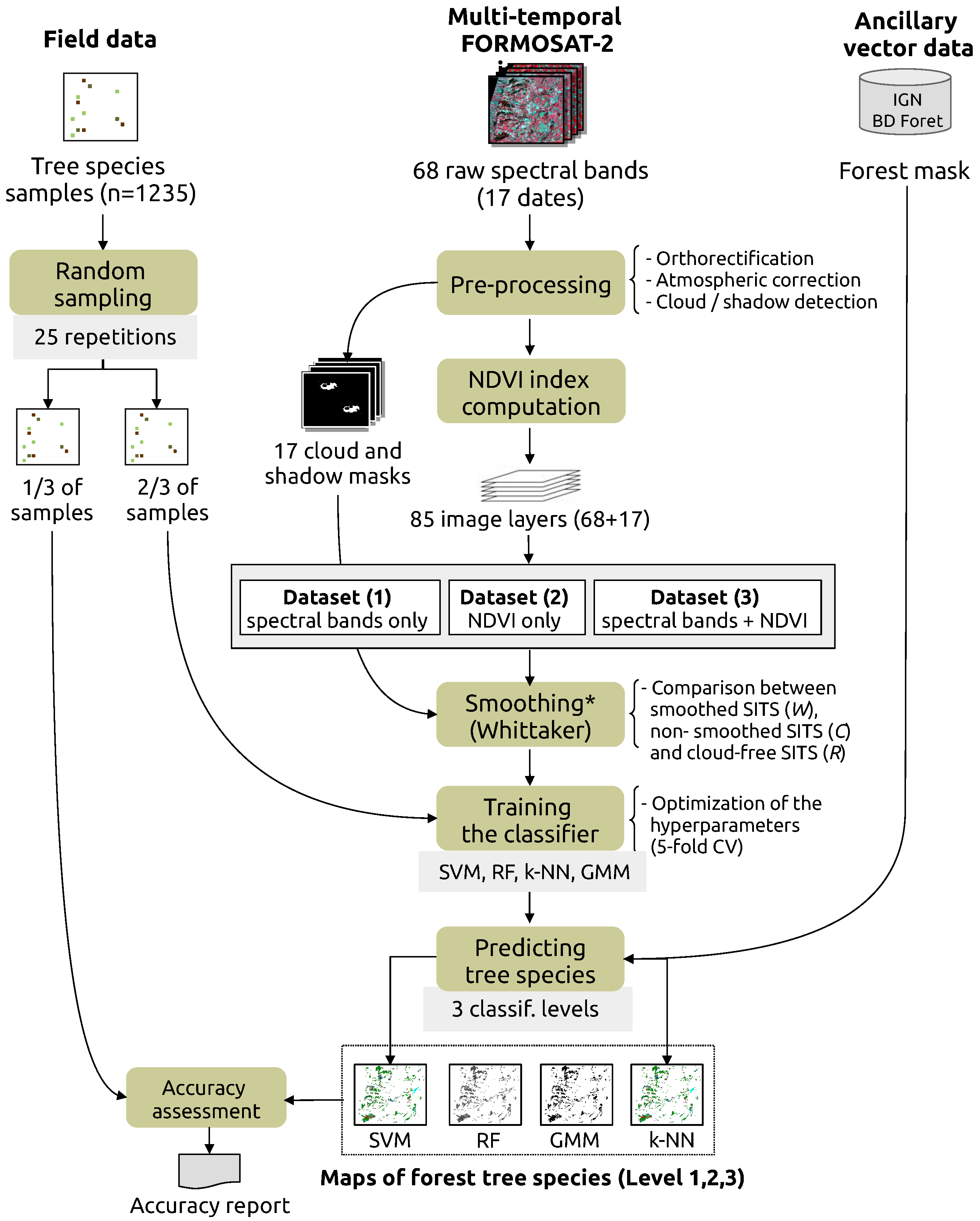
2.2. Image Data and Forest Map
2.3. Field Data
3. Methods
3.1. Smoothing of Temporal Profiles
3.2. Training and Validating the Models
4. Results
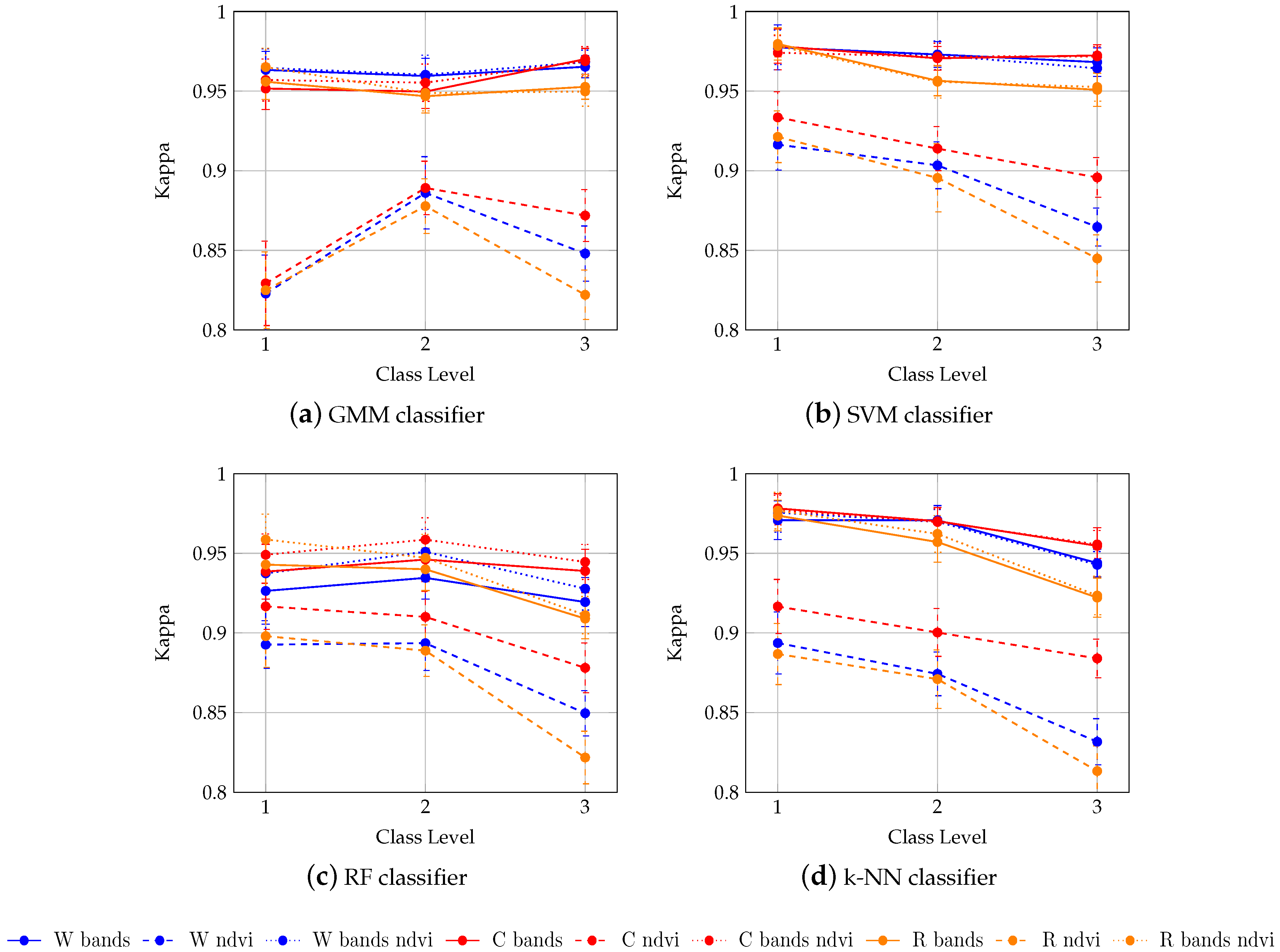
4.1. Influence of the Classifier
4.2. Influence of the Spectral Features
4.3. Influence of the Smoothing
4.4. Confusions between Species
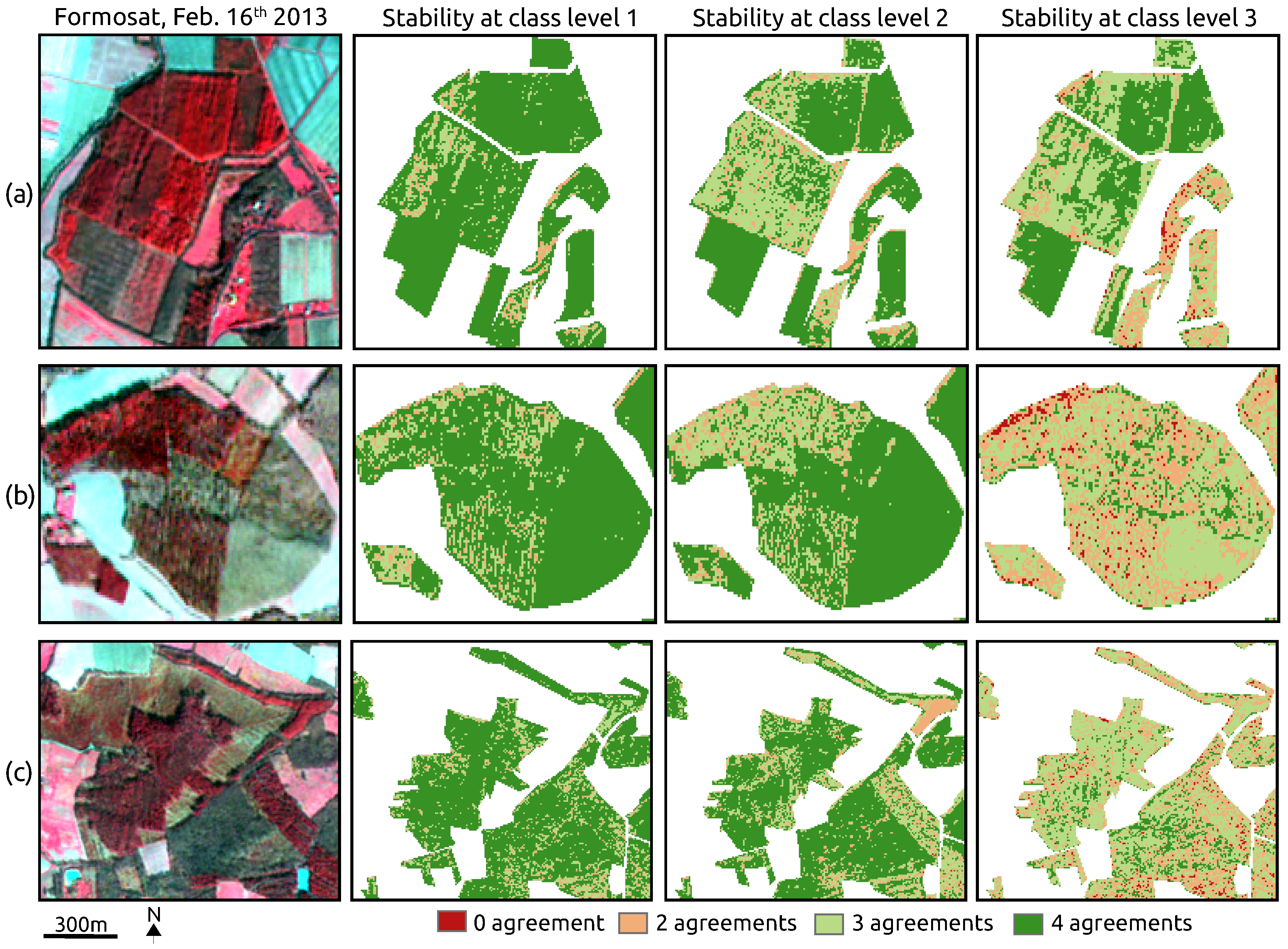
4.5. Classification Stability
5. Discussion
6. Conclusions
- The classification performance is slighlty influenced by the classifier. RBF-SVM classifier demonstrated the best accuracy at the three levels of the class hierarchy. GMM performed the worst.
- There is any clear benefit of removing cloudy and shady pixels using the Whittaker smoother in our context, even if 32% of the reference pixels were contaminated at least once. By contrast, adding all the dates in the SITS instead of only the cloud-free and shadow-free images enables the classification accuracy to be increased.
- There is no benefit of adding NDVI to spectral bands to discriminate tree species. By contrast, using NDVI alone led to a significant decrease in classification performance, even if the dimensionality of the data is reduced.
- Classification uncertainty exists for complex mixed forests, regarding the spatial disagreements that appear between the maps produced by all the classifiers. By contrast, a high consistency is observed within monospecific broadleaf plantations.
- Among the broadleaf tree species, Oak and Black locust are the most difficult to discriminate. For conifers, the lowest accuracy is observed for Douglas fir.
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A. Confusion Matrix in Pixels from the Smoothed Wbands Dataset and the SVM Classifier
| Reference Class | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Predicted Class | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| 1 | 29.00 | 0.64 | 0.04 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 2 | 0 | 37.04 | 0.04 | 0.12 | 0 | 0.12 | 0.16 | 0.32 | 0.68 | 0.72 | 0.48 | 0 | 0 |
| 3 | 0 | 0.20 | 49.92 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 4 | 0 | 0 | 0 | 20.04 | 0 | 0 | 0 | 0.32 | 0 | 0 | 0 | 0.40 | 0 |
| 5 | 0 | 0.56 | 0 | 0.12 | 49.88 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 6 | 0 | 0.24 | 0 | 0 | 0 | 27.72 | 0.04 | 0 | 0 | 0 | 0.16 | 0 | 0 |
| 7 | 0 | 0.04 | 0 | 0 | 0 | 0.16 | 71.80 | 0 | 0 | 0 | 0 | 0 | 0 |
| 8 | 0 | 0.24 | 0 | 0.08 | 0 | 0 | 0 | 20.60 | 0.92 | 0.40 | 0 | 0 | 0 |
| 9 | 0 | 0.04 | 0 | 0.56 | 0.12 | 0 | 0 | 0.64 | 27.52 | 0.12 | 0 | 0 | 0 |
| 10 | 0 | 0 | 0 | 0.52 | 0 | 0 | 0 | 0.12 | 0.56 | 17.72 | 0 | 0.44 | 0 |
| 11 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 20.36 | 0 | 0 |
| 12 | 0 | 0 | 0 | 1.56 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 25.16 | 0 |
| 13 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.32 | 0 | 0 | 0 | 16.00 |
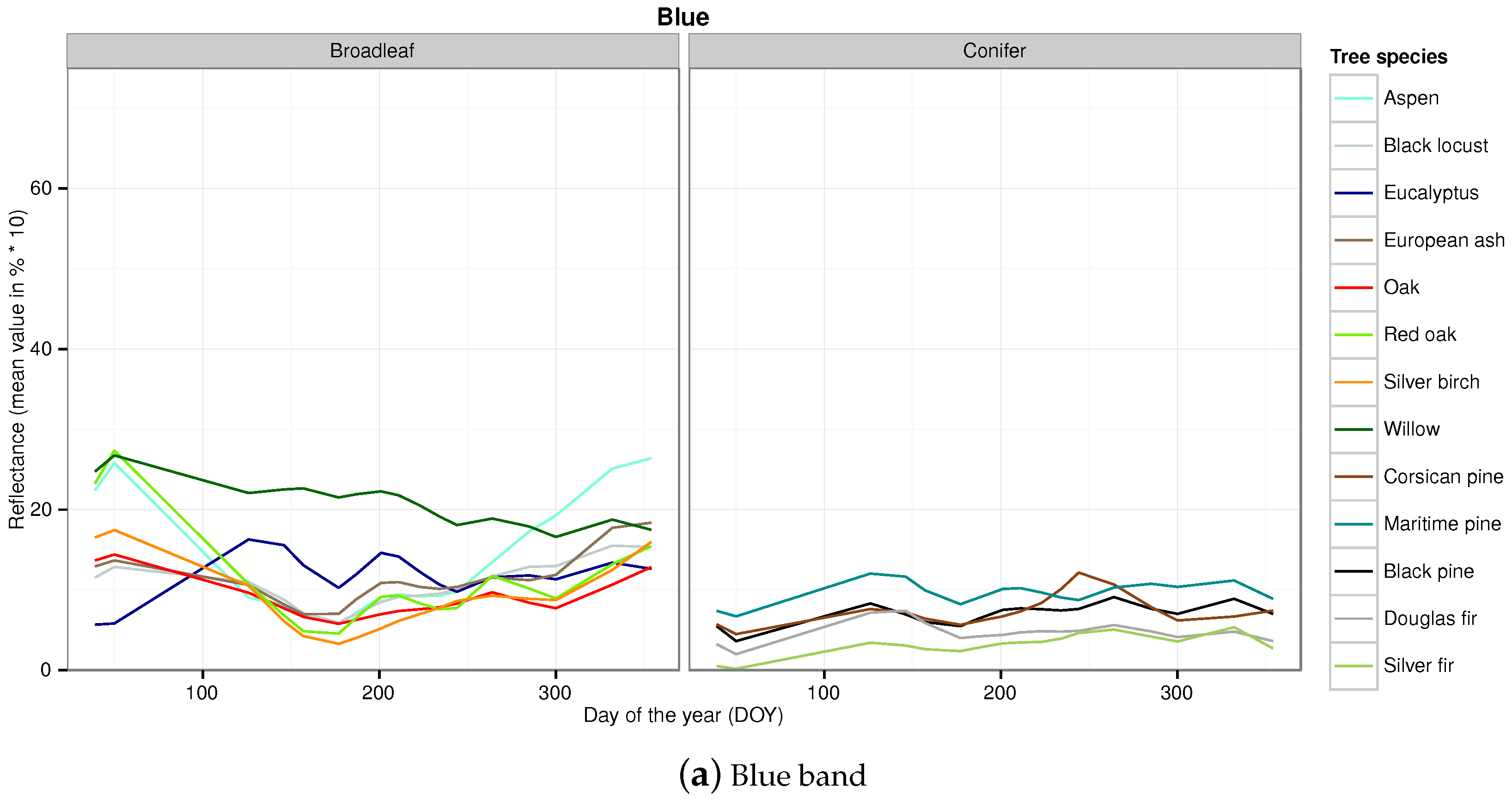
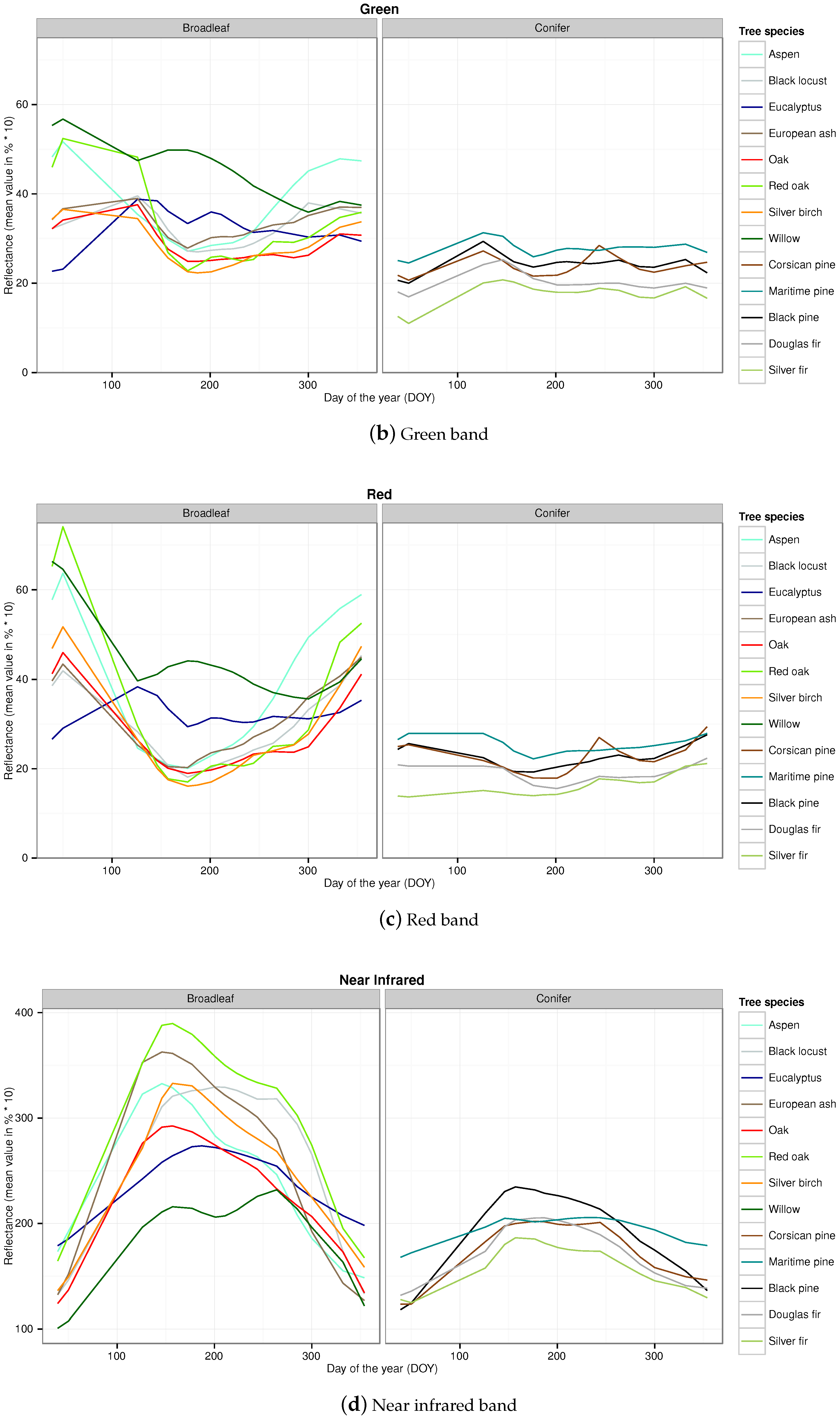
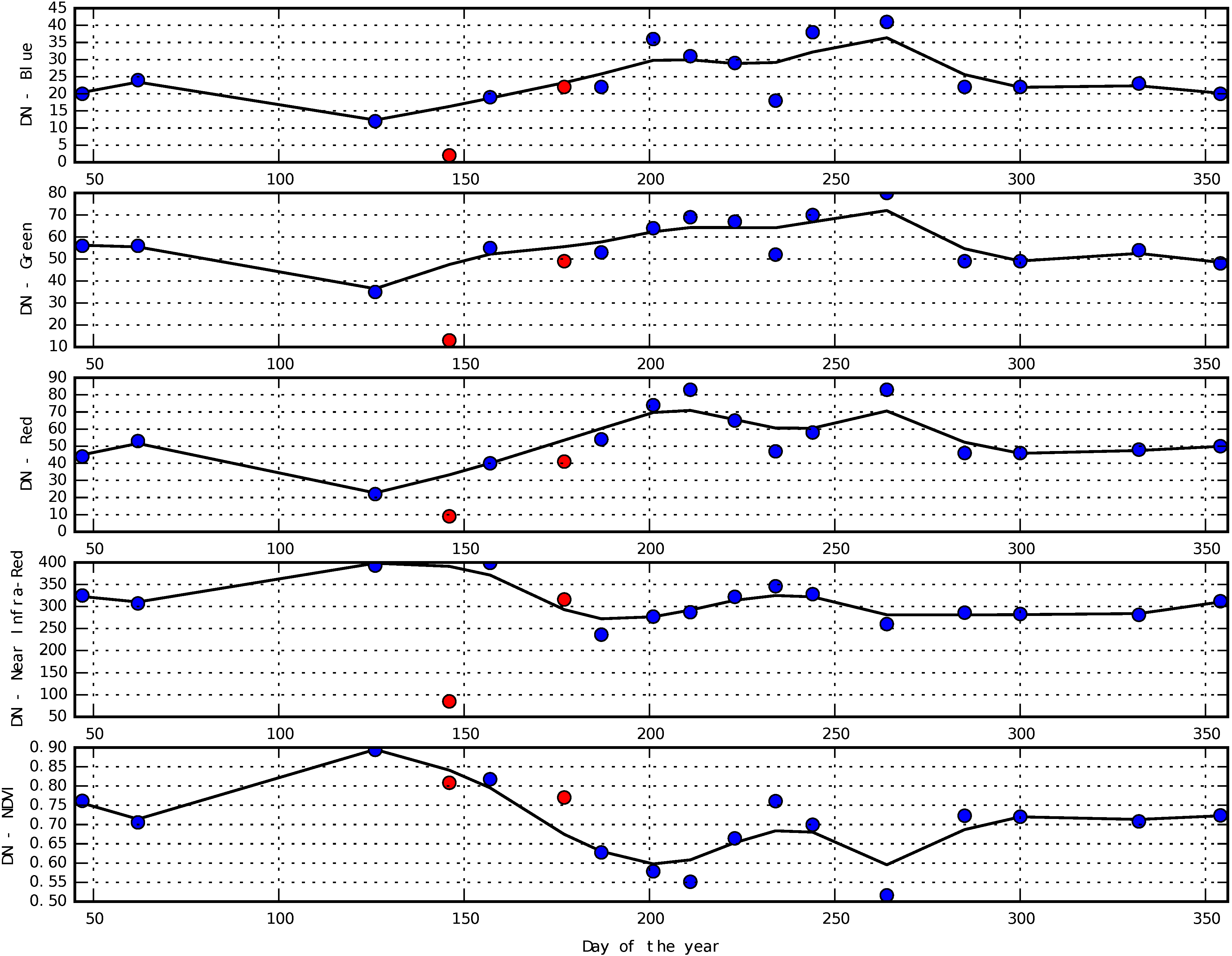
Appendix B. Temporal Signatures in Each Spectral Band of the SITS for Each Broadleaf and Conifer Tree Species
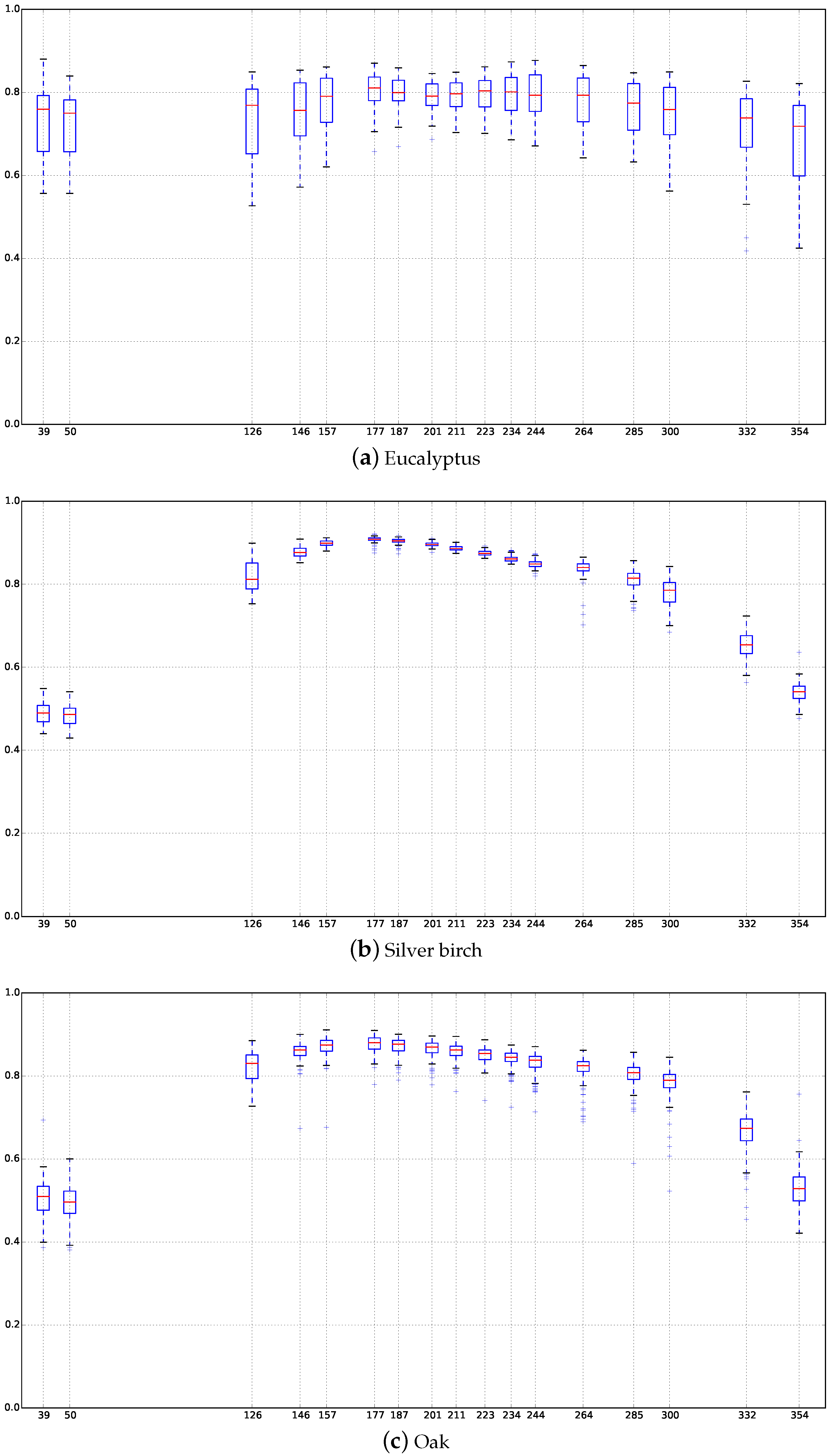
Appendix C. Boxplots of the NDVI Index of the SITS for Each Broadleaf and Conifer Tree Species

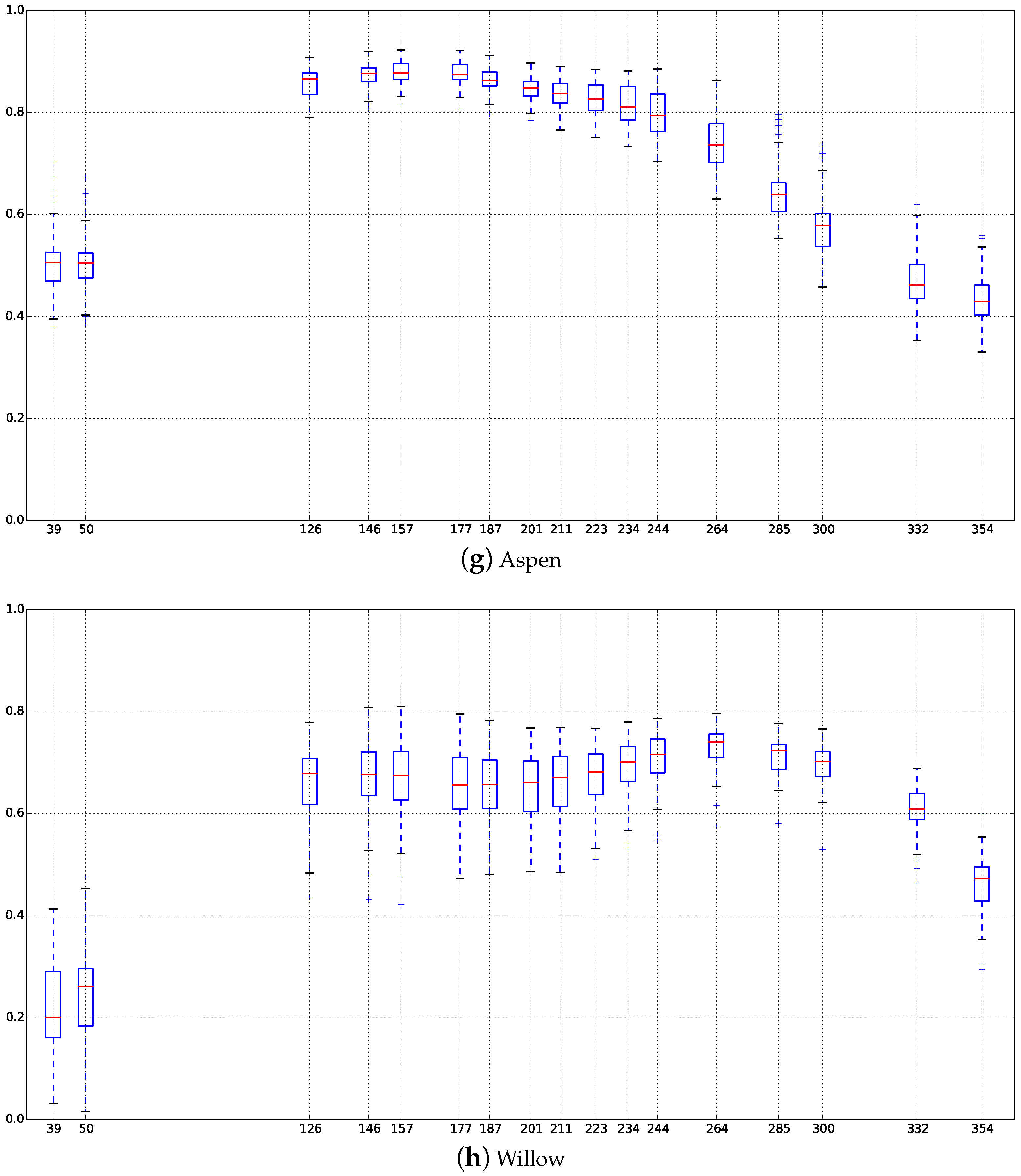
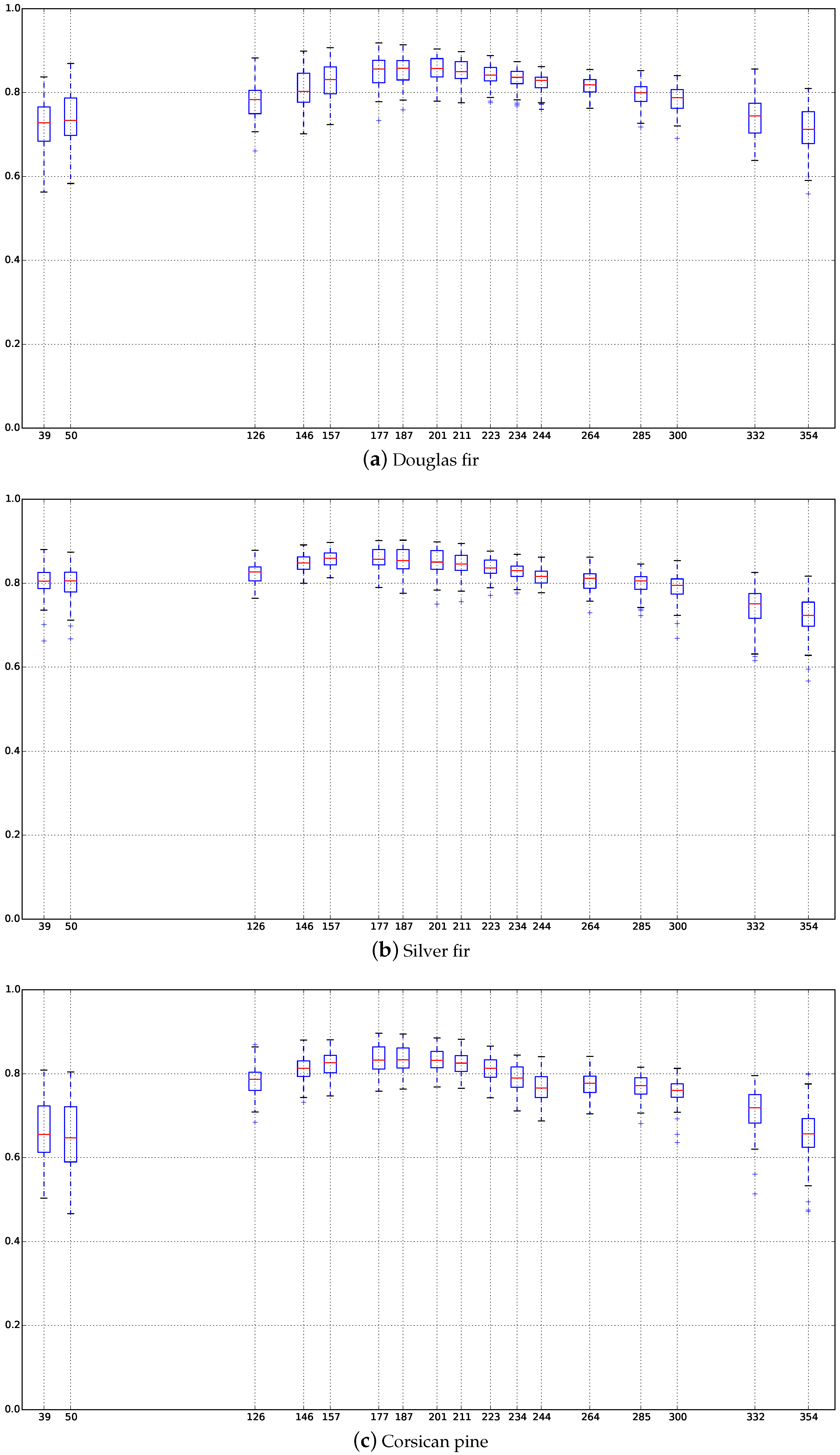
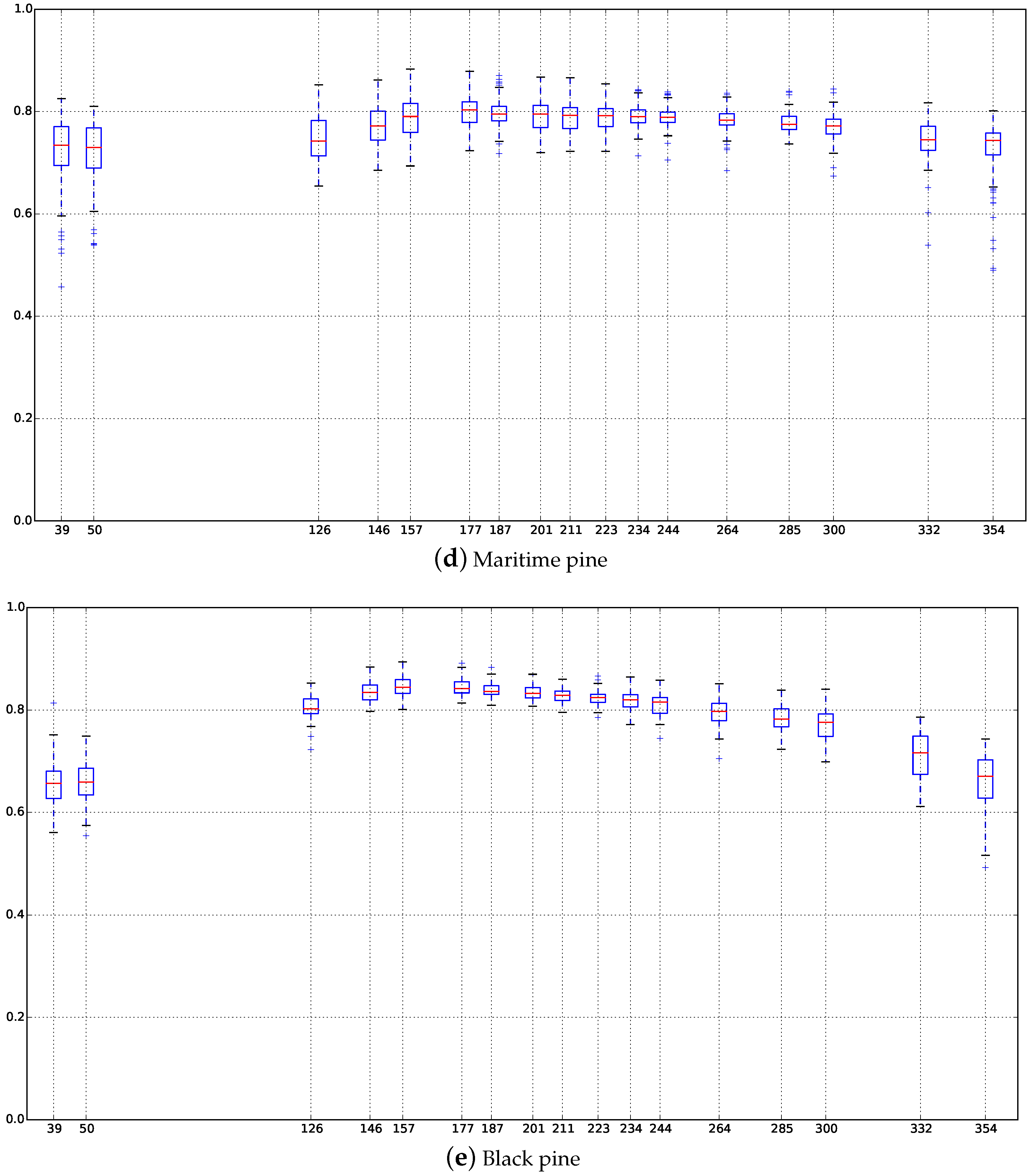
Appendix D. Smoothing of Temporal Profiles Using Whittaker
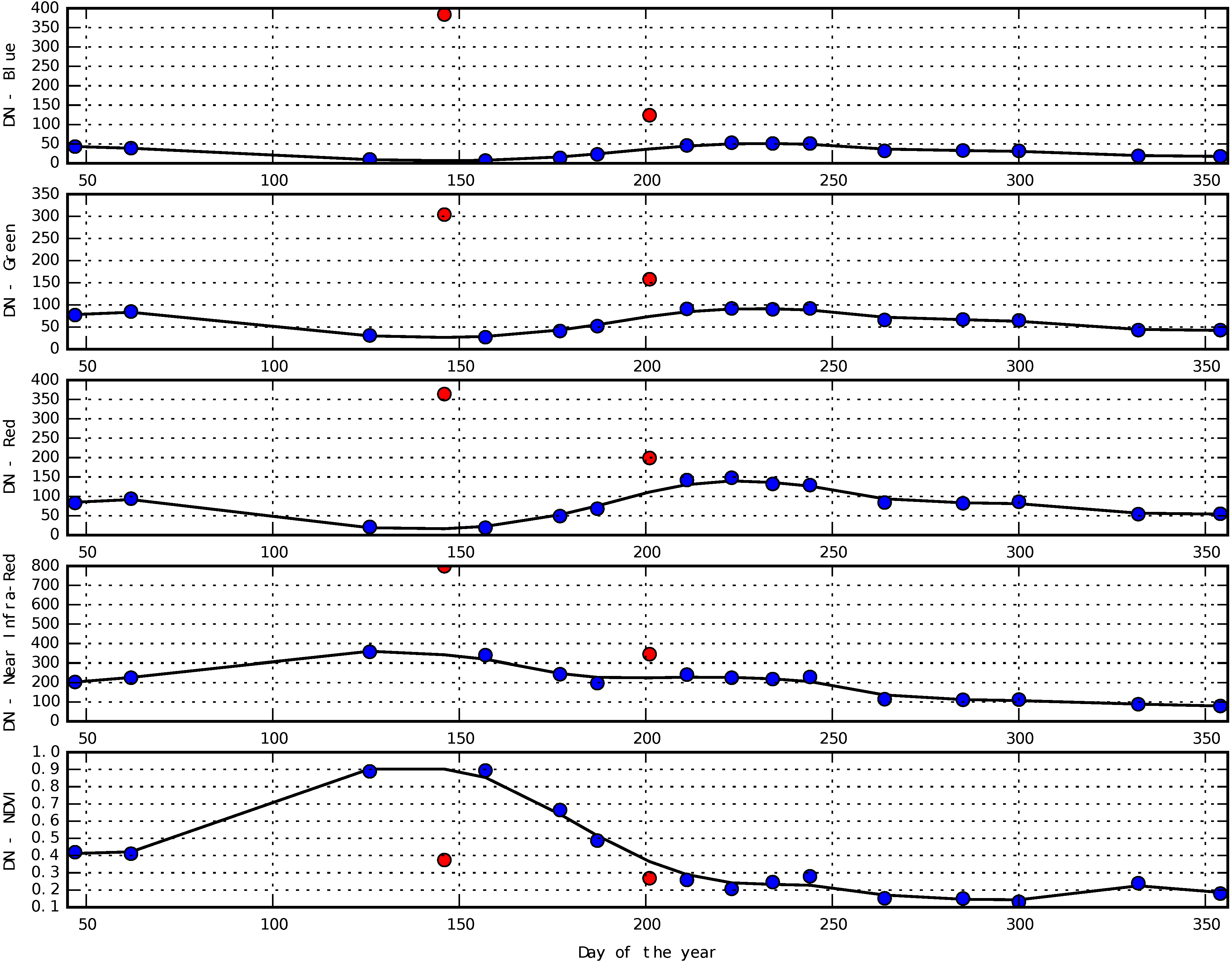
References
- Assessment, M.E. Ecosystems & Human Well-Being: Synthesis; Island Press: Washington, DC, USA, 2005. [Google Scholar]
- Gamfeldt, L.; Snall, T.; Bagchi, R.; Jonsson, M.; Gustafsson, L.; Kjellander, P.; Ruiz-Jaen, M.C.; Fröberg, M.; Stendahl, J.; Philipson, C.D.; et al. Higher levels of multiple ecosystem services are found in forests with more tree species. Nat. Commun. 2013, 4, 1340. [Google Scholar] [CrossRef] [PubMed]
- Iverson, L.R.; McKenzie, D. Tree-species range shifts in a changing climate: Detecting, modeling, assisting. Landsc. Ecol. 2013, 28, 879–889. [Google Scholar] [CrossRef]
- Thompson, I.; Mackey, B.; McNulty, S.; Mosseler, A. Forest Resilience, Biodiversity, and Climate Change. A Synthesis of the Biodiversity/Resilience/Stability Relationship in Forest Ecosystems; Technical Series No. 43; Secretariat of the Convention on Biological Diversity: Montreal, QC, Canada, 2009. [Google Scholar]
- Guyot, V.; Castagneyrol, B.; Vialatte, A.; Deconchat, M.; Selvi, F.; Bussotti, F.; Jactel, H. Tree diversity limits the impact of an invasive forest pest. PLoS ONE 2015, 10, e0136469. [Google Scholar] [CrossRef] [PubMed]
- Hansen, M.C.; Potapov, P.V.; Moore, R.; Hancher, M.; Turubanova, S.A.; Tyukavina, A.; Thau, D.; Stehman, S.V.; Goetz, S.J.; Loveland, T.R.; et al. High-resolution global maps of 21st-century forest cover change. Science 2013, 342, 850–853. [Google Scholar] [CrossRef] [PubMed]
- Thompson, S.D.; Nelson, T.A.; White, J.C.; Wulder, M.A. Mapping dominant tree species over large forested areas using Landsat Best-Available-Pixel image composites. Can. J. Remote Sens. 2015, 41, 203–218. [Google Scholar] [CrossRef]
- Guisan, A.; Zimmermann, N.E. Predictive habitat distribution models in ecology. Ecol. Model. 2000, 135, 147–186. [Google Scholar] [CrossRef]
- Franklin, J. Mapping Species Distributions: Spatial Inference and Prediction; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar]
- Iverson, L.R.; Prasad, A.M.; Matthews, S.N.; Peters, M. Estimating potential habitat for 134 eastern US tree species under six climate scenarios. For. Ecol. Manag. 2008, 254, 390–406. [Google Scholar] [CrossRef]
- Brus, D.J.; Hengeveld, G.M.; Walvoort, D.J.; Goedhart, P.W.; Heidema, A.H.; Nabuurs, G.J.; Gunia, K. Statistical mapping of tree species over Europe. Eur. J. For. Res. 2012, 131, 145–157. [Google Scholar] [CrossRef]
- Holmgren, P.; Thuressopn, T. Satellite remote sensing for forestry planning — A review. Scand. J. For. Res. 1998, 13, 90–110. [Google Scholar] [CrossRef]
- Boyd, D.S.; Danson, F.M. Satellite remote sensing of forest resources: Three decades of research development. Prog. Phys. Geogr. 2005, 29, 1–26. [Google Scholar] [CrossRef]
- Nagendra, H. Using remote sensing to assess biodiversity. Int. J. Remote Sens. 2001, 22, 2377–2400. [Google Scholar] [CrossRef]
- Meyer, P.; Staenzb, K.; Ittena, K.I. Semi-automated procedures for tree species identification in high spatial resolution data from digitized colour infrared-aerial photography. ISPRS J. Photogramm. Remote Sens. 1996, 51, 5–16. [Google Scholar] [CrossRef]
- Wulder, M.A.; Franklin, S.E. Remote Sensing of Forest Environments: Concepts and Case Studies; Kluwer Academic Publishers: Dordrecht, The Netherlands, 2003. [Google Scholar]
- Brandtberg, T. Individual tree-based species classification in high spatial resolution aerial images of forests using fuzzy sets. Fuzzy Sets Syst. 2002, 132, 371–387. [Google Scholar] [CrossRef]
- Erikson, M. Species classification of individually segmented tree crowns in high-resolution aerial images using radiometric and morphologic image measures. Remote Sens. Environ. 2004, 91, 469–477. [Google Scholar] [CrossRef]
- Franklin, S.E.; Hall, R.J.; Moskal, L.M.; Maudie, A.J.; Lavigne, M. Incorporating texture into classification of forest species composition from airborne multispectral images. Int. J. Remote Sens. 2000, 21, 61–79. [Google Scholar] [CrossRef]
- Kayitakire, F.; Giot, P.; Defourny, P. Discrimination automatique de peuplements forestiers à partir d’orthophotos numériques couleur: Un cas d’etude en Belgique. Can. J. Remote Sens. 2002, 28, 629–640. [Google Scholar] [CrossRef]
- Waser, L.T.; Ginzler, C.; Kuechler, M.; Baltsavias, E.; Hurni, L. Semi-automatic classification of tree species in different forest ecosystems by spectral and geometric variables derived from Airborne Digital Sensor (ADS40) and RC30 data. Remote Sens. Environ. 2011, 115, 76–85. [Google Scholar] [CrossRef]
- Carleer, A.; Wolff, E. Exploitation of very high resolution satellite data for tree species identification. Photogramm. Eng. Remote Sens. 2004, 70, 135–140. [Google Scholar] [CrossRef]
- Immitzer, M.; Atzberger, C.; Koukal, T. Tree species classification with random forest using very high spatial resolution 8-band WorldView satellite data. Remote Sens. 2012, 4, 2661–2693. [Google Scholar] [CrossRef]
- Lin, C.; Popescu, S.C.; Thomson, G.; Tsogt, K.; Chang, C.I. Classification of tree species in overstorey canopy of subtropical forest using QuickBird images. PLoS ONE 2015, 10, e0125554. [Google Scholar] [CrossRef] [PubMed]
- Wolter, P.T.; Mladenoff, D.J.; Host, G.E.; Crow, T.R. Improved forest classification in the northern Lake States using multi-temporal Landsat imagery. Photogramm. Eng. Remote Sens. 1995, 61, 1129–1143. [Google Scholar]
- Foody, G.M.; Hill, R.A. Classification of tropical forest classes from Landsat TM data. Int. J. Remote Sens. 1996, 17, 2353–2367. [Google Scholar] [CrossRef]
- Cochrane, M.A. Using vegetation reflectance variability for species level classification of hyperspectral data. Int. J. Remote Sens. 2000, 21, 2075–2087. [Google Scholar] [CrossRef]
- Féret, J.B.; Asner, G.P. Tree species discrimination in tropical forests using airborne imaging spectroscopy. IEEE Trans. Geosci. Remote Sens. 2012, 51, 73–84. [Google Scholar] [CrossRef]
- Ghiyamat, A.; Shafri, H.Z.; Mahdiraji, G.A.; Shariff, A.R.M.; Mansor, S. Hyperspectral discrimination of tree species with different classifications using single- and multiple-endmember. Int. J. Appl. Earth Obs. Geoinf. 2013, 23, 177–191. [Google Scholar] [CrossRef]
- George, R.; Padaliab, H.; Kushwahab, S.P. Forest tree species discrimination in western Himalaya using EO-1 Hyperion. Int. J. Appl. Earth Obs. Geoinf. 2014, 28, 140–149. [Google Scholar] [CrossRef]
- Heinzel, J.; Koch, B. Exploring full-waveform LiDAR parameters for tree species classification. Int. J. Appl. Earth Obs. Geoinf. 2011, 13, 152–160. [Google Scholar] [CrossRef]
- Ke, Y.; Quackenbush, L.J.; Im, J. Synergistic use of QuickBird multispectral imagery and LIDAR data for object-based forest species classification. Remote Sens. Environ. 2010, 114, 1141–1154. [Google Scholar] [CrossRef]
- Dalponte, M.; Bruzzone, L.; Gianelle, D. Tree species classification in the Southern Alps based on the fusion of very high geometrical resolution multispectral/hyperspectral images and LiDAR data. Remote Sens. Environ. 2012, 123, 258–270. [Google Scholar] [CrossRef]
- Engler, R.; Waser, L.T.; Zimmermann, N.E.; Schaub, M.; Berdos, S.; Ginzler, C.; Psomas, A. Combining ensemble modeling and remote sensing for mapping individual tree species at high spatial resolution. For. Ecol. Manag. 2013, 310, 64–73. [Google Scholar] [CrossRef]
- Ghosh, A.; Fassnacht, F.E.; Joshia, P.K.; Koch, B. A framework for mapping tree species combining hyperspectral and LiDAR data: Role of selected classifiers and sensor across three spatial scales. Int. J. Appl. Earth Obs. Geoinf. 2014, 26, 49–63. [Google Scholar] [CrossRef]
- Holmgren, J.; Persson, A.; Soderman, U. Species identification of individual trees by combining high resolution LiDAR data with multispectral images. Int. J. Remote Sens. 2008, 29, 1537–1552. [Google Scholar] [CrossRef]
- Schriver, J.R.; Congalton, R.G. Evaluating seasonal variability as an aid to cover-type mapping from Landsat Thematic Mapper data in the Northeast. Photogramm. Eng. Remote Sens. 1995, 61, 321–327. [Google Scholar]
- Mickelson, J.G.; Civco, D.L.; Silander, J.A. Delineating forest canopy species in the northeastern United States using multi-temporal TM imagery. Photogramm. Eng. Remote Sens. 1998, 64, 891–904. [Google Scholar]
- Dymond, C.C.; Mladenoff, D.J.; Radeloff, V.C. Phenological differences in Tasseled Cap indices improve deciduous forest classification. Remote Sens. Environ. 2002, 80, 460–472. [Google Scholar] [CrossRef]
- Zhu, X.; Liu, D. Accurate mapping of forest types using dense seasonal Landsat time-series. ISPRS J. Photogramm. Remote Sens. 2014, 96, 1–11. [Google Scholar] [CrossRef]
- Cano, E.; Denux, J.P.; Bisquert, M.; Hubert-Moy, L.; Chéret, V. Improved forest mapping based on MODIS time series and landscape stratification. Int. J. Remote Sens. 2016, in press. [Google Scholar]
- Key, T.; Warner, T.A.; McGraw, J.B.; Fajvan, M.A. A comparison of multispectral and multitemporal information in high spatial resolution imagery for classification of individual tree species in a temperate hardwood forest. Remote Sens. Environ. 2001, 75, 100–112. [Google Scholar] [CrossRef]
- Hill, R.A.; Wilson, A.K.; George, M.; Hinsley, S.A. Mapping tree species in temperate deciduous woodland using time-series multi-spectral data. Appl. Veg. Sci. 2010, 13, 86–99. [Google Scholar] [CrossRef]
- Tigges, J.; Lakes, T.; Hostert, P. Urban vegetation classification: Benefits of multitemporal RapidEye satellite data. Remote Sens. Environ. 2013, 136, 66–75. [Google Scholar] [CrossRef]
- Dedieu, G.; Karnieli, A.; Hagolle, O.; Jeanjean, H.; Cabot, F.; Ferrier, P.; Yaniv, Y. VENμS mission: A joint Israel-French Earth Observation scientific mission with High spatial and temporal resolution capabilities. In Second Recent Advances in Quantitative Remote Sensing; Sobrino, J.A., Ed.; Publicacions de la Universitat de València: Valencia, Spain, 2006; pp. 517–521. [Google Scholar]
- Boureau, J.G. Manuel d’interprétation des Photographies Aériennes Infrarouges—Application aux Milieux Forestiers et Naturels; Inventaire Forestier National: Saint-Jean-de-la-Ruelle, France, 2008; p. 268. [Google Scholar]
- Hagolle, O.; Dedieu, G.; Mougenot, B.; Debaecker, V.; Duchemin, B.; Meygret, A. Correction of aerosol effects on multi-temporal images acquired with constant viewing angles: Application to Formosat-2 images. Remote Sens. Environ. 2008, 112, 1689–1701. [Google Scholar] [CrossRef]
- Hagolle, O.; Dedieu, G.; Mougenot, B.; Debaecker, V.; Duchemin, B.; Meygret, A. A multi-temporal and multi-spectral method to estimate aerosol optical thickness over land, for the atmospheric correction of Formosat-2, Landsat, VENμS and Sentinel-2 Images. Remote Sens. 2015, 7, 2668–2691. [Google Scholar] [CrossRef]
- Hagolle, O.; Huc, M.; Pascual, D.V.; Dedieu, G. A multi-temporal method for cloud detection, applied to Formosat-2, VENμS, Landsat and Sentinel-2 Images. Remote Sens. Environ. 2010, 114, 1747–1755. [Google Scholar] [CrossRef]
- Eilers, P. A perfect smoother. Anal. Chem. 2011, 75, 3299–3304. [Google Scholar] [CrossRef]
- Atzberger, C.; Eilers, P. Evaluating the effectiveness of smoothing algorithms in the absence of ground reference measurements. Int. J. Remote Sens. 2011, 32, 3689–3709. [Google Scholar] [CrossRef]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Kavzoglu, T.; Colkesen, I. Kernel functions analysis for support vector machines for land cover classification. Int. J. Appl. Earth Obs. Geoinf. 2009, 11, 352–359. [Google Scholar] [CrossRef]
- Heinzel, J.; Koch, B. Investigating multiple data sources for tree species classification in temperate forest and use for single tree delineation. Int. J. Appl. Earth Obs. Geoinf. 2012, 18, 101–110. [Google Scholar] [CrossRef]
- Mantero, P.; Moser, G.; Serpico, S. Partially supervised classification of remote sensing images through SVM-based probability density estimation. IEEE Trans. Geosci. Remote Sens. 2005, 43, 559–570. [Google Scholar] [CrossRef]
- Mountrakis, G.; Im, J.; Ogole, C. Support vector machines in remote sensing: A review. ISPRS J. Photogramm. Remote Sens. 2011, 66, 247–259. [Google Scholar] [CrossRef]
- Hastie, T.J.; Tibshirani, R.J.; Friedman, J.H. The Elements of Statistical Learning: Data Mining, Inference, and Prediction; Springer Series in Statistics; Springer: New York, NY, USA, 2009. [Google Scholar]
- Shao, Y.; Lunetta, R.; Wheeler, B.; Iiames, J.; Campbell, J. An evaluation of time-series smoothing algorithms for land-cover classifications using MODIS-NDVI multi-temporal data. Remote Sens. Environ. 2016, 174, 258–265. [Google Scholar] [CrossRef]
- Congalton, R.G. A review of assessing the accuracy of classifictions of remotely sensed data. Remote Sens. Environ. 1991, 37, 35–46. [Google Scholar] [CrossRef]
- Foody, G.M. Sample size determination for image classification accuracy assessment and comparison. Int. J. Remote Sens. 2009, 30, 5273–5291. [Google Scholar] [CrossRef]
- Foody, G.M.; Mathur, A. The use of small training sets containing mixed pixels for accurate hard image classification: Training on mixed spectral responses for classification by a SVM. Remote Sens. Environ. 2006, 103, 179–189. [Google Scholar] [CrossRef]
- Dash, M.; Liu, H. Feature selection for classification. Intell. Data Anal. 1997, 1, 131–156. [Google Scholar] [CrossRef]
- Fauvel, M.; Dechesne, C.; Zullo, A.; Ferraty, F. Fast forward feature selection of hyperspectral images for classification with Gaussian mixture models. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 2824–2831. [Google Scholar] [CrossRef]
- Sun, Y.; Wong, A.K.; Kamel, M.S. Classification of imbalanced data: A review. Int. J. Pattern Recognit. Artif. Intell. 2009, 23, 687–719. [Google Scholar] [CrossRef]
- Graves, S.J.; Asner, G.P.; Martin, R.E.; Anderson, C.B.; Colgan, M.S.; Kalantari, L.; Bohlman, S.A. Tree species abundance predictions in a tropical agricultural landscape with a supervised classification model and imbalanced data. Remote Sens. 2016, 8. [Google Scholar] [CrossRef]
- Triepke, F.; Brewer, C.; Leavell, D.; Novak, S. Mapping forest alliances and associations using fuzzy systems and nearest neighbor classifiers. Remote Sens. Environ. 2008, 112, 1037–1050. [Google Scholar] [CrossRef]
- Plourde, L.; Ollinger, S.; Smith, M.L.; Martin, M. Estimating species abundance in a northern temperate forest using spectral mixture analysis. Photogramm. Eng. Remote Sens. 2007, 73, 829–840. [Google Scholar] [CrossRef]
- Hammond, T.; Verbyla, D. Optimistic bias in classification accuracy assessment. Int. J. Remote Sens. 1996, 7, 1261–1266. [Google Scholar] [CrossRef]
- Friedl, M.A.; Woodcock, C.; Gopal, S.; Muchoney, D.; Strahler, A.H.; Barker-Schaaf, C. Note on procedures used for accuracy assessment in land cover maps derived from AVHRR data. Int. J. Remote Sens. 2000, 21, 1073–1077. [Google Scholar] [CrossRef]
- Chen, D.; Wei, H. The effect of spatial autocorrelation and class proportion on the accuracy measures from different sampling designs. ISPRS J. Photogramm. Remote Sens. 2009, 64, 140–150. [Google Scholar] [CrossRef]
- Zhen, Z.; Quackenbush, L.; Stehman, S.; Zhang, L. Impact of training and validation sample selection on classification accuracy and accuracy assessment when using reference polygons in object-based classification. Int. J. Remote Sens. 2001, 22, 2377–2400. [Google Scholar] [CrossRef]

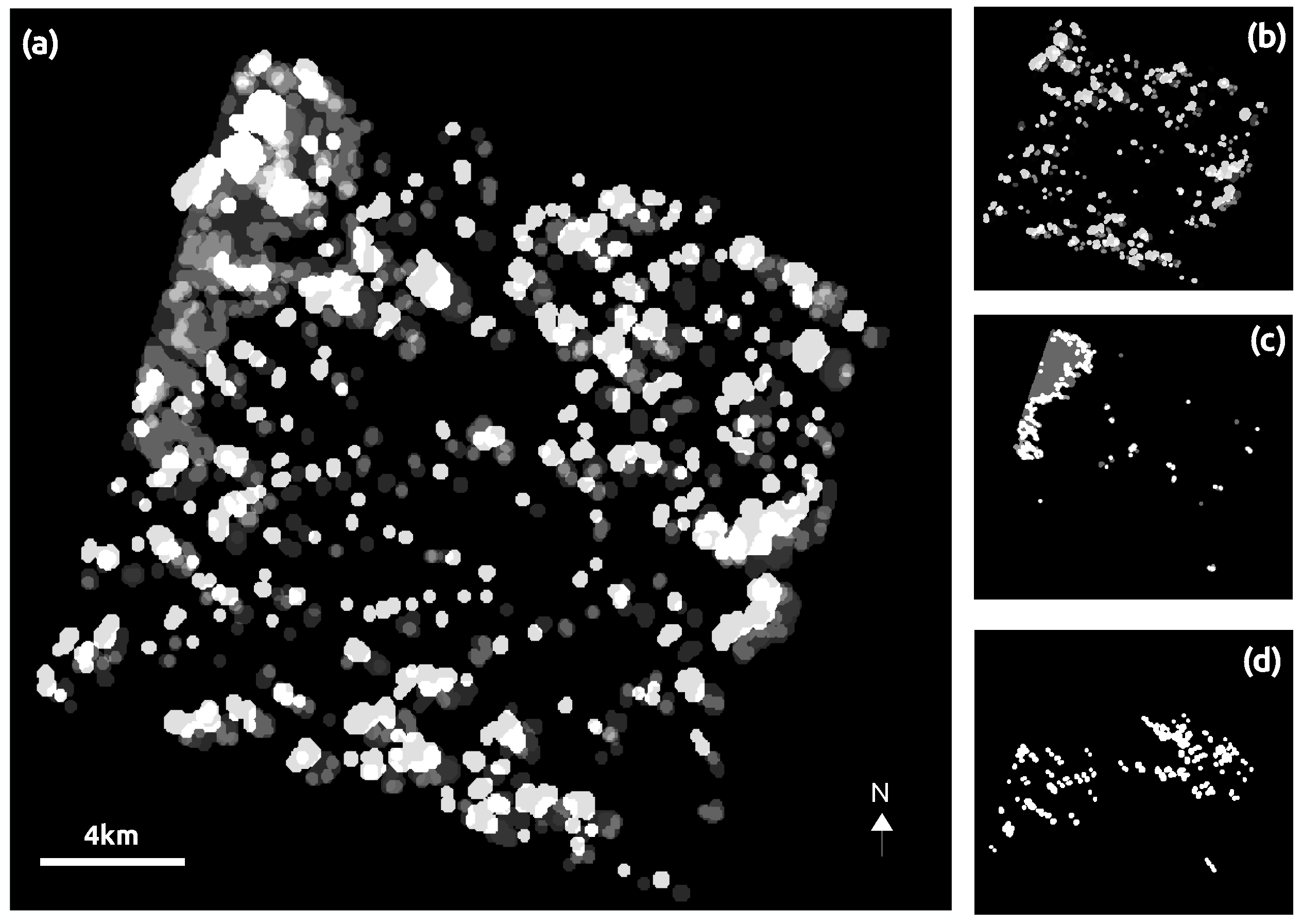
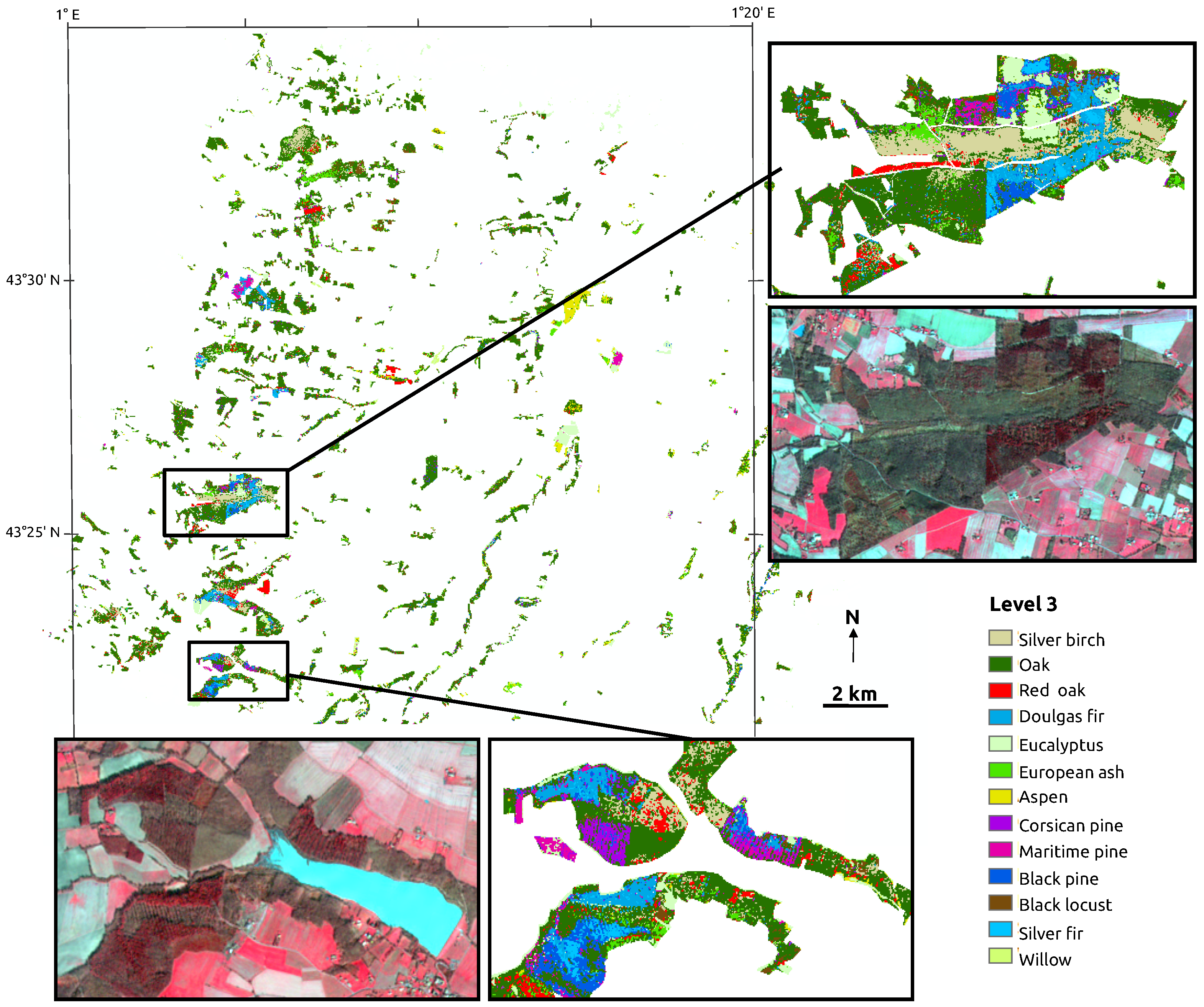

| Level 1 | Level 2 | Level 3 | Sample Size |
|---|---|---|---|
| Broadleaf | Deciduous | Silver birch (Betula pendula) | 85 |
| Broadleaf | Deciduous | Oak (Quercus robur/pubescens/petraea) | 113 |
| Broadleaf | Deciduous | Red oak (Quercus rubra) | 145 |
| Broadleaf | Deciduous | European ash (Fraxinus excelsior) | 80 |
| Broadleaf | Deciduous | Aspen (Populus tremula) | 209 |
| Broadleaf | Deciduous | Black locust (Robinia pseudoacacia) | 59 |
| Broadleaf | Deciduous | Willow (Salix spp.) | 51 |
| Broadleaf | Evergreen | Eucalyptus (Eucalyptus spp.) | 148 |
| Conifer | Pine | Corsican pine (Pinus nigra subsp. laricio) | 62 |
| Conifer | Pine | Maritime pine (Pinus pinaster) | 87 |
| Conifer | Pine | Black pine (Pinus nigra) | 55 |
| Conifer | Other conifer | Douglas fir (Pseudotsuga menziesii) | 66 |
| Conifer | Other conifer | Silver fir (Abies alba) | 75 |
| Dataset | Composition |
|---|---|
| W | Smoothed time series based on Whittaker including spectral bands only (17 dates) |
| W | Smoothed time series based on Whittaker including NDVI only (17 dates) |
| W | Smoothed time series based on Whittaker including spectral bands and NDVI (17 dates) |
| C | Non-smoothed (cloudy) time series including spectral bands only (17 dates) |
| C | Non-smoothed (cloudy) time series including NDVI only (17 dates) |
| C | Non-smoothed (cloudy) time series including spectral bands and NDVI (17 dates) |
| R | Non-smoothed time series with no cloud coverage or cloud shadows on forests including spectral bands only (14 dates) |
| R | Non-smoothed time series with no cloud coverage or cloud shadows on forests including NDVI only (14 dates) |
| R | Non-smoothed time series with no cloud coverage or cloud shadows on forests including spectral bands and NDVI (14 dates) |
| GMM | SVM | RF | k-NN | |
|---|---|---|---|---|
| Level 1/all datasets | 0.91 ± 0.02 | 0.96 ± 0.01 | 0.93 ± 0.02 | 0.95 ± 0.01 |
| Level 2/all datasets | 0.93 ± 0.01 | 0.95 ± 0.01 | 0.93 ± 0.01 | 0.94 ± 0.01 |
| Level 3/all datasets | 0.92 ± 0.01 | 0.93 ± 0.01 | 0.90 ± 0.01 | 0.91 ± 0.01 |
| Reference Class | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Predicted Class | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| 1 | 100 | 1.64 | 0.08 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 2 | 0 | 94.97 | 0.08 | 0.52 | 0 | 0.43 | 0.22 | 1.45 | 2.27 | 3.80 | 2.29 | 0 | 0 |
| 3 | 0 | 0.51 | 99.84 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 4 | 0 | 0 | 0 | 87.13 | 0 | 0 | 0 | 1.45 | 0 | 0 | 0 | 1.54 | 0 |
| 5 | 0 | 1.44 | 0 | 0.52 | 99.76 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 6 | 0 | 0.62 | 0 | 0 | 0 | 99.00 | 0.06 | 0 | 0 | 0 | 0.76 | 0 | 0 |
| 7 | 0 | 0.10 | 0 | 0 | 0 | 0.57 | 99.72 | 0 | 0 | 0 | 0 | 0 | 0 |
| 8 | 0 | 0.62 | 0 | 0.35 | 0 | 0 | 0 | 93.64 | 3.07 | 2.11 | 0 | 0 | 0 |
| 9 | 0 | 0.10 | 0 | 2.43 | 0.24 | 0 | 0 | 2.91 | 91.73 | 0.63 | 0 | 0 | 0 |
| 10 | 0 | 0 | 0 | 2.26 | 0 | 0 | 0 | 0.55 | 1.87 | 93.46 | 0 | 1.69 | 0 |
| 11 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 96.95 | 0 | 0 |
| 12 | 0 | 0 | 0 | 6.78 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 96.77 | 0 |
| 13 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1.07 | 0 | 0 | 0 | 100 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sheeren, D.; Fauvel, M.; Josipović, V.; Lopes, M.; Planque, C.; Willm, J.; Dejoux, J.-F. Tree Species Classification in Temperate Forests Using Formosat-2 Satellite Image Time Series. Remote Sens. 2016, 8, 734. https://doi.org/10.3390/rs8090734
Sheeren D, Fauvel M, Josipović V, Lopes M, Planque C, Willm J, Dejoux J-F. Tree Species Classification in Temperate Forests Using Formosat-2 Satellite Image Time Series. Remote Sensing. 2016; 8(9):734. https://doi.org/10.3390/rs8090734
Chicago/Turabian StyleSheeren, David, Mathieu Fauvel, Veliborka Josipović, Maïlys Lopes, Carole Planque, Jérôme Willm, and Jean-François Dejoux. 2016. "Tree Species Classification in Temperate Forests Using Formosat-2 Satellite Image Time Series" Remote Sensing 8, no. 9: 734. https://doi.org/10.3390/rs8090734
APA StyleSheeren, D., Fauvel, M., Josipović, V., Lopes, M., Planque, C., Willm, J., & Dejoux, J.-F. (2016). Tree Species Classification in Temperate Forests Using Formosat-2 Satellite Image Time Series. Remote Sensing, 8(9), 734. https://doi.org/10.3390/rs8090734